Redes neuronales: así de sencillo (Parte 94): Optimización de la secuencia de entrada

Introducción

Un enfoque habitual al procesar series temporales es mantener intacta la disposición original de los pasos temporales. Se supone que el orden histórico es el más óptimo. Sin embargo, la mayoría de los modelos existentes carecen de mecanismos explícitos para explorar las relaciones entre segmentos distantes dentro de cada serie temporal, que de hecho pueden tener fuertes dependencias. Por ejemplo, los modelos basados en redes convolucionales (CNN) utilizados para el aprendizaje de series temporales sólo pueden captar patrones dentro de una ventana temporal limitada. En consecuencia, cuando se analizan series temporales en las que los patrones importantes abarcan ventanas temporales más largas, estos modelos tienen dificultades para captar eficazmente esta información. El uso de redes profundas permite aumentar el tamaño del campo receptivo y resuelve parcialmente el problema. Pero el número de capas convolucionales necesarias para cubrir toda la secuencia puede ser demasiado grande, y sobredimensionar el modelo conduce al problema del gradiente evanescente.

Cuando se utiliza en modelos de arquitectura el Transformer, la eficacia de la detección de dependencias a largo plazo depende en gran medida de muchos factores. Entre ellas figuran la longitud de la secuencia, diversas estrategias de codificación posicional y la tokenización de los datos.

Tales pensamientos llevaron a los autores del artículo «Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations» a la idea de encontrar el uso óptimo de la secuencia histórica. ¿Podría haber una mejor organización de las series temporales que permitiera un aprendizaje de la representación más eficiente dada la tarea que nos ocupa?

En el artículo, los autores presentan un mecanismo sencillo y listo para usar llamado Segment, Shuffle, Stitch (S3), diseñado para aprender a optimizar la representación de series temporales. Como su nombre indica, S3 funciona segmentando una serie temporal en múltiples segmentos no solapados, barajando estos segmentos en el orden más óptimo y combinando después los segmentos barajados en una nueva secuencia. Cabe señalar aquí que el orden de barajado de los segmentos se aprende para cada tarea específica.

Además, S3 integra la serie temporal original mediante una operación de suma ponderada aprendible con una versión barajada, que conserva información clave de la secuencia original.

S3 actúa como un mecanismo modular diseñado para integrarse a la perfección con cualquier modelo de análisis de series temporales, lo que se traduce en un procedimiento de entrenamiento más suave con un error reducido. Dado que S3 se entrena junto con la red troncal, los parámetros de barajado se actualizan a propósito, adaptándose a las características de los datos de origen y del modelo subyacente para reflejar mejor la dinámica temporal. Además, S3 puede apilarse para crear una barajada más detallada con un mayor nivel de granularidad.

El algoritmo propuesto tiene muy pocos hiperparámetros que ajustar y requiere pocos recursos computacionales adicionales.

Para evaluar la eficacia de los enfoques propuestos, los autores del método integran S3 en varias arquitecturas neuronales, incluyendo CNN y modelos basados en Transformer. La evaluación del rendimiento en varios conjuntos de datos de problemas de clasificación de predicciones univariantes y multivariantes demuestra que la adición de S3 conduce a una mejora significativa de la eficacia del modelo entrenado, en igualdad de condiciones. Los resultados muestran que la integración de S3 en métodos modernos puede proporcionar una mejora del rendimiento de hasta el 39,59% en tareas de clasificación. En cuanto a las tareas de previsión de series temporales unidimensionales y multidimensionales, la eficacia del modelo puede aumentar un 68,71% y un 51,22%, respectivamente.

1. Algoritmo S3

Veamos con más detalle el método S3 propuesto.

Para los datos de entrada, el método utiliza una serie temporal multidimensional X compuesta por T pasos temporales y C canales, que se divide en N segmentos no intersecantes.

Consideramos el caso general de una serie temporal multivariante, aunque el método también funciona bien con series temporales univariantes. En realidad, una serie temporal unidimensional puede considerarse un caso especial de una serie multidimensional, cuando el número de canales C es igual a 1.

El objetivo del método es reordenar de forma óptima los segmentos para formar una nueva secuencia X, lo que nos permitirá captar mejor las principales relaciones y dependencias temporales dentro de una serie temporal. Esto, a su vez, conduce a una mejor comprensión de la tarea objetivo.

Los autores del método S3 proponen una solución al problema anterior en tres etapas: Segmentación, mezclado y combinación.

El módulo Segment divide la secuencia original X en N segmentos no intersecantes, cada uno de los cuales contiene τ pasos temporales donde τ = T/N. El conjunto de segmentos puede representarse como S = {s1, s2, . . . , sn}.

Los segmentos se introducen en el módulo Shuffle, que utiliza un vector de mezcla P = {p1, p2, . . . , pn} para reordenar los segmentos en el orden óptimo. Cada parámetro de barajado pj del vector P coincide con el segmento sj de la matriz S. Básicamente, P es un conjunto de pesos aprendibles optimizados por la red que controla la posición y prioridad de un segmento en una secuencia reordenada.

El proceso de barajado es bastante sencillo e intuitivo: cuanto mayor sea el valor de pj, mayor será la prioridad del segmento sj en una secuencia barajada. Una secuencia barajada Sshuffled puede representarse como:

Permutar S basándose en el orden ordenado P no es diferenciable por defecto porque implica operaciones discretas e introduce discontinuidades. Los métodos de clasificación suave aproximan el orden de clasificación asignando probabilidades que reflejan cuánto mayor es cada elemento en comparación con los demás. Aunque esta aproximación es diferenciable por naturaleza, puede introducir ruido e imprecisiones, lo que hace que la clasificación no sea intuitiva. Para conseguir una ordenación y barajado diferenciables que sean tan precisos e intuitivos como los métodos tradicionales, los autores del método introducen varios pasos intermedios. Estos pasos crean un camino para que los gradientes fluyan a través de los parámetros de barajado P..

Primero obtenemos los índices que ordenan los elementos de P utilizando σ = Argsort(P). Tenemos una lista de tensores S = {s1, s2, s3, ... sn}, que queremos reordenar en base a la lista de índices σ = {σ1, σ2, ..., σn} de forma diferenciable. A continuación, creamos una matriz U de tamaño (τ × C) × n × n, en la que repetimos cada si N veces.

Después formamos una matriz Ω de tamaño n x n, en la que cada fila j tiene un elemento distinto de cero en la posición k = σj. Convertimos la matriz Ω en una matriz binaria escalando cada elemento distinto de cero a 1 utilizando un factor de escala. Este proceso crea un camino para que los gradientes fluyan a través de P durante la retropropagación.

Realizando el producto de Hadamard entre U y Ω, obtenemos una matriz V, en la que cada fila j tiene un elemento distinto de cero k igual a sk. Sumando sobre la última dimensión y transponiendo la matriz resultante, obtenemos la matriz barajada final Sbarajada.

El uso de una matriz multidimensional P nos permite introducir parámetros adicionales que permiten al modelo capturar representaciones más complejas. Por ello, los autores del método S3 introducen un hiperparámetro λ para determinar la dimensionalidad de P. A continuación, realizamos la suma de P sobre las primeras λ - 1 dimensiones para obtener un vector unidimensional P, que luego se utiliza para calcular los índices de permutación σ = Argsort(P).

Este enfoque permite aumentar el número de parámetros de barajado, capturando así dependencias más complejas en los datos de series temporales sin afectar a las operaciones de ordenación.

En el paso final , el módulo Stitch concatena los segmentos barajados Sshuffled para crear una secuencia barajada X.

Para preservar la información presente en el orden original de las series temporales analizadas, realizan una suma ponderada de las secuencias original y mixta con parámetros w1 y w2, que también se optimizan mediante el entrenamiento del modelo principal.

Considerando S3 como un nivel modular, podemos apilarlos en una arquitectura neuronal. Definamos ϕ como un hiperparámetro que determina el número de capas S3. Por simplicidad y para evitar definir un hiperparámetro de segmento independiente para cada capa S3, los autores del método definen un parámetro θ como multiplicador del número de segmentos en las capas posteriores.

Cuando se apilan varias capas S3, cada nivel ℓ de 1 a ϕ segmenta y baraja los datos de entrada basándose en la salida de la capa anterior.

Todos los parámetros aprendibles de S3 se actualizan junto con los parámetros del modelo, y no se introducen pérdidas intermedias para las capas S3. Esto garantiza que los niveles S3 se entrenen de acuerdo con una tarea específica y un nivel básico.

En los casos en los que la longitud de la secuencia de entrada X no es divisible por el número de segmentos N, recurrimos a truncar los primeros T mod N pasos temporales de la secuencia de entrada. Para garantizar que no se pierden datos y que las formas de entrada y salida son las mismas, volvemos a añadir posteriormente las muestras truncadas al principio de la salida de la capa S3 final.

A continuación se muestra la visualización original del método.

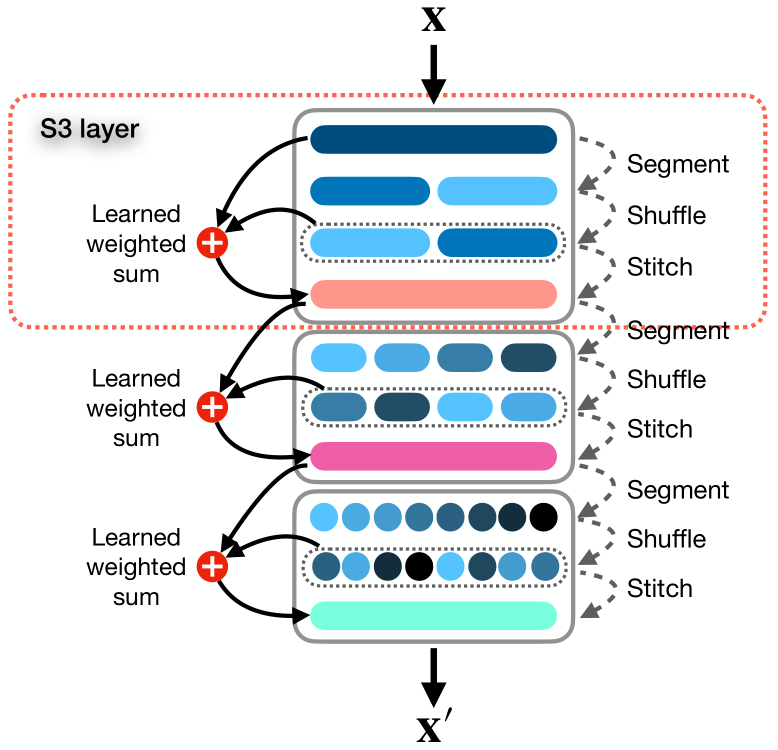
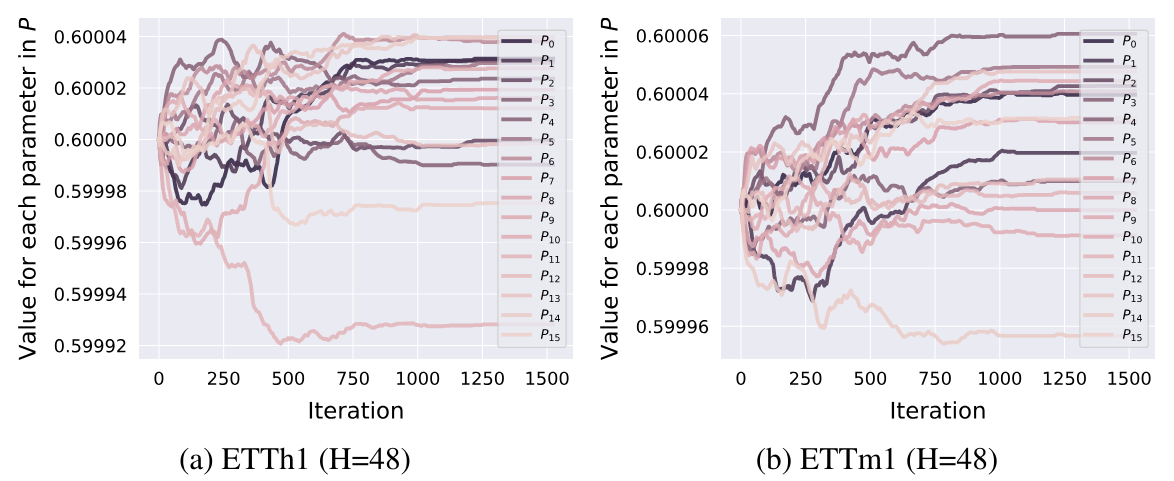
Cabe añadir aquí que, basándose en los resultados de los experimentos presentados en el documento, los parámetros de permutación se ajustan en la fase inicial del entrenamiento. Después se fijan y no cambian más adelante.

2. Implementación en MQL5

Tras considerar los aspectos teóricos del método S3, pasamos a la parte práctica de nuestro artículo en la que implementamos los enfoques propuestos en MQL5. Pero antes de empezar a escribir código, pensemos en la arquitectura de los enfoques propuestos a la luz de nuestros desarrollos actuales.

2.1 Arquitectura de soluciones

Para determinar el orden de clasificación de los datos, los autores del método S3 utilizan un vector de parámetros aprendibles P. En nuestra biblioteca, los parámetros aprendibles sólo existen en las capas neuronales. Bueno, podemos usar una capa neuronal para generar prioridades de segmentos. En este caso, el entrenamiento de parámetros se puede realizar utilizando los métodos disponibles dentro de la capa neuronal. Pero hay un matiz: necesitamos alimentar la capa neuronal con entradas para las que no están previstos los parámetros de entrenamiento. La situación es bastante simple: introducimos un vector fijo lleno de "1" en dicha capa neuronal.

Este enfoque nos permite resolver inmediatamente el problema de la matriz multidimensional de permutaciones.PAG'. Para cambiar la dimensión de esta matriz (los autores del método S3 definieron el hiperparámetro λ), solo necesitamos cambiar el tamaño del vector de datos original. El resto de la funcionalidad permanece sin cambios. La suma de parámetros individuales para cada segmento ya está implementada dentro de nuestra capa neuronal. El tamaño de los resultados de dicha capa neuronal es igual al número de segmentos.

Para traducir las prioridades de los segmentos al dominio de los valores probabilísticos, utilizaremos la función SoftMax.

Utilizaremos un enfoque similar para los parámetros de ponderación de la influencia de las secuencias originales y mezcladas. Esta vez el tamaño del resultado de la capa es 2. Como función de activación de esta capa utilizaremos la sigmoidea.

Éstos eran parámetros que se podían aprender. En cuanto al algoritmo para ordenar segmentos en orden ascendente o descendente de probabilidades, necesitaremos implementar esta funcionalidad.

En teoría, el orden de clasificación (ascendente o descendente) de las prioridades de los segmentos individuales no importa. Porque aprenderemos el orden de permutación de segmentos. En consecuencia, durante el proceso de entrenamiento, el modelo distribuirá prioridades según el orden de clasificación especificado. Es importante aquí que el orden de clasificación durante el entrenamiento y el funcionamiento del modelo permanezca inalterado.

Para permitir la propagación del error de gradiente al vector de prioridad P, los autores del método propusieron un algoritmo bastante complejo, en el que crean matrices multidimensionales y entradas duplicadas. Lo que genera costes computacionales adicionales y un mayor consumo de memoria. ¿Podemos ofrecer una opción más eficiente?

Veamos el proceso propuesto por los autores delS3 método, analizando las acciones y resultados.

En primer lugar, se forma una matriz U, que es una copia múltiple de los datos originales. Me gustaría excluir este procedimiento, que reducirá el consumo de memoria asociado al almacenamiento de una matriz grande y los recursos informáticos que se gastan al copiar los datos.

La segunda matriz Ω es una matriz binaria que en su mayor parte está llena de valores cero. El número de valores distintos de cero es igual al número de segmentos de la secuencia analizada (N). El número de elementos cero es N - 1 veces mayor. En este caso, deberíamos utilizar una matriz dispersa, lo que reducirá tanto el consumo de memoria como los costes computacionales al multiplicar matrices.

A continuación, según el algoritmo S3, se produce una multiplicación de matrices por elementos, seguida de una suma a lo largo de la última dimensión y la transposición de la matriz resultante.

Como resultado de todas las operaciones anteriores, obtenemos simplemente un tensor original barajado. Una simple operación de permutación de elementos del tensor requerirá menos recursos y se ejecutará más rápido.

Los autores desarrollaron un algoritmo de permutación tan complejo para implementar la propagación del gradiente de error al vector de prioridad P. Esto es en parte una «trampa» de la diferenciación automática de PyTorch, que los autores del método utilizaron al construir su algoritmo.

Estamos construyendo algoritmos de avance y retropropagación. Por supuesto, esto aumenta nuestros costes de construcción de algoritmos, pero también nos da mayor flexibilidad a la hora de construir procesos. Por lo tanto, en el paso de avance, podemos sustituir las operaciones anteriores por un barajado directo de los datos. Obviamente, este es un enfoque más eficaz.

Ahora tenemos que decidir sobre la cuestión de la propagación del gradiente de error. Al barajar las entradas, cada segmento participa en el tensor de salida una sola vez. En consecuencia, todo el gradiente de error se propaga al segmento correspondiente. En otras palabras, al distribuir el gradiente de error en los datos de entrada, tenemos que realizar la permutación inversa de los segmentos. Esta vez trabajaremos con el tensor de gradiente de error.

La segunda cuestión: Cómo propagar el gradiente de error al vector de prioridad. Aquí el algoritmo es un poco más complicado. En el paso de avance, utilizamos una prioridad para todo el segmento. Por lo tanto, en el paso de retropropagación tenemos que recoger el gradiente de error de todo el segmento en una prioridad. Para ello, debemos multiplicar el vector de entrada del segmento deseado por el segmento correspondiente del tensor de gradiente de error.

Además, al construir una matriz binaria Ω, utilizamos factores de escala para convertir los elementos distintos de cero en 1. Obviamente, para convertir un número distinto de cero en 1, hay que dividirlo por el mismo número o multiplicarlo por el número recíproco. Por lo tanto, los factores de escala son iguales a la inversa de los números de prioridad. Esto significa que el valor del gradiente de error obtenido anteriormente debe dividirse por la prioridad del segmento.

Cabe señalar que la prioridad del segmento no debe ser igual a «0». El uso de la función SoftMax nos permite excluir esta opción. Pero no excluye valores suficientemente pequeños, cuya división puede conducir a valores suficientemente grandes del gradiente de error.

Además, el uso de la función SoftMax al formar las probabilidades de las prioridades de los segmentos garantiza que todos los valores estén en el intervalo (0, 1). Obviamente, los segmentos con menor prioridad reciben un gradiente de error mayor, porque la división por un número menor que 1 da un resultado mayor que el dividendo.

Así que estos fueron los momentos sutiles de este algoritmo. Con esto en mente, ahora podemos pasar a implementarlo en código. Empecemos con la implementación en el lado del contexto OpenCL.

2.2 Creación de núcleos OpenCL

Como siempre, empezamos aplicando algoritmos feed-forward. En el lado del programa OpenCL, primero creamos el núcleo FeedForwardS3.

Me gustaría recordar aquí que implementaremos la generación de probabilidades de distribución de segmentos y la suma ponderada de la secuencia original y barajada en capas neuronales anidadas. Esto significa que este núcleo recibe datos ya preparados en forma de parámetros.

Por lo tanto, nuestro núcleo recibe punteros a 5 búferes de datos y 2 constantes en parámetros. Los 3 búferes contienen las entradas: la secuencia original, las probabilidades de los segmentos y los pesos. Otros dos búferes están destinados a registrar las salidas del núcleo. En uno de ellos escribiremos la secuencia de salida, y en el segundo los índices de barajado de segmentos que necesitaremos al realizar las operaciones de retropropagación.

En las constantes, especificaremos el tamaño de ventana de un segmento y el número total de elementos de la secuencia.

Tenga en cuenta que en la segunda constante especificamos el tamaño del vector de entrada y no el número de segmentos o pasos temporales. En el tamaño de la ventana del segmento también especificamos el número de elementos de la matriz, no los pasos temporales. Por lo tanto, ambas constantes deben ser divisibles por el tamaño del vector de un paso temporal sin resto.

__kernel void FeedForwardS3(__global float* inputs,
                            __global float* probability,
                            __global float* weights,
                            __global float* outputs,
                            __global float* positions,
                            const int window,
                            const int total
                           )
  {
   int pos = get_global_id(0);
   int segments = get_global_size(0);

Planeamos lanzar el núcleo en un espacio de tareas unidimensional basado en el número de segmentos de la secuencia analizada. En el cuerpo del núcleo, identificamos inmediatamente el flujo actual y también determinamos el número total de segmentos en función del número de tareas en ejecución.

En el caso de que el tamaño total de la entrada no sea múltiplo del tamaño de la ventana de un segmento, reducimos el número total de segmentos en 1.

   if((segments * window) > total)
      segments--;

En el siguiente paso, ordenamos las prioridades de los segmentos para determinar su secuencia. Sin embargo, no organizaremos el algoritmo de clasificación en su forma pura. En su lugar, determinaremos la posición del segmento analizado en la secuencia. Para determinar la posición de 1 elemento, sólo necesitamos 1 pasada por el vector de probabilidad del segmento. Sin embargo, al ordenar un vector, necesitaremos varias pasadas por el vector de probabilidad y la sincronización de los hilos de cálculo.

Aquí dividimos el algoritmo en 2 ramas, dependiendo del índice del hilo actual. La primera rama es el caso general y se utiliza si el índice del hilo actual es menor que el número de segmentos. Teniendo en cuenta que el índice del primer hilo es igual a 0, la formulación dada de la condición puede parecer extraña. Anteriormente, al considerar casos en los que el tamaño de la entrada no era múltiplo del tamaño de la ventana de segmentos, redujimos el valor de la variable del número de segmentos. Y en este caso, el último hilo seguirá la 2ª rama del algoritmo para determinar la posición del segmento.

En general, para determinar la posición del segmento correspondiente al hilo de operaciones en curso, fijamos su prioridad en una constante local. Ejecutamos un bucle desde el primer segmento hasta el actual, en el que contamos el número de elementos con una prioridad menor o igual a la actual. Para el caso de la ordenación descendente, determinamos el número de elementos con una prioridad mayor o igual que el segmento actual.

A continuación, organizamos un bucle desde el siguiente segmento hasta el último, en el que sumamos el número de elementos con una prioridad estrictamente menor (estrictamente mayor si la ordenación es descendente).

Tras completar las operaciones de ambos bucles, obtenemos la posición del segmento actual en la secuencia global.

   int segment = 0;
   if(pos < segments)
     {
      const float prob = probability[pos];
      for(int i = 0; i < pos; i++)
        {
         if(probability[i] <= prob)
            segment++;
        }
      for(int i = pos + 1; i < segments; i++)
        {
         if(probability[i] < prob)
            segment++;
        }
     }

La división de una pasada por el vector de prioridad en 2 bucles se realiza para el caso especial de tener 2 o más elementos con la misma prioridad. En este caso, se da prioridad al elemento que está antes en la secuencia original. Bien, podríamos construir un algoritmo con un bucle, pero en este caso, antes de comparar las prioridades, tendríamos que comprobar en cada iteración si el segmento estaba antes o después del actual en la secuencia original.

En la segunda rama del algoritmo de casos especiales, simplemente asignamos el número de segmento a su orden en la secuencia. En el caso especial mencionado, todos los segmentos completos se mezclarán y el último (no completo) permanecerá en su lugar.

   else
      segment = pos;

Ahora que hemos determinado la posición del segmento en la secuencia barajada, podemos moverlo. Para ello, definimos los desplazamientos en los búferes de entrada y salida.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Guardamos inmediatamente una posición determinada en el búfer correspondiente.

   positions[pos] = (float)segment;

No olvidemos la suma ponderada de las secuencias original y mixta. Naturalmente, para evitar la copia innecesaria de datos en el búfer de resultados, guardaremos inmediatamente la suma ponderada de 2 segmentos de las secuencias original y mezclada. Para ello, guardamos los parámetros de pesaje en constantes locales.

   const float w1 = weights[0];
   const float w2 = weights[1];

Creamos un bucle con un número de iteraciones igual al tamaño de la ventana de un segmento, en el que sumamos los elementos de 2 secuencias teniendo en cuenta los pesos y guardamos los valores obtenidos en el búfer de resultados.

   for(int i = 0; i < window; i++)
     {
      if((shift_in + i) >= total || (shift_out + i) >= total)
         break;
      outputs[shift_out + i] = w1 * inputs[shift_in + i] + w2 * inputs[shift_out + i];
     }
  }

Después de construir el núcleo de paso de propagación hacia adelante (feed-forward), pasamos a trabajar en el paso de retropropagación. Aquí empezamos a trabajar con la construcción del kernel InsideGradientS3, en el que distribuimos el gradiente de error al nivel de la capa anterior y las prioridades de los segmentos. En los parámetros del núcleo, añadimos punteros a los búferes de los gradientes de error correspondientes se añaden a los búferes previamente considerados.

__kernel void InsideGradientS3(__global float* inputs,
                               __global float* inputs_gr,
                               __global float* probability,
                               __global float* probability_gr,
                               __global float* weights,
                               __global float* outputs_gr,
                               __global float* positions,
                               const int window,
                               const int total
                              )
  {
   size_t pos = get_global_id(0);

El núcleo se lanzará en un espacio de tareas unidimensional en función del número de segmentos de la secuencia analizada. En el cuerpo del núcleo, identificamos inmediatamente el hilo de operaciones actual. En este caso, no es necesario determinar el número total de segmentos.

A continuación, cargamos las constantes determinadas durante el paso de avance desde los búferes de datos.

   int segment = (int)positions[pos];
   float prob = probability[pos];
   const float w1 = weights[0];
   const float w2 = weights[1];

Después determinamos el desplazamiento en los búferes de datos.

   const int shift_in = segment * window;
   const int shift_out = pos * window;

Y declararemos variables locales para los datos intermedios.

   float grad = 0;
   float temp = 0;

En el siguiente paso, creamos un bucle con un número de iteraciones igual al tamaño de la ventana del segmento, en el que recogemos el gradiente de error para la prioridad del segmento.

   for(int i = 0; i < window; i++)
     {
      if((shift_out + i) >= total)
         break;
      temp = outputs_gr[shift_out + i] * w1;
      grad += temp * inputs[shift_in + i];

Al mismo tiempo, transferimos el gradiente de error al búfer de la capa anterior. Durante el pase de avance, sumamos la secuencia original y la barajada. Por lo tanto, cada elemento de entrada debe recibir el gradiente de error de 2 hilos con el peso correspondiente.

      inputs_gr[shift_in + i] = temp + outputs_gr[shift_in + i] * w2;
     }

Antes de escribir el gradiente de error de prioridad del segmento en el búfer de datos correspondiente, dividimos el valor de salida por la probabilidad del segmento actual.

   probability_gr[segment] = grad / prob;
  }

Al núcleo de propagación de gradiente considerado anteriormente le falta un punto: la propagación del gradiente de error en los pesos de las secuencias original y mezclada. Para implementar esta funcionalidad, crearemos un núcleo independiente WeightGradientS3.

Aquí hay que decir que el enfoque general que utilizamos, cuando el gradiente de error de 1 elemento se recoge en cada hilo individual, no es muy eficaz en este caso. Esto se debe al reducido número de elementos del vector de pesos. Como puede ver, aquí sólo hay 2. Sin embargo, es mejor disponer de más hilos paralelos para reducir el tiempo total dedicado al entrenamiento del modelo. Para conseguir este efecto, crearemos dos grupos de hilos de trabajo, cada uno de los cuales recogerá el gradiente de error de su parámetro.

__kernel void WeightGradientS3(__global float *inputs,
                               __global float *positions,
                               __global float *outputs_gr,
                               __global float *weights_gr,
                               const int window,
                               const int total
                              )
  {
   size_t l = get_local_id(0);
   size_t w = get_global_id(1);

En consecuencia, el núcleo se lanzará en un espacio de tareas bidimensional. La primera dimensión define el número de hilos paralelos en un grupo. Y la segunda dimensión indica el índice del parámetro para el que se recoge el gradiente de error.

A continuación, declaramos un array local, en el que cada hilo del grupo guardará su parte del trabajo.

   __local float temp[LOCAL_ARRAY_SIZE];

Dado que el número de hilos de trabajo no puede ser mayor que el tamaño de la matriz local declarada, nos vemos obligados a limitar el número de «caballos de trabajo».

   size_t ls = min((uint)get_local_size(0), (uint)LOCAL_ARRAY_SIZE);

En la primera etapa, cada subproceso recoge su parte de gradientes de error independientemente de los demás subprocesos del grupo de trabajo. Para ello, ejecutamos un bucle sobre los elementos del búfer de gradiente de error a la salida de la capa actual, empezando por el elemento con el índice del grupo de trabajo del hilo actual hasta el último de la matriz, con un paso igual al número de «caballos de trabajo».

En el cuerpo del bucle, primero determinamos el desplazamiento hasta el elemento correspondiente en la memoria intermedia de datos de origen. Este desplazamiento depende del índice del peso para el que recogemos el gradiente de error. Para el segundo peso, el desplazamiento en las memorias intermedias de gradiente del error de capa y los datos de entrada es el mismo.

   if(l < ls)
     {
      float val = 0;
      //---
      for(int i = l; i < total; i += ls)
        {
         int shift_in = i;

Como para el primer desplazamiento, primero definimos un segmento en el búfer de gradiente de error. A continuación, a partir del vector de permutación, extraemos el segmento correspondiente en la secuencia original. Sólo entonces podremos calcular el desplazamiento en el búfer de entrada hasta el elemento requerido.

         if(w == 0)
           {
            int pos = i / window;
            shift_in = positions[pos] * window + i % window;
           }

Dados los índices de los elementos correspondientes en ambas memorias intermedias de datos, calculamos el gradiente de error para el peso en esa posición y lo añadimos a la variable de acumulación.

         val += outputs_gr[i] * inputs[shift_in];
        }
      temp[l] = val;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Una vez completadas todas las iteraciones del bucle, escribimos la suma acumulada del gradiente de error en el elemento correspondiente de la matriz de memoria local e implementamos una barrera de sincronización para los hilos del grupo de trabajo.

En el segundo paso, sumamos los valores de los elementos de la matriz local.

   int t = ls;
   do
     {
      t = (t + 1) / 2;
      if(l < t && (l + t) < ls)
        {
         temp[l] += temp[l + t];
         temp[l + t] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(t > 1);

Al final de las operaciones del núcleo, el primer subproceso del grupo de trabajo transfiere el gradiente de error total al elemento correspondiente de la memoria intermedia global.

   if(l == 0)
      weights_gr[w] = temp[0];
  }

Tras distribuir los gradientes de error de todos los elementos en función de su impacto en el resultado global, solemos pasar a trabajar en los algoritmos de actualización de parámetros. Pero en el marco de este artículo, hemos organizado todos los parámetros entrenables dentro de las capas neuronales anidadas. Por consiguiente, los algoritmos de actualización de los parámetros ya están previstos en los objetos mencionados. Por lo tanto, aquí estamos completando las operaciones en el lado OpenCL y pasamos a trabajar con el programa principal.

2.3. Creación de la clase CNeuronS3.

Para implementar los enfoques propuestos en el lado del programa principal, creamos una nueva clase de capa neuronal CNeuronS3. A continuación se presenta su estructura.

class CNeuronS3   :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iSegments;
   //---
   CNeuronBaseOCL    cOne;
   CNeuronConvOCL    cShufle;
   CNeuronSoftMaxOCL cProbability;
   CNeuronConvOCL    cWeights;
   CBufferFloat      cPositions;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      feedForwardS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradientsS3(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronS3(void)   {};
                    ~CNeuronS3(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronS3;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual CLayerDescription* GetLayerInfo(void);
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En la clase, declaramos 2 variables y 5 objetos anidados. Las variables almacenarán el tamaño de ventana de un segmento y el número total de segmentos de la secuencia. En cuanto a los objetos anidados, los tendremos en cuenta al implementar los métodos de nuestra clase.

Todos los objetos de la clase se declaran estáticos. Esto nos permite dejar el constructor y el destructor de la clase «vacíos». La inicialización de todos los objetos anidados se realiza en el método Init. Como siempre, en los parámetros de este método recibimos los parámetros principales de la arquitectura de la clase del llamante. Presta atención a los 2 parámetros siguientes:

• window — tamaño de ventana de 1 segmento;
• numNeurons — el número de neuronas de la capa.

En estos parámetros indicamos el número de elementos de la matriz en lugar de los pasos de la serie temporal. Sin embargo, su valor debe ser múltiplo del tamaño del vector que describe un paso temporal. En otras palabras, para facilitar la implementación construimos una clase para trabajar con series temporales unidimensionales. Aquí, el usuario es responsable de mantener la integridad de los pasos temporales de una serie temporal multidimensional dentro de los segmentos.

bool CNeuronS3::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                     uint window, uint numNeurons, 
                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

En el cuerpo del método, primero llamamos al mismo método de la clase padre, que controla los parámetros recibidos e inicializa los objetos heredados. Recuerde controlar la ejecución de los métodos llamados.

Tras inicializar correctamente los objetos heredados, guardamos el tamaño de ventana de 1 segmento y determinamos inmediatamente el número total de segmentos.

   iWindow = MathMax(window, 1);
   iSegments = (numNeurons + window - 1) / window;

A continuación, inicializamos los objetos internos de la clase. En primer lugar, inicializamos una capa neuronal fija de valores únicos, que se utilizará como entrada para generar las prioridades de permutación de segmentos y los parámetros ponderados de suma de secuencias. Aquí primero inicializamos la capa neuronal y luego forzamos el llenado del buffer de resultados con valores individuales.

   if(!cOne.Init(0, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buffer = cOne.getOutput();
   if(!buffer || !buffer.BufferInit(buffer.Total(),1))
      return false;
   if(!buffer.BufferWrite())
     return false;

Preste atención a los dos puntos siguientes. En primer lugar, creamos una capa de 1 neurona. Como recordarás, cuando estábamos trabajando en la arquitectura de nuestra implementación, dijimos que el número de neuronas en una capa dada indicaría la dimensión de la matriz de permutación. No veo el sentido de utilizar una matriz multidimensional. Desde un punto de vista matemático, sin el uso de funciones de activación intermedias, la función lineal de sumar el producto de varias variables por una constante degenera en el producto de una variable por la constante utilizada.

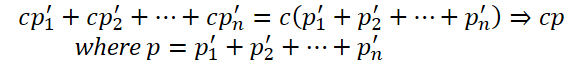
Desde este punto de vista, un aumento de los parámetros sólo conduce a un aumento de la complejidad computacional con un impacto cuestionable en la eficacia del modelo.

Por otra parte, ésta es sólo mi opinión. Así que puedes comprobarlo experimentalmente.

El segundo punto es la indicación de «0» conexiones salientes para esta capa anidada. Planeamos utilizar este objeto como datos iniciales para 2 capas neuronales. Fue la presencia de 2 capas posteriores lo que nos obligó a recurrir a un pequeño truco. Nuestra capa neuronal base está diseñada de tal manera que contiene una matriz de pesos sólo para 1 capa posterior. Pero tenemos una clase de capas neuronales convolucionales, que contiene matrices de coeficientes de peso para las conexiones entrantes. Utilizar 1 elemento de entrada y múltiples prioridades de permutación en la salida no es, por decirlo suavemente, exactamente un escenario adecuado para utilizar una capa convolucional. Pero espera.

Se garantiza que un elemento de entrada nos dará 1 parámetro aprendible en el filtro de convolución. Además, podemos proporcionar fácilmente el tamaño del vector de permutación especificando el número necesario de filtros de convolución. En este caso, especificaremos sólo 1 elemento de convolución. De este modo transferiremos los parámetros aprendibles a las capas neuronales posteriores.

   if(!cShufle.Init(0, 1, OpenCL, 1, 1, iSegments, 1, optimization, iBatch))
      return false;
   cShufle.SetActivationFunction(None);

Como ya se ha comentado, trasladamos las prioridades de permutación al dominio de la probabilidad mediante la función SoftMax.

   if(!cProbability.Init(0, 2, OpenCL, iSegments, optimization, iBatch))
      return false;
   cProbability.SetActivationFunction(None);
   cProbability.SetHeads(1);

Hacemos lo mismo con el objeto de generar parámetros de suma ponderada de secuencias. La diferencia es que aquí utilizamos sigmoide como función de activación.

   if(!cWeights.Init(0, 3, OpenCL, 1, 1, 2, 1, optimization, iBatch))
      return false;
   cWeights.SetActivationFunction(SIGMOID);

Y al final del método de inicialización, creamos un búfer para registrar los índices de permutación de los segmentos.

   if(!cPositions.BufferInit(iSegments, 0) || !cPositions.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

La clase contiene dos nuevos métodos (feedForwardS3 y calcInputGradientsS3). Colocan los núcleos de programa OpenCL creados previamente en la cola de ejecución. Como se puede adivinar, el primer método pone en cola la ejecución del kernel feed-forward, y el segundo método pone en cola los dos kernels de distribución de gradiente de error restantes. En artículos anteriores, ya hemos hablado del algoritmo para colocar el núcleo en la cola de ejecución. Estos métodos se basan en un algoritmo similar, por lo que no los consideraremos ahora. Puede encontrar el código de estos métodos en el archivo adjunto. El archivo adjunto contiene también el código completo de todos los programas utilizados en la preparación del artículo.

El algoritmo feed-forward de nuestra clase se construye en el método feedForward. Al igual que el método de la clase padre con el mismo nombre, el método recibe como parámetros un puntero al objeto de la capa neuronal anterior, que contiene los datos de entrada.

Antes de llamar al método de colocación del núcleo de avance en la cola, necesitamos preparar las prioridades de las permutaciones de segmentos y los parámetros para ponderar la suma de las secuencias original y barajada. Y aquí hay que señalar que los datos iniciales de los procesos indicados son un vector fijo de valores unitarios. Por consiguiente, sus valores no dependen de los datos iniciales y no cambian durante el funcionamiento del modelo. Los valores especificados sólo pueden cambiar cuando los parámetros de aprendizaje cambian durante el proceso de aprendizaje. Esto significa que su recálculo sólo es necesario durante el proceso de aprendizaje. Para recalcular los valores, llamamos al método feed-forward de los objetos anidados correspondientes.

bool CNeuronS3::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(bTrain)
     {
      if(!cWeights.FeedForward(cOne.AsObject()))
         return false;
      if(!cShufle.FeedForward(cOne.AsObject()))
         return false;
      if(!cProbability.FeedForward(cShufle.AsObject()))
         return false;
     }

A continuación, barajamos la secuencia original llamando al método para poner el núcleo de paso adelante en la cola de ejecución.

   if(!feedForwardS3(NeuronOCL))
      return false;
//---
   return true;
  }

Recuerde que debe controlar la ejecución de las operaciones.

No hay nada inesperado en el algoritmo del método de distribución de gradiente. El método sólo se llama durante el proceso de aprendizaje y no necesitamos comprobar el modo de funcionamiento actual del modelo.

En los parámetros, el método recibe un puntero al objeto de la capa anterior, al que debe pasarse el gradiente de error, e inmediatamente llamamos al método para poner en cola los núcleos de distribución del gradiente de error creados anteriormente.

bool CNeuronS3::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!calcInputGradientsS3(NeuronOCL))
      return false;

A continuación, pasamos el gradiente de error a la capa de parámetros de prioridad de barajado de segmentos.

   if(!cShufle.calcHiddenGradients(cProbability.AsObject()))
      return false;

No tiene sentido seguir propagando el gradiente de error hasta el nivel de la capa fija. Por lo tanto, omitiremos este procedimiento. Sólo tenemos que corregir el gradiente de error obtenido para las posibles funciones de activación.

   if(cWeights.Activation() != None)
      if(!DeActivation(cWeights.getOutput(), cWeights.getGradient(), cWeights.getGradient(), cWeights.Activation()))
         return false;
   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(),NeuronOCL.getGradient(),NeuronOCL.getGradient(),NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Tenga en cuenta que llamamos al método para desactivar los gradientes de error sólo si hay uno en el objeto correspondiente.

Tras propagar el gradiente de error a todos los elementos de nuestro modelo en función de su influencia en el resultado global, tenemos que ajustar los parámetros del modelo para reducir el error global. Esto es bastante sencillo. Para ajustar los parámetros de la capa CNeuronS3, basta con llamar a los métodos de actualización de los parámetros de los objetos anidados correspondientes.

bool CNeuronS3::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWeights.UpdateInputWeights(cOne.AsObject()))
      return false;
   if(!cShufle.UpdateInputWeights(cOne.AsObject()))
      return false;
//---
   return true;
  }

Con esto concluimos la descripción de los métodos de nuestra nueva clase. No es posible describir todos los métodos de nuestra nueva clase en un artículo, pero puede estudiarlos usted mismo ya que todos los códigos se proporcionan en el archivo adjunto. Allí encontrará el código completo de esta clase y todos sus métodos.

2.4 Arquitectura modelo

Después de crear la nueva clase de capa, la implementamos en nuestro modelo de arquitectura. Creo que es obvio que agregaremos la clase CNeuronS3 a la arquitectura del codificador de estado del entorno. Dentro de este artículo, no entraré en detalle sobre la arquitectura del Encoder, ya que está completamente copiada del artículo anterior. Detengámonos sólo en las capas neuronales añadidas, que colocamos inmediatamente después de la capa de datos de origen.

Permítanme recordarles que nuestros modelos de prueba se construyen para analizar datos históricos en el marco temporal H1. Para el análisis, utilizamos los últimos 120 compases de la historia, cada uno de los cuales se describe mediante 9 parámetros.

#define        HistoryBars             120           //Depth of history
#define        BarDescr                9             //Elements for 1 bar description

Mientras preparábamos este artículo, implementamos 3 capas consecutivas que barajan las entradas en el codificador. Para la primera capa, utilizamos segmentos de 12 pasos temporales (horas).

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 12*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

En la segunda capa, reducimos el tamaño del segmento a 4 pasos temporales.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = 4*BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y en el último, barajamos cada paso temporal.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronS3;
   descr.count = prev_count;
   descr.window = BarDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Más arquitectura también está completamente copiada de los anteriores artículos sin ningún cambio. Esto significa que no hicimos ningún cambio en el algoritmo de los programas para interactuar con el entorno, entrenar y probar los modelos. En el archivo adjunto encontrará el código completo de todos los programas utilizados.

3. Pruebas

Hemos construido los algoritmos de los enfoques propuestos. Ahora, pasemos a la fase quizá más emocionante: probar y evaluar los resultados.

Como se ha indicado anteriormente, no hemos realizado ningún cambio en los programas de interacción medioambiental mientras trabajábamos en este artículo. Esto significa que podemos utilizar un conjunto de datos de entrenamiento recogidos previamente para entrenar modelos.

Permítanme recordarles que para entrenar los modelos, utilizamos los registros de los pases del programa de interacción ambiental en el probador de estrategias MetaTrader 5 utilizando datos históricos reales del instrumento EURUSD, marco de temporalidad H1, para todo el año 2023.

En el primer paso, entrenamos el codificador del estado del entorno. Este modelo se entrena para predecir los datos de los 24 elementos siguientes de la serie temporal analizada.

#define        NForecast               24            //Number of forecast

En otras palabras, nuestro modelo intenta predecir el movimiento de los precios para el día siguiente. Al construir la política de comportamiento de nuestro Agente, no nos basamos en la previsión recibida, sino en el estado oculto del codificador. Por lo tanto, al entrenar el modelo, no estamos tan interesados en una previsión precisa del próximo movimiento, evaluamos la capacidad del codificador para capturar y cifrar en su estado oculto las principales tendencias y tendencias del próximo movimiento de precios.

El modelo Encoder se entrena únicamente para analizar el estado del mercado sin tener en cuenta el estado de la cuenta y las posiciones abiertas. Por lo tanto, la actualización del conjunto de datos de entrenamiento durante el proceso de entrenamiento del modelo no proporcionará información adicional. Esto nos permite entrenar el modelo en un conjunto de datos creado previamente hasta obtener el resultado deseado.

Basándonos en los resultados del primer paso de entrenamiento, podemos evaluar el impacto de nuestra nueva capa en los datos iniciales obtenidos por el modelo. Aquí debo señalar que el modelo presta casi la misma atención a las secuencias barajadas y a las originales. Un poco más de atención a este último.

En la primera capa, el coeficiente de la secuencia barajada era de 0,5039, y el de la secuencia original, de 0,5679. Al mismo tiempo, la secuencia se baraja casi por completo. Sólo el segmento con índice 7 permaneció en su posición. Y la mezcla es totalmente aleatoria. No hay ni un solo par de elementos que simplemente se intercambien.

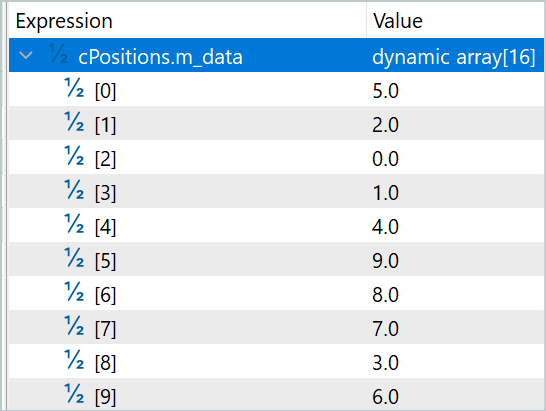
En la siguiente capa, ambos coeficientes aumentaron ligeramente hasta 0,6386 y 0,6574, respectivamente. No facilitaré la lista de permutaciones, ya que se ha multiplicado por tres. Ya no contiene segmentos no barajados.

En la tercera capa, se presta más atención a la secuencia original, pero el coeficiente de la secuencia barajada sigue siendo bastante alto. Los parámetros cambiaron a 0,5064 y 0,7089, respectivamente.

Los resultados obtenidos pueden evaluarse de distintas maneras. En mi opinión, el modelo busca la racionalidad en la comparación por pares de segmentos.

El resultado obtenido es bastante interesante, pero nos interesa más el impacto en la política final del Agente. Una vez entrenado el codificador, pasamos a la segunda fase de entrenamiento de nuestros modelos. En esta fase, entrenamos la política Actor y el modelo Critic. El funcionamiento de estos modelos depende en gran medida del estado de la cuenta y de las posiciones abiertas en el momento analizado. Por lo tanto, nuestro proceso de aprendizaje será iterativo, alternando entre el entrenamiento de los modelos y la recogida de datos adicionales sobre la interacción con el entorno. Esto nos permitirá afinar y optimizar la política de comportamiento del Agente.

Durante el proceso de formación, pudimos entrenar una política para que generara beneficios tanto durante el periodo de formación como durante el periodo de prueba. A continuación se presentan los resultados de los entrenamientos.

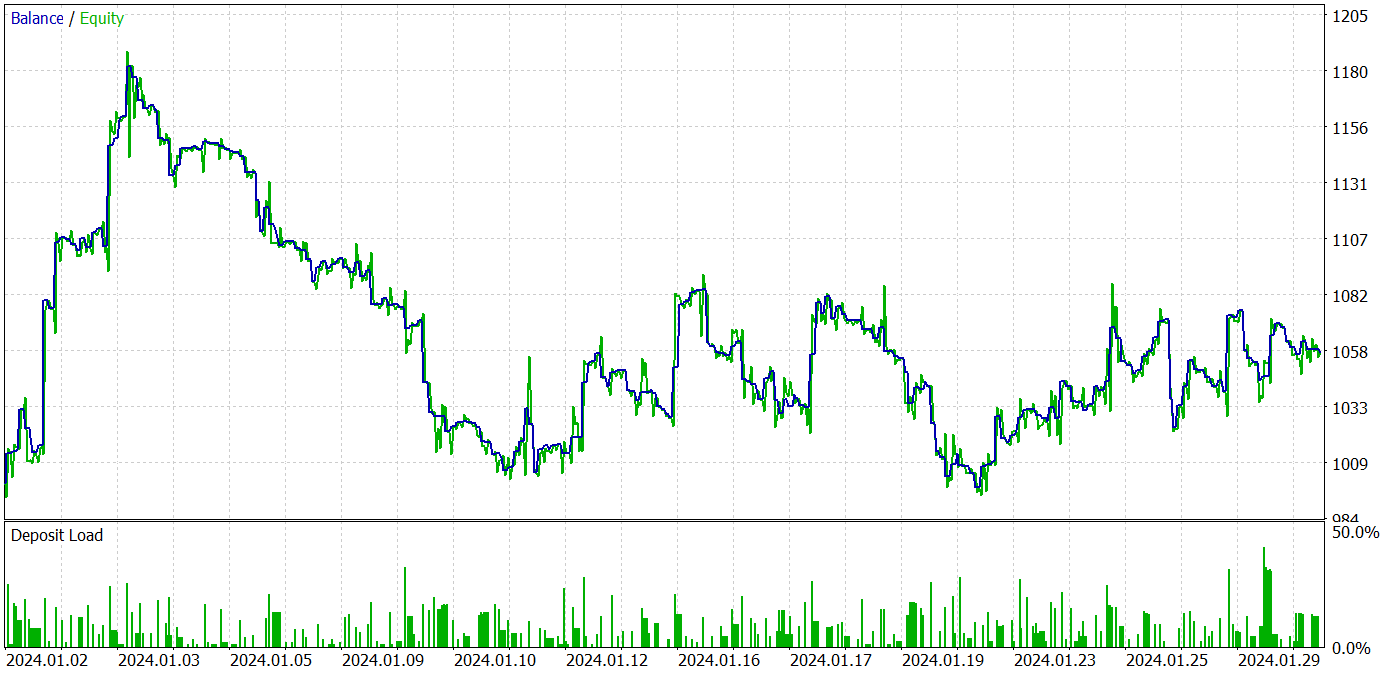
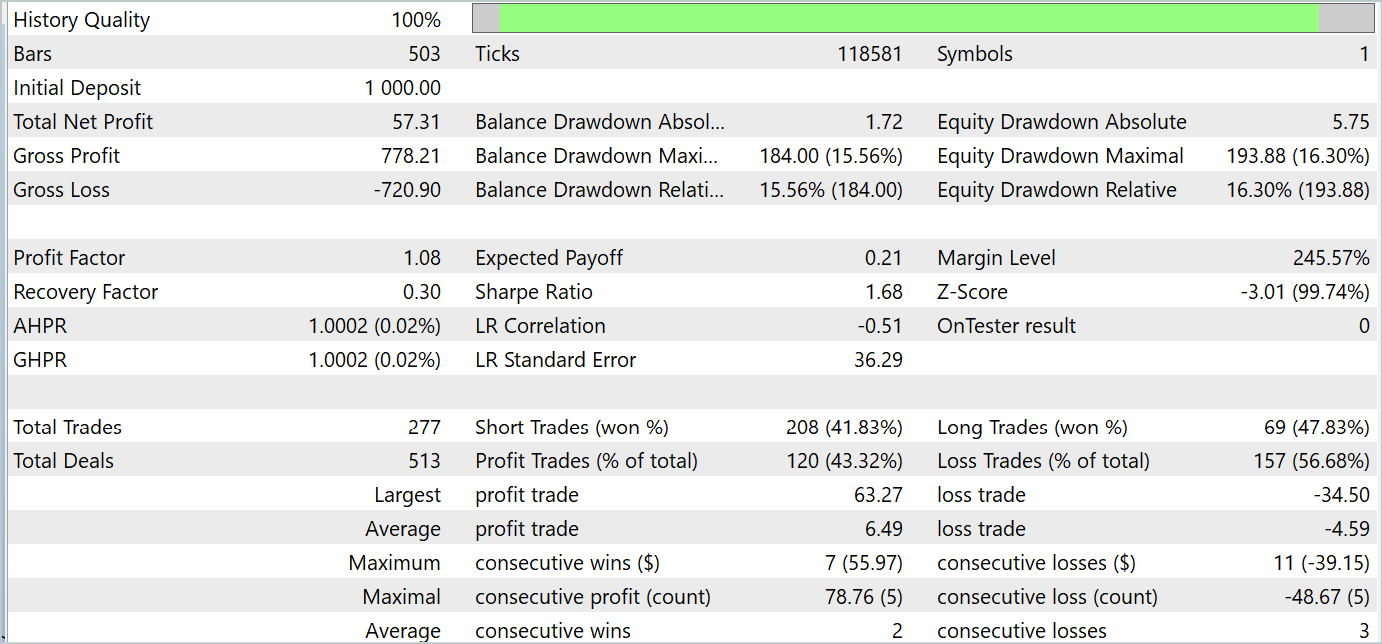
A pesar de los beneficios recibidos, el gráfico del balance no tiene buen aspecto. El modelo aún necesita algunas mejoras. Si observa más de cerca el informe de pruebas, puede destacar los lunes y viernes menos rentables. El miércoles, por el contrario, el modelo genera el máximo beneficio.

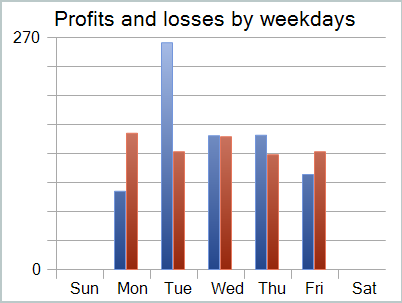
Por lo tanto, limitar el funcionamiento del modelo a determinados días de la semana aumentará la rentabilidad general del modelo. Pero esta hipótesis requiere pruebas más detalladas en un conjunto de datos más representativo.

Conclusión

En este artículo, analizamos un método bastante interesante para optimizar secuencias de series temporales: S3. El método fue presentado en el artículo "Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations". La idea principal del método es mejorar la calidad de la representación de series temporales. La aplicación de S3 conduce a una mayor precisión de la clasificación y estabilidad del modelo.

En la parte práctica de nuestro artículo, hemos construido nuestra visión de los enfoques propuestos utilizando MQL5. Hemos entrenado y probado modelos utilizando los enfoques propuestos. Los resultados son bastante interesantes.

Referencias

• Segment, Shuffle, and Stitch: A Simple Mechanism for Improving Time-Series Representations
• Otros artículos de esta serie

Programas utilizados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Expert Advisor	Colección de ejemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para la recolección de ejemplos utilizando el método Real-ORL
3	Study.mq5	Expert Advisor	EA para el entrenamiento del modelo
4	StudyEncoder.mq5	Expert Advisor	EA de entrenamiento del codificador
5	Test.mq5	Expert Advisor	EA de prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Código base	Biblioteca OpenCL