母集団最適化アルゴリズム：極値から抜け出す力（第I部）

MetaTrader 5 — 例 | 12 8月 2024, 13:25

Andrey Dik

内容

1. はじめに
2. タスクの設定
3. コードの変更
4. アルゴリズム
5. 予備的結論

1. はじめに

これはユニークな研究であり、私の記事のうち1つのディスカッション中に生じた質問に答える中で思いついたものです。読者がこの研究の価値とオリジナリティを評価してくれれば嬉しいです。

この研究に至る私の考えやアイデアは、このテーマに深く没頭し、科学的研究に情熱を注いだ結果です。私は、この研究が研究者や実務家の注目を集めるアルゴリズム最適化の分野への重要な貢献になると信じています。

この実験では、アルゴリズムが極値から抜け出す能力評価することを目的としたテストをおこなうことを提案します。最初の反復で、エージェントを探索空間の全フィールドにランダムに配置する代わりに、最小値に配置します。実験の目的は、最大値を探索することです。

このようなシナリオでは、アルゴリズムのすべての探索エージェントが一点に位置するため、退化した集団という興味深い現象に直面することになります。これは、個体群の多様性が最小化される、時間の凍結のような瞬間です。このシナリオは人為的なものですが、興味深い結論を得ることができ、母集団の多様性を減らすことが結果に与える影響を評価することができます。アルゴリズムはこのようなボトルネックから抜け出し、最大値を達成できるはずです。

このような最適化アルゴリズムのストレステストでは、エージェントの相互作用、協力や競争の秘密を明らかにし、これらの要因が最適値を達成するスピードにどのように影響するかを理解することができます。このような分析により、アルゴリズムの効率的な運用における母集団の多様性の重要性を理解する上で新たな地平が開かれ、より良い結果を得るためにこの多様性を維持するための戦略を開発することが可能になります。

実験をおこなうには、まず最初のエポックで適応度関数を測定する前に、最小値の座標を用いて、アルゴリズムの外側でエージェントの座標を強制的に初期化する必要があります。

このような実験によって、極めて困難な条件に対する耐性や、制限を克服する能力を評価することができます。

2. タスクの設定

深い谷間にいて、濃い闇に包まれていると想像してください。目隠しされ、周りの世界を見ることができません。冷たい風が顔に吹きつけるのを感じます。まるで胸から破裂しようとするかのように心臓が激しく鼓動し、不安と不確実性が際立ちます。

あなたは最初の一歩を踏み出します。足が地面を感じます。あなたは谷に沿って徐々に進み、一歩一歩自由に近づき、心は決意で満たされます。そして淵にたどり着くと、息をのむような絶景が目の前に広がります。ガラスのような平原が無限のキャンバスのように目の前に広がります。遠くにそびえる孤立した切り立った崖は、驚きと挑戦の入り混じった感情を呼び起こします。しかし、この美しいパノラマにもかかわらず、まだ見ることができません。

あなたは、自分の感覚と直感を頼りに、進むべき方向を決め、最も高い崖の頂上に到達します。さて、Megacityテストの離散関数に基づくアルゴリズムがこの難題に直面したとしましょう。あなたと同じように、このアルゴリズムの能力には限界があり、環境を直接見たり感じたりすることはできません。計算能力とロジックを駆使して、最も高い崖の頂上までの最良の道を決めなければなりません。したがって、Megacityテストの離散関数に関するこの問題は、あなたと同じように不確実性に直面しているアルゴリズムにとって難しい挑戦なのです。

しかし、このような状況では、Hilly関数とForest関数にも難しい問題が引き起こされます。アルゴリズムの今後のタスクの複雑さを理解するために、これらの身近な関数を見てみましょう。

Hilly ロード

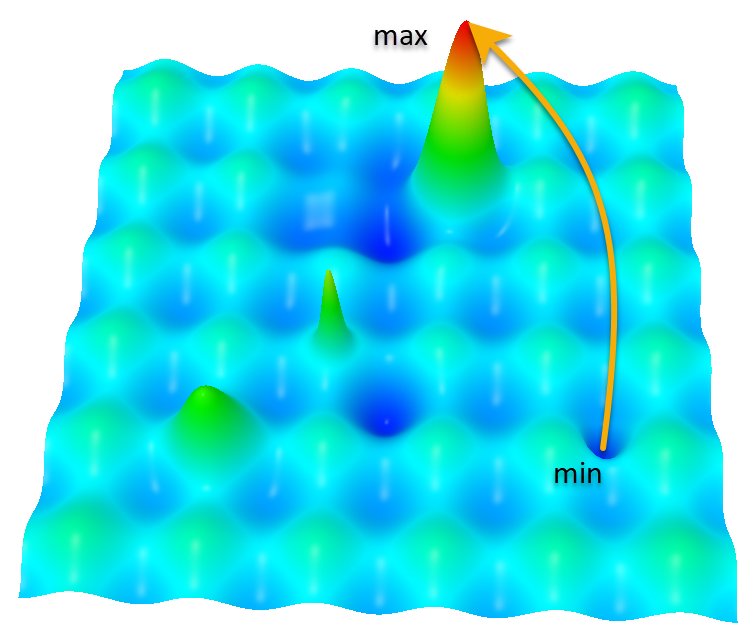
Hilly関数

Forestロード

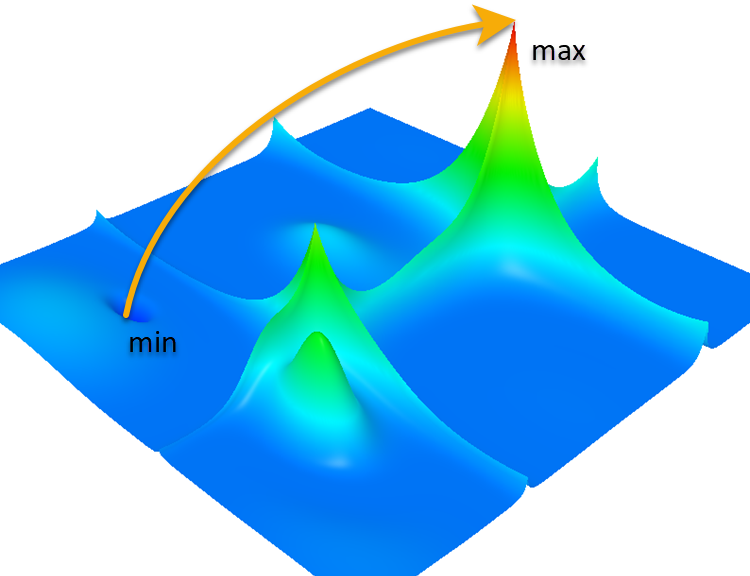
Forest関数

Megacityロード

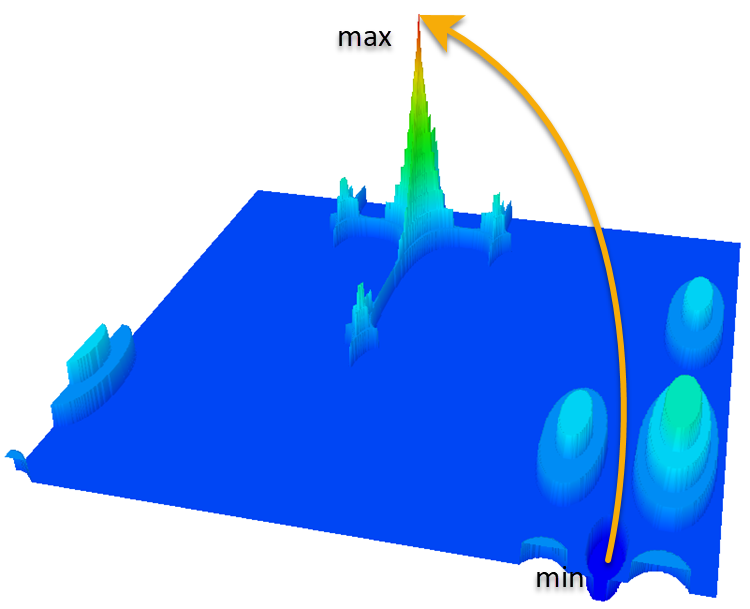
Megacity関数

自分がアルゴリズムであり、計算能力と論理的思考を具現化したものだと想像してみてください。あなたはただの紙の上のコードや方程式の羅列ではなく、命を吹き込まれ、研究者の役割を担います。あなたの心は疑問と仮説で満たされ、目の前に立ちはだかる謎を解こうと努力します。あなたはデータと情報の世界に没頭し、重要な要素を分析、比較、強調し、計算能力をフル回転させています。さまざまなモデルやシナリオを構築し、問題解決への可能な道筋を探り、さまざまな組み合わせや選択肢を試します。そして、あなたの創造性が新たな発見につながります。しかし、解決への道は必ずしも容易ではありません。乗り越えられないと思われる困難に直面しても、あなたはあきらめません。障害や雑念を1つずつ乗り越え、一歩一歩ゴールに近づいていきます。そして最後に、解決策が見つかったとき、それは悟りの瞬間のようなものです。あなたの心は理解という明るい光で照らされ、すべてがうまくいくのがわかります。

この図の文脈では、最適化アルゴリズムは、多くの極大値を持つ複雑なトポロジーを持つ関数を最大化するタスクに直面しています。以下は問題の詳細です。

極大値：始点(min)から終点(max)までの道のりで、アルゴリズムは多くの極大値に遭遇します。このため、アルゴリズムが最大値に達することなく、局所的な罠にはまってしまうことがあります。これが、最適化問題における大きな問題です。例えば、勾配降下ベースのアルゴリズムは、最も近い最大値まで「登る」傾向があり、それが極大値であれば「立ち往生」します。

高次元：多次元空間の関数を考える場合、極大値の数が急激に増え、問題が複雑になります。高次元では空間が「空」になり、アルゴリズムがしがみつくものがなくなるため、問題はさらに難しくなります。

関数曲面の複雑さ：関数曲面は山あり谷ありで非常に複雑になり、最適化プロセスに時間がかかります。そのためには、アルゴリズムが極大値を飛び越え、最大値まで上昇できる必要があります。

収束と収束スピード：関数の最大値へのアルゴリズムの収束は、始点から終点の距離のために遅くなる可能性があり、目標を達成するために追加の反復を必要とする可能性があります。

領域研究：アルゴリズムは、さらに最大値を求めて領域を探索する必要があるかもしれません。これは計算量の増加につながる可能性があります。

問題の説明を要約すると、エージェントが探索空間において一様に分布した状態で移動を開始する典型的な最適化の状況と、既存の情報を「明らかにする」だけでなく、むしろ未知の領域を探索し、知識や経験を拡大する必要がある状況との違いを強調することができます。このように問題を設定することは、以前の最適化セッションで得られた解がすでにあり、既存の情報を単に結晶化するのではなく、この解の「点」から出発したい場合に、特に価値があります。

3. コードの変更

エージェントを1点に配置するには、テスト関数の最小値の座標を適切な母集団エージェントに割り当てます。一般的に、この手順は次のようになります。

if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].c [i * 2]     = f.GetMinFuncX ();
      AO.a [set].c [i * 2 + 1] = f.GetMinFuncY ();
    }
  }
}

アルゴリズムによっては、単にエージェントを探索空間の一点に配置するだけでは不十分なものもあります。追加情報を入力する必要があります。例えば、SDSmアルゴリズムの場合、各座標に対応するセクタも指定する必要があります。一方、BGAアルゴリズムを使用する場合、座標値を実数表現から2進表現に変換する必要があり、アルゴリズムコードに追加の変更が必要となります。BGAの場合、ある時点でのエージェントの位置は次のようになります。

//==================
if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].DoubleToGene (f.GetMinFuncX (), i * 2);
      AO.a [set].DoubleToGene (f.GetMinFuncY (), i * 2 + 1);
    }

    AO.a [set].ExtractGenes ();
  }
}
//==================

このコードからわかるように、座標から遺伝子のバイナリコードへの変換がここでおこなわれます。私は現在、エージェントを希望する座標に配置するプロセスの統一に取り組んでいます。この研究では、現状のソースコードを紹介します。ほとんどすべてのアルゴリズムは、そのアーキテクチャの性質上、カスタムテストベッドを必要としました。アルゴリズムの最新情報は新しい記事でお届けするのでご期待ください。母集団における座標の配置を簡素化し、それらを統一することで、共通の標準がもたらされます。

4. アルゴリズム

独自のテストにおけるアルゴリズムの動作分析に移ります。最悪の結果を示したアルゴリズムについて考察を始めましょう。特に驚きなのは、標準的なテストではかなり上位に位置していたのに、今回のような変わったテストでは成績が悪かったことです。このことは、アルゴリズムの成功は、その全体的な効率だけでなく、問題の特定の条件や特性に適応する能力にも依存する可能性があることを示唆しています。このような予想外の結果は、さまざまな文脈における最適化アルゴリズムの性能をより深く理解するために、さまざまなテストや研究を実施することの重要性を浮き彫りにしています。

以下は、アルゴリズムに関するレポートです。

C_AO_FSS:50;0.01;0.8：アルゴリズム名と外部パラメータ
5 Hilly's：テスト関数の名前とテスト中の番号
Func runs:10000：実行回数
result:0.32457068874346456：得られた結果。0.0はテスト関数の最小値、1.0は最大値。数値が高いほど良い
All score:1.33084：得点の合計値。数値が高いほど良い

差分進化(DE)

C_AO_DE:50;0.2;0.8
=============================
5 Hilly's; Func runs:10000; result:0.0
25 Hilly's; Func runs:10000; result:0.0
500 Hilly's; Func runs:10000; result:0.0
=============================
5 Forest's; Func runs:10000; result:0.0
25 Forest's; Func runs:10000; result:0.0
500 Forest's; Func runs:10000; result:0.0
=============================
5 Megacity's; Func runs:10000; result:0.0
25 Megacity's; Func runs:10000; result:0.0
500 Megacity's; Func runs:10000; result:0.0
=============================
All score:0.00000

残念ながら、ランキング表の中で最も強力なアルゴリズムの1つでさえ、私たちのテストでは完全に不合格でした。この場合、エージェントは自分が停滞し、動くことができないことに気づきました。この失敗の理由は、エージェントのそれぞれの新しい位置が、他の3つのエージェントの位置に依存しており、もしエージェントがすべて同じ地点に着いた場合、どのエージェントも座標を更新することができないということです。この状況は、エージェント間の相互作用を注意深く分析し、最適化問題を成功させるためにエージェントの動きを適切に制御することの重要性を浮き彫りにしています。このような予期せぬ失敗は、このような複雑さに効果的に対処できるアルゴリズムの開発において、さらなる研究と改善の動機付けとなるかもしれません。

テストに完全に失敗した他のアルゴリズムについては、テストベンチのプリントアウトは提供しません。

電磁アルゴリズム(EM)

EMアルゴリズムには、最適化中にエージェントの座標を更新できないという問題がありました。この場合、電磁引力の影響で粒子が崩壊し、エージェントが結合して塊になりました。

重力探索アルゴリズム(GSA)

重力の力によって、すべてのオブジェクトは一点に集まり、そこに留まることになりました。ブラックホールのように、中心に引き寄せられたのです。

人工蟻コロニーアルゴリズム(ACOm)

このアルゴリズムの問題点は、フェロモンの匂いに基づいて移動する蟻の移動経路がないことでした。この場合、蟻は1つの地点からスタートしたため、蟻と蟻の間の経路が形成されず、蟻の移動や行動の調整が困難になりました。

魚群検索(FSS)

C_AO_FSS:50;0.01;0.8
=============================
5 Hilly's; Func runs:10000; result:0.32457068874346456
25 Hilly's; Func runs:10000; result:0.27938488291267094
500 Hilly's; Func runs:10000; result:0.2343201202260512
=============================
5 Forest's; Func runs:10000; result:0.18964347858030822
25 Forest's; Func runs:10000; result:0.16146315945349987
500 Forest's; Func runs:10000; result:0.14145987387955847
=============================
5 Megacity's; Func runs:10000; result:0.0
25 Megacity's; Func runs:10000; result:0.0
500 Megacity's; Func runs:10000; result:0.0
=============================
All score:1.33084

このアルゴリズムでは、魚は前回と前々回の反復の適応度の差を利用して移動方向を決定します。Hilly関数とForest関数では、魚は風景の変化を感知しますが、Megacityの平坦な表面でアルゴリズムを実行すると、魚は混乱して方向感覚を失います。勾配のある滑らかな表面でスタートするときには、魚の驚くべき行動が起こります。しかし、スタート地点が穴の中ではなく、極値の頂点にある場合、魚はHilly関数やForest関数でも移動する可能性は低いです。

等方的焼きなまし(SIA)

C_AO_SIA:100:0.01:0.1
=============================
5 Hilly's; Func runs:10000; result:0.32958446477979136
25 Hilly's; Func runs:10000; result:0.32556359155723036
500 Hilly's; Func runs:10000; result:0.27262289744765306
=============================
5 Forest's; Func runs:10000; result:0.1940720887058382
25 Forest's; Func runs:10000; result:0.1935893813273654
500 Forest's; Func runs:10000; result:0.16409411642496857
=============================
5 Megacity's; Func runs:10000; result:0.0
25 Megacity's; Func runs:10000; result:0.0
500 Megacity's; Func runs:10000; result:0.0
=============================
All score:1.47953

等方性焼きなましアルゴリズムは、FSSの動作を彷彿とさせるが、大きな違いがあるユニークな特徴の組み合わせを示します。このアルゴリズムでは、出発点からのさまざまな方向への移動がFSSよりもエネルギッシュかつ能動的におこなわれ、最適解を見つけるための旺盛な創造性が感じられます。FSSと同様に、等方性焼きなましアルゴリズムは、適応度関数値の違いを利用して動きを誘導します。しかし、この運動は温度の漸減に影響され、時間の経過とともに粒子が空間のある地点で「凍結」します。

進化戦略((PO)ES)

C_AO_(PO)ES:100:10:0.025:8.0
=============================
5 Hilly's; Func runs:10000; result:0.32231823718105856
25 Hilly's; Func runs:10000; result:0.3228736374003839
500 Hilly's; Func runs:10000; result:0.2797261292300971
=============================
5 Forest's; Func runs:10000; result:0.19410491957153192
25 Forest's; Func runs:10000; result:0.1875135077472832
500 Forest's; Func runs:10000; result:0.15801830580073034
=============================
5 Megacity's; Func runs:10000; result:0.1292307692307692
25 Megacity's; Func runs:10000; result:0.12553846153846154
500 Megacity's; Func runs:10000; result:0.08198461538461577
=============================
All score:1.80131

このアルゴリズムは、すべてのテストを成功裏に完了できたリストの中で最初のものでした。「成功裏に完了」という言葉は、かなり断定的な表現に思えますが、実際には、少なくともゼロ以外の何らかの結果で各テストに合格しています。驚くべきことに、母集団は別々のグループに分かれる傾向があります。しかし、アルゴリズムの最初の熱狂は短時間しか続かず、エージェントは最初の最も近い丘ですぐに探索をやめてしまいます。おそらくすでに成功を収めていると想定しているためです。

特に興味深いのは、グループに分かれたエージェントが、それぞれの方向に移動することで観察者に楽観的な気持ちを抱かせるが、すぐに失望が訪れることです。あるグループが顕著な地位の向上を達成すると、他のすべてのグループがすぐに方向転換し、リーダーに向かって殺到します。こうした瞬間は、喜びから失望まで、さまざまな感情や思いを呼び起こします。このアルゴリズムにおけるエージェントの相互作用は、あらゆる驚きと変わりやすさを持つ人生に似ています。

モンキーアルゴリズム(MA)

C_AO_MA:50;0.01;0.9;50
=============================
5 Hilly's; Func runs:10000; result:0.32874856274894027
25 Hilly's; Func runs:10000; result:0.30383823957660194
500 Hilly's; Func runs:10000; result:0.2475564907358033
=============================
5 Forest's; Func runs:10000; result:0.20619304546795353
25 Forest's; Func runs:10000; result:0.1733511102614089
500 Forest's; Func runs:10000; result:0.14786586882293234
=============================
5 Megacity's; Func runs:10000; result:0.17538461538461542
25 Megacity's; Func runs:10000; result:0.1436923076923077
500 Megacity's; Func runs:10000; result:0.09555384615384681
=============================
All score:1.82218

このアルゴリズムの文脈では、たとえその方向が間違っていることが判明しても、サルは選ばれた方向にかなり孤立したやり方で動き続けます。このユニークな行動により、エージェントはより効率的に空間を探索し、出発点からより遠くへと広がっていきます。彼らは長い「未知への飛躍」を遂げ、これは特に離散Megacity関数では印象的です。この関数では、水平面上での適応度の増加がなく、遠隔地への到達が容易になります。

しかし、この探索能力にもかかわらず、利用可能な反復回数が終わりに近づくにつれ、主目的を達成するには不十分であることが判明します。アルゴリズムの魅力的な視覚的挙動に注目することは重要で、それはまさに群れをなすサルのカオス的な動きに似ています。これは、驚くべき光景を作り出し、さらなる研究と改良への関心を呼び起こします。

焼きなまし(SA)

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Hilly's; Func runs:10000; result:0.3266993983850477
25 Hilly's; Func runs:10000; result:0.30166692301946135
500 Hilly's; Func runs:10000; result:0.2545648344562219
=============================
5 Forest's; Func runs:10000; result:0.1939959116807614
25 Forest's; Func runs:10000; result:0.17721159702946082
500 Forest's; Func runs:10000; result:0.15159936395874307
=============================
5 Megacity's; Func runs:10000; result:0.2584615384615384
25 Megacity's; Func runs:10000; result:0.15292307692307697
500 Megacity's; Func runs:10000; result:0.10135384615384675
=============================
All score:1.91848

焼きなましアルゴリズムでは、その「相対的な」SIA（ちなみに、ランキングではずっと上位を占めている）とは異なり、挙動はよりカオス的で、可視化すると肉眼でもわかるほどです。しかし、この「焼きなまし」のカオス的な性質は、わずかに良い結果を得るのに役立っています。ただし、これらの成果は、このアルゴリズムを傑出したアルゴリズムの殿堂に不朽の名声を刻むほどのものではありません。改善は顕著であり、評価に値します。

ホタルアルゴリズム(FAm)

C_AO_FAm:50;0.1;0.3;0.1
=============================
5 Hilly's; Func runs:10000; result:0.32461162859403175
25 Hilly's; Func runs:10000; result:0.31981492599317524
500 Hilly's; Func runs:10000; result:0.25932958993768923
=============================
5 Forest's; Func runs:10000; result:0.2124297717365277
25 Forest's; Func runs:10000; result:0.21595138588924906
500 Forest's; Func runs:10000; result:0.1577543024576405
=============================
5 Megacity's; Func runs:10000; result:0.2246153846153846
25 Megacity's; Func runs:10000; result:0.1987692307692308
500 Megacity's; Func runs:10000; result:0.12084615384615457
=============================
All score:2.03412

FAは私の好きなアルゴリズムの1つです。その魅力は、美しい名前そのものだけでなく、その背景にあるエレガントなアイデア、そしてホタルのエレガントな行動にも表れています。この神秘的な発光生物は、瞬時に最寄りの極値に接近することができます。そのスピードは本当に追跡するのが難しいほどです。しかし、エージェントが極大値から抜け出せず、それ以上探索できず、大域的最適解に到達できない場合、この素晴らしいショーの後に停滞が起こります。

苛立たしいように見えるかもしれませんが、この停滞の瞬間がアルゴリズムを改善するチャンスを開くのです。局所的な落とし穴を克服するメカニズムを導入することで、FAは効率と精度の新たな地平を切り開くことができます。このように、ホタルが止まった瞬間でさえ、私たちは終わりを見るのではなく、新たな始まりを見るのです。この驚くべきアルゴリズムを改良し、開発する機会です。

細菌採餌最適化(BFO)

C_AO_BFO:50;0.01;0.3;100
=============================
5 Hilly's; Func runs:10000; result:0.3226339934200066
25 Hilly's; Func runs:10000; result:0.2925193012197403
500 Hilly's; Func runs:10000; result:0.2554221763445149
=============================
5 Forest's; Func runs:10000; result:0.2111053636851011
25 Forest's; Func runs:10000; result:0.20536292110181784
500 Forest's; Func runs:10000; result:0.15743855819242952
=============================
5 Megacity's; Func runs:10000; result:0.27999999999999997
25 Megacity's; Func runs:10000; result:0.19415384615384618
500 Megacity's; Func runs:10000; result:0.11735384615384695
=============================
All score:2.03599

細菌は適応度を増やさなくても移動力を維持することができるため、長距離を効率的に拡散することができます。この点では上で説明したアルゴリズムよりも優れています。この驚くべき現象は、特にMegacity環境において顕著です。細菌は驚異的な移動力と生存能力を発揮し、多様で複雑な環境にうまく適応することができます。この文脈において、細菌は新しい領域を開拓し、植民地化する真のパイオニアとなります。これは、生物の世界における細菌のユニークな能力と重要性を強調しています。

荷電系探索(CSS)

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Hilly's; Func runs:10000; result:0.38395827586082376
25 Hilly's; Func runs:10000; result:0.3048219687002418
500 Hilly's; Func runs:10000; result:0.2895158695448419
=============================
5 Forest's; Func runs:10000; result:0.2699906934238054
25 Forest's; Func runs:10000; result:0.19451237087137088
500 Forest's; Func runs:10000; result:0.18498127715987073
=============================
5 Megacity's; Func runs:10000; result:0.16923076923076924
25 Megacity's; Func runs:10000; result:0.13846153846153847
500 Megacity's; Func runs:10000; result:0.12276923076923094
=============================
All score:2.05824

意外なことに、このアルゴリズムは今回のテストではまったく予想外の力を発揮し、部外者の評価では下から2番目といういつもの指標を上回りました。今回、CSSは真ん中あたり（下から12番目）に終わりました。この変化の謎には独自の説明があります。アルゴリズムの方程式に従う静電荷は、電荷の半径内に入ると反発力と相互作用し始めます。これにより、周囲の検索空間に爆発的に拡散することができます。このプロセスは見た目に美しいだけでなく、実用的な応用の可能性も秘めています。

爆竹のような発射能力は、CSSの新たな可能性を切り開きます。例えば、このアルゴリズムを、他の最適化アルゴリズムでエージェントの最適な位置を決定するための解の「アイデア」の源と考えることもできるし、CSSが母集団の退化を避けるのに役立つハイブリッド解にうまく組み込むこともできます。このように、今回のテストにおけるCSSの予想外の成功は、感動的であるだけでなく、CSSの応用に新たな展望を開くものでもあります。

苗木の播種と育成アルゴリズム (SSG)

C_AO_SSG:50;0.3;0.5;0.4;0.1
=============================
5 Hilly's; Func runs:10000; result:0.3284133103606342
25 Hilly's; Func runs:10000; result:0.3246280774155864
500 Hilly's; Func runs:10000; result:0.2808547975998361
=============================
5 Forest's; Func runs:10000; result:0.194115963123826
25 Forest's; Func runs:10000; result:0.19754974771110584
500 Forest's; Func runs:10000; result:0.17111478002239264
=============================
5 Megacity's; Func runs:10000; result:0.25846153846153846
25 Megacity's; Func runs:10000; result:0.23353846153846156
500 Megacity's; Func runs:10000; result:0.14158461538461614
=============================
All score:2.13026

このアルゴリズムは、HillyやForestのような勾配関数でその潜在能力を発揮し、標準的なランキングで上位にランクされます。ただし、その効率は勾配に正の変化がある場合にのみ十分に発揮されます。それ以外の場合、母集団はすぐに劣化し、個体は1つの最良の局所点に収束します。これは、最適化アルゴリズムの結果を洗練するためにSSG法を使用する可能性を開きます。

5. 予備的結論

アルゴリズムに厳しい初期条件を課したこのユニークな研究実験では、探索空間におけるエージェントの標準的なランダムな一様配置の下では隠されたままだった、様々なアルゴリズムの魅力的な特徴を数多く発見しました。実生活でもそうであるように、生物は極限状態でその内なる可能性を発揮します。

また、いくつかのアルゴリズムが最上位から最下位に転落するなど、予想外のテスト結果も見られました。これにより、特殊な最適化問題におけるアルゴリズムの能力に基づいた使い方をよりよく理解することができるとともに、アルゴリズムの長所と短所をより深く理解することができます。また、各アルゴリズムのプラスとマイナスの面の両方がより明確になったことで、より効果的に長所を生かし、短所を補うことができるようになりました。さらに、この研究はハイブリッドアルゴリズムの作成に関する理解を深めることに貢献し、異なる手法の長所を組み合わせて最適な結果を得ることを可能にします。

次回も引き続き、アルゴリズムの性質と振る舞いについて考察し、結論を導き出したいと思います。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14352

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

DoEasy - サービス関数（第1回）：価格パターン

この記事では、時系列データを使用して価格パターンを検索するメソッドの開発に着手します。パターンには、どのようなタイプのパターンにも共通する、一定のパラメータセットがあります。この種のデータはすべて、基となる抽象パターンのオブジェクトクラスに集約されます。今回は、抽象パターンクラスとピンバーパターンクラスを作成します。

ニューラルネットワークが簡単に（第78回）：Transformerを用いたデコーダなしの物体検出器（DFFT）

この記事では、取引戦略の構築という問題を別の角度から見てみようと思います。将来の値動きを予測するのではなく、過去のデータの分析に基づいた取引システムの構築を試みます。

因果推論における傾向スコア

本稿では、因果推論におけるマッチングについて考察します。マッチングは、データセット内の類似した観測を比較するために使用されます。これは因果関係を正しく判定し、バイアスを取り除くために必要なことです。著者は、訓練されていない新しいデータではより安定する、機械学習に基づく取引システムを構築する際に、これがどのように役立つかを説明しています。傾向スコアは因果推論において中心的な役割を果たし、広く用いられています。

効率的な最適化のバックボーンとしての母集団アルゴリズムの基本クラス

この記事は、最適化手法の適用を単純化するために、様々な母集団アルゴリズムを1つのクラスにまとめるというユニークな研究の試みです。このアプローチは、ハイブリッド型を含む新しいアルゴリズム開発の機会を開くだけでなく、普遍的な基本テストスタンドの構築にもつながります。このスタンドは、特定のタスクに応じて最適なアルゴリズムを選択するための重要なツールとなります。