群体优化算法：抵抗陷入局部极值（第一部分）

MetaTrader 5 — 示例 | 14 十一月 2024, 09:41

406

Andrey Dik

1.概述

这是一项独特的研究，这个想法是我在回答讨论我的一篇文章时出现的问题时产生的。我希望读者能够欣赏这部作品的价值和原创性。

这项研究的想法和理念源自我对这个主题的深入研究和对科学研究的热情。我相信这项工作可能会成为算法优化领域的重要贡献，吸引研究人员和从业者的关注。

在这个实验中，我建议进行一项测试，旨在评估算法对陷入局部极值的抵抗力，而不是在整个搜索空间的第一次迭代中随机放置代理，而是将它们放置在全局最小值中。实验的目的是寻找全局最大值。

在这种情况下，算法的所有搜索代理都位于一个点上，我们面临着一个有趣的现象 - 退化群体。这就像时间凝固的瞬间，群体的多样性降至最低。虽然这种情况是人为的，但它使我们能够获得有趣的结论并评估减少群体多样性对结果的影响。该算法应该能够摆脱这种瓶颈并实现全局最大值。

在这种优化算法的压力测试中，我们可以揭示代理交互、合作或竞争的秘密，并了解这些因素如何影响实现最优的速度。这种分析为理解群体多样性对于算法有效运行的重要性开辟了新的视野，并使我们能够制定维持这种多样性的策略，以取得更好的结果。

为了开展实验，我们需要首先在算法外部使用全局最小值的坐标强制初始化代理的坐标，然后再测量第一个历元的适应度函数。

这样的实验将使我们能够评估对极端困难条件的抵抗力和克服限制的能力。

2.设定任务

想象一下你处在一个深谷，周围是浓重的黑暗。你的眼睛被蒙住了，使你无法看清周围的世界。你感觉到一阵冷风吹过你的脸，你的心脏剧烈跳动，仿佛要冲出你的胸膛，强化着你的焦虑和不确定性。

你从迈出第一步开始前进。你的脚感觉到地面，你逐渐沿着山谷移动，每一步都更接近自由，你的头脑充满了决心。最后，当你到达边缘时，一幅令人惊叹的景色在你面前展开。平坦的平原就像一块无尽的画布在你面前展开。远处孤立的陡峭悬崖唤起了人们惊奇和挑战的混合感觉。然而，尽管有如此美丽的全景，你仍然看不到它。

您决定依靠自己的感觉和直觉来确定移动的方向，并到达最高悬崖的顶部。现在想象一下，基于 Megacity 测试离散函数的算法面临这个艰巨的任务。这种算法和你一样，受到其能力的限制，无法直接看到或感知环境。它必须运用其计算技能和逻辑来决定到达最高悬崖顶部的最佳路径。因此，这个关于 Megacity 测试离散函数的问题对于像你一样面临不确定性的算法来说是一个艰难的挑战。

然而，在这种情况下，Hilly 函数和 Forest 函数也带来了一个难题。让我们看一下这些熟悉的函数，以了解算法即将完成的任务的复杂性。

Hilly 之路

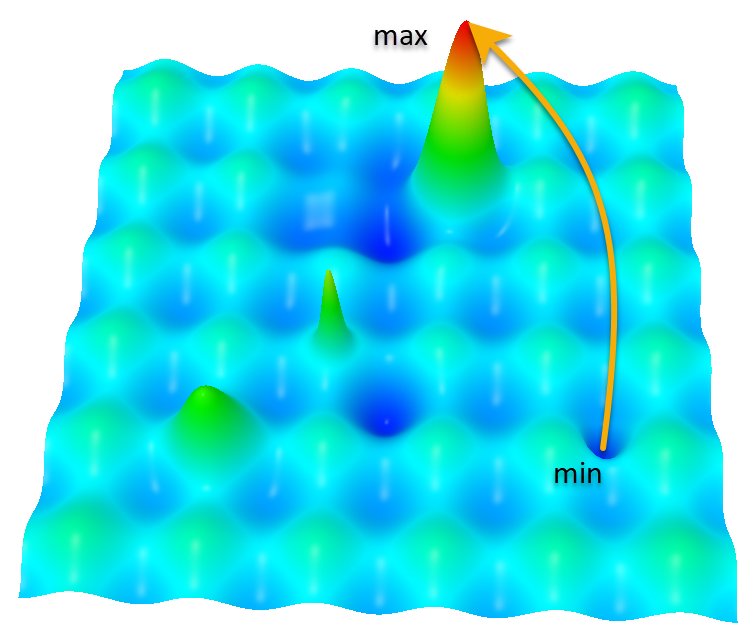
Hilly 函数

Forest 之路

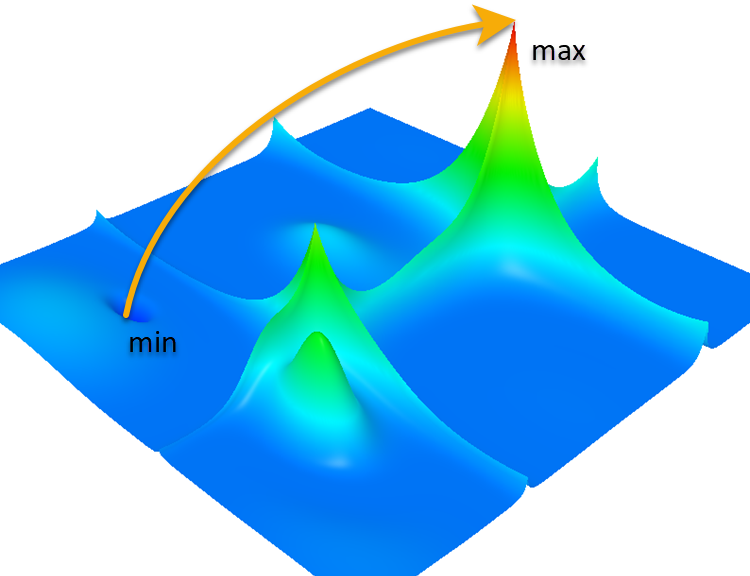
Forest 函数

Megacity 之路

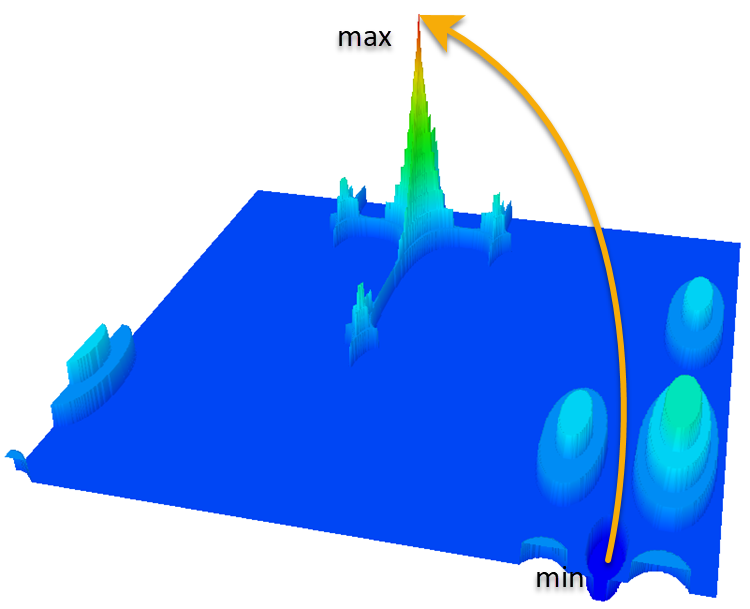
Megacity 函数

想象一下，你是一个算法，是计算能力和逻辑思维的体现。你不仅仅是纸上枯燥的代码或方程式，你活了过来，扮演了研究人员的角色。你的脑海里充满了问题和假设，你努力解决摆在你面前的谜团。你沉浸在数据和信息的世界中，分析、比较和突出关键因素，而你的计算能力正在全力以赴。你开始构建不同的模型和场景，探索解决问题的可能途径，尝试不同的组合和选项，你的创造力会带来新的发现。但解决问题的道路并不总是一帆风顺的。你面临着看似无法克服的挑战，但你不会放弃。你克服一个又一个的障碍和干扰，每一步都更接近你的目标。最后，当你找到解决方案时，就像突然顿悟一样。你的头脑被理解的明亮之光照亮，你看到所有的部分都各就各位。

在这幅图的背景下，优化算法面临的任务是最大化具有许多局部最大值的复杂拓扑的函数。以下是该问题的更详细描述：

局部最大值。从起点（标记为“最小值”）到终点（标记为“最大值”）的途中，该算法会遇到许多局部最大值。这可能导致算法陷入局部陷阱而无法达到全局极值。这是优化问题中的一个主要问题。例如，基于梯度下降的算法倾向于“爬升”到最近的最大值，如果它是局部最大值，那么它们就会“卡住”。

高维度。如果我们考虑多维空间中的函数，那么局部最大值的数量会急剧增加，这使问题变得复杂。在高维度中，空间变得“空”，由于算法没有任何可以依附的东西，这让问题变得更加困难。

函数表面复杂性。函数表面可能非常复杂，具有许多峰和谷，这使得优化过程更加耗时。这要求算法能够跳过局部最大值并攀爬到全局最大值。

收敛与收敛速度。由于终点与起点之间的距离较大，算法收敛到函数最大值的速度可能会变慢，可能需要额外的迭代才能达到目标。

区域研究。该算法可能需要额外探索该区域以寻找全局最大值，这会导致计算复杂度增加。

为了总结问题的描述，我们可以强调典型优化情况和情况之间的区别，在典型优化情况下，代理在均匀分布的搜索空间中开始移动，而在这种情况下，不仅需要“揭示”现有信息，而且需要探索和扩展他们的知识和经验到未知领域。在我们已在之前的优化会话中获得一些解决方案，并且我们希望从这个解决方案“点”开始，而不是简单地具体化现有信息的情况下，以这种方式设定问题变得特别有价值。

3.代码改动

为了将代理放置在某一点，将测试函数全局最小值的坐标分配给适当的群体代理。一般来说，这个过程是这样的：

if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].c [i * 2]     = f.GetMinFuncX ();
      AO.a [set].c [i * 2 + 1] = f.GetMinFuncY ();
    }
  }
}

对于某些算法来说，简单地将代理放置在搜索空间中的某一点是不够的，还要输入附加信息。例如在 SDSm 算法的情况下，还需要为每个坐标指定对应的扇区。另一方面，当使用 BGA 算法时，需要将坐标值从实数表示转换为二进制表示，这需要对算法代码进行额外的更改。对于 BGA，代理在某一点的位置将如下所示：

//==================
if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].DoubleToGene (f.GetMinFuncX (), i * 2);
      AO.a [set].DoubleToGene (f.GetMinFuncY (), i * 2 + 1);
    }

    AO.a [set].ExtractGenes ();
  }
}
//==================

从该代码可以看出，坐标到基因二进制代码的必要转换就发生在这里。我目前正在致力于统一将代理放置在所需坐标的过程。本研究展示了源代码的当前状态。由于其架构特性，几乎每种算法都需要定制的测试平台。请继续关注新文章以获取有关算法的更新。简化在群体中放置坐标的过程以及它们的统一，以达到共同的标准。

4.算法

继续分析我们独特测试中算法的行为，我们开始讨论表现最差的算法。尤其令人惊讶的是，其中一些之前在标准测试中排名相当高的算法在我们这项不寻常的测试中表现不佳。这表明算法的成功不仅取决于其整体效率，还取决于其适应问题特定条件和特征的能力。这些意想不到的结果凸显了进行各种测试和研究的重要性，以便更深入地了解优化算法在不同环境下的性能。

以下是算法运行的报告，应按如下方式阅读：

C_AO_FSS:50;0.01;0.8 - 算法名称和外部参数
5 Hilly's - 测试函数的名称及其在测试中的编号
Func runs:10000 - 运行次数
result:0.32457068874346456 - 获得的结果，其中 0.0 是测试函数的最小值，1.0 是最大值。值越高越好
All score:1.33084 - 得分的总值，值越高越好

差异进化（DE）

C_AO_DE:50;0.2;0.8
=============================
5 Hilly's; Func runs:10000; result：0.0
25 Hilly's；Func runs：10000; result：0.0
500 Hilly's；Func runs：10000; result：0.0
=============================
5 Forest's; Func runs：10000; result：0.0
25 Forest's; Func runs：10000; result：0.0
500 Forest's; Func runs：10000; result：0.0
=============================
5 Megacity's; Func runs:10000; result：0.0
25 Megacity's; Func runs:10000; result：0.0
500 Megacity's；Func runs：10000; result：0.0
=============================
All score:0.00000

不幸的是，排名表中即使是最强大的算法之一也完全未能通过我们的测试。在这种情况下，代理们会发现自己停滞不前，无法移动。失败的原因是，每个代理的新位置都依赖于其他三个代理的位置，如果他们最终都位于同一点，那么它们都无法更新他们的坐标。这种情况强调了仔细分析代理之间的相互作用并充分控制其运动以成功完成优化问题的重要性。此类意外故障可能会促使进一步研究和改进能够有效处理此类复杂性的算法。

对于其他完全未通过测试的算法，我不会提供测试台的打印输出。

电磁算法（EM）

EM 算法在优化过程中遇到了无法更新代理坐标的问题。在这种情况下，粒子在电磁引力的影响下崩溃，使得代理结合成一个块。

引力搜索算法（GSA）

引力导致所有物体都聚集在一点并停留在那里 - 它们被吸引到中心，类似于黑洞。

人工蚁群算法（ACOm）

该算法的问题在于缺乏根据信息素气味移动的蚂蚁的移动路径。在这种情况下，由于蚂蚁都是从一个点出发，它们之间的路径没有形成，导致蚂蚁的行动在移动和协调上遇到困难。

鱼群搜索 (FSS)

C_AO_FSS:50;0.01;0.8
=============================
5 Hilly's; Func runs:10000; result：0.32457068874346456
25 Hilly's；Func runs：10000; result：0.27938488291267094
500 Hilly's；Func runs：10000; result：0.2343201202260512
=============================
5 Forest's; Func runs：10000; result：0.18964347858030822
25 Forest's; Func runs：10000; result：0.16146315945349987
500 Forest's; Func runs：10000; result：0.14145987387955847
=============================
5 Megacity's; Func runs:10000; result：0.0
25 Megacity's; Func runs:10000; result：0.0
500 Megacity's；Func runs：10000; result：0.0
=============================
All score:1.33084

在该算法中，鱼利用上一次迭代和前一次迭代之间的适应度差异来确定其运动方向。虽然在 Hilly 和 Forest 函数中鱼可以感知地貌的变化，但在 Megacity 的平坦表面上运行算法会使鱼感到困惑，使它们失去方向感。当鱼开始在具有坡度的光滑表面上活动时，就会发生令人惊奇的行为。然而，如果起点位于局部极值的顶部，而不是在洞中，那么即使在 Hilly 和 Forest 函数中，鱼也不太可能移动。

模拟各向同性退火（SIA）

C_AO_SIA:100:0.01:0.1
=============================
5 Hilly's; Func runs:10000; result：0.32958446477979136
25 Hilly's；Func runs：10000; result：0.32556359155723036
500 Hilly's；Func runs：10000; result：0.27262289744765306
=============================
5 Forest's; Func runs：10000; result：0.1940720887058382
25 Forest's; Func runs：10000; result：0.1935893813273654
500 Forest's; Func runs：10000; result：0.16409411642496857
=============================
5 Megacity's; Func runs:10000; result：0.0
25 Megacity's; Func runs:10000; result：0.0
500 Megacity's；Func runs：10000; result：0.0
=============================
All score:1.47953

模拟各向同性退火算法表现出独特的特征组合，让人联想到 FSS 操作，但又有显著差异。在该算法中，从起点向不同方向的移动比在FSS中更有活力和积极性，在寻找最优解的过程中营造出一种充满活力的创造力的感觉。与FSS类似，各向同性退火模拟算法利用适应度函数值的差异来引导运动。然而，这里的运动受到温度逐渐下降的影响，随着时间的推移，导致粒子在空间的某些点“冻结”。

进化策略（(PO)ES）

C_AO_(PO)ES:100:10:0.025:8.0
=============================
5 Hilly's; Func runs:10000; result：0.32231823718105856
25 Hilly's；Func runs：10000; result：0.3228736374003839
500 Hilly's；Func runs：10000; result：0.2797261292300971
=============================
5 Forest's; Func runs：10000; result：0.19410491957153192
25 Forest's; Func runs：10000; result：0.1875135077472832
500 Forest's; Func runs：10000; result：0.15801830580073034
=============================
5 Megacity's; Func runs:10000; result：0.1292307692307692
25 Megacity's; Func runs:10000; result：0.12553846153846154
500 Megacity's；Func runs：10000; result：0.08198461538461577
=============================
All score:1.80131

该算法是列表中第一个能够成功完成所有测试的算法。尽管“成功完成”一词的使用似乎相当武断，但事实上它通过了每一项检查，并且至少获得了除零之外的一些结果。值得注意的是，群体有分成不同组别的趋势。然而，算法最初的热情只能持续很短的时间 - 代理很快就会停止在第一个最近的山丘上搜索，可能认为它们已经取得了成功。

特别有趣的是，一开始，代理分成几组，通过向不同的方向移动，激发了观察者的乐观情绪，但失望很快就来了：一旦其中一个组在其位置上取得明显的改善，所有其他组就会立即改变方向，冲向领导者。这些时刻唤起了复杂的感受和情绪 - 从喜悦到失望。该算法中代理的交互类似于生活，充满惊喜和多变。

猴子算法（MA）

C_AO_MA:50;0.01;0.9;50
=============================
5 Hilly's; Func runs:10000; result：0.32874856274894027
25 Hilly's；Func runs：10000; result：0.30383823957660194
500 Hilly's；Func runs：10000; result：0.2475564907358033
=============================
5 Forest's; Func runs：10000; result：0.20619304546795353
25 Forest's; Func runs：10000; result：0.1733511102614089
500 Forest's; Func runs：10000; result：0.14786586882293234
=============================
5 Megacity's; Func runs:10000; result：0.17538461538461542
25 Megacity's; Func runs:10000; result：0.1436923076923077
500 Megacity's；Func runs：10000; result：0.09555384615384681
=============================
All score:1.82218

在该算法的背景下，猴子会继续以相当孤立的方式朝着选定的方向移动，即使那个方向被证明是错误的。这种独特的行为使得代理能够更有效地探索空间，并从起点扩散得更远。它们向未知领域迈出了一大步，在离散 Megacity 函数中尤其令人印象深刻，其中水平表面上没有适应度增量，这有助于到达遥远的区域。

然而，尽管具有这种探索能力，但随着可用迭代次数的结束，它仍不足以实现主要目标。值得注意的是，该算法具有令人着迷的视觉行为，它真正类似于猴群中混乱的运动，创造了令人惊叹的奇观，并激发了人们对其进一步研究和改进的兴趣。

模拟退火（SA）

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Hilly's; Func runs:10000; result：0.3266993983850477
25 Hilly's；Func runs：10000; result：0.30166692301946135
500 Hilly's；Func runs：10000; result：0.2545648344562219
=============================
5 Forest's; Func runs：10000; result：0.1939959116807614
25 Forest's; Func runs：10000; result：0.17721159702946082
500 Forest's; Func runs：10000; result：0.15159936395874307
=============================
5 Megacity's; Func runs:10000; result：0.2584615384615384
25 Megacity's; Func runs:10000; result：0.15292307692307697
500 Megacity's；Func runs：10000; result：0.10135384615384675
=============================
All score:1.91848

在模拟退火算法中，与其“相对” SIA（顺便说一下，它在排名中占据更高的位置）不同，其行为更加混乱，甚至在可视化中肉眼可见。然而，“退火”模拟的这种混乱性质有助于实现稍好一些的结果。然而，这些成就并不足以让该算法在优秀算法名人堂中永垂不朽，但是其进步是显而易见的，值得认可。

萤火虫算法（FAm）

C_AO_FAm:50;0.1;0.3;0.1
=============================
5 Hilly's; Func runs:10000; result：0.32461162859403175
25 Hilly's；Func runs：10000; result：0.31981492599317524
500 Hilly's；Func runs：10000; result：0.25932958993768923
=============================
5 Forest's; Func runs：10000; result：0.2124297717365277
25 Forest's; Func runs：10000; result：0.21595138588924906
500 Forest's; Func runs：10000; result：0.1577543024576405
=============================
5 Megacity's; Func runs:10000; result：0.2246153846153846
25 Megacity's; Func runs:10000; result：0.1987692307692308
500 Megacity's；Func runs：10000; result：0.12084615384615457
=============================
All score:2.03412

FA 是我最喜欢的算法之一。它的吸引力不仅体现在美丽的名字本身，还体现在它背后优雅的理念，以及萤火虫优雅的行为。这些神秘的发光生物能够瞬间接近最近的局部极值，速度之快让人难以追踪它们。然而，当代理发现自己陷入局部最大值，无法进一步探索并达到全局最优时，这场精彩的表演就会陷入停滞。

尽管看起来令人沮丧，但这种停滞却为改进算法提供了机会。通过引入机制来克服局部缺陷，FA 可以实现效率和准确性的新高度。因此，即使在萤火虫停止的瞬间，我们看到的不仅仅是结束，而是一个新开始 - 改进和发展这种神奇算法的机会。

细菌觅食优化 (BFO)

C_AO_BFO:50;0.01;0.3;100
=============================
5 Hilly's; Func runs:10000; result：0.3226339934200066
25 Hilly's；Func runs：10000; result：0.2925193012197403
500 Hilly's；Func runs：10000; result：0.2554221763445149
=============================
5 Forest's; Func runs：10000; result：0.2111053636851011
25 Forest's; Func runs：10000; result：0.20536292110181784
500 Forest's; Func runs：10000; result：0.15743855819242952
=============================
5 Megacity's; Func runs:10000; result：0.27999999999999997
25 Megacity's; Func runs:10000; result：0.19415384615384618
500 Megacity's；Func runs：10000; result：0.11735384615384695
=============================
All score:2.03599

细菌无需提高适应度就能保持其流动性的能力是其能有效地长距离传播的关键因素，在这方面的表现优于上面讨论的算法。这一神奇现象在 Megacity 环境中尤为明显，细菌表现出惊人的流动性和生存能力，使它们能够成功适应多样化和复杂的环境。在这种背景下，细菌成为真正的先驱者，探索和殖民新领土，这强调了它们在生物世界中的独特能力和重要性。

充电系统搜索 (CSS)

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Hilly's; Func runs:10000; result：0.38395827586082376
25 Hilly's；Func runs：10000; result：0.3048219687002418
500 Hilly's；Func runs：10000; result：0.2895158695448419
=============================
5 Forest's; Func runs：10000; result：0.2699906934238054
25 Forest's; Func runs：10000; result：0.19451237087137088
500 Forest's; Func runs：10000; result：0.18498127715987073
=============================
5 Megacity's; Func runs:10000; result：0.16923076923076924
25 Megacity's; Func runs:10000; result：0.13846153846153847
500 Megacity's；Func runs：10000; result：0.12276923076923094
=============================
All score:2.05824

令人惊讶的是，这个算法在这次测试中表现得完全出乎意料，超越了其通常的指标，在评级中位列外部算法中倒数第二。这次，CSS 排名居中（倒数第十二）。这种转变的奥秘有其自己的解释：静电荷遵循算法方程，当它们落在电荷半径范围内时，开始与排斥力相互作用，这使它们能够在周围的搜索空间中爆炸性地扩散。这一过程不仅具有视觉吸引力，而且具有实际应用的潜力。

像爆竹一样发射的能力为 CSS 开辟了新的可能性。例如，我们可以将该算法视为确定其他优化算法的代理最佳位置的解决方案“思想”的来源，或者我们可以成功地将其集成到混合解决方案中，其中 CSS 将有助于避免群体退化。因此，CSS在这次测试中意外的成功不仅令人鼓舞，而且为其应用开辟了新的视角。

幼苗播种及成长算法（SSG）

C_AO_SSG:50;0.3;0.5;0.4;0.1
=============================
5 Hilly's; Func runs:10000; result：0.3284133103606342
25 Hilly's；Func runs：10000; result：0.3246280774155864
500 Hilly's；Func runs：10000; result：0.2808547975998361
=============================
5 Forest's; Func runs：10000; result：0.194115963123826
25 Forest's; Func runs：10000; result：0.19754974771110584
500 Forest's; Func runs：10000; result：0.17111478002239264
=============================
5 Megacity's; Func runs:10000; result：0.25846153846153846
25 Megacity's; Func runs:10000; result：0.23353846153846156
500 Megacity's；Func runs：10000; result：0.14158461538461614
=============================
All score:2.13026

该算法在梯度函数（如 Hilly 或 Forest）上展现了其潜力，并在标准排名中名列前茅。然而，只有在梯度出现正向变化的情况下，其效率才能充分体现出来。否则，群体数量会迅速退化，个体会收敛到一个最佳局部点，这为使用 SSG 方法细化优化算法的结果提供了可能性。

5.初步结论

在这个独特的研究实验中，算法受到严格的初始条件的限制，我们发现了各种算法的许多令人着迷的特征，这些特征隐藏在搜索空间中代理的标准随机均匀放置之下。正如现实生活中一样，生物在极端条件下也会显露出其内在的潜力。

我们还看到一些算法出现了意外的测试结果，包括从顶部跌至底部。这使我们能够更好地理解如何根据算法的能力在专门的优化问题中使用算法，并更深入地了解算法的优势和劣势。它还更清楚地揭示了每种算法的优点和缺点，从而使它们能够更有效地发挥各自的优势并弥补各自的弱点。此外，该研究有助于更好地理解混合算法的创建，从而可以结合不同方法的优势以获得最佳结果。

在下一篇文章中，我们将继续考虑算法的属性和行为，并得出结论。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14352

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.