Algoritmos de optimización de la población: Resiliencia ante el estancamiento en los extremos locales (Parte I)

Contenido:

1. Introducción
2. Planteamiento de la tarea
3. Código, cambios necesarios
4. Discusión de los algoritmos
5. Resultados preliminares

1. Introducción

El presente es un estudio único, cuya idea se me ocurrió al responder a las preguntas que surgieron durante una discusión sobre uno de mis artículos. Espero que los lectores sepan apreciar el valor y la originalidad de este artículo.

Las reflexiones e ideas que me ha impulsado a esta investigación son fruto de una profunda inmersión en el tema y de la pasión por la investigación científica, y creo que este trabajo puede resultar una contribución importante al campo de la optimización algorítmica, atrayendo la atención de investigadores y profesionales.

En este experimento, le propongo realizar una prueba destinada a evaluar la estabilidad de los algoritmos ante el atascamiento en los extremos locales y, en lugar de colocar aleatoriamente a los agentes en la primera iteración sobre todo el campo del espacio de búsqueda, colocarlos en el mínimo global. La tarea del experimento consistirá en encontrar el máximo global.

En un escenario así, en el que todos los agentes de búsqueda del algoritmo se ubican en un único punto, nos encontramos con un fenómeno interesante: una población degenerada. Esto resulta similar a un momento de congelación temporal en el que la diversidad de una población se reduce al mínimo. Aunque este escenario sea artificial, aporta datos interesantes y nos permite evaluar el impacto de la reducción de la diversidad en la población sobre el resultado. El algoritmo debe ser capaz de escapar de ese cuello de botella y alcanzar un máximo global.

En este tipo de pruebas de estrés para algoritmos de optimización, podemos desvelar los misterios de la interacción, la cooperación o la competición entre agentes, y comprender cómo influyen estos factores en la velocidad a la que se alcanza el óptimo. Estos análisis abren nuevos caminos para comprender la importancia de la diversidad en una población para que los algoritmos funcionen de forma eficaz, y nos permiten desarrollar estrategias para mantener esta diversidad y obtener mejores resultados.

Para el experimento, necesitaremos inicializar de forma previa las coordenadas de los agentes forzosamente fuera respecto al algoritmo, usando las coordenadas del mínimo global, antes de medir la función de aptitud en la primera época.

Este experimento evaluará la resistencia a condiciones extremadamente difíciles, así como la capacidad de superar dichas limitaciones.

2. Planteamiento de la tarea

Imagine que se encuentra en la profunda hondonada de un valle rodeado de una densa oscuridad. Sus ojos están vendados, privándole de la capacidad de ver el mundo que le rodea. Siente un viento frío que le cala el rostro y su corazón late con fuerza, como si quisiera salirse del pecho, aumentando su ansiedad e incertidumbre.

Empieza a moverse dando el primer paso hacia delante. Sus pies sienten el suelo y poco a poco avanza por la hondonada, cada paso le acerca más a la libertad y su mente se llena de determinación. Finalmente, al llegar al borde, se abre ante usted una vista impresionante. Una llanura lisa como el cristal se extiende ante usted como un lienzo sin límites, los escarpados acantilados que se alzan en la distancia evocan sentimientos encontrados de asombro y desafío. Sin embargo, a pesar de la existencia de este hermoso panorama, usted aún no puede verlo.

Así que decide confiar en sus sentidos e intuición para determinar la dirección que debe tomar para llegar a la cima del acantilado más alto. Imaginemos ahora que a esta difícil tarea se enfrenta un algoritmo sobre la función discreta de prueba Megacity. Este algoritmo, al igual que usted, está limitado por sus capacidades y no puede ver ni percibir el entorno directamente. El algoritmo debe utilizar su capacidad de cálculo y su lógica para decidir cuál es el mejor camino hacia la cima del acantilado más alto. Por consiguiente, este problema sobre la función discreta de prueba Megacity será un reto difícil para un algoritmo que, como usted, se enfrenta a la dificultad y la incertidumbre.

Sin embargo, las funciones Hilly y Forest también plantean un problema difícil en un entorno de esta clase. Vamos a echar un vistazo desde fuera a estas funciones tan familiares para apreciar la complejidad de la tarea que tienen por delante los algoritmos.

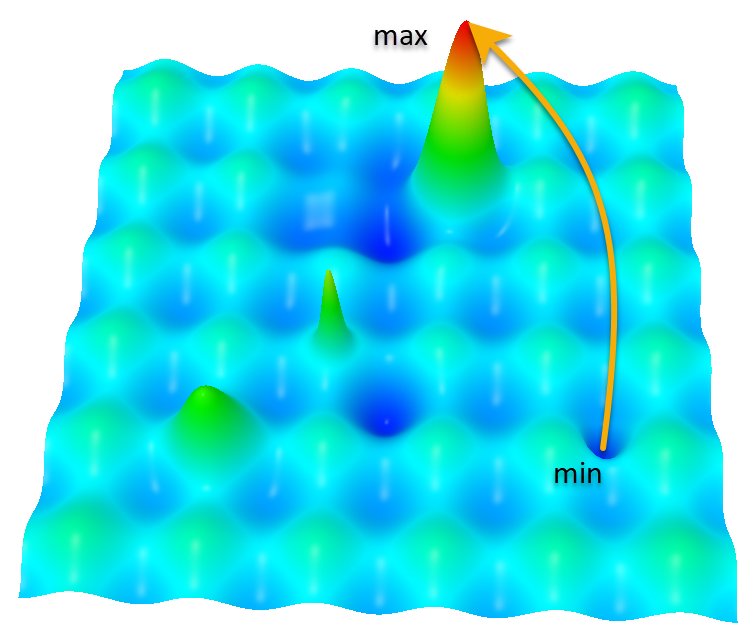
Función Hilly

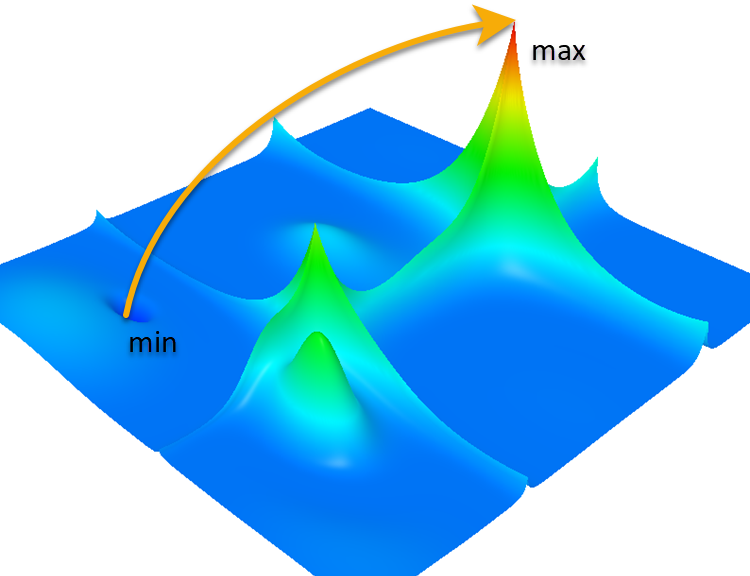
Función Forest

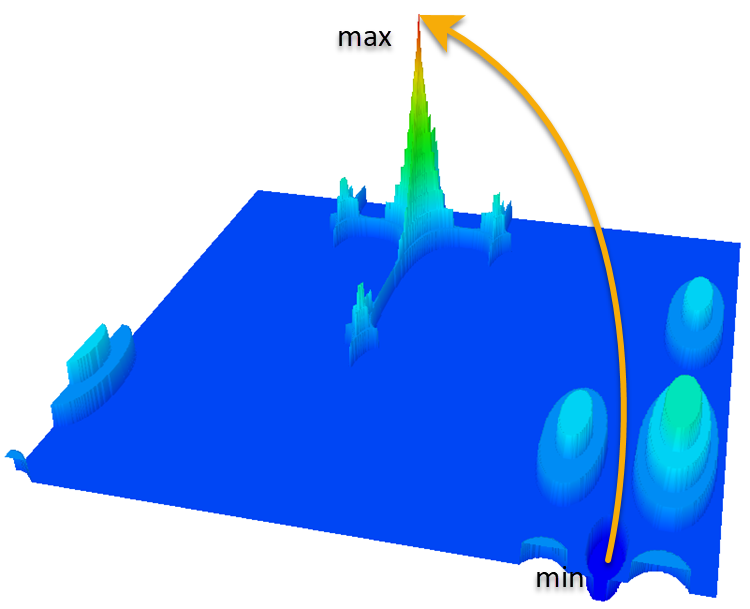
Función Megacity

Imagine que es un algoritmo, la personificación de la potencia de cálculo y el pensamiento lógico. Usted no representa solo frías líneas de código o fórmulas sobre un papel, todo lo contrario: cobra vida y asume el papel de investigador. Su mente se llena de preguntas e hipótesis, y se esfuerza por resolver el misterio que se presenta ante usted. Está inmerso en un mundo de datos e información, analizando, comparando y destacando factores clave, con sus capacidades informáticas trabajando a pleno rendimiento. Empieza a construir diferentes modelos y escenarios, a explorar posibles formas de resolver el problema y a probar distintas combinaciones y opciones, y su creatividad le lleva a nuevos descubrimientos. Pero el camino hacia la solución no siempre es fácil. Se enfrenta a retos y complejidades que pueden parecer insuperables, pero no se rinde. Supera los obstáculos y las distracciones uno a uno, acercándose a su objetivo con cada paso. Finalmente, cuando encuentra una solución, es como un momento de iluminación. Su mente se llena con la brillante luz de la comprensión y ve que todos los elementos encajan. ¿Lo ha entendido?

En el contexto de esta imagen, el algoritmo de optimización se enfrenta al problema de maximizar una función que posee una topología compleja con muchos máximos locales. Aquí tenemos una descripción más detallada del problema:

• Máximos locales. En el camino desde el punto inicial (etiquetado como "min") hasta el punto final (etiquetado como "max"), el algoritmo encuentra muchos máximos locales, y esto puede hacer que el algoritmo se quede "atascado" en una trampa local sin alcanzar el extremo global. Este es un problema importante en los problemas de optimización, por ejemplo, para los algoritmos basados en el descenso de gradiente; normalmente "suben" al máximo más cercano, y si este es un máximo local, entonces se quedan "atascados".

• Alta dimensionalidad. Si consideramos una función en un espacio multidimensional, el número de máximos locales aumentará drásticamente, lo cual complica el problema. En dimensiones elevadas, el espacio se vuelve "vacío", lo cual dificulta aún más el problema debido a que el algoritmo no tiene nada a lo que aferrarse.
  

• Complejidad de la superficie de la función. La superficie de la función puede ser muy compleja, con muchos picos y valles, lo que hace que el proceso de optimización lleve más tiempo. Para ello, el algoritmo deberá ser capaz de saltar los máximos locales y ascender hasta el máximo global. 

• Convergencia y tasa de convergencia. La convergencia del algoritmo al máximo de la función puede ralentizarse debido a la distancia del punto final al punto inicial, lo cual puede requerir iteraciones adicionales para alcanzar el objetivo.

• Estudio del dominio. Es posible que el algoritmo tenga que explorar más a fondo el dominio en busca de un máximo global, factor que puede aumentar la complejidad computacional.

Para resumir la descripción del problema, existe una diferencia entre una situación típica de optimización, en la que los agentes comienzan su movimiento en el espacio de búsqueda uniformemente distribuidos, y una situación en la que no es necesario simplemente "descubrir" información ya disponible, sino más bien explorar y ampliar nuestros conocimientos y experiencia en partes inexploradas del espacio. Esta formulación del problema resulta especialmente útil cuando ya disponemos de algunas soluciones obtenidas en sesiones de optimización anteriores, y pretendemos partir de este "punto" de la solución, en lugar de limitarnos a cristalizar la información disponible.

3. Código, cambios necesarios

Para colocar los agentes en un punto, asignaremos las coordenadas del mínimo global de la función de prueba a las coordenadas correspondientes de los agentes de la población. En términos generales, este procedimiento será el siguiente:

if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].c [i * 2]     = f.GetMinFuncX ();
      AO.a [set].c [i * 2 + 1] = f.GetMinFuncY ();
    }
  }
}

Para algunos algoritmos, no bastará con situar a los agentes en un punto del espacio de búsqueda, sino que se necesitará información adicional. Por ejemplo, en el caso del algoritmo SDSm, también deberá especificarse el sector correspondiente a cada coordenada. Por otro lado, al utilizar el algoritmo BGA, deberemos convertir los valores de las coordenadas de una representación real a una representación binaria, lo cual implicará cambios adicionales en el código del algoritmo. Para BGA, la ubicación de los agentes en un único punto tendrá el aspecto que vemos:

//==================
if (epochCNT == 1)
{
  for (int set = 0; set < ArraySize (AO.a); set++)
  {
    for (int i = 0; i < funcCount; i++)
    {
      AO.a [set].DoubleToGene (f.GetMinFuncX (), i * 2);
      AO.a [set].DoubleToGene (f.GetMinFuncY (), i * 2 + 1);
    }

    AO.a [set].ExtractGenes ();
  }
}
//==================

Como se desprende de este código, aquí sucederá la transformación necesaria de las coordenadas en un código binario de genes. Actualmente estoy trabajando para unificar el proceso de colocación de agentes en las coordenadas correctas. El material que estudiamos hoy presenta los códigos fuente en su estado actual. Casi todos los algoritmos requerían un banco de pruebas individual debido a las peculiaridades de su arquitectura. Permanezca atento a los nuevos artículos que se publiquen para estar al día de los algoritmos. Simplificación y unificación del proceso de colocación de coordenadas en la población.

4. Discusión de los algoritmos

Pasando ya al análisis del comportamiento de los algoritmos dentro de nuestras pruebas únicas, procederemos a discutir los algoritmos que han obtenido peores resultados. Lo que resulta especialmente sorprendente es que algunos de ellos, que antes habían ocupado puestos bastante altos en las clasificaciones de las pruebas estándar, han obtenido malos resultados en nuestra inusual prueba. Esto sugiere que el éxito de los algoritmos puede depender no solo de su eficacia general, sino también de su capacidad para adaptarse a condiciones específicas y a las características de la tarea. Estos resultados inesperados ponen de relieve la importancia de realizar diversas pruebas y estudios para conocer mejor el rendimiento de los algoritmos de optimización en contextos distintos.

A continuación le mostramos los informes del funcionamiento de los algoritmos:

• C_AO_FSS:50;0.01;0.8 - nombre y parámetros externos del algoritmo
  
• 5 Hilly's - nombre de la función de prueba y su número en la prueba
  
•  Func runs: 10000 - número de inicios
  
• result: 0.32457068874346456 - resultado obtenido, donde 0.0 es el mínimo de la función de prueba y 1.0 es el máximo, cuanto mayor sea el valor, mejor.
  
• All score: 1,33084 - valor total de los puntos obtenidos, cuanto mayor sea el valor, mejor
  

Evolución diferencial, DE

C_AO_DE:50;0.2;0.8
=============================
5 Hilly's; Func runs: 10000; result: 0.0
25 Hilly's; Func runs: 10000; result: 0.0
500 Hilly's; Func runs: 10000; result: 0.0
=============================
5 Forest's; Func runs: 10000; result: 0.0
25 Forest's; Func runs: 10000; result: 0.0
500 Forest's; Func runs: 10000; result: 0.0
=============================
5 Megacity's; Func runs: 10000; result: 0.0
25 Megacity's; Func runs: 10000; result: 0.0
500 Megacity's; Func runs: 10000; result: 0.0
=============================
All score: 0.00000

Por desgracia, incluso uno de los algoritmos más potentes de la tabla de clasificación ha fracasado completamente en nuestra prueba. En este caso, los agentes se han quedado estancados, sin moverse de su posición. La razón de este fallo es que cada nueva posición de un agente depende de las posiciones de los otros tres agentes, y si todos acaban en el mismo punto, ninguno de ellos podrá actualizar sus coordenadas. Esta situación pone de manifiesto la importancia de analizar cuidadosamente las interacciones entre los agentes y gestionar adecuadamente sus movimientos para realizar con éxito la tarea de optimización. Estos fallos inesperados pueden motivar nuevas investigaciones y mejoras en el desarrollo de algoritmos que puedan afrontar eficazmente tales complejidades.

En el caso de los demás algoritmos que no han superado la prueba, no proporcionaremos la impresión del banco de pruebas.

Algoritmo electromagnético, EM

El algoritmo EM se ha encontrado con el problema de no poder actualizar las coordenadas de los agentes durante el proceso de optimización. En este caso, hemos observado el colapso de las partículas bajo la influencia de la atracción electromagnética, lo cual ha provocado que los agentes se combinen en un único grupo.

Algoritmo de búsqueda gravitacional, GSA

Las fuerzas gravitatorias hacen que todos los objetos se encuentren en un punto y permanezcan allí: son atraídos hacia el centro, de manera similar a un agujero negro.

Algoritmo de colonias de hormigas, ACOm

El problema de este algoritmo ha sido la falta de vías para que las hormigas se desplacen guiadas por los olores de las feromonas. En este caso, como las hormigas parten de un punto, no se forman los caminos entre ellas, lo cual ha dificultado el movimiento y la coordinación de las hormigas.

Búsqueda de bancos de peces, FSS

C_AO_FSS:50;0.01;0.8
=============================
5 Hilly's; Func runs: 10000; result: 0.32457068874346456
25 Hilly's; Func runs: 10000; result: 0.27938488291267094
500 Hilly's; Func runs: 10000; result: 0.2343201202260512
=============================
5 Forest's; Func runs: 10000; result: 0.18964347858030822
25 Forest's; Func runs: 10000; result: 0.16146315945349987
500 Forest's; Func runs: 10000; result: 0.14145987387955847
=============================
5 Megacity's; Func runs: 10000; result: 0.0
25 Megacity's; Func runs: 10000; result: 0.0
500 Megacity's; Func runs: 10000; result: 0.0
=============================
All score: 1.33084

En este algoritmo, los peces utilizan la diferencia de aptitud entre la última iteración y la anterior para determinar su dirección de desplazamiento, pero en las funciones Hilly y Forest los peces perciben los cambios en el paisaje, y la ejecución del algoritmo en la superficie plana de Megacity confunde a los peces al desorientarlos. El sorprendente comportamiento de los peces se pone de manifiesto cuando parten en superficies lisas que presentan un gradiente. Sin embargo, si el punto de partida está en la cima de un extremo local y no en un valle, incluso en las funciones Hilly y Forest, es poco probable que los peces se desplacen.

Recocido isotrópico simulado, SIA

C_AO_SIA:100:0.01:0.1
=============================
5 Hilly's; Func runs: 10000; result: 0.32958446477979136
25 Hilly's; Func runs: 10000; result: 0.32556359155723036
500 Hilly's; Func runs: 10000; result: 0.27262289744765306
=============================
5 Forest's; Func runs: 10000; result: 0.1940720887058382
25 Forest's; Func runs: 10000; result: 0.1935893813273654
500 Forest's; Func runs: 10000; result: 0.16409411642496857
=============================
5 Megacity's; Func runs: 10000; result: 0.0
25 Megacity's; Func runs: 10000; result: 0.0
500 Megacity's; Func runs: 10000; result: 0.0
=============================
All score: 1.47953

El algoritmo de recocido isotrópico simulado presenta una combinación única de características que recuerdan al rendimiento de SFS, pero con diferencias significativas. En este algoritmo, el movimiento en distintas direcciones desde el punto de partida resulta más enérgico y activo que en SFS, lo cual genera una sensación de creatividad exuberante en la búsqueda de la solución óptima. De forma similar a SFS, el algoritmo de recocido isotrópico simulado explota las diferencias en los valores de la función de aptitud para la dirección del movimiento. En este caso, sin embargo, el movimiento se ve afectado por un descenso gradual de la temperatura, que acaba provocando la "congelación" de las partículas en determinados puntos del espacio.

Estrategias evolutivas, (PO)ES

C_AO_(PO)ES:100:10:0.025:8.0
=============================
5 Hilly's; Func runs: 10000; result: 0.32231823718105856
25 Hilly's; Func runs: 10000; result: 0.3228736374003839
500 Hilly's; Func runs: 10000; result: 0.2797261292300971
=============================
5 Forest's; Func runs: 10000; result: 0.19410491957153192
25 Forest's; Func runs: 10000; result: 0.1875135077472832
500 Forest's; Func runs: 10000; result: 0.15801830580073034
=============================
5 Megacity's; Func runs: 10000; result: 0.1292307692307692
25 Megacity's; Func runs: 10000; result: 0.12553846153846154
500 Megacity's; Func runs: 10000; result: 0.08198461538461577
=============================
All score: 1.80131

Este algoritmo ha sido el primero de la lista capaz de superar con éxito todas las pruebas. Aunque la expresión "superar con éxito" parece categórica, en realidad ha superado cada una de ellas, al menos con algún resultado distinto a cero. Lo notable del proceso ha sido la tendencia de la población a separarse en grupos distintos. No obstante, el entusiasmo inicial del algoritmo dura poco: los agentes dejan rápidamente de buscar en la primera elevación cercana, probablemente pensando que ya han tenido éxito.

Resulta especialmente divertido que al principio los agentes, divididos en grupos, inspiren optimismo al observador moviéndose en distintas direcciones, pero la decepción no tarda en llegar: en cuanto uno de los grupos consigue una mejora notable de la situación, el resto de ellos cambia instantáneamente de dirección, precipitándose hacia el líder. Estos momentos evocan todo un abanico de sentimientos y emociones, desde la euforia hasta la decepción. La interacción de los agentes en este algoritmo se parece a la vida, con todas sus sorpresas y cambios.

Algoritmo del mono, MA

C_AO_MA:50;0.01;0.9;50
=============================
5 Hilly's; Func runs: 10000; result: 0.32874856274894027
25 Hilly's; Func runs: 10000; result: 0.30383823957660194
500 Hilly's; Func runs: 10000; result: 0.2475564907358033
=============================
5 Forest's; Func runs: 10000; result: 0.20619304546795353
25 Forest's; Func runs: 10000; result: 0.1733511102614089
500 Forest's; Func runs: 10000; result: 0.14786586882293234
=============================
5 Megacity's; Func runs: 10000; result: 0.17538461538461542
25 Megacity's; Func runs: 10000; result: 0.1436923076923077
500 Megacity's; Func runs: 10000; result: 0.09555384615384681
=============================
All score: 1.82218

En el contexto de este algoritmo, los monos siguen moviéndose en una dirección elegida de forma bastante aislada, aunque dicha dirección resulte ser la equivocada. Este comportamiento único permite a los agentes explorar el espacio de manera más eficiente al extenderse más allá del punto de partida. Realizan "saltos a lo desconocido" lejanos, especialmente impresionantes en la función discreta Megacity, en la que no hay incremento de adaptación en las superficies horizontales, lo cual favorece el alcance de regiones lejanas.

Sin embargo, esta capacidad exploratoria resulta insuficiente para alcanzar el objetivo principal, ya que el número de iteraciones disponibles llega a su fin. Cabe destacar el fascinante comportamiento visual del algoritmo, que realmente se parece al movimiento caótico de los monos en manada, creando un espectáculo asombroso y generando interés por su investigación y mejora ulteriores.

Recocido simulado, SA

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Hilly's; Func runs: 10000; result: 0.3266993983850477
25 Hilly's; Func runs: 10000; result: 0.30166692301946135
500 Hilly's; Func runs: 10000; result: 0.2545648344562219
=============================
5 Forest's; Func runs: 10000; result: 0.1939959116807614
25 Forest's; Func runs: 10000; result: 0.17721159702946082
500 Forest's; Func runs: 10000; result: 0.15159936395874307
=============================
5 Megacity's; Func runs: 10000; result: 0.2584615384615384
25 Megacity's; Func runs: 10000; result: 0.15292307692307697
500 Megacity's; Func runs: 10000; result: 0.10135384615384675
=============================
All score: 1.91848

En el algoritmo de recocido simulado (a diferencia de su "pariente", el SIA, que, por cierto, ocupa una posición mucho más alta en el ranking), el comportamiento resulta más caótico, cosa que se aprecia incluso a simple vista en la visualización. No obstante, esta naturaleza caótica de la imitación del "recocido" tiene un efecto favorable, ya que ayuda a obtener resultados ligeramente mejores. Aunque estos logros no son lo bastante importantes como para inmortalizar este algoritmo en el salón de la fama de los algoritmos más destacados, la mejora resulta notable y merece reconocimiento.

Algoritmo de luciérnagas, FAm

C_AO_FAm:50;0.1;0.3;0.1
=============================
5 Hilly's; Func runs: 10000; result: 0.32461162859403175
25 Hilly's; Func runs: 10000; result: 0.31981492599317524
500 Hilly's; Func runs: 10000; result: 0.25932958993768923
=============================
5 Forest's; Func runs: 10000; result: 0.2124297717365277
25 Forest's; Func runs: 10000; result: 0.21595138588924906
500 Forest's; Func runs: 10000; result: 0.1577543024576405
=============================
5 Megacity's; Func runs: 10000; result: 0.2246153846153846
25 Megacity's; Func runs: 10000; result: 0.1987692307692308
500 Megacity's; Func runs: 10000; result: 0.12084615384615457
=============================
All score: 2.03412

El FA es uno de mis algoritmos favoritos. Su atractivo no reside solo en lo bonito del nombre en sí, sino también en la elegante idea que tiene detrás, así como en el elegante comportamiento de las luciérnagas. Estas místicas criaturas resplandecientes son capaces de acercarse de forma instantánea a los extremos locales más cercanos a tal velocidad que resulta realmente difícil seguirles la pista. Sin embargo, tras este espléndido espectáculo, se produce un estancamiento cuando los agentes se atascan en máximos localizados, privados de la oportunidad de explorar más el espacio y alcanzar un óptimo global.

Este momento de estancamiento, aunque pueda parecer frustrante, abre una oportunidad de mejora en el algoritmo. Introduciendo mecanismos que ayuden a superar las trampas localizadas, el FA puede ganar nuevos horizontes de eficacia y precisión. Así, incluso en los momentos en que las luciérnagas se detienen, vemos no solo un final, sino un nuevo comienzo: una oportunidad para mejorar y hacer evolucionar este asombroso algoritmo.

Algoritmo de forrajeo bacteriano, BFO

C_AO_BFO:50;0.01;0.3;100
=============================
5 Hilly's; Func runs: 10000; result: 0.3226339934200066
25 Hilly's; Func runs: 10000; result: 0.2925193012197403
500 Hilly's; Func runs: 10000; result: 0.2554221763445149
=============================
5 Forest's; Func runs: 10000; result: 0.2111053636851011
25 Forest's; Func runs: 10000; result: 0.20536292110181784
500 Forest's; Func runs: 10000; result: 0.15743855819242952
=============================
5 Megacity's; Func runs: 10000; result: 0.27999999999999997
25 Megacity's; Func runs: 10000; result: 0.19415384615384618
500 Megacity's; Func runs: 10000; result: 0.11735384615384695
=============================
All score: 2.03599

La capacidad de las bacterias para mantener su movilidad incluso sin necesidad de aumentar su aptitud es un factor clave que les permite propagarse eficazmente a grandes distancias, superando en este aspecto a los algoritmos que hemos comentado antes. Este notable fenómeno resulta especialmente pronunciado en Megacity, donde las bacterias muestran una asombrosa capacidad de movilidad y supervivencia, lo cual les permite adaptarse con éxito a entornos diversos y complejos. En este contexto, las bacterias se convierten en auténticas pioneras que exploran y colonizan nuevos territorios, poniendo de relieve sus capacidades únicas y su importancia en el mundo de los organismos vivos.

Algoritmo de búsqueda de sistema cargado, CSS

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Hilly's; Func runs: 10000; result: 0.38395827586082376
25 Hilly's; Func runs: 10000; result: 0.3048219687002418
500 Hilly's; Func runs: 10000; result: 0.2895158695448419
=============================
5 Forest's; Func runs: 10000; result: 0.2699906934238054
25 Forest's; Func runs: 10000; result: 0.19451237087137088
500 Forest's; Func runs: 10000; result: 0.18498127715987073
=============================
5 Megacity's; Func runs: 10000; result: 0.16923076923076924
25 Megacity's; Func runs: 10000; result: 0.13846153846153847
500 Megacity's; Func runs: 10000; result: 0.12276923076923094
=============================
All score: 2.05824

Sorprendentemente, este algoritmo ha obtenido unos resultados bastante inesperados en esta prueba, superando su rendimiento habitual, según el cual, ocupa el penúltimo lugar entre los rezagados de la clasificación. Esta vez, el CSS ha sorprendido a todos al situarse en una posición intermedia (duodécimo por la cola). El misterio de esta transformación tiene una explicación: las cargas electrostáticas que se someten a las fórmulas del algoritmo empiezan a interactuar con fuerzas repulsivas al caer dentro del radio de carga, lo cual les permite propagarse explosivamente por el espacio de búsqueda circundante. Este proceso no solo es visualmente atractivo, sino que también tiene posibilidades de aplicación práctica.

Con esta capacidad, la de dispararse como un fuego artificial, el CSS abre nuevos usos. Por ejemplo, se podría considerar este algoritmo como una fuente de "soluciones-idea" para determinar la posición óptima de los agentes para otros algoritmos de optimización, o integrarlo con éxito en soluciones híbridas en las que el CSS puede ayudar a evitar la degeneración de la población. Así pues, el inesperado éxito del CSS en esta prueba no solo es inspirador, sino que abre nuevas perspectivas para su aplicación.

Algoritmo de siembra y crecimiento de árboles, SSG

C_AO_SSG:50;0.3;0.5;0.4;0.1
=============================
5 Hilly's; Func runs: 10000; result: 0.3284133103606342
25 Hilly's; Func runs: 10000; result: 0.3246280774155864
500 Hilly's; Func runs: 10000; result: 0.2808547975998361
=============================
5 Forest's; Func runs: 10000; result: 0.194115963123826
25 Forest's; Func runs: 10000; result: 0.19754974771110584
500 Forest's; Func runs: 10000; result: 0.17111478002239264
=============================
5 Megacity's; Func runs: 10000; result: 0.25846153846153846
25 Megacity's; Func runs: 10000; result: 0.23353846153846156
500 Megacity's; Func runs: 10000; result: 0.14158461538461614
=============================
All score: 2.13026

Este algoritmo revela su potencial en funciones de gradiente como Hilly o Forest y ocupa un lugar destacado en las clasificaciones estándar. Sin embargo, su eficacia solo se manifiesta plenamente cuando se produce un cambio positivo en el gradiente. De lo contrario, la población se degrada rápidamente y los individuos convergen a un único mejor punto local, lo cual abre la posibilidad de aplicar el método SSG para afinar los resultados de los algoritmos de optimización.

5. Resultados preliminares

En este experimento de investigación único, en el que los algoritmos se han sometido a condiciones iniciales estrictas, descubrimos muchas características fascinantes de varios algoritmos que permanecían ocultas con la colocación uniforme aleatoria estándar de los agentes en el espacio de búsqueda. Al igual que ocurre en la vida real, los organismos liberan su potencial interior en condiciones extremas.

Asimismo, hemos visto algunos resultados inesperados en las pruebas de algunos algoritmos, como su caída de los primeros puestos a los últimos. Esto nos permite comprender mejor cómo utilizar los algoritmos según sus capacidades en problemas de optimización especializados, y profundizar en sus puntos fuertes y débiles. También ha puesto de relieve los aspectos positivos y negativos de cada algoritmo, lo cual nos ha permitido aprovechar mejor sus puntos fuertes y compensar sus puntos débiles. Además, esta investigación contribuye a una mejor comprensión de la creación de algoritmos híbridos al permitir combinar los puntos fuertes de distintos métodos para lograr resultados óptimos.

En el próximo artículo, continuaremos analizando las propiedades y el comportamiento de los algoritmos y resumiremos los resultados.