ニューラルネットワークが簡単に（第52回）：楽観論と分布補正の研究

MetaTrader 5 — トレーディングシステム | 10 1月 2024, 10:05

318

Dmitriy Gizlyk

はじめに

Q関数学習の安定性を高めるための基本的な要素のひとつは、経験再生バッファの使用です。バッファを増やすことで、より多様な環境との相互作用の例を集めることが可能になります。これにより、モデルは環境のQ関数をよりよく研究し、再現することができます。この手法は、Actor-Criticファミリーのアルゴリズムを含む様々な強化学習アルゴリズムで広く使われています。

しかし、逆の見方もあります。学習過程において、Actorの行動は、経験再生バッファに保存された例とは次第に異なっていきます。モデルパラメータの更新を繰り返せば繰り返すほど、この差は大きくなります。これはActor方策の訓練効率の低下につながります。可能性のある解決策のひとつが、論文「 Reinforcement Learning with Optimistic Exploration and Distribution Correction」（2021年10月）で紹介されています。この手法の著者は、分布補正推定法(DICE)をSoft Actor-Criticアルゴリズムに適応させることを提案しました。

同時に、この手法の著者はさらに別のニュアンスにも注意を払いました。Soft Actor-Critic法では、方策の訓練中に最小限の行動評価をおこないます。このアプローチの実際的な使用は、環境に関する悲観的で不十分な調査と、行動の同質性を指向する傾向を示しています。この影響を最小化するために、論文の著者は楽観的研究Actorモデルの追加訓練を提案しました。その結果、楽観的なActorモデルと環境との相互作用の例と、訓練された目標モデルの行動分布との間のギャップがさらに大きくなります。

しかし、分布推定値の補正と楽観的Actorモデルの研究を併用することで、目標モデルの学習結果を改善することができます。

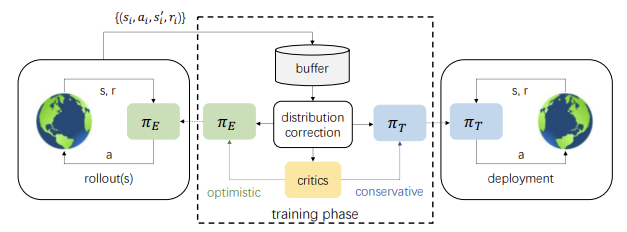
1.楽観論の研究

楽観論を用いた環境調査に関する最初のアイデアは、「Exploration with Optimistic Actor-Critic」（2019年10月）で述べられています。その著者は、Actorの貪欲な更新とCriticの悲観的な評価の組み合わせが、エージェントの知らない行動の回避につながることに気づきました。この現象は「悲観的過小探索」と呼ばれています。さらに、ほとんどのアルゴリズムは研究の方向性について知らされていません。無作為にサンプリングされた行動は、現在の平均値の反対側に位置する可能性が高い一方、一般に、特定の分野では他の分野よりもはるかに多くの行動を必要とします。これらの現象を修正するために、状態行動価値関数の下限信頼区間と上限信頼区間を近似するOptimistic ActorCritic (OAC)アルゴリズムが提案されました。これにより、楽観論の原則を、上限を用いた有向性調査の不確実性の中で用いることができるようになりました。同時に、下限は行動の過大評価を避けるのに役立ちます。

この手法の著者は、楽観的Actor Criticのアイデアを拾い上げ、発展させました。Soft Actor-Criticの場合と同様に、2つのCriticモデルを訓練します。しかし同時に、πеと目標 πтリサーチという2つのActorモデルも訓練します。

πе方策はQUB Q関数値の近似上限を最大化するように学習します。同時に、πтは訓練中のQLBQ関数の下界の近似を最大化します。OACは、Soft Actor-Criticと比較して、πеを含む研究がより効率的なサンプリングの利用を可能にすることを示しています。

QUB Q関数の近似的な上限を得るために、まず両Criticの評価の平均と分散を計算します。

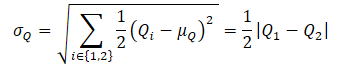
次に、式を使ってQUBを定義します。

ここでβUB ∈ Rは楽観度を管理します。

QLB Q関数の近似下界は次のように表されることにご注意ください。

βLB=1の悲観度では、QLBはCriticの評価の最小値に等しくなります。

Optimistic Actor-Criticは、πеと πтの間に最大KLダイバージェンス制約を適用し、、πеの閉じた解を得ることができ、訓練を安定させます。同時にこれは、Criticの誤った評価を正す可能性のある、より有益な行動をおこなう上でのπеの可能性を制限します。この制限により、πеは、Criticの最小限の評価に基づいて保守的に訓練されたπт方策によって生成された行動と大きく異なる行動を生成することができません。

SAC+DICEアルゴリズムでは、分布補正を加えることで、楽観的な方針ですべての探索の可能性を解き放つためのKL制約の使用を排除しています。この場合、方策の学習時に偏った勾配推定値を明示的に補正することで、学習の安定性が保たれます。

Q関数の過大評価を防ぐためにActorの行動方針πтを訓練する間、Soft Actor-Critic法と同様に、CriticとしてQLBの近似下界を用います。ただし、πт(s,a)/dD(s,a比を用いたサンプリング分布の調整が加わります。次のような訓練ゴールを得ます。

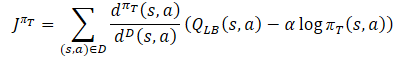
ここで、dπт(s,a)は現在の方策の状態行動分布を表し、dD(s,a)は経験再生バッファからの状態行動分布を定義します。このような学習目標の勾配は、目標方策を学習する際に偏った推定値を使用するこれまでのActor-Critic学習アルゴリズムとは異なり、方策勾配の不偏推定値を提供します。

πеの研究方針は、Q関数の推定値に対する楽観的なバイアスを研究し、誤った推定値を効果的に修正する経験を積むべきです。そこで著者らは、目的関数のCriticとして、Optimistic Actor-Critic QUBと同様の近似上限値を用いることを提案しました。πе方策とQ関数のより良い推定値の最終的な目標は、πт目標方策のより正確な勾配の推定を容易にすることです。したがって、πе損失関数のサンプリング分布は、πт行動方針と一致するはずです。その結果、この手法の著者は、Actorの目標方策の損失関数と同じ補正係数を使うことを提案しています。

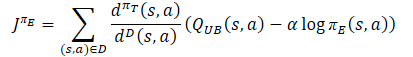
Criticについては、先に述べた「Soft Actor-Critic」からのアプローチが踏襲されています。目標モデルのQ関数の下界を使用してモデルを訓練します。ただし、ActorとCriticの訓練に同じサンプルを使うことの効率性を証明する研究は数多くあります。そのため、Criticsの損失関数には分布補正係数も加えられました。

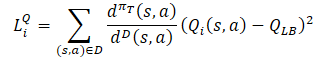
ご覧のように、分布補正係数は、上記のすべてから最も多くの疑問を投げかけるものです。詳しく考えてみましょう。

2.分布補正

分布補正推定法(DICE)アルゴリズムファミリーは、オフ方策評価(OPE)補正の問題を解決するために設計されています。これらの方法によって、D静的リトライバッファに基づく1ステップの方策値、つまり正規化された期待報酬の推定量を訓練することができます。DICEは分布補正係数を推定する不偏推定量を受け取ります。

分布補正係数を推定するために、著者らはDICE最適化構造を採用しました。DICE最適化構造は、様々な正則化を伴うミニマックス線形分布プログラムとして定式化することができます。DICEアルゴリズムを方策外の強化学習設定に直接適用することは、重要な最適化の課題を提起します。評価なし学習では、固定されたゴール方策と、十分な状態-動作空間をカバーする静的なリプレイバッファが仮定されますが、RLではゴール方策と経験再生バッファは学習中に変化します。そのため、SAC+DICE法の作者は、これらの困難を克服するためにいくつかの修正を加えています。今、数学の世界に飛び込んで、これらの修正にこだわるつもりはありません。元の記事をご覧ください。ここでは、提案された修正の結果として得られた損失関数のみを紹介します。

ここでζ(s,a)とv(s,a)はニューラルネットワークのモデルであり、λは調整可能なラグランジュ係数です。ζ(s,a)は分布補正係数を近似し、v(s,a)は一種のCriticです。訓練を安定させるために、Criticと同様にパラメータをソフト更新したv 目標モデルを使用します。

すべてのパラメータを最適化するために、著者らはアダム法の使用を提案しています。

上記のすべてが、単一のSAC+DICEアルゴリズムに一般化されます。従来のオフ方策強化学習アルゴリズムと同様に、πе楽観的探索方策に従って環境とのインタラクションを逐次実行し、そのデータを経験再生バッファに保存します。各訓練ステップにおいて、本アルゴリズムはまず、上記の損失関数に関してSGDを用いてモデルとDICEパラメータ（v, ζ, λ）を更新します。

そして、更新されたモデルからζ分布の補正比を計算します。

そして、ζを使ってRLを訓練し、πт、πе、Q1、Q2を更新します。

各訓練ステップの最後に、Q1、Q2、vの目標モデルがソフト的に更新されます。

3.MQL5を使用した実装

理論的な部分を読んでいるうちに、訓練されたモデルとパラメータの数が急激に増えていることに気づかれたかもしれません。実際、学習済みモデルの数は3つから6つに増えました。両者の関係はより複雑になります。同時に、Actorの行動方針のモデルを1つ受け取ることも期待しています。すべてのルーチンワークをユーザーから隠すために、アプローチを少し変更し、訓練全体を別のクラスCNET_SAC_DICEで包みます。新しいクラスは、CNetニューラルネットワークモデルの基本クラスの後継となります。クラス本体では、5つの学習可能モデルと3つの目標モデルを宣言します。ここでは、いくつかの内部変数も宣言します。その機能性については、実装時に見ていくことにしましょう。

class CNet_SAC_DICE  : protected CNet
  {
protected:
   CNet              cActorExploer;
   CNet              cCritic1;
   CNet              cCritic2;
   CNet              cTargetCritic1;
   CNet              cTargetCritic2;
   CNet              cZeta;
   CNet              cNu;
   CNet              cTargetNu;
   float             fLambda;
   float             fLambda_m;
   float             fLambda_v;
   int               iLatentLayer;
   //---
   float             fLoss1;
   float             fLoss2;
   float             fZeta;
   //---
   vector<float>     GetLogProbability(CBufferFloat *Actions);

public:
   //---
                     CNet_SAC_DICE(void);
                    ~CNet_SAC_DICE(void) {}
   //---
   bool              Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1);
   //---
   virtual bool      Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, 
                           vector<float> &ActionsLogProbab, CBufferFloat *NextState, 
                           CBufferFloat *NextSecondInput, float reward, float discount, float tau);
   virtual void      GetLoss(float &loss1, float &loss2)    {  loss1 = fLoss1; loss2 = fLoss2;  }
   //---
   virtual bool      Save(string file_name, bool common = true);
   bool              Load(string file_name, bool common = true);
  };

当初は6つの学習可能なモデルを挙げていましたが、5つしか宣言していないことにご注意ください。宣言されたモデルの中で、Actorの目標方針はありません。しかし、訓練全体の目的は、まさにそれを得ることにあります。先に述べたように、この新しいクラスはベースとなるニューラルネットワーククラスの後継です。つまり、それ自体が学習モデルなのです。従って、基本的なActor方策の訓練は、親クラスを使っておこなわれます。

また、新たに作成されるCNet_SAC_DICEクラスは、モデルの訓練にのみ使用されます。運用中、追加モデルのオブジェクトを作成することは意味がなく、不必要なリソースの消費となります。そのため、作戦中は基本的なモデルオブジェクトを使用する予定です。以上のことから、新しいクラスにはフォワードパスやバックワードパスのメソッドはありません。すべての機能は、Studyメソッドで実装されます。

もちろん、ファイルのSaveやLoadを扱うメソッドもあります。まず必要なことから始めていきます。

クラスのコンストラクタでは、内部変数を初期値で初期化します。内部オブジェクトはすべて静的に宣言され、初期化の対象にはなりません。したがって、デストラクタでメモリをクリアする必要はありません。

CNet_SAC_DICE::CNet_SAC_DICE(void)  :  fLambda(1.0e-5f),
                                       fLambda_m(0),
                                       fLambda_v(0),
                                       fLoss1(0),
                                       fLoss2(0),
                                       fZeta(0)
  {
  }

モデルの完全な初期化はCreateメソッドでおこなわれます。メソッドのパラメータには、すべての使用モデルのアーキテクチャの記述の動的配列と、分析された環境の状態の圧縮された表現を持つActorの潜在層のIDを渡します。

メソッド本体では、まずActorモデルを作成します。楽観的モデルは、cActorExploerオブジェクトに作成されます。目標モデルは、継承されたツールを使ってクラス本体に作成されます。

bool CNet_SAC_DICE::Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer)
  {
   ResetLastError();
//---
   if(!cActorExploer.Create(actor) || !CNet::Create(actor))
     {
      PrintFormat("Error of create Actor: %d", GetLastError());
      return false;
     }
//---
   if(!opencl)
     {
      Print("Don't opened OpenCL context");
      return false;
     }

作成されたOpenCLコンテキストポインタをすぐに確認します。

次に、両Criticの学習可能なモデルを作成します。

   if(!cCritic1.Create(critic) || !cCritic2.Create(critic))
     {
      PrintFormat("Error of create Critic: %d", GetLastError());
      return false;
     }

その後にDICEのブロックオブジェクトと目標モデルが続きます。

   if(!cZeta.Create(zeta) || !cNu.Create(nu))
     {
      PrintFormat("Error of create function nets: %d", GetLastError());
      return false;
     }
//---
   if(!cTargetCritic1.Create(critic) || !cTargetCritic2.Create(critic) ||
      !cTargetNu.Create(nu))
     {
      PrintFormat("Error of create target models: %d", GetLastError());
      return false;
     }

すべてのモデルの作成に成功したら、それらを1つのOpenCLコンテキストに渡します。

   cActorExploer.SetOpenCL(opencl);
   cCritic1.SetOpenCL(opencl);
   cCritic2.SetOpenCL(opencl);
   cZeta.SetOpenCL(opencl);
   cNu.SetOpenCL(opencl);
   cTargetCritic1.SetOpenCL(opencl);
   cTargetCritic2.SetOpenCL(opencl);
   cTargetNu.SetOpenCL(opencl);

そして、モデルパラメータを目標コピーにコピーします。また、各ステップでの作戦実行を制御することも忘れてはなりません。

   if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), 1.0) ||
      !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), 1.0) ||
      !cTargetNu.WeightsUpdate(GetPointer(cNu), 1.0))
     {
      PrintFormat("Error of update target models: %d", GetLastError());
      return false;
     }

必要なオブジェクトの作成に成功したら、データを内部変数に移し、メソッドを終了します。

   fLambda = 1.0e-5f;
   fLambda_m = 0;
   fLambda_v = 0;
   fZeta = 0;
   iLatentLayer = latent_layer;
//---
   return true;
  }

クラスの内部オブジェクトを初期化した後、CNET_SAC_DICE::Studyモデル訓練メソッドに進みます。このクラスのパラメータには、モデルの訓練の1ステップに必要なすべての情報が含まれています。ここに、環境の現状と未来があります。この場合、各状態は履歴データとバランス状態の2つのデータバッファに記述されます。ここには、行動バッファと報酬変数も表示されます。また、割引率や目標モデルのソフト更新のための変数もあります。初めて、元の方策の確率の対数のベクトルを追加します（例の収集に使用）。

bool CNet_SAC_DICE::Study(CArrayFloat *State,
                          CArrayFloat *SecondInput,
                          CBufferFloat *Actions,
                          vector<float> &ActionsLogProbab,
                          CBufferFloat *NextState,
                          CBufferFloat *NextSecondInput,
                          float reward,
                          float discount,
                          float tau)
  {
//---
   if(!Actions || Actions.Total()!=ActionsLogProbab.Size())
      return false;

メソッド本体では、まず小さな制御ブロックを配置し、行動バッファへのポインタの関連性と、そのサイズと確率対数ベクトルのサイズの対応を確認します。他のバッファへのポインタは、呼び出されたメソッドで制御されるため、確認しません。

制御ブロックの通過に成功した後は、現在の方針を考慮して、目標モデルによるその後の状態評価を実行します。そのためにまず、保守的なActor方策のダイレクトパスを導入します。現在の状態を表す生データを前処理し、この状態から行動ベクトルを予測するために使用します。得られたデータをCriticsの2つの目標モデルとDICEブロックのvモデルに渡します。

   if(!CNet::feedForward(NextState, 1, false, NextSecondInput))
      return false;
   if(!cTargetCritic1.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1) ||
      !cTargetCritic2.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1))
      return false;
//---
   if(!cTargetNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1))
      return false;

次のステップは、現在の状態データの準備です。後続の状態と同様に、現在の保守的なActorモデルを使用して、現在の状態の記述を前処理します。

   if(!CNet::feedForward(State, 1, false, SecondInput))
      return false;
   CBufferFloat *output = ((CNeuronBaseOCL*)((CLayer*)layers.At(layers.Total() - 1)).At(0)).getOutput();
   output.AssignArray(Actions);
   output.BufferWrite();

ここでは、フォワードパスの結果を置き換える小技を披露します。現在のActor方策で得られた行動の代わりに、経験再現バッファから行動テンソルを最後のニューラル層の結果バッファに保存します。この操作の目的は、行動と環境からの報酬の対応関係を維持することです。フォワードパス中に他の行動が形成された可能性が高いことは認識しています。しかし、CNeuronSoftActorCriticニューラル層は、その内部オブジェクトの深さにおける行動とその確率の分布を研究しています。リバースパスの間に、経験再生バッファからの行動に対応する分位数と確率が決定されます。この場合、不偏勾配はこれらの分位数まで正確に通過し、Actorモデルをより正確に、歪みなく学習させることができます。

現在の環境状態データを準備した後、ブロックDICEモデルをフォワードパスすることができます。操作の実行を制御することを忘れないでください。

   if(!cNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this)))
      return false;
   if(!cZeta.feedForward(GetPointer(this), iLatentLayer, GetPointer(this)))
      return false;

SAC+DICEアルゴリズムに従い、まずブロックDICEのモデルとパラメータを更新します。しかし、パラメータを更新する前に、v、ζ、λの損失関数の値を計算する必要があります。

損失関数の値を得るためには、現在の保守的な方針と、例証ベースの収集中の環境との相互作用における状態-作用確率比の目標値が必要であることにご注意ください。ここで言っておかなければならないのは、環境の状態を表す過去のデータは、Actorの方針には依存しないということです。さらに、私たちは現在の状態を、決断を下し、その後の行動の軌跡を構築するための出発点として認識しています。その結果、初期状態の確率は1に等しいと認識されます。

方策の学習中、行動の確率分布だけが学習された戦略に従って変化します。したがって、目標値は2つの方策における行動確率の比となります。操作では、確率比の代わりに確率対数の差を使用します。この場合、すべての行動の確率を掛け合わせるのではなく、それらの対数の和を使い、指数で値を復元します。

   vector<float> nu, next_nu, zeta, ones;
   cNu.getResults(nu);
   cTargetNu.getResults(next_nu);
   cZeta.getResults(zeta);
   ones = vector<float>::Ones(zeta.Size());
   vector<float> log_prob = GetLogProbability(output);
   float policy_ratio = MathExp((log_prob - ActionsLogProbab).Sum());
   vector<float> bellman_residuals = next_nu * discount * policy_ratio - nu + policy_ratio * reward;
   vector<float> zeta_loss = zeta * (MathAbs(bellman_residuals) - fLambda) * (-1) + MathPow(zeta, 2.0f) / 2;
   vector<float> nu_loss = zeta * MathAbs(bellman_residuals) + MathPow(nu, 2.0f) / 2.0f;
   float lambda_los = fLambda * (ones - zeta).Sum();

損失関数の値を決定した後、誤差勾配を定義し、パラメータを更新します。まず、ラグランジュ係数の値を更新します。パラメータ調整では、アダム法のアルゴリズムを使用します。

//--- update lambda
   float grad_lambda = (ones - zeta).Sum() * (-lambda_los);
   fLambda_m = b1 * fLambda_m + (1 - b1) * grad_lambda;
   fLambda_v = b2 * fLambda_v + (1 - b2) * MathPow(grad_lambda, 2);
   fLambda += lr * fLambda_m / (fLambda_v != 0.0f ? MathSqrt(fLambda_v) : 1.0f);

次に、v, ζモデルのパラメータを更新する必要があります。損失関数の値を定義したのであって、目標値を定義したのではないことに留意してください。さらに、それぞれのモデルの損失関数は個別で、これまで私たちが使ってきたものとは大きく異なります。現在のところ、モデルの基本的な損失関数に操作を当てはめることはしません。その代わり、すぐに誤差勾配を計算します。結果の値を適切なモデルバッファに転送し、モデルパラメータ全体に誤差勾配を伝播させましょう。

まず、Vモデルのパラメータを更新します。

//---
   CBufferFloat temp;
   temp.BufferInit(MathMax(Actions.Total(), SecondInput.Total()), 0);
   temp.BufferCreate(opencl);
//--- update nu
   int last_layer = cNu.layers.Total() - 1;
   CLayer *layer = cNu.layers.At(last_layer);
   if(!layer)
      return false;
   CNeuronBaseOCL *neuron = layer.At(0);
   if(!neuron)
      return false;
   CBufferFloat *buffer = neuron.getGradient();
   if(!buffer)
      return false;
   vector<float> nu_grad = nu_loss * (zeta * bellman_residuals / MathAbs(bellman_residuals) + nu);
   if(!buffer.AssignArray(nu_grad) || !buffer.BufferWrite())
      return false;
   if(!cNu.backPropGradient(output, GetPointer(temp)))
      return false;

次にζモデルに対して同様の操作をおこないます。

//--- update zeta
   last_layer = cZeta.layers.Total() - 1;
   layer = cZeta.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   vector<float> zeta_grad = zeta_loss * (zeta - MathAbs(bellman_residuals) + fLambda) * (-1);
   if(!buffer.AssignArray(zeta_grad) || !buffer.BufferWrite())
      return false;
   if(!cZeta.backPropGradient(output, GetPointer(temp)))
      return false;

この時点で、DICEブロックのパラメータを更新し、強化学習手順に直接移行しています。まず、両Criticの直接対決を実施します。この場合、ブロックのDICEオブジェクトのパラメータを更新する際に、すでにこの操作をおこなっているので、Actorのダイレクトパスはおこないません。

//--- feed forward critics
   if(!cCritic1.feedForward(GetPointer(this), iLatentLayer, output) ||
      !cCritic2.feedForward(GetPointer(this), iLatentLayer, output))
      return false;

次に、DICEパラメータの更新と同様に、損失関数の値を決定します。しかし、その前に少し準備作業をしましょう。モデル訓練の安定性を高めるため、分布補正係数を正規化し、現在のActor方策を考慮して目標Criticモデルによって予測される基準値を計算します。

   vector<float> result;
   if(fZeta == 0)
      fZeta = MathAbs(zeta[0]);
   else
      fZeta = 0.9f * fZeta + 0.1f * MathAbs(zeta[0]);
   zeta[0] = MathPow(MathAbs(zeta[0]), 1.0f / 3.0f) / (10.0f * MathPow(fZeta, 1.0f / 3.0f));
   cTargetCritic1.getResults(result);
   float target = result[0];
   cTargetCritic2.getResults(result);
   target = reward + discount * (MathMin(result[0], target) - LogProbMultiplier * log_prob.Sum());

目標値が存在するにもかかわらず、分布補正係数の使用がそれになじまないため、Criticのモデルをバックパスするという基本的な方法を実施することができません。そこで、誤差勾配を計算し、その結果をニューラル層のバッファに直接転送し、その後にモデル上に勾配を分布させるという、上記で開発した手法を使用します。

//--- update critic1
   cCritic1.getResults(result);
   float loss = zeta[0] * MathPow(result[0] - target, 2.0f);
   if(fLoss1 == 0)
      fLoss1 = MathSqrt(loss);
   else
      fLoss1 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * loss);
   float grad = loss * 2 * zeta[0] * (target - result[0]);
   last_layer = cCritic1.layers.Total() - 1;
   layer = cCritic1.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   if(!buffer.Update(0, grad) || !buffer.BufferWrite())
      return false;
   if(!cCritic1.backPropGradient(output, GetPointer(temp)) || 
      !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer))
      return false;

同時に、モデルの平均誤差を計算し、それをユーザーに見せることで、モデルの学習プロセスを視覚的に制御します。

2つ目のCriticについても同様の操作を繰り返す。

//--- update critic2
   cCritic2.getResults(result);
   loss = zeta[0] * MathPow(result[0] - target, 2.0f);
   if(fLoss2 == 0)
      fLoss2 = MathSqrt(loss);
   else
      fLoss2 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * loss);
   grad = loss * 2 * zeta[0] * (target - result[0]);
   last_layer = cCritic2.layers.Total() - 1;
   layer = cCritic2.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   if(!buffer.Update(0, grad) || !buffer.BufferWrite())
      return false;
   if(!cCritic2.backPropGradient(output, GetPointer(temp)) || 
      !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer))
      return false;

Criticのパラメータを更新した後、Actorの方策の更新に移ります。まずは保守的なActorの方針を更新します。ここでは、Q関数値の下限と現在の行動の確率分布を考慮して目標値を計算します。得られた値を分布補正係数で補正し、クリティックのモデルを通して誤差勾配を描きます。まず、Criticの訓練モードを無効にします。

//--- update policy
   cCritic1.getResults(result);
   float mean = result[0];
   float var = result[0];
   cCritic2.getResults(result);
   mean += result[0];
   var -= result[0];
   mean /= 2.0f;
   var = MathAbs(var) / 2.0f;
   target = zeta[0] * (mean - 2.5f * var + discount * log_prob.Sum() * LogProbMultiplier) + result[0];
   CBufferFloat bTarget;
   bTarget.Add(target);
   cCritic2.TrainMode(false);
   if(!cCritic2.backProp(GetPointer(bTarget), GetPointer(this)) ||
      !backPropGradient(SecondInput, GetPointer(temp)))
     {
      cCritic2.TrainMode(true);
      return false;
     }

Actorの楽観的研究方策のパラメータを更新する前に、指定されたモデルをフォワードパスし、結果バッファの値を置き換えます（悲観的モデルで前回おこなったように）。

次に、楽観係数を考慮して目標値を再計算し、誤差勾配をCriticモデルに分配します。

//--- update exploration policy
   if(!cActorExploer.feedForward(State, 1, false, SecondInput))
     {
      cCritic2.TrainMode(true);
      return false;
     }
   output = ((CNeuronBaseOCL*)((CLayer*)cActorExploer.layers.At(layers.Total() - 1)).At(0)).getOutput();
   output.AssignArray(Actions);
   output.BufferWrite();
   cActorExploer.GetLogProbs(log_prob);
   target = zeta[0] * (mean + 2.0f * var + discount * log_prob.Sum() * LogProbMultiplier) + result[0];
   bTarget.Update(0, target);
   if(!cCritic2.backProp(GetPointer(bTarget), GetPointer(cActorExploer)) ||
      !cActorExploer.backPropGradient(SecondInput, GetPointer(temp)))
     {
      cCritic2.TrainMode(true);
      return false;
     }
   cCritic2.TrainMode(true);

操作が完了したら、Critic訓練モードをオンにし、目標モデルのパラメータを更新します。

   if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), tau) ||
      !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), tau) ||
      !cTargetNu.WeightsUpdate(GetPointer(cNu), tau))
     {
      PrintFormat("Error of update target models: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

モデルの訓練方法に関する作業は完了しました。さて、次はファイルを扱うメソッドの構築です。まず、モデルを保存するメソッドを作成します。以前に説明した同様の方法とは異なり、すべてのデータを1つのファイルに保存することはしません。対照的に、各訓練済みモデルは個別のファイルを受け取ります。これによって、それぞれのモデルを独立して使うことができるようになります。

パラメータにおいて、データ保存メソッド CNet_SAC_DICE::Saveは、共有ターミナルフォルダ内の共通ファイル名（拡張子なし）と保存フラグを受け取ります。メソッド本体では、結果のテキスト変数にファイル名があるかどうかを即座に確認します。

bool CNet_SAC_DICE::Save(string file_name, bool common = true)
  {
   if(file_name == NULL)
      return false;

次に、与えられた名前と「.set」という拡張子を持つファイルを作成します。内部変数の値が保存されます。

   int handle = FileOpen(file_name + ".set", (common ? FILE_COMMON : 0) | FILE_BIN | FILE_WRITE);
   if(handle == INVALID_HANDLE)
      return false;
   if(FileWriteFloat(handle, fLambda) < sizeof(fLambda) ||
      FileWriteFloat(handle, fLambda_m) < sizeof(fLambda_m) ||
      FileWriteFloat(handle, fLambda_v) < sizeof(fLambda_v) ||
      FileWriteInteger(handle, iLatentLayer) < sizeof(iLatentLayer))
      return false;
   FileFlush(handle);
   FileClose(handle);

その後、モデルを保存するためのメソッドをひとつずつ呼び出し、操作のプロセスを制御します。ここでは、指定されたファイル名に注意を払う価値があります。保守的な方策を持つActorは、ファイル名の接尾辞として「Act.nnw」を受け取ります（以前にActorについて指定したとおりです）。楽観的なActorモデルは、接尾辞が「ActExp.nnw」のファイルを受け取ります。また、Criticsとv modelsの目標モデルのみを保存します。対応する学習済みモデルは保存されません。

   if(!CNet::Save(file_name + "Act.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cActorExploer.Save(file_name + "ActExp.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetCritic1.Save(file_name + "Crt1.nnw", fLoss1, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetCritic2.Save(file_name + "Crt2.nnw", fLoss2, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cZeta.Save(file_name + "Zeta.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetNu.Save(file_name + "Nu.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   return true;
  }

データロード法では、データがセットされた順番に厳密に操作を繰り返します。この場合、学習済みモデルと目標モデルは、同じ対応するファイルから読み込まれます。

bool CNet_SAC_DICE::Load(string file_name, bool common = true)
  {
   if(file_name == NULL)
      return false;
//---
   int handle = FileOpen(file_name + ".set", (common ? FILE_COMMON : 0) | FILE_BIN | FILE_READ);
   if(handle == INVALID_HANDLE)
      return false;
   if(FileIsEnding(handle))
      return false;
   fLambda = FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   fLambda_m = FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   fLambda_v =   FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   iLatentLayer =  FileReadInteger(handle);;
   FileClose(handle);
//---
   float temp;
   datetime dt;
   if(!CNet::Load(file_name + "Act.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cActorExploer.Load(file_name + "ActExp.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cCritic1.Load(file_name + "Crt1.nnw", fLoss1, temp, temp, dt, common) ||
      !cTargetCritic1.Load(file_name + "Crt1.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cCritic2.Load(file_name + "Crt2.nnw", fLoss2, temp, temp, dt, common) ||
      !cTargetCritic2.Load(file_name + "Crt2.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cZeta.Load(file_name + "Zeta.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cNu.Load(file_name + "Nu.nnw", temp, temp, temp, dt, common) ||
      !cTargetNu.Load(file_name + "Nu.nnw", temp, temp, temp, dt, common))
      return false;

これらのモデルを読み込んだ後、1つのOpenCLコンテキストに転送します。

   cActorExploer.SetOpenCL(opencl);
   cCritic1.SetOpenCL(opencl);
   cCritic2.SetOpenCL(opencl);
   cZeta.SetOpenCL(opencl);
   cNu.SetOpenCL(opencl);
   cTargetCritic1.SetOpenCL(opencl);
   cTargetCritic2.SetOpenCL(opencl);
   cTargetNu.SetOpenCL(opencl);
//---
   return true;
  }

これで CNet_SAC_DICEクラスに関する研究は完了です。添付ファイルに全メソッドの完全なコードがあります。覚えていらっしゃるかもしれませんが、前述した訓練法のパラメータは、行動確率の対数ベクトルを示しています。しかし、これまでそのようなデータを経験再生バッファに保存したことはありませんでした。そのため、ファイル「..\SAC&DICE\Trajectory.mqh」に示されているSState状態アクション記述構造体に対応する配列を追加する必要があります。配列のサイズは行動の数に等しくなります。

struct SState
  {
   float             state[HistoryBars * BarDescr];
   float             account[AccountDescr - 4];
   float             action[NActions];
   float             log_prob[NActions];
   //---
                     SState(void);
   //---
   bool              Save(int file_handle);
   bool              Load(int file_handle);
   //--- overloading
   void              operator=(const SState &obj)
     {
      ArrayCopy(state, obj.state);
      ArrayCopy(account, obj.account);
      ArrayCopy(action, obj.action);
      ArrayCopy(log_prob, obj.log_prob);
     }
  };

構造体をコピーしてファイルを操作するメソッドのアルゴリズムに配列を追加することを忘れないでください。全構造体コードは添付ファイルにあります。

モデルの作成と訓練に移りましょう。モデルアーキテクチャについては、Soft Actor-Critic法を説明した記事からそのまま移しました。同時に、vモデルとζモデル用に別々のアーキテクチャを作ることはしませんでした。Criticアーキテクチャを使用しました。

モデルの訓練では、前回と同様に3つのEAを使用します。

Research：事例データベースの収集
Study：モデルの訓練
Test：得られた結果の確認

Research EAのサンプルデータベースのデータを収集する際には、楽観的なActor方策（接尾辞が「ActExp.nnw」のファイル）を使用します。しかし、訓練されたモデルをテストするために、保守的なモデル（接尾辞が「Act.nnw」のファイル）を使用します。対応するファイルのモデルを読み込む際には、この点に注意する必要があります。また、経験値再生バッファにデータを収集する際には、行動分布確率の対数の読み込みを追加することを忘れないでください。EAの全コードは添付ファイルにあります。

Study訓練EAは最大の変化を遂げました。これは驚くべきことではありません。私たちは、その機能の大部分をCNET_SAC_DICEクラスの学習訓練メソッドに移しました。

まず、モデルを含むライブラリを変更することから始めます。

#include "Net_SAC_DICE.mqh"

グローバル変数ブロックでは、新しく作成された CNet_SAC_DICEクラスのモデルを1つだけ宣言します。同時に、データバッファの数も増やす。これは、以前は訓練の異なる段階で2つの状態に1つのバッファを使うことができたからです。今度は、後続の2つの状態に関する情報を同時にモデルに伝えなければなりません。

STrajectory          Buffer[];
CNet_SAC_DICE        Net;
//---
float                dError;
datetime             dtStudied;
//---
CBufferFloat         bState;
CBufferFloat         bAccount;
CBufferFloat         bActions;
CBufferFloat         bNextState;
CBufferFloat         bNextAccount;

これまでと同様、EA初期化メソッドでは、まずモデルの学習用に経験値再生バッファを読み込みます。

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

その後、1つのモデルを読み込みます。モデルがまだ作成されていない場合は、モデルのアーキテクチャの記述の配列を形成し、1つのモデルだけを作成し、すべてのアーキテクチャの記述をそのモデルに渡します。操作結果の確認は一度だけです。

上述したように、DICEブロックモデルに対するCriticのアーキテクチャを説明します。しかし、他の選択肢も可能です。このブロック用に独自のモデルを作成する場合は、ソースデータの一次処理のブロックとしてActorモデルを使用することにご注意ください。これはまさに、モデル訓練アルゴリズム全体を構築する方法です。モデルアーキテクチャを作成する際にそれに従うか、メソッドアルゴリズムに適切な変更を加える必要があります。

//--- load models
   if(!Net.Load(FileName, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *critic = new CArrayObj();
      if(!CreateDescriptions(actor, critic))
        {
         delete actor;
         delete critic;
         return INIT_FAILED;
        }
      if(!Net.Create(actor, critic, critic, critic, LatentLayer))
        {
         delete actor;
         delete critic;
         return INIT_FAILED;
        }
      delete actor;
      delete critic;
     }

「単一モデルのみ」というのは、完全には正確ではないかもしれません。訓練プロセスでは、6つの更新モデルと3つの目標モデルを作成します。すべてのモデルは新しいクラスの中で作成され、ユーザーからは見えないようになっています。トップレベルでは、1つのクラスしか扱いません。

EAの初期化方法の最後に、モデルの訓練イベントを生成します。

   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

すべての操作が正常に完了したら、EAの初期化手順を完了します。

次のステップは、Trainモデルを直接訓練する手順です。

前回と同様に、EAの外部パラメータで指定された反復回数に従って、この関数の本体に訓練サイクルを配置します。

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i<0)
        {
         iter--;
         continue;
        }

ループの中では、モデル訓練の現在の反復の軌跡と個々のステップをサンプリングします。

次に、準備作業をおこない、必要なデータを事前に宣言したデータバッファに収集します。まず、その後の環境の状態を表す過去のデータをバッファリングします。

      //--- Target
      bNextState.AssignArray(Buffer[tr].States[i + 1].state);
      float PrevBalance = Buffer[tr].States[i].account[0];
      float PrevEquity = Buffer[tr].States[i].account[1];
      if(PrevBalance==0)
        {
         iter--;
         continue;
        }
      bNextAccount.Clear();
      bNextAccount.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
      bNextAccount.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[2]);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[3]);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      bNextAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

別のバッファでは、口座のステータスの説明を作成し、タイムスタンプを追加します。

同様に、分析された環境の状態を記述するバッファを用意します。

      bState.AssignArray(Buffer[tr].States[i].state);
      PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bAccount.Clear();
      bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bAccount.Add(Buffer[tr].States[i].account[2]);
      bAccount.Add(Buffer[tr].States[i].account[3]);
      bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

そして、完了した行動をバッファに移します。確率対数はベクトルに読み込まれます。

      bActions.AssignArray(Buffer[tr].States[i].action);
      vector<float> log_prob;
      log_prob.Assign(Buffer[tr].States[i].log_prob);

この段階で準備作業は完了します。1回の訓練反復に必要なデータは、すでにデータ・バッファに収集されています。パラメータに必要なデータを渡して、モデルのCNet_SAC_DICE::Study訓練メソッドを呼び出します。

      if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), log_prob,
                    GetPointer(bNextState), GetPointer(bNextAccount),
                    Buffer[tr].Revards[i] - DiscFactor * Buffer[tr].Revards[i + 1], DiscFactor, Tau))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

経験再生バッファでは、報酬は累計として保存されることにご注意ください。ここで、個々のステップの正味報酬をモデル訓練法に移します。欠損データは目標モデルによって予測されます。

モデルの訓練操作をすべてクラスの訓練メソッドに実装しました。あとはメソッド操作の結果を確認するだけです。その後、モデルの訓練プロセスをユーザーに知らせます。

      if(GetTickCount() - ticks > 500)
        {
         float loss1, loss2;
         Net.GetLoss(loss1, loss2);
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), loss1);
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), loss2);
         Comment(str);
         ticks = GetTickCount();
        }
     }

ループの反復が完了したら、コメントフィールドをクリアし、EAのシャットダウンプロセスを開始します。

   Comment("");
//---
   float loss1, loss2;
   Net.GetLoss(loss1, loss2);
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", loss1);
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", loss2);
   ExpertRemove();
//---
  }

このように、モデルの訓練操作を別のクラスメソッドに置くことで、メインプログラム側のコードと人件費を大幅に削減することができます。同時にこのアプローチは、モデル訓練の柔軟性と、それを調整するユーザーの能力を低下させます。どちらのアプローチにもプラス面とマイナス面があります。具体的なアプローチの選択は、目の前のタスクと個人の好みによります。

EAのすべてのコードと記事で使用したすべてのプログラムは、添付ファイルにあります。

4.検証

モデルは2023年1月～5月のEURUSD H1のヒストリカルデータで訓練されました。指標のパラメータとすべてのハイパーパラメータはデフォルト値に設定されました。訓練の過程で、訓練セットで利益を生み出すことができるモデルが得られました。

モデル訓練結果

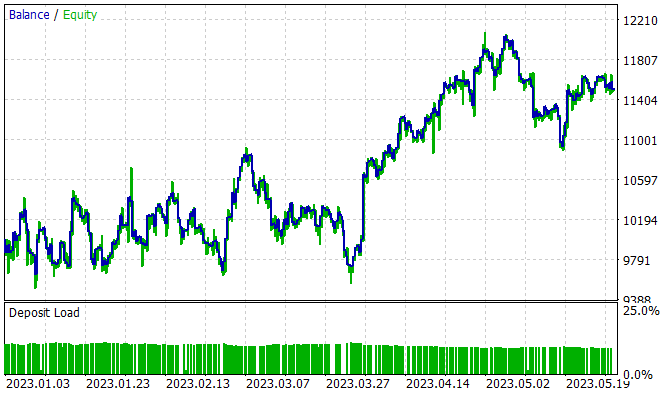
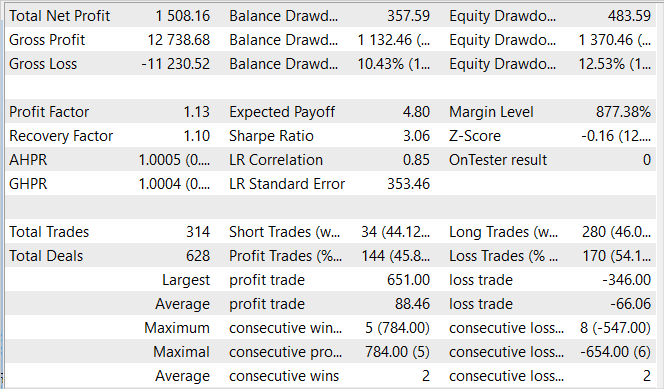
5か月の訓練期間中、このモデルは15％の利益を得ることができました。314のポジションが建てられ、うち45.8%は利益で決済されました。最大利益の取引は最大損失のほぼ2倍を上回ります。さらに、平均利益率は平均損失率より1/3高くなっています。1.13というプロフィットファクターを得ることができたのは、この利益と損失の比率のおかげです。

いつものように、新しいデータに対するモデルの効率にはもっと興味があります。馴染みのないデータに対するモデルの一般化能力とパフォーマンスは、ストラテジーテスターで2023年6月の履歴データを用いてテストされました。ご覧の通り、テスト期間は訓練セットの直後にあります。これにより、訓練サンプルとテストサンプルの最大限の均質性が保証されます。テスト結果を以下に示します。

テスト結果

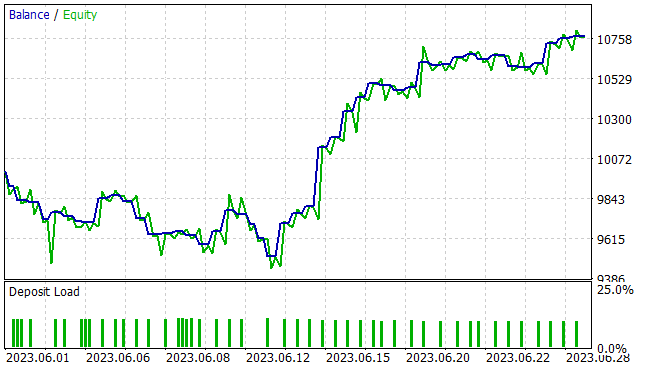
提示されたチャートは、月初めの10日間にドローダウンがあったことを示しています。しかし、その後は月末まで黒字の時期が続きます。その結果、EAは1か月間で7.7%の利益を獲得し、エクイティの最大ドローダウンは5.46%でした。残高に関しては、ドローダウンはさらに小さく、4.87％を超えることはありませんでした。

テスト結果

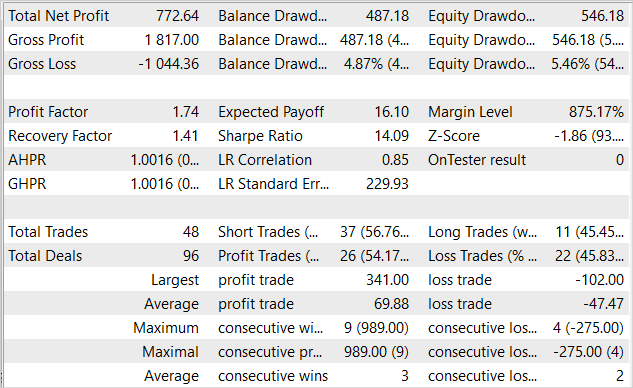
テスト結果の表は、テスト中にEAが両方向で取引をおこなったことを示しています。合計48のポジションが開かれました。そのうち54.17%は黒字決算でした。利益を生んだ取引の最大値は、負け取引最大値の3倍以上です。平均的な利益取引は、平均的な損失取引の半分です。定量的に言えば、平均して3つの利益を生む取引に対して2つの利益を生まない取引があります。この結果、プロフィットファクターは1.74、リカバリーファクターは1.41となりました。

結論

本稿では、Soft Actor-Criticアルゴリズムの2つの主な修正方向に基づいて、Actor-Criticファミリーの別のアルゴリズムであるSAC+DICEアルゴリズムを検討しました。環境研究の楽観的モデルを用いることで、環境研究の領域を広げることができます。この研究は、一般的な方策の収益性を高める方向でおこなわれています。もちろん、これは環境研究方策と学習保守方策の配分の断絶につながります。勾配の不偏推定値を得るために、修正DICEアプローチを用い、訓練可能な分布補正係数を導入しました。これらにより、モデル訓練の効率を高めることが可能になります。これは記事の実践的な部分で確認されました。

MQL5を用いて提案アルゴリズムを実装しました。この実装では、モデルの訓練プロセスを別のクラスメソッドに移行するアプローチが示されました。これにより、メインプログラム側の作業を大幅に減らし、使い方をシンプルにすることができます。

新しいデータで訓練し、訓練されたモデルをテストしました。テスト結果で、実装が効率的であることを証明しました。訓練されたモデルは、得られた経験を新しいデータに反映させることができました。テスト中、EAは利益を上げました。

しかし、紹介されたプログラムはすべて、この技術を使う可能性を示しているに過ぎません。これらは実際の金融市場で使用する準備ができていません。EA は、実際の市場で使用される前に、改良し、追加のテストをおこなう必要があります。

リンク

楽観的Actor Criticによる探索

楽観的探索と分布補正による強化学習

ニューラルネットワークが簡単に（第49回）：Soft Actor-Critic

ニューラルネットワークが簡単に（第50回）：Soft Actor-Critic (モデル最適化)

ニューラルネットワークが簡単に（第51回）：Behavior-Guided Actor-Critic (BAC)

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	Study.mq5	EA	エージェント訓練EA
3	Test.mq5	EA	モデルテストEA
4	Trajectory.mqh	クラスライブラリ	システム状態記述構造
5	Net_SAC_DICE.mqh	クラスライブラリ	モデルクラス
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13055

添付されたファイル |

ZIPをダウンロード

MQL5.zip (411.75 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークが簡単に（第53回）：報酬の分解

報酬関数を正しく選択することの重要性については、すでに何度かお話ししました。報酬関数は、個々の行動に報酬またはペナルティを追加することでエージェントの望ましい行動を刺激するために使用されます。しかし、エージェントによる信号の解読については未解決のままです。この記事では、訓練されたエージェントに個々のシグナルを送信するという観点からの報酬分解について説明します。

リプレイシステムの開発 - 市場シミュレーション（第17回）：ティックそしてまたティック(I)

ここでは、非常に興味深いものを実装する方法を見ていきますが、同時に、非常にわかりにくい点があるため非常に難しくなります。起こり得る最悪の事態は、自分をプロだと思っている一部のトレーダーが、資本市場におけるこれらの概念の重要性について何も知らないことです。さて、ここではプログラミングに焦点を当てていますが、私たちが実装しようとしているものにとって最も重要なのは市場取引に伴う問題のいくつかを理解することです。

リプレイシステムの開発 - 市場シミュレーション（第18回）：ティックそしてまたティック(II)

明らかに、現在の指標は1分足を作成するのに理想的な時間からは程遠いです。それが最初に修正することです。同期の問題を解決するのは難しくありません。難しそうに思えるかもしれませんが、実際はとても簡単です。前回の記事の目的は、チャート上の1分足を作成するために使用されたティックデータを気配値ウィンドウに転送する方法を説明することであったため、必要な修正はおこないませんでした。

MetaTrader 5でのモンテカルロ並べ替え検定

この記事では、Metatrader 5のみを使用して、任意のエキスパートアドバイザー（EA)でシャッフルされたティックデータに基づいて並べ替え検定を実施する方法を見てみましょう。