ニューラルネットワークが簡単に（第49回）：Soft Actor-Critic

MetaTrader 5 — トレーディングシステム | 18 12月 2023, 09:45

297

Dmitriy Gizlyk

はじめに

連続行動空間での強化学習を使用して問題を解決するためのアルゴリズムについて引き続き学習します。前回の記事では、方策勾配アルゴリズム(DDPG)アルゴリズムとTD3 (Twin Delayed Deep Deterministic policy gradient)アルゴリズムについて検討しました。この記事では、別のアルゴリズムであるSoft Actor-Critic (SAC)に焦点を当てます。このアルゴリズムは最初に「Soft Actor-Critic:Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor」（2018年1月）稿で紹介されました。この手法はTD3とほぼ同時に発表されました。いくつかの類似点がありますが、アルゴリズムに違いもあります。SACの主な目標は、方策の最大エントロピーを考慮して期待される報酬を最大化することであり、これにより確率的環境でさまざまな最適な解を見つけることができます。

1.Soft Actor-Criticアルゴリズム

SACアルゴリズムを検討する際には、それがTD3メソッドの直接の子孫ではない（またその逆も同様）ことにすぐに注意する必要があります。しかし、それらにはいくつかの類似点があります。特に、以下の点です。

どちらも方策外のアルゴリズムである
どちらもDDPGメソッドを利用する
どちらも2つのCriticを使用する

ただし、前に説明した2つの方法とは異なり、SACは確率的Actor方策を使用します。これにより、アルゴリズムはActorの行動の最大限の多様性を考慮して、さまざまな戦略を探索し、最適な解を見つけることができます。

環境の確率性について言えば、S状態でA行動を実行すると、[Rmin,Rmax]以内でPsaの確率でR報酬が得られることがわかります。

Soft Actor-Criticは、確率的方策を持つActorを使用します。これは、S状態のActorが特定のPa'確率で行動空間全体からA'行動を選択できることを意味します。言い換えれば、各特定の状態におけるActorの方策により、特定の最適な行動を1つ選択するのではなく、可能な行動のいずれかを（ただし、ある程度の確率で）選択することができます。訓練中に、Actorは最大の報酬を得る確率分布を学習します。

確率的Actor方策のこの特性により、さまざまな戦略を探索し、決定論的方策の使用時に隠れている可能性がある最適な解を発見することができます。さらに、確率的Actor方策では、環境の不確実性が考慮されます。ノイズやランダムな要因が発生した場合、そのような方策は環境と効果的に相互作用するさまざまな行動を生成できるため、より回復力と適応性が高くなります。

ただし、Actorの確率論的方策を訓練すると、訓練も調整されます。古典的な強化学習は、期待される利益を最大化することを目的としています。訓練中に、各S行動に対して、より高い収益性をもたらす可能性が最も高いA*行動を選択します。この決定論的アプローチは、St→At→St+1⇒Rという明確な関係を構築し、確率的動作の余地を残しません。確率的方策を訓練するために、Soft Actor-Criticアルゴリズムの作成者は、エントロピー正則化を報酬関数に導入しました。

この文脈におけるエントロピー(H)は、政策の不確実性または多様性の尺度です。ɑ>0パラメータは、環境の研究とモデルの操作の間のバランスをとることを可能にする温度係数です。

ご存知のとおり、エントロピーは確率変数の不確実性の尺度であり、次の方程式によって決定されます。

ここでは、[0,1]の範囲で行動を選択する確率の対数について話していることに注意してください。この許容値の範囲では、エントロピー関数のグラフは減少しており、正の値の領域にあります。したがって、行動を選択する確率が低いほど、報酬は高くなり、モデルは環境を探索することが奨励されます。

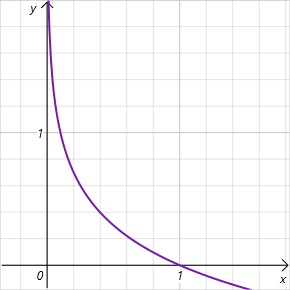
ご覧のとおり、この点で、ɑハイパーパラメータの選択には非常に高い要件が提示されています。現在、SACアルゴリズムを実装するにはさまざまなオプションがあります。従来の固定パラメータのアプローチもあります。パラメータが徐々に減少する実装がよく見られます。ɑ=0の場合、決定論的な強化学習に到達することが簡単にわかります。さらに、学習中にモデル自体によってɑパラメータを最適化するためのさまざまなアプローチがあります。

Criticの訓練に移りましょう。TD3と同様に、SACは損失関数としてMSEを使用して2つのCriticモデルを並行して訓練します。将来状態の予測値には、2つのCriticターゲットモデルの小さい方の値が使用されます。ただし、ここには2つの重要な違いがあります。

1つ目は、上で説明した報酬関数です。システムの次の状態のコストに適用される割引係数を考慮して、現在とその後の状態の両方にエントロピー正則化を使用します。

2番目の違いはActorです。SACはターゲットActorモデルを使用しません。現在およびその後の状態で行動を選択するには、訓練された1つのActorモデルが使用されます。したがって、将来の報酬の達成は現在の方策を使用して達成されることを強調します。さらに、単一のActorモデルを使用すると、メモリとコンピューティングリソースのコストが削減されます。

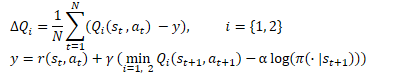
Actor方策を訓練するには、DDPGアプローチを使用します。Criticモデルを通じて予測された行動コストの誤差勾配を逆伝播することにより、行動エラー勾配を取得します。しかし、TD3（Critic1モデルのみを使用）とは異なり、SACの著者らは、推定行動コストが低いモデルを使用することを提案しています。

ここでもう1つ何かがあります。訓練中に方策を変更すると、システムの特定の状態におけるActorの行動が変化します。さらに、確率的Actor方策の使用も、Actor行動の多様性に貢献します。同時に、他のエージェントの行動に対する報酬を使用して、経験再生バッファのデータに基づいてモデルを訓練します。この場合、Actorの訓練の過程で、予測される報酬を最大化する方向に進むという理論的な仮定に基づいています。つまり、どのS状態でも、π新しい新しい方策を使用した行動コストがπ古い方策の行動コストを下回らないということです。

これはかなり主観的な仮定ですが、モデルの訓練パラダイムと完全に一致しています。発生する可能性のあるエラーを蓄積しないように、Actor方策の更新を考慮して、訓練中に経験再生バッファをより頻繁に更新することをお勧めします。

ターゲットモデルの更新は、TD3と同様のτ因子を使用して平滑化されます。

TD3方式との違いがさらに1つあります。Soft Actor-Criticアルゴリズムは、Actorの訓練とターゲットモデルの更新に遅延を使用しません。ここでは、すべてのモデルが各訓練ステップで更新されます。

Soft Actor-Criticアルゴリズムを要約してみましょう。

エントロピー正則化が報酬関数に導入されます。
訓練の開始時に、Actorモデルと2つのCriticモデルがランダムパラメータで初期化されます。
環境との対話の結果として、経験再生バッファが埋められます。環境、行動、その後の状態、報酬の状態をそのまま維持します。
経験再生バッファを埋めた後、モデルを訓練します。

経験再生バッファから一連のデータをランダムに抽出します。
Actorの現在の方策を考慮して、将来の状態に対する行動を決定します。
少なくとも2つのターゲットCriticsモデルの現在の方策を使用して、将来の状態の予測値を決定します。
Criticモデルを更新します。
Actor方策を更新します。
対象モデルを更新します。

モデルの訓練プロセスは反復的であり、目的の結果が得られるか、Critics損失関数グラフの最小値に到達するまで繰り返されます。

2.MQL5を使用した実装

Soft Actor-Criticアルゴリズムの理論的な概要を説明したので、MQL5を使用したその実装に進みます。最初に直面するのは、特定の行動の確率を決定することです。実際、これはActor方策の表形式の実装に対する非常に単純な質問です。しかし、ニューラルネットワークを使用する場合、問題が発生します。結局のところ、私たちは環境条件や実行された行動に関する統計を保持していません。これはモデルのカスタマイズ可能なパラメータに「組み込まれて」います。これに関連して、分散型Q学習について思い出しました。覚えていらっしゃるかもしれませんが、期待される報酬の確率分布を研究することについて話しました。分散型Q学習により、指定された数の固定間隔の報酬値の確率分布を取得できるようになりました。完全にパラメータ化されたQ関数(FQF)モデルを使用すると、間隔値とその確率の両方を調べることができます。

2.1 新しいニューラル層クラスの作成

CNeuronFQFクラスから継承して、提案されたCNeuronSoftActorCriticアルゴリズムを実装するための新しいニューラル層クラスを作成します。新しいクラスのメソッドのセットは非常に標準的ですが、独自の特徴もあります。

特に、ここでの実装では、カスタムのエントロピー正則化パラメータを使用することにしました。この目的のために、cAlphasニューラル層が追加されました。この実装では、CNeuronConcatenate型の層を使用します。比率のサイズを決定するために、出力で現在の状態と分位数分布の埋め込みを使用します。

さらに、エントロピー値を記録するための別のバッファを追加しました。これは後で報酬関数で使用します。

追加された両方のオブジェクトは静的に宣言されているため、クラスのコンストラクタとデストラクタを空のままにすることができます。

class CNeuronSoftActorCritic  :  public CNeuronFQF
  {
protected:
   CNeuronConcatenate   cAlphas;
   CBufferFloat         cLogProbs;
 
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronSoftActorCritic(void) {};
                    ~CNeuronSoftActorCritic(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint actions, uint quantiles, 
                          uint numInputs, ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      calcAlphaGradients(CNeuronBaseOCL *NeuronOCL);
   virtual bool      GetAlphaLogProbs(vector<float> &log_probs)       { return (cLogProbs.GetData(log_probs) > 0); }
   virtual bool      CalcLogProbs(CBufferFloat *buffer);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override        const                 {  return defNeuronSoftActorCritic;          }
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

まず、Initクラス初期化メソッドを見ていきます。メソッドのパラメータは、親クラスの同様のメソッドのパラメータを完全に繰り返します。メソッド本体で親クラスのメソッドをすぐに呼び出します。必要なコントロールはすべて親クラスに実装されているため、この手法は頻繁に使用されます。継承されたすべてのオブジェクトの初期化も同様に実行されます。親クラスメソッドの結果を1回確認することで、前述の操作の完全な制御が置き換えられます。追加したオブジェクトを初期化するだけです。

まず、ɑ比計算層を初期化します。上で述べたように、現在の状態の埋め込みをこのモデルの入力に送信します。そのサイズは前のニューラル層のサイズと等しくなります。さらに、現在の層の出力に分位点分布を追加します。これは内部層cQuantile2（親クラスで宣言および初期化）に含まれます。cAlphas層の出力では、個々の行動ごとに温度係数を取得します。したがって、層のサイズは行動の数と等しくなります。

係数は負であってはなりません。この要件を満たすために、この層の活性化関数としてシグモイドを定義しました。

メソッドの最後に、エントロピーバッファをゼロ値で初期化します。そのサイズも行動の数に等しくなります。現在のOpenCLコンテキストにバッファをすぐに作成します。

bool CNeuronSoftActorCritic::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                  uint actions, uint quantiles, uint numInputs, 
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronFQF::Init(numOutputs, myIndex, open_cl, actions, quantiles, numInputs, optimization_type, batch))
      return false;
//---
   if(!cAlphas.Init(0, 0, OpenCL, actions, numInputs, cQuantile2.Neurons(), optimization_type, batch))
      return false;
   cAlphas.SetActivationFunction(SIGMOID);
//---
   if(!cLogProbs.BufferInit(actions, 0) || !cLogProbs.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

次に、フォワードパスの実装に進みます。ここでは、分位数と確率分布を訓練するプロセスを親クラスから変更せずに借用します。ただし、温度係数を決定し、エントロピー値を計算するプロセスを追加する必要があります。さらに、温度の計算にはcAlphas層を介した直接パスの呼び出しが含まれますが、エントロピー値の決定は「0」から実装する必要があります。

Actorの行動ごとにエントロピーを計算する必要があります。現段階では、大きな行動は起こらないと予想されます。すべてのソースデータはOpenCLコンテキストメモリ内にあるため、操作をこの環境に転送するのは論理的です。まず、この機能を実装するプログラムのSAC_AlphaLogProbsOpenCLカーネルを作成します。

カーネルパラメータでは、5つのデータバッファと2つの定数を渡します。

outputs：結果バッファには、各行動の分位値の確率加重合計が含まれます
quantiles：平均分位値（cQuantile2内層結果バッファ）
probs：確率テンソル（cSoftMax内部層の結果バッファ）
alphas：温度係数のベクトル
log_probs：エントロピー値のベクトル（この場合、結果を記録するためのバッファ）
count_quants：各行動の分位数
activation：活性化関数の型

CNeuronFQFクラスは、出力で活性化関数を使用しません。それはクラスの背後にある考え方そのものと矛盾しているとさえ言えます。結局のところ、期待される報酬の分位数の平均値の分布は、モデルの訓練中の実際の報酬自体によって制限されます。ここでの場合、層の出力での連続分布からActorの行動の特定の値が期待されます。さまざまな技術的またはその他の状況により、エージェントに許可される行為の範囲が制限される場合があります。活性化関数を使用すると、これが可能になります。しかし、実際の行動の確率を決定した後、活性化関数が適用される真の確率推定値を取得することが非常に重要です。したがって、このカーネルにその実装を追加しました。

__kernel void SAC_AlphaLogProbs(__global float *outputs,
                                __global float *quantiles,
                                __global float *probs,
                                __global float *alphas,
                                __global float *log_probs,
                                const int count_quants,
                                const int activation
                               )
  {
   const int i = get_global_id(0);
   int shift = i * count_quants;
   float quant1 = -1e37f;
   float quant2 = 1e37f;
   float prob1 = 0;
   float prob2 = 0;
   float value = outputs[i];

カーネル本体の現在の操作フローを特定します。分析中の行動のシリアル番号が表示されます。次に、分位数バッファと確率バッファのシフトを決定します。

次にローカル変数を宣言します。特定の行動の確率を判断するには、最も近い2つの分位数を見つける必要があります。quant1変数には、最低分位数の平均値を書き込みます。quant2変数には、一番上に最も近い分位数の平均値が含まれます。初期段階では、指定された変数を明らかに極値で初期化します。対応する確率をprob1変数とprob2変数に格納し、ゼロ値で初期化します。実際、私たちの理解では、そのような極端な値が得られる確率は「0」です。

バッファからローカル変数値に目的の値を保存します。

OpenCLコンテキストの特定のメモリ構成により、ローカル変数へのアクセスは、グローバルメモリバッファからデータを取得するよりも何倍も高速になります。ローカル変数を操作することで、OpenCLプログラム全体のパフォーマンスが向上します。

目的の値をローカル変数に保存したので、ニューラル層の演算結果のバッファに活性化関数を簡単に適用できます。

   switch(activation)
     {
      case 0:
         outputs[i] = tanh(value);
         break;
      case 1:
         outputs[i] = 1 / (1 + exp(-value));
         break;
      case 2:
         if(value < 0)
            outputs[i] = value * 0.01f;
         break;
      default:
         break;
     }

次に、すべての平均分位値を検索し、最も近い値を探すサイクルを調整します。

ここで、平均分位値を並べ替えていないことに注意してください。加重平均の決定はこれによって影響を受けず、以前は不必要な演算の実行を避けてきました。したがって、高い確率で、目的の値に最も近い分位点は、分位点バッファの隣接する要素には配置されません。したがって、すべての値を反復処理します。

両方の変数に同じ分位値の値を書き込まないようにするために、下限には論理演算子「>=」を使用し、上限には厳密に「<」を使用します。分位点が以前に保存されたものに近い場合、以前に宣言された対応する変数の値を分位点の平均値とその確率に書き換えます。

   for(int q = 0; q < count_quants; q++)
     {
      float quant = quantiles[shift + q];
      if(value >= quant && quant1 < quant)
        {
         quant1 = quant;
         prob1 = probs[shift + q];
        }
      if(value < quant && quant2 > quant)
        {
         quant2 = quant;
         prob2 = probs[shift + q];
        }
     }

ループのすべての反復が完了すると、ローカル変数には最も近い分位数のデータが含まれます。必要な値はその範囲内のどこかにあります。ただし、行動の確率分布に関する私たちの知識は、研究された分布によってのみ制限されます。この場合、2つの最も近い分位数間の確率の線形依存性の仮定を使用します。分位数が十分に大きい場合、実際の行動領域の値の分布範囲が限られていることを考慮すると、私たちの仮定は真実から遠く離れていません。

   float prob = fabs(value - quant1) / fabs(quant2 - quant1);
   prob = clamp((1-prob) * prob1 + prob * prob2, 1.0e-3f, 1.0f);
   log_probs[i] = -alphas[i] * log(prob);
  }

行動の確率を決定した後、行動のエントロピーを決定し、結果の値に温度係数を乗算します。高すぎるエントロピー値を避けるために、確率の下限を0.001に制限しました。

それではメインプログラムに移りましょう。ここでは、CNeuronSoft ActorCritic::feedForwardクラスのフォワードパスメソッドを作成します。

覚えていらっしゃるとおり、ここでは継承されたオブジェクトの仮想メソッドの機能を広く活用しています。したがって、メソッドパラメータは、以前に説明したすべてのクラスの同様のメソッドを完全に繰り返します。

メソッド本体では、まず親クラスのフォワードパスメソッドと、温度係数を計算するための同様の層メソッドを呼び出します。ここでは、これらのメソッドの実行結果を確認するだけです。

bool CNeuronSoftActorCritic::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronFQF::feedForward(NeuronOCL))
      return false;
   if(!cAlphas.FeedForward(GetPointer(cQuantile0), cQuantile2.getOutput()))
      return false;

次に、報酬関数のエントロピー成分を計算する必要があります。これをおこなうために、上で説明したカーネルを起動するプロセスを準備します。分析する行動の数に応じて、1次元のタスク空間で実行します。

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};

いつものように、カーネルを実行キューに入れる前に、初期データをそのパラメータに渡します。

   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_alphas, cAlphas.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_log_probs, cLogProbs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_probs, cSoftMax.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_quantiles, cQuantile2.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_count_quants, (int)(cSoftMax.Neurons() / global_work_size[0])))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

バッファのチェックはおこなっていないことに注意してください。実際、使用されるすべてのバッファは、親クラスメソッドと温度比を計算する層を直接渡す段階ですでにチェックされています。未チェックのまま残っているのは、カーネル操作の結果を記録するための内部バッファだけです。しかし、これは内部オブジェクトです。その作成は、クラスオブジェクトの初期化段階で制御されました。外部プログラムからオブジェクトにアクセスすることはできません。ここでエラーが発生する可能性は非常に低いです。したがって、プログラムを高速化するためにそのようなリスクを負います。

メソッドの最後に、カーネルを実行キューに配置し、操作の結果を確認します。

   if(!OpenCL.Execute(def_k_SAC_AlphaLogProbs, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

この場合、カーネルを実行キューに入れた結果をチェックしていますが、カーネル内で操作を実行した結果はチェックしていないことをもう一度指摘しておきます。結果を取得するには、cLogProbsバッファデータをメインメモリに読み込む必要があります。この機能はGetAlphaLogProbsメソッドに実装されています。メソッドコードは1つの文字列に収まり、クラス構造記述ブロックで提供されます。

リバースパス機能の作成に進みましょう。機能の主要部分は、親クラスのメソッドにすでに実装されています。奇妙に思われるかもしれませんが、ニューラル層を介して誤差勾配を分配する方法さえ再定義するつもりはありません。実際のところ、エントロピー正則化の誤差勾配の分布は、一般的な構造に完全には適合しません。Criticモデルの最後の層から行動によって誤差勾配を取得します。エントロピー正則化自体を報酬関数に含めました。したがって、その誤差も報酬予測のレベル、つまりCritic結果層のレベルになります。ここで2つの質問があります。

追加の勾配バッファを導入すると、リバースパスメソッドの仮想化モデルが混乱します。
Actorのリバースパスの段階では、Criticのエラーに関するデータがまったくありません。モデル全体の新しいプロセスを構築する必要があります。

物事を単純化するために、モデル内の逆伝播プロセスを完全に修正することなく、エントロピー正則化誤差の勾配のみに対して新しい並列プロセスを作成しました。

まず、OpenCLプログラムでカーネルを作成します。そのコードはとても簡単です。結果として得られる誤差勾配にエントロピーを乗算するだけです。次に、温度比を計算するために、層の活性化関数の導関数によって結果の値を調整します。

__kernel void SAC_AlphaGradients(__global float *outputs,
                                 __global float *gradient,
                                 __global float *log_probs,
                                 __global float *alphas_grad,
                                 const int activation
                                )
  {
   const int i = get_global_id(0);
   float out = outputs[i];
//---
   float grad = -gradient[i] * log_probs[i];
   switch(activation)
     {
      case 0:
         out = clamp(out, -1.0f, 1.0f);
         grad = clamp(grad + out, -1.0f, 1.0f) - out;
         grad = grad * max(1 - pow(out, 2), 1.0e-4f);
         break;
      case 1:
         out = clamp(out, 0.0f, 1.0f);
         grad = clamp(grad + out, 0.0f, 1.0f) - out;
         grad = grad * max(out * (1 - out), 1.0e-4f);
         break;
      case 2:
         if(out < 0)
            grad = grad * 0.01f;
         break;
      default:
         break;
     }
//---
   alphas_grad[i] = grad;
  }

ここで、計算を簡素化するために、単純に勾配にlog_probsバッファの値を乗算していることに注意してください。覚えていらｓｓｈさるとおり、フォワードパス中、ここでは温度比を考慮してエントロピー値を設定しました。数学的な観点からは、バッファからの値をこの値で割る必要があります。ただし、温度の場合は活性化関数としてシグモイドを使用します。したがって、その値は常に[0,1]の範囲内になります。1未満の正の数で割ると、誤差勾配が増加するだけです。この場合、意図的にこれをおこないません。

SAC_AlphaGradientsカーネルの作業が終了したら、メインプログラムの作業に進み、CNeuronSoft ActorCritic::calcAlphaGradientsメソッドを作成します。この段階では、まずカーネルを実行キューに入れ、その後内部オブジェクトのメソッドを呼び出します。そのため、プロセスを開始する前に制御ユニットを手配します。

bool CNeuronSoftActorCritic::calcAlphaGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getGradient() ||
      !NeuronOCL.getGradientIndex()<0)
      return false;

次に、カーネルのタスク空間を定義し、入力データをそのパラメータに渡します。

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_outputs, cAlphas.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_alphas_grad, cAlphas.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_gradient, NeuronOCL.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaGradients, def_k_sac_alg_log_probs, cLogProbs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaGradients, def_k_sac_alg_activation, (int)cAlphas.Activation()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

その後、カーネルを実行キューに入れて、操作の実行を監視します。

   if(!OpenCL.Execute(def_k_SAC_AlphaGradients, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }

メソッドの最後で、内部温度係数計算層のリバースパスメソッドを呼び出します。

   return cAlphas.calcHiddenGradients(GetPointer(cQuantile0), cQuantile2.getOutput(), cQuantile2.getGradient());
  }

さらに、CNeuronSoft ActorCritic::updateInputWeightsニューラル層のパラメータを更新するメソッドをオーバーライドします。このメソッドのアルゴリズムは非常にシンプルです。親クラスと内部オブジェクトの同様のメソッドのみを呼び出します。このメソッドの完全なコードは添付ファイルにあります。ここには、新しいクラスのファイルを操作するためのメソッドを含む、記事で使用されているすべてのメソッドとクラスの完全なコードもありますが、これについてはここでは説明しません。

2.2 CNetクラスに変更を加える

新しいクラスが完成したら、作成されたカーネルを処理するための定数を宣言します。また、コンテキストオブジェクトとOpenCLプログラムの初期化プロセスに新しいカーネルを追加する必要があります。新しいカーネルを作成するたびにこの機能について50回以上検討してきましたので、これについては詳しく説明しません。

私たちのライブラリ機能では、ユーザーが特定のニューラル層に直接アクセスすることはできません。インタラクションプロセス全体は、CNetクラスレベルで全体としてモデルの機能を通じて構築されます。エントロピーコンポーネントの値を取得するために、CNet::GetLogProbsメソッドを作成します。

メソッドはパラメータで、値を設定するためのベクトルへのポインタを受け取ります。

メソッド本体では、オブジェクトのレベルを段階的に下げたコントロールのブロックを配置します。まず、ニューラル層の動的配列オブジェクトの存在を確認します。次に、1レベル下に進み、最後のニューラル層のオブジェクトへのポインタを確認します。次に、さらに下に進み、最後の神経層の種類を確認します。これは新しいCNeuronSoft ActorCritic層になります。

bool CNet::GetLogProbs(vectorf &log_probs)
  {
//---
   if(!layers)
      return false;
   int total = layers.Total();
   if(total <= 0 || !layers.At(total - 1))
      return false;
   CLayer *layer = layers.At(total - 1);
   if(!layer.At(0) || layer.At(0).Type() != defNeuronSoftActorCritic)
      return false;
//---
   CNeuronSoftActorCritic *neuron = layer.At(0);

すべてのレベルの制御を正常に通過した後でのみ、神経層の同様の方法に目を向けます。

   return neuron.GetAlphaLogProbs(log_probs);
  }

この段階ではモデルの最後の層のみに限定されていることに注意してください。つまり、層はActorの最終層としてのみ使用できます。

さらに、このメソッドはバッファからデータを読み取るだけであり、計算は開始しません。したがって、それを呼び出すことは、Actorを直接通過した後でのみ意味を持ちます。実際、これは制限ではありません。実際、エントロピーの正則化は、一次データの収集とモデルの訓練中に報酬を形成するためにのみ使用されます。これらのプロセスでは、行動の生成から実行までのActorのフォワードパスが主です。

リバースパスの必要に応じて、CNet::AlphasGradientメソッドを作成します。上で述べたように、エントロピーによる勾配の分布は、以前に構築したプロセスの範囲を超えています。これはメソッドのアルゴリズムにも反映されています。Criticのためにそれを呼び出すような方法でメソッドを構築しました。メソッドのパラメータで、Actorオブジェクトへのポインタを渡します。

このメソッドの制御ユニットのアルゴリズムは、それに応じて構築されます。まず、Actorオブジェクトへのポインタが最新であること、および最新のCNeuronSoft ActorCritic層が含まれていることを確認します。

bool CNet::AlphasGradient(CNet *PolicyNet)
  {
   if(!PolicyNet || !PolicyNet.layers)
      return false;
   int total = PolicyNet.layers.Total();
   if(total <= 0)
      return false;
   CLayer *layer = PolicyNet.layers.At(total - 1);
   if(!layer || !layer.At(0))
      return false;
   if(layer.At(0).Type() != defNeuronSoftActorCritic)
      return true;
//---
   CNeuronSoftActorCritic *neuron = layer.At(0);

制御ブロックの2番目の部分は、最後のCritic層に対して同様のチェックを実行します。ここで、ニューラル層の種類に制限はありません。

   if(!layers)
      return false;
   total = layers.Total();
   if(total <= 0 || !layers.At(total - 1))
      return false;
   layer = layers.At(total - 1);

すべてのコントロールを正常に通過した後、新しいニューラル層の勾配を分散するメソッドに移ります。

   return neuron.calcAlphaGradients((CNeuronBaseOCL*) layer.At(0));
  }

公平を期すために、完全にパラメータ化されたモデルを使用すると、個々の行動の確率を決定できます。ただし、真に確率的なActor方策を作成することはできません。Actorの確率論には、学習された分布からの行動のサンプリングが含まれますが、これはOpenCLコンテキスト側では実行できません。変分自動エンコーダでは、同様の問題を解決するために、再パラメータ化とメインプログラム側で生成されたランダム値のベクトルを使用したトリックを使用しました。ただし、この場合、サンプリングのために確率分布を読み込む必要があります。代わりに、例のデータベースを収集する段階で、（TD3と同様に）計算された値の何らかの環境で値をサンプリングし、そのような行動のエントロピーをモデルに尋ねます。これらの目的のために、CNet::CalcLogProbsメソッドを作成します。そのアルゴリズムはGetLogProbsメソッドの構築に似ていますが、前のアルゴリズムとは異なり、パラメータでサンプリングされた値を含むデータバッファへのポインタを受け取ります。同じバッファ内のメソッド操作の結果として、それらの確率を受け取ります。

すべてのクラスとそのメソッドの完全なコードは、添付ファイルにあります。

2.3 モデル訓練EAの作成

モデルの新しいオブジェクトを作成する作業が完了したら、モデルの作成と訓練のプロセスの調整に進みます。前と同様に、3つのEAを使用します。

Research：事例データベースの収集
Study：モデルの訓練
Test：得られた結果の確認

記事を短くして時間を節約するために、、問題のアルゴリズムを整理するには前の記事から同様のＥＡのバージョンに加えられた変更点のみに焦点を当てます。

まずはモデルのアーキテクチャです。ここでは最後のActor層のみを変更し、新しいCNeuronSoft ActorCriticクラスに置き換えました。（FQFメソッドの作成者が推奨しているように）行動の数と各行動の32分位数によって層サイズを指定しました。

前回の記事の実験と同様に、活性化関数としてシグモイドを使用しました。

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//--- Actor
.........
.........
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftActorCritic;
   descr.count = NActions;
   descr.window_out = 32;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- Critic
.........
.........
//---
   return true;
  }

「...\Soft ActorCritic\Research.mq5」EAアルゴリズムは、ほとんど変更せずに前の記事から転送されました。履歴データ収集ブロックも取引操作ブロックも何も変更されていません。環境報酬に関してはOnTick関数のみに変更が加えられました。上で述べたように、Soft Actor-Criticアルゴリズムは、報酬関数にエントロピー正則化を追加します。

以前と同様に、口座残高の相対的な変化を補償として使用します。また、ポジションがない場合のペナルティも追加します。しかし、次にエントロピー正則化を追加する必要があります。このために、上記のCalcLogProbsメソッドを作成しました。1つ注意点があります。このクラスの分位分布には、活性化関数までの値が格納されます。意思決定プロセスでは、Actorモデルの活性化された結果を使用します。Actorの出力で活性化関数としてシグモイドを使用します。

数学的変換を通じて、次のようになります。

このプロパティを使用して、サンプリングされた行動を必要な形式に調整してみましょう。次に、データをベクターからデータバッファに転送し、可能であれば、情報をOpenCLコンテキストメモリに転送します。

このような準備作業が完了したら、Actorに実行された行動のエントロピーを要求します。

温度比を考慮して6つの行動のエントロピーが得られたことに注意してください。しかし、私たちの報酬は、現在の状態と行動全体を評価する1つの数字です。この実装では、合計エントロピー値を使用しました。これは、複雑なイベントの確率がその構成要素イベントの確率の積に等しいため、確率と対数のコンテキストによく適合します。そして、積の対数は、個々の因子の対数の合計に等しくなります。ただし、他のアプローチもあるかもしれません。個々のケースに対するそれらの適切性は、訓練中にチェックできます。実験することを恐れないでください。

void OnTick()
  {
//---
.........
.........
//---
   float reward = Account[0];
   if((buy_value + sell_value) == 0)
      reward -= (float)(atr / PrevBalance);
   for(ulong i = 0; i < temp.Size(); i++)
      sState.action[i] = temp[i];
   temp.Clip(0.001f, 0.999f);
   temp = MathLog((temp - 1.0f) * (-1.0f) / temp) * (-1);
   Result.AssignArray(temp);
   if(Result.GetIndex() >= 0)
      Result.BufferWrite();
   if(Actor.CalcLogProbs(Result))
     {
      Result.GetData(temp);
      reward += temp.Sum();
     }
   if(!Base.Add(sState, reward))
      ExpertRemove();
  }

最も重要な変更は、「...\Soft ActorCritic\Study.mq5」EAのモデル訓練に加えられました。指定されたEAのTrain関数を詳しく見てみましょう。ここで、モデルの訓練プロセス全体が整理されます。

関数の開始時に、以前と同様に、経験再生バッファから一連のデータをサンプリングします。

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));

次に、将来の状態の予測値を決定します。TD3メソッドの実装では、アルゴリズムは同様のプロセスを繰り返します。唯一の違いは、ターゲットActorモデルが存在しないことです。ここでは、訓練可能なActorモデルを使用して、将来の状態での行動を決定します。

      //--- Target
      State.AssignArray(Buffer[tr].States[i + 1].state);
      float PrevBalance = Buffer[tr].States[i].account[0];
      float PrevEquity = Buffer[tr].States[i].account[1];
      Account.Clear();
      Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i + 1].account[2]);
      Account.Add(Buffer[tr].States[i + 1].account[3]);
      Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
      //---
      if(Account.GetIndex() >= 0)
         Account.BufferWrite();

ソースデータバッファにデータを入力し、ActorのフォワードパスメソッドとCriticの2つのターゲットモデルを呼び出します。

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         ExpertRemove();
         break;
        }
      //---
      if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
         !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

TD3メソッドと同様に、予測された状態コストの最小値を使用してCriticを訓練します。ただし、この場合はエントロピーコンポーネントを追加します。

      vector<float> log_prob;
      if(!Actor.GetLogProbs(log_prob))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      TargetCritic1.getResults(Result);
      float reward = Result[0];
      TargetCritic2.getResults(Result);
      reward = Buffer[tr].Revards[i] + DiscFactor * (MathMin(reward, Result[0]) + log_prob.Sum() - Buffer[tr].Revards[i + 1]);

ここで、軌跡を保存する過程で、割引係数を考慮して通過の終了までの累積報酬額を保存したことに注意してください。この場合、新しい状態への個々の遷移に対する報酬には、エントロピーの正則化が含まれます。Criticモデルを訓練するには、更新された方策の使用を考慮して、保存されている累積報酬を調整します。これをおこなうために、エントロピーコンポーネントと再生バッファに保存されたこの状態の累積報酬経験を考慮して、後続の状態の最小予測コストの差を計算します。結果の値を割引係数で調整し、現在の状態の保存された値に追加します。この場合、行動のコストはモデルを最適化するプロセスでは減少しないという仮定を使用します。

次に、Criticsモデルを訓練する段階に進みます。これをおこなうには、データバッファにシステムの現在の状態を書き込みます。

      //--- Q-function study
      State.AssignArray(Buffer[tr].States[i].state);
      PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      Account.Update(0, (Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      Account.Update(1, Buffer[tr].States[i].account[1] / PrevBalance);
      Account.Update(2, (Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      Account.Update(3, Buffer[tr].States[i].account[2]);
      Account.Update(4, Buffer[tr].States[i].account[3]);
      Account.Update(5, Buffer[tr].States[i].account[4] / PrevBalance);
      Account.Update(6, Buffer[tr].States[i].account[5] / PrevBalance);
      Account.Update(7, Buffer[tr].States[i].account[6] / PrevBalance);
      //---
      Account.BufferWrite();

この場合、OpenCLコンテキスト内に講座状態記述バッファが存在するかどうかはチェックされないことに注意してください。データを保存した直後に、データをコンテキストに転送するメソッドを呼び出すだけです。これは、すべてのモデルが同じOpenCLコンテキストで動作するという事実によって可能になります。このアプローチの利点についてはすでに説明しました。ターゲットモデルでフォワードパスメソッドを呼び出すと、コンテキスト内にバッファがすでに作成されています。そうしないと、実行時にエラーが発生します。したがって、この段階では不必要な検証に時間とリソースを浪費することはもうありません。

データを読み込んだ後、Actorのフォワードパスメソッドを呼び出し、報酬のエントロピーコンポーネントをロードします。

      if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      //---
      Actor.GetLogProbs(log_prob);

この段階では、Criticsの順方向および逆方向のパッセージに必要なデータがすべて揃っています。しかし、この段階で、著者のアルゴリズムからわずかに逸脱しました。実際、このメソッドの作成者は、Criticsのパラメータを更新した後、Actorの方策を更新するために最小スコアを持つCriticを使用することを提案しています。私たちの観察によると、推定値の偏差にもかかわらず、実際の誤差の勾配は実質的に変化していません。そこで私は、Criticsモデルを単純に置き換えることにしました。偶数回目の反復では、経験再生バッファからの行動に基づいてCritic2モデルを更新します。最初のCriticの評価に基づいてActorの方策を訓練します。

      Actions.AssignArray(Buffer[tr].States[i].action);
      if(Actions.GetIndex() >= 0)
         Actions.BufferWrite();
//---
      if((iter % 2) == 0)
        {
         if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Clear();
         Result.Add(reward-log_prob.Sum());
         if(!Critic1.backProp(Result, GetPointer(Actor)) ||
            !Critic1.AlphasGradient(GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Update(0,Buffer[tr].Revards[i]);
         if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
        }

奇数回の反復でCriticモデルの使用を変更します。

      else
        {
         if(!Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Clear();
         Result.Add(reward);
         if(!Critic2.backProp(Result, GetPointer(Actor)) ||
            !Critic2.AlphasGradient(GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Result.Update(0,Buffer[tr].Revards[i]);
         if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
        }

リバースパスメソッドが呼び出される順序に注意してください。まず、リバースCriticパスを実行します。次に、エントロピーコンポーネントに勾配を渡します。次に、Actorのプライマリデータ処理ブロックを介してリバースパスを実行します。これにより、畳み込み層をCriticの要件に合わせて調整することができます。これをすべておこなった後、Actorの完全なリバースパスを実行して、その行動の方策を最適化します。

関数操作の最後に、ターゲットモデルを更新し、訓練プロセスを視覚的に監視するためにユーザーに情報メッセージを表示します。

      //--- Update Target Nets
      TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau);
      TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
      //---
      if(GetTickCount() - ticks > 500)
        {
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError());
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }
   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError());
   ExpertRemove();
//---
  }

EAの完全なコードは、添付ファイルに記載されています。そこにはテストEAコードもあります。これに加えられた変更は、プライマリデータ収集EAの変更と同様であるため、ここでは詳しく説明しません。

3.検証

このモデルは、2023年1月から5月までのEURUSDH1の履歴データに基づいて訓練およびテストされました。指標のパラメータとすべてのハイパーパラメータはデフォルト値に設定されました。

残念なことに、この記事の執筆中に、訓練セットで利益を生み出すことができるモデルを訓練できなかったことを認めなければなりません。テスト結果によると、私のモデルは5か月の訓練期間中に3.8%減少しました。

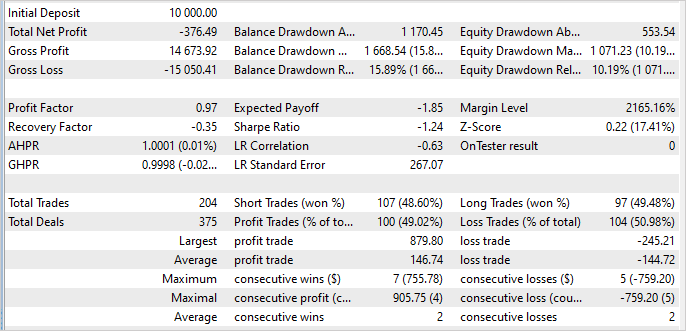
良い面としては、利益を得る最大取引額は、1取引あたりの最大損失額の3.6倍です。勝ち取引の平均は負け取引の平均よりわずかに高いだけです。しかし、収益性の高い取引の割合は49%です。本来、この1%では「0」に達するのに十分ではありませんでした。

訓練セット外のデータについては、状況はほとんど変わりませんでした。収益性の高い取引の割合さえ51%に増加しました。しかし、収益性の高い取引の平均規模は減少し、再び損失が発生しました。

訓練セット外のテスト

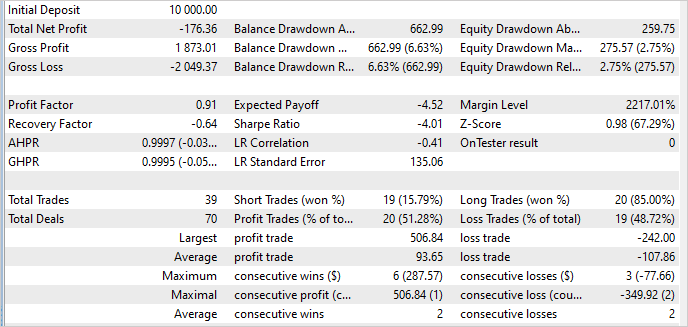
訓練セット外のモデルの安定性はプラスの要因です。しかし、どうすれば損失をなくせるかという問題は残ります。おそらく、その理由は、アルゴリズムの変更、またはより市場調査を刺激する温度比率の上昇にあると考えられます。

さらに、サンプリングされた行動値が分散しすぎていることが原因である可能性があります。「0」に近い確率で行動をサンプリングすると、高いエントロピーによって報酬が膨張し、これによりActorの方策が歪められます。原因を特定するには追加の検査が必要です。その結果を皆さんと共有します。

結論

この記事では、連続行動空間で問題を解決するために設計されたSoft Actor-Critic (SAC)アルゴリズムを紹介しました。これは、方策のエントロピーを最大化するという考えに基づいており、エージェントがさまざまな戦略を探索し、行動の最大の多様性を考慮して確率的環境で最適な解を見つけることができます。

この方法の著者らは、訓練目的関数に追加されるエントロピー正則化を使用することを提案しました。これにより、アルゴリズムが新しい行動の探索を促進し、特定の戦略に固執しすぎるのを防ぐことができます。

MQL5を使用してこのメソッドを実装しましたが、残念ながら、収益性の高い戦略を訓練することはできませんでした。ただし、訓練されたモデルは、訓練セットの内外で安定したパフォーマンスを示します。これは、得られた経験を一般化し、それを未知の環境条件に移すこの手法の能力を示しています。

収益性の高いActor方策を訓練する機会を探すことを目標に設定しました。結果は後ほどご紹介します。

参考文献リスト

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	サンプルコレクションEA
2	Study.mq5	EA	エージェント訓練EA
3	Test.mq5	EA	モデルテストEA
4	Trajectory.mqh	クラスライブラリ	システム状態記述構造
5	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
6	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/12941

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1294.79 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

リプレイシステムの開発 - 市場シミュレーション（第13回）：シミュレーターの誕生（III）

ここでは、次回以降の仕事に関連するいくつかの要素を簡略化します。シミュレーターが生成するランダム性を視覚化する方法も説明しましょう。

離散ハートレー変換

この記事では、スペクトル分析と信号処理の方法の1つである離散ハートレー変換について説明します。信号のフィルタリング、スペクトルの分析などが可能になります。DHTの能力は離散フーリエ変換の能力に劣りません。ただし、DFTとは異なり、DHTは実数のみを使用するため、実際の実装がより便利であり、その適用結果はより視覚的です。

リプレイシステムの開発 - 市場シミュレーション（第9回）：カスタムイベント

ここでは、カスタムイベントがどのようにトリガーされ、指標でどのようにリプレイ/シミュレーションサービスの状態がレポートされるかを見ていきます。

MQL5の構造体とデータ表示メソッド

この記事では、MqlDateTime、MqlTick、MqlRates、MqlBookInfoの各構造体と、それらからデータを表示するメソッドについて見ていきます。構造体のすべてのフィールドを表示するためには、標準的なArrayPrint()関数があります。この関数では、配列に含まれるデータを便利な表形式で、扱われる構造体の型とともに表示します。