MetaTrader 5 / Торговые системы
English 中文 Español Deutsch 日本語 Português
preview
Нейросети — это просто (Часть 52): Исследование с оптимизмом и коррекцией распределения

Нейросети — это просто (Часть 52): Исследование с оптимизмом и коррекцией распределения

MetaTrader 5 — Торговые системы | 1 августа 2023, 13:04
1 093 16
Dmitriy Gizlyk
Dmitriy Gizlyk

Введение

Один из базовых элементов повышения стабильности обучения Q-функции является использование буфера воспроизведения опыта. Увеличение буфера дает возможность собрать больше разнообразных примеров взаимодействия со средой. Что в целом позволяет нашей модели более качественно изучить и воспроизвести Q-функцию окружающей среды. Данный прием широко используется в различных алгоритмах обучения с подкреплением, в том числе и алгоритмах семейства Актер-Критик.

Но есть и обратная сторона медали. В процессе обучения действия Актера все больше отличаются от примеров, сохраненных в буфере воспроизведения опыта. И чем больше итераций обновления параметров модели, тем больше эта разница. Что приводит к снижению эффективности обучения политики Актера. Один из вариантом решения данной проблемы был представлен в статье "Off-policy Reinforcement Learning with Optimistic Exploration and Distribution Correction" (октябрь 2021г.) Авторы метода предложили адаптировать метод корректировки распределения Distribution Correction Estimation (DICE) к алгоритму Soft Actor-Critic.

Вместе с тем авторы метода обратили внимание еще на один момент. В процессе обучения политик метод Soft Actor-Critic использует минимальную оценку действий. Опыт практического использования такого подхода демонстрирует склонность к пессимистическому недостаточному исследованию окружающей среды и направленной однородности действий. Для минимизации этого эффекта авторы статьи предложили дополнительно обучать оптимистическую исследовательскую модель Актера. Что в свою очередь ещё больше увеличивает разрыв между примера взаимодействия оптимистической модели Актера с окружающей средой и распределения действий обучаемой целевой модели.

Однако совместное использование коррекции оценок распределения и исследования оптимистической модели Актера позволяют улучшить результат обучения целевой модели.


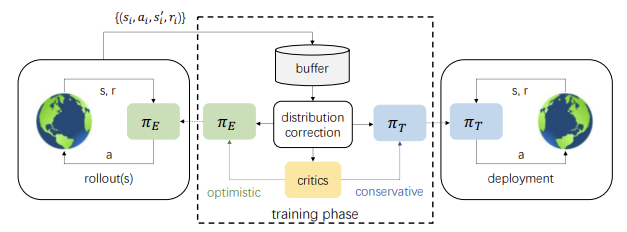
1. Исследование с оптимизмом

Надо сказать, что первые идеи об исследовании окружающей среды с оптимизмом были опубликованы в статье "Better Exploration with Optimistic Actor-Critic" (октябрь 2019г.). Именно ее авторы обратили внимание, что сочетание жадного обновления актера с пессимистичной оценкой критика приводит к избеганию действий, о которых агент не знает. Данное явление было названо "пессимистическим недоисследованием". Кроме того, большинство алгоритмов не информированы о направлении исследования. Случайным образом семплированые действия с равной вероятностью расположены по противоположные стороны от текущего среднего значения. В то время, как обычно нам нужны действия, предпринимаемые в определенных направлениях, гораздо больше, чем в других. Для коррекции этих явлений был предложен алгоритм Optimistic Actor Critic (OAC), который аппроксимирует нижнюю и верхнюю доверительные границы функции ценности состояния-действия. Это позволило использовать принцип оптимизма в неопределенности выполнения направленного исследования с использованием верхней границы. В то же время нижняя граница помогает избежать переоценки действий.

Авторы рассматриваемого в данной статье метода подхватили и развили идеи Optimistic Actor Critic. Как и в Soft Actor-Critic мы будем обучать 2 модели Критиков. Но вместе с тем, мы будем обучать и 2 модели Актера: исследования πе и целевой πт.

Политика πе обучается максимизации приближенной верхней границы значений Q-функции QUB. Одновременно πт в процессе обучения максимизирует приближение нижней границы Q-функции QLB. OAC показывает, что исследование с использованием πе позволяет достигать более эффективного использования выборки по сравнению с Soft Actor-Critic.

Для получения приближенной верхней границы Q-функции QUB сначала вычисляются среднее значение и дисперсия оценок обоих Критиков:

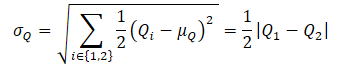
Далее мы определяет QUB по формуле:

где βUB ∈ R и управляет уровнем оптимизма.

Обратите внимание, что предыдущая приближенная нижняя граница Q-функции QLB может быть выражена как

При уровне пессимизма βLB = 1 QLB равняется минимальной из оценок Критиков.

В Optimistic Actor-Critic применяется ограничение максимального расхождение KL между πе и πт, что позволяет получить закрытое решение для πе и стабилизирует обучение. В то же время это ограничивает потенциал πе в выполнении более информативных действий, которые потенциально могут скорректировать ложные оценки критиков. Так как это ограничение не позволяет πе генерировать действия, которые сильно отличаются от генерируемых политикой πт, обучаемой консервативно на основе минимальной оценки критиков.

В алгоритме SAC+DICE добавление коррекции распределений позволяет отказаться от использования ограничения KL для раскрытия всех возможностей исследования оптимистической политикой. При этом стабильность обучения сохраняется путем явной коррекции смещенной оценки градиента при обучении политики.

В процессе обучения поведенческой политики Актера πт для предотвращения переоценки Q-функции используется приближенная нижняя граница QLB в качестве критика, как и в методе Soft Actor-Critic. Но добавляется корректировка распределение выборки с помощью отношения dπт(s,a)/dD(s,a). Получаем следующую обучающую цель:

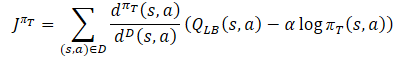
где dπт(s,a) представляет собой распределение состояние-действие текущей политики, а dD(s,a) — распределение состояние-действие из буфера воспроизведения опыта. Градиент такой обучающей цели предоставляет несмещенную оценку градиента политики, в отличие от предыдущих алгоритмов обучения Актер-Критик, использующих смещенную оценку при обучении целевой политики.

Политика исследования πе должна изучать оптимистичное смещение относительно оцененных значений Q-функции, чтобы собирать опыт для эффективной коррекции ложных оценок. Поэтому авторы метода предложили использовать приближенную верхнюю границу, аналогично Optimistic Actor-Critic QUB в качестве Критика в целевой функции. Конечной целью политики πе и лучшей оценки Q-функции является облегчение более точной оценки градиента для целевой политики πт. Поэтому распределение выборки для функции потерь πе должно быть согласовано с поведенческой политикой πт. Как следствие, авторы метода предлагают использовать тот же коэффициент коррекции, что и для функции потерь целевой политики Актера.

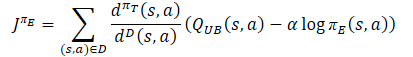
Касательно Критиков сохраняется ранее рассмотренный подход из Soft Actor-Critic. И для их обучения используется нижняя граница Q-функции целевых моделей. Однако, существует ряд исследований, в которых доказывается эффективность использования одних выборок для обучения Актеров и Критиков. Поэтому в функцию потерь Критиков был также добавлен коэффициент коррекции распределений.

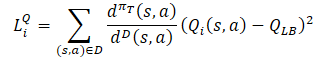
Как можно заметить, из всего описанного выше наибольшее количество вопросов вызывает коэффициент коррекции распределения. О нем продолжение нашей статьи.


2. Коррекция распределения

Семейство алгоритмов Distribution Correction Estimation (DICE) предназначено для решения задачи коррекции оценки без вмешательства (Off-Policy Evaluation - OPE). Данные методы позволяют обучить оценщик значения политики, то есть нормализованной ожидаемой награды за один шаг, на основе статического буфера повтора D. DICE получает несмещенный оценщик, который оценивая коэффициент коррекции распределения. 

Для оценки коэффициента коррекции распределения авторы метода адаптировали схему оптимизации DICE, которая может быть сформулирована как минимаксная линейная программа распределения с различными регуляризациями. Прямое применение алгоритмов DICE к настройкам обучения с подкреплением вне политики вызывает значительные трудности с оптимизацией. Обучение с оценкой без вмешательства предполагает фиксированную целевую политику и статический буфер повтора с достаточным покрытием пространства состояний-действий, а в RL целевая политика и буфер воспроизведения опыта меняются в процессе обучения. Поэтому авторы метода SAC+DICE вносят несколько модификации, чтобы преодолеть эти сложности. Мы не будем сейчас погружаться в математику и останавливаться на рассмотрении этих модификаций. Все желающие могут найти их в оригинальной статье. Приведем лишь функции потерь, полученные в результате предложенных модификаций.

Здесь ζ(s,a) и v(s,a) являются моделями нейронных сетей, а λ — настраиваемый коэффициент Лагранжа. ζ(s,a) аппроксимирует коэффициент коррекции распределения. А v(s,a) являет собой подобие критика. И для стабилизации процесса обучения, аналогично Критику, мы будем использовать целевую модель v с мягким обновлением её параметров.

Для оптимизации всех параметров авторы предлагают использовать метод Adam.

Все выше сказанное обобщается в единый алгоритм SAC+DICE. Как и в случае с обычными алгоритмами обучения с подкреплением вне политики, мы последовательно выполняем взаимодействие с окружающей средой, следуя оптимистической политике исследования πе, и сохраняем данные в буфер воспроизведения опыта. На каждом шаге обучения рассматриваемый алгоритм сначала обновляет модели и параметры DICE (v, ζ, λ) с использованием SGD относительно приведенных выше функций потерь.

После чего вычисляем поправочное отношение распределения ζ из обновленной модели.

Затем, с использованием ζ, выполняем обучение RL для обновления πт, πе, Q1 и Q2.

В завершении каждого шага обучения производится мягкое обновление целевых моделей Q1, Q2 и v.



3. Реализация средствами MQL5

При прочтении теоретической части, думаю, вы заметили, как резко увеличивается число обучаемых моделей и параметров. Фактически, число обучаемых моделей возросло с 3 до 6. Процесс их взаимодействия усложняется. В то же время на выходе мы ожидаем получить одну модель поведенческой политики Актера. И чтобы скрыть всю рутинную работу от пользователя мы немного изменим наш подход и обернем весь процесс обучения в отдельный класс CNet_SAC_DICE. Наш новый класс будет наследником базового класса моделей нейронных сетей CNet. В теле класса мы объявим 5 обучаемых моделей и 3 целевых модели. Тут же мы объявим и ряд внутренних переменных, с функционалом которых мы познакомимся в процессе реализации.

class CNet_SAC_DICE  : protected CNet
  {
protected:
   CNet              cActorExploer;
   CNet              cCritic1;
   CNet              cCritic2;
   CNet              cTargetCritic1;
   CNet              cTargetCritic2;
   CNet              cZeta;
   CNet              cNu;
   CNet              cTargetNu;
   float             fLambda;
   float             fLambda_m;
   float             fLambda_v;
   int               iLatentLayer;
   //---
   float             fLoss1;
   float             fLoss2;
   float             fZeta;
   //---
   vector<float>     GetLogProbability(CBufferFloat *Actions);

public:
   //---
                     CNet_SAC_DICE(void);
                    ~CNet_SAC_DICE(void) {}
   //---
   bool              Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1);
   //---
   virtual bool      Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, 
                           vector<float> &ActionsLogProbab, CBufferFloat *NextState, 
                           CBufferFloat *NextSecondInput, float reward, float discount, float tau);
   virtual void      GetLoss(float &loss1, float &loss2)    {  loss1 = fLoss1; loss2 = fLoss2;  }
   //---
   virtual bool      Save(string file_name, bool common = true);
   bool              Load(string file_name, bool common = true);
  };

Обратите внимание, что вначале мы говорили о 6 обучаемых моделях. А объявили только 5 моделей. Среди объявленных моделей нет целевой политики Актера. А ведь цель всего процесса обучения именно в получении данной политики. Дело в том, что наш новый класс, как уже было сказано ранее, является наследником базового класса нейронной сети. А значит и сам является обучаемой моделью. Поэтому обучение основной политики Актера будет осуществляться средствами родительского класса.

Также надо сказать, что создаваемый новый класс CNet_SAC_DICE будет использоваться только для обучения модели. В процессе эксплуатации создание объектов дополнительных моделей не имеет смысла и является излишним потреблением ресурсов. Поэтому мы планируем в процессе эксплуатации использовать базовые объекты моделей. В связи с вышесказанным в новом классе отсутствуют методы прямого и обратного проходов. Весь функционал будет реализован в методе Study.

И конечно присутствуют методы работы с файлами Save и Load. Но обо всем по порядку.

В конструкторе класса мы инициализируем внутренние переменные начальными значениями. Все внутренние объекты объявлены статично и не подлежат инициализации. Соответственно и в деструкторе нам нет необходимости очищать память, что позволяет оставить деструктор пустым.

CNet_SAC_DICE::CNet_SAC_DICE(void)  :  fLambda(1.0e-5f),
                                       fLambda_m(0),
                                       fLambda_v(0),
                                       fLoss1(0),
                                       fLoss2(0),
                                       fZeta(0)
  {
  }

Полная инициализация моделей осуществляется в методе Create. В параметрах метода мы будем передавать динамические массивы описания архитектуры всех используемых моделей и идентификатор латентного слоя Актера со сжатым представлением анализируемого состояния окружающей среды.

В теле метода мы сначала создадим модели Актеров. Оптимистическая модель создается в объекте cActorExploer. А целевая модель в теле нашего класса унаследованными средствами.

bool CNet_SAC_DICE::Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer)
  {
   ResetLastError();
//---
   if(!cActorExploer.Create(actor) || !CNet::Create(actor))
     {
      PrintFormat("Error of create Actor: %d", GetLastError());
      return false;
     }
//---
   if(!opencl)
     {
      Print("Don't opened OpenCL context");
      return false;
     }

Сразу же проверяем созданный указатель контекста OpenCL.

Далее мы создаем обучаемые модели обоих Критиков.

   if(!cCritic1.Create(critic) || !cCritic2.Create(critic))
     {
      PrintFormat("Error of create Critic: %d", GetLastError());
      return false;
     }

А затем объекты DICE блока и целевые модели.

   if(!cZeta.Create(zeta) || !cNu.Create(nu))
     {
      PrintFormat("Error of create function nets: %d", GetLastError());
      return false;
     }
//---
   if(!cTargetCritic1.Create(critic) || !cTargetCritic2.Create(critic) ||
      !cTargetNu.Create(nu))
     {
      PrintFormat("Error of create target models: %d", GetLastError());
      return false;
     }

После успешного создания всех моделей перенесем их в единый контекст OpenCL.

   cActorExploer.SetOpenCL(opencl);
   cCritic1.SetOpenCL(opencl);
   cCritic2.SetOpenCL(opencl);
   cZeta.SetOpenCL(opencl);
   cNu.SetOpenCL(opencl);
   cTargetCritic1.SetOpenCL(opencl);
   cTargetCritic2.SetOpenCL(opencl);
   cTargetNu.SetOpenCL(opencl);

И скопируем параметры моделей в их целевые копии. При этом не забываем контролировать выполнения операций на каждом шаге.

   if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), 1.0) ||
      !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), 1.0) ||
      !cTargetNu.WeightsUpdate(GetPointer(cNu), 1.0))
     {
      PrintFormat("Error of update target models: %d", GetLastError());
      return false;
     }

После успешного создания всех необходимых объектов мы перенесем данные во внутренние переменные и завершаем работу метода.

   fLambda = 1.0e-5f;
   fLambda_m = 0;
   fLambda_v = 0;
   fZeta = 0;
   iLatentLayer = latent_layer;
//---
   return true;
  }

После инициализации внутренних объектов класса мы переходим к работе над методом обучения модели CNet_SAC_DICE::Study.  В параметрах данного класса мы получаем всю информацию, необходимую для одного шага обучения модели. Здесь текущее и последующее состояния окружающей среды. При этом каждое состояние описывается в 2 буферах данных: исторические данные и состояние баланса. Здесь же вы увидите буфер действий и переменная вознаграждения. Так же есть переменные для коэффициентов дисконтирования и мягкого обновления целевых моделей. Мы впервые добавляем вектор логарифмов вероятности исходной политики (используемой при сборе примеров).

bool CNet_SAC_DICE::Study(CArrayFloat *State,
                          CArrayFloat *SecondInput,
                          CBufferFloat *Actions,
                          vector<float> &ActionsLogProbab,
                          CBufferFloat *NextState,
                          CBufferFloat *NextSecondInput,
                          float reward,
                          float discount,
                          float tau)
  {
//---
   if(!Actions || Actions.Total()!=ActionsLogProbab.Size())
      return false;

В теле метода мы сначала организуем небольшой контрольный блок, в котором проверим актуальность указателя на буфер действий и соответствие его размера и размера вектора логарифмов вероятностей. Мы не проверяем указатели на остальные буферы, так их контроль реализован в вызываемых методах.

После успешного прохождения контрольного блока мы осуществляем оценки последующего состояния целевыми моделями с учетом текущей политики. Для этого мы сначала осуществляем прямой проход нашей консервативной политики Актера. Его мы используем для предварительной обработки сырых данных описания текущего состояния и прогнозирования вектора действий из этого состояния. Полученные данные мы передаем в 2 целевые модели Критиков и модель v из блока DICE.

   if(!CNet::feedForward(NextState, 1, false, NextSecondInput))
      return false;
   if(!cTargetCritic1.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1) ||
      !cTargetCritic2.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1))
      return false;
//---
   if(!cTargetNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1))
      return false;

Следующим этапом мы подготовим данные текущего состояния. Как и для последующего состояния, мы используем текущую модель консервативного Актера для предварительной обработки описания текущего состояния.

   if(!CNet::feedForward(State, 1, false, SecondInput))
      return false;
   CBufferFloat *output = ((CNeuronBaseOCL*)((CLayer*)layers.At(layers.Total() - 1)).At(0)).getOutput();
   output.AssignArray(Actions);
   output.BufferWrite();

Здесь же мы выполняем небольшой трюк с подменой результатов прямимого прохода. Вместо полученных действий текущей политики Актера мы сохраним в буфер результатов последнего нейронного слоя тензор действий из буфера воспроизведения опыта. Цель данной операции в сохранении соответствия между действием и вознаграждением от окружающей среды. Да, мы осознаём, что в процессе прямого прохода с большой долей вероятности были сформированы иные действия. Но наш нейронный слой CNeuronSoftActorCritic в недрах своих внутренних объектов изучает распределение действий и их вероятностей. И при обратном проходе будут определены квантили и вероятности, соответствующие действиям из буфера воспроизведения опыта. При этом несмещенный градиент пройдет именно в эти квантили, что позволит точнее и без искажений обучать модель Актера.

После подготовки данных текущего состояния окружающей среды мы можем осуществить прямой проход моделей DICE блока. И, конечно, не забываем контролировать процесс выполнения операций.

   if(!cNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this)))
      return false;
   if(!cZeta.feedForward(GetPointer(this), iLatentLayer, GetPointer(this)))
      return false;

В соответствии с алгоритмом SAC+DICE вначале мы осуществляем обновление моделей и параметров DICE блока. Но перед обновлением параметров нам необходимо вычислить значения функций потерь для v, ζ, λ.

Обратите внимание, что для получения значения функций потерь нам необходимо целевое значение отношения вероятностей состояния-действий в текущей консервативной политике и при взаимодействии с окружающей средой во время сбора базы примеров. Здесь надо сказать, что исторические данные описания состояния окружающей среды не зависят от политики Актера. Более того, текущее состояния мы воспринимаем как начальную точку для принятия решения и построения последующей траектории действий. Следовательно, вероятность начального состояния воспринимается равной 1, ведь мы в нем находимся.

В процессе обучения политики изменяется лишь вероятностное распределения действий в соответствии с выученной стратегией. Поэтому нашим целевым значением будет отношение вероятностей действий в двух политиках. В процессе операций вместо отношения вероятностей мы будем использовать разницу логарифмом вероятностей. При этом вместо умножения вероятностей всех действий мы воспользуемся суммой их логарифмов с восстановлением значения через экспоненту. 

   vector<float> nu, next_nu, zeta, ones;
   cNu.getResults(nu);
   cTargetNu.getResults(next_nu);
   cZeta.getResults(zeta);
   ones = vector<float>::Ones(zeta.Size());
   vector<float> log_prob = GetLogProbability(output);
   float policy_ratio = MathExp((log_prob - ActionsLogProbab).Sum());
   vector<float> bellman_residuals = next_nu * discount * policy_ratio - nu + policy_ratio * reward;
   vector<float> zeta_loss = zeta * (MathAbs(bellman_residuals) - fLambda) * (-1) + MathPow(zeta, 2.0f) / 2;
   vector<float> nu_loss = zeta * MathAbs(bellman_residuals) + MathPow(nu, 2.0f) / 2.0f;
   float lambda_los = fLambda * (ones - zeta).Sum();

После определения значений функции потерь мы определим градиенты ошибок и обновим параметры. Сначала мы обновляем значения коэффициента Лагранжа. В процессе корректировки параметра мы используем алгоритм метода Adam.

//--- update lambda
   float grad_lambda = (ones - zeta).Sum() * (-lambda_los);
   fLambda_m = b1 * fLambda_m + (1 - b1) * grad_lambda;
   fLambda_v = b2 * fLambda_v + (1 - b2) * MathPow(grad_lambda, 2);
   fLambda += lr * fLambda_m / (fLambda_v != 0.0f ? MathSqrt(fLambda_v) : 1.0f);

Далее нам необходимо обновить параметры моделей v, ζ. Следует сказать, что мы определили значения функций потерь, а не целевых значений. При этом функция потерь для каждой модели индивидуальна и сильно отличается от ранее используемых нами. И сейчас мы не будем подгонять операции под базовую функцию потерь нашей модели. Вместо этого мы сразу вычислим градиент ошибки. Перенесем полученное значение в соответствующий буфер модели и распространим градиент ошибки по параметрам модели.

Вначале мы обновим параметры модели v.

//---
   CBufferFloat temp;
   temp.BufferInit(MathMax(Actions.Total(), SecondInput.Total()), 0);
   temp.BufferCreate(opencl);
//--- update nu
   int last_layer = cNu.layers.Total() - 1;
   CLayer *layer = cNu.layers.At(last_layer);
   if(!layer)
      return false;
   CNeuronBaseOCL *neuron = layer.At(0);
   if(!neuron)
      return false;
   CBufferFloat *buffer = neuron.getGradient();
   if(!buffer)
      return false;
   vector<float> nu_grad = nu_loss * (zeta * bellman_residuals / MathAbs(bellman_residuals) + nu);
   if(!buffer.AssignArray(nu_grad) || !buffer.BufferWrite())
      return false;
   if(!cNu.backPropGradient(output, GetPointer(temp)))
      return false;

А затем выполним аналогичные операции для модели ζ.

//--- update zeta
   last_layer = cZeta.layers.Total() - 1;
   layer = cZeta.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   vector<float> zeta_grad = zeta_loss * (zeta - MathAbs(bellman_residuals) + fLambda) * (-1);
   if(!buffer.AssignArray(zeta_grad) || !buffer.BufferWrite())
      return false;
   if(!cZeta.backPropGradient(output, GetPointer(temp)))
      return false;

На этом этапе мы обновили параметры DICE блока и переходим непосредственно к процедуре обучения с подкреплением. Вначале осуществляем прямой проход обоих Критиков. В данном случае мы не осуществляем прямой проход Актера, так как данную операцию мы уже выполнили при обновлении параметров объектов DICE блока.

//--- feed forward critics
   if(!cCritic1.feedForward(GetPointer(this), iLatentLayer, output) ||
      !cCritic2.feedForward(GetPointer(this), iLatentLayer, output))
      return false;

Далее, как и при обновлении DICE параметров, мы определим значения функций потерь. Но сначала проведем небольшую подготовительную работу. Для повышения стабильности обучения модели нормализуем коэффициент коррекции распределения и посчитаем эталонное значение, спрогнозированное целевыми моделями критиков с учетом текущей политики Актера.

   vector<float> result;
   if(fZeta == 0)
      fZeta = MathAbs(zeta[0]);
   else
      fZeta = 0.9f * fZeta + 0.1f * MathAbs(zeta[0]);
   zeta[0] = MathPow(MathAbs(zeta[0]), 1.0f / 3.0f) / (10.0f * MathPow(fZeta, 1.0f / 3.0f));
   cTargetCritic1.getResults(result);
   float target = result[0];
   cTargetCritic2.getResults(result);
   target = reward + discount * (MathMin(result[0], target) - LogProbMultiplier * log_prob.Sum());

Несмотря на наличие целевого значения мы не можем осуществить базовый метод обратного прохода моделей критиков, так как в него не вписывается использование коэффициента коррекции распределения. Поэтому мы применяем выше проработанный прием с расчетом градиента ошибки и прямым его переносом в буфер нейронного слоя результатов с последующим распределением градиентов по модели.

//--- update critic1
   cCritic1.getResults(result);
   float loss = zeta[0] * MathPow(result[0] - target, 2.0f);
   if(fLoss1 == 0)
      fLoss1 = MathSqrt(loss);
   else
      fLoss1 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * loss);
   float grad = loss * 2 * zeta[0] * (target - result[0]);
   last_layer = cCritic1.layers.Total() - 1;
   layer = cCritic1.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   if(!buffer.Update(0, grad) || !buffer.BufferWrite())
      return false;
   if(!cCritic1.backPropGradient(output, GetPointer(temp)) || 
      !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer))
      return false;

Одновременно, мы считаем среднюю ошибку модели, которую будем демонстрировать пользователю для визуального контроля процесса обучения модели.

Повторяем операции для второго критика.

//--- update critic2
   cCritic2.getResults(result);
   loss = zeta[0] * MathPow(result[0] - target, 2.0f);
   if(fLoss2 == 0)
      fLoss2 = MathSqrt(loss);
   else
      fLoss2 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * loss);
   grad = loss * 2 * zeta[0] * (target - result[0]);
   last_layer = cCritic2.layers.Total() - 1;
   layer = cCritic2.layers.At(last_layer);
   if(!layer)
      return false;
   neuron = layer.At(0);
   if(!neuron)
      return false;
   buffer = neuron.getGradient();
   if(!buffer)
      return false;
   if(!buffer.Update(0, grad) || !buffer.BufferWrite())
      return false;
   if(!cCritic2.backPropGradient(output, GetPointer(temp)) || 
      !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer))
      return false;

После обновления параметров Критиков мы переходим к обновлению политик Актеров. Первой мы обновим политику консервативного Актера. Здесь мы рассчитываем целевое значение с учетом нижней границы значений Q-функции и текущего вероятностного распределения действий. Полученное значение скорректируем на коэффициент коррекции распределений и проведем градиент ошибки через модель Критика. Предварительно мы отключим режим обучения данного критика.

//--- update policy
   cCritic1.getResults(result);
   float mean = result[0];
   float var = result[0];
   cCritic2.getResults(result);
   mean += result[0];
   var -= result[0];
   mean /= 2.0f;
   var = MathAbs(var) / 2.0f;
   target = zeta[0] * (mean - 2.5f * var + discount * log_prob.Sum() * LogProbMultiplier) + result[0];
   CBufferFloat bTarget;
   bTarget.Add(target);
   cCritic2.TrainMode(false);
   if(!cCritic2.backProp(GetPointer(bTarget), GetPointer(this)) ||
      !backPropGradient(SecondInput, GetPointer(temp)))
     {
      cCritic2.TrainMode(true);
      return false;
     }

Перед обновлением параметров оптимистической исследовательской политики Актера, мы осуществляем прямой проход указанной модели и подмену значений буфера результатов (как мы ранее сделали для пессимистической модели).

После чего пересчитаем целевое значение с учетом коэффициента оптимизма и распределим градиент ошибки через модель критика.

//--- update exploration policy
   if(!cActorExploer.feedForward(State, 1, false, SecondInput))
     {
      cCritic2.TrainMode(true);
      return false;
     }
   output = ((CNeuronBaseOCL*)((CLayer*)cActorExploer.layers.At(layers.Total() - 1)).At(0)).getOutput();
   output.AssignArray(Actions);
   output.BufferWrite();
   cActorExploer.GetLogProbs(log_prob);
   target = zeta[0] * (mean + 2.0f * var + discount * log_prob.Sum() * LogProbMultiplier) + result[0];
   bTarget.Update(0, target);
   if(!cCritic2.backProp(GetPointer(bTarget), GetPointer(cActorExploer)) ||
      !cActorExploer.backPropGradient(SecondInput, GetPointer(temp)))
     {
      cCritic2.TrainMode(true);
      return false;
     }
   cCritic2.TrainMode(true);

После завершения операций включаем режим обучения критика и обновляем параметры целевых моделей.

   if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), tau) ||
      !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), tau) ||
      !cTargetNu.WeightsUpdate(GetPointer(cNu), tau))
     {
      PrintFormat("Error of update target models: %d", GetLastError());
      return false;
     }
//---
   return true;
  }

На этом мы завершаем работу над методом обучения моделей и переходим к построению методов работы с файлами. Первым мы создаем метод сохранения моделей. Здесь надо сказать, что в отличии от ранее рассмотренных аналогичных методов, мы не будем сохранять все данные в одном файле. Напротив, каждая обучаемая модель получит отдельный файл. Это позволит нам использовать каждую отдельно взятую модель независимо от других.

В параметрах метод сохранения данных CNet_SAC_DICE::Save получит общее имя файла (без расширения) и флаг сохранения в общей папке терминалов. В теле метода мы сразу проверяем наличие имени файла в полученной текстовой переменной.

bool CNet_SAC_DICE::Save(string file_name, bool common = true)
  {
   if(file_name == NULL)
      return false;

Далее мы создаем файл с заданным именем и расширением ".set" с последующим сохранением в него значений внутренних переменных.

   int handle = FileOpen(file_name + ".set", (common ? FILE_COMMON : 0) | FILE_BIN | FILE_WRITE);
   if(handle == INVALID_HANDLE)
      return false;
   if(FileWriteFloat(handle, fLambda) < sizeof(fLambda) ||
      FileWriteFloat(handle, fLambda_m) < sizeof(fLambda_m) ||
      FileWriteFloat(handle, fLambda_v) < sizeof(fLambda_v) ||
      FileWriteInteger(handle, iLatentLayer) < sizeof(iLatentLayer))
      return false;
   FileFlush(handle);
   FileClose(handle);

После чего мы поочередно вызываем методы сохранения моделей и контролируем процесс выполнения операций. Здесь стоит обратить внимание на указываемые имена файлов. Актер с консервативной политикой получает суффикс имения файла "Act.nnw" (как мы и ранее указывали для Актеров. А вот модель оптимистического Актера получила файл с суффиксом "ActExp.nnw". Кроме того, мы сохраняем только целевые модели Критиков и v-модели. Соответствующие обучаемые модели не сохраняются.

   if(!CNet::Save(file_name + "Act.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cActorExploer.Save(file_name + "ActExp.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetCritic1.Save(file_name + "Crt1.nnw", fLoss1, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetCritic2.Save(file_name + "Crt2.nnw", fLoss2, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cZeta.Save(file_name + "Zeta.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   if(!cTargetNu.Save(file_name + "Nu.nnw", 0, 0, 0, TimeCurrent(), common))
      return false;
//---
   return true;
  }

В методе загрузки данных мы повторяем операции в четком соответствии с порядком записи данных. При этом обучаемые и целевые модели загружаются из одних соответствующих файлов.

bool CNet_SAC_DICE::Load(string file_name, bool common = true)
  {
   if(file_name == NULL)
      return false;
//---
   int handle = FileOpen(file_name + ".set", (common ? FILE_COMMON : 0) | FILE_BIN | FILE_READ);
   if(handle == INVALID_HANDLE)
      return false;
   if(FileIsEnding(handle))
      return false;
   fLambda = FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   fLambda_m = FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   fLambda_v =   FileReadFloat(handle);
   if(FileIsEnding(handle))
      return false;
   iLatentLayer =  FileReadInteger(handle);;
   FileClose(handle);
//---
   float temp;
   datetime dt;
   if(!CNet::Load(file_name + "Act.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cActorExploer.Load(file_name + "ActExp.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cCritic1.Load(file_name + "Crt1.nnw", fLoss1, temp, temp, dt, common) ||
      !cTargetCritic1.Load(file_name + "Crt1.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cCritic2.Load(file_name + "Crt2.nnw", fLoss2, temp, temp, dt, common) ||
      !cTargetCritic2.Load(file_name + "Crt2.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cZeta.Load(file_name + "Zeta.nnw", temp, temp, temp, dt, common))
      return false;
//---
   if(!cNu.Load(file_name + "Nu.nnw", temp, temp, temp, dt, common) ||
      !cTargetNu.Load(file_name + "Nu.nnw", temp, temp, temp, dt, common))
      return false;

После загрузки данных моделей мы переносим их в единый контекст OpenCL.

   cActorExploer.SetOpenCL(opencl);
   cCritic1.SetOpenCL(opencl);
   cCritic2.SetOpenCL(opencl);
   cZeta.SetOpenCL(opencl);
   cNu.SetOpenCL(opencl);
   cTargetCritic1.SetOpenCL(opencl);
   cTargetCritic2.SetOpenCL(opencl);
   cTargetNu.SetOpenCL(opencl);
//---
   return true;
  }

На этом мы завершаем работу над классом CNet_SAC_DICE. C полным колом всех его методов Вы можете познакомиться во вложении. А мы продолжаем нашу работу. И тут надо вспомнить, что в параметрах выше рассмотренного метода обучения указывается вектор логарифмов вероятностей действий. Но таких данных мы ранее не сохраняли в буфер воспроизведения опыта. Следовательно, сейчас нам необходимо добавить соответствующий массив в структуру описания состояние-действие SState, которая представлена в фале "..\SAC&DICE\Trajectory.mqh". Размер массива равен количеству действий.

struct SState
  {
   float             state[HistoryBars * BarDescr];
   float             account[AccountDescr - 4];
   float             action[NActions];
   float             log_prob[NActions];
   //---
                     SState(void);
   //---
   bool              Save(int file_handle);
   bool              Load(int file_handle);
   //--- overloading
   void              operator=(const SState &obj)
     {
      ArrayCopy(state, obj.state);
      ArrayCopy(account, obj.account);
      ArrayCopy(action, obj.action);
      ArrayCopy(log_prob, obj.log_prob);
     }
  };

Не забываем добавить массив в алгоритм методов копирования структуры и работы с файлами. С полным кодом структуры можно ознакомиться во вложении.

А мы переходим к созданию и обучению моделей. Касательно архитектуры моделей можно сказать, что она перенесена без изменений из статьи описания метода Soft Actor-Critic. При этом мы не создавали отдельных архитектур для v и ζ моделей. Для них мы использовали архитектуру критика.

В процессе обучения модели, как и ранее, мы используем 3 советника:

  • Research — сбор базы примеров
  • Study — обучение моделей
  • Test — проверка полученных результатов.

Здесь надо сказать, что при сборе данных для базы примеров в советнике Research мы используем оптимистическую политику Актера (файл с суффиксом "ActExp.nnw"). А вот для тестирования обученной модели мы будем использовать консервативную модель (файл с суффиксом "Act.nnw"). И на это следует обратить внимание при загрузке моделей в соответствующих файлах. Кроме того, при сборе данных в буфер воспроизведения опыта не забываем добавить загрузку логарифма вероятностей распределения действий. Ну а с полным кодом советников вы можете ознакомиться во вложении.

Максимальных изменений претерпел советник обучения Study. Это и не удивительно. Огромную часть его функционала мы перенесли в метод обучения Study класса CNet_SAC_DICE.

Начинаем мы с изменения библиотеки, содержащей нашу модель.

#include "Net_SAC_DICE.mqh"

В блоке глобальных переменных мы объявляем только одну модель нового созданного класса CNet_SAC_DICE. Но при этом увеличиваем количества буферов данных. Это связано с тем, что ранее мы могли один буфер использовать для двух состояний на разных этапах обучения. Сейчас же нам придется одновременно передавать информацию о 2 последующих состояниях в модель.

STrajectory          Buffer[];
CNet_SAC_DICE        Net;
//---
float                dError;
datetime             dtStudied;
//---
CBufferFloat         bState;
CBufferFloat         bAccount;
CBufferFloat         bActions;
CBufferFloat         bNextState;
CBufferFloat         bNextAccount;

В методе инициализации советника OnInit мы, как и прежде, сначала загружаем буфер воспроизведения опыта для обучения моделей.

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

После чего загружаем только одну модель. Если модель ещё не создана, то формируем массивы описания архитектуры моделей и создаем только одну модель, передав ей все описания архитектур. И только один раз проверяем результат выполнения операций.

Как уже было сказано выше, для моделей DICE блока мы передаем описание архитектуры критика. Но возможны и другие варианты. Создавая свои модели для данного блока, обратите внимание на использование модели Актера в качестве блока первичной обработки исходных данных. Именно таким образом мы выстроили весь алгоритм обучения модели. И нужно либо следовать ему при создании архитектур моделей, либо вносить соответствующие правки в алгоритм метода.

//--- load models
   if(!Net.Load(FileName, true))
     {
      CArrayObj *actor = new CArrayObj();
      CArrayObj *critic = new CArrayObj();
      if(!CreateDescriptions(actor, critic))
        {
         delete actor;
         delete critic;
         return INIT_FAILED;
        }
      if(!Net.Create(actor, critic, critic, critic, LatentLayer))
        {
         delete actor;
         delete critic;
         return INIT_FAILED;
        }
      delete actor;
      delete critic;
     }

Говоря "только одну модель" я, конечно, лукавлю. Ведь в процессе обучения мы создаем 6 обновляемых моделей и 3 целевых. Просто все модели создаются внутри нашего нового класса и скрыты от пользователя. На верхнем уровнем мы работаем только с одним классом.

В завершение метода инициализации советника генерируем событие обучения модели.

   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

После успешного выполнения всех операций завершаем процедуру инициализации советника.

И следующим этапом мы переходим к работе над процедурой непосредственного обучения моделей Train.

В теле данной функции мы, как и ранее, организовываем цикл обучения по числу итераций, указанному во внешних параметрах советника.

void Train(void)
  {
   int total_tr = ArraySize(Buffer);
   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int tr = (int)((MathRand() / 32767.0) * (total_tr - 1));
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i<0)
        {
         iter--;
         continue;
        }

Внутри цикла мы семплируем траекторию и отдельный шаг для текущей итерации обучения моделей.

Далее мы проведем подготовительную работу и соберем необходимы данные в ранее объявленные буфера данных. Сначала мы перенесем в буфер исторические данные описания последующего состояния окружающей среды.

      //--- Target
      bNextState.AssignArray(Buffer[tr].States[i + 1].state);
      float PrevBalance = Buffer[tr].States[i].account[0];
      float PrevEquity = Buffer[tr].States[i].account[1];
      if(PrevBalance==0)
        {
         iter--;
         continue;
        }
      bNextAccount.Clear();
      bNextAccount.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
      bNextAccount.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[2]);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[3]);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
      bNextAccount.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      bNextAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
      bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

В другом буфер мы сформируем описание состояния счета и добавим временные метки.

Аналогичным образом подготовим буферы с описанием анализируемого состояния окружающей среды.

      bState.AssignArray(Buffer[tr].States[i].state);
      PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bAccount.Clear();
      bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bAccount.Add(Buffer[tr].States[i].account[2]);
      bAccount.Add(Buffer[tr].States[i].account[3]);
      bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1);
      bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

Затем мы перенесем в буфер выполненные действия. А логарифм вероятностей загрузим в вектор.

      bActions.AssignArray(Buffer[tr].States[i].action);
      vector<float> log_prob;
      log_prob.Assign(Buffer[tr].States[i].log_prob);

На этом этапе мы завершаем подготовительную работу и в буферах данных уже собраны все данные, необходимые для одной итерации обучения. Мы вызываем метод обучения нашей модели CNet_SAC_DICE::Study, передав в параметрах необходимые данные.

      if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), log_prob,
                    GetPointer(bNextState), GetPointer(bNextAccount),
                    Buffer[tr].Revards[i] - DiscFactor * Buffer[tr].Revards[i + 1], DiscFactor, Tau))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }

Обратите внимание, что в буфере воспроизведения опыта мы сохраняли вознаграждения накопительным итогом. Сейчас же в метод обучения модели мы передаем чистое вознаграждение за один отдельно взятый шаг. Недостающие данные будут спрогнозированы целевыми моделями.

Все операции обучения моделей мы вынесли в метод обучения нашего класса. И сейчас нам достаточно только проверить результат выполнения операций метода. После чего проинформируем пользователя о процессе обучения модели.

      if(GetTickCount() - ticks > 500)
        {
         float loss1, loss2;
         Net.GetLoss(loss1, loss2);
         string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", 
                                    iter * 100.0 / (double)(Iterations), loss1);
         str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", 
                                    iter * 100.0 / (double)(Iterations), loss2);
         Comment(str);
         ticks = GetTickCount();
        }
     }

По завершении всех итераций цикла мы очищаем поле комментариев и инициализируем процедуру завершения работы советника.

   Comment("");
//---
   float loss1, loss2;
   Net.GetLoss(loss1, loss2);
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", loss1);
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", loss2);
   ExpertRemove();
//---
  }

Как можно заметить, вынесение операций обучения модели в отдельный метод класса позволяет значительно сократить код и трудозатраты на стороне основной программы. Но вместе с тем, такой поход снижается гибкость процесса обучения модели и возможности пользователя для его корректировки. Оба подхода имеют свои положительные и отрицательные стороны. И выбор конкретного подхода зависит от поставленной задачи и личных предпочтений.

С полным кодом данного советника, как и всех программ, используемых в статье, вы можете ознакомиться во вложении.



4. Тестирование

Обучение модели осуществлялось на исторических данных инструмента EURUSD тайм-фрейм H1 за период январь — май 2023 года. Параметры индикаторов и все гиперпараметры использовались установленные по умолчанию. В процессе обучения была получена модель, способная генерировать прибыль на обучающей выборке.

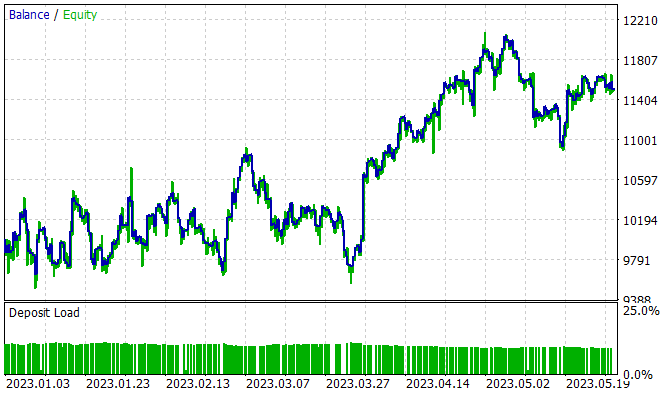
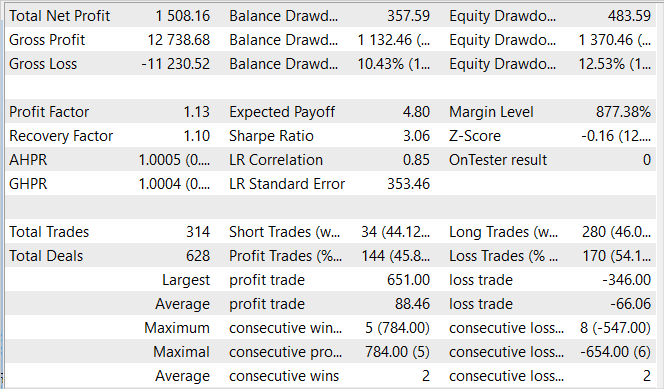
Результаты обучения модели

Результаты обучения модели

За 5 месяцев периода обучения модель смогла заработать 15% прибыли. Было открыто 314 позиций, 45,8% из которых закрыты с прибылью. Максимальная прибыльная сделка почти в 2 раза превышает максимальный убыток. При этом средняя прибыльная сделка на 1/3 превышает средний убыток. Именно такое соотношение прибылей и убытков позволило получить профит-фактор на уровне 1.13.

Но для нас, как всегда, гораздо больший интерес представляет эффективность работы модели на новых данных. Способность к обобщению и работа модели на незнакомых данных была проверена в тестере стратегий на исторических данных за июнь 2023 года. Как можно заметить, период тестирования следует непосредственно за обучающей выборкой. Это обеспечивает максимальную однородность обучающей и тестовой выборок. Результаты тестирования представлены ниже.

Результаты тестирования

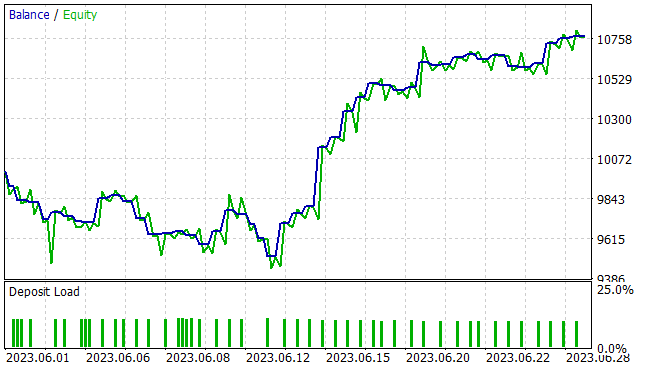
На представленном графике видна зона просадки в первой декаде месяца. Но далее идет период доходности, который продолжается до конца месяца. И в результате за месят советник получил прибыль 7.7%, при максимальной просадке по Эквити 5.46%. По балансу же просадка была ещё меньше и не превысила 4.87%.

Результаты тестирования

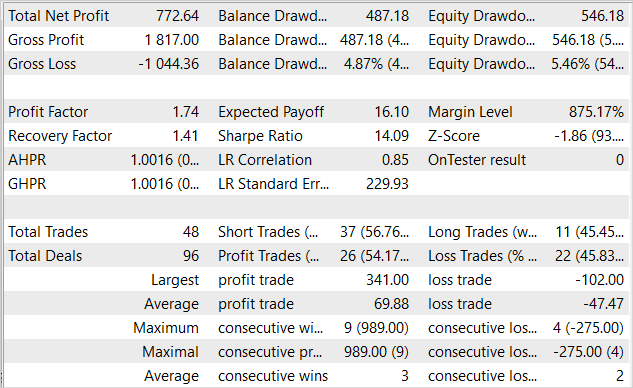
Из таблицы результатов тестирования видно, что в процессе тестирования советник совершал разнонаправленные торговые операции. Всего было открыто 48 позиций. И 54.17% из них было закрыто с прибылью. При этом максимальная прибыльная сделка более чем в 3 раза превышает максимальную убыточную сделку. А средняя прибыльная сделка пости на половину превышает среднюю убыточную сделку. В количественном выражение в среднем на 3 прибыльных сделки приходится 2 убыточных. Все это дало профит-фактор на уровне 1.74, а фактор восстановления 1.41.



Заключение

В данной статье мы познакомились ещё с одним алгоритмом из семейства Актер-Критик — алгоритм SAC+DICE, который основан на 2 основных направлениях модификации алгоритма Soft Actor-Critic. Использование оптимистической модели исследования окружающей среды позволяет расширить зону исследования окружающей среды. При этом исследование осуществляется направленно в направлении повышения доходности общей политики. Конечно, это ведет к разрыву распределений политик исследования окружающей среды и обучающейся консервативной политики. Для получения не смещенной оценки градиентов используется модифицированный подход DICE и вводится обучаемый коэффициент коррекции распределений. Все месте это позволяет повысить эффективность обучения моделей, что и было подтверждено в практической части нашей статьи.

Нами был реализован предложенный алгоритм средствами MQL5. В ходе данной реализации был продемонстрирован подход вынесения процесса обучения модели в отдельный метод класса. Это позволяет значительно сократить работу на стороне основной программы и упростить использование.

Мы обучили и протестировали обученную модель на новых данных. Результаты тестирования продемонстрировали эффективность нашей реализации. Обученная модель смогла перенести полученный опыт на новые данные. И в ходе тестирования советник получил прибыль.

Однако, все представленные программы лишь демонстрируют возможность использования технологии. И не готовы для использования на реальных финансовых рынках. Перед их использование требуется доработка советников и дополнительное всестороннее тестирование.


Ссылки

  • Better Exploration with Optimistic Actor-Critic
  • Off-policy Reinforcement Learning with Optimistic Exploration and Distribution Correction
  • Нейросети — это просто (Часть 49): Мягкий Актер-Критик (Soft Actor-Critic)
  • Нейросети — это просто (Часть 50): Soft Actor-Critic (оптимизация модели)
  • Нейросети — это просто (Часть 51): Актер-критик, управляемый поведением (BAC)

    • Программы, используемые в статье

    # Имя Тип Описание
    1 Research.mq5 Советник Советник сбора примеров
    2 Study.mq5  Советник Советник обучения агента
    3 Test.mq5 Советник Советник для тестирования модели
    4 Trajectory.mqh Библиотека класса Структура описания состояния системы
    5 Net_SAC_DICE.mqh Библиотека класса
    		Класс модели
    6 NeuroNet.mqh Библиотека класса Библиотека классов для создания нейронной сети
    7 NeuroNet.cl Библиотека Библиотека кода программы OpenCL


    Прикрепленные файлы |
    Загрузить ZIP
    MQL5.zip (411.19 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Последние комментарии | Перейти к обсуждению на форуме трейдеров (16)
    Viktor Kudriavtsev
    Viktor Kudriavtsev | 14 авг. 2023 в 06:15
    Дмитрий а почему эта сеть открывает все сделки ровно 1 лотом, при обучении на всех тестах, и не пытается менять лот? Не пытается ставить дробные лота и больше 1 лота тоже выставлять не хочет. Инструмент EURUSD.  Параметры обучения как у Вас.
    Dmitriy Gizlyk
    Dmitriy Gizlyk | 14 авг. 2023 в 14:41
    Viktor Kudriavtsev #:
    Дмитрий а почему эта сеть открывает все сделки ровно 1 лотом, при обучении на всех тестах, и не пытается менять лот? Не пытается ставить дробные лота и больше 1 лота тоже выставлять не хочет. Инструмент EURUSD.  Параметры обучения как у Вас.

    На последнем слое Актера мы используем сигмоиду в качестве функции активации, что ограничивает значения в диапазоне [0,1]. Для TP и SL мы используем множитель, чтобы скорректировать значения. Объем лота не корректируется. Следовательно, 1 лот это максимальное возможное значение.

    //--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftActorCritic;
   descr.count = NActions;
   descr.window_out = 32;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
    Viktor Kudriavtsev
    Viktor Kudriavtsev | 14 авг. 2023 в 16:43
    Dmitriy Gizlyk #:

    На последнем слое Актера мы используем сигмоиду в качестве функции активации, что ограничивает значения в диапазоне [0,1]. Для TP и SL мы используем множитель, чтобы скорректировать значения. Объем лота не корректируется. Следовательно, 1 лот это максимальное возможное значение.

    Понятно, Спасибо.

    JimReaper
    JimReaper | 15 авг. 2023 в 20:34
    ENJOY <3

    //+------------------------------------------------------------------+
    //| Expert tick function                                             |
    //+------------------------------------------------------------------+
    void OnTick()
    {
    //---
       if(!IsNewBar())
          return;
    //---
       int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates);
       if(!ArraySetAsSeries(Rates, true))
          return;
    //---
       RSI.Refresh();
       CCI.Refresh();
       ATR.Refresh();
       MACD.Refresh();
       Symb.Refresh();
       Symb.RefreshRates();
    //---
       float atr = 0;
       for(int b = 0; b < (int)HistoryBars; b++)
          {
             float open = (float)Rates[b].open;
             float rsi = (float)RSI.Main(b);
             float cci = (float)CCI.Main(b);
             atr = (float)ATR.Main(b);
             float macd = (float)MACD.Main(b);
             float sign = (float)MACD.Signal(b);
             if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
                continue;
             //---
             int shift = b * BarDescr;
             sState.state[shift] = (float)(Rates[b].close - open);
             sState.state[shift + 1] = (float)(Rates[b].high - open);
             sState.state[shift + 2] = (float)(Rates[b].low - open);
             sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f);
             sState.state[shift + 4] = rsi;
             sState.state[shift + 5] = cci;
             sState.state[shift + 6] = atr;
             sState.state[shift + 7] = macd;
             sState.state[shift + 8] = sign;
          }
       bState.AssignArray(sState.state);
    //---
       sState.account[0] = (float)AccountInfoDouble(ACCOUNT_BALANCE);
       sState.account[1] = (float)AccountInfoDouble(ACCOUNT_EQUITY);
    //---
       double buy_value = 0, sell_value = 0, buy_profit = 0, sell_profit = 0;
       double position_discount = 0;
       double multiplyer = 1.0 / (60.0 * 60.0 * 10.0);
       int total = PositionsTotal();
       datetime current = TimeCurrent();
       for(int i = 0; i < total; i++)
          {
             if(PositionGetSymbol(i) != Symb.Name())
                continue;
             double profit = PositionGetDouble(POSITION_PROFIT);
             switch((int)PositionGetInteger(POSITION_TYPE))
                {
                case POSITION_TYPE_BUY:
                   buy_value += PositionGetDouble(POSITION_VOLUME);
                   buy_profit += profit;
                   break;
                case POSITION_TYPE_SELL:
                   sell_value += PositionGetDouble(POSITION_VOLUME);
                   sell_profit += profit;
                   break;
                }
             position_discount += profit - (current - PositionGetInteger(POSITION_TIME)) * multiplyer * MathAbs(profit);
          }
       sState.account[2] = (float)buy_value;
       sState.account[3] = (float)sell_value;
       sState.account[4] = (float)buy_profit;
       sState.account[5] = (float)sell_profit;
       sState.account[6] = (float)position_discount;
       sState.account[7] = (float)Rates[0].time;
    //---
       bAccount.Clear();
       bAccount.Add((float)((sState.account[0] - PrevBalance) / PrevBalance));
       bAccount.Add((float)(sState.account[1] / PrevBalance));
       bAccount.Add((float)((sState.account[1] - PrevEquity) / PrevEquity));
       bAccount.Add(sState.account[2]);
       bAccount.Add(sState.account[3]);
       bAccount.Add((float)(sState.account[4] / PrevBalance));
       bAccount.Add((float)(sState.account[5] / PrevBalance));
       bAccount.Add((float)(sState.account[6] / PrevBalance));
       double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01');
       bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
       x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1);
       bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
       x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1);
       bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
       x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1);
       bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
    //---
       if (bAccount.GetIndex() >= 0 && !bAccount.BufferWrite())
          return;
    //---
       if (!Actor.feedForward(GetPointer(bState), 1, false, GetPointer(bAccount)))
          return;
    //---
       PrevBalance = sState.account[0];
       PrevEquity = sState.account[1];
    //---
       vector<float> temp;
       Actor.getResults(temp);
       float delta = MathAbs(ActorResult - temp).Sum();
       ActorResult = temp;
    //---
       double min_lot = Symb.LotsMin();
       double step_lot = Symb.LotsStep();
       double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point();
       if (temp[0] >= temp[3])
          {
             temp[0] -= temp[3];
             temp[3] = 0;
          }
       else
          {
             temp[3] -= temp[0];
             temp[0] = 0;
          }
    //--- buy control
       if (temp[0] < min_lot || (temp[1] * MaxTP * Symb.Point()) <= stops || (temp[2] * MaxSL * Symb.Point()) <= stops)
          {
             if (buy_value > 0)
                CloseByDirection(POSITION_TYPE_BUY);
          }
       else
          {
             double buy_lot = min_lot + MathRound((double)(temp[0] - min_lot) / step_lot) * step_lot;
             double buy_tp = NormalizeDouble(Symb.Ask() + temp[1] * MaxTP * Symb.Point(), Symb.Digits());
             double buy_sl = NormalizeDouble(Symb.Ask() - temp[2] * MaxSL * Symb.Point(), Symb.Digits());
             if (buy_value > 0)
                TrailPosition(POSITION_TYPE_BUY, buy_sl, buy_tp);
             if (buy_value != buy_lot)
                {
                   if (buy_value > buy_lot)
                      ClosePartial(POSITION_TYPE_BUY, buy_value - buy_lot);
                   else
                      Trade.Buy(buy_lot - buy_value, Symb.Name(), Symb.Ask(), buy_sl, buy_tp);
                }
          }
    //--- sell control
       if (temp[3] < min_lot || (temp[4] * MaxTP * Symb.Point()) <= stops || (temp[5] * MaxSL * Symb.Point()) <= stops)
          {
             if (sell_value > 0)
                CloseByDirection(POSITION_TYPE_SELL);
          }
       else
          {
             double sell_lot = min_lot + MathRound((double)(temp[3] - min_lot) / step_lot) * step_lot;
             double sell_tp = NormalizeDouble(Symb.Bid() - temp[4] * MaxTP * Symb.Point(), Symb.Digits());
             double sell_sl = NormalizeDouble(Symb.Bid() + temp[5] * MaxSL * Symb.Point(), Symb.Digits());
             if (sell_value > 0)
                TrailPosition(POSITION_TYPE_SELL, sell_sl, sell_tp);
             if (sell_value != sell_lot)
                {
                   if (sell_value > sell_lot)
                      ClosePartial(POSITION_TYPE_SELL, sell_value - sell_lot);
                   else
                      Trade.Sell(sell_lot - sell_value, Symb.Name(), Symb.Bid(), sell_sl, sell_tp);
                }
          }
    // Calculate initial rewards
       float iRewards = bAccount[0];
       vector<float> log_prob;
       Actor.GetLogProbs(log_prob);
    // Normalize ATR to the range [0, 1]
       float minATR = -100.0; // Adjust these values based on your data
       float maxATR = 100.0;
       float norm_atr = (atr - minATR) / (maxATR - minATR);
    // Define weights for normalization
       float minWeight = 0.0;
       float maxWeight = 1.0;
    // Normalize initial rewards and normalized ATR based on weights
       float norm_iRewards = (iRewards - minWeight) / (maxWeight - minWeight);
       float norm_norm_atr = (norm_atr - minWeight) / (maxWeight - minWeight);
    // Calculate penalty for no trades
       double penalty = (buy_value + sell_value) == 0 ? (norm_norm_atr + atr / (PrevBalance + LogProbMultiplier)) : 0.0;
    // Update rewards and log probabilities
       for (ulong i = 0; i < temp.Size(); i++)
          {
             sState.action[i] = temp[i];
             sState.log_prob[i] = log_prob[i];
          }
    // Calculate increment based on log_prob_sum
       float iRewards_increment = MathLog((float)PrevBalance);
    // Adjust rewards based on initial norm_iRewards
       if (norm_iRewards != 0)
          {
             norm_iRewards += norm_norm_atr + iRewards_increment;
          }
    // Apply Z-score normalization to norm_iRewards
       float meanRewards = -10.0; // Calculate the mean of rewards over time
       float stdRewards = 10.0;  // Calculate the standard deviation of rewards over time
       float normalized_iRewards = (norm_iRewards - meanRewards) / stdRewards;
    // Apply power transformation to enhance data distribution (e.g., Box-Cox transform)
       float power = 0.5; // Adjust the power parameter as needed
       float transformed_reward = (pow(1 + normalized_iRewards, power) - 1) / power;
    // Apply exponential transformation to enhance data distribution
       float ZReward = (transformed_reward - (LogProbMultiplier)) / (5 - (LogProbMultiplier));
       float Mreward = MathLog10(ZReward + 1);
       float reward = (Mreward - (-1.0f)) / (0.4f - (-1.0f));
    Apply square root transformation
    Calculate the mapped values back to the range [1, 100]
       float SRQTreward = sqrt(reward);
    Print the rewards and other information
       Print("Buy Value: ", buy_value);
       Print("Sell Value: ", sell_value);
       Print("Temperature: ", temp);
    Print("Temperature Size: ", temp. Size());
       Print("iRewards: ", iRewards);
       Print("Normalized ATR: ", norm_norm_atr);
       Print("Normalized iRewards: ", normalized_iRewards);
       Print("Transformed Reward: ", transformed_reward);
       Print("Trajectory Reward: ", ZReward);
       Print("MATHLOG: ", Mreward);
       Print("Scaled Reward: ", reward);
       Print("SRQT Reward: ", SRQTreward);
    Add state and normalized rewards to the trajectory
    if (! Base.Add(sState, reward))
          {
    ExpertRemove(); Handle the case when adding to Base fails
          }
    }
    //+------------------------------------------------------------------+



    //+------------------------------------------------------------------+
    //|                                                                  |
    //+------------------------------------------------------------------+
    bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
    {
    //---
       CLayerDescription *descr;
    //---
       if(!actor)
          {
             actor = new CArrayObj();
             if(!actor)
                return false;
          }
       if(!critic)
          {
             critic = new CArrayObj();
             if(!critic)
                return false;
          }
    //--- Actor
       actor.Clear();
    //--- Input layer
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       int prev_count = descr.count = (HistoryBars * BarDescr);
       descr.window = 0;
       descr.activation = None;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 1
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 7;
       descr.step = 3;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 2
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 5;
       descr.step = 2;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 3
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 3;
       descr.step = 1;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 4
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 5
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       prev_count = descr.count = 512;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 6
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 6;
       descr.step = 2;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 7
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 4;
       descr.step = 2;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 8
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count - 1;
       descr.window = 2;
       descr.step = 1;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 9
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConvOCL;
       prev_count = descr.count = prev_count;
       descr.window = 8;
       descr.step = 8;
       descr.window_out = 8;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 10
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBatchNormOCL;
       descr.count = prev_count;
       descr.batch = 1000;
       descr.activation = None;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 11
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 12
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       prev_count = descr.count = 512;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 13
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConcatenate;
       descr.count = LatentCount;
       descr.window = prev_count;
       descr.step = AccountDescr;
       descr.optimization = ADAM;
       descr.activation = SIGMOID;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 14
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 15
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       prev_count = descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 16
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = prev_count;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 17
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronSoftActorCritic;
       descr.count = NActions;
       descr.window_out = 32;
       descr.optimization = ADAM;
       descr.activation = SIGMOID;
       if(!actor.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- Critic
       critic.Clear();
    //--- Input layer
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       prev_count = descr.count = LatentCount;
       descr.window = 0;
       descr.activation = None;
       descr.optimization = ADAM;
       if(!critic.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 1
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronConcatenate;
       descr.count = 1024;
       descr.window = prev_count;
       descr.step = 6;
       descr.optimization = ADAM;
       descr.activation = LReLU;
       if(!critic.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 2
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!critic.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 3
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
       if(!critic.Add(descr))
          {
             delete descr;
             return false;
          }
    //--- layer 4
       if(!(descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1024;
       descr.activation = LReLU;
       descr.optimization = ADAM;
    if(!critic. Add(descr))
          {
             delete descr;
             return false;
          }
    --- layer 5
    if(!( descr = new CLayerDescription()))
          return false;
       descr.type = defNeuronBaseOCL;
       descr.count = 1;
       descr.optimization = ADAM;
       descr.activation = None;
    if(!critic. Add(descr))
          {
             delete descr;
             return false;
          }
    //---
       return true;
    }
    JimReaper
    JimReaper | 17 авг. 2023 в 03:05
    Thanks 
    Торговые транзакции. Структуры запросов и ответов, описание и вывод в журнал Торговые транзакции. Структуры запросов и ответов, описание и вывод в журнал
    В статье рассмотрим работу со структурами торговых запросов — для создания запроса, его предварительной проверки перед отправкой на сервер, ответ сервера на торговый запрос и структуру торговых транзакций. Создадим простые удобные функции для отправки торговых приказов на сервер и, на основе всего рассмотренного, создадим советник-информер о торговых транзакциях.
    Прогнозирование с помощью моделей ARIMA в MQL5 Прогнозирование с помощью моделей ARIMA в MQL5
    В этой статье мы продолжаем разработку класса CArima для построения моделей ARIMA, добавляя интуитивно понятные методы прогнозирования.
    Простая торговая стратегия возврата к среднему Простая торговая стратегия возврата к среднему
    Возврат к среднему - это метод контртрендовой торговли, при котором трейдер ожидает, что цена вернется к некоторой форме равновесия, которое обычно измеряется средним значением или другим статистическим показателем усредненной тенденции.
    Как стать успешным поставщиком сигналов на MQL5.com Как стать успешным поставщиком сигналов на MQL5.com
    Основная цель статьи — предоставить простой пошаговый путь, пройдя по которому вы сможете стать лучшим поставщиком сигналов на MQL5.com. Опираясь на свои знания и опыт, я объясню, что нужно, чтобы стать успешным поставщиком сигналов, в том числе, как найти, протестировать и оптимизировать хорошую стратегию. Кроме того, я дам советы по публикации вашего сигнала, написанию убедительного описания и эффективному продвижению и управлению.