
ニューラルネットワーク:理論~実践
はじめに
今日、トレーダーはだれしもニューラルネットワークについて聞いたことがあり、それを使うのがかっこいいということがわかっています。多数の人がニューラルネットワークを利用してディールを行える人はスーパーヒューマンだと思っています。本稿ではニューラルネットワークのアーキテクチャを説明し、アプリケーションについて記述し、実用例を示していこうと思います。
ニューラルネットワークのコンセプト
人工的なニューラルネットワークのニューラルネットワークは学習能力において人間の神経組織をシミュレートする試みを基にした人工知能の研究分野の一つであり、それを適用することで人間の脳内処理のおおざっぱなシミュレーションを構築することができるものです。
十分興味をそそるものである人口ニューラルネットワークは人工ニューロンから作成されます。
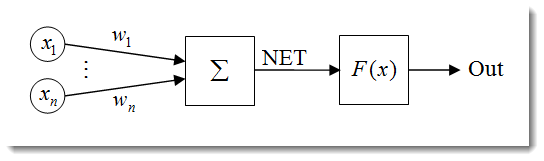
図1 人工ニューロンモデル
ニューロン構造は以下のユニットの組合せとして表現することができます。
- インプット
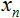
- ウェイト
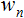
- 転送関数および
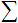 ネットインプット
ネットインプット 
- 活性化関数
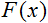
- アウトプット
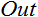
ニューラルネットワークにはもっとも重要な一つとなることを学習する能力を持つ数多くのプロパティがあります。学習プロセスによりウェイトが変化することになります![]() 。
。

![]() ここにニューロンのネットインプットがあります。
ここにニューロンのネットインプットがあります。
![]()
それからネットインプットはのちに取り上げる活性化関数によってアウトプットに変換されます。簡単に言えば、ニューラルネットワークはインプットとしてシグナルを受け取り結果をアウトプットする「ブラックボックス」に見えるかもしれません。
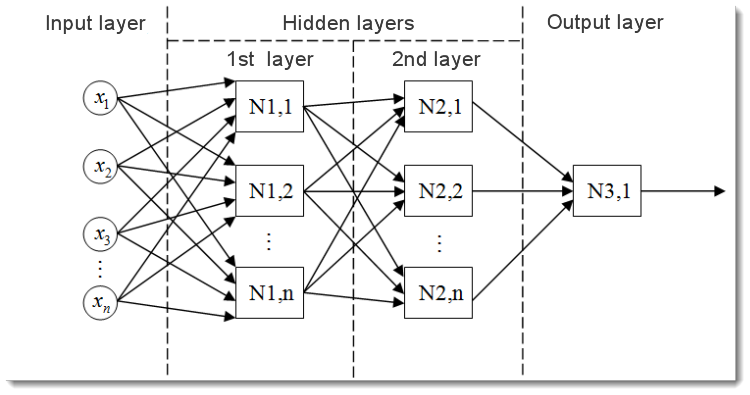
図2 多層ニューラルネットワークモデル
これが多層ニューラルネットワークの概観です。それを以下を満たしています。
- 入力層 ネットワーク中にデータを配布するが計算はまったく行いません。この階層のアウトプットは次の階層(非表示またはアウトプット)のインプットにシグナルを変換します。
- 出力層 通常ニューラルネットワーク全体のアウトプットを生成するニューロンを一つ(または複数の場合もあります)持ちます。このシグナルは EA の将来の制御ロジックにあります。
- 非表示層 インプット階層からアウトプット階層へシグナルを変換する標準ニューロンの階層です。 そのインプットは前層のアウトプットで、またそのアウトプットは次の層のインプットの役目をします。
この例ではニューラルネットワークには2つ非表示層があります。ただしもっと多くの非表示層を持つニューラルネットワークもありえます。
入力データの標準化
入力データの標準化はすべての入力データが標準化されるプロセスです。すなわちレンジ [0,1] または [-1,1]までの減少です。標準化が行われると、入力データはニューロンに別の影響を与えます。誤った判断をさせてしまうのです。別の言い方をすれば、異なる桁を持つ値をどうやって比較することができるのか?です。
標準的形式の標準化式は以下です。
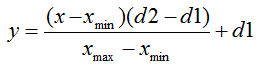
ここで
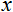 - 標準化される値
- 標準化される値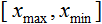 - х 値レンジ
- х 値レンジ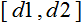 - 値 x が減るレンジ
- 値 x が減るレンジ
例を使って説明します。
レンジ [0,10]から n入力データを持っているとすると、![]() = 0 and
= 0 and ![]() = 10です。データをレンジ [0,1]まで減らすと、
= 10です。データをレンジ [0,1]まで減らすと、![]() = 0 and
= 0 and ![]() = 1です。これで値を式に代入し、入力データnから任意のx に対して標準化値を計算することができます。
= 1です。これで値を式に代入し、入力データnから任意のx に対して標準化値を計算することができます。
これが MQL5に実装された場合、以下のようになります。
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
まずアウトプット値の上下限を指定し、インディケータの最小値および最大値を取得します(インディケータからデータをコピーすることが残されていますが、たとえば最終 10 の値があり得ます)。最後にすべてのインプット要素(異なるバーのインディケータ値)を標準化し、のちに使用するため結果を配列に格納します。
活性化関数
活性化関数はニューロンのアウトプットを計算する関数です。受け取るインプットは入力のすべてのプロダクツ合計とそれぞれに応じたウェイト(以降『加重和』)を表します。
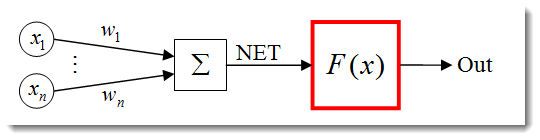
図3 線で囲まれた活性化関数を持つ人工ニューロンモデル
標準形式の活性化関数式は以下のようになります。
![]()
ここで
 は活性化関数です。
は活性化関数です。-
 はニューロンのアウトプットを計算する初期段階で取得される加重和です。
はニューロンのアウトプットを計算する初期段階で取得される加重和です。  は活性化関数の閾値です。ハード閾値関数に対してのみ使用され、その他関数では値はゼロです。
は活性化関数の閾値です。ハード閾値関数に対してのみ使用され、その他関数では値はゼロです。
活性化関数の主なタイプは以下です。
-
単位ステップ関数 または ハード閾値関数
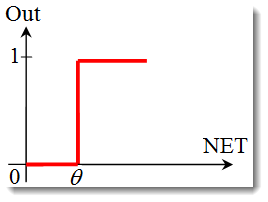
関数は以下の式で記述されます。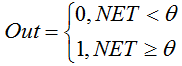
加重和が指定値より小さい場合、活性化関数はゼロを返します。加重和が指定値より大きい場合、活性化関数は1を返します。 -
シグモイド関数
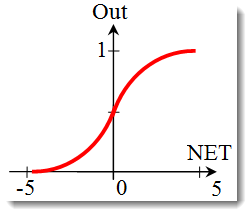
シグモイド関数を記述する式は以下のようになります。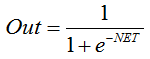
それは連続シグナルを伴い多層ニューラルネットワークその他ネットワークで多用されます。関数平滑化および連続性はひじょうにポジティブなプロパティです。 -
を記述する式
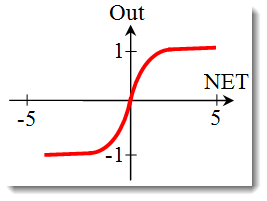
式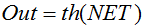 または
または 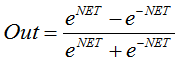
それもまた連続シグナルを伴うネットワークで多用されます。そこでは負の値が返されるのが特殊です。
活性化関数の変形
前項で活性化関数タイプを取り上げました。まだ考察すべき重要な事柄がもうひとつあります。関数傾斜(はーろ閾値関数以外)です。シグモイド関数を詳しく見ていきます。
関数グラフを見ると、レンジ [-5,5]で関数がなめらかなのが簡単に判ります。インプット10、アウトプット1の単一ニューロンで構成されるネットワークがあるとします。ここで変数の上下値を計算してみます![]() 。各インプットは標準化された値(入力データ標準化ですでに述べています)を取ります。たとえばレンジ [-1,1]からです。
。各インプットは標準化された値(入力データ標準化ですでに述べています)を取ります。たとえばレンジ [-1,1]からです。
関数が負の引数でも差別化できるので負のインプット値を用います。ウェイトも同じレンジから選択します。インプットとウェイトのすべての可能な組合せで次のように![]() レンジ [-10,10] において極値を取得します。
レンジ [-10,10] において極値を取得します。

MQL5では式は次のように記述されます。
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
ここで指定されたレンジにおいて活性化関数をプロットする必要があります。シグモイド関数を例に取ります。 Excelエクセルを利用するのがもっとも簡単です。
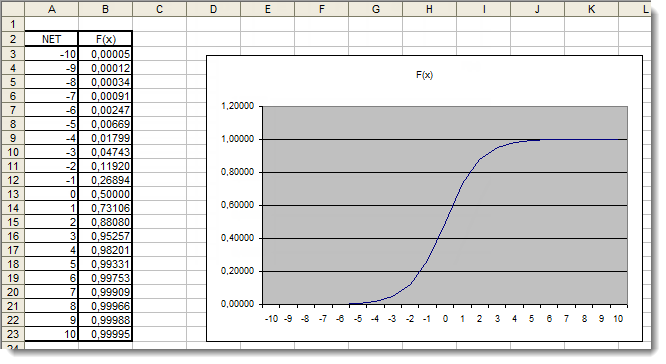
図4 シグモイド関数の Excel グラフ
ここではレンジ [-5,5] 外の引数値は確実に結果になんの影響もないことが明確に判ります。このことは値範囲が不完全であることを示します。これを修正します。引数に値レンジを拡張できる別の係数dを追加します。
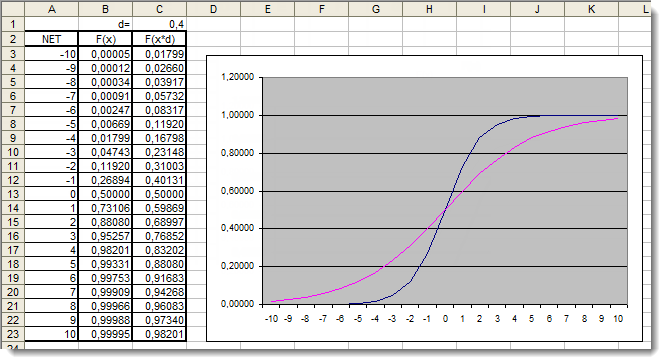
図5 追加係数を適用したシグモイド関数の Excel グラフ
グラフを今一度見てみます。関数を変形する別の係数 d=0.4 を追加しました。表での値比較はこれでより均一に分布されていることを示します。 uniformly よって結果は以下のように記述できます。
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
ここで双曲正接活性化関数をよく見てみます。前関数の検討で取り上げた理論は飛ばして、さっそく実用的アプリケーションに取り掛かります。ここでの違いはアウトプットが [-1,1]のレンジにあることだけです。加重和もまたレンジ [-10,10]からの値を取ります。
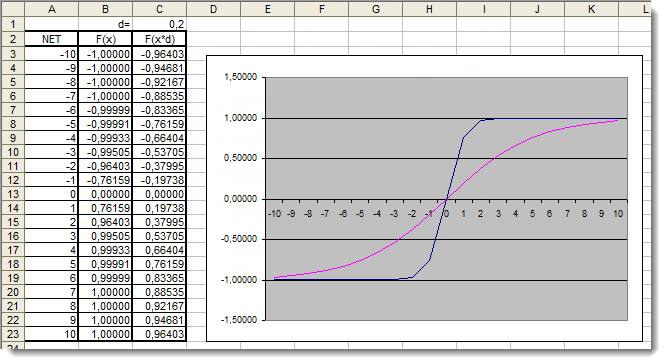
図6 追加係数を適用した双曲正接関数の Excel グラフ
グラフは関数の形が追加の係数d=0.2により改善されたことを示しています。よって結果は以下のように記述できます。
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
この方法であらゆる活性化関数の形を変更し改善するこができます。
アプリケーション
では実用的アプリケーションに移ります。まず、ニューロンのネットインプットを計算します。続いて活性化関数を追加します。ニューロンのネットインプットを計算する式を思い出します。

double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
詳しく見ていきます。
- ニューロンのネットインプット
 およびインプット
およびインプット 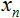 と ウェエイト
と ウェエイト 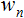 の配列を2つ格納するための変数を宣下することから始めました。
の配列を2つ格納するための変数を宣下することから始めました。 - これら変数はすべての関数の外側でそれら関数にグローバルスコープ(プログラムのどこからもアクセス可能なように)まっさきに宣言されています。
- 初期化関数 OnInit() (実際他のどんな関数でもありえますが)では、インプット配列とウェイト配列を書いています。
- この後にループ n<3 の合計をします。これはインプットとそのそれぞれに対するウェイトが3つしか持たないためです。
- そのあと加重されたインプット変数を追加し変数に格納しました
 。
。
これで最初のタスクは完了です。合計を取得しました。ここから活性化関数の番です。以下は活性化関数 項で検討した活性化関数を計算するコードです。
ユニットステップ関数またはハード閾値関数
double Out; if(NET>=x) Out=1; else Out=0;
シグモイド関数
double Out = 1/(1+exp(-NET));
双曲正接関数
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
すべてをまとめます。
実装をより簡単にするため単一ニューロンでできているネットワークを取ります。それをネットワークと呼ぶのはたしかに少々無理がありますが、重要なことは原理を理解することです。最終的に多層ニューラルネットワークは前のニューロン層のアウトプットが次の層のインプットの役割をするのと同様のニューロンで構成されています。
われわれは記事"A Quick Start or a Short Guide for Beginners"で開発され紹介されているExpert Advisorをわずかに変更したバージョンを使用していきます。そのため、たとえば移動平均eトレンドインディケータを相対強度指数 オシレータに置き換えます。インディケータのパラメータおよびそのシーケンスに関する情報は内蔵の「ヘルプ」にあります。
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
まず初めにすべきことはわれわれのネットワークをトレーニングすることです。ウェイトを最適化します。
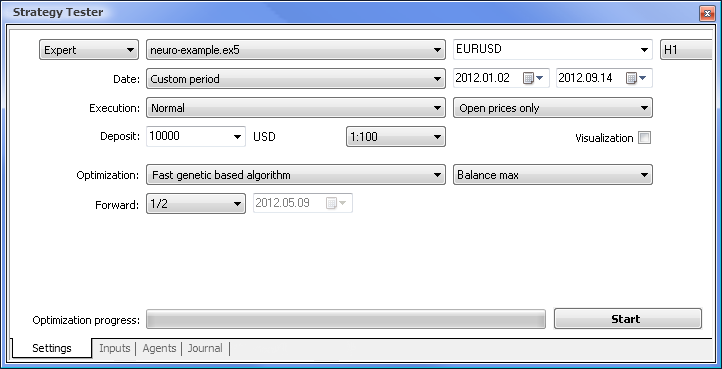
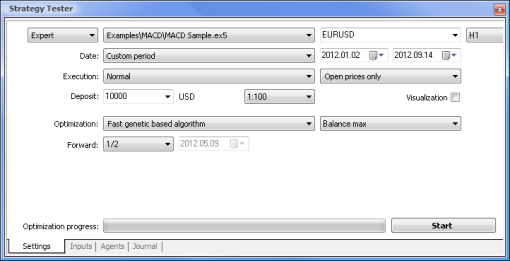
図7 必要なパラメータセットを持つストラテジーテスタ
以下のパラメータを使用して最適化を実行します。
- 日付 - たとえば年初からの期間が長いほど曲線のあてはめは起こりにくくなり、結果はよりよくなります。
- 実行 - 通常。始値のみチックモード『毎』に検証を行う意味はありません。なぜならここでの Expert Advisor は現在値以外インディケータの最終10の値を取るにすぎないからです。
- 最適化 は速度の遅い完全アルゴリズムを用いて実行するよう設定することが可能です。にもかかわらず遺伝的最適化はアルゴリズムにアクセスするときは特に便利になる高速の結果を出します。結果が満足のいくものであれば、より正確な結果を得るために速度の遅い完全アルゴリズムを用いて実行してみることもできます。
- 先送り を1/2かそれ以上 にすることで次の最適化まで EA が取得した結果を生成するのにどのくらい時間がかかるか査定することができます。
- 時間枠 および 通貨ペア は必要に応じて設定できます。
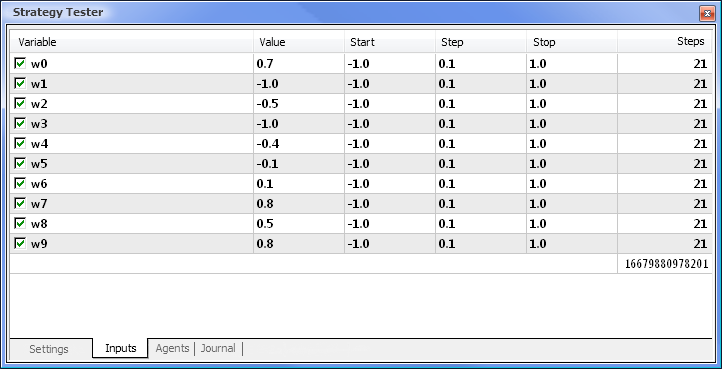
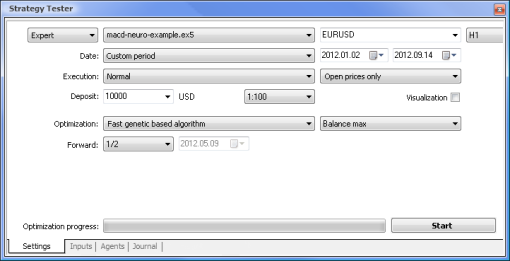
図8 最適化のためのパラメータおよびそれに応じたレンジの設定
最適化はすべてのウェイトとレンジに関して実行されます。「設定」タブに戻り、「開始」ボタンをクリックして最適化を始めます。
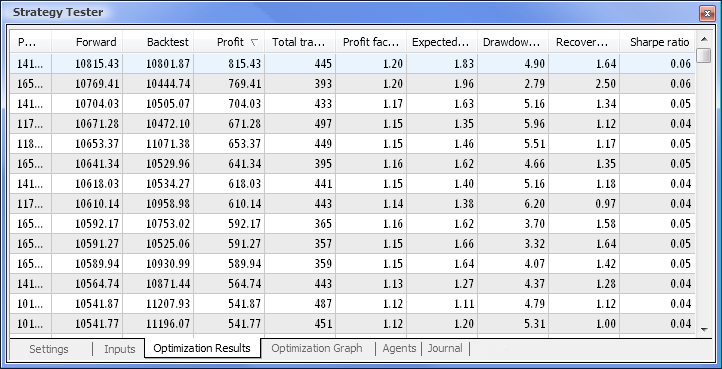
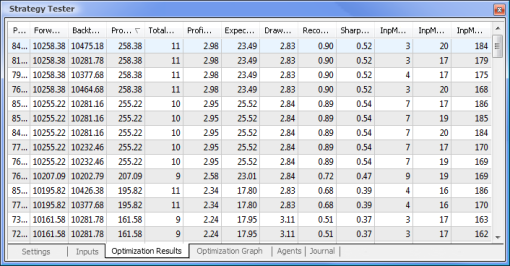
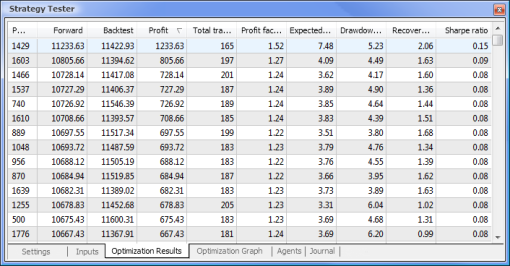
図9 最適化に続いて取得されるデータ
最適化が完了したら、「最適化結果」タブで最大収益値(パラメータの一つでソートするには適切な列見出しをクリックします)を持つパスを選択します。そうすると必要に応じてその他のパラメータを査定し望むパスを選択することができます。
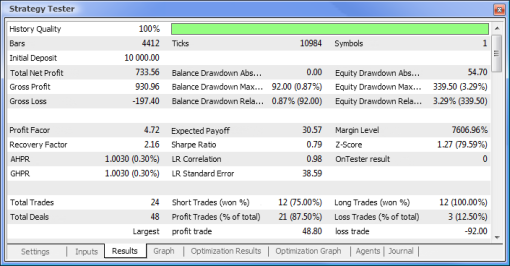
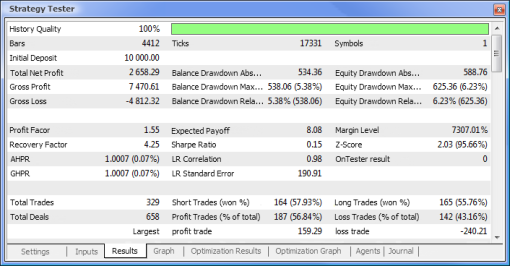
必要なパスの上でダブルクリックすると「結果」および「グラフ」タブに示される結果を検証を起動します。
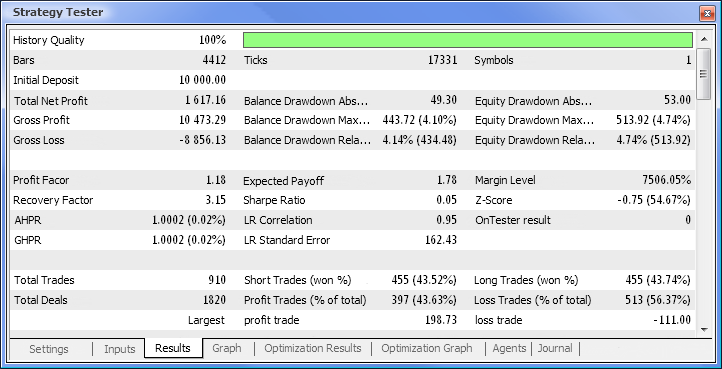
図10 検証レポート
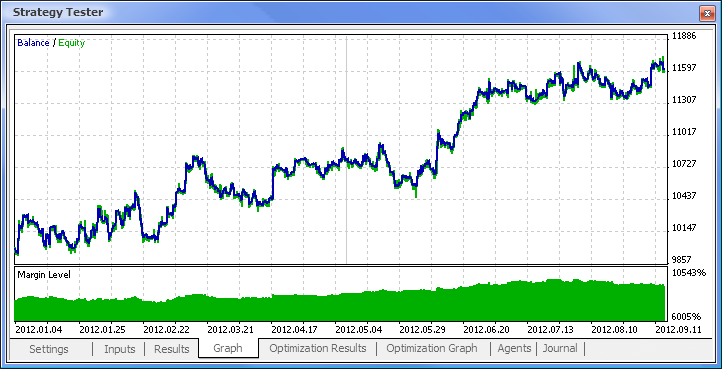
図11 残高チャート
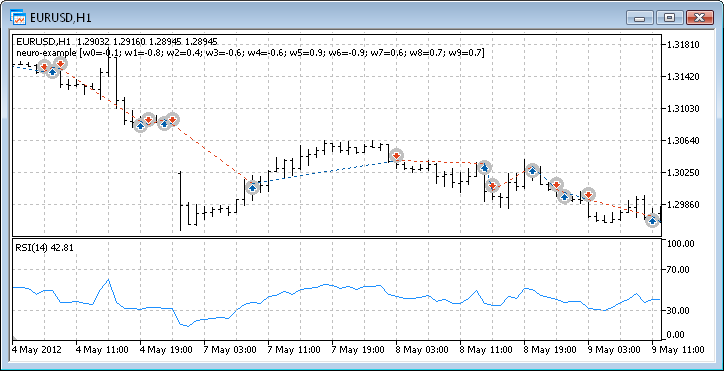
図12 Expert Advisorのトレーディング処理
よって最終的に結果を得、スタートとしてはこの結果はかなり良いものです。しかしここではニューロンはただ一つであることを忘れないでください。ここでの結果は明らかに粗いものですが、それだけでも収益を上げることができるということは認めざるをえません。
Advantages of Neural Networks
ここでニューラルネットワーク駆動 EAの標準ロジックに基づくEAを比較してみます。ターミナルと一体となる「MACD サンプル Expert Advisor」の最適化および検証結果を MACDに基づくニューラルネットワーク駆動 EAの結果と比較します。
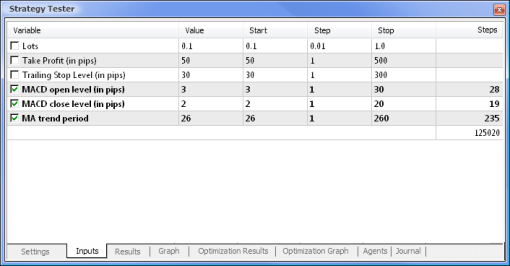
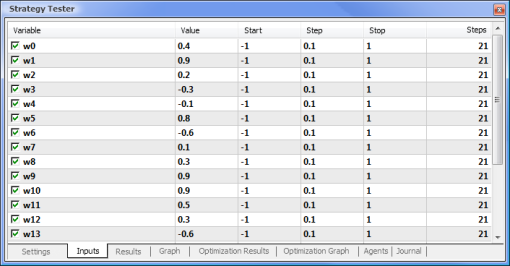
テイクプロフィット値およびトレーリングストップ値は、ニューラルネットワーク駆動 EAにはないため最適化には含まれません。これから検証していくどちらの Expert Advisors も以下のパラメータについてMACDを基にしています。
- 高速移動平均期間: 12
- 低速移動平均期間: 26
- 差の平均化期間: 9
- 価格タイプ: 終値
また必要な通貨ペアといj間枠を設定することもできますが、ここでは変更なしで、それぞれ通貨ペア- EURUSD、時間枠- H1とします。どちらも検証期間は同じで、始値を用いて年始からとします。
| MACD サンプル | 移動平均 - ニューロ - 例 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
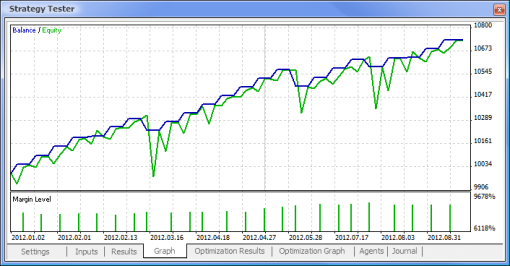 |
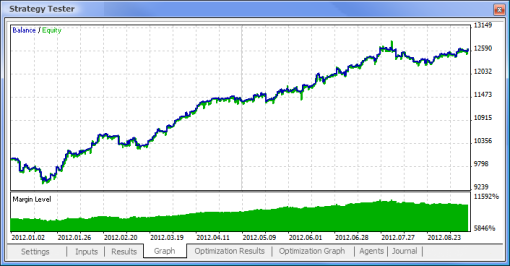 |
検証済み Expert Advisorsの主要パラメータを比較します。
| パラメータ | MACD サンプル | 移動平均 - ニューロ - 例 |
|---|---|---|
| トータル純利益 | 733,56 | 2 658,29 |
| 初期投資額からの残高ドローダウン | 0,00 | 534,36 |
| 最大資本ドローダウン | 339,50 (3,29%) | 625,36 (6,23%) |
| プロフィットファクター | 4,72 | 1,55 |
| リカバリーファクター | 2,16 | 4,25 |
| 期待利得 | 30,57 | 8,08 |
| シャープレシオ | 0,79 | 0,15 |
| トレード総額 | 24 | 329 |
| ディール総額 | 48 | 658 |
| トレード利益(トータルの% ) | 21 (87,50%) | 187 (56,84%) |
| 平均トレード利益額 | 44,33 | 39,95 |
| 平均連続勝利 | 5 | 2 |
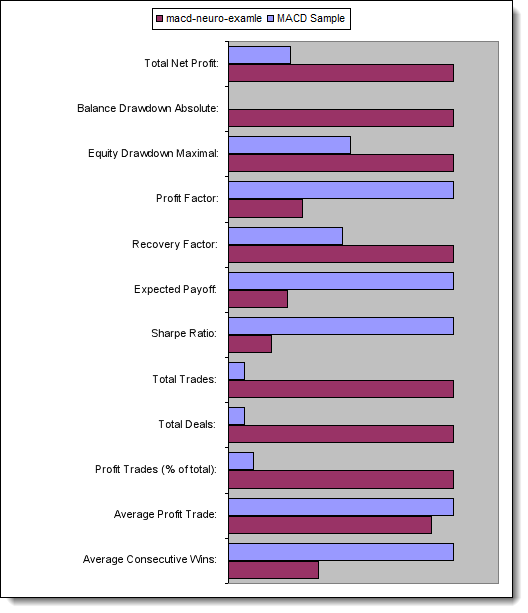
図13 主要パラメータ比較
おわりに
本稿ではニューラルネットワークを用いて EA を設計する際必要な知識の要点を取り上げました。そしてニューロンとニューラルネットワークのストラクチャを示し、活性化関数とその変形法、最適化および入力データの標準化のあらましを述べました。またニューラルネットワーク駆動 EAの標準ロジックに基づきEA の比較も行いました。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/497
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 トレード戦略の統計的実行
トレード戦略の統計的実行
 MetaTraderのマーケットからトレードロボットを購入し、インストールする方法
MetaTraderのマーケットからトレードロボットを購入し、インストールする方法
 標準ライブラリのトレーディングストラテジークラスの探求- ストラテジーのカスタマイズ
標準ライブラリのトレーディングストラテジークラスの探求- ストラテジーのカスタマイズ
 その他のアプリのためにMetaTrader5の取引価格を準備する方法
その他のアプリのためにMetaTrader5の取引価格を準備する方法
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
バックテストでは1回しか取引できない
重要な質問です:
RSIのN過去値は14(N=14)に設定されています。
入力数は10(過去の値)です。
何か問題があるのでしょうか?MLの結果が不安定になるのでは?
回答お願いします。
ありがとうございます。
重要な質問だ:
RSIのN個の過去値は14(N=14)に設定されています。
入力の数は10(過去の値)です。
何か問題があるのでしょうか?MLの結果が不安定なのでは?
回答お願いします。
ありがとうございます。
14はRSIインジケータを計算する期間です。入力はRSIバッファから10個の値です。