
取引における道徳的期待値
この記事では、歴史的持続性を維持するために通貨単位としてドゥカートを使用します。ドゥカートの代わりに、使い慣れた他の通貨をいつでも置き換えることができます。
数学的期待値
取引における数学的期待値は、取引戦略の効率性を評価するために使用される指標の1つです。このような数学的期待値のユーザー(およびそれ以上)については、「トレーディングにおける数学:トレード結果の推定方法.」稿で詳しく説明しています。
ただし、今興味があるのは数学的期待値の確率論的定義です。たとえば、私があなたに、10%の確率で100ドゥカートを獲得して90%の確率で10ドゥカートを失うゲームを提供するとします。そのようなゲームの数学的期待値は、E = 0.1 * 100 + 0.9 * (-10) = 1ドゥカートとなります。したがって、数学的な期待値を使用して期待リターンを判断できます。たとえば、このゲームを100回プレイすると、初回入金が100ドゥカート増加すると仮定できます。
直観的に、数学的な期待が大きければ大きいほど、そのようなゲームに参加することがより興味深いものになることが示唆されます。たとえば、ゲームの賞金を200ドゥカートに増やすと、数学的な期待値も11に増加し、100ゲームからの期待収益性は1100ドゥカートに増加します。そして、数学的な期待値が+100,500だったらどうでしょう。夢のようですね。そう思いませんか。
もしそう思うなら、今日はあなたの人生で最も幸せな日のうちの1つです。この無限期待ゲームをプレイすることをお勧めします。想像してみてください。1時間かそれよりも早く、超億万長者になるのです。
ただし、このゲームには1つの小さな不便さがあります。参加するには、少額の参加料、たとえば100ドゥカートを支払う必要があるということです。わかりました、これは少し酷いですね。50ドゥカートとしましょう。いえいえ、特別割引を提供させてください。25ドゥカートをお支払いになれば、この素晴らしいゲームをすぐに開始できます。
参加料を振込まれる間に、このゲームのルールをお教えししましょう。まず、コイントスの表裏を予想してください。それから私がコインを投げて、あなたが当たれば、私はあなたに1ドゥカートを払います。2回目が当たれば2ドゥカート、3回目が当たれば4ドゥカートを払います。当たるたびに、以前の賞金が2倍になるのです。50回目の後、私があなたに支払わなければならないドゥカートの数を想像してみてください。そして100回目の後は?そのような数字はまだまったく発明されておらず、世界のすべての富はあなたの賞金に比べれば些細なものです。
はずれたらゲームオーバーです。もう一度参加料をお支払いいただくと、最初からゲームを開始できます。
何となくですが、誰も私と一緒にそのようなゲームをしたくないと思うのです。なぜでしょうか。一方では、無限の数学的期待値があります。
一方、内なる声は、25ドゥカートでも、そのような無限大のために払うには高すぎることを示唆しています。この矛盾は「サンクトペテルブルクのパラドックス」と呼ばれています。
道徳的期待値
1738年に、ダニエル・ベルヌーイは、「Specimen theoriae novae de mensura sortis」(Exposition of a New Theory on the Measurement of Risk)を発表しました。この作品で彼は、どのゲームにおいても、期待される利益を最大化するのではなく、プレイヤーにとっての効用を最大化する必要があることを示唆しました。
この仮定は、次の例で説明できます。2人の異なるプレイヤーがいるとします。1人は100ドゥカートの資本を持ち、もう1人は1000ドゥカートの資本を持っています。この2人に、10ドゥカートのペイオフが期待されるゲームが提供されます。明らかに、最初のプレイヤーにとって、そのようなゲームはより興味深いものになります。なぜなら、2番目のプレイヤーの資本が1%増加するだけなのに対して、最初のプレイヤーが勝った場合、その資本は10%増加するからです。言い換えれば、同じ勝利は、2番目のプレイヤーよりも最初のプレイヤーにとってより有益になるのです。
この仮定に基づいて、ダニエル・ベルヌーイは期待効用方程式を導出しました。Depositはプレイヤーが利用できる資金、Profitは期待されるペイオフ、Lossは損失の可能性、pは勝つ確率であると仮定しましょう。この場合、道徳的期待値の方程式は次のようになります。
道徳的期待値と数学的期待値の主な違いは、道徳的期待値はプレイヤーの資本に依存し、暗黙のうちにゲームのリスクを考慮に入れるということです。
たとえば、先ほど提案したゲームの1つを考えてみましょう。10%の確率で200ドゥカートを獲得でき、90%の確率で10ドゥカートを失う可能性があります。このゲームの数学的期待値はすべてのプレイヤーで同じで、0.1*200 + 0.9*(-10) = 11ドゥカートです。しかし、道徳的期待値は異なり、もう少し情報が得られます。
最初にあなたのドゥカートをテーブルの上に並べて数えてください。メリットとデメリットを比較検討して、このゲームをプレイすることに同意するかどうかを決定します。
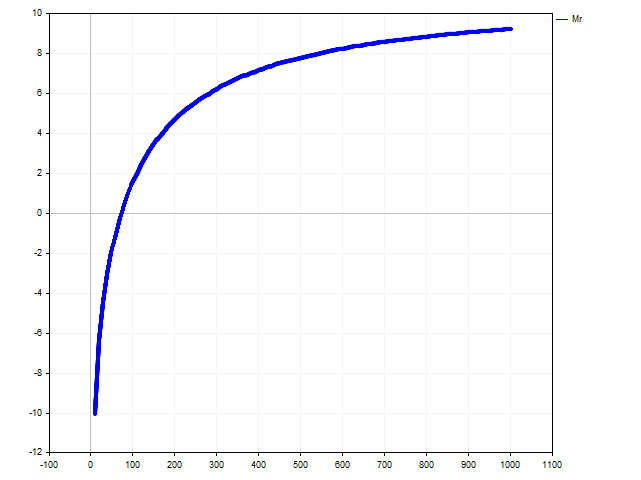
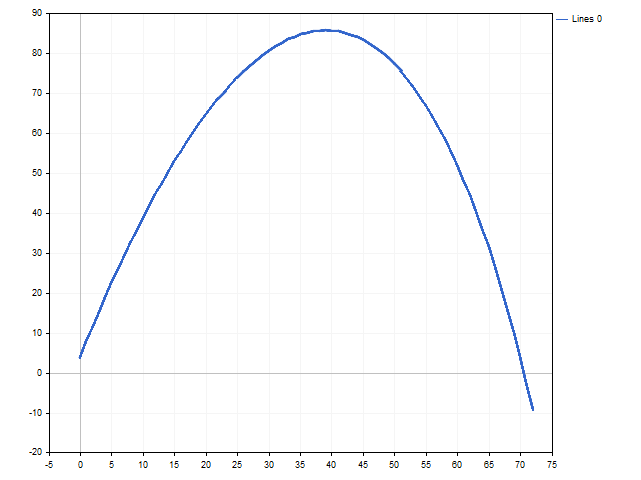
- プレイすることに同意し、所持金が73.74ドゥカートを超えている場合、すべてが順調です。リスクと機会は正しく計算されています。
- 正確に73.74ドゥカートなら、薄い氷の上を歩いていることになります。非常に薄い氷の上です。
- 73.74ドゥカート未満の場合は、ご自分のアドレナリン中毒に対処する他の方法を探す必要があるかもしれません。沖合でお腹を空かした人食いサメに餌をやるとかです。
- 73.74ドゥカートを超えているのにこのゲームを放棄した場合、人生で最も興味深い瞬間を逃している可能性が十分にあります。
この不思議な73.74ドゥカートという合計はどこから来たのか、疑問に思われるかもしれません。それは、このゲームの道徳的期待値から来ています。
合理的なプレイヤーの場合、道徳的期待値は厳密に正でなければなりません。
不等式Deposit > 73.74から解を見つけるのは簡単です。以下の画像は、プレイヤーの資本によって道徳的期待値がどのように変化するかを示しています。
取引における道徳的期待値
一部の取引戦略には、損切りと利食いの設定が含まれます。このような取引戦略では、道徳的期待値を使用することができます。この場合、道徳的期待値を適用するためのいくつかのオプションが可能です。
ポジションを開くとき、トレーダーは取引口座の正確な残高を知っています。また、勝つ確率を見積もることができます(これについては以下で説明します)。他のすべてのポジションパラメータは変数として表されます。
- SL:ポイント単位でのポジションの始値と損切りの差(正の整数)
- TP:ポイント単位でのポジションの始値と利食いの差;
- PV:ポイントあたりの預金通貨の1コスト
- Lot:ポジションボリューム
この場合、このポジションに対する道徳的期待値は次のようになります。
道徳的期待値を適用する最初の方法は、3つの変数のうち任意の2つの値(SL、TP、およびLot)が事前に設定されている場合にのみ可能です。
たとえば、ポジションを開くときは、ポジションボリュームとその利食いを設定します。すると、この取引の損切りレベルを推定できます。その値は、道徳的期待値が正になるようなものでなければなりません。言い換えれば、可能な最大の損切り値を見つけます。
これをおこなう方法を象徴的に見てみましょう。まず、補助変数の値を見つける必要があります。
すると、損切りは不等式によって制限されます。
ロットと損切りが指定されている場合、利食いレベルを見積もることができます。
すると、この取引の利食いは次のようになります。
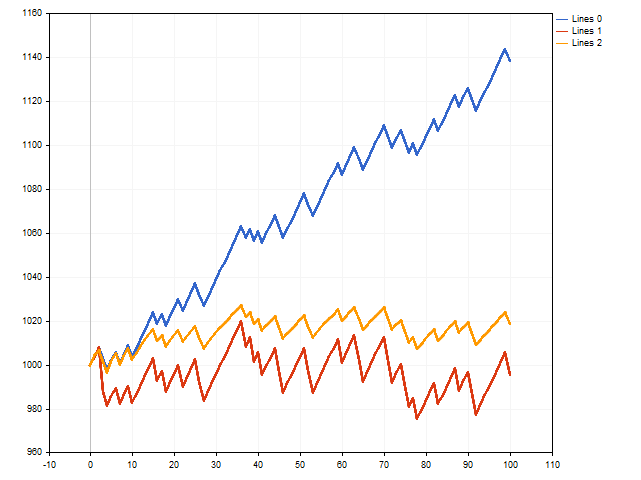
これは理論でした。それでは、実際に何ができるか見てみましょう。それには、取引の実行をシミュレートするスクリプトを作成します。同時に、固定損切りと利食い、フローティング損切りとフローティング利食いの3つのオプションをチェックします。
一見すると、損切りと利食いが固定されたオプション(青い線)が勝ちです。
ただし、可能な限り最大の損切りと最小の利食いを使用したことを覚えておく必要があります。損切りをわずかに減らし、利食いを増やすことで、これらの境界から離れるとどうなるでしょうか。すると、状況が変わる可能性があります。
赤い線は変動損切りでの取引の結果を示し、オレンジ色の線は変動利食いでの取引の結果を示します。ご覧のとおり、変動利食いは取引結果にプラスの影響を与える可能性があります。
道徳的期待値と資金管理
道徳的期待値の方程式を2つの部分に分けてみましょう。条件付きで最初の部分を有益と呼びましょう。
2番目の部分は不採算と呼ばれます。
儲かる部分をよく見てみると、ロットの増加がその成長につながっていることがわかります。しかし、同じロットの増加は、不採算部分の減少につながります。その結果、不採算部分がゼロ(またはマイナスの値)になる可能性があります。この場合、そのような取引の道徳的期待値は否定的になります。覚えているように、これは最良の選択ではなく、合理的なトレーダーはそれを承認しません。
次のアイデアは、特定のロット値を見つけることです。これにより、方程式の収益性の高い部分と収益性のない部分の両方が同時に可能な最大値を取るようになります。次に、道徳的期待値は、与えられたSLとTPに対して最大になります。画像では、ロットサイズが大きくなるにつれて道徳的期待値がどのように変化するかを見ることができます。
数値の実験は肯定的な結果をもたらしました。それでは、最適なポジションサイズの式を導き出しましょう。これをおこなうには、lot変数に関する道徳的期待値の導関数を見つけ、それをゼロに等しくし、結果の方程式を解く必要があります。その結果、次の式が得られます。
式の角括弧で囲まれた部分に注目しましょう。そこにあるのは、数学的期待値を損切りと利食いで割ったものです。ロットを正しく計算するには、トランザクションの数学的期待値が厳密に正でなければならないことに注意してください。つまり、次の条件が常に満たされている必要があります。
ちなみに、角括弧内の分数を展開すると、ケリー基準が得られます。
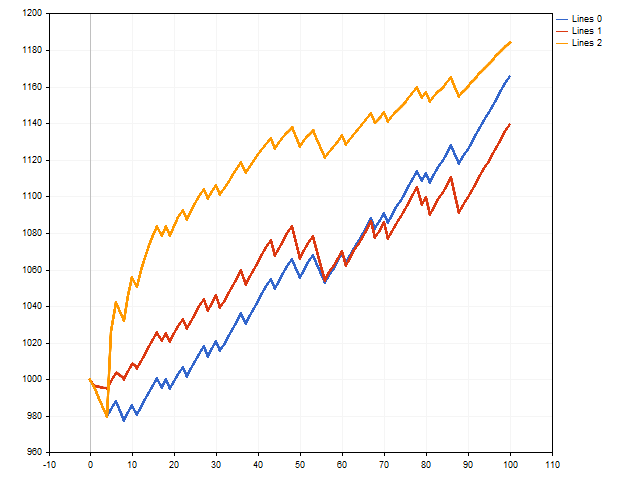
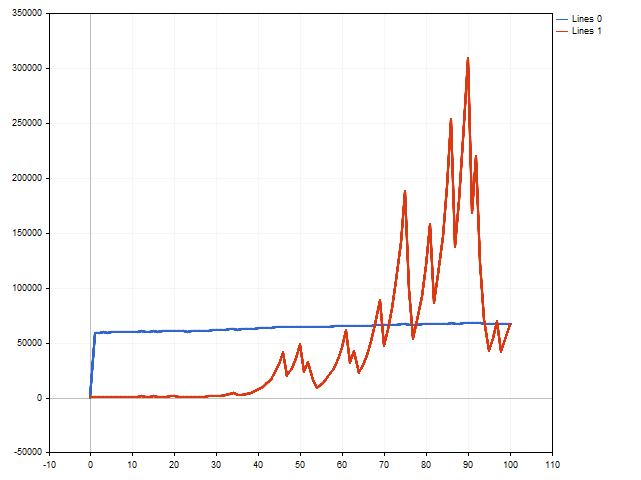
それでは、一連の取引をシミュレートしてみましょう。この取引では、道徳的期待値の助けを借りてロットが管理されます。ここでは、さまざまな結果が表示されます。たとえば、初回入金額が160倍以上に増加する可能性があります。
ただし、連続した負けトレードは、結果に最良ではない影響を与える可能性があります。次の図では、初回入金が約50倍に増加したことがわかります。これはかなり良いです。90番目のステップ近くで、初回入金が約300倍に増加したという事実を考慮しなければです。
危機管理
ご覧のように、道徳的期待値による資金管理は、印象的な利益と非常に明らかな損失の両方につながる可能性があります.これは、リスク管理の問題を提起します。
ここには2つの方法があります。1つ目(最も明白な方法)は、利用可能な預金全体を計算に使用するのではなく、その一部のみを使用することです。たとえば、固定金額を設定できます。また、現在の残高の割合を設定することもできます。いずれにせよ、これは取引時のリスクを軽減するのに役立ちます。
2番目のリスク管理オプションは、収益性の高い取引の確率の計算を変更することです。このオプションを詳しく見てみましょう。
nは取引の総数、mは勝った数です。すると、勝つ確率は次のように評価できます。
ただし、このアプローチは完全に正しいわけではありません。それで、すでに発生したイベントの頻度を推定するためです。代わりに、将来の取引で勝つ確率を取得する必要があります。
すでに15回の取引をおこない、そのうち10回が勝っているとしましょう。次のポジションを建てようとしています。その後、取引の総数は1増加しますが、勝ち取引の数は増加するか、同じままになる可能性があります。
これらのオプションの平均を取ってみましょう。ポジションで勝つ確率は次のようになります。
このようにして、Krichevsky–Trofimov推定量を取得します。記号形式では次のようになります。
シフトを追加すると、勝つ確率がわずかに低くなり、リスクが低くなります。
次のように確率推定を一般化しましょう。任意のシフトs >=1を導入します。すると、勝つ確率は次のようになります。
sを設定することで、かなり広い範囲でリスクを調整できます。sの値が大きいほど、リスクは低くなります。
残念ながら、リスクの軽減は、受け取る利益の額にも影響します。したがって、トレーダーには選択が強いられます。リスクが高いと大きな利益を得ることができますが、損失も非常に大きくなる可能性があります。リスクが低いと損失を減らすことができますが、利益は小さくなります。
リスクが取引にどのように影響するかを見てみましょう。2つの移動平均線の交点で最も単純なエキスパートアドバイザー(EA)を使用します。EAは次のパラメータでテストされました。
通貨ペア:ユーロドル
時間枠:H1
テスト期間:2021.01.01–2022.12.31
他のすべてのパラメータはデフォルトです。
テスト期間中に419回の取引がありました。残高グラフは次のようになります。
異なるリスク値について、次の結果が得られました。
| リスク | 総純利益 | 初期投資額からの残高ドローダウン | 利益率 | ペイオフの期待値 | 回復率 | マージンレベル |
|---|---|---|---|---|---|---|
| 0 | 42961.51 | 2699.05 | 1.18 | 102.53 | 1.72 | 89.20% |
| 25 | 28932.51 | 570.27 | 1.21 | 69.05 | 1.89 | 260.70% |
| 50 | 16836.83 | 230.64 | 1.21 | 40.18 | 1.92 | 309.53% |
ご覧のとおり、リスク削減は利益を減らしますが、取引戦略の他のパラメータを改善することができます。
結論
この記事の執筆時には、次のプログラムが使用されました。
| 名前 | 種類 | 詳細 |
|---|---|---|
| ME SL-TP | スクリプト | 取引の道徳的期待値に従って損切りと利食いの値が選択された場合に、取引の収益性がどのように変化するかを示すスクリプトです。スクリプトパラメータは次の通りです。
|
| ME Lot | スクリプト | ポジションサイズが取引の道徳的期待値にどのように影響するかを示すスクリプトです。 |
| ME MM | スクリプト | 道徳的期待の資産管理と固定ロット取引を比較するスクリプトです。作業の最後に、両方のオプションの取引結果と、合理的な固定ロットのサイズを示すメッセージが表示されます。 |
| Two_Moving_Averages_System | EA | 取引パフォーマンスに対するリスクの影響を評価できます。そのパラメータは次の通りです。
|
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/12134
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
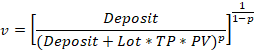


利益が出るトレードの確率と保証金次第です。大きなストップロスを使うのは、小さな値動きの可能性が高いからです。つまり、TP = 20 * SLの比率では、利益を取ってポジションを閉じる可能性が高くなります。しかし、これはすでに最適採算の理論に当てはまります。
新しい記事「 トレーディングにおける道徳的期待」が掲載されました:
アレクセイ・ポリャコフ 著
非常に独創的なトレーディング理論である!
いや、実に興味深い記事だ。そのような用語は高等教育にはないし、数学にもない。どうでもいいのか?)
現象を描写し、それに用語を与えることを妨げるものは何もない。
特にこのような狭い環境では。
いや、実に興味深い記事だ。そのような用語は高等教育にはないし、数学の世界だけだ) インディキターズや経済ニュースはどうなんだ?気にしないんですか?)
指標-そんなものがある
https://www.mql5.com/ja/articles/14494
ニュースについて書くつもりはない。複雑すぎるし、ファジーロジックとかいろいろあるし......。むしろ、サイクルについてお話ししたいと思います。
そして用語について。道徳的期待」というものがある。