MetaTrader 5 / 統計と分析
English Русский 中文 Español Deutsch Português
preview
データサイエンスと機械学習（第10回）：リッジ回帰

データサイエンスと機械学習（第10回）：リッジ回帰

MetaTrader 5 — 統計と分析 | 18 4月 2023, 12:21
528 0
Omega J Msigwa
Omega J Msigwa

はじめに 

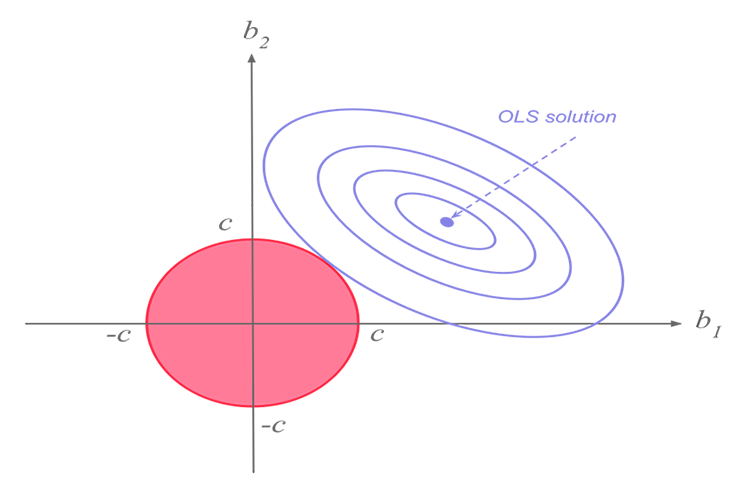
リッジ回帰は、独立変数の相関が高い場面で、重回帰モデルの係数を推定する方法です。この方法は、許容量のバイアスと引き換えに、パラメータ推定問題の効率を向上させます。一方、ラッソ (最小絶対収縮および選択演算子) は、変数の選択と正則化の両方を実行して、結果として得られる統計モデルの予測精度と解釈可能性を高める回帰分析方法です。ラッソはもともと線形回帰モデルのために定式化されたものです。この単純なケースは、推定量についてかなりのことを明らかにしています。これには、リッジ回帰やベストサブセット選択との関係、ラッソ係数推定といわゆるソフト閾値との関係などが含まれます。また、共変量が共線的であれば、（標準的な線形回帰のように）係数推定値が一意である必要はないことも明らかになります。

ここで、そもそもなぜこのようなモデルが必要なのかを理解するために、バイアス（偏り）とバリアンス（分散）という言葉を理解しましょう。


バイアス（偏り） 

機械学習が独立変数と応答変数の真の関係を捉えることができないことです。

このことは、モデルにとってどのような意味を持つのでしょうか。

  • バイアスが低い：バイアスの低いモデルは、目標関数の形についての仮定を少なくしている
  • バイアスが高い：バイアスが高いモデルは、より多くの仮定を立て、学習データセット内の関係を捉えることができる

    バリアンス（分散）

    バリアンスは、確率変数がその期待値からどれだけ異なるかを示します。
    バイアスを減らす方法：
    • モデルが学習不足なため、入力の特徴を増やす
    • 正則化項を減少させる
    • 一部の多項式機能を含むなど、より複雑な機能を使用する

    バリアンスを減らす方法：

    • 入力特徴量を減らす、モデルが学習不足なため、パラメータ数を減らす
    • あまり複雑なモデルは使わない
    • 学習データを増やす
    • 正則化項を増やす


    バイアスとバリアンスのトレードオフ

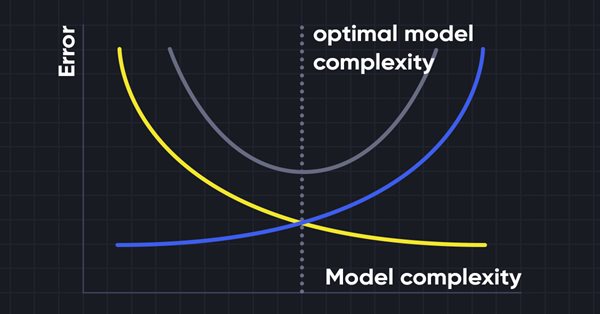
    機械学習モデルを構築する際には、モデルの過学習を避けるために、バイアスとバリアンスに注意することが本当に重要です。モデルが非常に単純でパラメータが少ない場合、バイアスは大きいがバリアンスは小さくなる傾向があり、逆に複雑なモデルはバイアスは小さいがバリアンスは大きくなることが多くなります。そのため、バイアスとバリアンスエラーのバランスを取る必要があります。これら2項のバランスを見つけることは、バイアスとバリアンスのトレードオフとして知られています。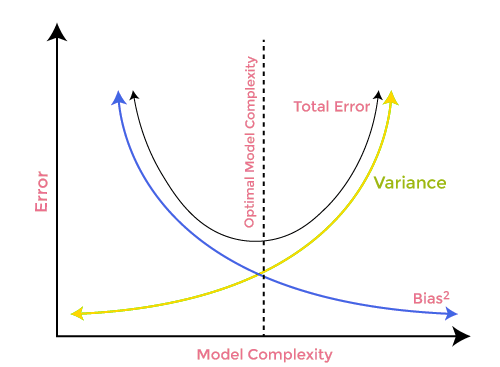
    モデルの正確な予測のためには、アルゴリズムには低いバイアスと低いバリアンスも必要ですが、バイアスとバリアンスは互いに負の関係にあるため、これは現実的に不可能です。
    バイアスを大きくすればバリアンスは小さくなり、その逆もまた真です。


    リッジ回帰

    リッジ回帰と投げ縄回帰は同じ使命を持っていますが、両者には大きな違いがあり、後ほど、数学の世界に飛び込み、それぞれのアルゴリズムが何を特徴としているのかを解明することになります。

    リッジ回帰の考え方

    線形相関のある測定値がたくさんある場合、最小二乗法は独立変数と目的変数の関係を反映するのに適していると確信することができます。

    下図は、マウスの大きさと体重をプロットした例です。


    しかし、2つの測定値を学習データセットとして残りをテストデータセットとした場合、最小二乗法でモデルを適合させると、残差の二乗和がゼロとなる完全適合となります。


    次に、このモデルを新しいデータセットでテストしてみましょう。



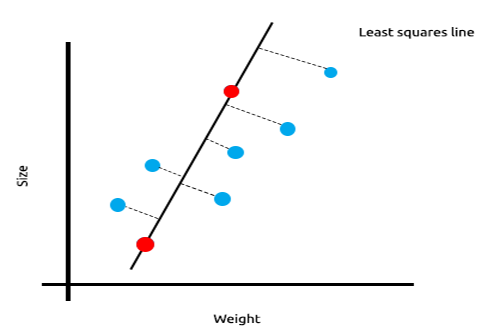
    学習データの二乗誤差の合計はゼロですが、テストデータの二乗残差の合計は大きく、モデルの分散が大きいことを意味します。機械学習の専門用語では、このモデルは学習データに過学習していると言います。

    リッジ回帰とラッソ回帰の主な考え方は、学習データにあまり合わないモデルを見つけることです。


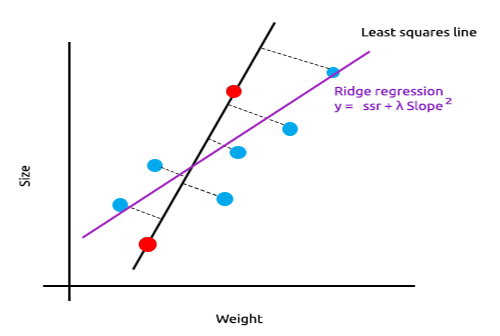
    リッジ回帰では、少量のバイアスを導入することで新しい線にして、分散の大幅な減少を得ることができます。リッジ回帰はわずかなバイアスを導入しているため、モデルはうまく適合しませんが、学習データとテストデータの両方から、長期的に信頼できるモデルを得ることができます。

    この正則化されたモデルを使うとき

    最小二乗法や線形回帰モデルで十分なのに、なぜL1normやL2Normを使うかと思われるかもしれません。

    これを理解するために、多変量線形回帰が学習済みデータセットでどのように実行されるかを見てみましょう。


    そこで、EURUSDのオシレータとボリューム指標のデータセットを用意しました。

    相関行列を見るまでもなく、これらの指標が回帰問題に適さないことは、これらの指標に詳しい人なら誰でも知っていることです。以下は、相関マトリックスです。

        ArrayPrint(matrix_utils.csv_header);
    Print(Matrix.CorrCoef(false));

    結果：

    CS      0       06:29:41.493    TestEA (EURUSD,H1)      "Stochastic" "Rsi"        "Volume"     "Bears"      "Bulls"      "EURUSD"    
CS      0       06:29:41.493    TestEA (EURUSD,H1)      [[1,0.680705511991766,0.02399740959375265,0.6910892641498844,0.7291018045506749,0.1490856367010467]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.680705511991766,1,0.07620207894739518,0.8184961346648213,0.8258569040865805,0.1567269000583347]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.02399740959375265,0.07620207894739518,1,0.3752014290536041,-0.1289026185114097,-0.1024017077869821]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.6910892641498844,0.8184961346648213,0.3752014290536041,1,0.7826404088603456,0.07283638913665436]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.7291018045506749,0.8258569040865805,-0.1289026185114097,0.7826404088603456,1,0.08392530400705019]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.1490856367010467,0.1567269000583347,-0.1024017077869821,0.07283638913665436,0.08392530400705019,1]]
    すべての指標に対するEURUSD列の相関が20%未満であることがわかります。ストキャスティクスとRSIは他よりも相関が高いようですが、それぞれ約14%と15%に留まっていることがわかります。ストキャスティクスのみから始まる線形回帰モデルを作成し、その後、独立変数や他の指標の読み方をどんどん追加していくことにしましょう。

    結果の表：

    独立変数 R2スコア(精度)
      ストキャスティクス     1.2 %
      ストキャスティクスとRSI     1.8 %
      ストキャスティクス、RSI、ボリューム     2.8 %
      ストキャスティクス、RSI、ボリューム、ベアーズパワー、ブルズパワー
      (すべての独立変数)    		     4.9%

    では、この表からどのような結論を引き出すことができるでしょうか。独立変数の数を増やすと、学習済み線形モデルの精度は、その変数が何であるかにかかわらず常に上昇します。この例で使用した独立変数の相関は非常に低いので、新しい独立変数が追加されるたびに精度がわずかに向上するのがわかりますが、変数の相関がそれぞれ30～40%程度ある場合は、そうではないかもしれません。これらの独立変数を与えすぎると、訓練フェーズでモデルの精度が最大90%に達することがあります。

    独立変数の増加はバリアンスを増加させます。.このモデルは過学習であるため、新しいデータセットでパフォーマンスが低下することは間違いありません。この問題を解決するために、リッジ回帰と投げ縄回帰の両方が導入されました。先に述べたように、ある種のバイアスを追加することで、バリアントが大幅に低下します。


    リッジ回帰理論

    リッジ回帰自体は、独立変数の相関が高い場合に、線形回帰モデルの係数を推定する手法です。

    リッジ回帰は、線形回帰モデルに多重共線性（高相関）がある場合に、最小二乗法による推定量の不正確さを解決するために、リッジ回帰推定量（RR）を作成することによって開発されました。これは、バリアントとバイアスが最小二乗法による推定量よりも小さいことが多く、より正確なリッジパラメータを提供します。

    リッジ推測機

    通常の最小二乗法推定量と同様に，単純リッジ推定量は次式で与えられます。 

    ここで、yは独立変数行列、Xはデザイン行列、Iは恒等行列で、λは0以上の値を持つリッジパラメータです。

    そのためのコードを書いてみましょう。

    CRidgeregression::CRidgeregression(matrix &_matrix)
 {
    
    n = _matrix.Rows();
    k = _matrix.Cols();
    
    pre_processing.Standardization(_matrix);
    m_dataset.Copy(_matrix);
    
    matrix_utils.XandYSplitMatrices(_matrix,XMatrix,yVector);
    
    YMatrix = matrix_utils.VectorToMatrix(yVector);
    
//---

    Id_matrix.Resize(k,k);
    
    Id_matrix.Identity();

 }

    関数コンストラクタでは3つの重要なことがおこないます。1つ目は、データの標準化です。多変量勾配降下や他の多くの機械学習手法と同様に、リッジ回帰は標準化されたデータセットで動作し、次にデータはx行列とy行列に分割され、最後に恒等行列が作成されます。

    L2Norm関数の内部：

    vector CRidgeregression::L2Norm(double lambda)
 {    
   matrix design = matrix_utils.DesignMatrix(XMatrix);
   
   matrix XT = design.Transpose();
   
   matrix XTX = XT.MatMul(design);
   
   matrix lamdaxI = lambda * Id_matrix;
   
   //Print("LambdaxI \n",lamdaxI);
   
   //Print("XTX\n",XTX);
   
   matrix sum_matrix = XTX + lamdaxI;
   
   matrix Inverse_sum = sum_matrix.Inv();
   
   matrix XTy = XT.MatMul(YMatrix);
   
   Betas = Inverse_sum.MatMul(XTy);
 
   #ifdef DEBUG_MODE
      Print("Betas\n",Betas);
   #endif 
   
  return(matrix_utils.MatrixToVector(Betas));
 }

    この関数は、先ほど見たリッジ回帰を使った係数の求め方の上式で指示されたとおりに、すべての処理をおこないます。

    この仕組みを理解するために、本連載の読者にはすでに馴染みのある別のデータセットを使ってみましょう。

    int OnInit()
  {
//---
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);
    
    ridge_reg = new CRidgeregression(Matrix);
    
    ridge_reg.L2Norm(0.3);
 }    

    リッジ回帰のランダムペナルティの値を0.3に設定したのは、この結果どうなるかを見るためです。次に、いよいよ関数を実行し、どんな係数が出るか見てみましょう。

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [[5.015577002384403e-16]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6013523727380532].

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3381524618200134]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.2119467984461254]] 。

    また、同じデータセットに対して線形回帰モデルを実行し、その係数も観察してみましょう。最小二乗法はデータセットを標準化しないので、モデルにデータを与える前に標準化もおこなってみましょう。

        matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);

    以下が出力です。

    CS 0 10:27:41.338 TestEA (EURUSD,H1) Betas

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [[-4.143037461930866e-14]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6034777119810752]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3363532376334173]

    CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.21126507562567]]

    係数が微妙に違うので、この関数が機能しているのでしょう。それぞれのモデルを訓練してテストし、最後にそれぞれのグラフをプロットすると、より理解が深まります。

    リッジ回帰自体はモデルではなく、線形回帰モデルで使用する必要のある係数の推定量なので、第3回で説明した線形回帰のクラスを少し変更しました。 

    線形回帰のクラスコンストラクタは、モデルが学習する場所です。これは、係数を保存して他の機能で使用するための領域です。モデルに係数を渡すことができる新しいコンストラクタを追加しました。これは、次に他の推定量を使用して、回帰モデルに使用させたい係数を取得する際に、最小限の労力でおこなうことができます。

    class CLinearRegression
  {
   public: 
                        CLinearRegression(matrix &Matrix_); //Least squares estimator
                        CLinearRegression(matrix<double> &Matrix_, double Lr, uint iters = 1000); //Lr by Gradient descent
                        CLinearRegression(matrix &Matrix_, vector &coeff_vector);
                        
                       ~CLinearRegression(void);


    リッジ回帰と線形回帰の比較

        Print("----> Ridge regression");
    
    ridge_reg = new CRidgeregression(Matrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(Matrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    double acc =0;
    
    vector ridge_predictions = Linear_reg.LRModelPred(Matrix,acc); //making the predictions and storing them to a vector
    
    delete(Linear_reg); //deleting that instance
    
    Print("----> Linear Regression");
   
    pre_processing.Standardization(Matrix);
     
    Linear_reg = new CLinearRegression(Matrix); //new Linear reg instance that gets coefficients by least squares
    
    vector linear_pred = Linear_reg.LRModelPred(Matrix,acc);

    出力：

    CS 0 11:35:52.153 TestEA (EURUSD,H1) ----> リッジ回帰

    CS 0 11:35:52.153 TestEA (EURUSD,H1) Betas

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [[-4.142058558619502e-14]

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.601352372738047].

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.3381524618200102].

    CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.2119467984461223]]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982949 Adjusted R 0.982926

    CS 0 11:35:52.154 TestEA (EURUSD,H1) ----> 線形回帰

    CS 0 11:35:52.154 TestEA (EURUSD,H1) Betas

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [[5.014846059117108e-16]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.6034777119810601]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.3363532376334217]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.2112650756256718]]

    CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982933 Adjusted R 0.982910

    すべてのデータを学習データとして使用した場合、モデルの性能は若干異なります。

    出力を保存して同じ軸にプロットすると、次のようなグラフになります。

    リッジ回帰と線形回帰の比較

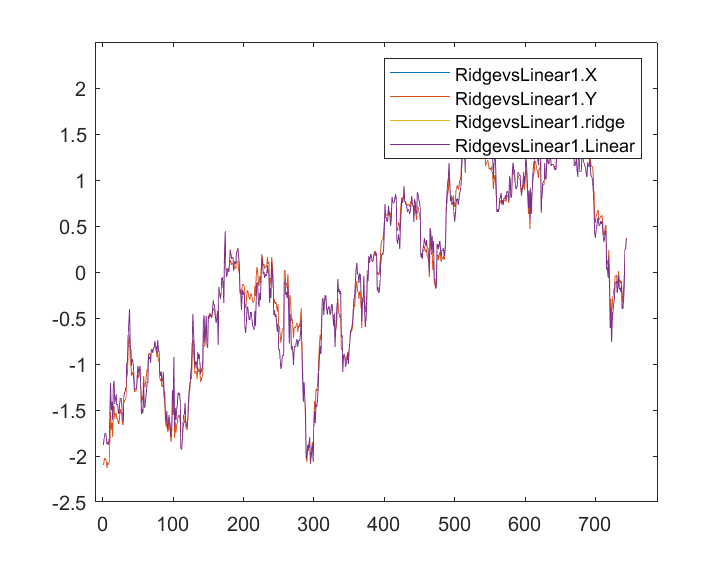
    線形モデルと青色でマークされた予測因子の違いはほとんどわかりません。リッジ回帰がデータセットにうまく適合していないことがわかるだけです。両モデルを1つずつ訓練してテストしてみましょう。

        matrix_utils.TrainTestSplitMatrices(Matrix,TrainMatrix,TestMatrix);
    
    Print("----> Ridge regression | Train ");
    
    ridge_reg = new CRidgeregression(TrainMatrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(TrainMatrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Ridge regression | Test");
    
    vector ridge_predictions = Linear_reg.LRModelPred(TestMatrix,acc); //making the predictions and storing them to a vector
    
    printf("Accuracy %.5f ",acc);
    
    delete(Linear_reg); //deleting that instance
    
    Print("\n----> Linear Regression | Train ");
     
    Linear_reg = new CLinearRegression(TrainMatrix); //new Linear reg instance that gets coefficients by least squares
    
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Linear Regression | Test ");
    
    vector linear_pred = Linear_reg.LRModelPred(TestMatrix,acc); 
    
    printf("Accuracy %.5f ",acc);
    

    出力：

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> リッジ回帰 | 訓練 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> リッジ回帰｜テスト

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78620 

    CS 0 13:27:40.744 TestEA (EURUSD,H1)

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> 線形回帰｜訓練 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> 線形回帰 | テスト 

    CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78540 

    リッジ回帰が独立変数を罰するために使用するペナルティが0.3と小さく、適切なペナルティを選択する方法がまだわかっていないことを考えると、両モデルとも訓練ではほぼ同じ精度でしたが、テストデータセットではわずかな違いがあったようです。

    λ値を10にすると、リッジ回帰の学習精度は0.97580から0.95760に下がり、テスト精度は0.78540から0.80050にわずかに上昇しました。


    適切なペナルティ値の選択(λ)

    λの正しい値を見つけるには、LEAVE ONE OUT CROSS VALIDATION (LOOCV)という手法を使う必要があります。なじみのない方のために説明すると、これはMLでいくつかのモデルの最適なパラメータを見つける手法です。これを達成する方法は次の通りです。すべてのデータセットを調べて、Iサンプルをデータセットから除外し、残りのデータセット(n-1)でモデルを訓練し、除外された1つのサンプルをテストサンプルとして使用します。n番目のサンプルまですべてのデータセットを調べ、最後に各反復ですべての値の損失を測定します。最後に、λの特定の値で最小損失関数がどこにあったかを見つけます。これは、最小のエラーを生成するものであり、その後の情報を読み込むめの最良のパラメータです。

    λの最適値を求めるために、交差検証クラスをインポートしてみましょう。

    #include <MALE5\cross_validation.mqh>
CCrossValidation *cross_validation;

    以下は、リッジ回帰のLOOCVのコードです。

    double CCrossValidation::LeaveOneOut(double init, double step, double finale)
 {
    matrix XMatrix;
    vector yVector;
    
    matrix_utils.XandYSplitMatrices(Matrix,XMatrix,yVector);
 
    matrix train = Matrix; vector test = {};
    
    int size = int(finale/step);
    vector validation_output(ulong(size));
    vector lambda_vector(ulong(size));
    
    vector forecast(n); 
    vector actual = yVector;
    
    double lambda = init;
    
     for (int i=0; i<size; i++)
       {
         lambda += step;
         
          for (ulong j=0; j<n; j++)
            {               
               train.Copy(Matrix);
               ZeroMemory(test);
               
               test = XMatrix.Row(j);
               
               matrix_utils.MatrixRemoveRow(train,j);
               
               vector coeff = {};
               double acc =0;
               
                switch(selected_model)
                  {
                   case  RIDGE_REGRESSION:

                        ridge_regression = new CRidgeregression(train);
                        coeff = ridge_regression.L2Norm(lambda); //ridge regression
                        
                        Linear_reg = new CLinearRegression(train,coeff);   

                        forecast[j] =  Linear_reg.LRModelPred(test);  
                        
                        //---
                        
                        delete (Linear_reg); 
                        delete (ridge_regression);
                        
                     break; 
                  }
            }
          
          validation_output[i] = forecast.Loss(actual,LOSS_MSE)/double(n); 
          
          lambda_vector[i] = lambda;
          
          #ifdef DEBUG_MODE
             printf("%.5f LOOCV mse %.5f",lambda_vector[i],validation_output[i]);
          #endif           
       }

//---

      #ifdef  DEBUG_MODE
         matrix store_matrix(size,2);
         
         store_matrix.Col(validation_output,0);
         store_matrix.Col(lambda_vector,1); 
         
         string name = EnumToString(selected_model)+"\\LOOCV.csv";
         
         string header[2] = {"Validation output","lambda"};
         matrix_utils.WriteCsv(name,store_matrix,header);
      #endif 
      
    return(lambda_vector[validation_output.ArgMin()]);
 }

    これを実行しましょう。

    int OnInit()
  {    
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",",");  
    
    ridge_reg = new CRidgeregression(Matrix);
    
    cross_validation = new CCrossValidation(Matrix,RIDGE_REGRESSION);
    
    double best_lambda = cross_validation.LeaveOneOut(0,1,10);
    
    Print("Best lambda ",best_lambda);

    出力：

    CS      0       10:12:51.346    ridge_test (EURUSD,H1)  1.00000 LOOCV mse 0.00020
CS      0       10:12:51.465    ridge_test (EURUSD,H1)  2.00000 LOOCV mse 0.00020
CS      0       10:12:51.576    ridge_test (EURUSD,H1)  3.00000 LOOCV mse 0.00020
CS      0       10:12:51.684    ridge_test (EURUSD,H1)  4.00000 LOOCV mse 0.00020
CS      0       10:12:51.788    ridge_test (EURUSD,H1)  5.00000 LOOCV mse 0.00020
CS      0       10:12:51.888    ridge_test (EURUSD,H1)  6.00000 LOOCV mse 0.00020
CS      0       10:12:51.987    ridge_test (EURUSD,H1)  7.00000 LOOCV mse 0.00021
CS      0       10:12:52.090    ridge_test (EURUSD,H1)  8.00000 LOOCV mse 0.00021
CS      0       10:12:52.201    ridge_test (EURUSD,H1)  9.00000 LOOCV mse 0.00021
CS      0       10:12:52.317    ridge_test (EURUSD,H1)  10.00000 LOOCV mse 0.00021
CS      0       10:12:52.319    ridge_test (EURUSD,H1)  Best lambda 1.0

    コードにバグがないと仮定すると、1～10まで検索したときのλの最適値は1です。このモデルのλの値はやや小さいことがわかるので、0から10まで、ステップサイズを0.01に設定してループを実行することにしました（合計1000回の反復）。完了するまでに5分ほどかかりましたが、λの最適値として0.09を取得できました。以下はプロットです。

    LOOCV

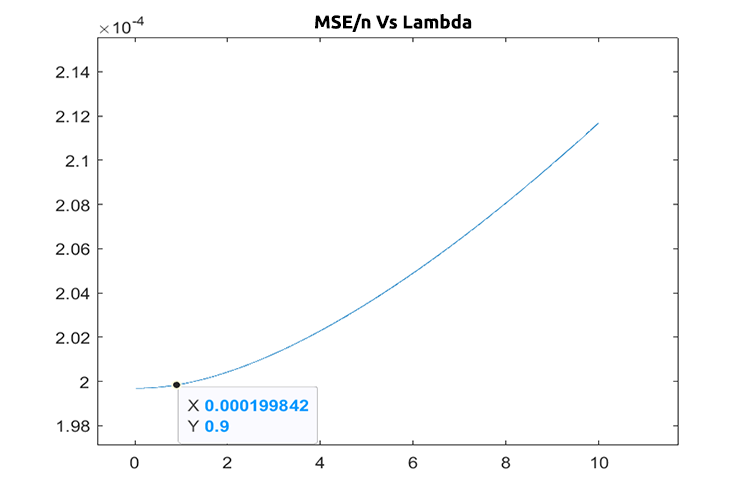
    これでリッジ回帰の部分はすべてうまくいきました。


    リッジ回帰のメリット

    • リッジ回帰推定量を使用することのメリットをいくつか見てみましょう。
    •  過学習からモデルを守ることができる
    •  モデルの複雑さを軽減できる
    •  多変量データセットにおいて、線形回帰に勝るとも劣らない性能を発揮する
    •  不偏推定量を必要としない

    リッジ回帰のデメリット

    •  最終モデルにすべての予測因子が含まれる
    •  特徴選択をおこなうことができない
    •  係数をゼロに向かって縮める
    •  バリアントとバイアスのトレードオフ


    最後に

    リッジ回帰は多変量解析の場合に回帰モデルの過学習を避けるのに役立ちますが、それでもモデルから不要な変数を自分で回避・削除することは重要です。今回のNASDAQ_DATAからRSI列を削除することもできたでしょう。なぜなら、RSI列がターゲット変数と相関していないことはおそらく誰もが知っているからです。この記事はここまでです。

    リッジ回帰の開発については、私のGitHubリポジトリで追跡してください。https://github.com/MegaJoctan/MALE5

    ファイル名 詳細
    cross_validation.mqh  sklearn交差検証と同様、LOOCVのような検証技法を含んでいます
    Linear regression.mqh  最小二乗法/線形回帰モデルを含んでいます
     matrix_utils.mqh  このユーティリティクラス関数は、追加の行列操作関数を含んでいます
     Preprocessing.mqh         sklearn.preprocessingと同様に、このクラスにはデータセットの操作や再スケーリングに使用できる関数が含まれています
     Ridge Regression.mqh  リッジ回帰モデルとその関連関数が含まれています
     ridge_test.mq5  本記事で説明したすべてのことをテストするために使用されるスクリプトです
     prepare_dataset.mq5  前回説明したオシレータ系指標のデータセットを作成するスクリプトで、データは、Oscillators.csvというファイルに格納されます
     NASDAQ_DATA.csv  このcsvファイルには、本記事で使用したデータセットが含まれています

    MetaQuotes Ltdにより英語から翻訳されました。
    元の記事: https://www.mql5.com/en/articles/11735

    添付されたファイル |
    ZIPをダウンロード
    MQL5.zip (142.77 KB)
    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この著者による他の記事

    ディスカッションに移動
    自動で動くEAを作る（第08回）：OnTradeTransaction 自動で動くEAを作る（第08回）：OnTradeTransaction
    今回は、受注システムに関する問題を迅速かつ効率的に処理するためのイベント処理システムの使用方法について紹介します。このシステムにより、EAは必要なデータを常に検索する必要がなくなり、より速く動作するようになります。
    MetaTrader 5におけるバイナリーオプション戦略のテストと最適化 MetaTrader 5におけるバイナリーオプション戦略のテストと最適化
    今回は、MetaTrader5でのバイナリーオプション戦略の確認と最適化をおこないます。
    ニューラルネットワークが簡単に（第34部）：FQF（Fully Parameterized Quantile Function、完全にパラメータ化された分位数関数） ニューラルネットワークが簡単に（第34部）：FQF（Fully Parameterized Quantile Function、完全にパラメータ化された分位数関数）
    分散型Q学習アルゴリズムの研究を続けます。以前の記事では、分散型の分位数Q学習アルゴリズムについて検討しました。最初のアルゴリズムでは、与えられた範囲の値の確率を訓練しました。2番目のアルゴリズムでは、特定の確率で範囲を訓練しました。それらの両方で、1つの分布のアプリオリな知識を使用し、別の分布を訓練しました。この記事では、モデルが両方の分布で訓練できるようにするアルゴリズムを検討します。
    MQL5クックブック - マクロ経済イベントデータベース MQL5クックブック - マクロ経済イベントデータベース
    この記事では、SQLiteエンジンに基づいてデータベースを処理する可能性について説明します。CDatabaseクラスは、OOP原則を便利かつ効率的に使用するために作成されました。その後、マクロ経済イベントのデータベースの作成と管理に関与しています。この記事では、CDatabaseクラスの複数のメソッドを使用する例を示します。