ニューラルネットワークが簡単に（第33部）：分散型Q学習における分位点回帰

MetaTrader 5 — トレーディングシステム | 28 3月 2023, 10:38

459

Dmitriy Gizlyk

はじめに

前回は、予測される報酬の確率分布を学習できる分散型Q学習に触れました。特定の値域で期待される報酬を受け取る確率を予測する方法を学びました。ただし、そのような範囲の数や報酬値の広がりは、モデルのハイパーパラメータになります。最適なパラメータを選択するためには、報酬値の分布に関する専門的な知識が必要となるとともに、ある種のテストをおこなう必要があります。

前回検討した可能な値の範囲全体を等しい範囲に分割する方法にも、欠点があると言わざるを得ません。それぞれの行動に対して、個々の範囲で報酬を受け取る確率を予測するために1つのニューロンを特定しましたが、実際には、多くの範囲で報酬を受け取る確率は0に等しいことがかなり多いです。つまり、資源を非効率に使っていることになります。いくつかの範囲を組み合わせれば、操作回数を減らすことができ、モデルの訓練や実行のスピードアップが期待できます。同時に、他の範囲で報酬を受け取る確率はかなり高いです。全体像をより完全に把握するために、この範囲をより小さく分割することができます。そうすれば、期待報酬の予測精度が向上しますが、私たちの方法では、異なるサイズの範囲を作成することはできません。これらの欠点は、2017年10月の「Distributional Reinforcement Learning with Quantile Regression」稿で提案した分位点回帰アルゴリズムを用いることで解決できます。

1.分位点回帰

分位点回帰は、説明変数の分布と目的変数のある分位点との関係をモデル化したものです。

分散型Q学習における分位点回帰の利用について検討を進める前に、提案するアルゴリズムが期待報酬の確率的分布の評価に反対側から迫っていることに触れておく必要があります。前回は、報酬値の可能性のある範囲を分割して説明しました。新しいアルゴリズムでは、受け取った報酬の集合をいくつかの等確率の分位点に分割します。そのメリットは何でしょうか。

分析された分位点の数のハイパーパラメータはありますが、同時に、可能な報酬値の範囲を限定することはありません。その代わりに、分位点の中央値を予測するモデルを訓練します。等確率の分位点を使うので、ゼロ確率の報酬を持つ分位点は存在しないことになります。さらに、報酬値がまばらな領域では、より大きな分位点を得ることができます。報酬が多くなる領域では、分位点が細かく分けられることになります。それによって、期待報酬の確率分布をより完全に把握することができます。さらに、この方法により、報酬値の密度がまばらな領域と増加した領域を動的に特定することができます。これらは、環境の状態により異なる場合があります。

しかし、同じQ学習であることに変わりはありません。処理自体は、ベルマン最適化方程式に基づいています。

ベルマン最適化方程式

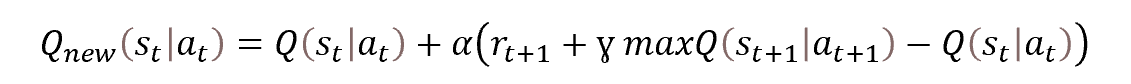
ただ、今回は1つの値ではなく、分布全体を定義する必要がありますが、基本的には課題は変わりません。では、その課題を詳しく見ていきましょう。

上述したように、訓練サンプルの報酬分布全体をN個の等積分量に分割します。各分位点は、分析されたランダム変数が所定の確率で超えない水準です。ここで、等確率分位とは、一定のステップを持つ分位であり、その集合は訓練データセット全体をカバーします。

実際には、訓練用データセットがあるとき、データセットから1つの要素を得る確率は1です。すべての要素が訓練データセットから取得されるため、他の選択肢はあり得ません。

集合をN個の等積分量に分割することは、訓練データセット全体をN個の同じ部分に分割することです。それぞれが同じ数の要素を含むことになります。部分集合の1つから要素を選ぶ確率は1/Nです。

分離分位点は、ある要素を選択する確率とその要素値の上限の2つのパラメータで特徴付けられます。また、分位点については、確率の累積で昇順に並び替えられることが条件となります。つまり、後続の各分位点の上限は前の分位点より高くなります。ある分位点の確率は、それ以前の分位点の確率を含みます。例えば、ある分布について、水準が15で、分位点が0.2というものがあります。つまり、分布全体の要素のうち、20%の値は15を超えないということです。確率のステップと最大分位点のレベルは、特定の分布に依存するため、比例しない場合があります。

ここで考えているアルゴリズムは、データセットを一定の確率のステップで分位に分割するものです。上限値の代わりに、分位の中央値を予測するようにモデルを訓練します。

モデルを訓練するには、目標値が必要です。あるデータセットの要素の完全なセットがあれば、簡単に平均値を求めることができますが、

実際には完全なセットがあるわけではありません。行動を取り、新しい状態に移行して初めて環境から報酬を受け取ることができます。ご覧のように、新しいモデル訓練アルゴリズムの使用は、環境との相互作用に影響を与えません。当初のQ学習では、平均的な期待報酬を予測するモデルを訓練していました。これは、学習係数を小さくして、モデルの結果を目標値に繰り返しシフトさせることでおこないました。このように、学習過程では、モデル結果は常に現在の目標値へのシフト力の影響を受けていることがわかります。多方向の力が釣り合う瞬間に平均値になります（図のような状態）。

新しいアルゴリズムの問題を解く際にも、同様の方法を用いることができます。でも、ひとつだけ注意があります。このアルゴリズムにより、集合の平均値を求めることができます。これは、第2分位です。それを純粋に適用すると、モデルの結果層のすべてのニューロンで同じ値を得ることになります。1つのニューロンのように、全部が同期して働くことになります。しかし、ここでは分析された分位点にわたる値の真の分布を得る必要があります。

分位点の性質を見てください。例えば、分析したデータセットの4分の1に当たる第1分位を考えてみます。要素の値間の距離を捨てると、分位点の1要素に対して、この分位点に入らない要素が全集合から3要素あるはずです。上の例に戻ると、第1四分位数で均衡を得るためには、分位点に対して価値減少の力が価値増加の力の3倍である必要があります。

したがって、各特定分位の値を求めるには、ベルマン方程式に補正係数を導入すればよいことになります。因子は、分位のレベルと偏差の方向によって異なります。

ここで、τは分位点の確率的な特性です。

学習過程では、経験値の再現とTarget Netの形で、古典的なQ学習アルゴリズムのヒューリスティックをすべて使用します。

2.MQL5での実装

アルゴリズムの理論的な側面を考慮したので、実用的な部分に話を移しましょう。MQL5を用いたアルゴリズムの実装方法を検討します。アルゴリズムを実装する際、ニューラル層の新しいアーキテクチャを作成することはありません。ただし、過程編成は別クラス「CQRDQN」に移行する予定です。これにより、エキスパートアドバイザー(EA)でのメソッドの使用が簡素化され、いくつかの実装の詳細からユーザーを保護することができます。新しいクラスの構造体を以下に示します。

class CQRDQN : protected CNet
  {
private:
   uint              iCountBackProp;
protected:
   uint              iNumbers;
   uint              iActions;
   uint              iUpdateTarget;
   matrix<float>     mTaus;
   //---
   CNet              cTargetNet;
public:
   /** Constructor */
                     CQRDQN(void);
                     CQRDQN(CArrayObj *Description)  { Create(Description, iActions); }
   bool              Create(CArrayObj *Description, uint actions);
   /** Destructor */~CQRDQN(void);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) 
                       { return        CNet::feedForward(inputVals, window, tem); }
   bool              backProp(CBufferFloat *targetVals, float discount,
                              CArrayFloat *nextState, int window = 1, bool tem = true); 
   void              getResults(CBufferFloat *&resultVals);
   int               getAction(void); 
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; } 
   bool              Save(string file_name, datetime time, bool common = true)
                       { return        CNet::Save(file_name, getRecentAverageError(),
                                                  (float)iActions, 0, time, common); }
   virtual bool      Save(const int file_handle);
   virtual bool      Load(string file_name, datetime &time, bool common = true);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)   const   {  return defQRDQN;   }
   virtual bool      TrainMode(bool flag) { return CNet::TrainMode(flag); } 
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result) 
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual void      SetUpdateTarget(uint batch)   { iUpdateTarget = batch; }
   virtual bool      UpdateTarget(string file_name);
   //---
   virtual bool      SetActions(uint actions);
  };

この新しいクラスは、当社のニューラルネットワークモデルの作業を整理するCNETクラスから派生したものです。つまり、モデルを操作するためのアルゴリズムを新たに構築することになります。

アルゴリズムの主要なパラメータを保存するために、以下の変数を作成します。

iNumbers - 1つの行動の分布を記述する集合のニューロン数
iActions - 可能な行動のバリエーションの数
iUpdateTarget - モデルパラメータTarget Netを更新する頻度
mTaus - 分母の確率的特性を書き込むための行列
cTargetNet - Target Netオブジェクトへのポインタ

mTaus行列では、各分位点における確率の中央値を書いていることに注意してください。

クラスコンストラクタで、これらの変数に初期値を設定します。

CQRDQN::CQRDQN()  :  iNumbers(31),
                     iActions(2),
                     iUpdateTarget(1000)
  {
   mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers;
   mTaus[0, 0] /= 2;
   mTaus = mTaus.CumSum(0);
   cTargetNet.Create(NULL);
   Create(NULL, iActions);
  }

ニューラルネットワークモデルを構成するCNetクラスと同様に、パラメータを持たないコンストラクタに加え、作成するモデルのアーキテクチャを指定したメソッドのオーバーロードを作成することにします。

                     CQRDQN(CArrayObj *Description)  { Create(Description, iActions); }

このメソッドはCreateメソッドで作成され、パラメータとして、モデルアーキテクチャとエージェントの可能な行動の数を記述した配列へのポインタを受け取ります。

bool CQRDQN::Create(CArrayObj *Description, uint actions)
  {
   if(actions <= 0 || !CNet::Create(Description))
      return false;

メソッド本体で、エージェント行動の数が正しく指定されているかどうかを確認します。同じ名前の親クラスのメソッドを呼び出します。モデルアーキテクチャを記述するオブジェクトに関するすべての必要な制御を含むとともに、モデル作成過程を実装するものです。ここでは、親クラスの操作の論理的な結果のみを確認します。

新しいモデルの作成に成功したら、作成したモデルの結果層を取ります。そのサイズと可能なエージェント行動の数に関する情報に基づいて、確率的な分位特性のmTaus行列に入力します。この行列の行数は、1つの行動に対する報酬の確率分布の大きさと同じです。訓練開始前に設定される各分位点の確率は、エージェントの可能なすべての行動に対して等しい固定ステップであるため、ここでは1行のベクトル行列を使用することにします。ベクトルではなく行列を使うのは、この解がさらに発展し、後に行動の確率分布が変化することを意味するからです。

   int last_layer = Description.Total() - 1;
   CLayer *layer = layers.At(last_layer);
   if(!layer)
      return false;
   CNeuronBaseOCL *neuron = layer.At(0);
   if(!neuron)
      return false;
   iActions = actions;
   iNumbers = neuron.Neurons() / actions;
   mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers;
   mTaus[0, 0] /= 2;
   mTaus = mTaus.CumSum(0);
   cTargetNet.Create(NULL);
//---
   return true;
  }

なお、最初のステップでは、Target Netをリセットしています。この方法は、訓練されていないモデルの絶対的にランダムな値で新しいモデルを訓練しないようにします。

フィードフォワードパスを実装するために、親クラスの同様のメソッドを利用します。

   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) 
                     { return CNet::feedForward(inputVals, window, tem); }

フィードバックワードメソッドbackPropについては、少し工夫が必要です。エージェントが行動するたびに、環境が報酬で反応することを思い出してください。古典的なQ学習過程では報酬方策を定義しています。取引において可能なエージェントの行動は相互に排他的であり、性質が反対であるため、実行した行動に対して環境が返した報酬によって、反対行動の報酬を決定することができます。この特徴に基づき、フィードバックワードパスの各反復で、可能なすべての行動の目標値を渡すことができます。そのため、高速かつ安定した学習が可能です。ただし、分散型Q学習過程では、各行動の目標値のベクトル全体を扱うことになります。前回は、モデル訓練EAでモデルターゲットテンソルを作成する過程を新たに構築しました。また、訓練したモデルがどのように機能するかを確認するために、取引EAで行動を実行する前にモデル結果をデコードするためのブロックを新たに作成しました。

新しいクラスを作ることで、この処理をユーザーから隠すことができます。そのため、モデルを使った作業はよりシンプルでわかりやすくなります。実際には、古典的なQ学習と同様、環境は行動ごとに離散的な報酬値だけを返し、この離散的な報酬を行動ごとの分布ベクトルに変換する全過程をフィードバックメソッドの本体で実装することになります。

新しいクラスを使って処理を実装することの利点を後ひとつ言及しなければなりません。ご存知のように、Q学習過程では、将来の報酬を予測するためにTarget Netを使用します。以前は2つのモデルを使い分ける必要がありましたが、Target Netを使ったすべての作業を、クラスのメソッド内に隠すことができるようになりました。こうすることで、より快適に作業ができるようになりますが、そのためにはフィードバックメソッドのパラメータを変更する必要がありました。この場合、バックプロパゲーションを正しく実行するためには、ユーザーから目標値やシステムの新しい状態を受け取ることが必要です。

バックワードパスメソッドの本体では、まず、受け取った目標値ベクトルへのポインタの正しさを確認します。また、結果のベクトルの大きさは、可能なエージェント行動の数に等しくなければなりません。

bool CQRDQN::backProp(CBufferFloat *targetVals, float discount,
 CArrayFloat *nextState=NULL, int window = 1, bool tem = true)
  {
//---
   if(!targetVals)
      return false;
   vectorf target;
   if(!targetVals.GetData(target) || target.Size() != iActions)
      return false;

その後、新しいシステム状態を記述するベクトルへのポインタの正しさを確認します。必要に応じて、フィードフォワードパスTarget Netを実装します。その後、可能な限り最大限の報酬を決定し、割引率を考慮して、環境から受け取る報酬を将来の収入に調整します。

   if(!!nextState)
     {
      if(!cTargetNet.feedForward(nextState, window, tem))
         return false;
      vectorf temp;
      cTargetNet.getResults(targetVals);
      if(!targetVals.GetData(temp))
         return false;
      matrixf q = matrixf::Zeros(1, temp.Size());
      if(!q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
         return false;
      temp = q.Mean(0);
      target = target + discount * temp.Max();
     }

以下の式でモデルパラメータを更新していきます。

ただし、メソッド本体に上記の式を実装する場合は、学習係数を使用しないことに留意してください。これにはちょっとした仕掛けがあります。ポイントは、メソッド本体では、どんなに奇妙に見えても、モデルパラメータを更新しないことです。私たちのモデルには、目標結果のベクトルしか作りません。一方、モデルのパラメータは親クラスのメソッド（同名）で更新されます。ターゲットモデルの結果のフルテンソルを親クラスのメソッドに渡すことになります。モデルのパラメータを更新する際には、学習係数を考慮します。

このステップでは、将来起こりうる利益も含めて、すでに環境からの報酬を得ているのです。目標値のベクトルを作るには、モデルのフィードフォワードパスの最新の結果だけが必要です。これは、ローカルのQ行列に読み込まれます。

   vectorf quantils;
   getResults(targetVals);
   if(!targetVals.GetData(quantils))
      return false;
   matrixf Q = matrixf::Zeros(1, quantils.Size());
   if(!Q.Row(quantils, 0) || !Q.Reshape(iActions, iNumbers))
      return false;

その後、モデルの目標値に対して必要なバッファを作成することができます。そのために、エージェントの各個別行動に対する分位レベルの目標値を、可能なものの中からベクトルとして作成する処理をループで構成することになります。なお、行列やベクトル演算の利用には、アルゴリズムを構築する際に、いくつかのコツや方法の変更が必要です。その反面、ループの使用を減らすことができます。一般的に、プログラムの実行速度が向上します。

この場合、ベクトル演算を使うことで、すべての行動と、可能な行動ごとの分布のすべての要素を反復するような入れ子ループのシステムを使う必要がなくなります。その代わりに、エージェントの可能な行動に対して1つのループだけを使用します。多くの場合、ループの繰り返し回数は、消去されたループの繰り返し回数の数十分の一になるはずです。ただし、その代償として、条件演算子が使えなくなります。ベクトルの2つの要素を比較して、比較結果によって行動を選択することはできず、

ベクトルの全要素に対して、両方の演算分岐を実行する必要があるのです。演算の期待結果を歪めないために、環境から受け取った報酬と最後のフィードフォワードパスの結果との差分のベクトルを2つ作成することにします。その後、1つのベクトルではマイナスの値をリセットし、2つのベクトルではプラスの値をリセットします。このように、得られたベクトルに、平均分位点への影響を調整する対応する係数を乗じることで、目的の補正値を得ることができます。受信したベクトルとフィードフォワードの最後の結果の合計が、モデルのフィードバックワードパスに必要な目標値を生成します。

   for(uint a = 0; a < iActions; a++)
     {
      vectorf q = Q.Row(a);
      vectorf dp = q - target[a], dn = dp;
      if(!dp.Clip(0, FLT_MAX) || !dn.Clip(-FLT_MAX, 0))
         return false;
      dp = (mTaus.Row(0) - 1) * dp;
      dn = mTaus.Row(0) * dn * (-1);
      if(!Q.Row(dp + dn + q, a))
         return false;
     }
   if(!targetVals.AssignArray(Q))
      return false;

すべてのループの繰り返しが完了したら、ターゲット値バッファの値を更新します。

次に、Target Netモデルの扱い方について、ちょっとした補助作業をおこないます。バックワードパスの反復カウンタを実装することになります。反復回数が閾値に達したら、Target Netモデルを更新します。

   if(iCountBackProp >= iUpdateTarget)
     {
#ifdef FileName
      if(UpdateTarget(FileName + ".nnw"))
#else
      if(UpdateTarget("QRDQN.upd"))
#endif
         iCountBackProp = 0;
     }
   else
      iCountBackProp++;

フィードバックの繰り返し閾値に達したときの比較演算子本体でのマクロ置換に注意してください。従来通り、Target Netのモデルを更新する際、モデル間のパラメータを直接コピーすることはしません。その代わり、モデルをファイルから保存し、復元します。この操作を実現するために、ファイル名が必要です。

すべてのモデルでは、FileNameマクロの置換を使用して、使用するEA、取引商品、時間枠に応じた固有のファイル名を生成しています。このマクロの代入は、EAで直接割り当てられます。今回実装したマクロ置換によって、EAでファイル名生成のためのマクロ置換の割り当てを確認することができます。そして、割り当てがあった場合は、それを使ってファイルの保存や復元をおこないます。ない場合は、デフォルトのファイル名が使用されます。

#define FileName        Symb.Name()+"_"+EnumToString(TimeFrame)+"_"+StringSubstr(__FILE__,0,StringFind(__FILE__,".",0))

このメソッドの最後で、親クラスのフィードバックワードメソッドを呼び出し、そこに用意されたターゲット結果テンソルをパラメータとして入力します。親クラスのメソッド操作の論理結果は、呼び出し元のプログラムに返されます。

   return CNet::backProp(targetVals);
  }

このように、フィードバックワードパスをおこなう際に確率分布モデルを使用することはユーザーから隠されています。環境は、各行動に対して1つの離散的な報酬しか返しません。フィードバックワードメソッドの呼び出しは、古典的なQ学習アルゴリズムと同様におこなわれるようになります。ただし、ユーザーは2つ目のTarget Netモデルを制御する必要がなくなりました。これによって、モデルの使い勝手が向上すると思いますが、フィードフォワードパスの疑問は残ります。

前述したように、フィードフォワードメソッドには親クラスメソッドが利用されます。フィードフォワードパスメソッドは操作の論理結果のみを返すので、フィードフォワード操作に直接悪影響を与えることはありません。フォワードパスの結果を得ようとすると、疑問が生じます。親クラスのメソッドは、モデルによって生成された完全な確率分布を返します。ここに、フィードフォワードの結果とフィードバックの目標との間にギャップがあるのです。そのため、フィードフォワードの結果を得るメソッドを再定義して、バックワードパスの目標値と比較できるようにする必要があります。

そこで役に立つのが、等確率分位点の利用です。これにより、エージェントの可能なアクションごとに生成された分布全体から平均値を簡単に見つけて、この値を期待される報酬として返すことができます。ここでは、行列演算も用いており、ループを用いずにアルゴリズム手法全体を構築することが可能です。

このメソッドの冒頭で、フィードフォワードパスの結果をデータバッファにコピーするために必要なすべての制御と操作を実装した、同名の親クラスのメソッドを呼び出します。得られたデータを行列に転送します。この行列は、可能なエージェント行動の数と同じ行数を持つ表形式行列に再フォーマットされます。この場合、各行は個々の行動に対する期待報酬の確率分布を持つベクトルです。したがって、エージェントのすべての可能な行動の平均値を決定するためには、行列関数Meanが1つだけ必要です。結果をデータバッファに転送し、呼び出し元に返すだけです。

void CQRDQN::getResults(CBufferFloat *&resultVals)
  {
   CNet::getResults(resultVals);
   if(!resultVals)
      return;
   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return;
     }
   matrixf q;
   if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
     {
      delete resultVals;
      return;
     }
//---
   if(!resultVals.AssignArray(q.Mean(1)))
     {
      delete resultVals;
      return;
     }
//---
  }

ここで、「元のQ学習が訓練する平均値に戻るなら、なぜこんなことをしたのだろう」と思われるかもしれません。数学的な説明は省きますが、1つだけ、実際の結果で確認できたことをお伝えします。集合平均の確率は、同じ集合からの部分集合の確率の平均と等しくありません。元のQ学習アルゴリズムは、集合平均の確率を学習します。しかし、分散型Q学習は、各分位に対して複数の平均値を学習します。そして、その確率的な値の平均を求めるのです。

科学的な研究や実践が示すように、一般に分位点回帰は様々な異常値の影響を受けにくいものです。これにより、モデルの学習過程がより安定します。しかも、そのような訓練の結果は、偏りが少なくなります。この手法の著者らは、57本のアタリゲームを対象に訓練したモデルの成果を、他のアルゴリズムで訓練したモデルの成果と比較して発表しました。このデータから、オリジナルのQ学習(DQN)の結果と比較して、平均で約4倍の結果が得られていることがわかります。以下は、元の記事 [6]の結果の表です。

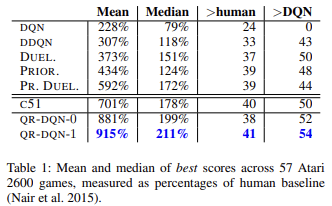
モデルの使い勝手の向上前回、すべての強化学習モデルをテストするEAを作成する際に、学習済みモデルのフィードフォワード結果をもとに行動を選択する様々な方法を作成しました。新しいクラスを作ることで、この機能を実行するメソッドを実装することができます。最大期待報酬に基づく貪欲な行動選択のために、getActionメソッドを作成しましょう。そのアルゴリズムは非常に単純です。上記のgetResultsメソッドは、フィードフォワードパスの結果を得るためにのみ使用することにします。得られたバッファから、最も値の高い要素を選択します。

int CQRDQN::getAction(void)
  {
   CBufferFloat *temp;
   getResults(temp);
   if(!temp)
      return -1;
//---
   return temp.Maximum(0, temp.Total());
  }

ɛ-greedy行動選択戦略は、環境学習度を上げるためのモデル学習の過程で使用されるため、実装しません。当社の報酬方策のため、これらのメソッドを使用する必要はありません。学習過程では、可能性のあるすべてのエージェント行動のターゲットを提供します。

2番目のgetSampleメソッドは、より大きな報酬がより大きな確率で得られる確率分布から、行動をランダムに選択するために使用されます。行列とデータバッファ間の不要なデータコピーをなくすため、getResultsメソッドのアルゴリズムを部分的に繰り返すことにします。

int CQRDQN::getSample(void)
  {
   CBufferFloat* resultVals;
   CNet::getResults(resultVals);
   if(!resultVals)
      return -1;
   vectorf temp;
   if(!resultVals.GetData(temp))
     {
      delete resultVals;
      return -1;
     }
   delete resultVals;
   matrixf q;
   if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers))
     {
      delete resultVals;
      return -1;
     }

その後、SoftMax関数を用いてフィードフォワードパスの結果を正規化します。これが行動選択確率となります。

   if(!q.Mean(1).Activation(temp, AF_SOFTMAX))
      return -1;
   temp = temp.CumSum();

確率の累積総和のベクトルを集め、得られた確率分布ベクトルからサンプリングを実装しましょう。

   int err_code;
   float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code);
   if(random >= 1)
      return (int)temp.Size() - 1;
   for(int i = 0; i < (int)temp.Size(); i++)
      if(random <= temp[i] && temp[i] > 0)
         return i;
//---
   return -1;
  }

サンプリング結果を呼び出し元のプログラムに返します。

フィードフォワードメソッドとバックワードメソッド、そしてモデルの結果を得るためのメソッドについて見てきました。しかし、まだまだ未解決の部分が多くあります。そのひとつが、モデル更新メソッド「Target Net - UpdateTarget」です。このメソッドは、バックプロパゲーションメソッドを説明する際に参照しました。このメソッドは別のクラスのメソッドから呼び出されるのですが、publicにしてユーザーがアクセスできるようにしました。ユーザー側からTarget Netの状態を制御する必要をなくしたのです。ただし、選択の自由を制限することはありません。必要であれば、ユーザーがすべてを制御することができます。

このメソッドのアルゴリズムは非常にシンプルです。単に現在のオブジェクトのsaveメソッドを最初に呼び出すだけです。そして、そのデータ復旧メソッドTarget Netを呼び出します。すべての操作について、実行過程を制御します。Target Netが正常に更新されたら、バックワード反復カウンタをリセットします。

bool CQRDQN::UpdateTarget(string file_name)
  {
   if(!Save(file_name, 0, false))
      return false;
   float error, undefine, forecast;
   datetime time;
   if(!cTargetNet.Load(file_name, error, undefine, forecast, time, false))
      return false;
   iCountBackProp = 0;
//---
   return true;
  }

オブジェクトクラスの違いに注目してください。新しいCQRDQNクラスで作業し、Target Netは親クラスCNetのインスタンスです。ポイントは、Target Netのフィードフォワード機能のみを使用している点です。このメソッドは、私たちのクラスでは変更されていません。従って、親クラスを使用することに問題はないはずです。同時に、CQRDQNクラスのインスタンスを使用する場合、Target Netについては、新しいインスタンスに対する内側のTarget Netオブジェクトが再帰的に作成されることになります。このような繰り返しは、致命的なミスにつながる可能性があります。そのため、このような些細なことが、プログラム全体の運用に大きな影響を与えることがあります。

分散型Q学習（QR-DQN）における分位点回帰アルゴリズムを実装した新しいクラスCQRDQNの主な機能を考えてみました。この手法は、2017年10月に「Reinforcement Learning with Quantile Regression」稿で紹介されました。

また、このクラスには、モデルを保存するためのメソッド(Save)と、後で復元するためのメソッド(Load)が実装されています。これらの方法の変化は、それほど複雑なものではありません。以下に添付したコードで勉強できます。次に、新しいクラスのテストに移ることを提案します。

3.テスト

それでは、モデルの訓練によって新しいクラスのテストを始めましょう。モデルを訓練するために、専用のEA QRDQN-learning.mq5が作成されています。Q学習のオリジナルEA「Q学習.mq5」をベースに作成したEAです。今回のEAでは、学習させるモデルのクラスを変更し、Target netモデルインスタンス宣言を削除しています。

CSymbolInfo          Symb;
MqlRates             Rates[];
CQRDQN               StudyNet;
CBufferFloat        *TempData;
CiRSI                RSI;
CiCCI                CCI;
CiATR                ATR;
CiMACD               MACD;

EA初期化メソッドでは、あらかじめ作成したファイルからモデルを読み込みます。全ニューラル層の学習モードを強制的にONにします。分析された履歴の深さは、ソースデータ層のサイズに等しく定義されます。許容される行動の領域の大きさをモデルに入力します。また、Target Netの更新期間も指定します。今回は、モデル更新の過程を自分で制御する予定なので、意図的に過大評価した値を示しました。

int OnInit()
  {
//---
.........
.........
//---
   if(!StudyNet.Load(FileName + ".nnw", dtStudied, false))
      return INIT_FAILED;
   if(!StudyNet.TrainMode(true))
      return INIT_FAILED;
//---
   if(!StudyNet.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   if(!StudyNet.SetActions(Actions))
      return INIT_PARAMETERS_INCORRECT;
   StudyNet.SetUpdateTarget(1000000);
//---
........
//---
   return(INIT_SUCCEEDED);
  }

モデルの実際の訓練プロセスはTrain関数で実行されます。.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

この関数では、訓練期間を定義し、過去のデータを読み込みます。この工程は完全に原型をとどめています。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

次に、モデルの訓練過程として、入れ子のループのシステムを実装します。外側ループでは、Target netモデルを更新するための訓練エポックをカウントダウンします。

   int total = bars - (int)HistoryBars - 240;
   bool use_target = false;
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int i = 0;
      uint ticks = GetTickCount();
      int count = 0;
      int total_max = 0;

ネストされたループの中で、フィードフォワードとバックワードパスを繰り返し実行します。ここではまず、その後の2つの状態を記述するための履歴データを用意します。1つは、訓練するモデルのフィードフォワードパスに使用されます。2つ目はTarget Netに使用されます。

      for(int batch = 0; batch < (Batch * UpdateTarget); batch++)
        {
         i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * total + 240);
         State1.Clear();
         State2.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;
         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE ||
               sign == EMPTY_VALUE)
               continue;
            //---
            if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) ||
               !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
               !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               break;
              }
            if(!use_target)
               continue;
            //---
            bar_t --;
            open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            rsi = (float)RSI.Main(bar_t);
            cci = (float)CCI.Main(bar_t);
            atr = (float)ATR.Main(bar_t);
            macd = (float)MACD.Main(bar_t);
            sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE ||
               sign == EMPTY_VALUE)
               continue;
            //---
            if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) || 
               !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) ||
               !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign))
              {
               PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
               break;
              }
           }

訓練しているモデルのフィードフォワードを実装します。

         if(IsStopped())
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            ExpertRemove();
            return;
           }
         if(State1.Total() < (int)HistoryBars * 12 ||
            (use_target && State2.Total() < (int)HistoryBars * 12))
            continue;
         if(!StudyNet.feedForward(GetPointer(State1), 12, true))
            return;

その後、エージェントのすべての可能な行動に対して報酬のバッチを生成し、メインモデルのフィードバックワードメソッドを呼び出します。

         Rewards.BufferInit(Actions, 0);
         double reward = Rates[i].close - Rates[i].open;
         if(reward >= 0)
           {
            if(!Rewards.Update(0, (float)(2 * reward)))
               return;
            if(!Rewards.Update(1, (float)(-5 * reward)))
               return;
            if(!Rewards.Update(2, (float) - reward))
               return;
           }
         else
           {
            if(!Rewards.Update(0, (float)(5 * reward)))
               return;
            if(!Rewards.Update(1, (float)(-2 * reward)))
               return;
            if(!Rewards.Update(2, (float)reward))
               return;
           }

なお、オーバーライドフィードバックワード方式に則り、報酬バッファだけでなく、それに続く現在の状態もメソッドに入力しています。また、Target Netoperationsのブロックを削除し、、将来の州の予想所得に対する報酬調整をおこないました。

         if(!StudyNet.backProp(GetPointer(Rewards), DiscountFactor, (use_target ? GetPointer(State2) : NULL), 12, true))
            return;

過程の進捗情報を銘柄チャートに出力します。

         if(GetTickCount() - ticks > 500)
           {
            Comment(StringFormat("%.2f%%", batch * 100.0 / (double)(Batch * UpdateTarget)));
            ticks = GetTickCount();
           }
        }

これで入れ子ループの操作は完了です。そしてそのすべての繰り返しで、現在のモデルの誤差を確認します。以前に達成した結果が改善された場合、現在のモデルの状態を保存し、Target Netを更新します。

      if(StudyNet.getRecentAverageError() <= min_loss)
        {
         if(!StudyNet.UpdateTarget(FileName + ".nnw"))
            continue;
         use_target = true;
         min_loss = StudyNet.getRecentAverageError();
        }
      PrintFormat("Iteration %d, loss %.8f", iter, StudyNet.getRecentAverageError());
     }
   Comment("");
//---
   PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
   ExpertRemove();
  }

これで、外側ループの動作と訓練関数全体の動作は完了です。それ以外のEAコードに変更はありません。すべてのクラスとプログラムのすべてのコードは、添付ファイルでご覧いただけます。

NetCreatorというツールを使って訓練モデルを作成しました。このモデルのアーキテクチャは、前回までの訓練モデルのアーキテクチャと同じです。最後のSoftMaxの正規化層を削除して、モデル結果エリアが、使用された報酬方策のどの結果も再現できるようにしました。

前回と同様、EURUSDの履歴データ、H1時間枠でモデルを学習させました。訓練データセットとして、過去2年間の履歴データを使用しました。

訓練したモデルの働きは、ストラテジーテスターで検証しました。テスト用のEAQRDQN-learning-test.mqが別途作成されています。また、EAは過去の記事の類似EAを参考に作成しました。そのコードはあまり変わっていません。コード全体は添付ファイルに記載されています。

ストラテジーテスターでは、2週間という短期間で利益を生み出す能力を発揮するモデルでした。半数以上の取引が利益をもって決済されました。取引あたりの平均利益は、平均損失のほぼ2倍でした。

モデルテストグラフ

モデルテスト結果

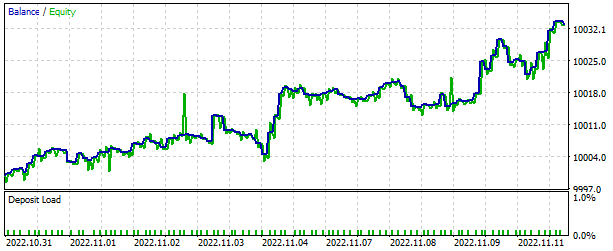
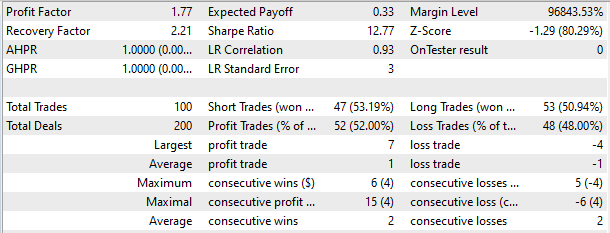
結論

今回は、もう1つの強化学習手法に触れてみました。この手法を実装するためのクラスを作成しました。モデルを訓練し、ストラテジーテスターでその動作結果を見てみました。得られた結果から、分散型Q学習における分位点回帰アルゴリズムを用いることで、実市場の問題を解決できるモデルを実装することが可能であると結論づけることができます。

繰り返しになりますが、記事で紹介しているプログラムはすべて技術実証を目的としたものであることにご留意ください。実際の取引に使用するためには、包括的なテストとともに、モデルやEAのさらなる改良が必要です。

参照文献

記事で使用されているプログラム

#	ファイル名	タイプ	詳細
1	QRDQN-learning.mq5	EA	モデルを最適化するためのEA
2	QRDQN-learning-test.mq5	EA	ストラテジーテスターでモデルをテストするためのEA
3	QRDQN.mqh	クラスライブラリ	QR-DQNモデルクラス
4	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークモデルを作成するためのライブラリ
5	NeuroNet.cl	コードベース	ニューラルネットワークモデルを作成するためのOpenCLプログラムコードライブラリ
6	NetCreator.mq5	EA	モデル構築ツール
7	NetCreatotPanel.mqh	クラスライブラリ	ツールを作成するためのクラスライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11752

添付されたファイル |

ZIPをダウンロード

MQL5.zip (85.24 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

自動で動くEAを作る（第06回）：口座の種類（I）

今日は、自動モードでシンプルかつ安全に動作するエキスパートアドバイザー(EA)を作成する方法を紹介します。このEAは、現状ではどんな状況でも機能しますが、まだ自動化には至っていません。まだ、いくつかの点で工夫が必要です。

データサイエンスと機械学習（第11回）：単純ベイズ、取引における確率論

確率を利用した取引は綱渡りのようなもので、正確さとバランス、そしてリスクに対する鋭い理解が必要です。取引の世界では、確率がすべてです。確率は、成功と失敗、利益と損失の違いになります。確率の力を活用することで、トレーダーは十分な情報に基づいた意思決定をおこない、リスクを効果的に管理し、経済的目標を達成することができます。つまり、経験豊富な投資家であれ、初心者のトレーダーであれ、確率を理解することは、取引の可能性を引き出す鍵になるのです。この記事では、確率を利用したエキサイティングな取引の世界を探求し、取引ゲームを次のレベルに引き上げる方法を紹介します。

自動で動くEAを作る（第07回）：口座の種類(II)

今日は、自動モードでシンプルかつ安全に動作するエキスパートアドバイザー(EA)を作成する方法を紹介します。トレーダーは、自動EAが何をしているのかを常に意識しておく必要があります。そうすれば、もしEAが「レールから外れた」場合、トレーダーはできるだけ早くチャートからEAを取り除き、状況をコントロールすることができます。

母集団最適化アルゴリズム：細菌採餌最適化(BFO)

大腸菌の採餌戦略は、科学者にBFO最適化アルゴリズムの作成を促しました。このアルゴリズムには、最適化に対する独自のアイデアと有望なアプローチが含まれており、さらに研究する価値があります。

目次