データサイエンスと機械学習（第11回）：単純ベイズ、取引における確率論
536
0
熱力学の第4法則：成功の確率がほぼ1でないなら、それは0に近い。
David J. Rose
はじめに
単純ベイズ分類器は、機械学習で分類タスクに使用される乱択アルゴリズムで、利用可能なエビデンスから仮説の確率を計算する、ベイズの定理に基づくものです。この確率的分類器は、シンプルでありながら様々な場面で有効なアルゴリズムで、分類に使用される特徴が互いに独立していることを前提としています。次は例です。身長、足のサイズ、体重、肩幅で人間（男性、女性）を分類する場合、このモデルはこれらの変数をすべて互いに独立したものとして扱い、この場合、足のサイズと身長が人間にとって関係あるとは考えません。
このモデルは、独立変数間のパターンを理解しようとしないので、情報に基づいた取引の意思決定に使用してみるべきだと思います。取引の世界でパターンを完全に理解できる人は誰もいないと思うので、単純ベイズがどのように機能するのか見てみましょう。
早速ですが、モデルインスタンスを呼び出して使ってみましょう。このモデルがどのような構成になっているかは、後ほど説明します。
訓練データの準備
この例では、5つの指標を選びました。そのほとんどはオシレーターとボリューム指標で、良い分類変数になると思います。また、これらは有限であるため、このアルゴリズムの中核をなすアイデアの1つである正規分布に適しています。ただし、これらの指標に限定されるものではないので、様々な指標やデータを自由に探索してください。
まず重要なことからです。
matrix Matrix(TrainBars, 6); int handles[5]; double buffer[]; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Preparing Data handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- vector col_v; for (ulong i=0; i<5; i++) //Independent vars { CopyBuffer(handles[i],0,0,TrainBars, buffer); col_v = matrix_utils.ArrayToVector(buffer); Matrix.Col(col_v, i); } //-- Target var vector open, close; col_v.Resize(TrainBars); close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars); for (int i=0; i<TrainBars; i++) { if (close[i] > open[i]) //price went up col_v[i] = 1; else col_v[i] = 0; } Matrix.Col(col_v, 5); //Adding independent variable to the last column of matrix //---
TF、bears_periodなどの変数は、上記コードの初めにある入力定義変数です。
教師あり学習なので、対象変数を作り上げる必要がありましたが、ロジックは簡単です。終値が始値を上回った場合、目的変数はクラス1に設定され、それ以外の場合はクラス0に設定されます。こうして目的変数が設定されました。以下は、データセット行列がどのように見えるかの概要です。
CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" "Target Var" CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-3.753148029472797e-06,0.008786246851970603,67.65238281791684,13489,55.24611392389958,0] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.002513216984025402,0.005616783015974569,50.29835423473968,12226,49.47293811405203,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.001829900272021678,0.0009700997279782353,47.33479153312328,7192,46.84320886771249,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004718485947447171,-0.0001584859474472733,39.04848493977027,6267,44.61564654651691,1] CS 0 13:21:15.457 Naive Bayes Test (EURUSD,H1) [-0.004517273669240485,-0.001367273669240276,45.4127802340401,3867,47.8438816641815,0]
そこで、データが確率分布に従うかどうかを確認するために、分布図で可視化することにしました。
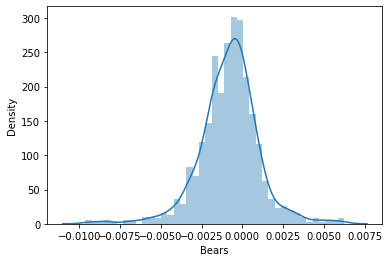
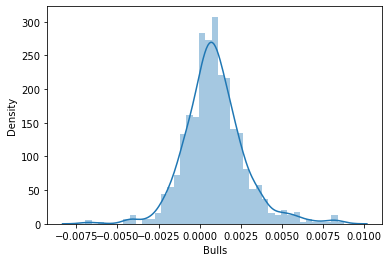
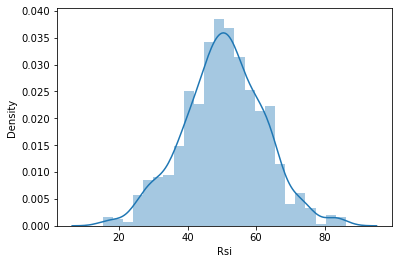
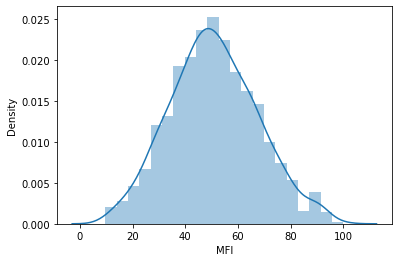
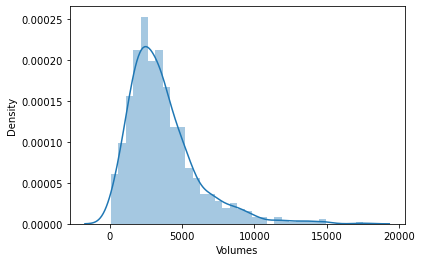
確率分布の種類を理解したい方のために、こちらの記事で紹介しています。
すべての独立変数の相関係数行列を詳しく見てみると、次のようになります。
string header[5] = {"Bears","Bulls","Rsi","Volumes","MFI"}; matrix vars_matrix = Matrix; //Independent variables only matrix_utils.RemoveCol(vars_matrix, 5); //remove target variable ArrayPrint(header); Print(vars_matrix.CorrCoef(false));
以下が出力です。
CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) "Bears" "Bulls" "Rsi" "Volumes" "MFI" CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [[1,0.7784600081627714,0.8201955846987788,-0.2874457184671095,0.6211980865273238] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.7784600081627714,1,0.8257210032763984,0.2650418244580489,0.6554288778228361] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.8201955846987788,0.8257210032763984,1,-0.01205084357067248,0.7578863565293196] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [-0.2874457184671095,0.2650418244580489,-0.01205084357067248,1,0.0531475992791923] CS 0 13:21:15.481 Naive Bayes Test (EURUSD,H1) [0.6211980865273238,0.6554288778228361,0.7578863565293196,0.0531475992791923,1]]
ボリュームと残りとの相関関係を除いて、すべての変数は相互に強く相関してことにお気づきでしょう。たとえばRSIとの相関係数がブルとベアの両方で約0.82だという偶然の一致もあります。ボリュームとMFIは、どちらもボリュームという共通のものからできているので、相関係数が0.62であるのには理由があります。ガウス単純ベイズはそんなことは一切気にしないので、先に進みますが、変数を確認して分析するのは良いアイデアだと思います。
モデルの訓練
ガウス単純ベイズの訓練は簡単で、非常に短時間で終了します。まずは、その正しいやり方を見てみましょう。
Print("\n---> Training the Model\n"); matrix x_train, x_test; vector y_train, y_test; matrix_utils.TrainTestSplitMatrices(Matrix,x_train,y_train,x_test,y_test,0.7,rand_state); //--- Train gaussian_naive = new CGaussianNaiveBayes(x_train,y_train); //Initializing and Training the model vector train_pred = gaussian_naive.GaussianNaiveBayes(x_train); //making predictions on trained data vector c= gaussian_naive.classes; //Classes in a dataset that was detected by mode metrics.confusion_matrix(y_train,train_pred,c); //analyzing the predictions in confusion matrix //---
関数TrainTestSplitMatricesは、データをx個の訓練行列とx個のテスト行列とそれぞれのターゲットベクトルに分割します。sklearn pythonのtrain_test_splitのようなものです。その核となる関数は、次のようなものです。
void CMatrixutils::TrainTestSplitMatrices(matrix &matrix_,matrix &x_train,vector &y_train,matrix &x_test, vector &y_test,double train_size=0.7,int random_state=-1)
デフォルトでは、データの70%が訓練データに分割され、残りはテストデータセットとして保持されます。この分割の詳細については、こちらをお読みください。
この関数で多くの人が混乱するのはrandom_stateです。Python MLコミュニティではrandom_state=42を選ぶことが多いのですが、この数値は、行列の行をシャッフルするための乱数を生成するための乱数シードを設定するもので、デバッグを容易にするために毎回同じものを生成することを保証するだけなので、どんな数値でも構いません。
この関数で得られた出力行列が、デフォルトの順序ではないことにお気づきでしょうか。この42の選択については、ディスカッションがいくつかあります。
以下は、このブロックのコードの出力です。
CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) ---> Training the Model CS 0 14:33:04.001 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> GROUPS [0,1] CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.002 Naive Bayes Test (EURUSD,H1) ---> Prior_proba [0.5457142857142857,0.4542857142857143] Evidence [382,318] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [[236,146] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) [145,173]] CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 0.0 0.62 0.62 0.54 0.62 382.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) 1.0 0.54 0.54 0.62 0.54 318.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Accuracy 0.58 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) Average 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) W Avg 0.58 0.58 0.58 0.58 700.0 CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1)
混同行列の分類レポートによると、訓練されたモデルは58%の精度を示しています。各クラスがどの程度正確に分類されたかを示す精度など、このレポートから理解できることはたくさんあります（詳細はこちら）。基本的に、クラス0はクラス1よりもよく分類されているようです。これは、モデルが他のクラス1よりも予測したためで、事前確率（データセットにおける主要な確率、一目でわかる確率）は言うに及ばず、理にかなっています。このデータセットでは、事前確率は次の通りです。
Prior_proba [0.5457142857142857,0.4542857142857143] エビデンス [382,318]。これは
事前確率 ＝エビデンス / 出来事/出力の総数
によって計算されます。この場合、事前確率 [382/700, 318/700]です。700は、1000データの70%を訓練データに分割した後の訓練データセットサイズであることを覚えていらっしゃるでしょうか。
ガウス単純ベイズモデルは、まずデータセットに出現するクラスの確率を調べ、それを使って将来何が起こるかを推測します。これはエビデンスに基づいて計算され、 他よりも高い確率につながるエビデンスがあるクラスが、訓練とテストの際にアルゴリズムによって優先されます。これは理にかなっていますよね。 これはこのアルゴリズムの欠点の1つです。あるクラスが訓練データに存在しない場合、モデルはそのクラスが存在しないと仮定し、そのクラスの確率をゼロにするからです。つまり、テストデータセットや将来のどの時点でも予測されることはないということです。
モデルのテスト
モデルのテストも簡単です。この時点ですでに学習済みのモデルのパラメータを持ってるGaussianNaiveBayes関数に新しいデータを差し込むだけです。
//--- Test Print("\n---> Testing the model\n"); vector test_pred = gaussian_naive.GaussianNaiveBayes(x_test); //giving the model test data to predict and obtain predictions to a vector metrics.confusion_matrix(y_test,test_pred, c); //Analysing the tested model
以下が出力です。
CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) ---> Testing the model CS 0 14:33:04.294 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Confusion Matrix CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [[96,54] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) [65,85]] CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Classification Report CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 0.0 0.60 0.64 0.57 0.62 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) 1.0 0.61 0.57 0.64 0.59 150.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Accuracy 0.60 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) Average 0.60 0.60 0.60 0.60 300.0 CS 0 14:33:04.418 Naive Bayes Test (EURUSD,H1) W Avg 0.60 0.60 0.60 0.60 300.0
テストデータセットでは、モデルの性能が若干向上し、訓練データの精度から2%向上した60%の精度が得られています。これは良いニュースです。
ガウス単純ベイズモデルストラテジーテスターについて
ストラテジーテスターで機械学習モデルを使ってもうまくいかないことが多いのですが、それは予測ができないからではなく、ストラテジーテスターの利益グラフを見るのが普通だからです。機械学習モデルが市場の次の方向性を推測できても、必ずしもそれで儲かるとは限りません。これは私がデータセットを収集し準備するのに使ったシンプルな論理では特にそうです。入力で与えられたTF PERIOD_H1（1時間）を使用して、各バーでデータセットが収集されています。
close.CopyRates(Symbol(),TF, COPY_RATES_CLOSE,0,TrainBars); open.CopyRates(Symbol(),TF, COPY_RATES_OPEN,0,TrainBars);
H1時間枠から1000本のバーを集め、その指標値を独立変数として読み取り、次に、ローソク足が強気だった場合はEAでクラス1を設定してそうでなければクラス0を設定することによって、目的変数を作成しました。 モデルは次のローソク足を予測するため、新しいローソク足で取引を開始し、前のローソク足を決済するようにしています。つまり、すべてのバーのすべてのシグナルでEAを取引させています。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if (!train_state) TrainTest(); train_state = true; //--- vector v_inputs(5); //5 independent variables double buff[1]; //current indicator value for (ulong i=0; i<5; i++) //Independent vars { CopyBuffer(handles[i],0,0,1, buff); v_inputs[i] = buff[0]; } //--- MqlTick ticks; SymbolInfoTick(Symbol(), ticks); int signal = -1; double min_volume = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); if (isNewBar()) { signal = gaussian_naive.GaussianNaiveBayes(v_inputs); Comment("SIGNAL ",signal); CloseAll(); if (signal == 1) { if (!PosExist()) m_trade.Buy(min_volume, Symbol(), ticks.ask, 0 , 0,"Naive Buy"); } else if (signal == 0) { if (!PosExist()) m_trade.Sell(min_volume, Symbol(), ticks.bid, 0 , 0,"Naive Sell"); } } }
この関数を実際の取引とストラテジーテスターの両方で動作させるために、ロジックを少し変更する必要がありました。指標のCopyBuffer()と訓練をTrainTest()関数内に移しました。この関数はOnTick関数で1回実行されます。この関数を頻繁に実行させて、非常に頻繁にモデルを訓練することもできますが、これを実践するのは皆さんにお任せします。
Init関数はCopyBuffer()やコピーレートメソッドに適した関数ではないので（この方法で使用するとストラテジーテスターでゼロ値を返す）、すべてをTrainTest()という関数に移しました。
int OnInit() { handles[0] = iBearsPower(Symbol(),TF, bears_period); handles[1] = iBullsPower(Symbol(),TF, bulls_period); handles[2] = iRSI(Symbol(),TF,rsi_period, rsi_price); handles[3] = iVolumes(Symbol(),TF,VOLUME_TICK); handles[4] = iMFI(Symbol(),TF,mfi_period,VOLUME_TICK ); //--- m_trade.SetExpertMagicNumber(MAGIC_NUMBER); m_trade.SetTypeFillingBySymbol(Symbol()); m_trade.SetMarginMode(); m_trade.SetDeviationInPoints(slippage); return(INIT_SUCCEEDED); }
シングルテスト （時間枠：1時間）
2023年1月1日から2023年2月14日（昨日)までの2ヶ月間テストを実施したところ、次のようになりました。
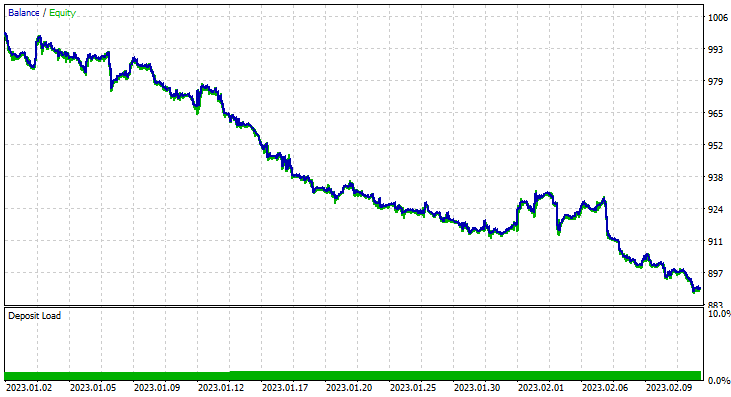
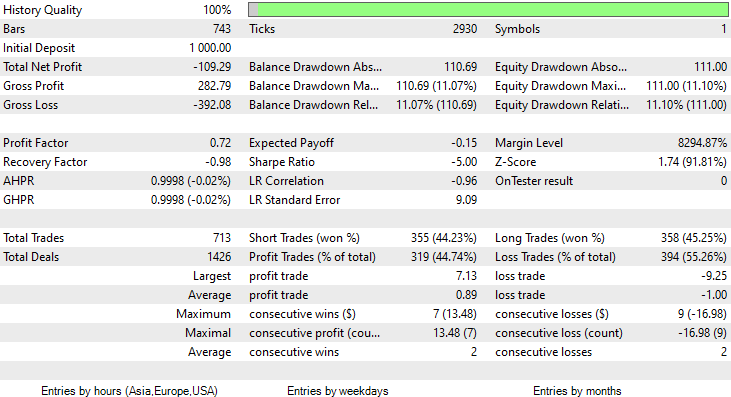
1000本の時足はほぼ41日と、訓練期間が長くないので、それに合わせて、2ヶ月という短い期間でテストすることにしました。TrainTest()関数はテスターでも実行されたので、モデルの学習対象となったローソクは700本です。
問題の正体
このモデルは、訓練データで60%の精度を示し、ストラテジーテスターに初印象を与えましたが、
CS 0 08:30:13.816 Tester initial deposit 1000.00 USD, leverage 1:100 CS 0 08:30:13.818 Tester successfully initialized CS 0 08:30:13.818 Network 80 Kb of total initialization data received CS 0 08:30:13.819 Tester Intel Core i5 660 @ 3.33GHz, 6007 MB CS 0 08:30:13.900 Symbols EURUSD: symbol to be synchronized CS 0 08:30:13.901 Symbols EURUSD: symbol synchronized, 3720 bytes of symbol info received CS 0 08:30:13.901 History EURUSD: history synchronization started .... .... .... CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Training the Model CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> GROUPS [0,1] CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.086 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 ---> Prior_proba [0.4728571428571429,0.5271428571428571] Evidence [331,369] CS 0 08:30:14.377 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Confusion Matrix CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [[200,131] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 [150,219]] CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Classification Report CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 _ Precision Recall Specificity F1 score Support CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 0.0 0.57 0.60 0.59 0.59 331.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 1.0 0.63 0.59 0.60 0.61 369.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Accuracy 0.60 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 Average 0.60 0.60 0.60 0.60 700.0 CS 0 08:30:14.378 Naive Bayes Test (EURUSD,H1) 2023.01.02 01:00:00 W Avg 0.60 0.60 0.60 0.60 700.0
その約束された精度やそれに近い利益ある取引をすることはできませんでした。以下が私の考察です。
- ロジックはどこか盲目的で、量と質をトレードしています。2ヶ月間で713回の取引とは、まったく大変な数です。これは反対方向に変える必要があります。このモデルをより長い時間枠で訓練し、より長い時間枠で取引することで、数少ない質の高い取引を得るのです。
- このテストでは、訓練のバーを削減しなければならないので、最近のデータでモデルを訓練したいと思います。
これらを実現するために、6H時間枠で最適化をおこない、Train Bars = 80、TF = 12時間で、新しいパラメータを使用して2ヶ月間テストをおこないました。本記事の最後にリンクされている*setファイルで、すべてのパラメータを確認してください。
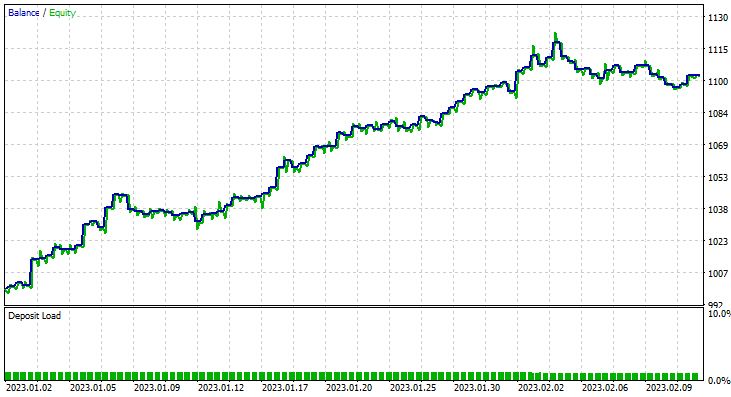
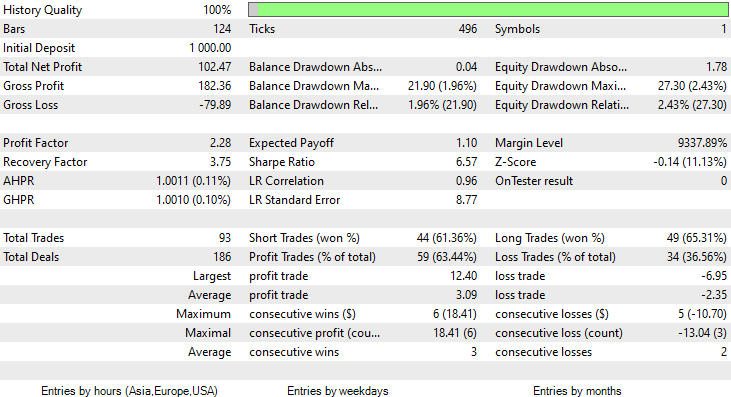
今回のガウス単純ベイズモデルの学習精度は58%でした。
おこなったのは2ヶ月間で93回の取引で1日平均2.3回です。これは健康的だと言えます。今回は、ガウス単純ベイズEAで63%の利益を伴う取引をおこない、10%の利益を出すことができました。
これでガウス単純ベイズモデルを使って、情報に基づいた取引の意思決定ができることがお分かりいただけたと思います。次にその特徴を見ていきましょう。
単純ベイズ理論
ガウス単純ベイズと混同しないようにしてください。
このアルゴリズムの名前の由来は次の通りです。
- 単純： 変数/特徴が独立であることはほとんどないが、それを前提にしている
-
ベイズ： ベイズの定理に基づいている
以下はベイズの定理の公式です。
ここで、
P(A|B) = 事後確率（観測された事象Bに対する仮説Aの確率）
P(B|A) = 尤度確率：仮説の確率が真であることを前提としたエビデンスの確率で、簡単に言うと、Aが真である場合にBが成立する確率
P(A) = Aの事前確率（エビデンスを観察する前の仮説の確率）
P(B) = 周辺確率（エビデンスの確率）
これらの数式における用語は、最初はわかりにくいかもしれません。それらは、作業するにつれて明らかになるので、お付き合いください。
分類機での作業
天気データセットで簡単な例を見てみましょう。ここでは、1列目の見通しに注目してください。それが理解できれば、他の列を独立変数として追加することは全く同じプロセスです。
| 見通し | テニスをする |
|---|---|
| 晴れ | いいえ |
| 晴れ | いいえ |
| 曇り | はい |
| 雨 | はい |
| 雨 | はい |
| 雨 | いいえ |
| 曇り | はい |
| 晴れ | いいえ |
| 晴れ | はい |
| 雨 | はい |
| 晴れ | はい |
| 曇り | はい |
| 曇り | はい |
| 雨 | いいえ |
では、同じことをMetaEditorでやってみましょう。
void OnStart() { //--- matrix Matrix = matrix_utils.ReadCsvEncode("weather dataset.csv"); int cols[3] = {1,2,3}; matrix_utils.RemoveMultCols(Matrix, cols); //removing Temperature Humidity and Wind ArrayRemove(matrix_utils.csv_header,1,3); //Removing column headers ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix x_matrix; vector y_vector; matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); }
単純ベイズは離散/非連続変数のみを対象としていることに留意してください。上記で動作を見た、連続変数を処理できるガウス単純ベイズと混同しないでください。この単純ベイズモデルの場合は異なります。そのため、この例では、文字列値からエンコードされた離散値を含むこのデータセットを使用することにしました。以下は、上記操作の出力です。
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) "Outlook" "Play" CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [[0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,0] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [1,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) [2,0]]
ということで、単純ベイズクラスのコンストラクタで事前確率を求めましょう。
CNaiveBayes::CNaiveBayes(matrix &x_matrix, vector &y_vector) { XMatrix.Copy(x_matrix); YVector.Copy(y_vector); classes = matrix_utils.Classes(YVector); c_evidence.Resize((ulong)classes.Size()); n = YVector.Size(); if (n==0) { Print("--> n == 0 | Naive Bayes class failed"); return; } //--- vector v = {}; for (ulong i=0; i<c_evidence.Size(); i++) { v = matrix_utils.Search(YVector,(int)classes[i]); c_evidence[i] = (int)v.Size(); } //--- c_prior_proba.Resize(classes.Size()); for (ulong i=0; i<classes.Size(); i++) c_prior_proba[i] = c_evidence[i]/(double)n; #ifdef DEBUG_MODE Print("---> GROUPS ",classes); Print("Prior Class Proba ",c_prior_proba,"\nEvidence ",c_evidence); #endif }
以下が出力です。
CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Prior Class Proba [0.3571428571428572,0.6428571428571429] CS 0 12:59:37.386 Naive Bayes theory script (EURUSD,H1) Evidence [5,9]
[いいえ、はい]の事前確率は約［0.36、0.64］です。
次に、晴れた日にテニスをする人の確率を知りたいとすると、次のようになります。
P（はい|晴れ）＝P（晴れ|はい） x P（はい） / P（晴れ）
簡単な英語で詳しく言うと次のようになります。
晴れた日に誰かがテニスする確率＝確率的に何回晴れていて、誰かがテニスしたか x 確率的に何回誰かがテニスをしたか / 確率的に何回一般的に晴れた日だったか。
P（晴れ|はい）＝2/9
P（はい）= 0.64
P（晴れ） = 5/14 = 0.357
ということで、最終的にP（はい|晴れ）= 0.333 x 0.64 / 0.357 =0.4となります。
（いいえ|晴れ）の確率はどうでしょうか。1-「はい」の確率＝1-0.5972＝0.4027で計算するのが近道ですが、次も見てみましょう。
P（いいえ|晴れ）= (3/5) x 0.36 / (0.357) =0.6
以下は、そのためのコードです。
vector CNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //vector to return if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, fetures columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; for (ulong j=0; j<v.Size(); j++) { if (v_features[i] == v[j] && classes[c] == YVector[j]) count++; } proba *= count==0 ? 1 : count/(double)c_evidence[c]; //do not calculate if there isn't enought evidence' } proba_v[c] = proba*c_prior_proba[c]; } return proba_v; }
この関数で提供される晴れの確率ベクトルは、以下の通りです。
2023.02.15 16:34:21.519 Naive Bayes theory script (EURUSD,H1) Probabilities [0.6,0.4]
しかし、この関数が確率を与えてくれるわけではないことは、間違いないでしょう。説明すると、そのシナリオで予測しようとしているデータセットにのみ2つのクラスがある場合、結果は確率ですが、それ以外の場合は、この関数の出力を確率項に検証する必要があります。これを達成するには簡単です。
この関数で出てきたベクトルの和をとり、各要素を総和で割ると、残ったベクトルが、合計すると1になる実確率値となります。
probability_v = v[i]/probability_v.Sum()
この小さな処理は、NaiveBayes()という関数内でおこなわれ、結果クラスまたはすべての中でより高い確率を持つクラスを予測します。
int CNaiveBayes::NaiveBayes(vector &x_vector) { vector v = calcProba(x_vector); double sum = v.Sum(); for (ulong i=0; i<v.Size(); i++) //converting the values into probabilities v[i] = NormalizeDouble(v[i]/sum,2); vector p = v; #ifdef DEBUG_MODE Print("Probabilities ",p); #endif return((int)classes[p.ArgMax()]); }
これだけです。単純ベイズはシンプルなアルゴリズムですが、ここで、本記事の序盤で使用したガウス単純ベイズに焦点を移しましょう。
ガウス単純ベイズ
ガウス単純ベイズは、特徴が正規分布に従うと仮定します。つまり、予測変数が離散ではなく連続変数である場合、これらの値がガウス分布からサンプリングされると仮定します。
正規分布の復習
正規分布は、平均値を中心に左右対称で、観測値のほとんどが中央のピークに集まり、平均値から離れた値の確率は両方向に等しく先細りになる連続確率分布です。同様に、分布の両端の外れ値もまれです。
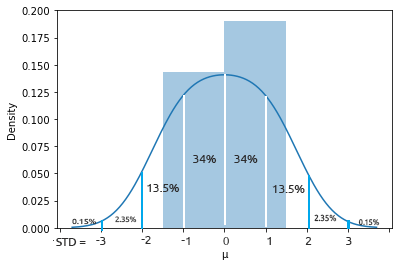
このベル型の確率曲線は非常に強力で、有用な統計分析ツールの1つです。平均から1標準偏差離れたものを見つける確率は約34%、ベル曲線の反対側でも34%なので、平均から1標準偏差離れた値を見つける確率は両側を合わせて約68%です。数学の授業をサボった方は、こちらをお読みください。
この正規分布/ガウス分布から、確率密度を求めたいので、以下の式で計算します。
ここで、
μ＝平均値
𝜎 = 標準偏差
x = 入力値
さて、ガウス単純ベイズはこれに依存しているので、そのコードを書いてみましょう。
class CNormDistribution { public: double m_mean; //Assign the value of the mean double m_std; //Assign the value of Variance CNormDistribution(void); ~CNormDistribution(void); double PDF(double x); //Probability density function }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::CNormDistribution(void) { } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CNormDistribution::~CNormDistribution(void) { ZeroMemory(m_mean); ZeroMemory(m_std); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CNormDistribution::PDF(double x) { double nurm = MathPow((x - m_mean),2)/(2*MathPow(m_std,2)); nurm = exp(-nurm); double denorm = 1.0/(MathSqrt(2*M_PI*MathPow(m_std,2))); return(nurm*denorm); }
ガウス単純ベイズモデルの作成
ガウス単純ベイズのクラスコンストラクタは、単純ベイズと似ているように見えます。ここではコンストラクタのコードを示して説明する必要はありません。以下は、確率の計算をおこなうメイン関数です。
vector CGaussianNaiveBayes::calcProba(vector &v_features) { vector proba_v(classes.Size()); //vector to return if (v_features.Size() != XMatrix.Cols()) { printf("FATAL | Can't calculate probability, fetures columns size = %d is not equal to XMatrix columns =%d",v_features.Size(),XMatrix.Cols()); return proba_v; } //--- vector v = {}; for (ulong c=0; c<classes.Size(); c++) { double proba = 1; for (ulong i=0; i<XMatrix.Cols(); i++) { v = XMatrix.Col(i); int count =0; vector calc_v = {}; for (ulong j=0; j<v.Size(); j++) { if (classes[c] == YVector[j]) { count++; calc_v.Resize(count); calc_v[count-1] = v[j]; } } norm_distribution.m_mean = calc_v.Mean(); //Assign these to Gaussian Normal distribution norm_distribution.m_std = calc_v.Std(); #ifdef DEBUG_MODE printf("mean %.5f std %.5f ",norm_distribution.m_mean,norm_distribution.m_std); #endif proba *= count==0 ? 1 : norm_distribution.PDF(v_features[i]); //do not calculate if there isn't enought evidence' } proba_v[c] = proba*c_prior_proba[c]; //Turning the probability density into probability #ifdef DEBUG_MODE Print(">> Proba ",proba," prior proba ",c_prior_proba); #endif } return proba_v; }
では、このモデルの性能を実際に見てみましょう。
性別データセットを使用します。
| 身長（フット） | 体重（ポンド） | 足のサイズ（インチ） | 人（0=男、1=女） |
|---|---|---|---|
| 6 | 180 | 12 | 0 |
| 5.92 | 190 | 11 | 0 |
| 5.58 | 170 | 12 | 0 |
| 5.92 | 165 | 10 | 0 |
| 5 | 100 | 6 | 1 |
| 5.5 | 150 | 8 | 1 |
| 5.42 | 130 | 7 | 1 |
| 5.75 | 150 | 9 | 1 |
//--- Gaussian naive bayes Matrix = matrix_utils.ReadCsv("gender dataset.csv"); ArrayPrint(matrix_utils.csv_header); Print(Matrix); matrix_utils.XandYSplitMatrices(Matrix, x_matrix, y_vector); gaussian_naive = new CGaussianNaiveBayes(x_matrix, y_vector);
以下が出力です。
CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> GROUPS [0,1] CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) CS 0 18:52:18.653 Naive Bayes theory script (EURUSD,H1) ---> Prior_proba [0.5,0.5] Evidence [4,4]
8人中4人が男性、残りの4人が女性であったため、モデルが主に男性または女性を予測する確率は半々でした。
身長5.3、体重140、足のサイズ7.5という新しいデータで、モデルを試してみましょう。この人が女性である可能性が高いことは、あなたも私も知っています。
vector person = {5.3, 140, 7.5}; Print("The Person is a ",gaussian_naive.GaussianNaiveBayes(person));
以下が出力です。
2023.02.15 19:14:40.424 Naive Bayes theory script (EURUSD,H1) The Person is a 1
素晴らしい、その人が女性であることは正しく予測されています。
ガウス単純ベイズモデルのテストは比較的簡単です。訓練した行列を渡すだけで、混同行列を使った予測精度を測定することができます。
CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Confusion Matrix CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [[4,0] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) [0,4]] CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Classification Report CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) _ Precision Recall Specificity F1 score Support CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 0.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) 1.0 1.00 1.00 1.00 1.00 4.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Accuracy 1.00 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) Average 1.00 1.00 1.00 1.00 8.0 CS 0 19:21:22.951 Naive Bayes theory script (EURUSD,H1) W Avg 1.00 1.00 1.00 1.00 8.0
学習精度は100%で、すべてのデータを学習データとして使用した場合、その人が男性か女性かを分類することができるのです。
単純ベイズ分類器とガウスベイズ分類器の長所
- データセットの分類に使用される最も簡単で高速な機械学習アルゴリズムの1つ
- 二値分類と多値分類の両方に使用可
- シンプルなだけに、多くのアルゴリズムが苦手とする多クラス分類で優れた性能を発揮することが多い
- テキスト分類の問題で最もよく使用される
単純ベイズ分類器とガウスベイズ分類器の欠点
単純ベイズは、分類のためのシンプルで効果的な機械学習アルゴリズムですが、考慮すべきいくつかの限界と欠点があります。
単純ベイズ
- 独立を前提にする：単純ベイズは、すべての特徴が互いに独立であると仮定していますが、これは実際には必ずしもそうであるとは限りません。この仮定は、特徴が互いに強く依存している場合、分類精度の低下につながる可能性があります。
- データのスパース性：単純ベイズは、クラスの事前分布と条件付き確率を正確に推定するために、各クラスに十分な学習例が存在することに依存しています。データセットが小さすぎると、推定値が不正確になり、分類性能が低下することがあります。
- 無関係な機能への感応度：単純ベイズは、分類タスクとの関連性にかかわらず、すべての特徴を平等に扱います。このため、データセットに無関係な特徴が含まれていると、分類性能が低下する可能性があります。データセットの中には、他の特徴よりも重要な特徴があることは否定できない事実です。
- 連続変数に対応できない：単純ベイズは、すべての特徴が離散的またはカテゴリ的であることを前提としており、連続変数を直接扱うことはできません。単純ベイズを連続変数で使用するためには、データを離散化する必要があり、情報損失や分類精度の低下につながる可能性があります。
- 限られた表現力：単純ベイズは線形決定境界しかモデル化できないため、より複雑な分類タスクには十分でない場合があります。これは、決定境界が非線形である場合に、パフォーマンスが低下する可能性があります。
- クラスのアンバランス：単純ベイズは、クラス間の例の分布が非常に不均衡な場合、クラスプリオが偏り、少数クラスの条件付き確率の推定がうまくいかない可能性があるため、パフォーマンスが低下することがあります。
ガウス単純ベイズ
ガウス単純ベイズには、上記に加えてさらに2つの欠点があります。
- 異常値に対して敏感：ガウス単純ベイズは、特徴量が正規分布していると仮定しているため、極値や外れ値が平均や分散の推定値に大きな影響を与える可能性があります。このため、データセットに異常値が含まれる場合は、分類性能が低下する可能性があります。
- 重い尾を持つ機能に不適：ガウス単純ベイズは、特徴量が有限の分散を持つ正規分布であると仮定します。特徴量がコーシー分布のような裾が重い分布である場合、アルゴリズムはうまく機能しないことがあります。
結論
機械学習モデルがストラテジーテスターで結果を出すには、モデルを訓練するだけでは不十分で、利益の上向きグラフが出来上がるようにしながら、性能を追求する必要があります。機械学習モデルをテストするには計算量が多すぎるモデルもあるので、必ずしもストラテジーテスターを使用する必要はないかもしれませんが、取引量や時間枠の最適化など、使用する理由が他に必ずあるはずです。どのようなモードであれ、実際の取引をおこなうことを決定する前に、ロジックについて慎重に分析する必要があります。
ご精読ありがとうございました。
このアルゴリズムの最新の開発と変更は、私のGitHubレポジトリ(https://github.com/MegaJoctan/MALE5)でご覧ください。
| ファイル | 内容・使用方法 |
|---|---|
| Naive Bayes.mqh | 単純ベイズモデルのクラス |
| Naive Bayes theory script.mq5 | ライブラリをテストするためのスクリプト |
| Naive Bayes Test.mq5 | 考察したモデルを用いて取引するためのEA |
| matrix_utils.mqh | 行列関数を追加 |
| metrics.mqh | MLモデルの性能を分析するための関数（混同行列など） |
| naive bayes visualize.py | モデルで使用されるすべての独立変数の分布図を描くためのPythonスクリプト |
| gender datasets.csv & weather dataset.csv | 本記事で例として使用したデータセット |
免責事項：この記事は教育目的のみのものです。取引はリスクの高いゲームです。読者はそれに関連するリスクをご存じだと思います。この記事で取り上げたこのような方法を使用することで発生する可能性のある損失や損害について、著者は責任を負いませんのでご了承ください。リスクにさらすのは失ってもいい資金だけにしてください。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/12184
ニューラルネットワークが簡単に（第33部）：分散型Q学習における分位点回帰
母集団最適化アルゴリズム：細菌採餌最適化(BFO)
自動で動くEAを作る（第06回）：口座の種類（I）
Murrayシステム再訪問
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索