
Нейросети — это просто (Часть 33): Квантильная регрессия в распределенном Q-обучении
Содержание
- Введение
- 1. Квантильная регрессия
- 2. Реализация средствами MQL5
- 3. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
В предыдущей статье мы познакомились с распределенным Q-обучением, которое позволяет изучить вероятностное распределение прогнозируемого вознаграждения. Мы научились прогнозировать вероятность получения ожидаемого вознаграждения в конкретном диапазоне значений. Но, как вы могли заметить, количество таких диапазонов и разброс значений вознаграждения являются гиперпараметрами модели. Следовательно, для выбора оптимальных параметров нам необходимы экспертные знания о распределении значений вознаграждений. И ряд тестов для подбора оптимальных гиперпараметров.
Надо сказать, что принятый нами подход разделения всего диапазона возможных значений на равные диапазоны также имеет свои недостатки. Для прогнозирования вероятности получения вознаграждения в каждом из отдельных диапазонов по каждому действию мы выделили по одному нейрону. На практике же довольно часто видим ситуацию, когда вероятность получения вознаграждения в большом количестве диапазонов ровна "0". А значит, мы неэффективно расходуем свои ресурсы. Можно было бы объединить некоторые диапазона для снижения количества выполняемых операций. И тем самым ускорить обучение и работу модели. В то же время вероятность получения вознаграждения в других диапазонах довольно велика. И для получения более полной картины нам бы хотелось разбить такой диапазон на более мелки составляющие. Что позволило бы повысить точность прогнозирования ожидаемого вознаграждения. Однако, наш подход не позволяет создавать диапазоны различных размеров. Эти недостатки решаются при использовании алгоритма квантильной регрессии, предложенного в октябре 2017 года в статье "Distributional Reinforcement Learning with Quantile Regression".
1. Квантильная регрессия
Квантильная регрессия моделирует взаимосвязь между распределением независимых переменных и определенными квантилями целевой переменной.
Начиная разговор об использовании квантильной регрессии в распределенном Q-обучении надо сказать, что предложенный алгоритм подходит с другой стороны к оценке вероятностного распределения ожидаемого вознаграждения. И если ранее мы разбивали диапазон возможных значений вознаграждения на разные участки. То в новом алгоритме мы разбиваем все множество получаемых вознаграждений на несколько равновероятностных квантилей. Что же это нам даёт?
У нас остаётся гиперпараметр количества анализируемых квантилей. Но при этом мы не ограничиваем диапазон возможных значений вознаграждений. Вместо этого мы обучаем свою модель прогнозировать медианные значения квантилей. И так как мы используем равновероятностные квантили, то у нас не будет квантилей с нулевой вероятностью получения вознаграждения. Более того, в области разрежения значений вознаграждений мы получим укрупненные квантили. А области большого скопления вознаграждений будут разбиты на более мелкие участки. Тем самым предоставляя нам более полную картину о вероятностном распределении ожидаемого вознаграждения. Более того, такой подход позволяет выявить не статичные области разряжения и повышенной плотности значений вознаграждений. Которые могут меняться в зависимости от состояния окружающей среды.
Тем не менее, это остаётся все то же Q-обучение. И процесс строится на уравнении оптимизации Беллмана.
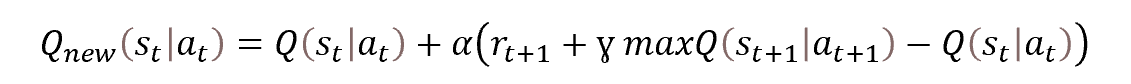
Только на это раз нам пред определить не одно значение, а целое распределение. Но, по сути, задача остаётся прежней. Давайте внимательнее посмотрим на поставленную задачу.
Как было сказано выше, мы разбиваем все распределение вознаграждений обучающей выборки на N равновероятных квантилей. Каждый квантиль представляет уровень, который анализируемая случайная величина не превышает с заданной вероятностью. Равновероятностными квантилями в данном случае я называю квантили с фиксированным шагом, общая совокупность которых покрывает всю обучающую выборку.
На практике мы имеем совокупность обучающей выборки. И вероятность получения одного из элементов из данной выборки равна "1". Другого просто не может быть. Ведь мы берем элементы из обучающей выборки.
Разбиение выборки на N равновероятных квантилей подразумевает, прежде всего, разбиение всей обучающей выборки на N равных частей. Каждая из которых будет содержать одинаковое количество элементов. И вероятность выбора элемента из одной из выборок составляет 1/N.
Отдельный квантиль характеризуется 2 параметрами: вероятность выбора элемента и верхняя граница значений его элементов. Надо сказать, что дополнительным условием квантилей является их сортировка по возрастанию с накоплением вероятностей. То есть, верхняя граница значений каждого последующего квантиля выше предыдущей. И вероятность квантиля включает вероятность предыдущих квантилей. К примеру, для некоего распределения мы имеем квантиль 0.2 с уровнем 15. Это значит, что значение 20% элементов всего распределения не превышает 15. При этом, шаг вероятностей и уровня максимальных значений квантилей могут быть не пропорциональными и зависят от конкретного распределения.
Рассматриваемый нами алгоритм подразумевает деление совокупности на квантили с фиксированным шагом вероятности. А вместо верхних границ, мы будем обучать модель прогнозировать медианные значения квантилей.
Для обучения модели нам необходимы целевые значения. При наличии полного набора элементов некой совокупности мы легко можем найти среднее значение.
Но на практике у нас нет полной совокупности. Вознаграждения мы получаем от среды только после совершения действия и перехода в новое состояние. Как видите, изменение алгоритма обучения модели не влияет на процесс взаимодействия со средой. В процессе оригинального Q-обучения мы обучали модель прогнозирования среднего ожидаемого вознаграждения. А достигали мы этого путем итерационного смещения результатов нашей модели к целевым показателям с небольшим коэффициентом обучения. Как можно заметить, в процессе обучения на результат работы нашей модели постоянно действует сила смещения в сторону текущего целевого значения. И среднего значения мы достигаем в тот момент, когда разнонаправленные силы уравновешивают друг друга (как показано на рисунке).

Аналогичный подход мы модем использовать и при решении задач рассматриваемого алгоритма. Но здесь есть одно обстоятельство. Указанный алгоритм позволяет найти среднее значение всей совокупности. Что составляет квантиль 0.5. Применяя его в чистом виде, мы получим одинаковые значения на всех нейронах слоя результатов нашей модели. Они все будут работать синхронно, как один нейрон. А мы бы хотели получить истинное распределение значений по анализируемым квантилям.
Давайте посмотрим на природу квантиля. К примеру, рассмотрим квантиль 0.25, что составляет четверть от анализируемой совокупности. Если мы отбросим расстояние между значениями элементов, то на каждый 1 элемент квантиля должно быть 3 элемента из общей совокупности не попадающих в данный квантиль. Возвращаясь к нашему примеру выше, для получения равновесия в точке квантиля 0.25 сила снижения значения должна быть в 3 раза больше силы увеличения значения квантиля.
Следовательно, для нахождения значения каждого конкретного квантиля нам достаточно ввести в уравнение Беллмана корректирующий коэффициент. Который будет зависеть от уровня квантиля и направления отклонения.
![]()
где τ — вероятностная характеристика квантиля.
При этом, в процессе обучения мы используем все эвристики классического Q-обучения в виде воспроизведения опыта и Target Net.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов алгоритма мы переходим к практической части данной статьи. И рассмотрим вариант реализации алгоритма средствами MQL5. В процессе реализации алгоритма мы не буем создавать новые архитектуры нейронных слоёв. Зато мы вынесем организацию процесса в отдельный класс CQRDQN. Что позволит нам упростить процесс использования метода в советниках и оградить пользователя от некоторых деталей реализации. Структура нового класса представлена ниже.
class CQRDQN : protected CNet { private: uint iCountBackProp; protected: uint iNumbers; uint iActions; uint iUpdateTarget; matrix<float> mTaus; //--- CNet cTargetNet; public: /** Constructor */ CQRDQN(void); CQRDQN(CArrayObj *Description) { Create(Description, iActions); } bool Create(CArrayObj *Description, uint actions); /** Destructor */~CQRDQN(void); bool feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { return CNet::feedForward(inputVals, window, tem); } bool backProp(CBufferFloat *targetVals, float discount, CArrayFloat *nextState, int window = 1, bool tem = true); void getResults(CBufferFloat *&resultVals); int getAction(void); int getSample(void); float getRecentAverageError() { return recentAverageError; } bool Save(string file_name, datetime time, bool common = true) { return CNet::Save(file_name, getRecentAverageError(), (float)iActions, 0, time, common); } virtual bool Save(const int file_handle); virtual bool Load(string file_name, datetime &time, bool common = true); virtual bool Load(const int file_handle); //--- virtual int Type(void) const { return defQRDQN; } virtual bool TrainMode(bool flag) { return CNet::TrainMode(flag); } virtual bool GetLayerOutput(uint layer, CBufferFloat *&result) { return CNet::GetLayerOutput(layer, result); } //--- virtual void SetUpdateTarget(uint batch) { iUpdateTarget = batch; } virtual bool UpdateTarget(string file_name); //--- virtual bool SetActions(uint actions); };
Новый класс мы создаём наследником от класса организации работы наших моделей нейронных сетей CNet. Это означает, что мы будем выстраивать новый алгоритм работы с моделью.
Для хранения ключевых параметров работы нашего алгоритма мы создадим переменные:
- iNumbers — количество нейронов в последовательности описания распределения одного действия;
- iActions — количество возможных вариантов действий;
- iUpdateTarget — частота обновления параметров модели Target Net;
- mTaus — матрица записи вероятностных характеристик квантилей;
- cTargetNet — указатель на объект Target Net.
Здесь надо обратить внимание, что в матрице mTaus мы запишем медианные значения вероятностей каждого квантиля.
В конструкторе класса мы зададим начальные значения указанных переменных.
CQRDQN::CQRDQN() : iNumbers(31), iActions(2), iUpdateTarget(1000) { mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers; mTaus[0, 0] /= 2; mTaus = mTaus.CumSum(0); cTargetNet.Create(NULL); Create(NULL, iActions); }
Как и в самом классе организации модели нейронной сети CNet, помимо конструктора без параметров мы создадим перегрузку метода с указанием архитектуры создаваемой модели.
CQRDQN(CArrayObj *Description) { Create(Description, iActions); }
Непосредственно создавать модель мы будем в методе Create. В параметрах данный метод получает указатель на массив описания архитектуры создаваемой модели и количество возможных действий агента.
bool CQRDQN::Create(CArrayObj *Description, uint actions) { if(actions <= 0 || !CNet::Create(Description)) return false;
В теле метода мы проверяем корректность указания параметра количества действий агента. И вызываем одноименный метод родительского класса, в котором организованы все необходимые контроли касательно объекта описания архитектуры создаваемой модели и выстроен сам процесс создания новой модели. Здесь мы лишь проверяем логический результат выполнения операций родительского класса.
После успешного создания новой модели мы возьмем слой результатов созданной модели. На основании информации о его размере и количестве возможных действий агента заполним матрицу вероятностных характеристик квантилей mTaus. Количество строк данной матрице равно размеру вероятностного распределения вознаграждения одного действия. И так как вероятности каждого квантиля у нас задаются перед началом обучения одинаковые для всех возможных действий агента с равным фиксированным шагом, то мы будем использовать матрицу-вектор с одной строкой. Использование именно матрицы, а не вектора, обусловлено "прицелом" на дальнейшее развитие с возможной вариативность вероятностных распределений по действиям.
int last_layer = Description.Total() - 1; CLayer *layer = layers.At(last_layer); if(!layer) return false; CNeuronBaseOCL *neuron = layer.At(0); if(!neuron) return false; iActions = actions; iNumbers = neuron.Neurons() / actions; mTaus = matrix<float>::Ones(1, iNumbers) / iNumbers; mTaus[0, 0] /= 2; mTaus = mTaus.CumSum(0); cTargetNet.Create(NULL); //--- return true; }
Обратите внимание, что на начальном этапе мы обнуляем Target Net. Такой подход используется с целью не допущения обучения новой модели на абсолютно случайные величины не обученной модели.
Для организации прямого прохода мы будем полностью эксплуатировать аналогичный метод родительского класса.
bool feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { return CNet::feedForward(inputVals, window, tem); }
А вот с методом обратного backProp прохода нам придется немного поработать. Напомню, что реакцией среды на каждое действие наше агента является вознаграждение. При организации процесса классического Q-обучения мы определили политику вознаграждений. И так как в процессе трейдинга возможные действия агента являются взаимоисключающими и носят противоположный характер, то по вознаграждению среды на одно действие мы можем определить какое было бы вознаграждение на противоположное действие. Это позволяет нам на каждой итерации обратного прохода передавать нам целевые значения для всех возможных действий. Что делает процесс обучения стабильнее и быстрее. Но в процессе распределенного Q-обучения мы имеем дело с целым вектором целевых значений для каждого действия. И в предыдущей статье мы строили новый процесс создания тензора целевых значений модели в советнике обучения модели. Равно как и новый блок расшифровки результатов модели перед совершением действия в торговом советнике проверки работы обученной модели.
Сейчас, благодаря созданию нового класса мы можем скрыть этот процесс от пользователя. И сделать его работу с моделью более простой и понятной. Аналогичной работе с моделью классического Q-обучения. Когда среда возвращает только дискретное значение вознаграждения на каждое действие. А весь процесс перевода этого дискретного вознаграждения в вектор распределения для каждого действия мы организуем в теле метода обратного прохода.
Надо сказать и ещё об одном преимуществе использования нового класса организации процесса. Как вы знаете, в процессе Q-обучения используется Target Net для прогнозирования будущего вознаграждения. И ранее пользователю необходимо было работать с 2 моделями. Теперь мы можем скрыть всю работу с Target Net внутри методов нашего класса. И тем самым облегчить работу пользователя. Но это потребовало изменение параметров метода обратного прохода. И в таком варианте для корректного выполнения процесса обратного прохода помимо целевых значений мы ожидаем получить от пользователя и новое состояние системы.
В теле метода обратного прохода сначала мы проверяем корректность полученного указателя на вектор целевых значений. А также размер полученного вектора должен быть равен количеству возможных действий агента.
bool CQRDQN::backProp(CBufferFloat *targetVals, float discount, CArrayFloat *nextState=NULL, int window = 1, bool tem = true) { //--- if(!targetVals) return false; vectorf target; if(!targetVals.GetData(target) || target.Size() != iActions) return false;
Затем мы проверяем корректность указателя на вектор описания нового состояния системы. И, при необходимости, осуществляем прямой проход Target Net. После чего определяем максимально возможное вознаграждение и корректируем полученное от среды вознаграждение на будущий доход с учетом коэффициента дисконтирования.
if(!!nextState) { if(!cTargetNet.feedForward(nextState, window, tem)) return false; vectorf temp; cTargetNet.getResults(targetVals); if(!targetVals.GetData(temp)) return false; matrixf q = matrixf::Zeros(1, temp.Size()); if(!q.Row(temp, 0) || !q.Reshape(iActions, iNumbers)) return false; temp = q.Mean(0); target = target + discount * temp.Max(); }
Для обновления параметров модели мы будем использовать формулу.
![]()
Однако, стоит обратить внимание, что при реализации приведенной формулы в теле данного метода мы не будем использовать коэффициент обучения. Здесь кроется небольшая хитрость. Дело в том, что в теле данного метода, как бы ни показалось странным, мы не обновляем параметры модели. Мы лишь создаём вектор целевых результатов для нашей модели. А непосредственно обновление параметров модели будет осуществляться в одноименном методе родительского класса. В который мы будем передавать полный тензор целевых результатов модели. И уже при обновлении параметров модели мы будем учитывать коэффициент обучения.
На данном этапе мы уже имеем вознаграждение от среды с учетом возможных будущих выгод. И для создания вектора целевых значений нам недостаёт лишь последних результатов прямого прохода нашей модели. Их мы загрузим в локальную матрицу Q.
vectorf quantils; getResults(targetVals); if(!targetVals.GetData(quantils)) return false; matrixf Q = matrixf::Zeros(1, quantils.Size()); if(!Q.Row(quantils, 0) || !Q.Reshape(iActions, iNumbers)) return false;
После этого мы можем создать необходимый буфер целевых значений для нашей модели. Для этого мы в цикле построим процесс создания вектора целевых значений уровней квантилей по каждому отдельному действию агента из числа возможных. Хочу обратить внимание, что использование матричных и векторных операций требует некоторых ухищрений и изменения подходов при построении алгоритмов. Но при этом позволяет сократить использование циклов. Что в целом позволяет повысить скорость выполнения программы.
В данном случае использование векторных операций позволяет нам отказаться от системы вложенных циклов. В которых мы бы перебирали все действия и все элементы распределения по каждому возможному действию агента. Вместо этого мы используем лишь 1 цикл перебора возможных действий агента. Число итераций которого в большинстве случаев будут в десятки раз меньше числа итераций исключенного цикла перебора элементов вероятностного распределения. Но платой за это послужил отказ от условного оператора. Мы не можем просто сравнить 2 элемента векторов для выбора действия в зависимости от результата сравнения.
И нам предстоит выполнить обе ветки операций для всех элементов векторов. Чтобы при этом не исказить ожидаемый результат операций мы создадим 2 вектора разностей между полученным от среды вознаграждением и результатом последнего прямого прохода. После чего в одном векторе обнулим отрицательные значения, а во втором — положительные. Таким образом, после умножения полученных векторов на соответствующие коэффициенты корректировки силы влияния на среднее значения квантиля мы получим желаемые корректирующие значения. Сумма полученных векторов и последних результатов прямого прохода даст необходимые нам целевые значения для обратного прохода нашей модели.
for(uint a = 0; a < iActions; a++) { vectorf q = Q.Row(a); vectorf dp = q - target[a], dn = dp; if(!dp.Clip(0, FLT_MAX) || !dn.Clip(-FLT_MAX, 0)) return false; dp = (mTaus.Row(0) - 1) * dp; dn = mTaus.Row(0) * dn * (-1); if(!Q.Row(dp + dn + q, a)) return false; } if(!targetVals.AssignArray(Q)) return false;
После завершения всех итераций цикла мы обновляем значения буфера целевых значений.
Далее мы выполняем небольшую вспомогательную работу по организации работы с моделью Target Net. Мы реализуем счетчик итераций обратных проходов. И при достижении порогового числа итераций осуществляем обновление модели Target Net.
if(iCountBackProp >= iUpdateTarget) { #ifdef FileName if(UpdateTarget(FileName + ".nnw")) #else if(UpdateTarget("QRDQN.upd")) #endif iCountBackProp = 0; } else iCountBackProp++;
Обратите внимание на макроподстановки в теле оператора сравнения при достижении порогового значения итераций обратного прохода. Как и ранее, при обновлении модели Target Net мы не осуществляем прямое копирование параметров из одной модели в другую. Вместо этого мы используем механизм сохранения и восстановления модели из файла. Для осуществления такой итерации нам необходимо имя файла.
Во всех своих моделях я использовал макроподстановку FileName для генерирования уникального имени файла в зависимости от используемого советника, инструмента и таймфрейма. Данная макроподстановка назначается непосредственно в советнике. А организованная здесь макроподстановка позволяет нам проверить назначение макроподстановки генерирования имени файла в советнике. И при наличии таковой, использовать её для операций сохранения и восстановления файла. В случае же отсутствия таковой будет использоваться заданное по умолчанию имя файла.
#define FileName Symb.Name()+"_"+EnumToString(TimeFrame)+"_"+StringSubstr(__FILE__,0,StringFind(__FILE__,".",0))
В завершение нашего метода мы вызываем метод обратного прохода родительского класса и передадим ему в параметрах подготовленный тензор целевых результатов. А логический результат выполнения операций метода родительского класса вернем вызывающей программе.
return CNet::backProp(targetVals);
}
Таким образом мы скрыли от пользователя использование модели с вероятностным распределением при осуществлении обратного прохода. И среда нам возвращает только по одному дискретному вознаграждению для каждого действия. Сейчас вызов метода обратного прохода осуществляется аналогично классическому Q-обучению. Но при этом мы избавили пользователя от необходимости контроля второй модели Target Net. Что, на мой взгляд, повышает юзабилити нашей модели. Но остается открытый вопрос прямого прохода.
Как было указано выше, для прямого прохода эксплуатируется метод родительского класса. Непосредственно на операции прямого прохода это не оказывает отрицательного слияния. Ведь метод прямого прохода возвращает лишь логический результат выполнения операций. Вопрос возникает при попытке получить результаты прямого прохода. Здесь методы родительского класса вернут полное вероятностное распределение, сформированное моделью. И тут возникает разрыв шаблонов между результатами прямого прохода и целевыми значениями обратного прохода. Следовательно, нам предстоит переопределить метод получения результатов прямого прохода, чтобы они стали сопоставимыми с используемыми целевыми результатами обратного прохода.
Здесь надо сказать, что мы не зря использовали равновероятностные квантили. Именно благодаря этому мы можем просто взять среднее значение из всего сформированного распределения по каждому возможному действию агента и вернуть это значение в качестве ожидаемого вознаграждения. И здесь нам опять на помощь приходят матричные операции. Именно благодаря им нам удалось построить алгоритм метода полностью без использования циклов.
Вначале метода мы вызываем одноименный метод родительского класса, в котором реализованы все необходимые контроли и операции для копирования результатов прямого прохода в буфер данных. Полученные данные мы переносим в матрицу. Которую затем переформатируем в табличную матрицу с числом строк равным числу возможных действий агента. В таком случае каждая строка представляет собой вектор вероятностного распределения ожидаемого вознаграждения по каждому отдельно взятому действию агента. И тогда нам достаточно лишь одной матричной функции Mean для определения средних значений по всем возможным действиям агента. Нам остаётся лишь перенести полученный результат в буфер данных и вернуть его вызывающей программе.
void CQRDQN::getResults(CBufferFloat *&resultVals) { CNet::getResults(resultVals); if(!resultVals) return; vectorf temp; if(!resultVals.GetData(temp)) { delete resultVals; return; } matrixf q; if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers)) { delete resultVals; return; } //--- if(!resultVals.AssignArray(q.Mean(1))) { delete resultVals; return; } //--- }
И тут я ожидаю море недоумения и вопросов для чего мы все это делали если вернулись к среднему значению, которое и учит оригинальное Q-обучение. Не вдаваясь в глубокие дебри математики скажу одну истину, подтвержденную практическими результатами. Вероятность среднего значения выборки не равна среднему значению вероятностей подвыборок из этой же совокупности. Оригинальное Q-обучение учит вероятность среднего значения выборки. В то время как распределенное Q-обучение выучивает несколько средних по каждому квантилю. И затем мы берем уже среднее из этих вероятностных значений.
Как показывают научные труды и практика квантильная регрессия в целом менее подвержена влиянию различных выбросов. И это делает процесс обучения модели более стабильным. А результаты такого обучения менее смещенными. Авторы метода в своей статье приводят результаты обучения работы обученных моделей на 57 играх Атари в сравнении с достижениями моделей, обученных другими алгоритмами. Приведенные данные демонстрируют, что средний результат практически в 4 раза превышает результат оригинального Q-обучения (DQN). Ниже приведена таблица результатов из оригинальной статьи [6]
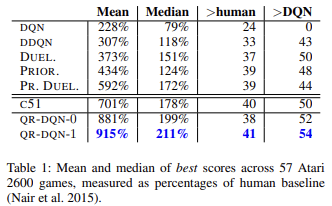
Повышаем юзабилити нашей модели. Ранее, при создании всех советников тестирования моделей обучения с подкреплением мы создавали различные методы выбора действия по результатам прямого прохода обученной модели. Создание нового класса позволяет нам организовать методы, выполняющие данный функционал. Для жадного выбора действия с максимальным ожидаемым вознаграждением мы создадим метод getAction. Его алгоритм довольно прост. Мы лишь воспользуемся выше описанным методом получения результатов прямого прохода getResults. Из полученного буфера результатов выберем элемент с максимальным значением.
int CQRDQN::getAction(void) { CBufferFloat *temp; getResults(temp); if(!temp) return -1; //--- return temp.Maximum(0, temp.Total()); }
Мы не реализуем ɛ-жадную стратегию выбора действия, так как она применяется в процессе обучения модели для повышения степени изучения среды. Наша политика вознаграждений позволяет отказаться от использования подобных методов. Ведь в процессе обучения мы даем целевые ориентиры сразу для всех возможных действий агента.
Второй метод getSample будет использоваться для случайного выбора действия из вероятностного распределения. В котором большая награда имеет большую вероятность. Для исключения излишних копирований данных между матрицами и буферами данных мы частично повторим алгоритм метода getResults.
int CQRDQN::getSample(void) { CBufferFloat* resultVals; CNet::getResults(resultVals); if(!resultVals) return -1; vectorf temp; if(!resultVals.GetData(temp)) { delete resultVals; return -1; } delete resultVals; matrixf q; if(!q.Init(1, temp.Size()) || !q.Row(temp, 0) || !q.Reshape(iActions, iNumbers)) { delete resultVals; return -1; }
После чего результаты прямого прохода нормализуем функцией SoftMax. Это и будут вероятности выбора действий агента.
if(!q.Mean(1).Activation(temp, AF_SOFTMAX)) return -1; temp = temp.CumSum();
Соберем вектор накопительных итогов вероятностей и проведем семплирование из полученного вектора вероятностного распределения.
int err_code; float random = (float)Math::MathRandomNormal(0.5, 0.5, err_code); if(random >= 1) return (int)temp.Size() - 1; for(int i = 0; i < (int)temp.Size(); i++) if(random <= temp[i] && temp[i] > 0) return i; //--- return -1; }
Результат семплирования вернем вызывающей программе.
Мы рассмотрели методы прямого и обратного проходов. А также методы получения результатов работы нашей модели. Но у на еще остаётся ряд не закрытых вопросов. И один из них — это метод обновления модели Target Net — UpdateTarget. Мы ссылались на это метод при рассмотрении метода обратного прохода. Несмотря на то, что данные метод вызывается из другого метода класса я решил сделать его публичным и предоставить доступ к нему пользователю. Да, мы оградили пользователя от необходимости контроля состояния Target Net. Тем не менее, мы не ограничиваем его свободу выбора. И, при желании, он может взять полный контроль в свои руки.
Алгоритм метода довольно прост. Мы просто сначала вызываем метод сохранения текущего объекта. А затем вызываем метод восстановления данных Target Net. При этом контролируем процесс выполнения операций. И после успешного обновления модели Target Net обнулим счетчик итераций обратного прохода.
bool CQRDQN::UpdateTarget(string file_name) { if(!Save(file_name, 0, false)) return false; float error, undefine, forecast; datetime time; if(!cTargetNet.Load(file_name, error, undefine, forecast, time, false)) return false; iCountBackProp = 0; //--- return true; }
Следует обратить внимание на разность классов объектов. Мы работаем в новом классе CQRDQN, а Target Net является экземпляром родительского класса CNet. Дело в том, что от Target Net мы используем только функционал прямого прохода. Данный метод не модифицировался в нашем классе. И не предвидится проблем в использовании родительского класса. В то же время, при использовании экземпляра класса CQRDQN для Target Net рекуррентно будет создан внутренний объект Target Net уже нового экземпляра. И такой рекуррентный процесс способен привести к критическим ошибкам. Поэтому столь незначительная деталь может иметь значительные последствия для работы всей программы.
Мы рассмотрели основной функционал нового класса CQRDQN, в котором реализован алгоритм квантильной регрессии в распределенном Q-обучении (QR-DQN). Метод был представлен в октябре 2017 года в статье "Distributional Reinforcement Learning with Quantile Regression".
В классе ещё были реализованы методы сохранения модели Save и её последующего восстановления Load. Внесенные в них изменения не столь сложны. И с ними Вы можете самостоятельно ознакомиться во вложении. А сейчас я предлагаю перейти к тестированию нового класса.
3. Тестирование
Тестирование работы нового класса мы начинаем с обучения модели. Для её обучения был создан советник "QRDQN-learning.mq5". Советник был создан на базе советника оригинального Q-обучения "Q-learning.mq5". Мы изменили в данном советнике класс обучаемой модели и убрали объявление экземпляра модели Target Net.
CSymbolInfo Symb;
MqlRates Rates[];
CQRDQN StudyNet;
CBufferFloat *TempData;
CiRSI RSI;
CiCCI CCI;
CiATR ATR;
CiMACD MACD; В методе инициализации советника мы загружаем модель из предварительно созданного файла. Принудительно включаем режим обучения всех нейронных слоев. Определяем глубину анализируемой истории по размеру слоя исходных данных. И передадим модели размер области допустимых действий. А также укажем период обновления Target Net. В данном случае я указал заведомо завышенное значение, так как планирую сам управлять процессов обновления моделей.
int OnInit() { //--- ......... ......... //--- if(!StudyNet.Load(FileName + ".nnw", dtStudied, false)) return INIT_FAILED; if(!StudyNet.TrainMode(true)) return INIT_FAILED; //--- if(!StudyNet.GetLayerOutput(0, TempData)) return INIT_FAILED; HistoryBars = TempData.Total() / 12; if(!StudyNet.SetActions(Actions)) return INIT_PARAMETERS_INCORRECT; StudyNet.SetUpdateTarget(1000000); //--- ........ //--- return(INIT_SUCCEEDED); }
Непосредственно процесс обучения модели осуществляется в функции Train.
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time);
В функции мы определяем период обучения и загружаем исторические данные. Этот процесс полностью сохранен в оригинальном исполнении.
int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh();
Далее мы организовываем систему вложенных циклов процесса обучения модели. Внешний цикл отсчитывает эпохи обучения по обновлению модели Target Net.
int total = bars - (int)HistoryBars - 240; bool use_target = false; //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int i = 0; uint ticks = GetTickCount(); int count = 0; int total_max = 0;
Во вложенном цикле мы повторяем итерации прямого и обратного прохода. Здесь мы вначале подготовим исторические данные для описания двух последующих состояний системы. Одно будет использоваться для прямого прохода обучаемой модели. А второе — Target Net.
for(int batch = 0; batch < (Batch * UpdateTarget); batch++) { i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * total + 240); State1.Clear(); State2.Clear(); int r = i + (int)HistoryBars; if(r > bars) continue; for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = r - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) || !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) || !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } if(!use_target) continue; //--- bar_t --; open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); rsi = (float)RSI.Main(bar_t); cci = (float)CCI.Main(bar_t); atr = (float)ATR.Main(bar_t); macd = (float)MACD.Main(bar_t); sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) || !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) || !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
И выполняем прямой проход обучаемой модели.
if(IsStopped()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } if(State1.Total() < (int)HistoryBars * 12 || (use_target && State2.Total() < (int)HistoryBars * 12)) continue; if(!StudyNet.feedForward(GetPointer(State1), 12, true)) return;
После чего формируем пакет вознаграждений за все возможные действия агента и вызываем метод обратного прохода основной модели.
Rewards.BufferInit(Actions, 0); double reward = Rates[i].close - Rates[i].open; if(reward >= 0) { if(!Rewards.Update(0, (float)(2 * reward))) return; if(!Rewards.Update(1, (float)(-5 * reward))) return; if(!Rewards.Update(2, (float) - reward)) return; } else { if(!Rewards.Update(0, (float)(5 * reward))) return; if(!Rewards.Update(1, (float)(-2 * reward))) return; if(!Rewards.Update(2, (float)reward)) return; }
Обратите внимание, что в соответствии с переопределенным методом обратного прохода, в параметрах методу мы передаем не только буфер вознаграждений, но и последующее текущее состояние. Вместе с тем, мы удалили блок работы с Target Net и корректировки вознаграждения на ожидаемый доход будущих состояний.
if(!StudyNet.backProp(GetPointer(Rewards), DiscountFactor, (use_target ? GetPointer(State2) : NULL), 12, true)) return;
И выводим информацию о прогрессе процесса на график инструмента.
if(GetTickCount() - ticks > 500) { Comment(StringFormat("%.2f%%", batch * 100.0 / (double)(Batch * UpdateTarget))); ticks = GetTickCount(); } }
На этом заканчиваются операции вложенного цикла. И после завершения всех его итераций мы проверяем текущую ошибку модели. При улучшении ранее достигнутых результатов мы сохраняем текущее состояние модели и обновляем Target Net.
if(StudyNet.getRecentAverageError() <= min_loss) { if(!StudyNet.UpdateTarget(FileName + ".nnw")) continue; use_target = true; min_loss = StudyNet.getRecentAverageError(); } PrintFormat("Iteration %d, loss %.8f", iter, StudyNet.getRecentAverageError()); } Comment(""); //--- PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); }
На этом завершаются операции внешнего цикла и функции обучения в целом. Остальной код советника был перенесен полностью без изменений. С полным кодом всех классов и программ можно ознакомиться во вложении.
Для обучения была создана модель с помощью инструмента NetCreator. Модель полностью повторила архитектуру обучаемой модели из предыдущей статьи. Я лишь удалил последний слой нормализации SoftMax, чтобы область результатов модели могла повторить любые результаты используемой политики вознаграждения.
Как всегда, обучение модели осуществлялось на исторических данных EURUSD, таймфрейм H1. В качестве обучающей выборки использовались исторические данные за 2 последних года.
Работа обученной модели была проверена в тестере стратегий. Для этого был создан советник "QRDQN-learning-test.mq". Советник также был создан на базе аналогичных советников из предыдущих статей. И его код не претерпел значительных изменений. В с его полным кодом можно ознакомиться во вложении.
В тестере стратегий модель продемонстрировала способность к генерации прибыли на коротком временном отрезке в 2 недели. Более половины совершенных торговых операций были закрыты с прибылью. При этом средняя прибыль по сделке практически в 2 раза превышала средний убыток.
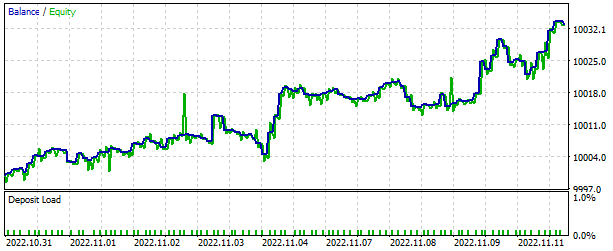
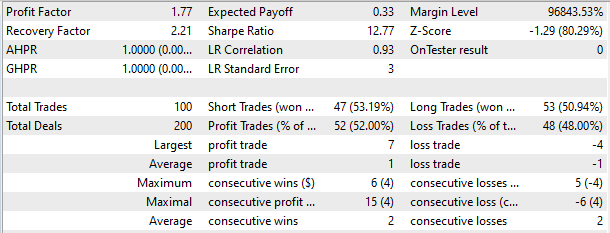
Заключение
В данной статье мы познакомились с ещё одним перспективным методом обучения с подкреплением. Нами была создан класс реализации рассмотренного метода. Мы обучили модель и посмотрели на результаты её работы в тестере стратегий. Полученные результаты позволяют сделать вывод о возможности использования алгоритма квантильной регрессии в распределенном Q-обучении для реализации моделей, способных решать реальные рыночные задачи.
Ещё раз хочу акцентировать внимание, что все приведенные в статье программы предназначены только для демонстрации технологии. Для использования моделей и советников в реальной торговле необходима их доработка и тщательное всестороннее тестирование.
Ссылки
- Нейросети — это просто (Часть 26): Обучение с подкреплением
- Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
- Нейросети — это просто (Часть 28): Policy gradient алгоритм
- Нейросети — это просто (Часть 32): Распределенное Q-обучение
- A Distributional Perspective on Reinforcement Learning
- Distributional Reinforcement Learning with Quantile Regression
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | QRDQN-learning.mq5 | Советник | Советник для оптимизации модели |
| 2 | QRDQN-learning-test.mq5 | Советник | Советник для тестирования модели в тестере стратегий |
| 3 | QRDQN.mqh | Библиотека классов | Класс организации модели QR-DQN |
| 4 | NeuroNet.mqh | Библиотека классов | Библиотека для организации моделей нейронных сетей |
| 5 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL для организации моделей нейронных сетей |
| 6 | NetCreator.mq5 | Советник | Инструмент создания моделей |
| 7 | NetCreatotPanel.mqh | Библиотека классов | Библиотека класса для создания инструмента |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торговой системы на основе индикатора DeMarker
Разработка торговой системы на основе индикатора DeMarker
 Разработка торговой системы на основе Индекса относительной бодрости Relative Vigor Index
Разработка торговой системы на основе Индекса относительной бодрости Relative Vigor Index
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
hi,
thanks for your hard work, appreciate your time and effort.
had to grab VAE from article #22 when I tried to compile QRDQN.
but running into this error,
'MathRandomNormal' - undeclared identifier VAE.mqh 92 8
Im guessing the VAE library in #22 is outdated?
hi,
thanks for your hard work, appreciate your time and effort.
had to grab VAE from article #22 when I tried to compile QRDQN.
but running into this error,
'MathRandomNormal' - undeclared identifier VAE.mqh 92 8
Im guessing the VAE library in #22 is outdated?
Hi, you can load updated files from this article https://www.mql5.com/ru/articles/11619
Hi, you can load updated files from this article https://www.mql5.com/en/articles/11619
thanks for your reply,
I did that and that error is fixed, but 2 more popped up.
one
'Create' - expression of 'void' type is illegal QRDQN.mqh 85 30
2
''AssignArray' - no one of the overloads can be applied to the function call QRDQN.mqh 149 19