Aproximación por fuerza bruta a la búsqueda de patrones (Parte II): Inmersión

Introducción

Hemos decidido continuar el tema iniciado en el artículo anterior y analizar en profundidad varias parejas de divisas usando una versión modificada de nuestro programa. En este sentido, el autor querría agradecer al usuario Aleksey Vyazmikin su contribución al desarrollo de la idea. El consejo de Alexey resultó muy útil en el plano técnico y fue el verdadero impulso para el desarrollo de la idea. En el próximo artículo, continuaremos trabajando en esta dirección y ofreceremos a los lectores datos y resultados mucho más interesantes. Es muy importante mostrar y hablar del nivel de efectividad del análisis de un pareja de divisas en particular a escala global y en su conjunto, y también mostrar las diferencias existentes en el futuro al analizar los intervalos temporales de duración máxima y mínima. Obviamente, como el tiempo y las capacidades informáticas de que disponemos son limitados, podemos abarcar solo unas pocas parejas de divisas y solo 1 marco temporal, pero, a nuestro juicio, esto es suficiente para tomar conocimiento de los patrones globales. Al analizar los datos, usaremos adicionalmente los datos del artículo anterior.

¿Por qué es tan interesante este tema?

Con mucha frecuencia, las ideas de los programadores de asesores expertos de MetaTrader 4 y MetaTrader 5 implican escribir toneladas de líneas de código y hacer innumerables pruebas y optimizaciones, así como back testing y forward testing. En la mayoría de los casos, no obtenemos lo que queremos. Algunos programadores terminan por aburrirse ante esta situación. Para ellos, el proceso de investigación y búsqueda se convierte en una rutina. Si el trabajo no nos ofrece ni dinero ni ninguna satisfacción moral, es muy probable que acabemos renunciando. Así que es mejor romper con la rutina y empezar a automatizar las acciones que una máquina puede realizar con éxito. Las máquinas no tienen emociones y son trabajadores ideales, a diferencia de los seres humanos. Claro está que una máquina no puede pensar de una forma tan amplia como una persona, pero tiene muchos recursos informáticos y puede implementar algunos procesos de manera más fácil y rápida. Existía la opción de comenzar a escribir una arquitectura de red neuronal propia capaz de evolucionar o comenzar con el enfoque más simple para resolver el problema. Decidimos usar el último enfoque. A pesar de su simplicidad, el proyecto deja espacio para la creatividad y el interés, en contraste con la simple programación de productos MQL. Es buena idea trabajar en una plantilla universal y desarrollarla más agregando gradualmente la funcionalidad necesaria. Podemos empezar con una plantilla simple y después crear nuevas plantillas para un principio de trabajo específico. Así, podemos ahorrarnos la aburrida rutina y continuar con nuestro desarrollo. Bueno, la pereza es el padre del progreso.

La nueva versión del programa de fuerza bruta y la lista de cambios de esta

Solo ha habido un cambio (aparentemente insignificante) en el programa: lo hemos resaltado en la figura con un marco rojo. Hemos tomado esta configuración de la segunda pestaña, donde ha mostrado su mejor faceta. Hemos añadido esta configuración porque, en realidad, influye fuertemente en la calidad de los resultados finales. El hecho es que al realizar el análisis en la primera pestaña, todos los resultados se ordenaron inicialmente según el indicador de calidad. Hemos utilizado como criterio de calidad el factor de beneficio o la esperanza matemática en puntos. Pero el programa no nos ha permitido valorar la forma del gráfico; para ello, hemos usado el factor de linealidad (similitud con una línea recta) como criterio de forma, lo cual nos ha ahorrado la necesidad de verificar cada opción visualmente. Si lo pensamos detenidamente, podemos llegar a la conclusión de que resulta más probable que los gráficos más rectos y suaves den finalmente una opción de alta calidad en la segunda pestaña, y también reducen la cantidad de opciones que serán descartadas por un filtro similar en la segunda pestaña. Para calcular este indicador, necesitamos una segunda pasada. Si este filtro está activo, la velocidad de la fuerza bruta disminuirá unas 2 veces, pero lo importante para nosotros no es la velocidad, sino la calidad total de los resultados primarios obtenidos, porque todo lo que suceda a continuación depende de su calidad.

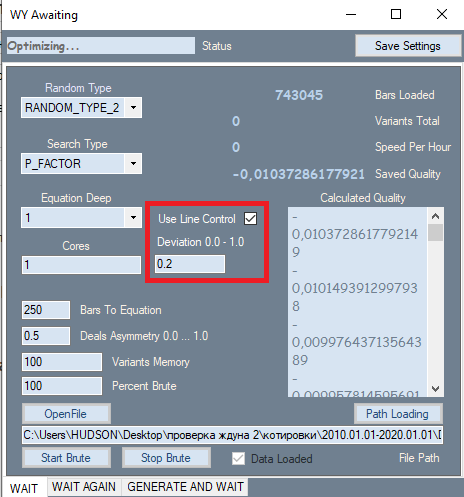
Además del filtro introducido, el polinomio en sí ha cambiado. Ahora el polinomio adopta como argumentos no solo los valores Close[i]-Open[i] de las barras específicas, sino también los siguientes valores:

• Close[i]-Open[i]
• High[i]-Open[i]
• Low[i]-Close[i]
• Low[i]-Open[i]
• High[i]-Close[i]

Ahora la fórmula incluye todos los datos de precio de una barra específica, a diferencia de la anterior versión del programa. Esto aumenta enormemente la complejidad del polinomio, lo cual provoca una disminución en la velocidad de la fuerza bruta. Pero ahora podemos elegir fórmulas de mercado mejores y más eficientes, siempre que haya suficientes recursos informáticos. Por supuesto, podríamos crear otras variables que implicaran estos datos, pero cuando estos valores se usan en el polinomio, también obtenemos la implementación de magnitudes que pueden ser una combinación lineal de los valores anteriores, por ejemplo: 

• C1*(High[i]-Close[i]) + C2*(Low[i]-Close[i]) = NewQuant
• si  C1 = 1 y C2 = -1
• NewQuant = (High[i]-Close[i]) - (Low[i]-Close[i]) =  High[i]-Low[i]
• en los demás casos
• NewQuant = (C1-C3)*(High[i]-Close[i])+(C2+C3)*(Low[i]-Close[i])  +  C3*((High[i]-Close[i]) - (Low[i]-Close[i])) = (C1-C3)*(High[i]-Close[i])+(C2-C3)*(Low[i]-Close[i]) +  C3*(High[i]-Low[i])

Es decir, a partir de una combinación lineal de variables, que a su vez constan de combinaciones lineales de otras variables, podemos componer nuevas variables sin ni siquiera incluirlas en la fórmula básica; el paso más fiable sería intentar no incluir aquellas variables que se puedan formar a partir de otras que ya están en la fórmula. Estas aparecerán durante la selección de coeficientes, dependiendo de los valores de los propios coeficientes.

El nuevo polinomio será mucho más complicado al final:

• Y = Suma(0,NC-1)( C[i]*Variante del producto(x[1]^p[1]*x[2]^p[2]...*x[N]^p[N]) )
  
• Summa(0,N)(p[i])=MaxPowOfPolinom
• NC: número total de términos en el polinomio, igual al número de coeficientes seleccionados
  

donde x [i] son ​​los argumentos que toma el polinomio, y p[i] es el grado al que elevamos este argumento. El grado total de todos los factores constituyentes no debe exceder el número que permitimos para nuestro polinomio, porque ninguna computadora puede manejar expansiones tan complejas. En nuestro caso, casi siempre utilizamos 1 grado, como último recurso 2 o 3, cuando el número de barras de la fórmula se acerca al mínimo. Pero la verdad es que usar grados superiores resulta ineficaz, incluso en los servidores. La potencia de procesamiento es insuficiente.

A continuación, mostramos las opciones para los argumentos. La suma final incluye todas las combinaciones de productos posibles:

1. x[i] =Close[i]-Open[i]
2. x[i] =High[i]-Open[i]
3. x[i] =Low[i]-Close[i]
4. x[i] =High[i]-Open[i]
5. x[i] =High[i]-Close[i]

También deberíamos aclarar por qué realizamos todas estas acciones con el polinomio. La cuestión es que, en última instancia, cualquier sistema se reduce a un conjunto de condiciones. Puede existir una o varias condiciones, lo cual no importa, porque las condiciones son una función lógica. Un conjunto de condiciones se puede transformar finalmente en una expresión booleana que retorne verdadero o falso. Dicha señal solo se puede interpretar como Sí o No. Pero resulta imposible determinar la fuerza de la señal o ajustar esta. Si usamos varios indicadores como señales, podremos ajustar por separado los parámetros de estos indicadores, lo cual causará un cambio en la expresión lógica final o un cambio en la señal, que eventualmente afectará el comercio. No obstante, esto resulta extremadamente inconveniente, porque al cambiar uno u otro parámetro de un indicador en particular, no sabremos cómo afectará al comercio.

La idea principal tras este enfoque era la simplicidad y la eficiencia. ¿Por qué exactamente este enfoque? Tiene varias ventajas:

• Singularidad de la función optimizada
• Intensidad de la señal respecto al valor de la función
• Facilidad de uso
• El único parámetro optimizado es el valor polinomial

Lo más importante es que no necesitamos seleccionar la cantidad de condiciones o su tipo. Esto se debe a que desde el inicio nos hemos acostumbrado a la idea de que en lugar de buscar un conjunto infinito de condiciones, podemos reducir todas estas condiciones a una sola función que dé un número fraccionario positivo o negativo en la salida. Dependiendo de la fiabilidad de una función en particular, podemos necesitar una señal más fuerte en el módulo. En algunas fórmulas, esto provocará una posible escalabilidad. Entendemos por escalabilidad la capacidad de amplificar una señal cuando el número de transacciones disminuye.

En general, la presente investigación, como en el caso de otras personas, lleva a una única conclusión: el deseo de reforzar la señal de entrada provoca una disminución inevitable en el número de transacciones durante un periodo de tiempo fijo. Dicho de forma sencilla: para cualquier función donde un componente aleatorio se encuentre inevitablemente presente, siempre existen puntos con un resultado más predecible que el de otros. Si nuestra función resulta lo suficientemente eficaz, podremos conseguir ciertos indicadores de predictibilidad al aumentar los requisitos respecto a la señal de esta función. Esto, claro está, no ocurre con todas las funciones que cumplen con nuestros requisitos primarios, pero, cuanto más estrictos sean estos requisitos, mejores serán las esperanzas matemáticas de los indicadores de rentabilidad de esas fórmulas que podemos encontrar iterando los coeficientes. Esto resulta igualmente cierto para el aumento de gradiente y otros métodos de búsqueda de patrones, así como para las redes neuronales.

Mucho depende de cuál sea la muestra de datos. Cuanto menor sea la muestra, mayor será la posibilidad de obtener un resultado aleatorio. Entendemos por resultado aleatorio aquel que no funciona o funciona de manera extremadamente ineficaz si el sistema final se pone a prueba con la historia global del símbolo del que se ha realizado la búsqueda del patrón.

Vamos a intentar responder a la pregunta de cómo la calidad del sistema comercial final depende en el futuro del tamaño del área analizada y la cantidad de trabajo requerido para encontrar este sistema. Primero, definimos la fórmula para la esperanza matemática del número de estrategias encontradas durante un intervalo temporal fijo:

• Mn(t) = W(t,F)*Ef(T,N,L)
• Mn -  esperanza matemática del número de estrategias encontradas que cumplen con nuestros requisitos
• W(t,F) = F*t - número resultante de variantes iteradas por unidad de tiempo
• Ef(T,N,L) = ? - eficiencia de la fuerza bruta que depende de la longitud del intervalo, el tipo de cotización, el número requerido de órdenes cerradas y el factor de linealidad necesario si se considera durante la fuerza bruta (este valor es igual a la probabilidad de que los resultados de la variante actual tome los valores necesarios y suficientes)
  
• N - número mínimo de transacciones permitido que resultaría suficiente para nuestra prueba
• L - factor de linealidad máximo permitido (como criterio de control adicional)
• F - frecuencia de iteración de las variantes de las estrategias

Resulta extremadamente difícil determinar la forma de la función Ef, pero podemos valorar aproximadamente qué aspecto tendrá y qué propiedades posee:

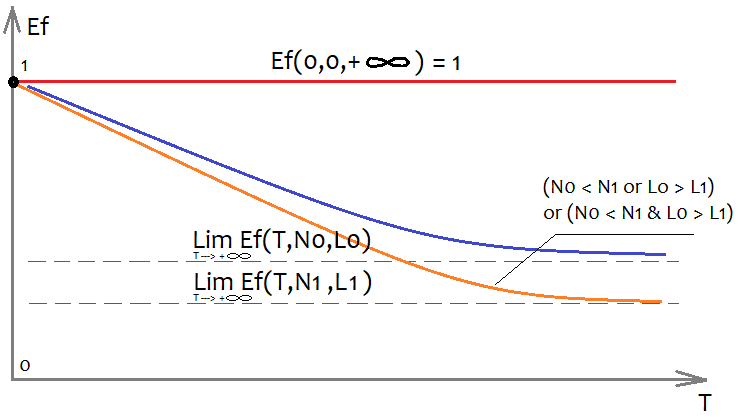
Para poder representar una función multidimensional en un plano, es necesario fijar todos sus argumentos con algún tipo de números, excepto el argumento con el que construimos el gráfico en sí. En nuestro caso, nos interesa la variable T, que indica la duración de la muestra analizada según el tiempo, si consideramos que estamos analizando un único marco temporal. Si omitimos esta suposición, entonces el tamaño de la muestra se podrá tomar como T; este hecho no modificará el aspecto de los gráficos. Obviamente, estamos interesados ​​en cómo los 2 argumentos restantes influirán en el aspecto del gráfico; hemos representado todo en la figura. Cuantas más transacciones queramos en la versión final, menos sistemas encontraremos que cumplan con nuestros requisitos, simplemente porque resulta mucho más fácil encontrar un sistema con menos transacciones. La misma consideración se aplica al factor de linealidad (desviación de una línea recta), con la única diferencia de que el mejor factor de linealidad es el menor (tiende a cero).

Si no fijamos el concepto de calidad del sistema (y este valor puede ser tanto un factor de beneficio como una esperanza matemática), también podremos introducir el concepto de calidad máxima del sistema encontrado. De la misma forma, podemos describir a grandes rasgos de qué depende:

• Mq=Mq(T,N,S)
• S - configuración elegida para la fórmula

Dicho de otra forma: la máxima calidad posible de una estrategia depende directamente de la eficacia de nuestra fórmula, así como de nuestros requisitos y la complejidad del intervalo. Al mismo tiempo, seguimos asumiendo que el comienzo del área es fijo y que cada variación del punto de inicio del entrenamiento es única y ofrece parámetros de inicio únicos. Es decir, seleccionando una fecha de inicio diferente para el área de entrenamiento, obtendremos un valor de eficiencia diferente y otros parámetros, así como la calidad final de los sistemas obtenidos.

También podemos llegar a entender que cada tipo de calidad posee su valor máximo, por ejemplo, la calidad máxima del factor de beneficio es infinita, pero es mejor no usar esta medida para el análisis, porque su valor máximo no está limitado, y por lo tanto, los modelos gráficos en los que tome parte serán más difíciles de comprender. Por consiguiente, vamos a utilizar P_FACTOR, nuestro propio análogo de este valor, que utilizaremos en lugar del original; no es de ninguna manera inferior a él, solo se encuentra en el rango [-1,1].

• P_FACTOR=(Profit-Loss)/(Profit+Loss)

Su máximo es igual a 1, por lo que resulta más adecuado trabajar con él. Aquí está la función que describe el máximo de este valor en función de T (área seleccionada y su muestra).

• Mx=Mx(T)

Si seleccionamos P_FACTOR como indicador o criterio de calidad, entonces Mx(T)=1, si, por ejemplo, elegimos la esperanza matemática, entonces se desconocerá la forma de esta función, pero sabremos que  Mx'(T) > 0 en toda la parte positiva del eje T, es decir, la derivada es positiva en cualquier punto, lo cual significa que la gráfica aumenta todo el tiempo.

Para el factor de beneficio, todo esto se verá así:

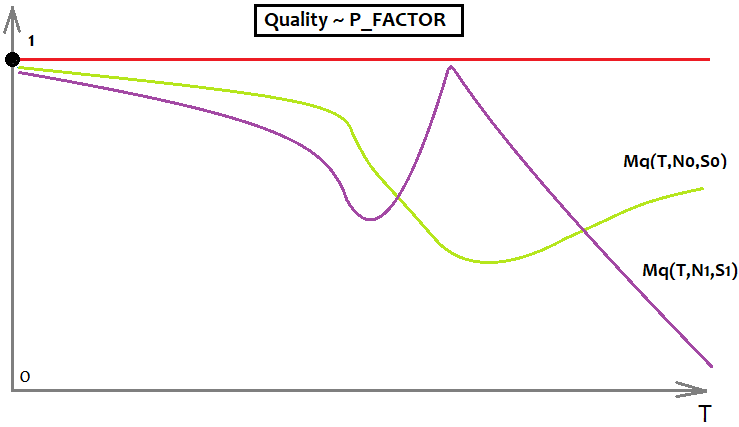
Aquí, por ejemplo, solo se muestra el límite superior del factor de beneficio y 2 gráficos que simbolizan 2 fórmulas diferentes con requisitos distintos. En el gráfico, la fórmula de color lima es mejor, ya que resulta mucho menos propensa a perder calidad cuando "T" tiende al infinito.

Para la esperanza matemática, todo se verá así:

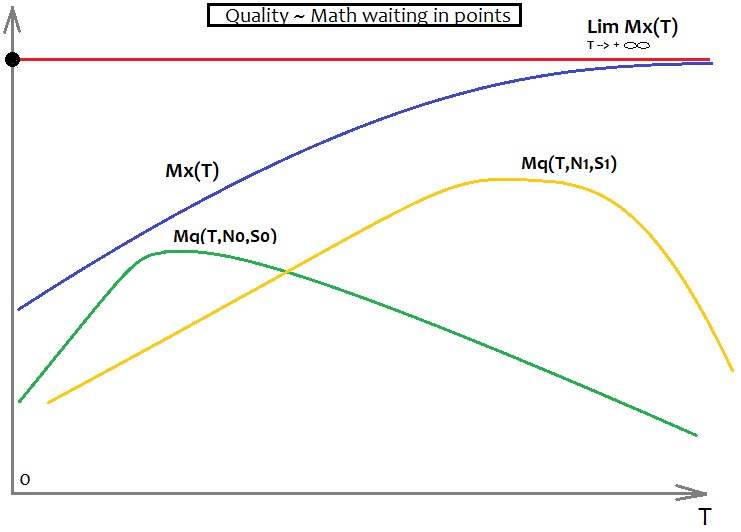
Aquí, nuevamente tenemos dos variantes para dos fórmulas diferentes con requisitos distintos. Además, tenemos Mx(T), que sirve como asíntota: Mq(T,N,S) no puede superar esta barrera. El Mq(T,N,S) ideal coincidirá con el gráfico Mx(T) e indicará que hemos encontrado el "santo grial". Esto, por supuesto, nunca sucederá en la realidad, pero es importante comprenderlo, pues resulta muy importante para tener una actitud correcta respecto al mercado, si, por supuesto, realmente queremos comprender qué es el mercado y valoramos nuestro tiempo.

En fórex, como en cualquier otra bolsa, resulta más correcto y preciso operar solo con los conceptos de la teoría de la probabilidad. Incluso escribiremos a continuación algunas reglas básicas de análisis matemático en fórex:

• Casi todas las cantidades no son fijas y son sustituidas por sus esperanzas matemáticas.
• Las esperanzas matemáticas de los valores de la muestra más grande tienden al resultado de la muestra global
• Utilice las probabilidades con mayor frecuencia

La fiabilidad de los datos del área no es más que una frecuencia de muestreo. Cuanto mayor sea la muestra, más amplio será el conjunto de datos de entrada, y más justa será la fórmula final. El hecho es que, como la muestra tiende al infinito, el resultado final tenderá a un valor límite fijo.

Los cambios en la plantilla y para qué son necesarios

Como hemos mejorado la lógica, necesitaremos modificar las funciones en la plantilla para garantizar que estas funcionen correctamente y obtengan los nuevos parámetros. La implementación de estas funciones resulta idéntica tanto en el programa como en el código de la plantilla. Las funciones originales se desarrollaron para trabajar con un valor, pero hemos añadido 4 más, por lo que tendremos que mejorarlas. En primer lugar, estos cambios deberían proporcionar fórmulas de mayor calidad; no sabemos las mejoras que ofrecerán los cambios, pero resulta obvio que todo mejorará. Cuantos más datos se usen en una fórmula, mayor será su capacidad de búsqueda.

Durante la redacción del artículo, encontramos un fallo en el código: las combinaciones de factores pueden repetirse, mientras que el orden de estos factores resulta caótico por las peculiaridades de la función que implementa el polinomio multidimensional. Esta función crea un árbol de llamadas, pero no puede controlar las permutaciones de elementos. Podemos evitar esto de dos formas:

1. Controlando todas las posibles permutaciones de factores
2. Compensando el número de factores duplicados en una fórmula dividiendo el coeficiente total por su número.

Nos decantamos por la segunda opción. La desventaja de este enfoque es que el coeficiente promedio tenderá a 0,5. Al menos, los factores no resultarán inútiles. Para este artículo, usamos un polinomio de grado 1 que no se ve influido por el error. Podemos calcular sin dificultad el número de combinaciones para un multiplicador con un grado total fijo:

• Comb=n!/(n-k)!
• n - es el número de posibles multiplicadores independientes
• k - es el grado total del término final

A continuación, mostramos la implementación de esta fórmula en el código:

double Combinations(int k,int n)
   {
   int i1=1;
   int i2=1;
   for ( int i=n; i<n-k; i-- ) i1*=i;
   for ( int i=n-k; i>1; i-- ) i2*=i;
   return double(i1/i2);
   }

Y así es como se transformó la función principal del polinomio final; los cambios se relacionan con un polinomio unidimensional, porque ahora no dependemos de 1 parámetro de barra, sino de 5. Obviamente, tenemos 4 matrices iniciales, pero en su forma básica: los datos de precios no se pueden utilizar solo como datos, necesitamos transformarlos en algunos valores más flexibles, como son la diferencia entre precios vecinos. Los precios vecinos pueden ser tanto las aperturas como los cierres de las barras, lo que sea, siempre que el valor final cuantificado contenga la diferencia en los precios de cierre.

double Val;
int iterator;
double PolinomTrade()//Polynomial for trading
   {
   Val=0;
   iterator=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Open[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Open[i+1]-Low[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(High[i+1]-Close[i+1])/Point;
         iterator++;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*(Close[i+1]-Low[i+1])/Point;
         iterator++;
         }

      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }
   }


///Fractal calculation of numbers
double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC,int deepStart,double Val0=1.0)//intermediary fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      } 
      
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Open[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Open[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Open[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(High[i+1]-Close[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(High[i+1]-Close[i+1])*Val0/Point;
         NumC++;
         }
      }

   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Low[i+1])*Val0;
         Deep(Ci0,Nums,deepC-1,deepStart,ValW);
         } 
      else 
         {
         ValStart+=(Ci0[NumC]/Combinations(deepStart,Nums*5))*(Close[i+1]-Low[i+1])*Val0/Point;
         NumC++;
         }
      }
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ ) Deep(Ci0,Nums,i+1,i+1);
   }

La función para el cálculo del tamaño de la matriz de coeficientes también se ha visto sometida a pequeños cambios. Simplemente, el ciclo es ahora 5 veces más largo:

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums*5; i++ )
      {
      if (deepC > 1) DeepN(Nums,deepC-1);
      else NumCAll++;
      }
   }

void CalcDeepN(int Nums,int deepC=1)
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ ) DeepN(Nums,i+1);
   } 

Necesitamos todas estas funciones para implementar el polinomio final. La POO resulta redundante aquí, pues resulta mejor utilizar funciones similares para construir un árbol de llamadas, especialmente para las fórmulas que no se pueden escribir explícitamente (como las expansiones multidimensionales). Resulta bastante difícil comprender su lógica, pero es posible. Los análogos de estas funciones se implementan dentro del programa C#. Desafortunadamente, los asesores adjuntos no tienen este código, pero sí que utilizan la versión anterior en su interior. Resulta bastante eficiente, aunque bastante torpe. El programa todavía se encuentra en la etapa de prototipo; lo mejoraremos y completaremos más adelante. Hasta ahora, el programa no ha resultado adecuado para analizar los patrones globales en PC normales. Todavía existen muchos fallos menores en el lado de nuestro programa, y seguimos detectando errores y corrigiéndolos. Entonces, el programa va adquiriendo una buena funcionalidad.

Análisis de los patrones encontrados

Una vez más, gracias a que nuestras capacidades informáticas resultan limitadas, al igual que el tiempo disponible, hemos tenido que limitar la cantidad de datos, pero aún así, será suficiente para sacar algunas conclusiones. En particular, para analizar los patrones globales, ha sido necesario usar solo gráficos de horas y solo un tiempo limitado para el análisis. Todas las pruebas se realizarán en MetaTrader 4. El caso es que la esperanza matemática de los patrones encontrados está al nivel del spread, y en MetaTrader 5, incluso cuando utilizamos la opción Configuración personalizada para el símbolo de prueba, el simulador utiliza un spread no inferior al valor registrado en la historia. El valor se ajusta en función de los datos de ticks reales del bróker actual y el margen en el área seleccionada. Esto se hace así para proteger al usuario contra resultados de prueba demasiado optimistas. Necesitábamos abstraernos de estos mecanismos, para lo cual elegimos el simulador de MetaTrader 4. 

Empezaremos con los patrones globales. Su esperanza matemática ha sido apenas de unos 8 puntos. Esto es así porque hemos tomado 50 velas para la fórmula, y solo hemos probado alrededor de 200,000 variantes en la primera pestaña para cada pareja de divisas y solo en 1 núcleo. Si el servidor fuera bueno, resultaría mucho más sencillo. Por ahora, seguimos así. La próxima versión del programa dependerá menos de la potencia computacional. En esta rama, queremos concentrarnos no solo en la esperanza matemática en puntos de los resultados, sino también en cómo su rendimiento influye en su comportamiento futuro.

Comenzaremos con la pareja EURUSD H1. Todo esto se pueso a prueba en el área 2010.01.01-2020.01.01 para tener la oportunidad de encontrar un patrón global:

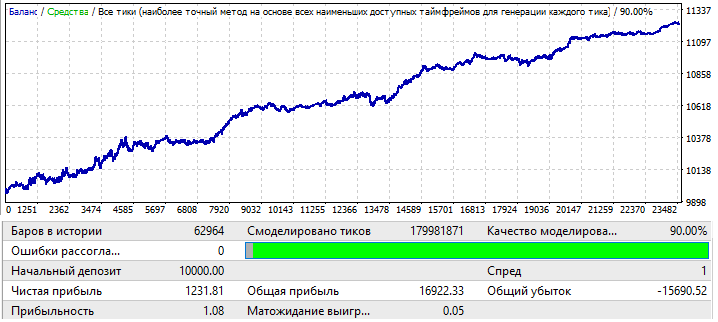
Los resultados no son nada del otro mundo, pero esto es todo lo que hemos logrado sacar de la pareja en el intervalo de tiempo dado. Podemos ver un patrón global, aunque no sea tan pronunciado considerando el factor de beneficio, pero sí que vemos que algo funciona aquí. Para la fuerza bruta, hemos utilizado 50 velas en la fórmula. En realidad, el resultado no resulta tan bueno como podríamos esperar, pero lo necesitamos. Más tarde, veremos por qué. Vamos a poner a prueba el mismo segmento en el periodo forward 2020.01.01-2020.11.01, para comprender su futuro rendimiento:

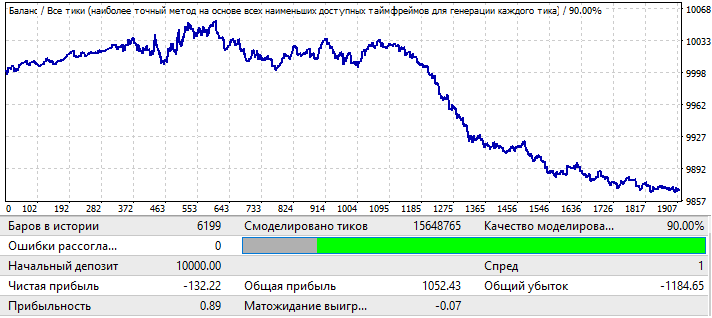
Esto no es lo que esperábamos, pero resulta bastante comprensible. Resulta que este análisis no es suficiente para ganar algo con la continuación del patrón. Y, en general, creemos que si analizamos los patrones globales, solo será partiendo de la base de que esto funcione durante al menos varios años más, en caso contrario, tal análisis no tiene ningún sentido. Al principio del gráfico, podemos ver que el patrón continúa funcionando, pero después de seis meses realmente se invierte; en general, tal análisis podría ser suficiente para comerciar durante varios meses, si, por supuesto, encontráramos parámetros lo suficientemente buenos para la prueba inicial. En este caso, hemos realizado el análisis según el valor P_Factor. Este valor es similar al Factor de beneficio, con la única diferencia de que toma valores [0...1]. 1 - 100% del beneficio. En la primera pestaña, el máximo de este indicador fue de aproximadamente 0.029. En consecuencia, el valor medio de todas las variantes encontradas fue de aproximadamente 0,02, lo cual dio un resultado similar.

El siguiente gráfico EURCHF:

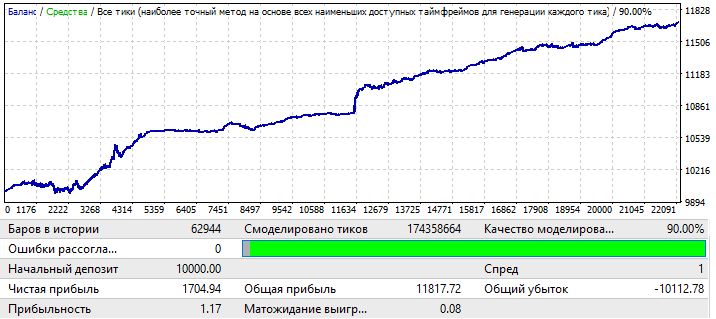
El resultado máximo para las variantes del gráfico en la primera pestaña de este programa fue de aproximadamente 0.057; su grado de predictibilidad es 2 veces superior al del gráfico anterior, lo cual también influyó en el Factor de Beneficio final, que en realidad es 0.09 más alto que el anterior. Veamos si la mejora en los indicadores globales afecta al periodo futuro:

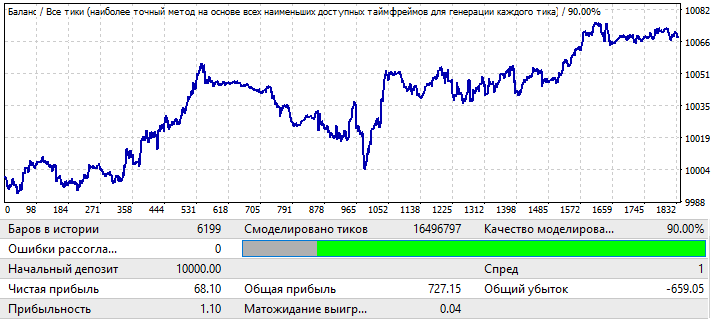
Podemos observar que el patrón prosigue durante todo el año; quizá no sea tan suave, es cierto, y el factor de beneficio resulta menor, pero, no obstante, podemos sacar conclusiones preliminares. De hecho, el factor de beneficio es menor porque existen áreas bastante grandes con un fuerte aumento en el balance en la prueba global, y han aumentado el factor de beneficio final. Y en los próximos años, si lo probamos, seguro que resultará prácticamente igual. La conclusión preliminar es que la mejora de la calidad y la apariencia del gráfico ha influido en su rendimiento futuro, sin importar qué pareja de divisas sea, pero es importante que, en este caso, nuestra configuración sea más aplicable a esta pareja de divisas en particular: esto ha dado el resultado. Si observamos con atención, el motivo de las ondas en el gráfico se puede ver en la prueba global, donde las fluctuaciones de equilibrio han aumentado considerablemente en los últimos años, y esto es solo su continuación.

Pasando al gráfico USDJPY:

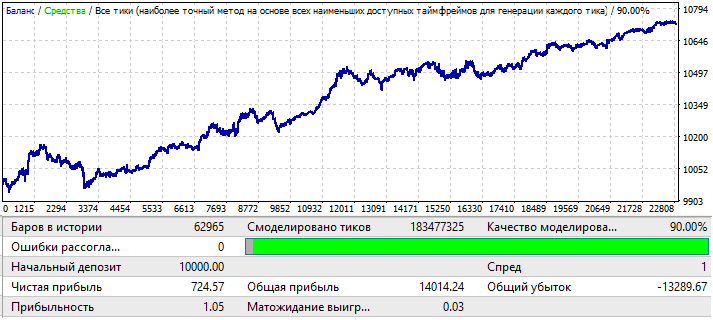
El gráfico es el más feo de todos, veamos qué ocurre en el periodo forward:

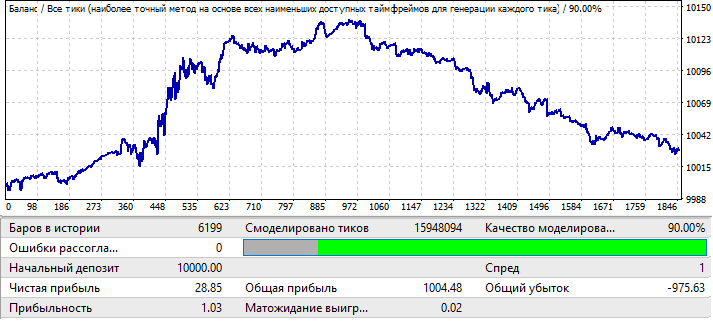
Parece estar en una zona positiva, pero su segunda mitad resulta muy similar a la del primer gráfico (EURUSD H1), que también comenzó con un movimiento ascendente, luego viró y tuvo un movimiento descendente casi en línea recta. Por ello, las conclusiones en el primer gráfico y aquí son las mismas. La calidad del resultado final no es lo suficientemente alta. Sin embargo, podríamos tener la esperanza de un par de meses de transacciones rentables con este patrón, siempre que la esperanza matemática y el factor de beneficio sean lo suficientemente buenos.

El último gráfico, USDCHF:

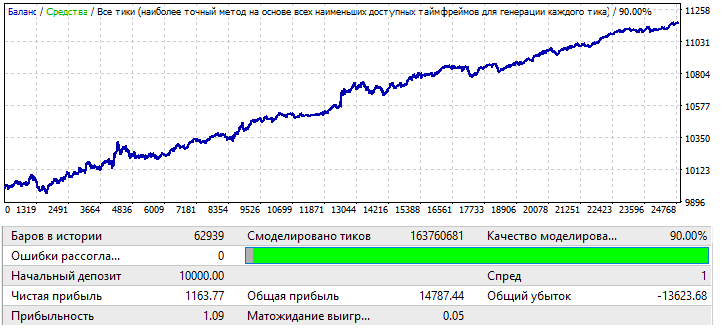
No es muy impresionante. Vamos a echar un vistazo al periodo forward:

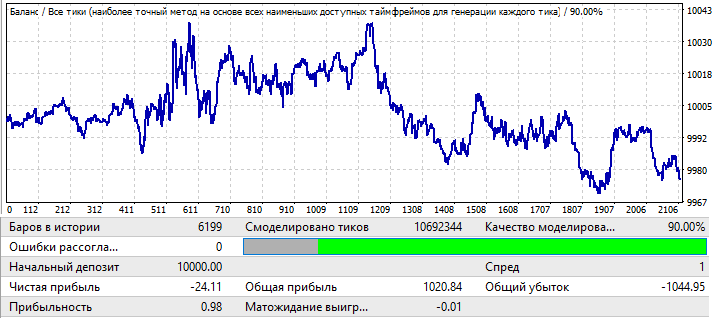
La imagen que vemos es la misma que en los otros gráficos, salvo por EURCHF. La eficiencia se mantiene hasta mediados de año; luego hay un viraje y el patrón se invierte.

Podemos extraer las siguientes conclusiones preliminares:

1. Claramente, EURCHF fue el mejor gráfico
2. EURCHF ha superado a todos tanto en el área de entrenamiento como en la prueba forward
3. En todos los gráficos, el patrón funciona hasta mediados de año, excepto para EURCHF.

De todo esto, podemos deducir que los indicadores de calidad en el área de entrenamiento influyen directamente en lo que vemos en el periodo forward, en particular, un aumento en el factor de beneficio del resultado final puede indicar que el resultado es mucho menos aleatorio que en otros gráficos que pueden indicar el hallazgo exitoso de un patrón global. Hay un dicho: "entre broma y broma, la verdad asoma". Podemos adaptar esto a fórex o cualquier otro mercado: "en entre patrón y patrón, la verdad asoma". Cuanto más fuertes sean los indicadores de prueba, mayor será esta porción de verdad.

Ahora, vamos a intentar modificar el tamaño de la muestra. Tomaremos 1 año. Intervalo 2017.01.01-2018.01.01 EURJPY H1. Y veremos cómo se comporta el patrón durante un mes en el futuro:

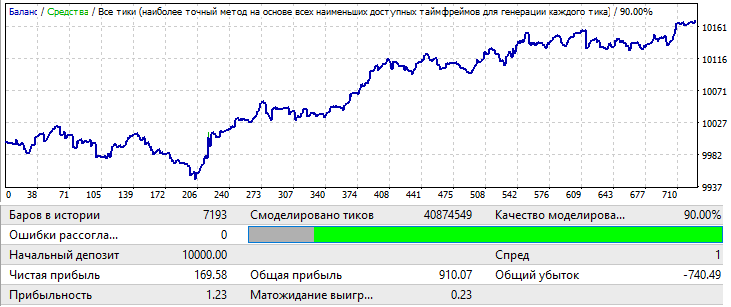
El gráfico no tiene muy buen aspecto, pero el factor de beneficio final y la esperanza matemática son ciertamente más altos que los de las variantes de 10 años. La muestra es 12 veces menor que las variantes iniciales; no obstante, estos datos también son datos y no debemos ignorarlos.

Tomaremos un periodo forward durante un mes en el futuro. Intervalo 2018.01.01-2018.02.01:

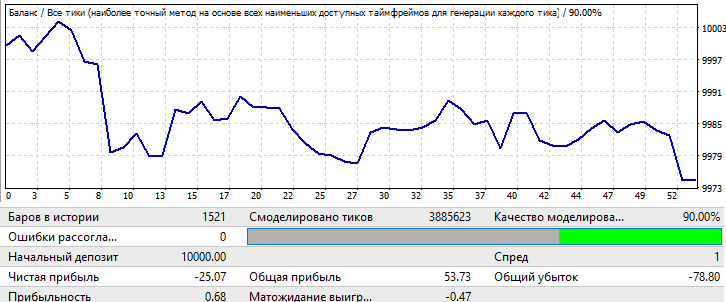
Este es solo un ejemplo para aclarar los razonamientos que veremos más adelante. Aquí el patrón se invierte casi de inmediato. Por desgracia, no podemos ofrecer más datos. Los cálculos y la configuración del software llevan mucho tiempo. De todas formas, esta información debería resultar suficiente para el primer análisis.

Análisis de la información

Una vez que los asesores han sido puestos a prueba, podemos sacar algunas conclusiones:

• La construcción de robots que implementen leyes globales y tengan una duración de trabajo suficiente es posible usando una simple iteración de números
• La duración del trabajo en el futuro depende directamente del tamaño de la muestra de datos
• La duración del trabajo depende directamente de la calidad de la prueba en el área de entrenamiento
• Al poner a prueba el periodo forward en todos los gráficos, la operatividad de los patrones globales se mantiene al menos durante 2-3 meses
• La probabilidad de encontrar un patrón que funcione durante al menos algunos años tiende al máximo cuando la calidad del resultado final en el área de fuerza bruta tiende al 100%
• Para buscar patrones globales, las diferentes configuraciones funcionan de manera distinta para diferentes parejas de divisas

En lo que respecta a los patrones locales, por ejemplo, de mes-año, aquí todo resulta totalmente diferente. En el último artículo analizamos patrones locales, pero sin utilizar las innovaciones introducidas por esta versión del programa. Cualquier modernización nos permite tener una visión más clara de los mismos problemas, eliminando información innecesaria. En general, con respecto a los patrones locales, podemos decir que:

• Siempre debemos jugar con el cambio de patrón
• Podemos usar martingale, pero con cuidado

Es decir, cuanto mayor sea la muestra, más tiempo permanecerá operativa en el futuro, y viceversa, cuanto menor sea la muestra, más rápido virará el patrón en el futuro, claro está, siempre que no haya optimización forward, que, por cierto, planeamos añadir más tarde, pero no en el próximo artículo: por ahora, hay tareas más prioritarias. En este caso, la inversión del patrón si aparece un área corta sucederá con toda garantía. De todas estas ideas, podemos extraer conclusiones que dictan 2 tipos de comercio:

1. La explotación de patrones globales
2. La explotación de patrones locales

En el primer caso, cuanto mayor sea el área de entrenamiento, más tiempo funcionará el patrón. No obstante, es mejor buscar nuevas fórmulas cada 2 o 3 meses. En cuanto a los patrones locales, las búsquedas deben realizarse todas las semanas mientras el mercado esté congelado. La calidad de los resultados no será alta, pero no debemos preocuparnos por el resultado, al menos podremos obtener algunos beneficios.

Ahora, intentaremos resumir todos los datos obtenidos como resultado de la investigación sobre patrones de diferentes escalas. Para hacer esto, presentaremos una función que muestra la esperanza matemática del beneficio de una orden concreta, así como una función que muestra el factor de beneficio, partiendo de que conozcamos el futuro, o al menos parcialmente. Podemos añadir cualquier otra función que caracterice métricas menos importantes. Un espacio de eventos o una variable aleatoria serán todas las posibles variantes de desarrollos de eventos en el futuro. Ahora, solo conocemos lo siguiente:

• Existen innumerables desarrollos posibles para la barra "F" en el futuro (se haya abierto una orden en ella o no)
• Para todas las variantes de desarrollo del futuro en las que se ha abierto una orden en una barra específica, esta orden tendrá una esperanza matemática en puntos y un factor de beneficio (imaginaremos que estamos realizando una prueba en una barra; solo las siguientes barras son siempre diferentes para cada orden)
• Para cada fórmula, todas estas cantidades serán diferentes
• Para las áreas con diferentes fechas de inicio en el futuro (el comienzo del futuro coincide con el final del área de entrenamiento) y diferente duración del área de entrenamiento (que equivale a diferentes fechas de inicio del área de entrenamiento), los parámetros finales buscados tomarán valores únicos

Todas estas afirmaciones se pueden transformar en fórmulas matemáticas. En lenguaje matemático, se escribirá así:

• MF=MF(T,I,F,S,R) — esperanza matemática de las órdenes en una barra específica en el futuro.
• PF=PF(T,I,F,S,R)  — factor de beneficio de las órdenes en una barra específica en el futuro. 
• T  — duración del área de entrenamiento (en este caso, el tamaño de la muestra o el número de barras, que es el mismo)
• I  — fecha de finalización del área de entrenamiento
• F  — número de la barra en el futuro, contando desde la fecha de finalización del entrenamiento
• S  — polinomio o algoritmo único (si el patrón se ha encontrado manualmente o programando un nuevo robot)
• R  — resultados logrados usando un polinomio o estrategia en particular (en otras palabras, cómo de bien se hemos realizado el trabajo para optimizar nuestra señal), incluyen el número de transacciones en el área de entrenamiento e indicadores como la esperanza matemática, el factor de beneficio y otros parámetros.

Usando como base los datos obtenidos por fuerza bruta en diferentes instrumentos y diferentes fechas, podemos dibujar las funciones anteriores en un gráfico (si usamos "F" como argumento):

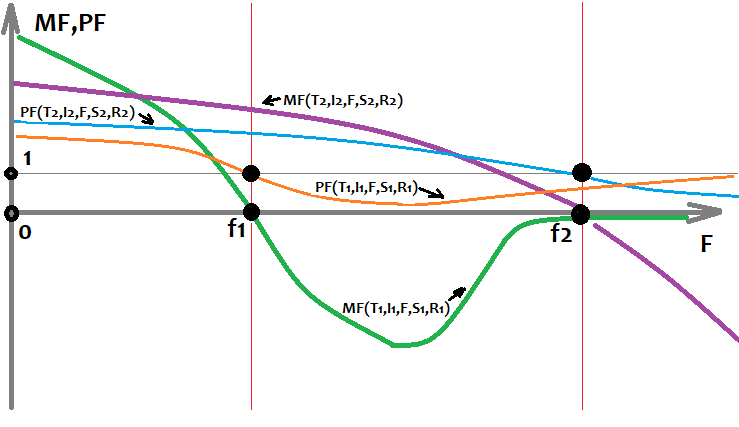
Este gráfico muestra 2 variantes únicas de estrategias que se han entrenado en diferentes áreas usando configuraciones distintas y han logrado diferentes resultados. Existen innumerables variantes de este tipo, pero todas tienen una duración y calidad del patrón original diferentes. Debemos entender que esto siempre va seguido de una inversión del patrón. Es posible que esta regla no funcione solo para patrones muy fuertes. Pero incluso para ellos, siempre existe el riesgo de que el gráfico vire, tal vez dentro de 5 años, pero lo hará. Las fórmulas más estables serán las que se encuentren a partir de la muestra más grande. Si las fórmulas se encuentran manualmente y se originan a partir de alguna teoría, dichas fórmulas en el futuro podrán funcionar indefinidamente. No obstante, no tenemos tales garantías al usar fuerza bruta u otros métodos de aprendizaje automático. Todo lo que tenemos es una valoración del tiempo de operación, que solo se puede realizar usando como base datos estadísticos. Este análisis resulta posible utilizando nuestro programa; no obstante, no puede ser implementado por una sola persona, debido a las limitaciones de tiempo y potencia computacional.

¿Qué es lo próximo?

El análisis de patrones globales ha demostrado que la potencia de una computadora ordinaria no es suficiente para realizar un análisis profundo y de alta calidad de grandes muestras (digamos, de 10 años o más), y de hecho, para una búsqueda de alta calidad, resulta necesario tomar muestras muy grandes. Quizá si ejecutamos el programa durante un par de meses en el servidor, entonces encontremos una o 2 buenas variantes, pero esta no es una tarea para una computadora estacionaria, eso seguro. Por consiguiente, necesitamos mejorar la eficiencia y al mismo tiempo aumentar la velocidad de iteración de las variantes. A nuestro juicio, podemos seguir desarrollando el programa de la siguiente manera:

1. Añadiendo la posibilidad de analizar las ventanas fijas del tiempo del servidor
2. Añadiendo la posibilidad de analizar en días fijos de la semana
3. Añadiendo la posibilidad de generar aleatoriamente ventanas temporales
4. Añadiendo la posibilidad de generar aleatoriamente una matriz de días de la semana permitidos para el comercio
5. Mejorando el segundo grado de análisis (pestaña de optimización), en concreto, la implementación de los cálculos multinúcleo y la corrección de errores del optimizador.

Los cambios enumerados según la idea, deberían aumentar en gran medida tanto la velocidad del programa como la variabilidad y calidad de las variables encontradas, y ya, finalmente, asegurar la disponibilidad de herramientas más o menos normales para el análisis de mercado.

Conclusión

Esperamos que el artículo haya sido de alguna utilidad para el lector. Nos ha parecido muy importante hablar de los patrones globales: un tema extremadamente difícil, ya que la potencia del programa es aún insuficiente para este tipo de análisis. Si tuviéramos un buen servidor de 30 núcleos, no resultaría difícil. En mejores condiciones,sería necesario dedicar mucho más tiempo a este análisis, tal vez un orden de magnitud temporal mayor.

Con suerte, resultará posible aumentar la potencia computacional en el futuro. El próximo artículo será más interesante. También hemos incluido algo de matemáticas para una mejor comprensión general, porque sin dicha comprensión, no podemos realizar un análisis efectivo incluso usando software útil; eso por no hablar de la iteración manual, la optimización, etc.

El ideal general del artículo era proporcionar información a aquellos que aún no han conseguido alcanzar siquiera estos pequeños resultados manualmente. Esta debería servir de ayuda a la hora de comprender los conceptos básicos de las ideas subyacentes que se usan al desarrollar robots.

Por último, querríamos destacar que no nos parece tan importante cómo se encuentra el patrón, si lo hemos encontrado manualmente o con la ayuda de una máquina. Si un patrón tiene ciertos indicadores de rentabilidad, entonces podremos considerarlo completamente funcional. De una forma u otra, ciertos parámetros de regularidad nos ofrecen algunas predicciones, al menos por un tiempo mínimo en el futuro, y este tiempo, grande o pequeño, resulta suficiente para obtener beneficios. Además, no deberíamos pensar que si hemos encontrado algún tipo de patrón de trabajo, este vaya a seguir funcionando. Para confirmar esto, necesitamos una muestra muy grande con un rendimiento comercial muy bueno en toda la muestra y un número suficiente de órdenes en relación con el tamaño de la muestra. Una cosa es encontrar un patrón y otra valorar su tiempo estimado de funcionamiento en el futuro. En nuestra opinión, esta cuestión resulta fundamental. ¿Qué sentido tiene buscar un patrón si no sabemos cuánto tiempo funcionará y qué tan bien lo hará? Sí, también hemos decidido compartir nuestro programa con todos, lo encontrará en el archivo. Asimismo, podrá hacer las preguntas que considere oportunas sobre la configuración por mensaje privado.