Características del Wizard MQL5 que debe conocer (Parte 26): Medias móviles y el exponente de Hurst

Introducción

Continuamos esta serie sobre técnicas con el Asistente MQL5 que se centran en métodos alternativos en el análisis financiero de series temporales en beneficio de los traders. Para este artículo, consideramos el Exponente de Hurst. Se trata de una métrica que nos indica si una serie temporal tiene una alta autocorrelación positiva o una autocorrelación negativa a largo plazo. Las aplicaciones de esta medida pueden ser muy amplias. ¿Cómo lo utilizaríamos? Bien, en primer lugar, calcularíamos el exponente de Hurst para determinar si el mercado está en tendencia (lo que normalmente nos daría un valor superior a 0,5) o si el mercado está en reversión de la media o en tendencia alcista (lo que nos daría un valor inferior a 0,5). Para este artículo, ya que estamos en una «temporada de mirar medias móviles» dado el último par de artículos, casaremos la información del Exponente de Hurst con la posición relativa del precio actual a una media móvil. La posición relativa del precio con respecto a una media móvil puede ser indicativa de la próxima dirección del precio, con una salvedad importante.

Tendría que saber si los mercados están en tendencia o si están oscilando (inversión de la media). Dado que podemos utilizar el Exponente de Hurst para responder a esta pregunta, se deduce que simplemente observaríamos dónde se encuentra el precio en relación con la media y, a continuación, realizaríamos una operación. Sin embargo, incluso esto puede ser un poco precipitado, dado que los mercados oscilantes tienden a estudiarse mejor en periodos de tiempo más cortos que los mercados tendenciales, que son más evidentes cuando se observan en periodos de tiempo mucho más largos. Por este motivo, necesitaríamos dos medias móviles distintas para sopesar la posición relativa del precio antes de poder evaluar una condición definitiva. Se trata de una media rápida para los mercados con oscilaciones o cambios medios, y de una media lenta para los mercados con tendencia, determinada por el exponente de Hurst. Así, cada tipo de mercado, tal y como lo establece el Exponente, tendría su propia media móvil. Por lo tanto, este artículo se centrará en el Análisis de rango reescalado, como un medio para estimar el exponente de Hurst. Revisaremos el proceso de estimación paso a paso y concluiremos con una clase de señal experta que implementa este exponente.

División de las series temporales

Según Wikipedia, la fórmula del Exponente de Hurst se presenta como:

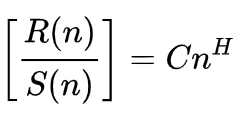
Donde:

• n : Es el tamaño de la muestra analizada.
• R() : Es el rango reescalado de la muestra.
• S() : Es la desviación estándar de la muestra.
• C : Es una constante.
• H : Es el exponente de Hurst.

Esta fórmula nos presenta inherentemente dos incógnitas, y la solución para encontrar tanto la constante C como el exponente buscado H es hacer una regresión de múltiples segmentos del conjunto muestreado. H es una potencia que aritméticamente significa que tomamos logaritmos en ambos lados de la ecuación para poder resolver H, y este es nuestro último paso, como veremos a continuación. Entonces, el primer paso es identificar o definir segmentos dentro de los datos muestreados.

El número mínimo de segmentos que podemos obtener de cualquier muestra es 2. El máximo que podemos obtener de una muestra depende del tamaño de la muestra, y la fórmula rudimentaria es el tamaño de la muestra dividido por 2. Ahora estamos buscando dos incógnitas, lo que significa que necesitamos más de un par de puntos para tener el mínimo de 2 ecuaciones como es la práctica. El número de ecuaciones o pares de puntos que podemos generar a partir de una muestra está dado por la mitad del tamaño de la muestra menos 1. Por lo tanto, un tamaño de muestra de 4 puntos de datos solo generará un par de puntos para la regresión, lo que claramente no será suficiente para encontrar el exponente de Hurst y la constante C.

Sin embargo, una muestra con 6 puntos de datos puede generar los 2 pares mínimos de puntos que podrían usarse para estimar el exponente y la constante. En la práctica, queremos que el tamaño de la muestra sea lo más grande posible porque, como se menciona en la definición, el exponente de Hurst es una propiedad "de largo plazo". Además, la fórmula de Wikipedia compartida anteriormente se aplica a las muestras a medida que n tiende a infinito. Por lo tanto, es importante que el tamaño de la muestra sea lo más grande posible para poder estimar un exponente de Hurst más representativo.

La división de la muestra en segmentos, donde cada conjunto de división/segmento genera un único par de puntos, es el "primer paso". Utilizo el "primer paso" porque en el enfoque que utilizamos para este artículo, como se muestra en el código fuente a continuación, no dividimos unilateralmente los datos y definimos todos los segmentos a la vez antes de pasar al siguiente paso, sino que para cada división calculamos el par de puntos que se asignan a partir de esa división de muestra. A continuación se muestra parte del código fuente que realiza esta operación:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   double _std = Data.Std();
   if(_std == 0.0)
   {  printf(__FUNCSIG__ + " uniform sample with no standard deviation! ");
      return;
   }
   int _t = Fraction(Data.Size(), 2);
   if(_t < 3)
   {  printf(__FUNCSIG__ + " too small sample size, cannot generate minimum 2 regression points! ");
      return;
   }
   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      int _rows = Fraction(Data.Size(), t);
      _segments.Init(_rows, t);
      int _r = 0, _c = 0;
      for(int s = 0; s < int(Data.Size()); s++)
      {  _segments[_r][_c] = Data[s];
         _c++;
         if(_c >= t)
         {  _c = 0;
            _r++;
            if(_r >= _rows)
            {  break;
            }
         }
      }
      
      ...

   }
   ...
}

Entonces, utilizamos una matriz en cada paso para registrar los segmentos no superpuestos de la muestra de datos. En la iteración general, comenzamos con el tamaño de segmento más pequeño, 2, y luego avanzamos hasta la mitad del tamaño de la muestra de datos. Es por esto que tenemos un paso de validación para el tamaño de la muestra de datos, donde verificamos y vemos si la mitad de su tamaño es al menos 3. Si es menor que tres, entonces no tiene sentido calcular el exponente de Hurst, ya que no podemos obtener al menos dos pares de puntos necesarios para la regresión en el último paso.

El otro paso de validación que realizamos en la muestra de datos es asegurarnos de que haya variabilidad entre los datos, esto se debe a que una desviación estándar de cero conduce a un número que no es válido o una división cero.

Ajuste de la media

Una vez que tenemos un conjunto de segmentos en una iteración dada (donde el número total de iteraciones está limitado a la mitad del tamaño de la muestra), necesitamos encontrar la media de cada segmento. Dado que nuestros segmentos están en una matriz, por filas, cada fila se puede recuperar como un vector. Una vez armados con el vector de cada fila podemos obtener fácilmente la media gracias a la función de media incorporada del vector y esto ahorra la necesidad de codificar innecesariamente. Luego, la media de cada segmento se resta de cada punto de datos en su segmento respectivo. Esto es lo que se llama ajuste de la media. Es importante en el proceso de análisis de cambio de escala de rango por varias razones.

En primer lugar, normaliza todos los datos en cada segmento, lo que garantiza que el análisis se centre en su fluctuación alrededor de su media en lugar de verse influenciado por los valores absolutos de cada punto de datos en un segmento. En segundo lugar, esta normalización sirve para reducir el sesgo hacia distorsiones y valores atípicos, que podrían dificultar la obtención de una escala de rango más representativa.

Esto además garantiza la coherencia entre todos los segmentos, de modo que sean más comparables que si se consideraran los valores absolutos sin esta normalización. Realizamos este ajuste dentro de MQL5 a través del siguiente código fuente:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
      ...

      vector _means;
      _means.Init(_rows);
      _means.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  vector _row = _segments.Row(r);
         _means[r] = _row.Mean();
      }
      
      ...
   }
   ...
}

Los tipos de datos matriciales y vectoriales son nuevamente indispensables no sólo para encontrar las medias, sino también para acelerar la normalización.

Desviación acumulada

Una vez que tenemos los segmentos ajustados a la media, debemos sumar estas desviaciones de la media para cada segmento para obtener las desviaciones acumuladas de cada segmento. Esto puede tomarse como una forma de reducción de dimensionalidad que sirve como base para el análisis a escala de rango. Realizamos esto de la siguiente manera dentro de nuestro código fuente:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      
      ...

      matrix _deviations;
      _deviations.Init(_rows, t);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _deviations[r][c] = _segments[r][c] - _means[r];
         }
      }
      vector _cumulations;
      _cumulations.Init(_rows);
      _cumulations.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _cumulations[r] += _deviations[r][c];
         }
      }

      ...

   }
   ...
}

Entonces, para recapitular brevemente, para cada valor "t" creamos un grupo de segmentos que dividen nuestra muestra de datos. De cada muestra, obtenemos su media y la restamos de los puntos de datos dentro del segmento respectivo. Esta resta sirve como una forma de normalización y, una vez realizada, esencialmente tenemos una matriz de puntos de datos donde cada fila es un segmento de la muestra de datos original. Como método para reducir las dimensiones de los segmentos, sumamos estas desviaciones de sus respectivas medias para que un segmento multidimensional nos dé un único valor. Esto implica que después de realizar las acumulaciones de desviación en la matriz, nos quedamos con un vector de sumas, y este vector está etiquetado como '_cumulations' en nuestra fuente anterior.

Rango reescalado y gráfico logarítmico

Una vez que tenemos las acumulaciones de desviaciones en todos los segmentos de un vector, el siguiente paso es simplemente encontrar el rango, que es la diferencia entre la desviación total más grande y la desviación total más pequeña. Tenga en cuenta que cuando registramos las desviaciones de cada punto de datos en los segmentos anteriores, no registramos el valor absoluto. Simplemente registramos el valor del segmento menos la media del segmento. Esto implica que es muy fácil que nuestras acumulaciones sumen cero. De hecho, esto es algo que debería someterse a una verificación de validación antes de continuar con los cálculos del exponente de Hurst, ya que puede conducir fácilmente a un resultado no válido. Esta validación no se realiza en el código fuente adjunto, y los lectores pueden sentirse libres de realizar estos ajustes. Realizamos este penúltimo paso en el siguiente código:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
       ...
       
       ...

      _points[t - 2][0] = log((_cumulations.Max() - _cumulations.Min()) / _std);
      _points[t - 2][1] = log(t);
   }
   LinearRegression(_points, H, C);
}

Como podemos ver en la parte del código fuente anterior, obtenemos los rangos acumulativos y también sus logaritmos naturales porque estamos buscando un exponente (potencia) y los logaritmos ayudan a resolver los exponentes. De la ecuación anterior, el tamaño de la muestra estaba en un lado de la ecuación, por lo tanto, también obtenemos su logaritmo natural y esto sirve como nuestro gráfico y, donde el gráfico x es el logaritmo natural del rango escalado dividido por la desviación estándar de la muestra de datos. Estos pares de puntos, x e y, son únicos para cada tamaño de segmento. Un tamaño de segmento diferente, dentro de la muestra de datos, representa otro par de puntos xy y cuanto más tengamos, más representativo será nuestro exponente de Hurst. Y como se mencionó anteriormente, el número total de posibles pares de puntos xy que podemos tener está limitado a la mitad del tamaño de la muestra de datos.

Entonces, nuestra matriz '_points' representa el logaritmo en el gráfico logarítmico encontrado en el análisis de rango reescalado. Es este gráfico el que sirve como entrada para los cálculos de regresión lineal.

Regresión lineal

La regresión lineal se realiza mediante una función separada del método 'Hurst'. Su código simple se comparte a continuación:

//+------------------------------------------------------------------+
// Function to perform linear regression
//+------------------------------------------------------------------+
void CSignalHurst::LinearRegression(matrix &Points, double &Slope, double &Intercept)
{  double _sum_x = 0.0, _sum_y = 0.0, _sum_xy = 0.0, _sum_xx = 0.0;
   for (int r = 0; r < int(Points.Rows()); r++)
   {  _sum_x += Points[r][0];
      _sum_y += Points[r][1];
      _sum_xy += (Points[r][0] * Points[r][1]);
      _sum_xx += (Points[r][0] * Points[r][0]);
   }
   Slope = ((Points.Rows() * _sum_xy) - (_sum_x * _sum_y)) / ((Points.Rows() * _sum_xx) - (_sum_x * _sum_x));
   Intercept = (_sum_y - (Slope * _sum_x)) / Points.Rows();
}

La Regresión lineal es el proceso mediante el cual llegamos a los coeficientes clave en la ecuación y = mx + c de un conjunto dado de puntos. Los coeficientes proporcionados definen la ecuación para la línea de mejor ajuste de estos puntos xy de entrada. Esta ecuación es importante para nosotros porque la pendiente de esta línea de mejor ajuste es el exponente de Hurst, mientras que la intersección con y sirve como constante C. Para este fin, la función 'LinearRegression' toma como entradas de referencia dos valores dobles que sirven como exponente de Hurst y marcador de posición de constante C, y al igual que la función 'Hurst', devuelve void.

Para este artículo nuestro objetivo principal es calcular el exponente de Hurst, sin embargo, parte de los resultados que obtenemos de este proceso, como ya se mencionó anteriormente, es la constante C. ¿Qué propósito tiene entonces esta constante C? Es una métrica de la variabilidad de una muestra de datos. Considere un escenario donde las series de precios de dos acciones tienen el mismo exponente de Hurst pero diferentes constantes C, donde una tiene una C de 7 y la otra una C de 21.

El valor del exponente similar indicaría que las dos acciones tienen características de "persistencia" similares, es decir, si el exponente de Hurst para ambas es inferior a 0,5, entonces ambas acciones tienden a revertir mucho a la media, mientras que si este exponente es superior a 0,5, entonces tienden a tener una tendencia mucho mayor en el largo plazo. Sin embargo, sus diferentes constantes C, a pesar de una acción de precios similar, apuntarían claramente a diferentes perfiles de riesgo. Esto se debe a que la constante C podría entenderse como un indicador de volatilidad. Las acciones con una constante C más alta tendrían oscilaciones de precios más amplias en sus promedios, a diferencia de las acciones con una constante C más pequeña. Esto podría implicar diferentes regímenes de tamaño de posiciones en las dos acciones, permaneciendo todos los demás factores constantes.

Compilación en una clase de señal

Utilizamos nuestros valores de exponente de Hurst generados para determinar las condiciones largas y cortas del símbolo negociado dentro de una clase de señal personalizada. El exponente de Hurst está destinado a capturar tendencias a muy largo plazo, por lo que, por definición, tiende a ser más preciso a medida que el tamaño de la muestra tiende a infinito. Sin embargo, para efectos prácticos, necesitamos medirlo a partir de un tamaño definido de precios históricos de los valores. Vamos a considerar uno de dos promedios móviles diferentes para evaluar nuestras condiciones largas/cortas, y por lo tanto, el tamaño del historial definido utilizado para calcular el exponente de Hurst se toma como la suma de los dos períodos utilizados para calcular estos dos promedios.

Esto puede no ser suficiente, porque como ya se mencionó, cuanto más largo sea el período de muestra de datos, más confiable será el exponente de Hurst por definición, por lo tanto, el lector puede realizar modificaciones según sea necesario para obtener un tamaño de historial que sea más representativo de su perspectiva. Como siempre, se adjunta el código fuente completo. Entonces, para cada una de las funciones de condición (larga y corta) comenzamos copiando los precios de cierre en un vector hasta el tamaño de nuestra muestra de datos. El tamaño de nuestra muestra de datos es la suma de los períodos largos y cortos.

Una vez que hemos hecho esto, calculamos el exponente de Hurst llamando a la función 'Hurst' y luego evaluamos el valor devuelto para determinar cómo se compara con 0,5. Se pueden realizar variaciones de esta implementación donde se agrega un umbral por encima y por debajo del valor 0,5, para limitar los puntos de entrada o de decisión. Si nuestro Hurst está por encima de 0,5 entonces hay persistencia y, por lo tanto, para la condición larga, buscaríamos ver si estamos por encima del promedio móvil del período lento (largo plazo). Si es así, esto podría indicar una posición alcista. Del mismo modo, para la condición corta, buscaríamos ver si estamos por debajo del promedio móvil del período lento y, si lo estamos, eso marcaría una apertura de posición corta.

En el caso de que el exponente de Hurst esté por debajo de 0,5, eso implicaría que estamos en un mercado de rango o de reversión a la media. En este caso, compararíamos el precio de oferta actual con el promedio móvil del período rápido. En la condición larga, si el precio está por debajo del promedio de movimiento rápido, eso indicaría una posición alcista. Por el contrario, en la condición corta, si el precio está por encima del promedio móvil del período rápido, eso es indicativo de la apertura de una posición corta. A continuación se comparte la implementación de estas dos condiciones:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::LongCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::ShortCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}

Pruebas y reportes de estrategia

Realizamos pruebas en el marco temporal de 4 horas para el par GBPCHF para el año 2023 y obtenemos los siguientes resultados:

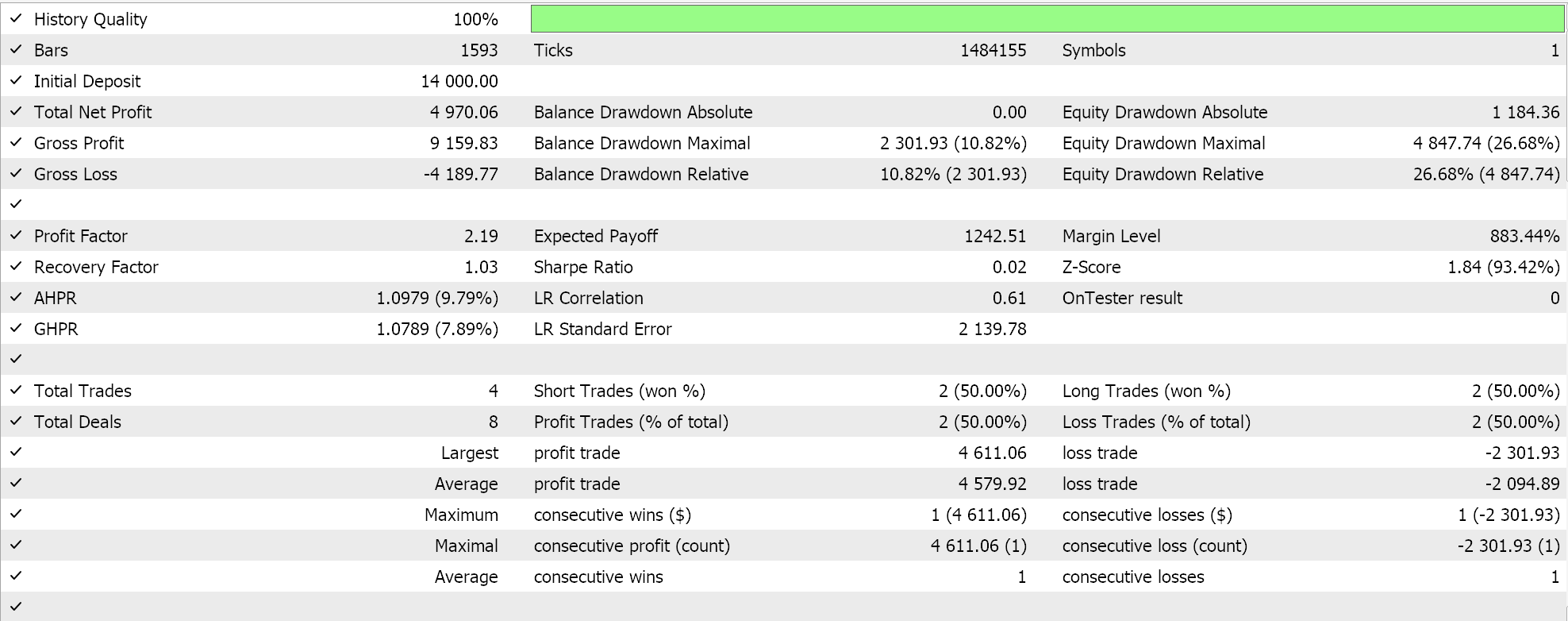
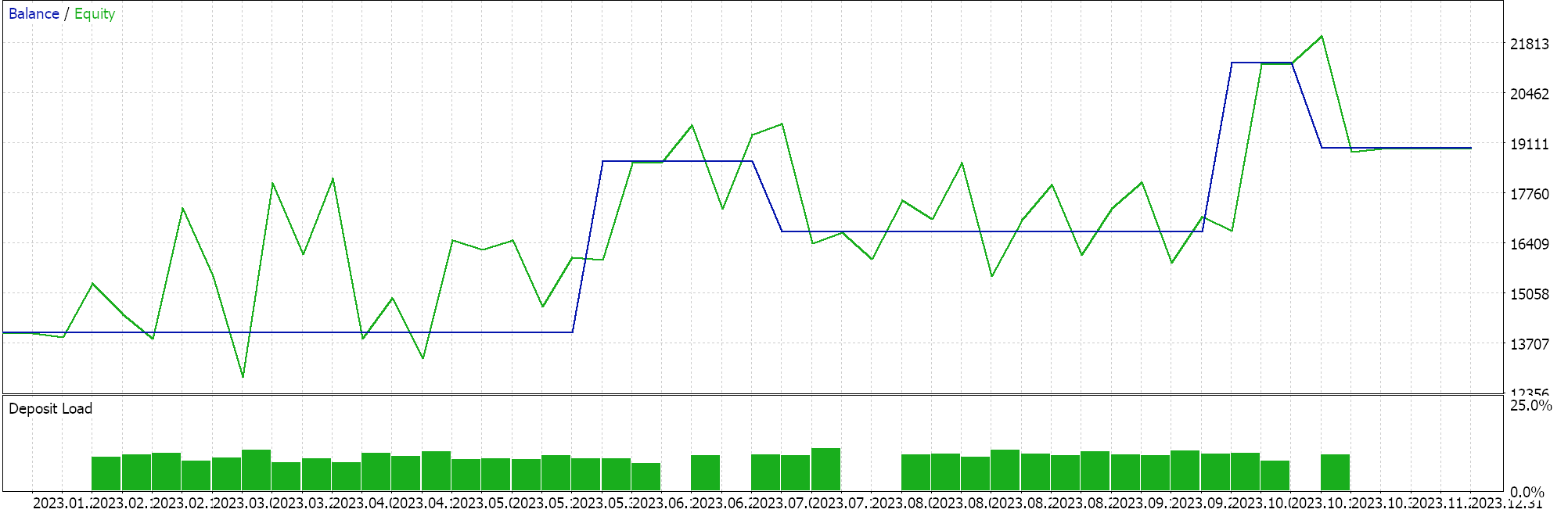
De nuestra prueba anterior, en el marco de tiempo de 4 horas no se están colocando muchas operaciones y esto podría ser una buena señal, ya que apunta a un Asesor Experto discriminante. Sin embargo, como siempre, antes de tomar una decisión sobre la eficacia del Experto, es necesario realizar pruebas durante periodos de tiempo más largos y, sobre todo, con marchas hacia delante.

Autocorrelación bruta como control

El exponente de Hurst afirma poder evaluar si una serie tiene rasgos persistentes (valores superiores a 0,5) o es antipersistente (valores inferiores a 0,5) actuando como una métrica de autocorrelación. Pero suponiendo que simplemente midiéramos las correlaciones de las series de datos sin tener que calcular este exponente y utilizáramos los resultados de nuestras mediciones reales de las correlaciones para evaluar las condiciones del mercado, ¿cuál sería la diferencia en el rendimiento de nuestro Asesor Experto?

Desarrollamos una clase de señal personalizada que, como cabría esperar, tiene menos funciones y simplemente evalúa en primer lugar cualquier correlación positiva durante el periodo de promediación más largo (más lento). Si existe una correlación positiva, la media móvil de este período más lento se utiliza para evaluar las configuraciones de seguimiento de tendencia, en las que los precios por encima de esta media son alcistas y los precios por debajo son bajistas. Sin embargo, si no existe una correlación positiva en los periodos más largos, se busca una correlación negativa en el periodo medio más corto (más rápido). En este caso, buscaríamos configuraciones de reversión a la media donde el precio por debajo de la media de movimiento rápido sería alcista mientras que el precio por encima sería bajista. El código para nuestra condición larga y corta es el siguiente:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAC::LongCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() < _ma.Mean())
               {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAC::ShortCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() > _ma.Mean())
               {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}

Realizamos ejecuciones de prueba casi similares para el mismo par GBPCHF en el marco temporal de 4 horas para el año 2023 y los resultados de nuestras mejores ejecuciones se presentan a continuación:

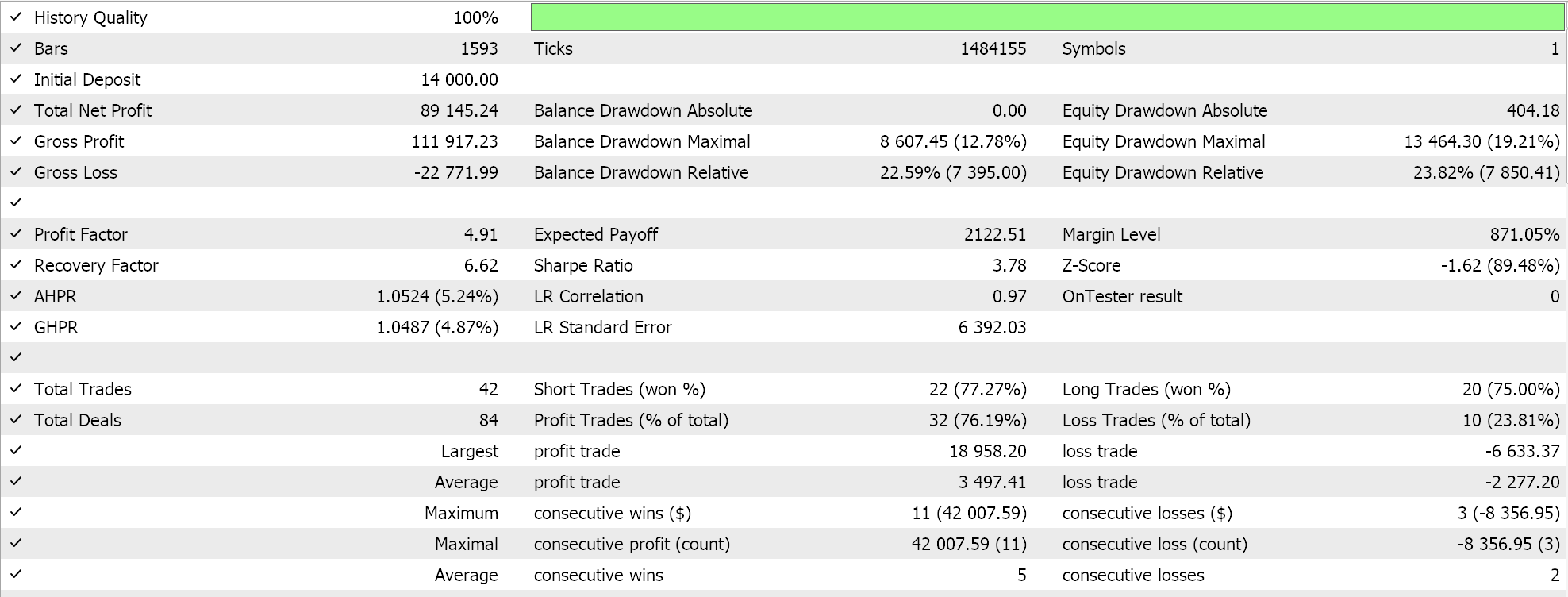
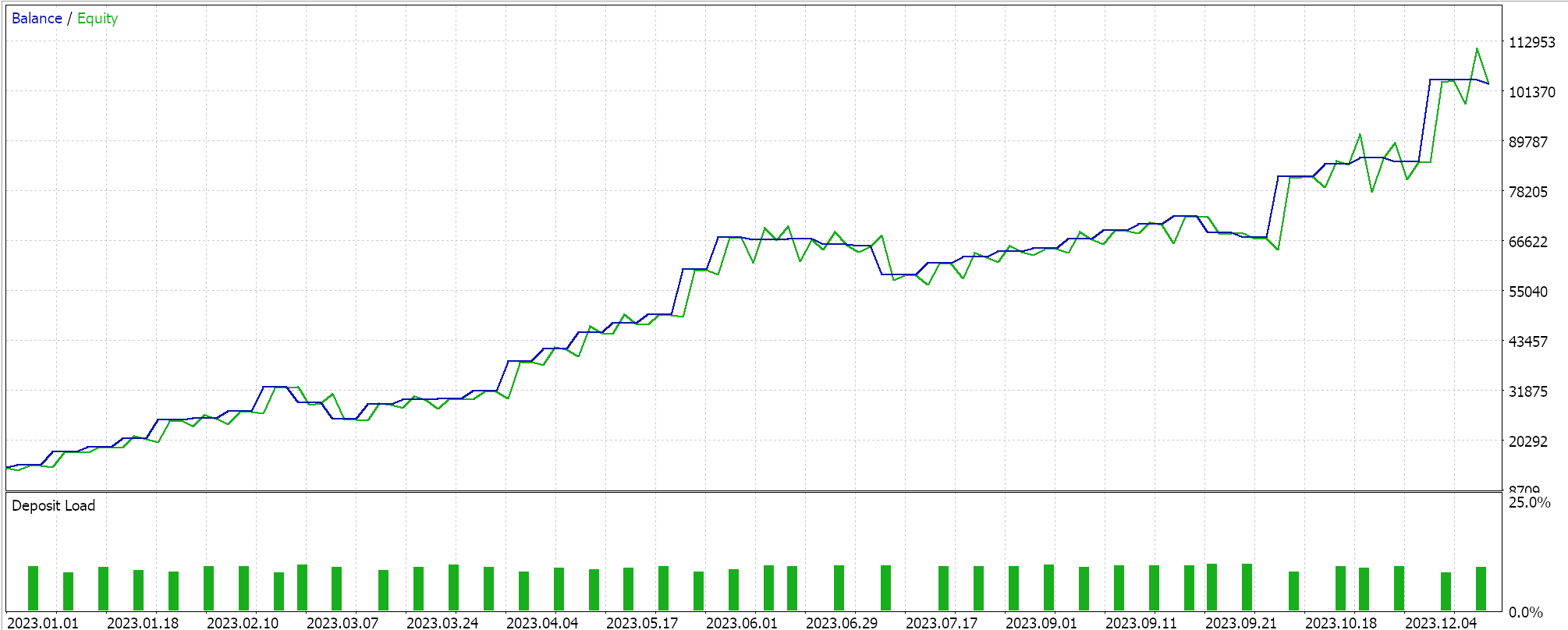
Tenemos claramente un salto o diferencia de rendimiento entre esta señal y la del Exponente de Hurst.

Conclusión

El exponente de Hurst se desarrolló a principios del siglo pasado, principalmente como herramienta para predecir los flujos y reflujos del río Nilo, una vez que se disponía de un conjunto de datos considerable de puntos de referencia. Desde entonces, se ha adoptado para una gama más amplia de aplicaciones, entre las que se encuentra el análisis de series temporales financieras. Para este artículo, hemos emparejado su exponente de serie temporal con medias móviles para distinguir mejor los mercados con tendencia de los mercados con reversión a la media al hacer una clase de señal personalizada.

A pesar de que las primeras pruebas que hemos realizado muestran claramente su potencial, aún queda mucho por hacer para justificar su uso, dado su rendimiento relativo frente a nuestra señal de autocorrelación bruta. Requiere muchos cálculos, filtra en exceso sus operaciones y sus mejores ejecuciones presentan una reducción excesiva, lo que resulta preocupante dado el intervalo de prueba relativamente pequeño utilizado para estas ejecuciones. Como siempre, las pruebas independientes podrían arrojar resultados diferentes e incluso más prometedores, y el lector está invitado a probarlos. El ensamblaje y compilación del código fuente adjunto en un Asesor Experto sigue las directrices que se encuentran aquí y aquí. Se recomienda que estas pruebas adicionales se realicen con datos reales del corredor y que abarquen un buen número de años.