Redes neuronales: así de sencillo (Parte 89): Transformador de descomposición de la frecuencia de señal (FEDformer)

Introducción

La previsión de series temporales a largo plazo es un problema largamente estudiado en diversas aplicaciones. Los modelos basados en el Transformer están dando resultados prometedores, pero la elevada complejidad computacional y los requisitos de memoria dificultan el uso del Transformer para modelar secuencias largas. Esto ha dado lugar a numerosos estudios que se han centrado en reducir el coste computacional del Transformer.

A pesar de los progresos realizados por los métodos de previsión de series temporales basados en el Transformer, en algunos casos estos no consiguen captar las características generales de la distribución de las series temporales. En este sentido, los autores del artículo "FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting" han tratado de proponer una solución a dicho problema. En el mencionado artículo, los autores comparan datos de series temporales reales con sus valores predichos obtenidos a partir delTransformer vainilla. Más abajo puede ver una captura de pantalla del artículo.

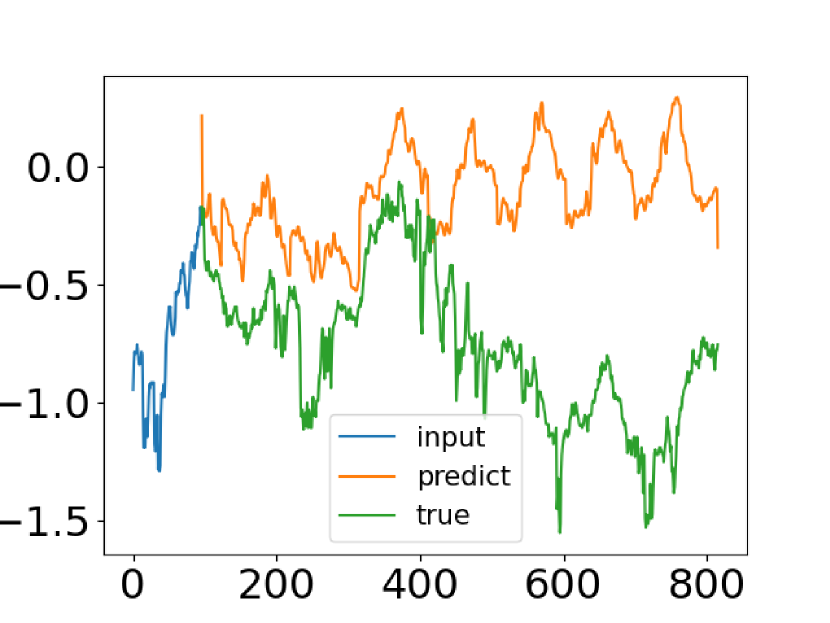
Podemos notar fácilmente que la distribución de las series temporales predichas es muy diferente de la verdadera. La discrepancia entre los valores previstos y los pronosticados puede explicarse por la atención puntual en el Transformer. Como la predicción para cada paso temporal se realiza de forma individual e independiente, es probable que el modelo no pueda preservar las propiedades y estadísticas globales de la serie temporal en su conjunto. Para resolver este problema, los autores del artículo exploran dos ideas.

La primera consiste en usar el método de descomposición de tendencias estacionales, muy utilizado en el análisis de series temporales. Los autores del artículo presentan una arquitectura de modelo especial que aproxima eficazmente la distribución de predicción a la distribución verdadera.

La segunda idea consiste en incorporar el análisis de Fourier al algoritmo del Transformer. En lugar de aplicar el Transformer a la dimensión temporal de una secuencia, los autores proponen analizar sus características frecuenciales, lo cual ayuda al Transformer a captar mejor las propiedades globales de las series temporales.

La combinación de las ideas propuestas se materializa en el Frequency Enhanced Decomposition Transformer o FEDformer, para abreviar.

Una de las cuestiones más importantes relacionadas con el FEDformer es qué subconjunto de componentes de frecuencia deberá utilizarse en el análisis de Fourier para representar las series temporales. En estos análisis, resulta más habitual conservar los componentes de baja frecuencia y descartar el componente de alta frecuencia. Sin embargo, esto podría no ser apropiado a la hora de pronosticar series temporales porque algunos cambios en las tendencias de las series temporales están asociados a acontecimientos importantes. Esta parte de la información puede perderse con la simple eliminación de todos los componentes de alta frecuencia de la señal. Los autores del método aceptan el hecho de que las series temporales suelen tener representaciones dispersas desconocidas que toman como fundamento la base de Fourier. Su análisis teórico ha demostrado que un subconjunto de componentes de frecuencia seleccionado aleatoriamente que incluya componentes de baja y alta frecuencia, ofrece una mejor representación de la serie temporal. Esta observación ha sido confirmada por numerosas investigaciones empíricas.

Además de mejorar la eficacia de las previsiones a largo plazo, la combinación del Transformer con el análisis de frecuencias reducirá el coste computacional de una complejidad cuadrática a lineal.

Los autores del documento resumen sus logros de la forma siguiente:

1. Se propone una arquitectura del Transformer de descomposición de señales con una característica de frecuencia mejorada y que utiliza expertos para descomponer las tendencias estacionales, lo cual mejora la capacidad de captar las propiedades globales de las series temporales.

2. Se proponen bloques de Fourier ampliados y bloques de wavelets mejorados en la arquitectura del Transformer para captar estructuras importantes en las series temporales mediante el análisis de las características de la frecuencia. Sirven para sustituir los bloques tanto de atención interna, como de atención cruzada.

3. Seleccionando aleatoriamente un número fijo de componentes de Fourier, el modelo propuesto logra una complejidad computacional y un coste de memoria lineales. La eficacia de este método de selección se ha probado tanto teórica como empíricamente.

4. Los experimentos realizados con seis conjuntos de datos de referencia de distintos ámbitos muestran que el modelo propuesto mejora el rendimiento de los métodos más avanzados en un 14,8% y un 22,6% para la predicción multivariante y univariante, respectivamente.

1. Algoritmo FEDformer

Debemos decir de entrada que los autores del método han presentado 2 variantes del modelo FEDformer. Una utiliza la base de Fourier para analizar las características frecuenciales de una serie temporal. Y la otra se basa en el uso de wavelets que permiten combinar análisis tanto en el dominio temporal como en el frecuencial.

La previsión de series temporales a largo plazo es un problema sequence-to-sequence. Denotaremos el tamaño de la secuencia de datos inicial como I y la secuencia prevista como O. Al mismo tiempo, D representará el tamaño del vector de descripción de un estado de una sola fila. A continuación, introduciremos un tensor de tamaño I*D en el Codificador, y el Decodificador recibirá la matriz (I/2+O)*D como entrada.

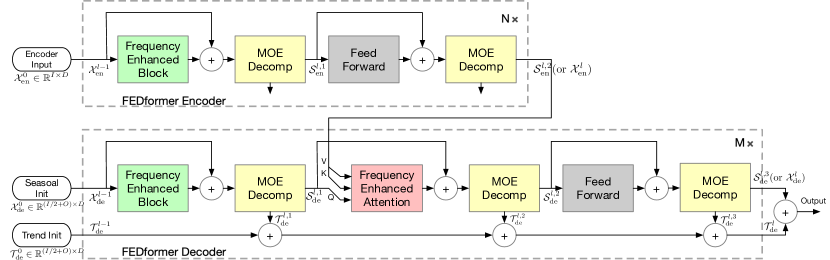
Como ya hemos mencionado, los autores del método han mejorado la arquitectura del Transformer introduciendo análisis de descomposición y distribución de tendencias estacionales. El Transformer actualizado es una arquitectura de descomposición profunda e incluye un bloque de estimación de frecuencia (FEB), un bloque de atención de frecuencia (FEA) y bloques de descomposición Mixture Of Experts (MOEDecomp).

El Сodificador FEDformer utiliza una estructura multinivel similar a la del Сodificador del Transformer. Un bloque independiente del mismo puede representarse usando las siguientes expresiones matemáticas:

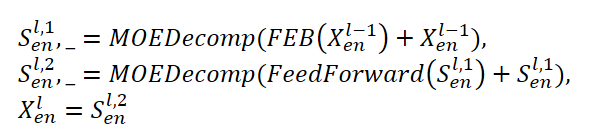
Aquí Sen representa el componente estacional extraído de los datos de origen en el bloque de descomposición MOEDecomp.

Para el módulo FEB, los autores del método proponen 2 versiones diferentes (FEB-f y FEB-w), que se implementan mediante el mecanismo de la transformada discreta de Fourier (DFT) y la transformada discreta de wavelet (DWT), respectivamente. En esta aplicación, sustituyen al bloque de Self-Attention.

El Descodificador también utiliza una estructura multinivel como el Сodificador. Pero la arquitectura de sus componentes resulta mucho más amplia y se describe mediante fórmulas:

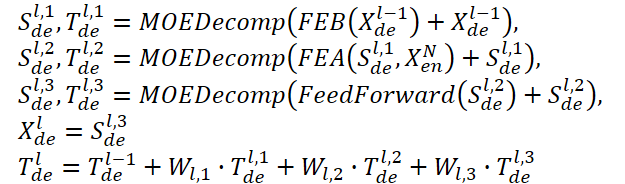
Sde y Tde representan el componente estacional y de tendencia tras el bloque de descomposición MOEDecomp, mientras que Wl  como proyección de la tendencia extraída. De forma semejante a FEB, FEA tiene dos versiones diferentes (FEA-f y FEA-w), que se implementan mediante la proyección DFT y DWT, respectivamente. El FEA se ha ejecutado con un diseño de atención y sustituye al bloque de atención transversal del Transformer vainilla.

La previsión final supone la suma de los dos componentes descompuestos refinados. El componente estacional se proyecta usando la matriz WS a la medición objetivo.

El modelo FEDformer propuesto utiliza la transformada discreta de Fourier (DFT), que permite descomponer la secuencia analizada en sus armónicos constituyentes (componentes sinusoidales). Para mejorar la eficacia del modelo, los autores del FEDformer utilizan la transformada rápida de Fourier (FFT).

Como ya hemos mencionado, el método utiliza un subconjunto aleatorio de la base de Fourier y la escala del subconjunto está limitada por un escalar. La selección del índice de modo antes de las operaciones de DFT y DFT inversa (IDFT ) nos permite regular aún más la complejidad computacional.

El bloque con rango de frecuencias extendido y transformada de Fourier (FEB-f) se utiliza tanto en el Codificador como en el Decodificador. Los datos de origen del bloque FEB-f se proyectan primero linealmente y luego se convierten del dominio temporal a características de frecuencia. A partir de las características de frecuencia obtenidas, se muestrean aleatoriamente M armónicos. A continuación, las características de frecuencia seleccionadas se multiplican por una matriz de núcleo parametrizada, que se inicializa con parámetros aleatorios y se ajusta durante el entrenamiento del modelo. El resultado se rellena con ceros hasta alcanzar la dimensionalidad de las características de frecuencia completas antes de realizar la transformada inversa de Fourier, que devuelve la secuencia analizada al dominio temporal. A continuación le mostramos la visualización del autor del bloque FEB-f.

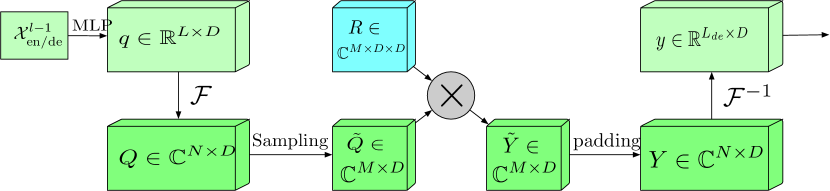
El bloque de atención de características de frecuencia mediante transformada discreta de Fourier (FEA-f) utiliza el enfoque canónico de la transformada con un pequeño añadido. Los datos de origen se convierten en representaciones Query, Key y Value. En la atención cruzada, Query procede del Descodificador, mientras que Key y Value se toman del Сodificador. Sin embargo, en FEA-f, transformamos Query, Key y Value utilizando la transformada de Fourier e implementamos un mecanismo de atención canónica similar en el dominio de la frecuencia. Aquí, al igual que en el bloque FEB-f, muestreamos aleatoriamente M armónicos para su análisis. El resultado de la operación de atención se completa con ceros hasta el tamaño de la secuencia original y se realiza la transformada inversa de Fourier. La estructura de FEA-f se muestra a continuación en la representación del autor.

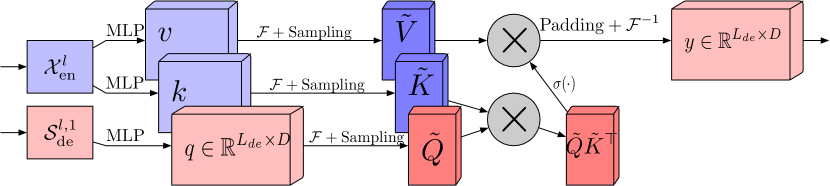
Mientras que la transformada de Fourier crea una representación de la señal en cuanto a las características frecuenciales, la transformada wavelet permite representar la señal tanto en el dominio de la frecuencia como en el del tiempo, lo cual ofrece un acceso eficaz a la información localizada sobre la señal original. La transformada multi-wavelet combina las ventajas de los polinomios ortogonales y de las wavelets. La representación multi-wavelet de una señal puede obtenerse usando el producto tensorial de las bases multiescala y multi-wavelet. Obsérvese que las bases a distintas escalas están relacionadas por el producto tensorial. Los autores del método FEDformer adaptan una representación wavelet no estándar para reducir la complejidad del modelo.

La arquitectura FEB-w difiere de la FEB-f en su mecanismo recursivo: los datos de origen se descomponen recursivamente en 3 partes y cada parte se procesa de forma individual. Para la descomposición wavelet, los autores del método proponen una matriz de descomposición de base wavelet de Legendre fija. Se usan tres módulos FEB-f para procesar la parte resultante de alta frecuencia, la parte de baja frecuencia y la parte restante de la descomposición wavelet, respectivamente. Con cada iteración, se crean un tensor de alta frecuencia procesado, un tensor de baja frecuencia procesado y un tensor de baja frecuencia sin procesar. Se trata de un enfoque descendente; el paso de descomposición realiza una reducción de la señal a la mitad. Los tres conjuntos de bloques FEB-f se comparten durante diferentes iteraciones de la descomposición. En cuanto a la reconstrucción wavelet, los autores del método también crean el tensor de salida de forma recursiva.

FEA-w contiene un paso de descomposición y un paso de reconstrucción similares a FEB-w. En este caso, los autores del FEDformer no modifican la etapa de reconstrucción. La única diferencia reside en la fase de descomposición. Esta usa la misma matriz para descomponer la señal en entidades de Query, Key y Value. Como mostramos arriba, el bloque FEB-w contiene tres bloques FEB-f para el procesamiento de la señal. Podemos considerar FEB-f como un sustituto del mecanismo de Self-Attention. Los autores del método usan un método sencillo para crear la atención cruzada mejorada con mejora de la frecuencia usando la descomposición wavelet, y sustituyendo cada FEB-f por un módulo FEA-f. Además, se ha añadido otro módulo FEA-f para procesar los restos más considerables.

Debido al patrón periódico complejo que suele observarse combinado con el componente de tendencia, en los datos reales la extracción de la tendencia puede resultar complicada cuando se combinan medias con una ventana fija. Para superar tal​problema, se desarrolló el bloque de descomposición Mixture Of Experts (MOEDecomp). Este contiene un conjunto de filtros de medias de distintos tamaños, diseñados para extraer varios componentes de tendencia de la señal original, y un conjunto de ponderaciones dependientes de los datos para combinarlos en la tendencia resultante.

El algoritmo completo del método FEDformer se muestra en la siguiente representación del autor.

2. Implementación con MQL5

Tras repasar los aspectos teóricos del método del FEDformer propuesto, debemos decir de inmediato que nuestra aplicación distará mucho de ser original. Usaremos los enfoques propuestos, pero no aplicaremos el algoritmo propuesto en su totalidad. El motivo reside en algunas de mis creencias personales al respecto.

Primero debemos decidir qué base vamos a utilizar DFT o DWT. La cuestión es bastante compleja y ambigua, y puede provocar que nos "rompamos la cabeza" con ella durante mucho tiempo. Pero nosotros actuaremos de forma mucho más simple. Vamos a pasar ahora a los resultados de las pruebas del método que presentamos en el artículo del autor.

Fíjese en la columna "Exchange". No entraremos en detalles sobre los datos con los que se ha probado el modelo, pero sí que se observa una clara superioridad del modelo que utiliza DWT. Es probable que, debido a una falta de periodicidad pronunciada en los datos de origen, la DFT sea incapaz de detectar cuándo cambian las tendencias. Al fin y al cabo, ignora el componente temporal de los datos de origen. Al mismo tiempo, la DWT, que analiza la señal en ambas dimensiones, es capaz de ofrecer datos predictivos más precisos. Creo que en una situación así nuestra elección a favor de la DWT será obvia.

2.1 Implementación de la DWT

Una vez decidida la base de implementación, primero implementamos la capacidad de descomposición wavelet en nuestra biblioteca. Para ello, crearemos un nuevo objeto CNeuronLegendreWavelets.

vamos a pensar un poco en la arquitectura del objeto que estamos creando. Como ya hemos mencionado, para la descomposición wavelet, los autores del método proponen usar una matriz fija de descomposición de base wavelet de Legendre. En otras palabras, para descomponer la señal, solo deberemos multiplicar el vector de la señal por la matriz de base wavelet.

En nuestra secuencia de datos inicial, tendremos que analizar varias señales paralelas de una serie temporal multimodal. En este caso, usaremos la misma matriz de base para cada serie temporal unitaria.

Este proceso será muy similar a la convolución con varios filtros, solo que en este caso el papel de la matriz de filtros lo desempeñará la matriz de base wavelet. Por ello, será bastante lógico crear un nuevo objeto como heredero de nuestra capa de convolución. Con previsión, podemos aprovechar al máximo los métodos heredados redefiniendo literalmente un par de ellos.

class CNeuronLegendreWavelets :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; } 

public:
                     CNeuronLegendreWavelets(void) {};
                    ~CNeuronLegendreWavelets(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWavelets;   }
  };

En la nueva estructura de la clase CNeuronLegendreWavelets presentada anteriormente, podemos ver solo 3 métodos redefinidos, uno de los cuales es el identificador de clase Type, que retorna una constante predefinida.

El segundo punto mencionado anteriormente es que usaremos una matriz fija de wavelets de base. Por lo tanto, no habrá parámetros entrenados en nuestra clase, y redefiniremos el método updateInputWeights con un "stub".

De hecho, solo tendremos que trabajar con el método de inicialización de objetos de la clase Init. En el nuevo método, no declararemos ninguna variable local ni ningún objeto. Y en el método de inicialización, solo tendremos que rellenar la matriz de wavelets de base.

Los autores del método proponen usar polinomios de Legendre como wavelets. Hemos elegido 9 polinomios de este tipo, cuya visualización se muestra a continuación.

Como podemos ver, los polinomios presentados en el gráfico permiten describir una gama bastante amplia de frecuencias.

También debemos señalar que el rango de valores admisibles de los polinomios presentados es [0, 1]. Y esto resultará muy cómodo. Ahora definiremos la longitud de la ventana de la secuencia analizada como 1. Y dividiremos el rango por el número de elementos de la secuencia. Al hacerlo, definiremos un paso de tiempo entre dos elementos vecinos de la secuencia, que formaremos inicialmente con un paso fijo. Y aquí, el marco temporal de los datos de origen recogidos será irrelevante. Analizaremos las características de frecuencia de la señal dentro de la ventana visible de la secuencia original.

Y aquí nos enfrentamos al problema de determinar el número de elementos de una secuencia en la fase de diseño del modelo. Antes de crear la matriz de base, deberemos especificar sus dimensiones. En esta fase, solo tendremos el número de filtros que hemos seleccionado, pero solo conoceremos el tamaño de la ventana de la secuencia analizada al inicializarse el modelo. En realidad, tendremos 2 maneras de salir de esta situación:

1. Determinar unas dimensiones estrictas para la matriz wavelet de base y rellenar sus valores directamente, mientras que el uso de una capa de convolución entrenada delante de la matriz nos permitirá trabajar con cualquier tamaño de la secuencia original.
2. Crear un algoritmo universal para rellenar la matriz de wavelets de base en la fase de inicialización del modelo para cualquier tamaño de datos iniciales.

La primera opción nos permitirá rellenar la matriz con valores fijos de cualquier forma disponible. Incluso podremos encontrar en Internet los coeficientes de wavelets de base que nos interesen. Pero, ¿cómo definir ese punto óptimo entre precisión y rendimiento? Además, los requisitos de precisión de las predicciones pueden cambiar mucho de una tarea a otra.

Y aquí, en mi opinión, la segunda opción parece mejor. Para implementarla, crearemos fórmulas de polinomios seleccionados como macrosustituciones. Estos son solo algunos de ellos (en el archivo adjunto figura la lista completa):

#define Legendre4(x)    (70*pow(x,4) - 140*pow(x,3) + 90*pow(x,2) - 20*x + 1)
#define Legendre6(x)    (924*pow(x,6) - 2772*pow(x,5) + 3150*pow(x,4) - 1680*pow(x,3) + \
                         420*pow(x,2) - 42*x + 1)
#define Legendre8(x)    (12870*pow(x,8) - 51480*pow(x,7) + 84084*pow(x,6) - 72072*pow(x,5) + \
                         34650*pow(x,4) - 9240*pow(x,3) + 1260*pow(x,2) - 72*x + 1)

Utilizando estas macrosustituciones, podremos obtener el valor del polinomio para cualquier valor discreto. Y tras finalizar el trabajo preparatorio, podremos pasar directamente a la descripción del algoritmo de inicialización del objeto de nuestra nueva clase CNeuronLegendreWavelets::Init.

En los parámetros del método, transmitiremos los parámetros clave de la arquitectura del objeto:

bool CNeuronLegendreWavelets::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                   uint window, uint step, uint units_count, 
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 9, units_count, 
                            optimization_type, batch))
      return false;

Y en el cuerpo del método, primero llamaremos al método homónimo de la clase padre.

Observe que en los parámetros del método de inicialización de la nueva clase solo obtendremos el tamaño de la ventana de la secuencia analizada y el número de elementos de la secuencia. Y cuando llamamos al método similar de la clase padre, necesitaremos añadir el paso de la ventana y el número de filtros. Ya hemos decidido antes el número de filtros: serán 9. Y el paso de la ventana analizada será igual a la ventana analizada.

Tras ejecutar con éxito el método de inicialización de la clase padre, nuestra matriz de parámetros de convolución se rellenará con valores aleatorios. Tendremos que rellenarla con los parámetros de base de la wavelet. Para ello, primero rellenaremos la matriz de pesos con valores cero. Este es un punto muy importante, ya que necesitamos poner a cero los parámetros de desplazamiento-bias establecidos.

   WeightsConv.BufferInit(WeightsConv.Total(), 0);

Y luego llenaremos la matriz de valores de wavelet de base en el ciclo:

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(i) / iWindow;
      if(!WeightsConv.Update(shift, Legendre4(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre6(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre8(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre10(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre12(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre16(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre18(k)))
         return false;
      shift += iWindow + 1;
      if(!WeightsConv.Update(shift, Legendre20(k)))
         return false;
     }

Vamos a transferir la matriz rellenada a la memoria contextual OpenCL:

   if(!!OpenCL)
      if(!WeightsConv.BufferWrite())
         return false;
//---
   return true;
  }

Luego finalizaremos el método.

Aquí debemos decir que en esta implementación heredaremos todas las demás funcionalidades necesarias para el correcto funcionamiento del objeto de la clase padre. Por lo tanto, finalizaremos esta clase y seguiremos adelante.

2.2 Bloque FED-w

En la siguiente etapa de nuestro trabajo, por así decirlo, iremos un paso más allá y crearemos nuestra visión del bloque FED-w, cuya funcionalidad se implementará en la clase CNeuronFEDW. La estructura de esta clase será la siguiente.

class CNeuronFEDW : public CNeuronBaseOCL
  {
protected:
   //---
   uint                    iWindow;
   uint                    iCount;
   //---
   CNeuronLegendreWavelets cWavlets;
   CNeuronBatchNormOCL     cNorm;
   CNeuronSoftMaxOCL       cSoftMax;
   CNeuronConvOCL          cFF[2];
   CNeuronBaseOCL          cReconstruct;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      Reconsruct(CBufferFloat* inputs, CBufferFloat *outputs);

public:
                     CNeuronFEDW(void) {};
                    ~CNeuronFEDW(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint count, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const                      {  return defNeuronFEDW; }
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
  };

Podemos observar que esta clase tiene una arquitectura más compleja en comparación con la anterior. En ella declararemos 2 variables locales para almacenar los parámetros clave. Y también declararemos una serie de objetos internos, cuyo propósito conoceremos durante la implementación. Todos los objetos se declararán de manera estática, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos".

La inicialización directa de todos los objetos anidados se realizará, como siempre, en el método CNeuronFEDW::Init. En los parámetros, al método se le transmitirán los parámetros básicos de la arquitectura del objeto. Entre ellos podremos destacar los parámetros fundamentales del tamaño de la ventana visible de datos (window) y el número de secuencias unitarias analizadas (count).

bool CNeuronFEDW::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint count, 
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, 
                            optimization_type, batch))
      return false;

En el cuerpo del método, primero llamaremos al método homónimo de la clase padre, lo cual, podemos decir, supone una regla en la implementación de nuestros objetos. Después, guardaremos los parámetros de arquitectura del objeto que se está inicializando en variables locales:

   iWindow = window;
   iCount = count;

Y luego inicializaremos los objetos internos en el orden en que se utilizarán más tarde.

En un primer momento, nos proponemos extraer las características de frecuencia de los datos de origen obtenidos. Para ello, utilizaremos una instancia de la clase CNeuronLegendreWavelets creada anteriormente:

   if(!cWavlets.Init(0, 0, OpenCL, iWindow, iWindow, iCount, optimization, iBatch))
      return false;
   cWavlets.SetActivationFunction(None);

Debemos decir que el bloque FED-w que estamos creando está muy simplificado en comparación con el método propuesto por los autores. Hemos renunciado a utilizar bloques DFT. A mi juicio, analizar aisladamente las características de frecuencia del componente temporal puede jugar en nuestra contra y reducir la calidad de las previsiones. Como mínimo, esto cuestionará la conveniencia de utilizar la DFT. Pero esa es mi opinión personal, y podría equivocarme.

Además, la eliminación del proceso de FFT, que lleva bastante tiempo, reducirá considerablemente los recursos informáticos necesarios durante el entrenamiento y el funcionamiento del modelo.

Considerando lo anteriormente dicho, he decidido mejorar el rendimiento del modelo aceptando los riesgos de un posible deterioro en la calidad de las predicciones.

Primero normalizaremos los datos obtenidos tras la descomposición wavelet utilizando una capa de normalización por lotes:

   if(!cNorm.Init(0, 1, OpenCL, 9 * iCount, 1000,optimization))
      return false;
   cNorm.SetActivationFunction(None);

Y luego estimaremos la proporción de cada uno de los filtros utilizados. Para ello, traduciremos los datos obtenidos al subespacio de probabilidad utilizando la función SoftMax.

   if(!cSoftMax.Init(0, 1, OpenCL, 9 * iCount, optimization, iBatch))
      return false;
   cSoftMax.SetHeads(iCount);
   cSoftMax.SetActivationFunction(None);

Obsérvese que evaluaremos cada canal unitario por separado.

A continuación, recuperaremos la serie temporal original partiendo de la representación probabilística usando la convolución inversa con nuestra matriz de base wavelet. El resultado se guardará en la capa de base anidada creada:

   if(!cReconstruct.Init(0, 2, OpenCL, iWindow, optimization, iBatch))
      return false;
   cReconstruct.SetActivationFunction(None);

Podemos ver que las operaciones anteriores realizan una especie de círculo cerrado: series temporales → descomposición wavelet → normalización → representación probabilística → series temporales. Pero a la salida obtendremos una representación bastante suavizada de la serie temporal original, que hemos pasado por una especie de filtro digital. Como resultado, obtendremos un filtrado de datos bastante eficaz con un mínimo de parámetros entrenados que solo están presentes en la capa de normalización por lotes. Y este bloque sustituirá a la Self-Attention en nuestra implementación.

Aquí debemos señalar que, en esencia, estamos sustituyendo los parámetros del modelo entrenado por wavelets predefinidas. Esto hará que nuestro modelo resulte más comprensible frente a una "caja negra" de parámetros entrenados, pero menos flexible. Asimismo, impondrá una carga adicional al arquitecto del modelo a la hora de encontrar las wavelets óptimas para la tarea en cuestión. Hemos puesto los polinomios wavelet en un bloque separado de macrosustituciones por una razón. Este enfoque nos permitirá experimentar fácilmente con diferentes wavelets en el camino hacia la búsqueda de las óptimas.

Pero regresemos al método de inicialización de nuestra clase. Detrás del bloque de filtro digital viene el conocido bloque FeedForward de la arquitectura del Transformer. Aquí utilizaremos una MLP de 2 capas sin cambios con LReLU entre ellas. Al igual que antes, utilizaremos objetos de capa convolucional para implementar el procesamiento de los canales independientes:

   if(!cFF[0].Init(0, 3, OpenCL, iWindow, iWindow, 4 * iWindow, iCount, optimization, iBatch))
      return false;
   cFF[0].SetActivationFunction(LReLU);
   if(!cFF[1].Init(0, 4, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iCount, optimization, iBatch))
      return false;
   SetActivationFunction(None);

Al final del método de inicialización, intercambiaremos el búfer del gradiente de error para minimizar las operaciones innecesarias de copiado de datos:

   if(Gradient != cFF[1].getGradient())
      SetGradient(cFF[1].getGradient());
//---
   return true;
  }

Una vez finalizada la inicialización de nuestro objeto, procederemos a implementar la pasada directa del modelo propuesto. De la anterior descripción del proceso planificado, cabe destacar la convolución inversa de las probabilidades obtenidas en una serie temporal.

La "convolución inversa" parece algo nuevo en nuestra aplicación. Sin embargo, hace mucho tiempo que aplicamos este proceso. Con la convolución inversa distribuimos el gradiente de error en la capa de convolución. Pero ahora necesitaremos la aplicación de dicho proceso dentro de la pasada directa.

La dificultad estriba en que todos los métodos de nuestras clases trabajarán con una lista fija de búferes de datos. Y esto nos permitirá no tener que pensar en los búferes de datos utilizados durante el proceso de construcción del modelo. Bastará con dar un puntero al objeto, y todos los búferes de datos ya estarán prescritos en el método. La "otra cara de la moneda" es que no podremos utilizar el método de pasada inversa para implementar el algoritmo en el marco de la pasada directa. No obstante, podremos crear un nuevo método en el que utilicemos un kernel creado anteriormente con los búferes y parámetros correctos que se le hayan transmitido.

Eso es lo que vamos a hacer. Vamos a crear el método CNeuronFEDW::Reconsruct, en cuyos parámetros transmitiremos los punteros a los búferes de probabilidades obtenidas y de la secuencia a reconstruir:

bool CNeuronFEDW::Reconsruct(CBufferFloat *sequence, CBufferFloat *probability)
  {
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = sequence.Total();

En el cuerpo del método, definiremos el espacio de tareas y transmitiremos todos los parámetros necesarios al kernel:

   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_w, 
                                                                     cWavlets.GetWeightsConv().GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_g, probability.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_o, probability.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_ig, sequence.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_outputs, probability.Total()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_step, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_in, (int)iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_out, (int)9))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_activation, (int)None))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_shift_out, (int)0))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Después, pondremos el kernel en la cola de ejecución:

   if(!OpenCL.Execute(def_k_CalcHiddenGradientConv, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Con esto completaremos el trabajo preparatorio, y podremos empezar a describir directamente el método de pasada directa de nuestra clase CNeuronFEDW::feedForward. Como siempre, en los parámetros del método de pasada directa transmitiremos un puntero al objeto de la capa anterior de nuestro modelo, que contiene los datos de origen requeridos:

bool CNeuronFEDW::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cWavlets.FeedForward(NeuronOCL.AsObject()))
      return false;

En el cuerpo del método, primero descompondremos la secuencia recibida en sus características de frecuencia constituyentes. Para ello, llamaremos al método de pasada directa del objeto anidado cWavlets.

A continuación, según el algoritmo propuesto, normalizaremos los datos obtenidos y los traduciremos a un subespacio probabilístico:

   if(!cNorm.FeedForward(cWavlets.AsObject()))
      return false;
   if(!cSoftMax.FeedForward(cNorm.AsObject()))
      return false;

Después de lo cual restauraremos la secuencia temporal:

   if(!Reconsruct(cReconstruct.getOutput(), cSoftMax.getOutput()))
      return false;

El algoritmo posterior será similar al algoritmo del Transformer clásico. Luego sumaremos y normalizaremos las secuencias temporales original y reconstruida:

   if(!SumAndNormilize(NeuronOCL.getOutput(), cReconstruct.getOutput(), cReconstruct.getOutput(),
                                                                        iWindow, true, 0, 0, 0, 1))
      return false;

Y pasaremos los datos a través del bloque FeedForward:

   if(!cFF[0].FeedForward(cReconstruct.AsObject()))
      return false;
   if(!cFF[1].FeedForward(cFF[0].AsObject()))
      return false;

A continuación, sumaremos y normalizaremos las secuencias temporales de los dos flujos de datos:

   if(!SumAndNormilize(cFF[1].getOutput(), cReconstruct.getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

La pasada directa estará ya implementada y podremos pasar a construir los métodos de pasada inversa. Primero crearemos el método de distribución del gradiente de error CNeuronFEDW::calcInputGradients:

bool CNeuronFEDW::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En el cuerpo del método primero comprobaremos que sea correcto el puntero al objeto de la capa anterior obtenido en los parámetros. Porque si no existe, la realización de las operaciones del método no tendrá sentido alguno.

Como recordará, en el método de inicialización de la clase, realizaremos el intercambio de los búferes de datos del gradiente de error. Y ahora podremos ir directamente a trabajar con el bloque FeedForward.

   if(!cFF[0].calcHiddenGradients(cFF[1].AsObject()))
      return false;
   if(!cReconstruct.calcHiddenGradients(cFF[0].AsObject()))
      return false;

De forma similar al flujo de datos en la pasada directa, en la pasada inversa distribuiremos el gradiente de error entre dos flujos de datos paralelos. Y en esta fase, sumaremos el gradiente de error de ambos flujos.

   if(!SumAndNormilize(Gradient, cReconstruct.getGradient(), cReconstruct.getGradient(), iWindow, false))
      return false;

A continuación, tendremos que transmitir el gradiente de error a través de la operación de convolución inversa. Obviamente, se trata de una operación de convolución común, pero hay otro problema. El método de pasada directa de la capa de convolución no funciona con los búferes de gradiente de error. Esta vez, haremos un pequeño truco: sustituiremos temporalmente los búferes de resultados de las capas por sus búferes de gradiente. Primero guardaremos los punteros a los búferes de datos intercambiados:

   CBufferFloat *temp_r = cReconstruct.getOutput();
   if(!cReconstruct.SetOutput(cReconstruct.getGradient(), false))
      return false;
   CBufferFloat *temp_w = cWavlets.getOutput();
   if(!cWavlets.SetOutput(cSoftMax.getGradient(), false))
      return false;

Luego realizaremos una pasada directa de la capa de convolución:

   if(!cWavlets.FeedForward(cReconstruct.AsObject()))
      return false;

Y retornaremos los búferes de datos a su posición original:

   if(!cWavlets.SetOutput(temp_w, false))
      return false;
   if(!cReconstruct.SetOutput(temp_r, false))
      return false;

A continuación, bajaremos el gradiente de error hasta la capa anterior:

   if(!cNorm.calcHiddenGradients(cSoftMax.AsObject()))
      return false;
   if(!cWavlets.calcHiddenGradients(cNorm.AsObject()))
      return false;
   if(!NeuronOCL.calcHiddenGradients(cWavlets.AsObject()))
      return false;

Y sumaremos el gradiente de error de los dos flujos de datos:

   if(!SumAndNormilize(NeuronOCL.getGradient(), cReconstruct.getGradient(), NeuronOCL.getGradient(),
                                                                            iWindow, false))
      return false;
//---
   return true;
  }

No deberemos olvidarnos controlar la ejecución de todas las operaciones. A continuación, finalizaremos el método.

La distribución del gradiente de error a todos los elementos de nuestro modelo irá seguida de la optimización de los parámetros del modelo entrenado. La funcionalidad para optimizar los parámetros de este objeto se implementará en el método CNeuronFEDW::updateInputWeights. El algoritmo del método es bastante sencillo, simplemente llamaremos a los métodos homónimos de los objetos anidados y comprobaremos el resultado de las operaciones según el resultado lógico de los métodos llamados.

bool CNeuronFEDW::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cFF[0].UpdateInputWeights(cReconstruct.AsObject()))
      return false;
   if(!cFF[1].UpdateInputWeights(cFF[0].AsObject()))
      return false;
   if(!cNorm.UpdateInputWeights(cWavlets.AsObject()))
      return false;
//---
   return true;
  }

Tenga en cuenta que en este método solo trabajaremos con objetos que contengan parámetros entrenables.

Aquí concluiremos nuestra análisis de los algoritmos para construir los métodos de las nuevas clases. Podrá leer el código completo de las clases consideradas y sus métodos en el archivo adjunto. Allí encontrará también el código completo de todos los programas usados en la elaboración del artículo.

Nótese que solo hemos creado nuestra propia visión del Сodificador de estados del algoritmo FEDformer propuesto. Al hacerlo, hemos omitido por completo el Descodificador. Se trata de una decisión consciente, que se relaciona con un enfoque basado en los principios de la obtención de una estrategia comercial rentable. El hecho es que, por extraño que parezca, no estamos tratando de predecir las condiciones del entorno posteriores con la mayor exactitud posible. Al fin y al cabo, afectarán indirectamente al trabajo de nuestro Agente. Si estuviéramos construyendo un algoritmo claro con reglas para el estado posterior, necesitaríamos la predicción más precisa del próximo movimiento del precio. No es así como vamos a construir la política de nuestro Agente.

Estamos entrenando al Сodificador para predecir futuros estados del entorno con el fin de obtener el estado oculto más informativo del Сodificador. El Actor, a su vez, extraerá el estado oculto del Codificador, que será esencialmente parte integrante del Actor y realizará la función de análisis del estado actual del entorno. Y, a partir del análisis del estado actual del entorno del Actor, se construirá su política de comportamiento.

Hay una línea muy fina que debemos entender. Así no gastaremos una cantidad excesiva de recursos en descomponer el estado oculto del Codificador para obtener la predicción más precisa de los futuros estados del entorno.

2.3 Arquitectura del modelo

Una vez construidos los objetos que constituyen los bloques de construcción de nuestro modelo, pasaremos a describir la arquitectura holística de los modelos entrenados. Debo decir que en este artículo he decidido combinar enfoques que, en apariencia, son completamente distintos. Incluso se podría decir que rivalizan. He decidido utilizar el enfoque propuesto con la descomposición wavelet de las series temporales como el procesamiento inicial de los datos de origen antes del método TiDE, discutido en el artículo anterior. Como consecuencia, hemos introducido cambios en la arquitectura del Сodificador del estado del entorno, que se representa en el método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En el cuerpo del método, como es habitual, primero comprobaremos la validez del puntero obtenido al array dinámico para registrar la arquitectura del modelo y, de ser necesario, crearemos una instancia del nuevo objeto.

Luego utilizaremos el objeto básico de la capa neuronal completamente conectada para obtener los datos brutos.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

El modelo, como siempre, recibirá datos de entrada "brutos", así que realizaremos su procesamiento inicial en la capa de normalización de datos por lotes:

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 10000;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, transpondremos los datos originales para que en las operaciones posteriores podamos analizar de forma independiente las secuencias unitarias de los indicadores utilizados:

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Después utilizaremos un bloque de 10 capas de FED-w:

//--- layer 3-12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFEDW;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.activation = None;
   for(int i = 0; i < 10; i++)
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

Y justo detrás del bloque estableceremos un Сodificador de series temporales completamente conectado:

//--- layer 13
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTiDEOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.window_out = NForecast;
   descr.step = 4;
     {
      int windows[] = {HistoryBars, 2 * EmbeddingSize, EmbeddingSize, 2 * EmbeddingSize, NForecast};
      if(ArrayCopy(descr.windows, windows) <= 0)
         return false;
     }
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, y al igual que antes, utilizaremos una capa convolucional de corrección del desplazamiento predictivo:

//--- layer 14
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.step = NForecast;
   descr.window_out = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Transpondremos los valores predichos a una representación de los datos originales:

//--- layer 15
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y retornaremos los parámetros estadísticos de la secuencia temporal de origen:

//--- layer 16
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Como podemos ver, los únicos cambios se dan en la arquitectura interna del Codificador. Por lo tanto, solo tendremos que cambiar el puntero a la capa del estado latente del Сodificador para extraer los datos. Mientras que la arquitectura del Actor y del Crítico permanecerá inalterada.

#define        LatentLayer             14

Además, no necesitaremos introducir cambios ni en los asesores de interacción con el entorno ni en los asesores de entrenamiento de modelos. El lector podrá ver su código completo en el archivo adjunto, mientras que la descripción de los algoritmos se encuentra en el artículo anterior.

3. Simulación

En este artículo presentamos el método FEDformer, que traslada el análisis de series temporales al dominio de las características de frecuencia. Es un método bastante interesante y prometedor. Asimismo, hemos hecho un trabajo considerable para implementar los enfoques propuestos con MQL5.

Una vez más, quisiera destacar que el artículo presenta una visión propia de la aplicación de los planteamientos propuestos, bastante distinta de la descripción del método presentada en el artículo del autor. Por lo tanto, las conclusiones extraídas de los resultados de las pruebas del modelo solo se aplicarán a esta implementación y no podrán extrapolarse totalmente al método del autor.

Como ya hemos dicho, los cambios solo han afectado a la arquitectura interna del Сodificador, lo cual significa que podremos utilizar muestras de entrenamiento recogidas previamente para entrenar los modelos.

Recordemos que para el entrenamiento offline del modelo, utilizaremos trayectorias de interacción con el entorno previamente recopiladas. Hemos recopilado datos históricos reales para todo el año 2023. Instrumento - EURUSD, marco temporal - H1. El modelo entrenado se ha puesto a prueba en el simulador de estrategias de MetaTrader 5 con los datos históricos de enero de 2024.

En la primera etapa, hemos entrenado el Сodificador de estados del entorno, minimizando el error entre las tasas de descripción reales de los estados del entorno posteriores y sus valores predichos. El Codificador solo analiza y predice los estados del entorno que son independientes de las acciones del Agente. Por ello, realizaremos un entrenamiento completo del Сodificador sin actualizar la muestra de entrenamiento.

En mi opinión, en esta fase ha mejorado la calidad de la predicción de los posteriores estados del entorno. Prueba de ello es la reducción de errores en el proceso de entrenamiento. Sin embargo, no hemos comparado gráficamente los valores reales y previstos para analizar su calidad con detalle.

En la segunda etapa iterativa, hemos implementado el entrenamiento de la política del Actor, que se realiza en paralelo con el modelo del Crítico, y que ofrece la evaluación más probable de las acciones del Actor. En esta fase, la exactitud de valoración del Actor tiene una importancia crítica para nosotros. Por lo tanto, hemos alternado el proceso de entrenamiento de los modelos y la actualización de los datos de la muestra de entrenamiento considerando la política actual del Actor.

Tras una serie de iteraciones como las anteriores, hemos logrado entrenar una política de comportamiento del Actor que generara beneficios tanto en el horizonte temporal del entrenamiento como en el de prueba. Ahora le presentamos los resultados de las pruebas.

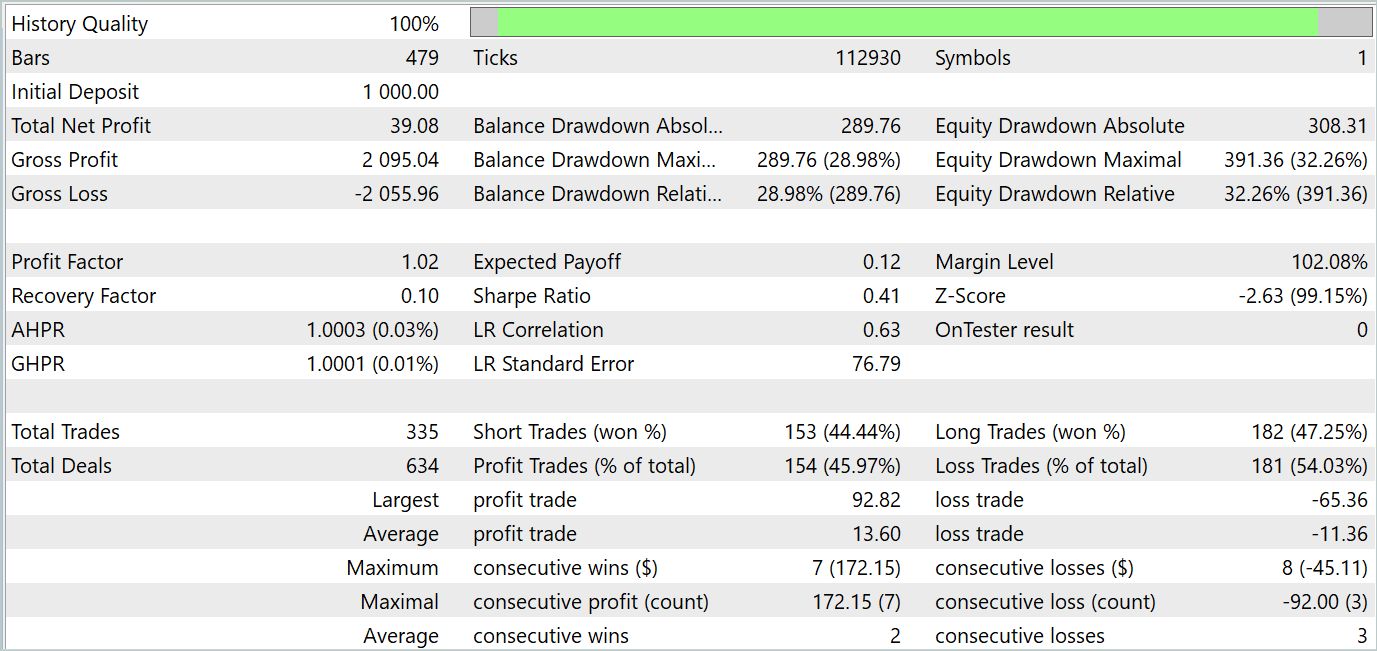
Como podemos ver, el gráfico de balance mantiene una tendencia general al alza. Al mismo tiempo, en el gráfico pueden distinguirse claramente 4 tendencias: 2 rentables y 2 no rentables. En el lado positivo, las tendencias rentables tienen más potencial. Esto nos permite acumular suficientes beneficios para no perder nuestro depósito en un periodo de pérdidas. Sin embargo, se observan maniobras arriesgadas. Durante el periodo de prueba, el factor de beneficio ha sido de solo 1,02, mientras que el porcentaje de transacciones rentables se ha situado justo por debajo del 46%.

En general, el modelo muestra potencial, pero hay que seguir trabajando para minimizar los periodos de pérdidas.

Conclusión

En este artículo, nos hemos familiarizado con el método FEDformer, propuesto para la previsión de series temporales a largo plazo. En este se ofrece un mecanismo de atención con aproximación frecuencial de bajo rango y descomposición mixta para controlar el desplazamiento de la distribución.

En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Asimismo, hemos entrenado y probado el modelo con datos históricos reales. Los resultados de las pruebas demuestran el potencial del modelo analizado, pero, al mismo tiempo, hay puntos que requieren una atención especial.

Enlaces

• FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de cobros de ejemplo Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL