
Neural networks made easy (Part 13): Batch Normalization
Contents
- Introduction
- 1. Theoretical Prerequisites for Normalization
- 2. Implementation
- 2.1. Creating a New Class for Our Model
- 2.2. Feed-Forward
- 2.3. Feed-Backward
- 2.4. Changes in the Neural Network Base Classes
- 3. Testing
- Conclusion
- References
- Programs Used in the Article
Introduction
In the previous article, we started considering methods aimed at increasing the convergence of neural networks and got acquainted with the Dropout method, which is used to reduce the co-adaptation of features. Let us continue this topic and get acquainted with the methods of normalization.
1. Theoretical Prerequisites for Normalization
Various approaches to data normalization are used in neural network application practice. However, all of them are aimed at keeping the training sample data and the output of the hidden layers of the neural network within a certain range and with certain statistical characteristics of the sample, such as variance and median. This is important, because network neurons use linear transformations which in the process of training shift the sample towards the antigradient.
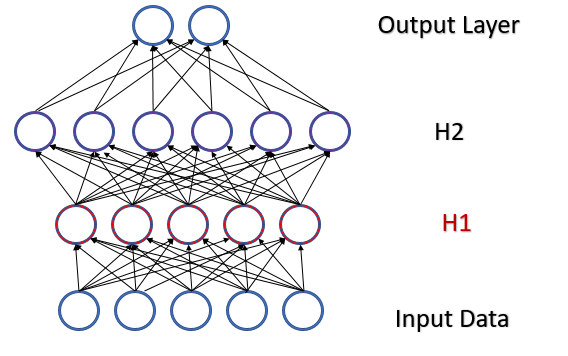
Consider a fully connected perceptron with two hidden layers. During a feed-forward pass, each layer generates a certain data set that serves as a training sample for the next layer. The result of the output layer is compared with the reference data. Then, during the feed-backward pass, the error gradient is propagated from the output layer through hidden layers towards the initial data. Having received an error gradient at each neuron, we update the weight coefficients, adjusting the neural network for the training samples of the last feed-forward pass. A conflict arises here: the second hidden layer (H2 in the figure below) is adjusted to the data sample at the output of the first hidden layer (H1 in the figure), while by changing the parameters of the first hidden layer we have already changed the data array. In other words, we adjust the second hidden layer to the data sample which no longer exists. A similar situation occurs with the output layer, which adjusts to the second hidden layer output which has already changed. The error scale will be even greater if we consider the distortion between the first and the second hidden layers. The deeper the neural network, the stronger the effect. This phenomenon is referred to as internal covariate shift.
Classical neural networks partly solve this problem by reducing the learning rate. Minor changes in weights do not entail significant changes in the sample distribution at the output of the neural layer. But this approach does not solve the scaling problem which appears with an increase in the number of neural network layers, and it also reduces the learning speed. Another problem of a small learning rate is that the process can get stuck on local minima, which we have already discussed in article 6.
In February 2015, Sergey Ioffe and Christian Szegedy proposed Batch Normalization as a solution to the problem of internal covariance shift [13]. The idea of the method is to normalize each individual neuron on a certain time interval with a shift in the median of the sample (batch) towards zero and to bring the sample variance to 1.
The normalization algorithm is as follows. First, the average value is calculated for the data batch.
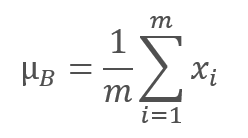
here m is the batch size.
Then the variance of the original batch is calculated.
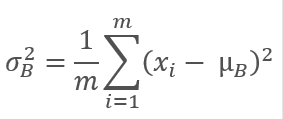
Batch data is normalized to bring the batch to the zero mean and to the variance of 1.
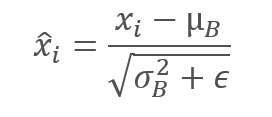
Note that the constant ϵ, a small positive number, is added to the batch variance in the denominator to avoid division by zero.
However, it turned out that such normalization can distort the influence of the original data. Therefore, the method authors have added one more step: scaling and shift. They have introduced two variables, γ and β, which are trained together with the neural network by gradient descent method.
![]()
The application of this method makes enables the obtaining of a data batch with the same distribution at each step of training, which makes neural network training more stable and allows an increase in the learning rate. In general, this method assists in improving the quality of training while reducing the time spent on neural network training.
However, this increases the cost of storing additional rates. Also, historical data of each neuron for the entire batch size should be stored for the calculation of the average value and dispersion. Here we can check the application of the exponential average. The figure below shows the graphs of the moving average and moving variance for 100 elements in comparison with the exponential moving average and exponential moving variance for the same 100 elements. The chart is built for 1000 random elements in the range between -1.0 and 1.0.
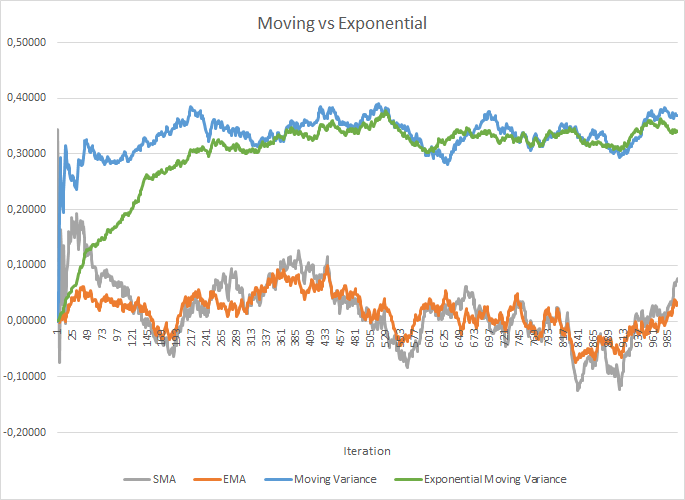
In this chart, the moving average and the exponential moving average approach each other after 120-130 iterations and then the deviation is minimal (so that it can be neglected). In addition, the exponential moving average graph is smoother. EMA can be calculated by knowing the previous value of the function and the current element of the sequence. Let us view the formula for the exponential moving average.
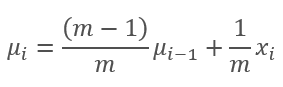 ,
,
where
- m is the batch size,
- i is an iteration.
It took a little more iterations (310-320) to bring the moving variance and the exponential moving variance graphs closer together, but the overall picture is similar. In the case of variance, the use of the exponential algorithm not only saves memory, but it also significantly reduces the number of calculations, since for the moving variance the deviation from the average would be calculated for the entire batch.
The experiments carried out by the method authors show that the use of the Batch Normalization method also serves as a regularizer. This reduces the need for other regularization methods, including the previously considered Dropout. Furthermore, later research show that the combined use of Dropout and Batch Normalization has a negative effect on the neural network learning results.
The proposed normalization algorithm can be found in various variations in modern neural network architectures. The authors suggest using Batch Normalization immediately before the nonlinearity (activation formula). The Layer Normalization method presented in July 2016 can be considered as one of the variations of this algorithm. We have already considered this method when studying the attention mechanism (article 9).
2. Implementation
2.1 Creating a New Class for Our Model
Now that we have considered the theoretical aspects, let us implement it in our library. Let us create a new class CNeuronBatchNormOCL to implement the algorithm.
class CNeuronBatchNormOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; ///< Pointer to the object of the previous layer uint iBatchSize; ///< Batch size CBufferDouble *BatchOptions; ///< Container of method parameters ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::BatchFeedForward().@param NeuronOCL Pointer to previous layer. ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateBatchOptionsMomentum() or ::UpdateBatchOptionsAdam() in depends on optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previous layer. public: /** Constructor */CNeuronBatchNormOCL(void); /** Destructor */~CNeuronBatchNormOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, uint batchSize, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (iBatchSize>1 ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (iBatchSize>1 ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (iBatchSize>1 ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (iBatchSize>1 ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (iBatchSize>1 ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradientBatch(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronBatchNormOCL; }///< Identificator of class.@return Type of class };
The new class will inherit from the CNeuronBaseOCL base class. By analogy with the CNeuronDropoutOCL class, let us add the PrevLayer variable. The data buffer replacement method demonstrated in the previous article will be applied when specifying the batch size less than "2", which will be saved to the iBatchSize variable.
The Batch Normalization algorithm requires saving of some parameters which are individual for each neuron of the normalized layer. In order not to generate many separate buffers for each individual parameter, we will create a single BatchOptions buffer of parameters with the following structure.

It can be seen from the presented structure that the size of the parameter buffer will depend on the applied parameter optimization method and, therefore, will be created in the class initialization method.
The set of class methods is already standard. Let us have a look at them. In the class constructor, let us reset the pointers to objects and set the batch size to one, which practically excludes the layer from the network operation until it is initialized.
CNeuronBatchNormOCL::CNeuronBatchNormOCL(void) : iBatchSize(1) { PrevLayer=NULL; BatchOptions=NULL; }
In the class destructor, delete the object of the parameter buffer and set the pointer to the previous layer to zero. Please note that we are not deleting the object of the previous layer, but only zeroing the pointer. The object will be deleted where it was created.
CNeuronBatchNormOCL::~CNeuronBatchNormOCL(void) { if(CheckPointer(PrevLayer)!=POINTER_INVALID) PrevLayer=NULL; if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; }
Now, consider the class initialization method CNeuronBatchNormOCL::Init. In the parameters, pass to the class the number of neurons of the next layer, an index for identifying the neuron, a pointer to the OpenCL object, the number of neurons in the normalization layer, the batch size and the parameter optimization method.
At the beginning of the method, call the relevant method of the parent class, in which the basic variables and data buffers will be initialized. Then save the batch size and set the layer activation function to None.
Please pay attention to the activation function. The use of this functionality depends on the architecture of the neural network. If the neural network architecture requires the inclusion of normalization before the activation function, as recommended by the authors of the method, then the activation function must be disabled on the previous layer and the required function must be specified in the normalization layer. Technically, the activation function is specified by calling the SetActivationFunction method of the parent class, after initializing a class instance. If normalization should be used after the activation function in accordance with the network architecture, the activation method should be specified in the previous layer and there will be no activation function in the normalization layer.
bool CNeuronBatchNormOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons,uint batchSize,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,numNeurons,optimization_type)) return false; activation=None; iBatchSize=batchSize; //--- if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; int count=(int)numNeurons*(optimization_type==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferInit(count,0)) return false; //--- return true; }
At the end of the method, we create a buffer of parameters. As mentioned above, the buffer size depends on the number of neurons in the layer and the parameter optimization method. When using SGD, we reserve 7 elements for each neuron; when optimizing by the Adam method, we need 9 buffer elements for each neuron. After successful creation of all buffers, exit the method with true.
The full code of all classes and their methods is available in the attachment.
2.2. Feed-Forward
As the next step, let us consider the feed-forward pass. Let us start by considering the direct pass BatchFeedForward. The kernel algorithm will be launched for each separate neuron.
The kernel receives in parameters pointers to 3 buffers: initial data, buffer of parameters and a buffer for writing the results. Additionally, pass in parameters the batch size, the optimization method and the neuron activation algorithm.
At the kernel beginning, check the specified size of the normalization window. If normalization is performed for one neuron, exit the method without performing further operations.
After successful verification, we get the stream identifier, which will indicate the position of the normalized value in the input data tensor. Based on the identifier, we can determine the shift for the first parameter in the tensor of normalization parameters. At this step, the optimization method will suggest the structure of the parameter buffer.
Next, calculate the exponential mean and variance at this step. Based on this data, calculate the normalized value for our element.
The next step of the algorithm of Batch Normalization is shifting and scaling. Earlier, during initialization, we filled the parameter buffer with zeros, so if we perform this operation "in its pure form" at the first step, we will receive "0". To avoid this, check the current value of the γ parameter and, if it is equal to "0", change its value to "1". Leave the shift at zero. Perform shifting and scaling in this form.
__kernel void BatchFeedForward(__global double *inputs, __global double *options, __global double *output, int batch int optimization, int activation) { if(batch<=1) return; int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- for(int i=0;i<(optimization==0 ? 7 : 9);i++) if(isnan(options[shift+i])) options[shift+i]=0; //--- double mean=(options[shift]*((double)batch-1)+inputs[n])/((double)batch); double delt=inputs[n]-mean; double variance=options[shift+1]*((double)batch-1.0)+pow(delt,2); if(options[shift+1]>0) variance/=(double)batch; double nx=delt/sqrt(variance+1e-6); //--- if(options[shift+3]==0) options[shift+3]=1; //--- double res=options[shift+3]*nx+options[shift+4]; switch(activation) { case 0: res=tanh(clamp(res,-20.0,20.0)); break; case 1: res=1/(1+exp(-clamp(res,-20.0,20.0))); break; case 2: if(res<0) res*=0.01; break; default: break; } //--- options[shift]=mean; options[shift+1]=variance; options[shift+2]=nx; output[n]=res; }
After obtaining the normalized value, let us check if we need to execute the activation function on this layer and perform the necessary actions.
Now, simply save the new values to the data buffers and exit the kernel.
The BatchFeedForward kernel building algorithm is rather straightforward and thus we can move on to creating a method for calling the kernel from the main program. This functionality will be implemented by the CNeuronBatchNormOCL::feedForward method. The method algorithm is similar to the relevant methods of other classes. The method receives in parameters a pointer to the previous neural network layer.
At the beginning of the method, check the validity of the received pointer and the pointer to the OpenCL object (as you might remember this is a replica of a standard library class for working with the OpenCL program).
At the next step, save the pointer to the previous layer of the neural network and check the batch size. If the size of the normalization window does not exceed "1", copy the type of the activation function of the previous layer and exit the method with the true result. This way we provide data for replacing buffers and exclude unnecessary iterations of the algorithm.
bool CNeuronBatchNormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- PrevLayer=NeuronOCL; if(iBatchSize<=1) { activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); return true; } //--- if(CheckPointer(BatchOptions)==POINTER_INVALID) { int count=Neurons()*(optimization==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(!BatchOptions.BufferInit(count,0)) return false; } if(!BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_inputs,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_output,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_optimization,(int)optimization)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_activation,(int)activation)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_BatchFeedForward,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch Feed Forward: %d",GetLastError()); return false; } if(!Output.BufferRead() || !BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
If, after all the checks, we have reached the launch of the direct pass kernel, we need to prepare the initial data for launching it. First, check the validity of the pointer to the parameter buffer of the normalization algorithm. Create and initialize a new buffer if necessary. Next, create a buffer in the video card memory and load the buffer contents.
Set the number of launched threads equal to the number of neurons in the layer and pass the pointers to the data buffers, along with the required parameters, to the kernel.
After the preparatory work, send the kernel for execution and read back the updated buffer data from the video card memory. Please note that data from two buffers are received from the video card: information from the algorithm output and a parameter buffer, in which we saved the updated mean, variance and normalized value. This data will be used in further iterations.
After the completion of the algorithm, delete the parameter buffer from the video card memory in order to free up memory for buffers of further layers of the neural network. Then, exit the method with true.
The full code of all classes and their methods from the library is available in the attachment.
2.3. Feed-Backward
The feed-backward pass again consists of two stages: error back propagation and updating of weights. Instead of usual weights, we will train parameters γ and β of the scaling and shifting function.
Let us start with the gradient descent functionality. Create the kernel CalcHiddenGradientBatch to implement its functionality. The kernel receives in parameters pointers to tensors of normalization parameters received from the next layer of gradients, previous layer output data (obtained during the last feed-forward pass) and tensors of previous layer gradients, to which the algorithm results will be written. The kernel will also receive in parameters the batch size, the type of the activation function, and the method for optimizing parameters.
As with the direct pass, at the kernel beginning check the batch size; if it is less than or equal to 1, then exit the kernel without performing other iterations.
The next step is to get the serial number of the thread and to determine the shift in the parameters tensor. These actions are similar to those described earlier in the feed-forward pass.
__kernel void CalcHiddenGradientBatch(__global double *options, ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer __global double *matrix_i, ///<[in] Tensor of previous layer output __global double *matrix_ig, ///<[out] Tensor of gradients at previous layer uint activation, ///< Activation type (#ENUM_ACTIVATION) int batch, ///< Batch size int optimization ///< Optimization type ) { if(batch<=1) return; //--- int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- double inp=matrix_i[n]; double gnx=matrix_g[n]*options[shift+3]; double temp=1/sqrt(options[shift+1]+1e-6); double gmu=(-temp)*gnx; double gvar=(options[shift]*inp)/(2*pow(options[shift+1]+1.0e-6,3/2))*gnx; double gx=temp*gnx+gmu/batch+gvar*2*inp/batch*pow((double)(batch-1)/batch,2.0); //--- if(isnan(gx)) gx=0; switch(activation) { case 0: gx=clamp(gx+inp,-1.0,1.0)-inp; gx=gx*(1-pow(inp==1 || inp==-1 ? 0.99999999 : inp,2)); break; case 1: gx=clamp(gx+inp,0.0,1.0)-inp; gx=gx*(inp==0 || inp==1 ? 0.00000001 : (inp*(1-inp))); break; case 2: if(inp<0) gx*=0.01; break; default: break; } matrix_ig[n]=clamp(gx,-MAX_GRADIENT,MAX_GRADIENT); }
Next, sequentially calculate the gradients for all functions of the algorithm.

And finally, propagate the gradient through the activation function of the previous layer. Save the resulting value to the gradient tensor of the previous layer.
Following the CalcHiddenGradientBatсh kernel, let us consider the CNeuronBatchNormOCL::calcInputGradients method which will start kernel execution from the main program. Similar to the relevant methods of other classes, the method receives in parameters a pointer to the object of the previous neural network layer.
At the beginning of the method, check the validity of the received pointer and of the pointer to the OpenCL object. After that, check the batch size. If it is less than or equal to 1, then exit the method. The result returned from the method will depend on the validity of the pointer to the previous layer, which was saved during the feed-forward pass.
If we move further along the algorithm, check the validity of the parameter buffer. If an error occurs, exit the method with the result false.
Please note that the propagated gradient belongs to the last feed-forward pass. That is why, at the last two points of control, we checked the objects participating in the feed-forward.
bool CNeuronBatchNormOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_ig,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_activation,NeuronOCL.Activation())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_optimization,(int)optimization)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_CalcHiddenGradientBatch,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch CalcHiddenGradient: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
As with the feed-forward pass, the number of kernel threads launched will be equal to the number of neurons in the layer. Send the contents of normalization parameter buffer to the video card memory and pass required tensor and parameter pointers to the kernel.
After performing all the above operations, run the kernel execution and calculate the resulting gradients from the video card memory into the corresponding buffer.
At the end of the method, remove the tensor of normalization parameters from the video card memory and exit the method with the result true.
After propagating the gradient, it is time to update the shift and scale parameters. To implement these iterations, create 2 kernels, according to the number of the previously described optimization methods, UpdateBatchOptionsMomentum and UpdateBatchOptionsAdam.
Let us start with the UpdateBatchOptionsMomentum method. The method receives in parameters pointers to two tensors: of normalization parameters and or gradients. Also, pass optimization method constants in the method parameters: the learning rate and the momentum.
At the beginning of the kernel, obtain the thread number and determine the shift in the tensor of the normalization parameters.
Using the source data, let us calculate delta for γ and β. For this operation, I used vector calculations with the 2-element double vector. This method allows the parallelizing of computations.
Adjust parameters γ, β and save the results in the appropriate elements of the normalization parameters tensor.
__kernel void UpdateBatchOptionsMomentum(__global double *options, ///<[in,out] Options matrix m*7, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer double learning_rates, ///< Learning rates double momentum ///< Momentum multiplier ) { const int n=get_global_id(0); const int shift=n*7; double grad=matrix_g[n]; //--- double2 delta=learning_rates*grad*(double2)(options[shift+2],1) + momentum*(double2)(options[shift+5],options[shift+6]); if(!isnan(delta.s0) && !isnan(delta.s1)) { options[shift+5]=delta.s0; options[shift+3]=clamp(options[shift+3]+delta.s0,-MAX_WEIGHT,MAX_WEIGHT); options[shift+6]=delta.s1; options[shift+4]=clamp(options[shift+4]+delta.s1,-MAX_WEIGHT,MAX_WEIGHT); } };
The UpdateBatchOptionsAdam kernel is built according to a similar scheme, but there are differences in the optimization method algorithm. The kernel receives in parameters pointers to the same parameter and gradient tensors. It also receives optimization method parameters.
At the beginning of the kernel, define the thread number and determine the shift in the parameter tensor.
Based on the data obtained, calculate the first and second moments. The vector calculations used here allow the calculation of moments for two parameters at the same time.
Based on the obtained moments, calculate the deltas and new parameter values. Calculation results will be saved into the corresponding elements of the tensor of normalization parameters.
__kernel void UpdateBatchOptionsAdam(__global double *options, ///<[in,out] Options matrix m*9, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer const double l, ///< Learning rates const double b1, ///< First momentum multiplier const double b2 ///< Second momentum multiplier ) { const int n=get_global_id(0); const int shift=n*9; double grad=matrix_g[n]; //--- double2 mt=b1*(double2)(options[shift+5],options[shift+6])+(1-b1)*(double2)(grad*options[shift+2],grad); double2 vt=b2*(double2)(options[shift+5],options[shift+6])+(1-b2)*pow((double2)(grad*options[shift+2],grad),2); double2 delta=l*mt/sqrt(vt+1.0e-8); if(isnan(delta.s0) || isnan(delta.s1)) return; double2 weight=clamp((double2)(options[shift+3],options[shift+4])+delta,-MAX_WEIGHT,MAX_WEIGHT); //--- if(!isnan(weight.s0) && !isnan(weight.s1)) { options[shift+3]=weight.s0; options[shift+4]=weight.s1; options[shift+5]=mt.s0; options[shift+6]=mt.s1; options[shift+7]=vt.s0; options[shift+8]=vt.s1; } };
To launch kernels from the main program, let us create the CNeuronBatchNormOCL::updateInputWeights method. The method receives in parameters a pointer to the previous neural network layer. Actually, this pointer will not be used in the method algorithm, but it is left for the inheritance of methods from the parent class.
At the beginning of the method, check the validity of the received pointer and of the pointer to the OpenCL object. Like for the previously considered CNeuronBatchNormOCL::calcInputGradients method, check the batch size and the validity of the parameter buffer. Load the contents of the parameter buffer into the video card memory. Set the number of threads equal to the number of neurons in the layer.
Further, the algorithm can follow two options, depending on the specified optimization method. Pass the initial parameters for the required kernel and restart its execution.
Regardless of the parameter optimization method, calculate the updated contents of the normalization parameters buffer and remove the buffer from the video card memory.
bool CNeuronBatchNormOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); //--- if(optimization==SGD) { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_learning_rates,eta)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_momentum,alpha)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsMomentum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsMomentum %d",GetLastError()); return false; } } else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_l,lr)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b2,b2)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsAdam,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsAdam %d",GetLastError()); return false; } } //--- if(!BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
After successful completion of the operations, exit the method with the result true.
Methods for buffer replacement were described in detail in the previous article and so I think they should not cause any difficulties. This also concerns operations with files (saving and loading a trained neural network).
The full code of all classes and their methods is available in the attachment.
2.4. Changes in the Neural Network Base Classes
Again, after creating a new class, let us integrate it into the general structure of the neural network. First, let us create an identifier for the new class.
#define defNeuronBatchNormOCL 0x7891 ///<Batchnorm neuron OpenCL \details Identified class #CNeuronBatchNormOCL
Next, define constant macro substitutions for working with new kernels.
#define def_k_BatchFeedForward 24 ///< Index of the kernel for Batch Normalization Feed Forward process (#CNeuronBathcNormOCL) #define def_k_bff_inputs 0 ///< Inputs data tensor #define def_k_bff_options 1 ///< Tensor of variables #define def_k_bff_output 2 ///< Tensor of output data #define def_k_bff_batch 3 ///< Batch size #define def_k_bff_optimization 4 ///< Optimization type #define def_k_bff_activation 5 ///< Activation type //--- #define def_k_CalcHiddenGradientBatch 25 ///< Index of the Kernel of the Batch neuron to transfer gradient to previous layer (#CNeuronBatchNormOCL) #define def_k_bchg_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_bchg_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_bchg_matrix_i 2 ///<[in] Tensor of previous layer output #define def_k_bchg_matrix_ig 3 ///<[out] Tensor of gradients at previous layer #define def_k_bchg_activation 4 ///< Activation type (#ENUM_ACTIVATION) #define def_k_bchg_batch 5 ///< Batch size #define def_k_bchg_optimization 6 ///< Optimization type //--- #define def_k_UpdateBatchOptionsMomentum 26 ///< Index of the kernel for Describe the process of SGD optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buom_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buom_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buom_learning_rates 2 ///< Learning rates #define def_k_buom_momentum 3 ///< Momentum multiplier //--- #define def_k_UpdateBatchOptionsAdam 27 ///< Index of the kernel for Describe the process of Adam optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buoa_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buoa_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buoa_l 2 ///< Learning rates #define def_k_buoa_b1 3 ///< First momentum multiplier #define def_k_buoa_b2 4 ///< Second momentum multiplier
In the neural network constructor CNet::CNet, let us add blocks which create new class objects and initialize new kernels (changes are highlighted in the code).
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
................
................
................
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
................
................
................
CNeuronBatchNormOCL *batch=NULL;
switch(desc.type)
{
................
................
................
................
//---
case defNeuronBatchNormOCL:
batch=new CNeuronBatchNormOCL();
if(CheckPointer(batch)==POINTER_INVALID)
{
delete temp;
return;
}
if(!batch.Init(outputs,0,opencl,desc.count,desc.window,desc.optimization))
{
delete batch;
delete temp;
return;
}
batch.SetActivationFunction(desc.activation);
if(!temp.Add(batch))
{
delete batch;
delete temp;
return;
}
batch=NULL;
break;
//---
default:
return;
break;
}
}
................
................
................
................
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(28);
................
................
................
................
opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward");
opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath");
opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum");
opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam");
//---
return;
}
Similarly, initiate new kernels when loading a pre-trained neural network.
bool CNet::Load(string file_name,double &error,double &undefine,double &forecast,datetime &time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return false; //--- ................ ................ ................ //--- if(CheckPointer(opencl)==POINTER_INVALID) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; else { //--- create kernels opencl.SetKernelsCount(28); ................ ................ ................ opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward"); opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath"); opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum"); opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam"); } } ................ ................ ................ ................ ................ }
Add a new type of neurons into the method that loads the pre-trained neural network.
bool CLayer::Load(const int file_handle) { iFileHandle=file_handle; if(!CArrayObj::Load(file_handle)) return false; if(CheckPointer(m_data[0])==POINTER_INVALID) return false; //--- CNeuronBaseOCL *ocl=NULL; CNeuronBase *cpu=NULL; switch(m_data[0].Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: ocl=m_data[0]; iOutputs=ocl.getConnections(); break; default: cpu=m_data[0]; iOutputs=cpu.getConnections().Total(); break; } //--- return true; }
Similarly, let us add a new type of neurons into dispatcher methods of the CNeuronBaseOCL base class.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- ................ ................ ................ CNeuronBatchNormOCL *batch=NULL; switch(TargetObject.Type()) { ................ ................ ................ case defNeuronBatchNormOCL: batch=TargetObject; temp=GetPointer(this); return batch.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
The full code of all classes and their methods is available in the attachment.
3. Testing
We continue to test new classes in the previously created Expert Advisors, which produces comparable data for the evaluation of the performance of individual elements. Let us test the normalization method base on the Expert Advisor from the article 12, replacing Dropout with Batch Normalization. The neural network structure of the new Expert Advisor is presented below. Here, the learning rate was increased from 0.000001 to 0.001.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*24; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=None; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
The Expert Advisor was tested on EURUSD, H1 timeframe. Data of 20 latest candlestick were input into the neural network, similarly to previous tests.
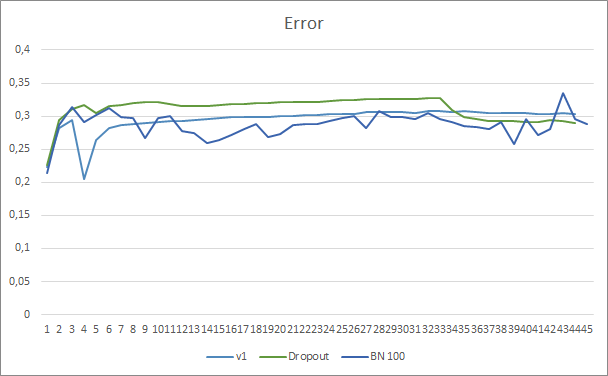
The neural network prediction error graph shows that the EA with batch normalization has a less smoothed graph, which can be caused by a sharp increase in the learning rate. However, the prediction error is lower than that of the previous tests almost throughout the test.
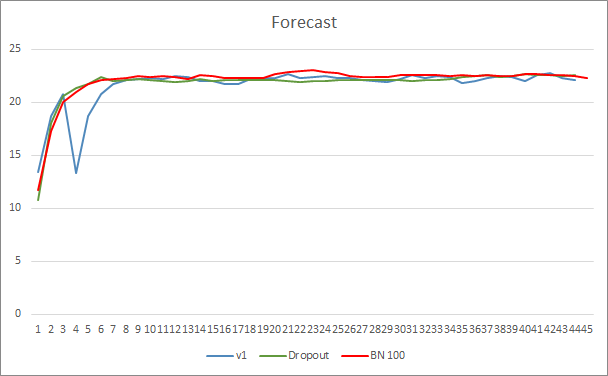
Prediction hit graphs of all three Expert Advisors are quite close and thus we cannot conclude that any of them is definitely better.
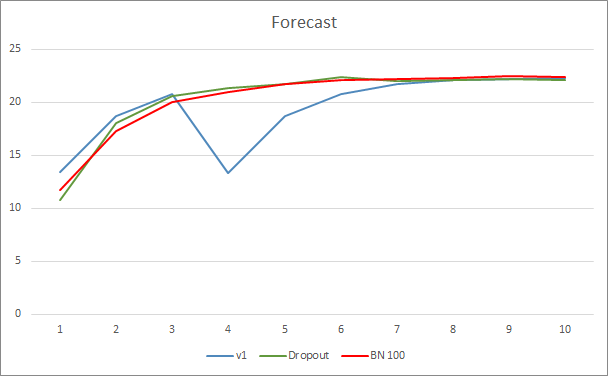
Conclusion
In this article, we continued considering methods aimed at increasing the convergence of neural networks and have added a Batch Normalization class to our library. Testing has shown that the use of this method can reduce the neural network error and increase the learning rate.
References
- Neural networks made easy
- Neural networks made easy (Part 2): Network training and testing
- Neural networks made easy (Part 3): Convolutional networks
- Neural networks made easy (Part 4): Recurrent networks
- Neural networks made easy (Part 5): Multithreaded calculations in OpenCL
- Neural networks made easy (Part 6): Experimenting with the neural network learning rate
- Neural networks made easy (Part 7): Adaptive optimization methods
- Neural networks made easy (Part 8): Attention mechanisms
- Neural networks made easy (Part 9): Documenting the work
- Neural networks made easy (Part 10): Multi-Head Attention
- Neural networks made easy (Part 11): A take on GPT
- Neural networks made easy (Part 12): Dropout
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- Layer Normalization
Programs Used in the Article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH_b.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the GTP architecture, with 5 attention layers + BatchNorm |
| 2 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 3 | NeuroNet.cl | Code Base | OpenCL program code library |
| 4 | NN.chm | HTML Help | A compiled Library Help CHM file. |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/9207
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Brute force approach to pattern search (Part IV): Minimal functionality
Brute force approach to pattern search (Part IV): Minimal functionality
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
HI. I am getting this error
CANDIDATE FUNCTION NOT VIABLE: NO KNOW CONVERSION FROM 'DOUBLE __ATTRIBUTE__((EXT_VECTOR_TYPE92000' TO 'HALF4' FOR 1ST ARGUMENT
2022.11.30 08:52:28.185 Fractal_OCL_AttentionMLMH_b (EURJPY,D1) OpenCL program create failed. Error code=5105
when using EA since article part 10 examples
Please any guess???
Thank you
Hi, can you send full log?
Hi. Thanks for help
Rogerio
Hi. Thanks for help
Rogerio
Hello Rogerio.
1. You don't create model.
2. Your GPU doesn't support double. Please, load last version from article https://www.mql5.com/ru/articles/11804
Hi Dmitriy
You wrote: You don't create model.
But How do I create a model ? I compile all program fonts and run the EA.
The EA creates a file on folder 'files' whith the extension nnw. this file isn't the model ?
Thanks
Hi Teacher Dmitriy
Now none of the .mqh compiles
for example when i try to compile the vae.mqh i obtain this error
'MathRandomNormal' - undeclared identifier VAE.mqh 92 8
I will try to start from the begning again.
One more question:When you put a new version of NeuroNet.mqh this version is fully compatible with the other olders EA ?
Thanks
rogerio
PS: Even deleting all files and directories and start with a new copy from PART 1 and 2 I can not more compile any code.
For exemple when a try to compile the code in fractal.mq5 a obtain this error:
cannot convert type 'CArrayObj *' to reference of type 'const CArrayObj *' NeuroNet.mqh 437 29
Sorry I realy wanted to understand your articles and code.
PS2: OK i removed the word 'const' on 'feedForward', 'calcHiddenGradients' and 'sumDOW' and now i could compile the Fractal.mqh and Fractal2.mqh