
Нейросети — это просто (Часть 13): Пакетная нормализация (Batch Normalization)
Содержание
- Введение
- 1. Теоретические предпосылки нормализации
- 2. Реализация
- 2.1. Создаем новый класс для нашей модели
- 2.2. Прямой проход
- 2.3. Обратный проход
- 2.4. Точечные изменения в базовых классах нейронной сети
- 3. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
В предыдущей статье мы начали рассмотрение методов повышения сходимости нейронных сетей при обучении и познакомились с Dropout, который применяется для снижения совместной адаптации признаков. В этой статье я предлагаю продолжить начатую тему и познакомиться с методами нормализации.
1. Теоретические предпосылки нормализации
В практике использования нейронных сетей используются различные подходы к нормализации данных. Но все они направлены на удержание данных обучающей выборки и выходных данных скрытых слоев нейронной сети в заданном диапазоне и с определенными статистическими характеристиками выборки, такими как дисперсия и медиана. Почему же это так важно, ведь мы помним, что в нейронах сети применяются линейные преобразования, которые в процессе обучения смещают выборку в сторону антиградиента.
Рассмотрим полносвязный перцептрон с 2-мя скрытыми слоями. При прямом проходе каждый слой генерирует некую совокупность данных, которые служат обучающей выборкой для последующего слоя. Результат работы выходного слоя сравнивается с эталонными данными и на обратном проходе распространяется градиент ошибки от выходного слоя через скрытые слои к исходным данным. Получив на каждом нейроне свой градиент ошибки мы обновляем весовые коэффициенты, подстраивая нашу нейронную сеть под обучающие выборки последнего прямого прохода. И здесь возникает конфликт: мы подстраиваем второй скрытый слой (H2 на рисунке ниже) под выборку данных на выходе первого скрытого слоя (на рисунке H1), в то время, как, изменив параметры первого скрытого слоя мы уже изменили массив данных. Т. е. мы подстраиваем второй скрытый слой под уже несуществующую выборку данных. Аналогичная ситуация и с выходным слоем, который подстраивается под уже измененный выход второго скрытого слоя. А если еще учесть искажение между первым и вторым скрытыми слоями, то масштабы ошибки увеличиваются. И чем глубже нейронная сеть, тем сильнее проявление этого эффекта. Это явление было названо внутренним ковариационным сдвигом.
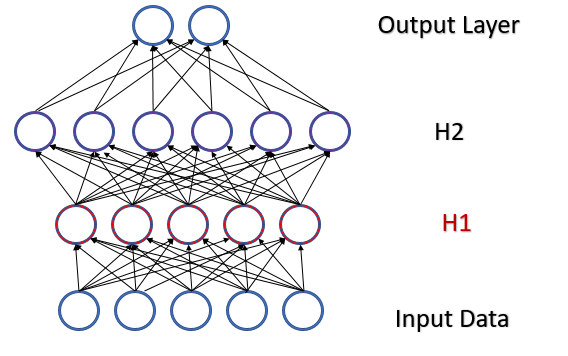
В классических нейронных сетях указанная проблема частично решалась уменьшением коэффициента обучения. Небольшие изменения весовых коэффициентов не сильно изменяют распределение выборки на выходе нейронного слоя. Но такой подход не решает масштабирования проблемы с ростом количества слоев нейронной сети и снижает скорость обучения. Еще одна проблема маленького коэффициента обучения — застревание в локальных минимумах, об этом мы уже говорили в статье [6].
В феврале 2015 года Sergey Ioffe и Christian Szegedy предложили метод пакетной нормализации данных (Batch Normalization) для решения проблемы внутреннего ковариационного сдвига[13]. Суть метода заключалась в нормализации каждого отдельного нейрона на некоем временном интервале со смещением медианы выборки к нулю и приведением дисперсии выборки к 1.
Алгоритм проведения нормализации следующий. Вначале по выборке данных считается среднее значение.
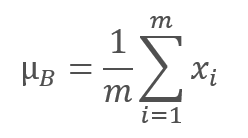
где m — размер выборки (batch).
Затем считаем дисперсию исходной выборки.
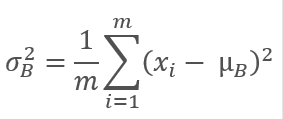
И нормализуем данные выборки приведя выборку к нулевому среднему и единичной дисперсии.
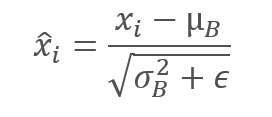
Обратите внимание, что в знаменателе к дисперсии выборки прибавляется константа ϵ, небольшое положительное число с целью исключить деление на ноль.
Но как оказалось, такая нормализация может исказить влияние исходных данных. Поэтому авторы метода добавили еще один шаг — масштабирование и смещение. Были введены 2 переменные γ и β, которые обучаются вместе с нейронной сетью методом обратного градиентного спуска.
![]()
Применение данного метода позволяет на каждом шаге обучения получать выборку данных с одинаковым распределением, что на практике делает обучение нейронной сети более стабильным и позволяет увеличить коэффициент обучения. В целом это позволит повысить качество обучения при меньших затратах времени на обучение нейронной сети.
Но в тоже время возрастают затраты на хранение дополнительных коэффициентов. А также для расчета скользящих средней и дисперсии требуется хранение в памяти исторических данных каждого нейрона на весь размер пакета. И тут можно посмотреть в сторону экспоненциальной средней. На рисунке ниже наглядно представлены графики скользящей средней и скользящей дисперсии на 100 элементов в сравнении с экспоненциальной скользящей средней и экспоненциальной скользящей дисперсии на те же 100 элементов. График был построен для 1000 случайных элементов из диапазона от -1.0 до 1.0.
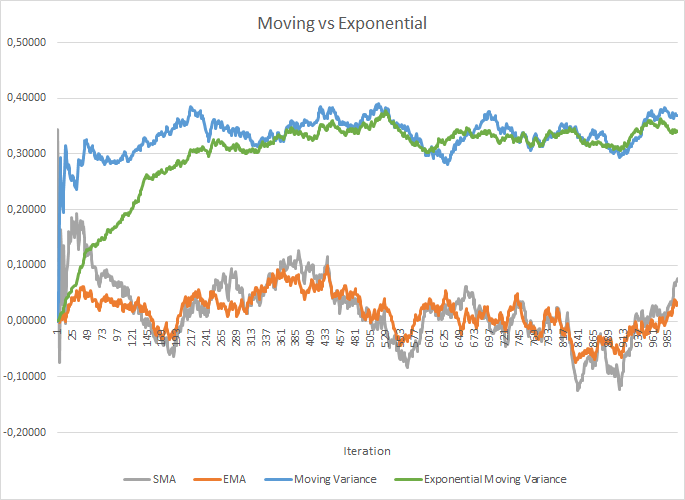
Как видно на графике, скользящая средняя и экспоненциальная скользящая средняя сближаются после 120-130 итераций и дальше отклонение минимально, которым можно пренебречь. К тому же график экспоненциальной скользящей средней имеет более сглаженный вид. А вот для расчета EMA достаточно предыдущего значения функции и текущего элемента последовательности. Напомню формулу экспоненциальной скользящей средней.
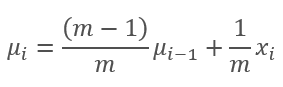 ,
,
где
- m — размер выборки (batch),
- i - итерация.
Для сближения графиков скользящей дисперсии и экспоненциальной скользящей дисперсии потребовалось чуть больше итераций (310-320), но в целом картина похожая. В случае с дисперсией применение экспоненциальной дает не только экономию памяти, но и значительно снижает количество вычислений, т.к. для скользящей дисперсии мы бы пересчитывали отклонение от средней для всего batch-а.
Эксперименты, проведенные авторами метода, показывают, что применение метода Batch Normalization выступает и в роли регуляризатора. Это позволяет отказаться от использования других методов регуляризации, в частности от рассмотренного ранее Dropout. Более того, есть более поздние работы, в которых показано, что совместное использование Dropout и Batch Normalization отрицательно сказывается на результатах обучения нейронной сети.
В современных архитектурах нейронных сетей предложенный алгоритм нормализации можно встретить в различных вариациях. Авторы предлагают использовать Batch Normalization непосредственно перед нелинейностью (формулой активации). Как одну из вариаций данного алгоритма можно рассматривать метод Layer Normalization, представленный в июле 2016 года. С ним мы встречались при изучении механизма внимания [9].
2. Реализация
2.1 Создаем новый класс для нашей модели
После рассмотрения теоретических аспектов метода посмотрим, как мы можем реализовать его в нашей библиотеке. Для реализации алгоритма создадим новый класс CNeuronBatchNormOCL.
class CNeuronBatchNormOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL *PrevLayer; ///< Pointer to the object of the previous layer uint iBatchSize; ///< Batch size CBufferDouble *BatchOptions; ///< Container of method parameters ///\ingroup neuron_base_ff virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); ///< \brief Feed Forward method of calling kernel ::BatchFeedForward().@param NeuronOCL Pointer to previos layer. ///\ingroup neuron_base_opt virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); ///< Method for updating weights.\details Calling one of kernels ::UpdateBatchOptionsMomentum() or ::UpdateBatchOptionsAdam() in depends of optimization type (#ENUM_OPTIMIZATION).@param NeuronOCL Pointer to previos layer. public: /** Constructor */CNeuronBatchNormOCL(void); /** Destructor */~CNeuronBatchNormOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, uint batchSize, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object. #param[in] numNeurons Number of neurons in layer @param optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolen result of operations. //--- virtual int getOutputIndex(void) { return (iBatchSize>1 ? Output.GetIndex() : PrevLayer.getOutputIndex()); } ///< Get index of output buffer @return Index virtual int getGradientIndex(void) { return (iBatchSize>1 ? Gradient.GetIndex() : PrevLayer.getGradientIndex()); } ///< Get index of gradient buffer @return Index //--- virtual int getOutputVal(double &values[]) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getOutputVal(CArrayDouble *values) { return (iBatchSize>1 ? Output.GetData(values) : PrevLayer.getOutputVal(values)); } ///< Get values of output buffer @param[out] values Array of data @return number of items virtual int getGradient(double &values[]) { return (iBatchSize>1 ? Gradient.GetData(values) : PrevLayer.getGradient(values)); } ///< Get values of gradient buffer @param[out] values Array of data @return number of items virtual CBufferDouble *getOutput(void) { return (iBatchSize>1 ? Output : PrevLayer.getOutput()); } ///< Get pointer of output buffer @return Pointer to object virtual CBufferDouble *getGradient(void) { return (iBatchSize>1 ? Gradient : PrevLayer.getGradient()); } ///< Get pointer of gradient buffer @return Pointer to object //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); ///< Method to transfer gradient to previous layer by calling kernel ::CalcHiddenGradientBatch(). @param NeuronOCL Pointer to next layer. //--- virtual bool Save(int const file_handle);///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle);///< Load method @param[in] file_handle handle of file @return logical result of operation //--- virtual int Type(void) const { return defNeuronBatchNormOCL; }///< Identificator of class.@return Type of class };
Новый класс будет наследоваться от базового класса CNeuronBaseOCL. По аналогии с классом CNeuronDropoutOCL добавим переменную PrevLayer. Продемонстрированный в предыдущей статье метод подмены буферов данных будем применять при указании размера batch-а мене "2", который будем сохранять в переменную iBatchSize.
Алгоритм Batch Normalization предусматривает сохранения ряда параметров индивидуальных для каждого нейрона нормализуемого слоя. Чтобы не плодить множество отдельных буферов для каждого отдельного параметра, создадим единый буфер параметров BatchOptions со следующей структурой.

Как видно из представленной структуры, размер буфера параметров будет зависеть от применяемого метода оптимизации параметров и, следовательно, будет создан в методе инициализации класса.
Набор методов класса уже стал стандартным и давайте рассмотрим их по порядку. В конструкторе класса обнулим указатели на объекты и зададим единичный размер batch-а, что практически исключает слой из работы сети до его инициализации.
CNeuronBatchNormOCL::CNeuronBatchNormOCL(void) : iBatchSize(1) { PrevLayer=NULL; BatchOptions=NULL; }
В деструкторе класса удалим объект буфера параметров и обнулим указатель на предыдущий слой. Обратите внимание, что мы не удаляем объект предыдущего слоя, а только обнуляем указатель. Объект будет удален там, где он и создавался.
CNeuronBatchNormOCL::~CNeuronBatchNormOCL(void) { if(CheckPointer(PrevLayer)!=POINTER_INVALID) PrevLayer=NULL; if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; }
Рассмотрим метод инициализации класса CNeuronBatchNormOCL::Init. В параметрах классу передаем количество нейронов последующего слоя, индекс для идентификации нейрона, указатель на объект OpenCL, количество нейронов в слое нормализации, размер batch-а и метод оптимизации параметров.
В начале метода вызовем одноименный метод родительского класса, в котором будут инициализированы базовые переменные и буфера данных. Затем сохраним размер batch-а и установим в None функцию активации слоя.
Здесь следует акцентировать внимание на функции активации. Включение данного функционала зависит от архитектуры выстраиваемой нейронной сети. Если архитектурой нейронной сети предусмотрено включение нормализации перед функцией активации, как рекомендуется авторами метода, то необходимо отключить функцию активации на предыдущем слое и указать необходимую функцию в слое нормализации. Технически указание функции активации осуществляется вызовом метода SetActivationFunction родительского класса после инициализации экземпляра класса. Если же архитектурой сети предусматривается использование нормализации после функции активации, то метод активации указывается в предыдущем слое, а слой нормализации остается без функции активации.
bool CNeuronBatchNormOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons,uint batchSize,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,numNeurons,optimization_type)) return false; activation=None; iBatchSize=batchSize; //--- if(CheckPointer(BatchOptions)!=POINTER_INVALID) delete BatchOptions; int count=(int)numNeurons*(optimization_type==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferInit(count,0)) return false; //--- return true; }
В заключении метода инициализации создадим буфер параметров. Как уже говорилось выше, размер буфера зависит от количества нейронов в слое и метода оптимизации параметров. При использовании SGD резервируем 7 элементов для каждого нейрона, а при оптимизации по методу Adam нам потребуется 9 элементов буфера на каждый нейрон. После успешного создания буфера заполним его нулями и выходим из метода с результатом true.
С полным кодом всех классов и их методов можно ознакомиться во вложении.
2.2. Прямой проход
Продолжаем дальше двигаться по алгоритму и рассмотрим метод прямого прохода. И начать предлагаю с рассмотрения кернела прямого прохода BatchFeedForward. Алгоритм кернела будем запускать для каждого отдельного нейрона.
В параметрах кернел получает указатели на 3 буфера: исходные данные, буфер параметров и буфер для записи результатов. Дополнительно в параметрах передадим размер batch-а, метод оптимизации и алгоритм активации нейрона.
В начале кернела проверим указанный размер окна нормализации. Если нормализация осуществляется по одному нейрону, выходим из метода без выполнения дальнейших операций.
После успешной проверки получим идентификатор потока, который укажет на позицию нормализуемой величины в тензоре входных данных. По ней определим смещение для первого параметра в тензоре параметров нормализации. На этом шаге метод оптимизации подскажет нам структуру буфера параметров.
Далее посчитаем экспоненциальную среднюю и дисперсию на данном шаге. По ним вычислим нормализованную величину нашего элемента.
Следующий шаг алгоритма пакетной нормализации — сдвиг и масштабирование. Напомню, что при инициализации мы заполнили буфер параметров нулями, поэтому проведение данной операции "в чистом виде" на первом шаге нам вернет "0". Чтобы этого не произошло, проверим текущее значение параметра γ и, если он равен "0", изменим его значение на "1". Смещение оставим нулевым. И в таком виде выполним сдвиг и масштабирование.
__kernel void BatchFeedForward(__global double *inputs, __global double *options, __global double *output, int batch int optimization, int activation) { if(batch<=1) return; int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- for(int i=0;i<(optimization==0 ? 7 : 9);i++) if(isnan(options[shift+i])) options[shift+i]=0; //--- double mean=(options[shift]*((double)batch-1)+inputs[n])/((double)batch); double delt=inputs[n]-mean; double variance=options[shift+1]*((double)batch-1.0)+pow(delt,2); if(options[shift+1]>0) variance/=(double)batch; double nx=delt/sqrt(variance+1e-6); //--- if(options[shift+3]==0) options[shift+3]=1; //--- double res=options[shift+3]*nx+options[shift+4]; switch(activation) { case 0: res=tanh(clamp(res,-20.0,20.0)); break; case 1: res=1/(1+exp(-clamp(res,-20.0,20.0))); break; case 2: if(res<0) res*=0.01; break; default: break; } //--- options[shift]=mean; options[shift+1]=variance; options[shift+2]=nx; output[n]=res; }
После получения нормализованной величины проверим необходимость выполнения функции активации на данном слое и выполним необходимые действия.
Теперь остается только сохранить новые значения в буферы данных и выйти из кернела.
Надеюсь, алгоритм построения кернела BatchFeedForward не вызывает вопросов, и мы можем перейти к созданию метода вызова кернела из основной программы. Этот функционал, как обычно, будет выполнять метод CNeuronBatchNormOCL::feedForward. Алгоритм метода похож на одноименные методы других классов. В параметрах метод получает указатель на предыдущий слой нейронной сети.
В начале метода проверим действительность полученного указателя и указателя на объект OpenCL (напомню, это реплика класса из стандартной библиотеки для работы с программой OpenCL).
На следующем шаге сохраним указатель на предыдущий слой нейронной сети и проверим размер batch-а. Если размер окна нормализации не более "1", скопируем тип функции активации предыдущего слоя и выйдем из метода с результатом true. Таким способом мы обеспечим данные для подмены буферов и исключим не нужные итерации алгоритма.
bool CNeuronBatchNormOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- PrevLayer=NeuronOCL; if(iBatchSize<=1) { activation=(ENUM_ACTIVATION)NeuronOCL.Activation(); return true; } //--- if(CheckPointer(BatchOptions)==POINTER_INVALID) { int count=Neurons()*(optimization==SGD ? 7 : 9); BatchOptions=new CBufferDouble(); if(!BatchOptions.BufferInit(count,0)) return false; } if(!BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_inputs,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_BatchFeedForward,def_k_bff_output,Output.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_optimization,(int)optimization)) return false; if(!OpenCL.SetArgument(def_k_BatchFeedForward,def_k_bff_activation,(int)activation)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_BatchFeedForward,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch Feed Forward: %d",GetLastError()); return false; } if(!Output.BufferRead() || !BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Если же после всех проверок мы дошли до запуска кернела прямого прохода, подготовим исходные данные для его запуска. Вначале проверим действительность указателя на буфер параметров алгоритма нормализации. При необходимости создадим и инициализируем новый буфер. Далее создадим буфер в памяти видеокарты и загрузим содержимое буфера.
Зададим количество запускаемых потоков по числу нейронов в слое и передадим кернелу указатели на буферы данных и требуемые параметры.
После проведения подготовительной работы отправим на выполнение кернел и считаем обратно из памяти видеокарты обновленные данные буферов. Обратите внимание, что мы получаем из видеокарты данные 2-х буферов: информацию с выхода алгоритма и буфер параметров, в который мы сохранили обновленную среднюю, дисперсию и нормализованную величину. Эти данные нам потребуются в последующих итерациях.
После завершения работы алгоритма удалим из памяти видеокарты буфер параметров, освобождая тем самым память для загрузки буферов последующих слоев нейронной сети и выходим из метода с результатом true.
С полным кодом всех классов и их методов нашей библиотеки можно ознакомиться во вложении.
2.3. Обратный проход
Обратный проход традиционно состоит из двух этапов: обратного распространения ошибки и обновления весовых коэффициентов. Только вместо привычных весовых коэффициентов мы будем обучать параметры γ и β функции масштабирования и сдвига.
Вначале рассмотрим функционал градиентного спуска. Для реализации его алгоритма создадим кернел CalcHiddenGradientBatch. В параметрах кернел получает указатели на тензоры параметров нормализации, поступивших от последующего слоя градиентов, выходных данных предыдущего слоя (полученных при последнем прямом проходе) и тензор градиентов предыдущего слоя нейронной сети, куда будут записываться результаты работы алгоритма. Также в параметрах кернелу будут передаваться размер batch-а, тип функции активации и метод оптимизации параметров.
Как и при прямом проходе, в начале кернела проверим размер batch-а и если он меньше или равен "1", то выходим из кернела без выполнения прочих итераций.
Следующим шагом получим порядковый номер нашего потока и определим смещение в тензоре параметров. Эти действия аналогичны описанным при прямом проходе.
__kernel void CalcHiddenGradientBatch(__global double *options, ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer __global double *matrix_i, ///<[in] Tensor of previous layer output __global double *matrix_ig, ///<[out] Tensor of gradients at previous layer uint activation, ///< Activation type (#ENUM_ACTIVATION) int batch, ///< Batch size int optimization ///< Optimization type ) { if(batch<=1) return; //--- int n=get_global_id(0); int shift=n*(optimization==0 ? 7 : 9); //--- double inp=matrix_i[n]; double gnx=matrix_g[n]*options[shift+3]; double temp=1/sqrt(options[shift+1]+1e-6); double gmu=(-temp)*gnx; double gvar=(options[shift]*inp)/(2*pow(options[shift+1]+1.0e-6,3/2))*gnx; double gx=temp*gnx+gmu/batch+gvar*2*inp/batch*pow((double)(batch-1)/batch,2.0); //--- if(isnan(gx)) gx=0; switch(activation) { case 0: gx=clamp(gx+inp,-1.0,1.0)-inp; gx=gx*(1-pow(inp==1 || inp==-1 ? 0.99999999 : inp,2)); break; case 1: gx=clamp(gx+inp,0.0,1.0)-inp; gx=gx*(inp==0 || inp==1 ? 0.00000001 : (inp*(1-inp))); break; case 2: if(inp<0) gx*=0.01; break; default: break; } matrix_ig[n]=clamp(gx,-MAX_GRADIENT,MAX_GRADIENT); }
Далее последовательно посчитаем градиенты по всем функциям алгоритма.

И в заключение проведем градиент через функцию активации предыдущего слоя. Полученное значение сохраним в тензор градиента предыдущего слоя.
Вслед за кернелом CalcHiddenGradientBatсh разберем метод CNeuronBatchNormOCL::calcInputGradients, который будет запускать выполнение кернела из главной программы. Как и одноименные методы других классов, в параметрах данный метод получает указатель на объект предыдущего слоя нейронной сети.
В начале метода, проверим действительность полученного указателя и указателя на объект OpenCL. После этого проверим размер batch-а. Если он меньше или равен "1", то выходим из метода. Результат, возвращаемый из метода будет зависеть от действительности сохраненного при прямом проходе указателя на предыдущий слой.
Если мы проходим дальше по алгоритму, то проверим действительность буфера параметров. В случае возникновения ошибки выходим из метода с результатом false.
Хочу обратить внимание, что спускаемый градиент относится к последнему прямому проходу. Поэтому в двух последних точках контроля мы проверяли объекты, участвующие в прямом проходе.
bool CNeuronBatchNormOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; //--- uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientBatch,def_k_bchg_matrix_ig,NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_activation,NeuronOCL.Activation())) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_batch,iBatchSize)) return false; if(!OpenCL.SetArgument(def_k_CalcHiddenGradientBatch,def_k_bchg_optimization,(int)optimization)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_CalcHiddenGradientBatch,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Batch CalcHiddenGradient: %d",GetLastError()); return false; } if(!NeuronOCL.getGradient().BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
Как и при прямом проходе, количество запускаемых потоков кернела будет равно количеству нейронов в слое. Отправим в память видеокарты содержимое буфера параметров нормализации и передадим кернелу указатели на требуемые тензоры и параметры.
После выполнения всех вышеописанных операций запустим кернел на выполнение и считаем полученные градиенты из памяти видеокарты в соответствующий буфер.
В заключение метода удаляем из памяти видеокарты тензор параметров нормализации и выходим из метода с результатом true.
После передачи градиента настало время обновить параметры сдвига и масштабирования. Для выполнения этих итераций создадим 2 кернела, по числу описанных ранее методов оптимизации, UpdateBatchOptionsMomentum и UpdateBatchOptionsAdam.
Вначале посмотрим на метод UpdateBatchOptionsMomentum. В параметрах метод получает указатели на 2 тензора: параметров нормализации и градиентов. Также в параметрах метода передадим константы метода оптимизации: обучающий коэффициент и моментум.
В начале кернела получим номер потока и определим смещение в тензоре параметров нормализации.
По исходным данным посчитаем размер дельты для γ и β. Для выполнения этой операции я воспользовался векторными вычислениями с вектором double из 2-х элементов. Такой способ позволяет распараллелить вычисления.
Скорректируем параметры γ, β и сохраним результаты в соответствующие элементы тензора параметров нормализации.
__kernel void UpdateBatchOptionsMomentum(__global double *options, ///<[in,out] Options matrix m*7, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer double learning_rates, ///< Learning rates double momentum ///< Momentum multiplier ) { const int n=get_global_id(0); const int shift=n*7; double grad=matrix_g[n]; //--- double2 delta=learning_rates*grad*(double2)(options[shift+2],1) + momentum*(double2)(options[shift+5],options[shift+6]); if(!isnan(delta.s0) && !isnan(delta.s1)) { options[shift+5]=delta.s0; options[shift+3]=clamp(options[shift+3]+delta.s0,-MAX_WEIGHT,MAX_WEIGHT); options[shift+6]=delta.s1; options[shift+4]=clamp(options[shift+4]+delta.s1,-MAX_WEIGHT,MAX_WEIGHT); } };
Кернел UpdateBatchOptionsAdam построен по аналогичной схеме, отличия в алгоритме самого метода оптимизации. В параметрах кернел получает указатели на все те же тензоры параметров и градиентов. Плюс получает параметры метода оптимизации.
В начале кернела определим номер потока и определим сдвиг в тензоре параметров.
По полученным данным посчитаем первый и второй момент. Здесь также применены векторные вычисления, которые позволяют вычислять моменты для 2-х параметров одновременно.
По полученным моментам посчитаем дельты и новые значения параметров. Результаты вычислений сохраним в соответствующие элементы тензора параметров нормализации.
__kernel void UpdateBatchOptionsAdam(__global double *options, ///<[in,out] Options matrix m*9, where m - Number of neurons in previous layer __global double *matrix_g, ///<[in] Tensor of gradients at current layer const double l, ///< Learning rates const double b1, ///< First momentum multiplier const double b2 ///< Second momentum multiplier ) { const int n=get_global_id(0); const int shift=n*9; double grad=matrix_g[n]; //--- double2 mt=b1*(double2)(options[shift+5],options[shift+6])+(1-b1)*(double2)(grad*options[shift+2],grad); double2 vt=b2*(double2)(options[shift+5],options[shift+6])+(1-b2)*pow((double2)(grad*options[shift+2],grad),2); double2 delta=l*mt/sqrt(vt+1.0e-8); if(isnan(delta.s0) || isnan(delta.s1)) return; double2 weight=clamp((double2)(options[shift+3],options[shift+4])+delta,-MAX_WEIGHT,MAX_WEIGHT); //--- if(!isnan(weight.s0) && !isnan(weight.s1)) { options[shift+3]=weight.s0; options[shift+4]=weight.s1; options[shift+5]=mt.s0; options[shift+6]=mt.s1; options[shift+7]=vt.s0; options[shift+8]=vt.s1; } };
Для запуска кернелов из основной программы создадим метод CNeuronBatchNormOCL::updateInputWeights. В параметрах метод получает указатель на предыдущий слой нейронной сети. По существу, данный указатель не будет использоваться в алгоритме метода, но оставлен для преемственности методов от родительского класса.
В начале метода проверим действительность полученного указателя и указателя на объект OpenCL. По аналогии с ранее рассмотренным методом CNeuronBatchNormOCL::calcInputGradients, проверим размер batch-а и действительность буфера параметров. Загрузим содержимое буфера параметров в память видеокарты. Зададим количество потоков равным количеству нейронов в слое.
Далее идет разветвление алгоритма в зависимости от заданного метода оптимизации. Передадим исходные параметры для требуемого кернела и запустим его выполнение.
Вне зависимости от метода оптимизации параметров считаем обновленное содержимое буфера параметров нормализации и удалим буфер из памяти видеокарты.
bool CNeuronBatchNormOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; //--- if(iBatchSize<=1) return (CheckPointer(PrevLayer)!=POINTER_INVALID); //--- if(CheckPointer(BatchOptions)==POINTER_INVALID || !BatchOptions.BufferCreate(OpenCL)) return false; uint global_work_offset[1]= {0}; uint global_work_size[1]; global_work_size[0]=Neurons(); //--- if(optimization==SGD) { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsMomentum,def_k_buom_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_learning_rates,eta)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsMomentum,def_k_buom_momentum,alpha)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsMomentum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsMomentum %d",GetLastError()); return false; } } else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_options,BatchOptions.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateBatchOptionsAdam,def_k_buoa_matrix_g,Gradient.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_l,lr)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateBatchOptionsAdam,def_k_buoa_b2,b2)) return false; ResetLastError(); //--- if(!OpenCL.Execute(def_k_UpdateBatchOptionsAdam,1,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateBatchOptionsAdam %d",GetLastError()); return false; } } //--- if(!BatchOptions.BufferRead()) return false; BatchOptions.BufferFree(); //--- return true; }
После успешного выполнения всех операций метода выходим с результатом true.
Методы подмены буферов были подробно описаны в предыдущей статье и, думаю, не вызовут затруднений в понимании. Как и методы работы с файлами (сохранение и загрузка обученной нейронной сети).
С полным кодом всех классов и их методов можно ознакомиться во вложении.
2.4. Точечные изменения в базовых классах нейронной сети
Ну и по традиции, после создания нового класса нужно его интегрировать в общую структуру нашей нейронной сети. Первое, что нужно сделать, это создать идентификатор нашего класса.
#define defNeuronBatchNormOCL 0x7891 ///<Batchnorm neuron OpenCL \details Identified class #CNeuronBatchNormOCL
Затем зададим макроподстановки констант работы с новыми кернелами.
#define def_k_BatchFeedForward 24 ///< Index of the kernel for Batch Normalization Feed Forward process (#CNeuronBathcNormOCL) #define def_k_bff_inputs 0 ///< Inputs data tenzor #define def_k_bff_options 1 ///< Tenzor of variables #define def_k_bff_output 2 ///< Tenzor of output data #define def_k_bff_batch 3 ///< Batch size #define def_k_bff_optimization 4 ///< Optimization type #define def_k_bff_activation 5 ///< Activation type //--- #define def_k_CalcHiddenGradientBatch 25 ///< Index of the Kernel of the Batch neuron to transfer gradient to previous layer (#CNeuronBatchNormOCL) #define def_k_bchg_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_bchg_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_bchg_matrix_i 2 ///<[in] Tensor of previous layer output #define def_k_bchg_matrix_ig 3 ///<[out] Tensor of gradients at previous layer #define def_k_bchg_activation 4 ///< Activation type (#ENUM_ACTIVATION) #define def_k_bchg_batch 5 ///< Batch size #define def_k_bchg_optimization 6 ///< Optimization type //--- #define def_k_UpdateBatchOptionsMomentum 26 ///< Index of the kernel for Describe the process of SGD optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buom_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buom_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buom_learning_rates 2 ///< Learning rates #define def_k_buom_momentum 3 ///< Momentum multiplier //--- #define def_k_UpdateBatchOptionsAdam 27 ///< Index of the kernel for Describe the process of Adam optimization options for the Batch normalization Neuron (#CNeuronBatchNormOCL). #define def_k_buoa_options 0 ///<[in] Options matrix m*(7 or 9), where m - Number of neurons in previous layer #define def_k_buoa_matrix_g 1 ///<[in] Tensor of gradients at current layer #define def_k_buoa_l 2 ///< Learning rates #define def_k_buoa_b1 3 ///< First momentum multiplier #define def_k_buoa_b2 4 ///< Second momentum multiplier
В конструкторе нейронной сети CNet::CNet добавим блоки создания объектов нового класса и инициализацию новых кернелов (изменения выделены заливкой).
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
................
................
................
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
................
................
................
CNeuronBatchNormOCL *batch=NULL;
switch(desc.type)
{
................
................
................
................
//---
case defNeuronBatchNormOCL:
batch=new CNeuronBatchNormOCL();
if(CheckPointer(batch)==POINTER_INVALID)
{
delete temp;
return;
}
if(!batch.Init(outputs,0,opencl,desc.count,desc.window,desc.optimization))
{
delete batch;
delete temp;
return;
}
batch.SetActivationFunction(desc.activation);
if(!temp.Add(batch))
{
delete batch;
delete temp;
return;
}
batch=NULL;
break;
//---
default:
return;
break;
}
}
................
................
................
................
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(28);
................
................
................
................
opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward");
opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath");
opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum");
opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam");
//---
return;
}
Аналогично инициируем новые кернелы при загрузке предварительно обученной нейронной сети.
bool CNet::Load(string file_name,double &error,double &undefine,double &forecast,datetime &time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return false; //--- ................ ................ ................ //--- if(CheckPointer(opencl)==POINTER_INVALID) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; else { //--- create kernels opencl.SetKernelsCount(28); ................ ................ ................ opencl.KernelCreate(def_k_BatchFeedForward,"BatchFeedForward"); opencl.KernelCreate(def_k_CalcHiddenGradientBath,"CalcHiddenGradientBath"); opencl.KernelCreate(def_k_UpdateBatchOptionsMomentum,"UpdateBatchOptionsMomentum"); opencl.KernelCreate(def_k_UpdateBatchOptionsAdam,"UpdateBatchOptionsAdam"); } } ................ ................ ................ ................ ................ }
Добавим новый тип нейронов в метод загрузки предварительно обученной нейронной сети.
bool CLayer::Load(const int file_handle) { iFileHandle=file_handle; if(!CArrayObj::Load(file_handle)) return false; if(CheckPointer(m_data[0])==POINTER_INVALID) return false; //--- CNeuronBaseOCL *ocl=NULL; CNeuronBase *cpu=NULL; switch(m_data[0].Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: ocl=m_data[0]; iOutputs=ocl.getConnections(); break; default: cpu=m_data[0]; iOutputs=cpu.getConnections().Total(); break; } //--- return true; }
Аналогично добавим новый тип нейронов в диспетчерские методы базового класса CNeuronBaseOCL.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- ................ ................ ................ CNeuronBatchNormOCL *batch=NULL; switch(TargetObject.Type()) { ................ ................ ................ case defNeuronBatchNormOCL: batch=TargetObject; temp=GetPointer(this); return batch.calcInputGradients(temp); break; } //--- return false; }
bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: case defNeuronMLMHAttentionOCL: case defNeuronDropoutOCL: case defNeuronBatchNormOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
С полным кодом всех классов и их методов можно ознакомиться во вложении.
3. Тестирование
Продолжаем тестирование новых классов в ранее созданных советниках, что дает нам сопоставимые данные для оценки работы отдельных элементов. Метод нормализации будем тестировать на базе советника из статьи [12], в котором заменим Dropout на Batch Normalization. Структура нейронной сети нового советника представлена ниже. При этом коэффициент обучения был увеличен с 0,000001 до 0,001.
//--- 0 CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=24; desc.optimization=ADAM; desc.activation=None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*24; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMLMHAttentionOCL; desc.window=24; desc.window_out=4; desc.step=8; //heads desc.layers=5; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=None; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuronBatchNormOCL; desc.window=100; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM;
Тестирование советника проводилось на инструменте EURUSD, таймфрейм H1. На вход нейронной сети подаются исторические данные за 20 последних свечей, как и в предыдущих тестах.
График ошибки предсказания нейронной сети показывает, что советник с нормализацией демонстрирует менее сглаженный график, что может быть вызвано резким увеличением коэффициента обучения. При этом сама ошибка предсказания ниже предыдущих тестов практически на всем протяжении теста.
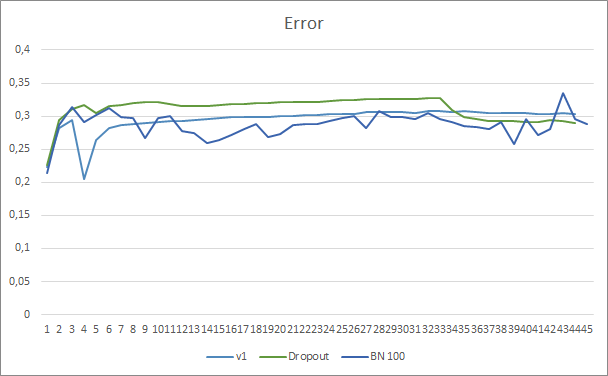
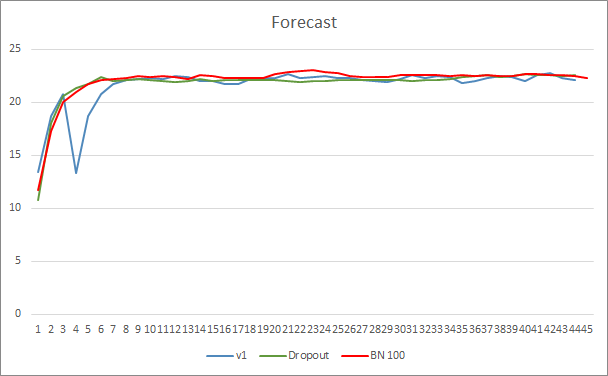
График попадания предсказанных паттернов всех трех советников довольно близок и не позволяет сказать о превосходстве какого-либо из методов.
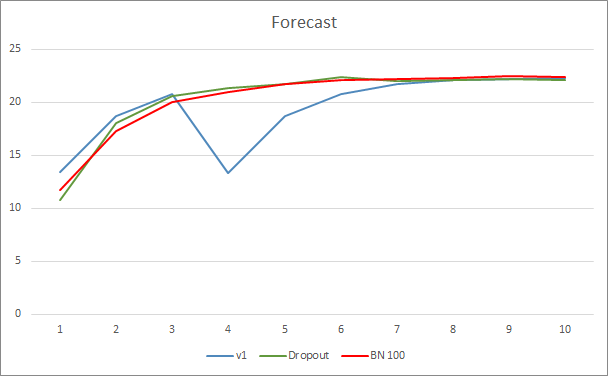
Заключение
В данной статье мы продолжили знакомство с методами повышения сходимости нейронных сетей и добавили в нашу библиотеку класс пакетной нормализации данных. Тестирование показало, что использование данного метода позволяет снизить ошибку нейронной сети и повысить скорость обучения.
Ссылки
- Нейросети — это просто
- Нейросети — это просто (Часть 2): обучение и тестирование сети
- Нейросети — это просто (Часть 3): сверточные сети
- Нейросети — это просто (Часть 4): рекуррентные сети
- Нейросети — это просто (Часть 5): многопоточные вычисления в OpenCL
- Нейросети — это просто (Часть 6): эксперименты с коэффициентом обучения нейронной сети
- Нейросети — это просто (Часть 7): Адаптивные методы оптимизации
- Нейросети — это просто (Часть 8): Механизмы внимания
- Нейросети — это просто (Часть 9): Документируем проделанную работу
- Нейросети — это просто (Часть 10): Multi-Head Attention (многоголовое внимание)
- Нейросети — это просто (Часть 11): Вариации на тему GPT
- Нейросети — это просто (Часть 12): Dropout
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- Layer Normalization
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Fractal_OCL_AttentionMLMH_b.mq5 | Советник | Советник с нейронной сетью классификации (3 нейрона в выходном слое) с использованием архитектуры GPT, 5 слоев внимания + BatchNorm |
| 2 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 3 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
| 4 | NN.chm | HTML-справка | Скомпилированный CHM-файл помощи по библиотеке. |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Шаблон проектирования MVC и возможность его использования
Шаблон проектирования MVC и возможность его использования
 Брутфорс-подход к поиску закономерностей (Часть IV): Минимальная функциональность
Брутфорс-подход к поиску закономерностей (Часть IV): Минимальная функциональность
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
при использовании советника с примерами из части 10 статьи
Пожалуйста, подскажите, что делать?
Спасибо
Здравствуйте, можете ли вы отправить полный журнал?
Здравствуйте. Спасибо за помощь
Рожерио
Здравствуйте. Спасибо за помощь
Рожерио
Здравствуйте, Роджерио.
1. Вы не создаете модель.
2. Ваш графический процессор не поддерживает удвоение. Пожалуйста, загрузите последнюю версию из статьи https://www.mql5.com/ru/articles/11804.
Здравствуйте Дмитрий
Вы написали: Вы не создаете модель.
Но как мне создать модель? Я компилирую все шрифты программы и запускаю советник.
Советник создает файл в папке 'files' с расширением nnw. этот файл не является моделью?
Спасибо
Здравствуйте, учитель Дмитрий
Теперь ни один из .mqh не компилируется.
Например, когда я пытаюсь скомпилировать vae.mqh, я получаю такую ошибку
'MathRandomNormal' - undeclared identifier VAE.mqh 92 8
Попробую начать с самого начала.
Еще один вопрос: когда вы выкладываете новую версию NeuroNet.mqh, эта версия полностью совместима с другими старыми версиями советника?
Спасибо
rogerio
PS: Даже удалив все файлы и каталоги и начав с новой копии с ЧАСТИ 1 и 2 я больше не могу скомпилировать никакой код.
Например, когда я пытаюсь скомпилировать код в fractal.mq5, я получаю эту ошибку:
cannot convert type'CArrayObj *' to reference of type 'const CArrayObj *' NeuroNet.mqh 437 29
Извините, я действительно хотел понять ваши статьи и код.
PS2: Хорошо, я удалил слово "const" в 'feedForward', 'calcHiddenGradients' и 'sumDOW' и теперь я могу скомпилировать Fractal.mqh и Fractal2.mqh