交易中的神经网络：优化时间序列预测变换器（LSEAttention）

MetaTrader 5 — 交易系统 | 12 九月 2025, 09:11

概述

多变量时间序列预测能跨越广泛的领域（金融、医疗保健、等）中扮演关键角色，其意向是基于历史数据预测未来值。该任务在长期预测中变得特别具有挑战性，长期预测所需模型，要能够有效捕获多变量时间序列数据中特征相关性、和长范围依赖关系。最近的研究越来越专注利用变换器架构进行时间序列预测，因为它具有强大的自注意力机制，擅长针对复杂的时态交互进行建模。然而，尽管其颇具潜力，但许多当代多变量时间序列预测方法仍严重依赖线性模型，这引发了人们对变换器在这种境况下真正有效性的担忧。

变换器架构核心的自注意力机制定义如下：

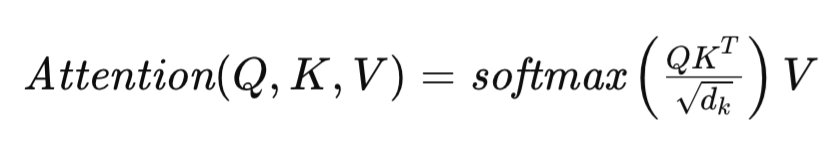
其中 Q、K、和 V 分别表示查询、主键、和数值矩阵，dk 代表描述每个序列元素的向量维数。该公式令变换器能够动态估算输入序列中不同元素的相关性，从而促进依据数据内部复杂依赖关系的建模。

变换器架构已有各种拟议的调整，以望提高其在长期时间序列预测任务中的性能。例如，FEDformer 集成了先进的傅里叶模块，可在时间和空间两者基础上达成线性复杂性，从而显著强化长期输入序列的可扩展性和效率。

另一方面，PatchTST 放弃了逐点注意力，转而采用补片级表征，专注于连续的区段，而非单个时间步长。该方式允许模型在多变量时间序列中捕获更广泛的语义信息，这对于长期预测的有效性至关重要。

在计算机视觉和自然语言处理等领域，注意力矩阵可能会遭受熵坍缩、或秩坍缩。由于基于时间的数据所固有的频繁波动，这个问题在时间序列预测中会进一步加剧，往往会导致模型性能大幅下降。熵坍缩的底层原因仍然知之甚少，这凸显了进一步研究其机制、及对模型普适性影响的必要性。这些挑战是题为《LSEAttention 是时间序列预测所需的一切》这篇论文的专注点。

1. LSEAttention 算法

多变量时间序列预测的目标是估算每个 C 通道最可能的未来值 P，表示为张量 Y ∈ RC×P。该预测基于长度 L 和 C 通道的历史时间序列数据，封装在输入矩阵 X ∈ RC×L 之中。该任务涉及训练一个由 ω 参数化的预测模型 fωRC×L →RC×P，将预测值和实际值之间的均方误差（MSE）最小化。

变换器严重依赖逐点自注意力机制来捕获时态关联。然而，这种依赖可能会导致一种称为注意力坍缩的现象，即注意力矩阵在不同的输入序列中收敛到近乎雷同的数值。这会导致模型对于数据的普适性很可怜。

LSEAttention 方法作者在 Softmax 函数计算的依赖系数、及 Log-Sum-Exp（LSE）运算之间进行了类比。他们推测该公式中的数值不稳定性，或许是注意力坍缩的根本原因。

函数的条件数量反映出它对小输入变化的敏感性。较高的条件数量表示输入中即使是微小的扰动也会导致显著的输出偏差。

在注意力机制的境况下，这般不稳定性可表现为过度注意力或熵坍缩，其特征是注意力矩阵含有极高的对角线值（表明上溢），以及非常低的对角线值（表明下溢）。

为了解决这些问题，作者提出了 LSEAttention 模块，其将 Log-Sum-Exp（LSE）技巧、与 GELU（高斯误差线性单位）激活函数集成到一起。LSE 技巧经由归一化减轻了上溢和下溢引起的数值不稳定性。Softmax 函数可由 LSE 重新表述如下：

其中 LSE(x) 的指数表示 log-sum-exp 函数的指数值，提升了数值稳定性。

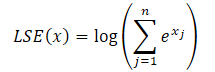
通过使用指数性质，任何指数项都可用两个指数项的乘积来表达。

其中 a 是用于归一化的常量。在实践中，最大值通常作为常数来用。将指数的乘积代入 LSE 公式，并取合计总值之外符号，我们得到：

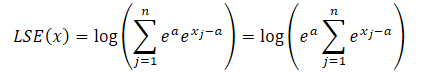
乘积的对数变成对数之和，指数的自然对数等于指数。这令我们能够简化所呈现的表达式：

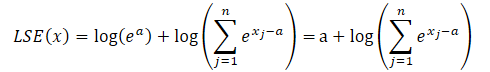
我们将生成的表达式代入 Softmax 函数，并用到指数性质：

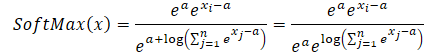
如您所见，常数指数值里共有的分子和分母被抵消了。自然对数的指数等于对数表达式。因此，我们得到了数值稳定的 Softmax 表达式。

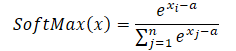
当用最大值作为常量（(a = max(x)）时，我们得到的 x-a 总是小于或等于 0。在这种情况下，x-a 的指数值位于 0 到 1 的范围内，不包括 0。相应地，函数的分母在 (1, n] 范围内。

此外，LSEAttention 框架作者还提议使用 GELU 激活函数，其可提供更平滑的概率激活。这有助于在应用指数函数之前平稳对数概率的极值，从而软化注意力分数的生硬转换。经过近似 ReLU 函数的平滑曲线，涉及标准正态分布的累积分布函数（CDF），GELU 降低了传统 ReLU 可能发生的激活急剧偏移。这一性质对于稳定基于变换器的注意力机制特别有益，其中突然的激活尖峰可能导致数值不稳定、及梯度爆炸。

GELU 函数的正式定义如下：

其中 Φ(x) 表示标准正态分布的 CDF。该公式确保 GELU 根据输入值的量级，给输入值应用不同程度的缩放，从而抑制极值的放大。GELU 的平滑、概率性质令输入激活能够逐渐过渡，从而减轻训练期间的梯度大幅波动。

当与 Log-Sum-Exp (LSE) 技巧结合运用时，该性质变得特别有价值，能数值稳定的措施归一化 Softmax 函数。LSE 和 GELU 协同，有效防止 Softmax 指数运算中的上溢和下溢，从而平稳注意力权重范围。通过确保跨词元之间注意力系数的良好分布，来协同强化变换器模型的健壮性。最终，这会导致更稳定的梯度，并改善训练期间的收敛性。

在传统的变换器架构中，前馈网络（FFN）模块中所用的 ReLU（整流线性单元）激活函数容易出现“濒死 ReLU” 问题，其中神经元可为所有负输入值输出零，从而变得失活。这会导致这些神经元的梯度为零，后果就是停滞它们的学习，并致训练不稳定。

为了解决这个麻烦，使用参数化的 ReLU（PReLU）函数作为替代。PReLU 为负值输入引入了可学习斜率，即使输入为负值，也允许非零输出。这种适应性不仅缓解了濒死 ReLU 问题，而且还开启了负值与正值激活之间的更平滑过渡，从而强化了模型在整个输入空间中的学习能力。负值的非零梯度存在，可支持更好的梯度流，这是训练更深度架构的基础。由此，运用 PReLU 能贡献整体训练的稳定性，并有助于维持激活表征，终致模型性能提升。

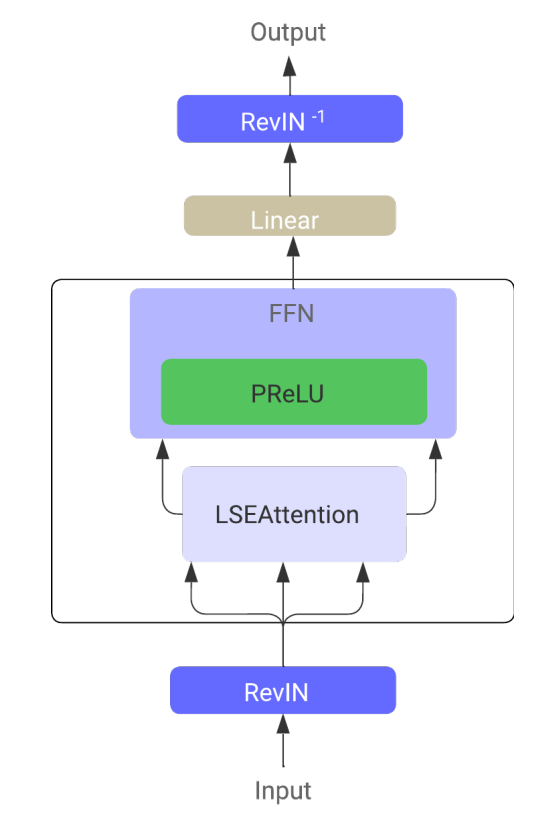
在 LSEAttention 时间序列变换器（LATST）架构中，作者还结合了可逆数据归一化，在解决时间序列预测任务中，训练数据和测试数据之间的分布差异方面，其被证明特别有效。

该架构保留了嵌入在 LSEAttention 模块中的传统时态自注意力机制。

总体而言，LATST 架构由单层变换器结构组成，并添加了替换模块，在保持注意力机制可靠性的同时，开启了自适应学习。这种设计促进了依据时态依赖关系有效建模，并在时间序列预测任务中激发性能。该框架的原始可视化提供如下。

2. 利用 MQL5 实现

在回顾了 LSEAttention 框架的理论层面之后，我们现在转向工作的实施部分，其中我们探索利用 MQL5 实现所提议技术的一种可能性。重点要注意，该实现与以前的实现有差别明显。具体地，我们不会创建一个新对象来实现所提出方法。取而代之，我们会将它们集成到以前开发的类中。

2.1调整 Softmax 层

我们研究处理 Softmax 函数层的 CNeuronSoftMaxOCL 类。在我们的模型独立组件、以及各种框架的部分，该类被广泛所用。举例，我们使用 CNeuronSoftMaxOCL 对象来构建基于依赖形态（CNeuronMHAttentionPooling）的池化模块，我们曾在最近的若干项研究中应用了该模块。因此，在该类的算法中协同数值稳定的 Softmax 计算，是合乎逻辑的。

为达成这一点，我们将修改 SoftMax_FeedForward 内核的行为。内核接收指向两个数据缓冲区的指针作为参数：一个用于输入值，另一个用于输出结果。

__kernel void SoftMax_FeedForward(__global float *inputs,
                                  __global float *outputs)
  {
   const uint total = (uint)get_local_size(0);
   const uint l = (uint)get_local_id(0);
   const uint h = (uint)get_global_id(1);

我们计划于二维任务空间之中执行该内核。第一个维度对应于单一单位序列中要归一化的数值数量。第二个维度表示这样的单元序列（或归一化头）的数量。我们将线程分组到每个独立单元序列中的工作组。

在内核主体中，我们首先在任务空间中辨别跨所有维度的当前线程。

然后，我们声明一个局部内存数组，其用于促进工作组内的数据交换。

   __local float temp[LOCAL_ARRAY_SIZE];

接下来，我们定义全局数据缓冲区中指向相关元素的偏移常量。

   const uint ls = min(total, (uint)LOCAL_ARRAY_SIZE);
   uint shift_head = h * total;

为了最大限度地减少对全局内存的访问，我们将输入值复制到局部变量中，并验证结果值。

   float inp = inputs[shift_head + l];
   if(isnan(inp) || isinf(inp) || inp<-120.0f)
      inp = -120.0f;

值得注意的是，我们将输入值限制为较低的阈值 -120，这近似于浮点格式中可表示的最小指数值。这充当防止下溢的额外措施。我们不对数值施加上限，因为潜在的上溢会通过减去最大值来解决。

接下来，我们判定当前单位序列中的最大值。这是经由一个循环来达成的，其内收集工作组中每个子组的最大值，并将它们存储在局部内存数组的元素当中。

   for(int i = 0; i < total; i += ls)
     {
      if(l >= i && l < (i + ls))
         temp[l] = (i > 0 ? fmax(inp, temp[l]) : inp);
      barrier(CLK_LOCAL_MEM_FENCE);
     }

然后，我们遍历局部数组，以便判定当前工作组的全局最大值。

   uint count = min(ls, (uint)total);
   do
     {
      count = (count + 1) / 2;
      if(l < ls)
         temp[l] = (l < count && (l + count) < total ? fmax(temp[l + count],temp[l]) : temp[l]);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
   float max_value = temp[0];
   barrier(CLK_LOCAL_MEM_FENCE);

得到的最大值存储在局部变量之中，我们要在该阶段确保线程同步。在对局部内存数组元素进行任何修改之前，工作组中的所有线程都必须保留正确的最大值，这一点至关重要。

现在，我们从每个原始输入中减去最大值。再次，我们检查下限。由于减去一个最大正值或许会将结果推到有效范围之外。然后我们计算已调整数值的指数。

   inp = fmax(inp - max_value, -120);
   float inp_exp = exp(inp);
   if(isinf(inp_exp) || isnan(inp_exp))
      inp_exp = 0;

配合后续两个循环，我们跨工作组汇总结果指数。循环结构类似于计算最大值的那个。我们只是修改了循环主体中的相应运算。

   for(int i = 0; i < total; i += ls)
     {
      if(l >= i && l < (i + ls))
         temp[l] = (i > 0 ? temp[l] : 0) + inp_exp;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (uint)total);
   do
     {
      count = (count + 1) / 2;
      if(l < ls)
         temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0);
      if(l + count < ls)
         temp[l + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

获得所有必需的数值后，我们现在能够将每个指数除以工作组内的指数之和，计算出最终的 Softmax 值。

//---
   float sum = temp[0];
   outputs[shift_head+l] = inp_exp / (sum + 1.2e-7f);
  }

该操作的结果将写入全局结果缓冲区中的相应元素。

需强调的重点是，在前向通验期间，针对 Softmax 计算所做的修改，无须在向后通验算法里修改。如本文前面讲述的数学推导所示，运用 LSE 技巧不会改变 Softmax 函数的最终输出。由此，输入数据对最终结果的影响维持不变。允许我们继续使用现有的梯度误差分布算法，而无需修改。

2.2修改相对注意力模块

重点要注意，Softmax 算法并不总是作为独立层运用。近期，我们涉及不同自注意力模块设计实现的几乎所有版本中，其逻辑都直接嵌入到统一的注意力内核当中。我们验证一下 CNeuronRelativeSelfAttention 模块。此处，修改后的自注意力机制的整个算法是在 MHRelativeAttentionOut 内核中实现的。当然，我们瞄准的是确保跨所有模型架构的训练过程稳定。因此，我们必须在所有这些内核中实现数值稳定的 Softmax。只要有可能，我们就会保留现有的内核参数和任务空间配置。同样的方式也用于升级 MHRelativeAttentionOut 内核。

不过，请注意，对内核参数或任务空间布局所做的任何更改，都必须反映在主程序的所有包装方法中，即内核排队以便执行。否则可能会导致内核调度期间出现严重的运行时错误。这不仅要应用于全局任务空间的修改，也要应用于工作组大小的更改。

__kernel void MHRelativeAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                     __global const float *k,         ///<[in] Matrix of Keys
                                     __global const float *v,         ///<[in] Matrix of Values
                                     __global const float *bk,        ///<[in] Matrix of Positional Bias Keys
                                     __global const float *bv,        ///<[in] Matrix of Positional Bias Values
                                     __global const float *gc,        ///<[in] Global content bias vector
                                     __global const float *gp,        ///<[in] Global positional bias vector
                                     __global float *score,           ///<[out] Matrix of Scores
                                     __global float *out,             ///<[out] Matrix of attention
                                     const int dimension              ///< Dimension of Key
                                    )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k_id = get_local_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_local_size(1);
   const int heads = get_global_size(2);

在内核主体中，如前，我们辨别任务空间中的当前线程，并定义所有必要的维度。

接下来，我们声明一组所需的常量，包括全局数据缓冲区、和辅助值的偏移量。

   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);

我们还定义了一个局部内存数组，用于每个工作组内的线程间数据交换。

   __local float temp[LOCAL_ARRAY_SIZE];

为了根据雏形自注意力算法计算注意力分数，我们首先在查询和主键张量的相应向量之间执行点积。然而，R-MAT 框架的作者添加了上下文依赖、和全局偏差项。由于所有向量的长度相等，因此这些运算可在单循环中执行，其中迭代次数等于向量大小。在循环主体中，我们执行元素乘法，然后求和。

//--- score
   float sc = 0;
   for(int d = 0; d < dimension; d++)
     {
      float val_q = q[shift_q + d];
      float val_k = k[shift_kv + d];
      float val_bk = bk[shift_kv + d];
      sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk;
     }
   sc = sc / koef;

生成的分数按向量维度的平方根缩放。根据雏形变换器作者的意思，该运算提升了模型稳定性。我们坚持这种举措。

然后调用 Softmax 函数将结果值转换为概率。此处，我们插入运算，以确保数值稳定性。首先，我们判定每个工作组内注意力分数的最大值。为此，我们将线程划分为多个子组，每个子组将其局部最大值写入局部内存数组中的元素。

//--- max value
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc));
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

然后我们循环整个数组，以找到全局最大值。

   uint count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] = (k_id < count && (k_id + count) < kunits ? 
                          fmax(temp[k_id + count], temp[k_id]) : 
                                                    temp[k_id]);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

然后在应用指数函数之前，减去该最大值来调整当前注意力分数。此处，我们还必须同步线程。因为在下一步中，我们将更改局部数组元素的值，而在工作组的所有线程使用之前覆盖最大元素值是要冒风险的。

   sc = exp(fmax(sc - temp[0], -120));
   if(isnan(sc) || isinf(sc))
      sc = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

接下来，我们计算工作组内所有指数的总和。如前，我们使用由顺序循环组成的两遍归约算法。

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   count = min(ls, (uint)kunits);
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

现在，我们就能将每个数值除以总和，将注意力分数转换为概率。

//--- score
   float sum = temp[0];
   if(isnan(sum) || isinf(sum) || sum <= 1.2e-7f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

出品概率被写入全局输出缓冲区的相应元素，我们在工作组内同步线程的执行。

最后，我们计算输入序列中每项的数值张量元素的加权和。我们将基于上面计算的注意力系数来加权。在序列的一个元素中，该运算将注意力系数向量乘以数值张量来表示，R-MAT 框架的作者往该张量里添加了全局偏差张量。

这是利用循环系统实现的，其中外部循环迭代数值张量的最后一个维度。

//--- out
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = sc * (val_v + val_bv);
      if(isnan(val) || isinf(val))
         val = 0;

在循环中，每个线程计算其对相应元素的贡献值，这些贡献值经工作组内的嵌套顺序缩减循环进行聚合。

      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

然后，其中一个线程将总和写入全局结果缓冲区的相应元素。

      //---
      if(k_id == 0)
         out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

之后，我们再次同步线程，然后再转入下一次循环迭代。

如早前讨论，针对 Softmax 函数所做的修改不会影响结果与输入数据的依赖性。因此，我们能够重用现有的反向传播算法，无需任何修改。

2.3GELU 激活函数

除了 Softmax 函数的数值稳定之外，LSEAttention 框架的作者还建议调用 GELU 激活函数。作者提议该函数的两个版本。其中之一呈现如下。

该激活函数的实现非常简单。我们只需将新变体添加到现有的激活函数处理程序中既可。

float Activation(const float value, const int function)
  {
   if(isnan(value) || isinf(value))
      return 0;
//---
   float result = value;
   switch(function)
     {
      case 0:
         result = tanh(clamp(value, -20.0f, 20.0f));
         break;
      case 1:  //Sigmoid
         result = 1 / (1 + exp(clamp(-value, -20.0f, 20.0f)));
         break;
      case 2:  //LReLU
         if(value < 0)
            result *= 0.01f;
         break;
      case 3:  //SoftPlus
         result = (value >= 20.0f ? 1.0f : (value <= -20.0f ? 0.0f : log(1 + exp(value))));
         break;
      case 4:  //GELU
         result = value / (1 + exp(clamp(-1.702f * value, -20.0f, 20.0f)));
         break;
      default:
         break;
     }
//---
   return result;
  }

然而，前馈通验表面看简单，然其背后还有一个更复杂的任务，即实现反向传播通验。这是因为 GELU 的推导取决于原始输入和 sigmoid 函数。它们在我们的标准实现中无一可用。

甚至，仅基于前馈通验的结果，无法准确表达 GELU 函数的推导。因此，我们不得不求助于某些启发式和近似法。

我们首先回顾一下 sigmoid 函数的形状。

对于大于 5 的输入值，sigmoid 接近 1，对于小于 –5 的输入，它接近 0。因此，对于 X 的足够负值，GELU 的推导趋向于 0，在于推导方程的左手因子接近于零。对于 X 的大正值，推导趋向于 1，因为两个乘法因子都收敛到 1。这一点由下图确认。

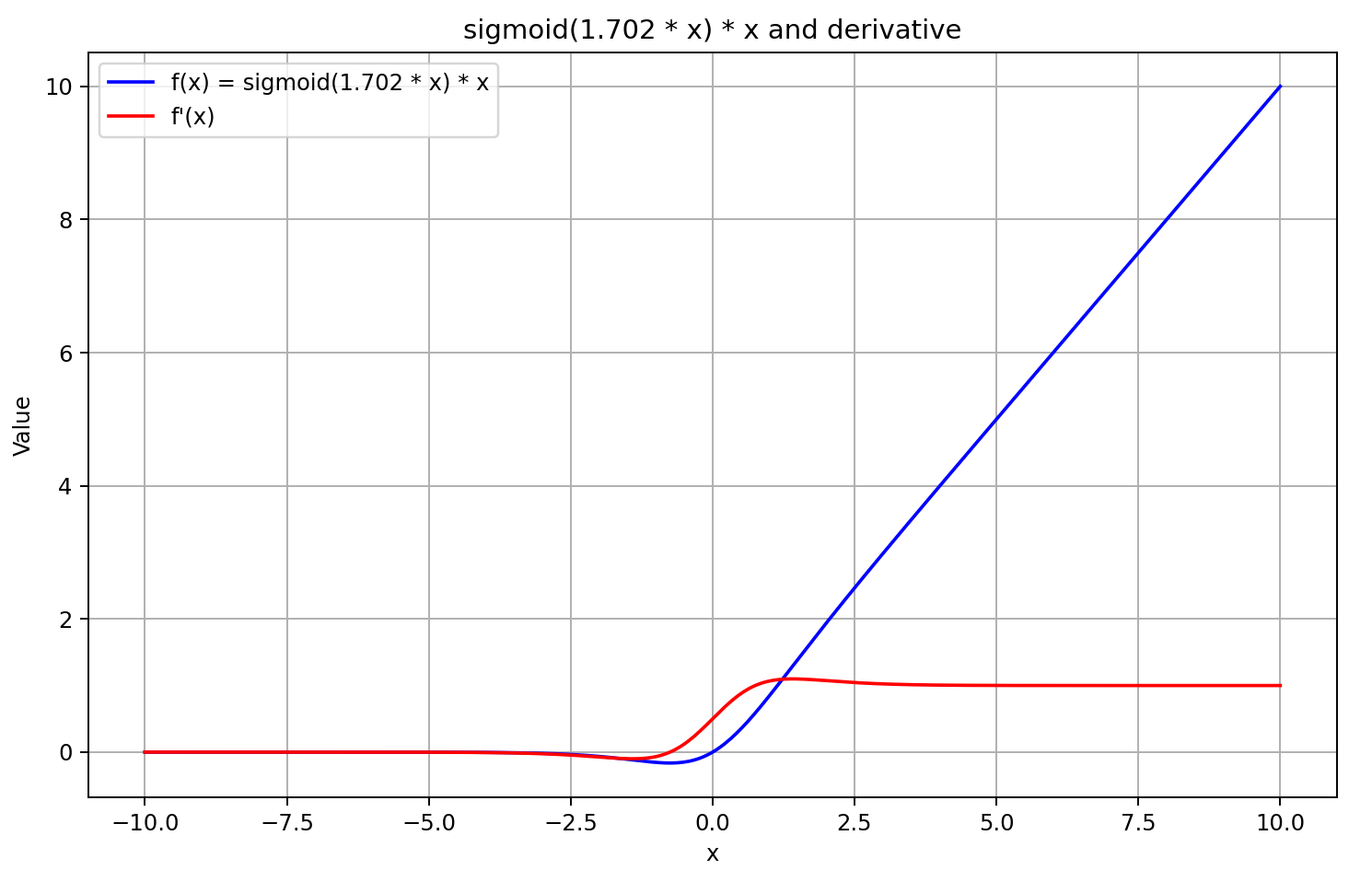
按这样的理解指导，我们推导近似值为前馈通验结果的 sigmoid，再乘以 5。该方法提供快速计算，并当 GELU 输出大于或等于 0 时，产生良好的近似值。然而，对于负的输出值，推导固定为 0.5，因此模型的进一步训练无法继续。实际上，推导应当接近 0，从而有效阻止误差梯度的传播。

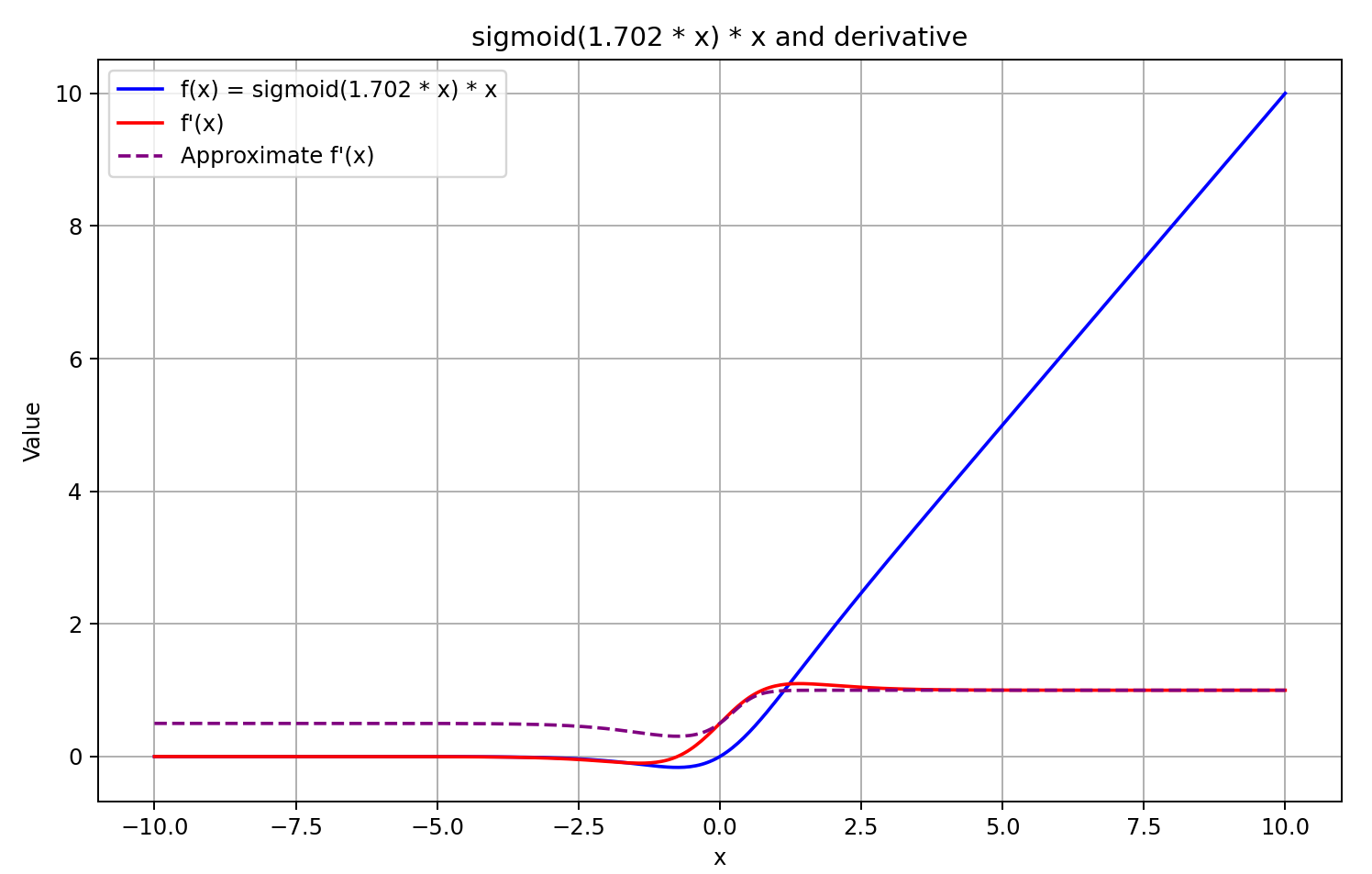
决策已做出。我们开始实现。为此，我们在推导计算函数中添加了另一种情况。

float Deactivation(const float grad, const float inp_value, const int function)
  {
   float result = grad;
//---
   if(isnan(inp_value) || isinf(inp_value) ||
      isnan(grad) || isinf(grad))
      result = 0;
   else
      switch(function)
        {
         case 0: //TANH
            result = clamp(grad + inp_value, -1.0f, 1.0f) - inp_value;
            result *= 1.0f - pow(inp_value, 2.0f);
            break;
         case 1:  //Sigmoid
            result = clamp(grad + inp_value, 0.0f, 1.0f) - inp_value;
            result *= inp_value * (1.0f - inp_value);
            break;
         case 2: //LReLU
            if(inp_value < 0)
               result *= 0.01f;
            break;
         case 3:  //SoftPlus
            result *= Activation(inp_value, 1);
            break;
         case 4:  //GELU
            if(inp_value < 0.9f)
               result *= Activation(5 * inp_value, 1);
            break;
         default:
            break;
        }
//---
   return clamp(result, -MAX_GRAD, MAX_GRAD);
  }

注意，仅当前馈通验的结果小于 0.9 时，我们才会计算激活推导。在所有其它情况下，假设推导为 1，这是准确的。这令我们能够降低梯度传播过程中的运算次数。

该框架作者建议调用 GELU 函数作为 FeedForward 模块层之间的非线性。在我们的 CNeuronRMAT 类中，该模块是使用反馈卷积模块 CResidualConv 实现的。我们修改了该模块层之间调用的激活函数。该操作在类初始化方法中完成。具体更新在代码中标有下划线。

bool CResidualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint window, uint window_out, uint count,
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * count, optimization_type, batch))
      return false;
//---
   if(!cConvs[0].Init(0, 0, OpenCL, window, window, window_out, count, optimization, iBatch))
      return false;
   if(!cNorm[0].Init(0, 1, OpenCL, window_out * count, iBatch, optimization))
      return false;
   cNorm[0].SetActivationFunction(GELU);
   if(!cConvs[1].Init(0, 2, OpenCL, window_out, window_out, window_out, count, optimization, iBatch))
      return false;
   if(!cNorm[1].Init(0, 3, OpenCL, window_out * count, iBatch, optimization))
      return false;
   cNorm[1].SetActivationFunction(None);
//---

........
........
........ 
//---
   return true;
  }

至此，我们实现了由 LSEAttention 框架作者提议的技术。完整代码的所有修改、以及准备本文时用到的所有程序的完整代码，都可在附件中找到。

需要注意的是，从上一篇文章中，所有的环境交互和模型训练程序都得到了充分的复用。类似地，模型架构保持不变。这令评估引入的优化的影响变得更加有趣，因为唯一的区别在于算法的改进。

3. 测试

在本文中，我们实现了 LSEAttention 框架作者提议的预测时间序列的雏形变换器算法的优化技术。如前所述，这项工作与我们早前的研究不同。我们没有像以前那样创建新的神经层。取而代之，我们将拟议的改进集成到之前已实现的组件之中。本质上，我们采用了上一篇文章中实现的 HypDiff 框架，并协同无需改变模型架构的算法优化。我们还修改了 FeedForward 模块中的激活函数。这些调整主要通过强化数值稳定性，来影响内部计算机制。诚然，我们感兴趣的是这些变化如何影响模型训练结果。

为了确保比较的公平性，我们完整地复刻了 HypDiff 模型训练算法。采用相同的训练数据集。不过，这次我们没有迭代更新训练集。虽然这或许会稍微降低训练性能，但它能准确比较算法优化前后的模型。

这些模型采用 2024 年第一季度的真实历史数据进行了评估。测试结果呈现如下。

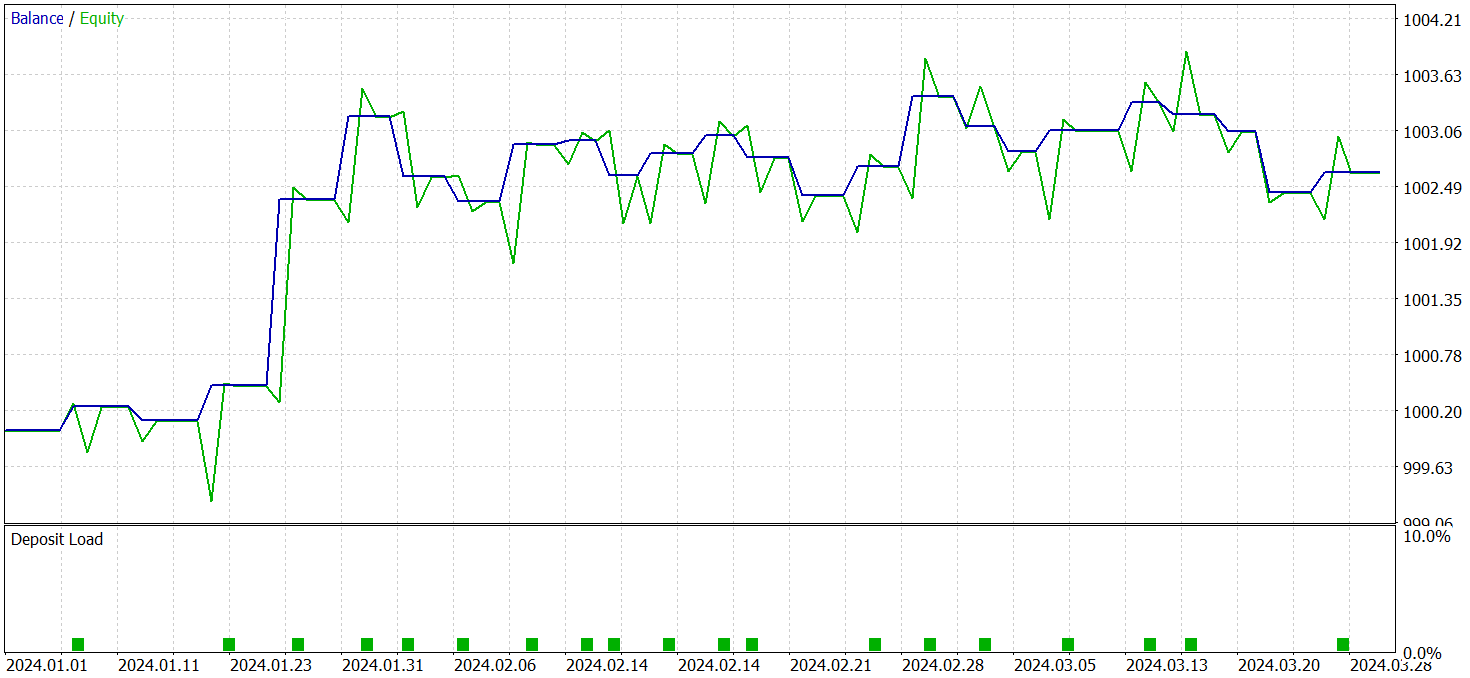
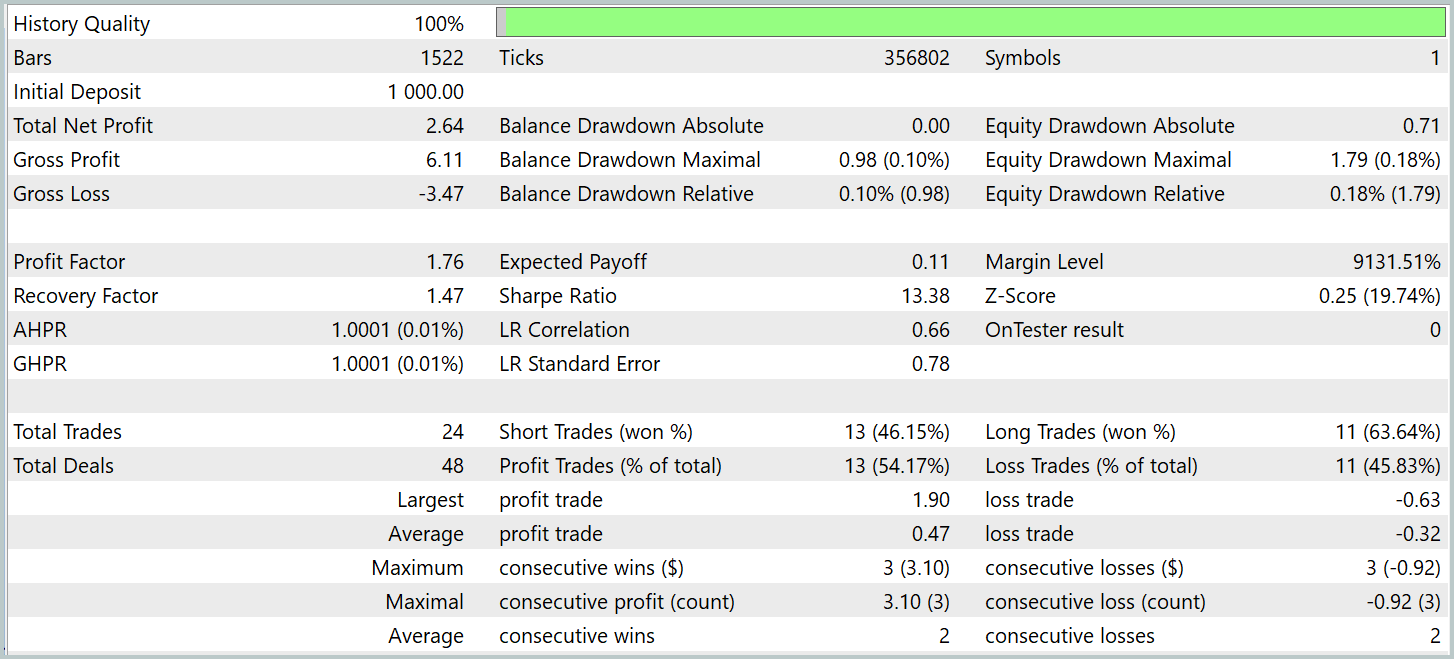
应当注意的是，修改前后的模型性能十分相似。在测试期间，更新后的模型执行了 24 笔交易。它与基准模型相比仅有一笔交易偏离，这落在误差范围之内。两种模型都完成了 13 笔盈利交易。唯一明显的改善是 2 月份没有疏缺。

结束语

LSEAttention 方法代表了注意力机制的演变，在需要对噪声和数据变异性具有高弹性的任务中特别有效。LSEAttention 的主要优点在于运用了对数平滑，这是调用 Log-Sum-Exp 函数实现。这令模型能够避免数值溢出、及梯度消失的问题，其在深度神经网络中至关重要。

在实践章节，我们利用 MQL5 实现了所提议方式，并将它们集成到之前开发的模块当中。我们依据真实历史数据训练并测试了模型。基于测试结果，我们能得出结论，这些方法提升了模型训练过程的稳定性。

参考

文章中所用程序

#	名称	类型	说明
1	Research.mq5	智能系统	收集示例的 EA 交易
2	ResearchRealORL.mq5	智能系统	利用 Real-ORL 方法收集示例的智能系统
3	Study.mq5	智能系统	模型训练 EA 交易系统
4	Test.mq5	智能系统	模型测试 EA 交易系统
5	Trajectory.mqh	类库	系统状态描述结构
6	NeuroNet.mqh	类库	创建神经网络的类库
7	NeuroNet.cl	函数库	OpenCL 程序代码库

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16360

附加的文件 |

下载ZIP

MQL5.zip (2123.05 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论

开发回放系统（第 72 部分）：异常通信（一）

我们今天创造的东西将很难理解。因此，在这篇文章中，我将只谈论初始阶段。请仔细阅读这篇文章，这是我们继续下一步的重要前提。本材料的目的纯粹是教学性的，因为我们只会学习和掌握所提出的概念，而没有实际应用。

迁移至 MQL5 Algo Forge（第 1 部分）：创建主存储库

在 MetaEditor 中处理项目时，开发人员经常需要管理代码版本。MetaQuotes 最近宣布迁移到 GIT，并推出具有代码版本控制和协作功能的 MQL5 Algo Forge。在本文中，我们将讨论如何更有效地使用新的和以前存在的工具。

新手在交易中的10个基本错误

新手在交易中会犯的10个基本错误: 在市场刚开始时交易, 获利时不适当地仓促, 在损失的时候追加投资, 从最好的仓位开始平仓, 翻本心理, 最优越的仓位, 用永远买进的规则进行交易, 在第一天就平掉获利的仓位,当发出建一个相反的仓位警示时平仓, 犹豫。

流动性攫取交易策略

流动性攫取交易策略是智能资金概念（SMC）的核心组成部分，旨在识别并利用市场中机构投资者的操作行为。该策略聚焦于高流动性区域（如支撑位或阻力位），在这些区域，大额订单可引发价格波动，随后市场恢复原有趋势。本文将详细阐释流动性攫取的概念，并概述如何在MQL5中开发流动性攫取交易策略的智能交易系统（EA）。