Datenwissenschaft und ML (Teil 44): Forex OHLC Zeitreihenprognose mit Vektor-Autoregression (VAR)
149
0
Inhalt
- Was ist Vektor-Autoregression (VAR)?
- Die Mathematik hinter dem Vektorautoregressionsmodell (VAR)
- Die dem VAR-Modell zugrunde liegende Annahmen
- Implementierung des VAR-Modells für OHLC-Werte in Python
- Prognosen außerhalb der Stichprobe mit VAR
- Herstellung des VAR-basierten Handelsroboters
- Abschließende Überlegungen
Was ist eine Vektor-Autoregression (VAR)?
Hierbei handelt es sich um ein traditionelles und statistisches Zeitreihenprognoseinstrument, das zur Untersuchung der dynamischen Beziehungen zwischen mehreren Zeitreihenvariablen verwendet wird. Im Gegensatz zu univariaten autoregressiven Modellen wie ARIMA (im vorherigen Artikel besprochen) die nur eine einzige Variable auf der Grundlage ihrer früheren Werte vorhersagen, untersuchen VAR-Modelle die Interkonnektivität vieler Variablen.
Sie erreichen dies, indem sie jede Variable als eine Funktion nicht nur ihrer früheren Werte, sondern auch der früheren Werte anderer Variablen im System modellieren. In diesem Artikel werden wir die Grundlagen der Vektorautoregression und ihre Anwendung auf den Handel untersuchen.
Ihr Ursprung
Die Vektorautoregression wurde erstmals in den 1960er Jahren von dem Wirtschaftswissenschaftler Clive Granger vorgestellt. Die bedeutenden Entdeckungen von Granger schufen den Rahmen für das Verständnis und die Modellierung der dynamischen Wechselwirkungen zwischen Wirtschaftsfaktoren. VAR-Modelle gewannen in den 1970er und 1980er Jahren in der Ökonometrie und Makroökonomie stark an Bedeutung.
Diese Technik ist eine multivariate Erweiterung der Autoregressionsmodelle (AR). Während traditionelle AR-Modelle wie ARIMA die Beziehung zwischen einer einzelnen Variablen und ihren verzögerten Werten analysieren, berücksichtigen VAR-Modelle mehrere Variablen gleichzeitig. In einem VAR-Modell wird jede Variable auf ihre eigenen verzögerten Werte sowie auf die verzögerten Werte der anderen Variablen im System regressiert.
Im vorangegangenen Artikel dieser Reihe haben wir ARIMA besprochen und festgestellt, dass es nicht in der Lage ist, mehrere Variablen in seinen Trainings- und Prognoseprozess einzubeziehen. In diesem Artikel werden wir VAR besprechen, das die meisten Leute als Vorgänger von ARIMA ansehen, da es darauf abzielt, das Problem der univariaten Zeitreihenprognose zu lösen.
Um diese einfache Technik (das Modell) zu verstehen, sollten wir uns ihre Mathematik ansehen.
Die Mathematik hinter dem Vektor-Autoregressions-Modell (VAR)
Der Hauptunterschied zwischen anderen autoregressiven Modellen (AR, ARMA und ARIMA) und dem VAR-Modell besteht darin, dass die erstgenannten Modelle unidirektional sind (die Vorhersagevariable beeinflusst die Zielvariable und nicht umgekehrt), während das VAR-Modell bidirektional ist.
Mathematisch kann ein VAR(p)-Modell mit „p“ Lags wie folgt dargestellt werden.
wobei:
- c = der konstante Term (Achsenabschnitt) des Modells
-
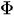= Koeffizient der Lags Y bis zur Ordnung p. -
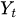= Der Wert der Zeitreihe zum Zeitpunkt t -
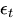= Der Fehlerterm zum Zeitpunkt t.
Ein K-dimensionales VAR-Modell der Ordnung P, bezeichnet als VAR(p), ergibt unter Berücksichtigung von k=2 die folgende Gleichung.
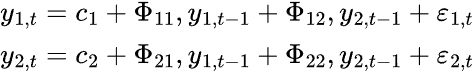
Beim VAR-Modell haben wir mehrere Zeitreihenvariablen, die sich gegenseitig beeinflussen; es wird als Gleichungssystem mit einer Gleichung pro Zeitreihenvariable modelliert. Nachstehend finden Sie die Formel in Form einer Matrix.
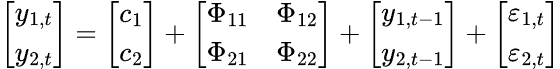
Die endgültige VAR-Gleichung lautet.
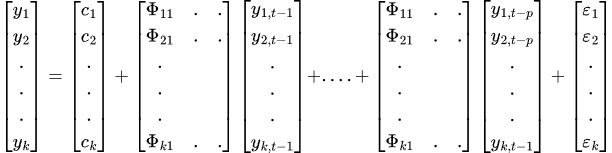
Um die Gültigkeit und Vertrauenswürdigkeit der mit dem VAR-Modell erzielten Ergebnisse zu gewährleisten, müssen verschiedene Annahmen und Anforderungen erfüllt werden.
Die dem VAR-Modell zugrunde liegende Annahmen
- Linearität
Wie aus der Formel hervorgeht, ist der VAR im Kern ein lineares Modell, sodass alle in diesem Modell verwendeten Variablen linear sein müssen (d. h. als gewichtete Summen verzögerter Werte ausgedrückt). - Stationarität
Alle in diesem Modell verwendeten Variablen müssen stationär sein, d. h. der Mittelwert, die Varianz und die Kovarianz jedes Merkmals der Zeitreihe müssen im Zeitverlauf konstant sein. Wir müssen alle nicht-stationären Merkmale in stationäre umwandeln, wenn wir welche im Datensatz haben. - Keine perfekte Multikollinearität zwischen Merkmalen
Damit VAR effektiv funktioniert, darf keine erklärende Variable eine exakte lineare Kombination von anderen sein. Dies ist wichtig, weil es hilft, singuläre Matrizen bei der OLS-Schätzung zu vermeiden (d. h.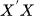
muss invertierbar sein). Wir müssen redundante Merkmale weglassen oder eine Regularisierungstechnik verwenden, um dieses Problem zu lösen. - Keine Autokorrelation in den Residuen
Es wird davon ausgegangen, dass die Residuen nicht seriell korreliert sind, sie sollten sich wie weißes Rauschen verhalten. Autokorrelation verzerrt Standardfehler und macht statistische Tests ungültig. - Ausreichende Beobachtungen
Der VAR geht davon aus, dass er genügend Daten für die Parameterschätzung erhalten hat. Wir müssen dieses Modell also mit so vielen Informationen wie möglich füttern, um maximale Effizienz zu erreichen.
Sehen wir uns nun an, wie man dieses Modell in der Programmiersprache Python umsetzen kann.
Implementierung des VAR-Modells für OHLC-Werte in Python
Beginnen wir mit der Installation aller Python-Abhängigkeiten. Die Datei requirements.txt befindet Sich im Abschnitt der Anhänge.
pip install -r requirements.txt
Importe
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import warnings # Suppress all warnings warnings.filterwarnings("ignore") sns.set_style("darkgrid")
Wir beginnen mit dem Import der OHLC-Werte für Open, High, Low und Close aus dem MetaTrader 5.
symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 if not mt5.symbol_select(symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error) quit() rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 10000) df = pd.DataFrame(rates) # convert rates into a pandas dataframe df
Ausgabe:
| time | open | high | low | close | tick_volume | spread | real_volume | |
|---|---|---|---|---|---|---|---|---|
| 0 | 611280000 | 1.00780 | 1.01050 | 1.00630 | 1.00760 | 821 | 50 | 0 |
| 1 | 611366400 | 0.99620 | 1.00580 | 0.99100 | 0.99600 | 2941 | 50 | 0 |
| 2 | 611452800 | 0.99180 | 0.99440 | 0.98760 | 0.99190 | 1351 | 50 | 0 |
| 3 | 611539200 | 0.99330 | 0.99370 | 0.99310 | 0.99310 | 101 | 50 | 0 |
| 4 | 611798400 | 0.97360 | 0.97360 | 0.97320 | 0.97360 | 81 | 50 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 9995 | 1748390400 | 1.13239 | 1.13453 | 1.12838 | 1.12910 | 153191 | 0 | 0 |
| 9996 | 1748476800 | 1.12918 | 1.13849 | 1.12105 | 1.13659 | 191948 | 0 | 0 |
| 9997 | 1748563200 | 1.13630 | 1.13901 | 1.13127 | 1.13470 | 186924 | 0 | 0 |
| 9998 | 1748822400 | 1.13435 | 1.14500 | 1.13412 | 1.14436 | 168697 | 0 | 0 |
| 9999 | 1748908800 | 1.14385 | 1.14549 | 1.13642 | 1.13708 | 147424 | 0 | 0 |
Wir haben 10000 Balken aus dem täglichen Zeitrahmen erhalten, was wir als sehr viel erachten können, da die Daten gemäß den Annahmen der Modelle ausreichend sein müssen.
Da wir dieses Modell auf OHLC-Werte anwenden wollen, lassen wir die anderen Spalten weg.
ohlc_df = df.drop(columns=[ "time", "tick_volume", "spread", "real_volume" ]) ohlc_df
Ich habe mich nur deshalb für die OHLC-Werte entschieden, weil ich glaube, dass zwischen diesen Werten eine starke Beziehung besteht, die uns das Modell aufzeigen könnte, ganz zu schweigen davon, dass diese vier Variablen die grundlegenden Merkmale sind, die wir aus Finanzinstrumenten extrahieren können.
Da dieses Modell von der Stationarität seiner Merkmale ausgeht, können wir feststellen, dass die OHLC-Werte nicht stationär sind, also machen wir sie stationär, indem wir jeden Wert einmal von seinem/ihren vorherigen Wert(en) unterscheiden.
stationary_df = pd.DataFrame() for col in df.columns: stationary_df["Diff_"+col] = df[col].diff() stationary_df.dropna(inplace=True) stationary_df
Ausgabe:
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| 1 | 0.00080 | 0.00180 | -0.01670 | -0.00950 |
| 2 | -0.00960 | -0.00840 | -0.01370 | -0.01880 |
| 3 | -0.01870 | -0.01930 | -0.00350 | -0.00190 |
| 4 | -0.00180 | -0.00210 | -0.00590 | -0.00870 |
| 5 | -0.00890 | -0.00310 | -0.01300 | -0.01200 |
| ... | ... | ... | ... | ... |
Optional können wir auf Stationarität prüfen, wenn wir uns bei den neu gewonnenen Variablen unsicher sind.
from statsmodels.tsa.stattools import adfuller for col in stationary_df.columns: result = adfuller(stationary_df[col]) print(f'{col} p-value: {result[1]}')
Ausgabe:
Diff_Open p-value: 0.0 Diff_High p-value: 1.0471939301334604e-28 Diff_Low p-value: 1.1015540451195308e-23 Diff_Close p-value: 0.0
Der P-Wert muss kleiner als 0,05 (<0,05) sein, damit die Daten als stationär gelten. Wie wir sehen können, ist der p-Wert kleiner als 0,05, sodass unsere Daten für den Moment gut sind.
Auch hier gilt, dass gemäß den VAR-Annahmen keine perfekte Multikollinearität zwischen den Merkmalen bestehen darf, sodass wir dies sicherstellen müssen.
stationary_df.corr()
Ausgabe:
| Diff_Open | Diff_High | Diff_Low | Diff_Close | |
|---|---|---|---|---|
| Diff_Open | 1.000000 | 0.565829 | 0.563516 | 0.036347 |
| Diff_High | 0.565829 | 1.000000 | 0.452775 | 0.564026 |
| Diff_Low | 0.563516 | 0.452775 | 1.000000 | 0.557139 |
| Diff_Close | 0.036347 | 0.564026 | 0.557139 | 1.000000 |
Die Korrelationsmatrix zwischen den Merkmalen scheint in Ordnung zu sein, wir können sogar den mittleren absoluten Korrelationskoeffizienten der gesamten Matrix überprüfen und sicherstellen, dass |p| < 0,8 ist.
print("Mean absolute |p|:", np.abs(np.corrcoef(stationary_df, rowvar=False).mean()))
Ausgabe:
Mean absolute |p|: 0.5924538886295351 Auswahl der besten Zahl für die Lags
Wir haben in der Formel gesehen, dass das VAR-Modell die Informationen aus der Vergangenheit (Lags) verwendet, um die Zukunft vorherzusagen; wir müssen wissen, welche Zahl für die Lags zu verwenden ist, um das beste Ergebnis zu erzielen. Glücklicherweise bietet die VAR-Funktion von „stats models“ die Möglichkeit, diesen Wert anhand einer Reihe von Kriterien zu bestimmen:
- AIC (Akaike Information Criterion)
- BIC (Bayesian/Schwarz Information Criterion)
- FPE (Final prediction Error)
- HQIC (Hannan-Quin Information Criterion)
# Select optimal lag using AIC lag_order = model.select_order(maxlags=30) print(lag_order.summary())
Ausgabe:
VAR Order Selection (* highlights the minimums) ================================================== AIC BIC FPE HQIC -------------------------------------------------- 0 -41.87 -41.87 6.537e-19 -41.87 1 -45.15 -45.14 2.457e-20 -45.15 2 -45.63 -45.60 1.530e-20 -45.62 3 -45.85 -45.81 1.225e-20 -45.84 4 -45.99 -45.94 1.065e-20 -45.97 5 -46.18 -46.12 8.805e-21 -46.16 6 -46.24 -46.17 8.256e-21 -46.22 7 -46.28 -46.20 7.951e-21 -46.25 8 -46.31 -46.22 7.708e-21 -46.28 9 -46.34 -46.24 7.471e-21 -46.31 10 -46.36 -46.24 7.368e-21 -46.32 11 -46.41 -46.28 6.979e-21 -46.37 12 -46.42 -46.28 6.890e-21 -46.38 13 -46.44 -46.28 6.806e-21 -46.38 14 -46.45 -46.28 6.730e-21 -46.39 15 -46.45 -46.28 6.697e-21 -46.39 16 -46.46 -46.28 6.628e-21 -46.40 17 -46.49 -46.29* 6.460e-21 -46.42 18 -46.50 -46.28 6.419e-21 -46.42 19 -46.50 -46.28 6.383e-21 -46.43 20 -46.50 -46.27 6.358e-21 -46.43 21 -46.51 -46.27 6.306e-21 -46.43 22 -46.52 -46.26 6.292e-21 -46.43 23 -46.53 -46.26 6.216e-21 -46.44 24 -46.53 -46.25 6.185e-21 -46.44 25 -46.54 -46.24 6.162e-21 -46.44 26 -46.54 -46.24 6.113e-21 -46.44 27 -46.55 -46.23 6.092e-21 -46.44 28 -46.55 -46.22 6.086e-21 -46.44 29 -46.56* -46.22 6.031e-21* -46.44* 30 -46.56 -46.21 6.033e-21 -46.44 --------------------------------------------------
Jede Zeile zeigt Werte für verschiedene lag_order. Ein mit einem Sternchen gekennzeichneter Wert ist der Mindestwert für dieses Kriterium und zeigt die „beste“ Verzögerungsreihenfolge nach diesem Kriterium an.
Laut dieser Zusammenfassung von lag_order
- Das beste Modell für AIC ist bei einem Lag von 29 (Wert -46,56)
- Das beste Modell für BIC ist bei einem Lag von 17 (Wert -46,29)
- Das beste Modell für FPE ist bei einem Lag von 29 (Wert -6,031e-21)
- Das beste Modell für HQIC ist bei einem Lag von 29 (Wert -46,44)
Meistens werden AIC- und BIC-Informationen verwendet, um ein Modell auszuwählen. Einfach ausgedrückt, neigt AIC dazu, komplexere Modelle auszuwählen (höhere Lags), während BIC die Komplexität stärker bestraft und oft einfachere Modelle auswählt.
HQIC ist der Mittelweg zwischen AIC und BIC, während sich FPE auf den Vorhersagefehler konzentriert.
Lassen Sie uns nun das Modell mit dem Wert für Lag gemäß den AIC-Kriterien anpassen.
# Fit the model with selected lag results = model.fit(lag_order.aic) print(results.summary())
Ausgabe:
Summary of Regression Results ================================== Model: VAR Method: OLS Date: Wed, 04, Jun, 2025 Time: 10:40:37 -------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21 -------------------------------------------------------------------- Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000 L1.diff_high 0.009878 0.004957 1.993 0.046 L1.diff_low 0.006869 0.005010 1.371 0.170 L1.diff_close 0.995718 0.004583 217.244 0.000 L2.diff_open -0.935345 0.015071 -62.062 0.000 L2.diff_high 0.007118 0.006749 1.055 0.292 L2.diff_low 0.022288 0.006819 3.268 0.001 L2.diff_close 0.939861 0.011863 79.226 0.000 L3.diff_open -0.906595 0.018115 -50.045 0.000 L3.diff_high 0.003072 0.007954 0.386 0.699 L3.diff_low 0.018535 0.008097 2.289 0.022 L3.diff_close 0.910898 0.015703 58.006 0.000 L4.diff_open -0.898803 0.020501 -43.841 0.000 L4.diff_high 0.003670 0.008912 0.412 0.681 L4.diff_low 0.015668 0.009103 1.721 0.085 L4.diff_close 0.886824 0.018628 47.606 0.000 L5.diff_open -0.867308 0.022560 -38.445 0.000 L5.diff_high 0.001318 0.009676 0.136 0.892 L5.diff_low -0.000027 0.009942 -0.003 0.998 L5.diff_close 0.884632 0.020996 42.133 0.000 ... ... ... L29.diff_open -0.005922 0.004617 -1.283 0.200 L29.diff_high 0.007026 0.004956 1.418 0.156 L29.diff_low 0.004387 0.005005 0.876 0.381 L29.diff_close 0.035169 0.010568 3.328 0.001 ================================================================================= Results for equation diff_high ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000008 0.000048 0.165 0.869 L1.diff_open -0.010294 0.038697 -0.266 0.790 L1.diff_high -0.887555 0.017570 -50.515 0.000 L1.diff_low -0.020634 0.017757 -1.162 0.245 L1.diff_close 0.969305 0.016245 59.667 0.000 L2.diff_open 0.006028 0.053418 0.113 0.910 L2.diff_high -0.838250 0.023920 -35.043 0.000 L2.diff_low -0.057396 0.024169 -2.375 0.018 L2.diff_close 0.914246 0.042047 21.744 0.000 L3.diff_open -0.160354 0.064208 -2.497 0.013 L3.diff_high -0.807663 0.028191 -28.650 0.000 L3.diff_low -0.042960 0.028698 -1.497 0.134 L3.diff_close 0.869460 0.055659 15.621 0.000 L4.diff_open -0.168775 0.072664 -2.323 0.020 L4.diff_high -0.785399 0.031589 -24.863 0.000 L4.diff_low -0.054113 0.032265 -1.677 0.094 L4.diff_close 1.013851 0.066026 15.355 0.000 L5.diff_open -0.146275 0.079959 -1.829 0.067 L5.diff_high -0.746785 0.034295 -21.775 0.000 L5.diff_low -0.098885 0.035238 -2.806 0.005 L5.diff_close 1.012989 0.074419 13.612 0.000 ... ... ... L27.diff_open 0.020345 0.053645 0.379 0.705 L27.diff_high -0.153391 0.028136 -5.452 0.000 L27.diff_low -0.065690 0.028874 -2.275 0.023 L27.diff_close 0.251005 0.062004 4.048 0.000 L28.diff_open -0.005863 0.040235 -0.146 0.884 L28.diff_high -0.087603 0.023901 -3.665 0.000 L28.diff_low 0.008246 0.024229 0.340 0.734 L28.diff_close 0.134924 0.051754 2.607 0.009 L29.diff_open -0.000480 0.016364 -0.029 0.977 L29.diff_high -0.051136 0.017564 -2.911 0.004 L29.diff_low 0.035083 0.017741 1.977 0.048 L29.diff_close 0.054123 0.037457 1.445 0.148 ================================================================================= Results for equation diff_low ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000005 0.000047 0.101 0.920 L1.diff_open 0.024212 0.038141 0.635 0.526 L1.diff_high -0.058570 0.017317 -3.382 0.001 L1.diff_low -0.904567 0.017501 -51.686 0.000 L1.diff_close 0.976598 0.016012 60.993 0.000 L2.diff_open 0.067049 0.052650 1.274 0.203 L2.diff_high -0.084679 0.023576 -3.592 0.000 L2.diff_low -0.866233 0.023822 -36.363 0.000 L2.diff_close 0.937652 0.041442 22.626 0.000 L3.diff_open 0.065284 0.063284 1.032 0.302 L3.diff_high -0.108128 0.027785 -3.892 0.000 L3.diff_low -0.791679 0.028285 -27.989 0.000 L3.diff_close 0.844047 0.054858 15.386 0.000 L4.diff_open 0.018366 0.071619 0.256 0.798 L4.diff_high -0.116216 0.031134 -3.733 0.000 L4.diff_low -0.747223 0.031801 -23.497 0.000 L4.diff_close 0.816060 0.065076 12.540 0.000 L5.diff_open -0.040872 0.078809 -0.519 0.604 L5.diff_high -0.110998 0.033802 -3.284 0.001 L5.diff_low -0.731241 0.034731 -21.054 0.000 L5.diff_close 0.832344 0.073348 11.348 0.000 ... ... ... L29.diff_open 0.024357 0.016128 1.510 0.131 L29.diff_high 0.026179 0.017312 1.512 0.130 L29.diff_low -0.072592 0.017486 -4.151 0.000 L29.diff_close 0.051738 0.036919 1.401 0.161 ================================================================================= Results for equation diff_close ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const 0.000013 0.000071 0.185 0.853 L1.diff_open 0.037592 0.057827 0.650 0.516 L1.diff_high 0.007085 0.026256 0.270 0.787 L1.diff_low 0.011658 0.026535 0.439 0.660 L1.diff_close -0.020373 0.024276 -0.839 0.401 L2.diff_open 0.150341 0.079825 1.883 0.060 L2.diff_high -0.035345 0.035745 -0.989 0.323 L2.diff_low -0.041114 0.036117 -1.138 0.255 L2.diff_close -0.012920 0.062832 -0.206 0.837 L3.diff_open -0.000054 0.095949 -0.001 1.000 L3.diff_high -0.047439 0.042126 -1.126 0.260 L3.diff_low 0.028500 0.042884 0.665 0.506 L3.diff_close -0.113979 0.083173 -1.370 0.171 L4.diff_open -0.083562 0.108585 -0.770 0.442 L4.diff_high -0.083193 0.047204 -1.762 0.078 L4.diff_low 0.055907 0.048215 1.160 0.246 L4.diff_close 0.026375 0.098665 0.267 0.789 L5.diff_open -0.148622 0.119487 -1.244 0.214 L5.diff_high -0.065192 0.051248 -1.272 0.203 L5.diff_low 0.011819 0.052658 0.224 0.822 L5.diff_close 0.125327 0.111207 1.127 0.260 ... ... ... L29.diff_open 0.002852 0.024453 0.117 0.907 L29.diff_high -0.011652 0.026247 -0.444 0.657 L29.diff_low -0.004191 0.026511 -0.158 0.874 L29.diff_close 0.070689 0.055974 1.263 0.207 ================================================================================= Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
Das VAR-Modell bietet, ähnlich wie andere statistische/traditionelle Zeitreihenmodelle, eine detaillierte Zusammenfassung der Modellleistung und seiner Merkmale. Diese Zusammenfassung hilft uns, das Modell im Detail zu verstehen, lassen Sie uns die Zusammenfassung des obigen Modells kurz analysieren.
-------------------------------------------------------------------- No. of Equations: 4.00000 BIC: -46.2188 Nobs: 9970.00 HQIC: -46.4425 Log likelihood: 175968. FPE: 6.03280e-21 AIC: -46.5571 Det(Omega_mle): 5.75774e-21
- Anzahl der Gleichungen: 4, bedeutet, dass das System (Modell) 4 endogene Variablen enthält: diff_open, diff_high, diff_low, diff_close.
- Nobs (Number of observations used bzw. Anzahl der verwendeten Beobachtungen): Da wir uns für das AIC-Kriterium entschieden haben, das 29 Lags verwendet, wurden 29+1 Merkmale nicht in den Trainingsprozess (Schätzung) einbezogen, da diese Werte zuvor als anfängliche Lags verwendet wurden.
- AIC, BIC, HQIC und FPE: Alle diese Werte sind negativ (normal), was ein gutes Zeichen für eine bessere Anpassung ist.
- Log-Wahrscheinlichkeit: Ein hoher positiver Wert weist auf eine gute Modellanpassung hin.
Jede Gleichung ergibt
Für jede Variable (diff_open, diff_high, diff_low und diff_close) sehen Sie.
- Koeffizienten
Diese stellen die Auswirkungen jeder verzögerten Variable (L1, L2 usw.) auf den aktuellen Wert dar. Je näher dieser Wert bei 1 liegt, desto positiver wirkt sich eine Variable auf die aktuelle Gleichungsvariable aus und umgekehrt.
Zum Beispiel.
Results for equation diff_open ================================================================================= coefficient std. error t-stat prob --------------------------------------------------------------------------------- const -0.000002 0.000013 -0.115 0.908 L1.diff_open -0.959329 0.010918 -87.867 0.000
Der Koeffizient von -0,959329 bedeutet hier, dass ein Anstieg des gestrigen (lag-1) Wertes von diff_open um 1 Einheit ist mit einem Rückgang des heutigen Wertes von diff_open um 0,959329 Einheiten verbunden, wobei alle anderen Variablen konstant bleiben. -
Std. Fehler
Sie geben die Genauigkeit der Koeffizientenschätzungen an. -
t-stat
Dies steht für statistische Signifikanz. Je größer der absolute Wert |t-stat| dieser Metrik ist, desto signifikanter ist die Variable. Ein großer absoluter Wert (z. B. |t|>2) zeigt statistische Signifikanz an.
Der Wert von |(-87,867)| = +87,876 ist groß und zeigt an, dass der Effekt der Variable diff_open bei lag-1 hoch signifikant ist (nicht zufällig). -
wahrscheinlich
Dies ist der p-Wert, der mit der t-Statistik jedes Koeffizienten verbunden ist. Sie gibt Aufschluss darüber, ob eine bestimmte verzögerte Variable einen signifikanten Einfluss auf den aktuellen Wert der abhängigen Variable hat.
Wenn der Wahrscheinlichkeitswert kleiner oder gleich 0,05 ist, ist eine Variable statistisch signifikant.
Residuale Korrelationsmatrix
Correlation matrix of residuals diff_open diff_high diff_low diff_close diff_open 1.000000 0.223818 0.241416 0.126479 diff_high 0.223818 1.000000 0.452061 0.770309 diff_low 0.241416 0.452061 1.000000 0.765777 diff_close 0.126479 0.770309 0.765777 1.000000
Dies zeigt die Korrelationen zwischen den Vorhersagefehlern verschiedener Gleichungen.
Eine hohe Korrelation zwischen diff_high/diff_close (0,77) und diff_low/diff_close (ungefähr: 0,766) deutet darauf hin, dass gemeinsame unerklärte Faktoren diese Paare beeinflussen.
Prognosen außerhalb der Stichprobe unter Verwendung von VAR
Ähnlich wie beim ARIMA-Modell, das im vorigen Artikel erörtert wurde, ist die Vorhersage von Daten, die außerhalb der Stichprobe liegen, unter Verwendung des VAR recht schwierig. Im Gegensatz zu Modellen des maschinellen Lernens müssen diese traditionellen Modelle regelmäßig mit neuen Informationen aktualisiert werden.
Lassen Sie uns eine Funktion für diese Aufgabe erstellen.
def forecast_next(model_res, symbol, timeframe): forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, model_res.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < model_res.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast, None # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]].values stationary_input = np.diff(input_data, axis=0)[-model_res.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = model_res.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast, None try: updated_data = np.vstack([model_res.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=model_res.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast, None return forecast, updated_model
Um eine Vorhersage zu erhalten, müssen wir das Modell mit dem ursprünglich trainierten Modell ausstatten und das neue Modell nach jeder Vorhersage aktualisieren, indem wir ihm eine Modellvariable neu zuweisen.
res_model = results # Initial model forecast, res_model = forecast_next(model_res=res_model, symbol=symbol, timeframe=timeframe) forecast_df = pd.DataFrame(forecast, columns=stationary_df.columns) print("next forecasted:\n", forecast_df)
Ausgabe:
next forecasted: diff_open diff_high diff_low diff_close 0 0.00435 0.003135 0.001032 -0.000655
Wir können den Trainings- und Vorhersageprozess vereinfachen, indem wir alle diese Elemente in einer Klasse zusammenfassen.
Datei VAR.py
import pandas as pd import numpy as np import MetaTrader5 as mt5 from statsmodels.tsa.api import VAR class VARForecaster: def __init__(self, symbol: str, timeframe: int): self.symbol = symbol self.timeframe = timeframe self.model = None def train(self, start_bar: int=1, total_bars: int=10000, max_lags: int=30): """Trains the VAR model using the collected OHLC from given bars from MetaTrader5 start_bar: int: The recent bar according to copyrates_from_pos total_bars: int: Total number of bars to use for training max_lags: int: The maximum number of lags to use """ self.max_lags = max_lags if not mt5.symbol_select(self.symbol, True): print("Failed to select and add a symbol to the MarketWatch, Error = ",mt5.last_error()) quit() rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, start_bar, total_bars) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return if total_bars < max_lags: print(f"Failed to train, max_lags: {max_lags} must be > total_bars: {total_bars}") return train_df = pd.DataFrame(rates) # convert rates into a pandas dataframe train_df = train_df[["open", "high", "low", "close"]] stationary_df = np.diff(train_df, axis=0) # Convert OHLC values into stationary ones by differenciating them self.model = VAR(stationary_df) # Select optimal lag using AIC lag_order = self.model.select_order(maxlags=self.max_lags) print(lag_order.summary()) # Fit the model with selected lag self.model_results = self.model.fit(lag_order.aic) print(self.model_results.summary()) def forecast_next(self): """Gets recent OHLC from MetaTrader5 and predicts the next differentiated prices Returns: np.array: predicted values """ forecast = None # Get required lags for prediction rates = mt5.copy_rates_from_pos(self.symbol, self.timeframe, 0, self.model_results.k_ar+1) # Get rates starting at the current bar to bars=lags used during training if rates is None or len(rates) < self.model_results.k_ar+1: print("Failed to get copy rates Error =", mt5.last_error()) return forecast # Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = np.diff(input_data, axis=0)[-self.model_results.k_ar:] # get the recent values equal to the number of lags used by the model try: forecast = self.model_results.forecast(stationary_input, steps=1) # predict the next price except Exception as e: print("Failed to forecast: ", str(e)) return forecast try: updated_data = np.vstack([self.model_results.endog, stationary_input[-1]]) # concatenate new/last datapoint to the data used during previous training updated_model = VAR(updated_data).fit(maxlags=self.model_results.k_ar) # Retrain the model with new data except Exception as e: print("Failed to update the model: ", str(e)) return forecast self.model = updated_model return forecast
Lassen Sie uns dies in einem Python-basierten Handelsroboter zusammenfassen.
Herstellung des VAR-basierten Handelsroboters
Angesichts der oben genannten Klasse, die uns beim Training und bei der Vorhersage des nächsten Wertes helfen kann, wollen wir die vorhergesagten Ergebnisse in eine Handelsstrategie einbeziehen.
Erstens haben wir im vorherigen Beispiel stationäre Werte verwendet, die durch Differenzierung der aktuellen Werte von den vorherigen Werten erzeugt wurden, um stationäre Werte zu erhalten. Auch wenn der Ansatz funktioniert, ist er nicht sehr praktisch, wenn es um den Aufbau einer Handelsstrategie geht.
Stattdessen sollten wir die Differenz zwischen dem Eröffnungs- und dem Höchstwert ermitteln, um festzustellen, um wie viel sich der Kurs gegenüber dem Eröffnungskurs nach oben bewegt, und die Differenz zwischen dem Eröffnungs- und dem Tiefstwert, um festzustellen, um wie viel sich der Kurs gegenüber dem Eröffnungskurs nach unten bewegt.
Wenn wir diese beiden Werte erhalten, einen für die Verfolgung der Aufwärtsbewegung der Kerze und den anderen für die Verfolgung der Abwärtsbewegung der Kerze, können wir die vorhergesagten Ergebnisse für die Festlegung von Stop-Loss- und Take-Profit-Werten verwenden.
Ändern wir nun die in unserem Modell verwendeten Merkmale.
# Prepare input data and make forecast input_data = pd.DataFrame(rates)[["open", "high", "low", "close"]] stationary_input = pd.DataFrame({ "high_open": input_data["high"] - input_data["open"], "open_low": input_data["open"] - input_data["low"] })
Bei den durch Differenzierung erhaltenen Merkmalen handelt es sich höchstwahrscheinlich um eine stationäre Variable (eine Überprüfung ist vorerst nicht erforderlich).
In der Hauptdatei des Roboters planen wir den Trainingsprozess und drucken die prognostizierten Werte aus.
Dateiname: VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time from VAR import VARForecaster symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model def get_next_forecast(): print(var_model.forecast_next()) schedule.every(1).minutes.do(get_next_forecast) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
Ausgabe:
[[0.00464001 0.00439884]]
Nun, da wir diese beiden separaten prognostizierten Ergebnisse für high_open und open_low haben, können wir eine einfache Handelsstrategie auf der Grundlage eines einfachen gleitenden Durchschnitts erstellen.
Dateiname: VAR-TradingRobot.py
import MetaTrader5 as mt5 import schedule import time import ta from VAR import VARForecaster from Trade.Trade import CTrade from Trade.SymbolInfo import CSymbolInfo from Trade.PositionInfo import CPositionInfo import numpy as np import pandas as pd symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 mt5_path = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # replace this with a desired MT5 path if not mt5.initialize(mt5_path): # initialize MetaTrader5 print("Failed to initialize MetaTrader5, error =", mt5.last_error()) quit() var_model = VARForecaster(symbol=symbol, timeframe=timeframe) var_model.train(start_bar=1, total_bars=10000, max_lags=30) # Train the VAR Model # Initlalize the trade classes MAGICNUMBER = 5062025 SLIPPAGE = 100 m_trade = CTrade(magic_number=MAGICNUMBER, filling_type_symbol=symbol, deviation_points=SLIPPAGE) m_symbol = CSymbolInfo(symbol=symbol) m_position = CPositionInfo() ##################################################### def pos_exists(pos_type: int, magic: int, symbol: str) -> bool: """Checks whether a position exists given a magic number, symbol, and the position type Returns: bool: True if a position is found otherwise False """ if mt5.positions_total() < 1: # no positions whatsoever return False positions = mt5.positions_get() for position in positions: if m_position.select_position(position): if m_position.magic() == magic and m_position.symbol() == symbol and m_position.position_type()==pos_type: return True return False def trading_strategy(): forecasts_arr = var_model.forecast_next().flatten() high_open = forecasts_arr[0] open_low = forecasts_arr[1] print(f"high_open: ",high_open, " open_low: ",open_low) # Get the information about the market rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, 50) # Get the last 50 bars information rates_df = pd.DataFrame(rates) if rates is None: print("Failed to get copy rates Error =", mt5.last_error()) return sma_buffer = ta.trend.sma_indicator(close=rates_df["close"], window=20) m_symbol.refresh_rates() if rates_df["close"].iloc[-1] > sma_buffer.iloc[-1]: # current closing price is above sma20 if pos_exists(pos_type=mt5.POSITION_TYPE_BUY, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.buy(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.ask(), sl=m_symbol.ask()-open_low, tp=m_symbol.ask()+high_open) else: # if the closing price is below the moving average if pos_exists(pos_type=mt5.POSITION_TYPE_SELL, symbol=symbol, magic=MAGICNUMBER) is False: # If a buy position doesn't exist m_trade.sell(volume=m_symbol.lots_min(), symbol=symbol, price=m_symbol.bid(), sl=m_symbol.bid()+high_open, tp=m_symbol.bid()-open_low) schedule.every(1).minutes.do(trading_strategy) while True: schedule.run_pending() time.sleep(60) else: mt5.shutdown()
Mit Hilfe der in diesem Artikel besprochenen Handelsklassen prüfen wir, ob eine Position der gleichen Art existiert; wenn nicht, eröffnen wir eine Position der gleichen Art. Die vorhergesagten Werte high_open und open_low werden für die Festlegung des Take-Profits und des Stop-Losses eines Handels für einen Kauf bzw. umgekehrt für einen Verkauf verwendet.
Ein einfacher gleitender Durchschnittsindikator der Periode (Fenster) = 20 wird als Bestätigungssignal verwendet. Wenn der aktuelle Schlusskurs über dem gleitenden Durchschnittsindikator liegt, eröffnen wir ein Kaufgeschäft; andernfalls tun wir das Gegenteil, um zu verkaufen.
Ausgabe:
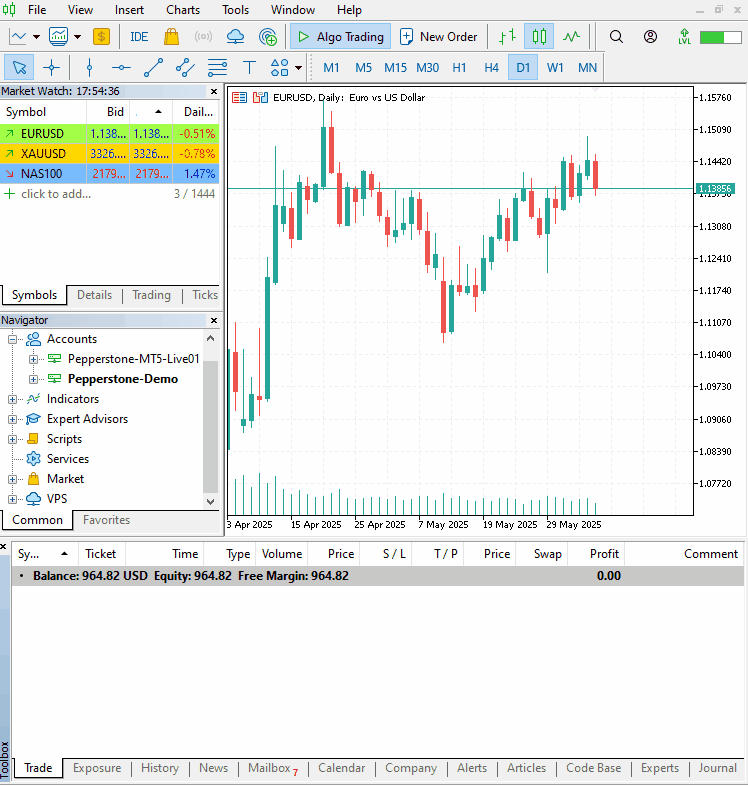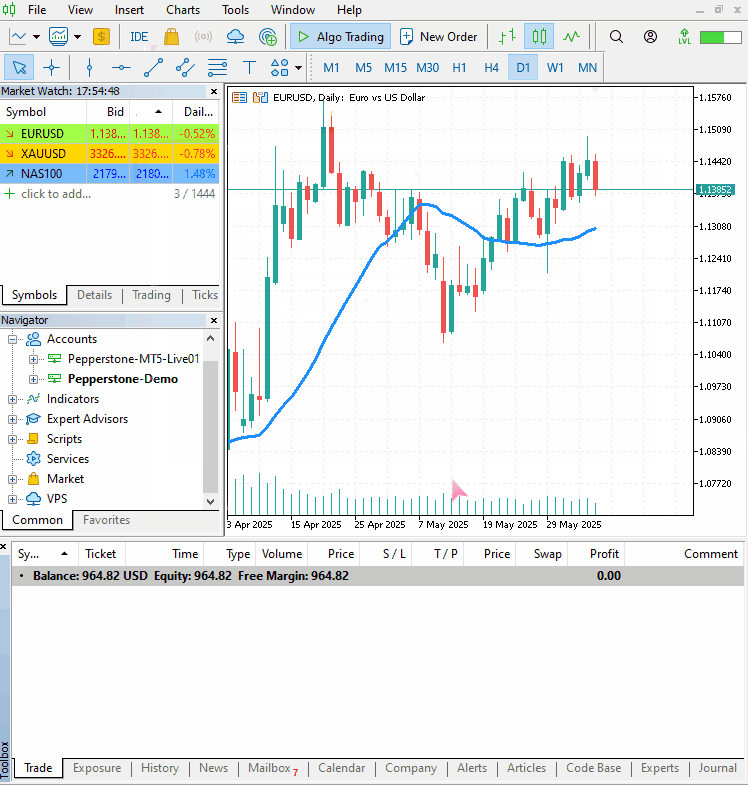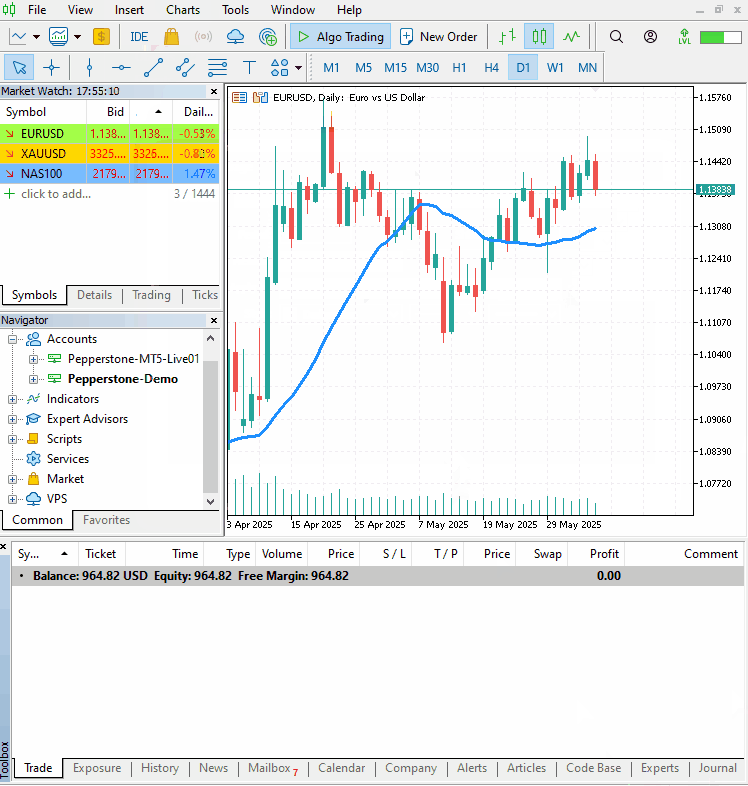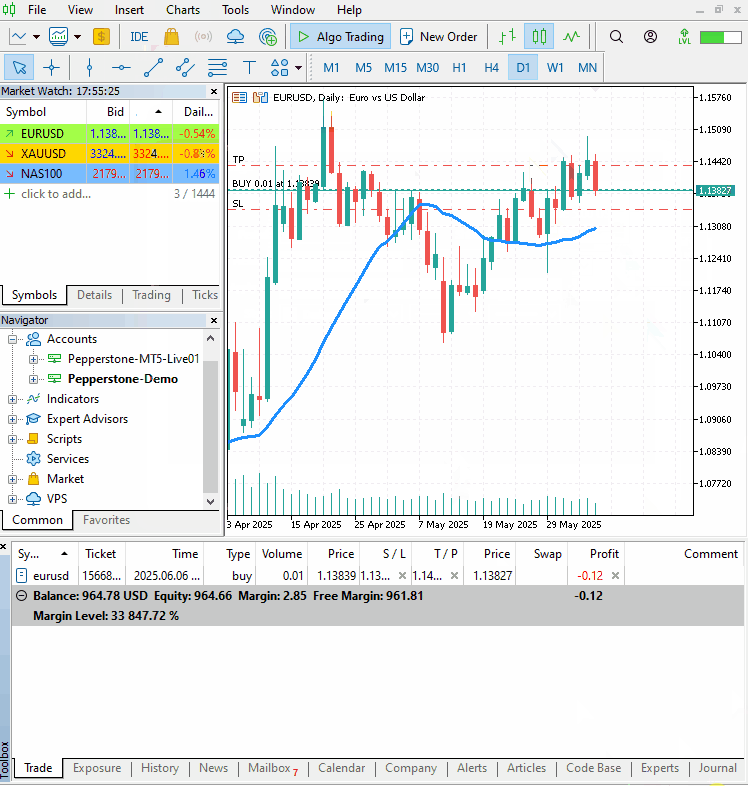
Abschließende Überlegungen
Die Vektor-Autoregression ist ein anerkanntes, klassisches Zeitreihenmodell mit der Fähigkeit, mehrere Regressionsmerkmale vorherzusagen, eine Fähigkeit, die die meisten maschinellen Lernmodelle nicht haben.
Diese Modelle bieten eine Reihe von Vorteilen, wie zum Beispiel:
- Eine flexible Lag-Struktur, die unterschiedliche Lag-Längen für verschiedene Variablen erlaubt,
- Sie erfassen Interdependenzen (dynamische Beziehungen zwischen Variablen),
- Sie haben keine strenge Exogenitätsannahme, wie sie in traditionellen Regressionsmodellen häufig vorkommt.
Zu ihren Nachteilen gehören unter anderem:
- Ihre Empfindlichkeit gegenüber stationären Variablen, da sie nur bei stationären Daten am besten funktionieren.
- Sie gehen von einer linearen Beziehung zwischen einer Variablen und ihren Lags aus, was auf den Finanzmärkten nicht immer möglich ist.
- Bei vielen Variablen und Lags kann es auch zu einer Überanpassung kommen.
Mit diesem Artikel wollte ich das Bewusstsein für dieses Modell, seine Zusammensetzung und seine Anwendung auf Handelsdaten schärfen, da ich im Internet nur wenige Informationen zu diesem speziellen Thema gefunden habe. Bitte zögern Sie nicht, die Idee Ihren Bedürfnissen entsprechend zu verbessern.
Mit freundlichen Grüßen.
Tabelle der Anhänge
| Dateiname | Beschreibung & Verwendung |
|---|---|
| Handel/* | MQL5-ähnliche Handelsklassen in der Sprache Python. |
| error_description.py | Enthält Beschreibungen von MetaTrader 5-Fehlercodes. |
| forex-ts-forecasting-using-var.ipynb | Ein Jupyter-Notebook mit Beispielen zu Lernzwecken. |
| VAR.py | Enthält die Klasse, die das VAR-Modell für das Training und die Erstellung von Prognosen verwendet. |
| VAR-TradingRobot.py | Ein Handelsroboter, der auf der Grundlage von Vorhersagen des VAR-Modells Kauf- und Verkaufstransaktionen eröffnet. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18371
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Erstellen eines Handelsadministrator-Panels in MQL5 (Teil XII): Integration eines Rechners für Forex-Werte
MQL5-Assistenz-Techniken, die Sie kennen sollten (Teil 70): Verwendung der Muster von SAR und RVI mit einem Exponential-Kernel-Netzwerk
Umstellung auf MQL5 Algo Forge (Teil 3): Verwendung externer Repositories für die eigenen Projekte
Meistern der Log-Einträge (Teil 8): Fehlereinträge, die sich selbst übersetzen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.