Training eines mehrschichtigen Perzeptrons unter Verwendung des Levenberg-Marquardt-Algorithmus

Einführung

Ziel dieses Artikels ist es, praktizierenden Händlern einen sehr effektiven Trainingsalgorithmus für neuronale Netze an die Hand zu geben - eine Variante der Newtonschen Optimierungsmethode, bekannt als Levenberg-Marquardt-Algorithmus. Er ist einer der schnellsten Algorithmen für das Training neuronaler Feed-Forward-Netze und wird nur vom Broyden-Fletcher-Goldfarb-Shanno-Algorithmus (L-BFGS) übertroffen.

Stochastische Optimierungsmethoden wie der stochastische Gradientenabstieg (SGD) und Adam eignen sich gut für das Offline-Training, wenn das neuronale Netz über lange Zeiträume hinweg eine Überanpassung aufweist. Wenn ein Händler, der neuronale Netze verwendet, möchte, dass sich das Modell schnell an die sich ständig ändernden Handelsbedingungen anpasst, muss er das Netz bei jedem neuen Balken oder nach einer kurzen Zeitspanne online neu trainieren. In diesem Fall sind die besten Algorithmen diejenigen, die zusätzlich zu den Informationen über den Gradienten der Verlustfunktion auch zusätzliche Informationen über die zweiten partiellen Ableitungen verwenden, was es ermöglicht, ein lokales Minimum der Verlustfunktion in nur wenigen Trainingsepochen zu finden.

Soweit ich weiß, gibt es derzeit keine allgemein verfügbare Implementierung des Levenberg-Marquardt-Algorithmus in MQL5. Es ist an der Zeit, diese Lücke zu schließen und dabei auch kurz auf die bekannten und einfachsten Optimierungsalgorithmen wie Gradientenabstieg, Gradientenabstieg mit Momentum und stochastischer Gradientenabstieg einzugehen. Am Ende des Artikels werden wir einen kleinen Test der Effizienz des Levenberg-Marquardt-Algorithmus und der Algorithmen aus der scikit-learn-Bibliothek für maschinelles Lernen durchführen.

Datensatz

Alle folgenden Beispiele verwenden zur einfacheren Darstellung synthetische Daten. Die Zeit wird als einzige Vorhersagevariable verwendet, und die Zielvariable, die wir mit Hilfe des neuronalen Netzes vorhersagen wollen, ist die Funktion:

1 + sin(pi/4*time) + NormDistr(0,sigma)

Diese Funktion besteht aus einem deterministischen Teil, der durch eine periodische Komponente in Form eines Sinus dargestellt wird, und einem stochastischen Teil - weißes Gauß-Rauschen. Insgesamt 81 Datenpunkte. Nachfolgend finden Sie ein Diagramm dieser Funktion und ihre Annäherung durch ein dreischichtiges Perzeptron.

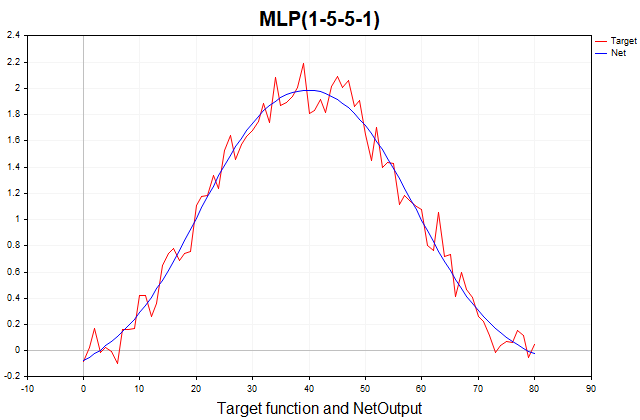
Abb. 1. Die Zielfunktion und ihre Approximation durch ein dreischichtiges Perzeptron

Gradientenabstieg

Beginnen wir mit der Implementierung des regulären Gradientenabstiegs, der einfachsten Methode für das Training neuronaler Netze. Ich werde ein sehr gutes Beispiel aus dem MQL5-Referenzbuch als Vorlage verwenden (Matrizen und Vektoren → Maschinelles Lernen). Ich habe es ein wenig modifiziert, indem ich die Möglichkeit hinzugefügt habe, die Aktivierungsfunktion für die letzte Schicht des Netzes auszuwählen und die Implementierung des Gradientenabstiegs universell zu machen, sodass sie nicht nur auf der quadratischen Verlustfunktion lernen kann, wie im Beispiel aus dem Referenzbuch implizit angenommen, sondern auf allen verfügbaren Verlustfunktionen in MQL5. Die Verlustfunktion ist von zentraler Bedeutung für das Training neuronaler Netze, und es lohnt sich manchmal, mit verschiedenen Funktionen zu experimentieren, die über den quadratischen Verlust hinausgehen. Hier ist die allgemeine Gleichung zur Berechnung des Fehlers der Ausgabeschicht (Delta):

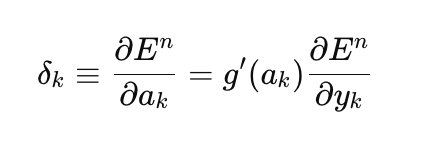
hier

• delta_k - Fehler der Ausgabeschicht,
• E - Verlustfunktion,
• g'(a_k) - Ableitung der Aktivierungsfunktion,
• a_k - Voraktivierung der letzten Schicht,
• y_k - vorhergesagter Wert des Netzes.

//--- Derivative of the loss function with respect to the predicted value       
matrix DerivLoss_wrt_y = result_.LossGradient(target,loss_func);  
matrix deriv_act;
  if(!result_.Derivative(deriv_act, ac_func_last)) 
     return false;      
 matrix  loss = deriv_act*DerivLoss_wrt_y;  // loss = delta_k

Die partiellen Ableitungen der Verlustfunktion in Bezug auf den vorhergesagten Wert des Netzes werden mit der Funktion LossGradient berechnet, während die Ableitung der Aktivierungsfunktion mit der Funktion Derivative berechnet wird. Im Referenzbeispiel wird die Differenz zwischen dem Zielwert und dem vorhergesagten Wert des Netzes, multipliziert mit 2, als Fehler der Ausgangsschicht verwendet.

matrix loss = (target - result_)*2; 

In der Literatur zum maschinellen Lernen wird der Fehler jeder Schicht des Netzes gewöhnlich als delta(D2,D1 usw.) und nicht als Verlust bezeichnet (siehe z. B. Bishop(1995)). Von nun an werde ich genau diese Notation im Code verwenden.         

Wie sind wir zu diesem Ergebnis gekommen? Dabei wird implizit davon ausgegangen, dass die Verlustfunktion die Summe der quadratischen Differenzen zwischen den Ziel- und den vorhergesagten Werten ist, und nicht der mittlere quadratische Fehler (MSE), der zusätzlich durch die Größe der Trainingsstichprobe normalisiert wird. Die Ableitung dieser Verlustfunktion ist genau gleich (Ziel - Ergebnis)*2. Da die letzte Schicht des Netzes die gleiche Aktivierungsfunktion verwendet, deren Ableitung gleich eins ist, kommen wir zu diesem Ergebnis. Wer also beliebige Verlustfunktionen und Aktivierungsfunktionen für die Ausgabeschicht zum Trainieren des Netzes verwenden möchte, muss die obige allgemeine Gleichung verwenden.

Trainieren wir nun unser Netzwerk mit der mittleren quadratischen Verlustfunktion. Aus Gründen der Übersichtlichkeit wurde das Diagramm in einer logarithmischen Skala dargestellt.

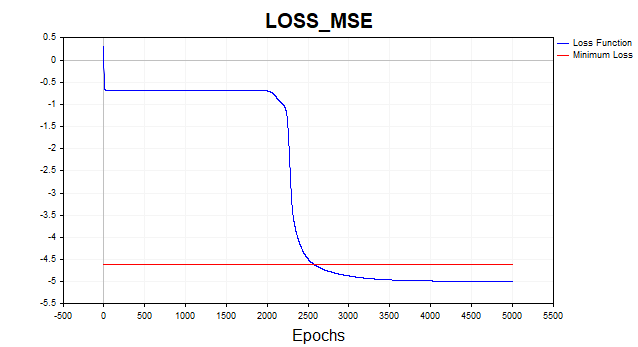
Abb. 2. MSE-Verlustfunktion, Gradientenabstieg

Im Durchschnitt benötigt der Gradientenabstiegsalgorithmus 1500-2000 Epochen (d. h. Durchläufe über den gesamten Trainingsdatensatz), um den minimalen Schwellenwert der Verlustfunktion zu erreichen. In diesem Fall habe ich zwei versteckte Schichten mit jeweils 5 Neuronen verwendet.

Die rote Linie im Diagramm zeigt den minimalen Schwellenwert der Verlustfunktion an. Sie ist definiert als die Varianz des weißen Gaußschen Rauschens. Hier habe ich Rauschen mit einer Varianz von 0,01 (0,1 sigma* 0,1 sigma) verwendet.

Was passiert, wenn wir dem neuronalen Netzmodell erlauben, unterhalb dieser Mindestschwelle zu lernen? Dann kommt es zu dem unerwünschten Phänomen der Netzüberanpassung. Es ist sinnlos zu versuchen, den Fehler der Verlustfunktion auf dem Trainingsdatensatz unter den Mindestschwellenwert zu bringen, da dies die Vorhersagekraft des Modells auf dem Testdatensatz beeinträchtigen wird. Hier sind wir mit der Tatsache konfrontiert, dass es unmöglich ist, eine Reihe genauer vorherzusagen, als es die statistische Streuung dieser Reihe erlaubt. Wenn wir das Training oberhalb der Mindestschwelle einstellen, haben wir ein weiteres Problem - das Netz wird untertrainiert sein. Das heißt, eine, die nicht in der Lage war, die vorhersehbare Komponente der Serie vollständig zu erfassen.

Wie Sie sehen können, muss der Gradientenabstieg eine ganze Reihe von Iterationen durchlaufen, um den optimalen Parametersatz zu erreichen. Beachten Sie, dass unser Datensatz ziemlich einfach ist. Für reale praktische Probleme erweist sich die Trainingszeit für den Gradientenabstieg als inakzeptabel. Eine der einfachsten Methoden zur Verbesserung der Konvergenz und Geschwindigkeit des Gradientenabstiegs ist die Momentumsmethode.

Gradientenabstieg mit Momentum

Die Idee hinter dem Gradientenabstieg mit Momentum besteht darin, die Trajektorie der Netzparameter während des Trainings zu glätten, indem die Parameter wie ein einfacher exponentieller Durchschnitt gemittelt werden. So wie wir die Zeitreihen der Preise von Finanzinstrumenten mit einem Durchschnitt glätten, um die Hauptrichtung hervorzuheben, glätten wir auch die Trajektorie eines parametrischen Vektors, der sich auf den Punkt eines lokalen Minimums unserer Verlustfunktion zubewegt. Zur besseren Veranschaulichung sehen wir uns ein Diagramm an, das zeigt, wie sich die Werte der beiden Parameter verändert haben - vom Beginn des Trainings bis zum Minimalpunkt der Verlustfunktion. Abb. 3 zeigt die Trajektorie ohne Verwendung eines Momentums. 

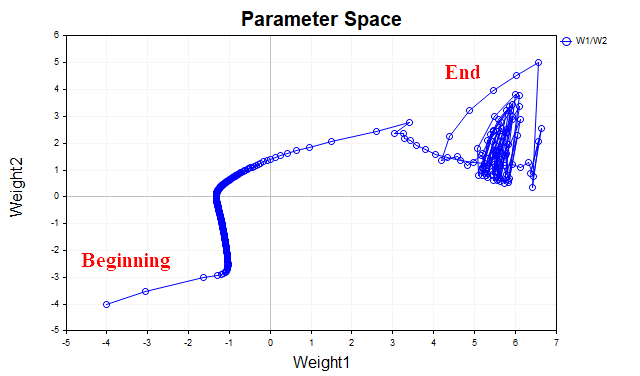
Abb. 3. Gradientenabstieg ohne Momentum

Es zeigt sich, dass der Parametervektor bei Annäherung an das Minimum chaotisch zu schwingen beginnt, sodass der optimale Punkt nicht erreicht werden kann. Um dieses Phänomen zu beseitigen, müssen wir die Lernrate verringern. Dann beginnt der Algorithmus natürlich zu konvergieren, aber der Zeitaufwand für die Suche kann sich erheblich erhöhen.

Abb. 4 zeigt die Trajektorie des Parametervektors unter Verwendung des Moments (mit dem Wert 0,9). Diesmal ist die Trajektorie glatter, und wir erreichen problemlos den optimalen Punkt. Jetzt können wir sogar die Lernrate erhöhen. Dies ist der Grundgedanke des Gradientenabstiegs mit Momentum, um den Konvergenzprozess zu beschleunigen.

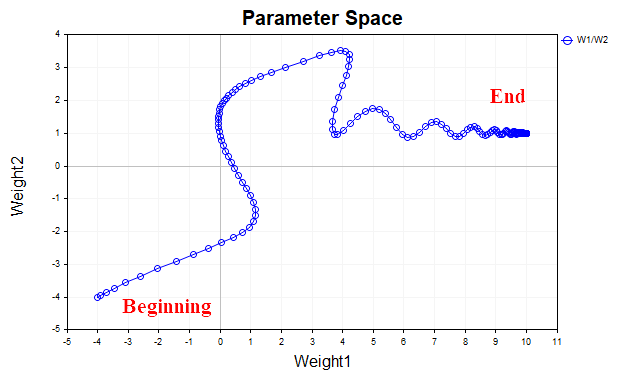
Abb. 4. Gradientenabstieg, Momentum (0.9)

Das Skript Momentum_SD implementiert den Gradientenabstiegsalgorithmus mit Momentum. Bei diesem Algorithmus habe ich beschlossen, eine ausgeblendete Schicht wegzulassen und die Gewichte und Verzerrungen des Netzes zu trennen, um die Wahrnehmung zu verbessern. Jetzt haben wir nur noch eine ausgeblendete Schicht mit 20 Neuronen anstelle von zwei ausgeblendeten Schichten mit je 5 Neuronen, wie im vorherigen Beispiel.

//+------------------------------------------------------------------+
//|                                                  Momentum_SD.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,  
   target_netpredict_plot
  };
  
matrix weights1, weights2,bias1,bias2;                      // network parameter matrices
matrix dW1,db1,dW2,db2;                                     // weight increment matrices
matrix n1,n2,act1,act2;                                     // neural layer output matrices
input int    layer1                  = 20;                  // neurons Layer 1
input int    Epochs                  = 1000;                // Epochs
input double lr                      = 0.1;                 // learning rate coefficient
input double sigma_                  = 0.1;                 // standard deviation synthetic data
input double gamma_                  = 0.9;                 // momentum 
input Plots  plot_                   = LossFunction_plot;   // display graph
input bool   plot_log                = false;               // Plot Log graph
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;      // Activation Layer1
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR;    // Activation Layer2
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;     // Loss function

double LossPlot[],target_Plot[],NetOutput[];
matrix ones_;
int Sample_,Features; 

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }
   ones_ = matrix::Ones(1,Sample_);  
      
   ulong start=GetMicrosecondCount(); 
//--- train the model
   if(!Train(data, target, Epochs))
      return;
   ulong end = (GetMicrosecondCount()-start)/1000;  
   Print("Learning time = " + (string)end + " msc");
//--- generate a test sample
    Func(data,target);
    StandartScaler(data);
//--- test the model
   Test(data, target);
//--- display graphs  
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
   ArrayResize(LossPlot,Epochs);
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      LossPlot[ep] = act2.Loss(target, loss_func);
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//---
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Cols(); i++)
     {
      NetOutput[i]  =act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features)  || !weights2.Init(1,layer1)) 
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))  
      return false;
//--- initialize the matrix of parameter increments
   dW1.Init(layer1,Features);
   dW2.Init(1, layer1);
   db1.Init(layer1,1);
   db2.Init(1,1);
   dW1.Fill(0);
   dW2.Fill(0);
   db1.Fill(0);
   db2.Fill(0);
//--- fill the parameter matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1,0.1);
   bias2.Random(-0.1,0.1);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  { 
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- Derivative of the loss function with respect to the predicted value
   matrix DerivLoss_wrt_y = act2.LossGradient(target.Transpose(),loss_func);
   matrix deriv_act2;
   n2.Derivative(deriv_act2, ac_func_last);
//--- D2   
   matrix  D2 = deriv_act2*DerivLoss_wrt_y; // error(delta) of the network output layer
//--- D1
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = D1*deriv_act1; // error (delta) of the first layer of the network
//--- update network parameters
   matrix  ones = matrix::Ones(data.Rows(),1);
   dW1 = gamma_*dW1 + (1-gamma_)*(D1.MatMul(data)) * lr;
   db1 = gamma_*db1 + (1-gamma_)*(D1.MatMul(ones)) * lr;
   dW2 = gamma_*dW2 + (1-gamma_)*(D2.MatMul(act1.Transpose())) * lr;
   db2 = gamma_*db2 + (1-gamma_)*(D2.MatMul(ones)) * lr;
   weights1 =  weights1 - dW1;
   weights2 =  weights2 - dW2;
   bias1    =  bias1    - db1;
   bias2    =  bias2    - db2;
//--- return result
   return true;
  }

Dank des Momentums konnte ich die Lerngeschwindigkeit von 0,1 auf 0,5 erhöhen. Jetzt konvergiert der Algorithmus in 150-200 Iterationen anstelle von 500 beim regulären Gradientenabstieg.

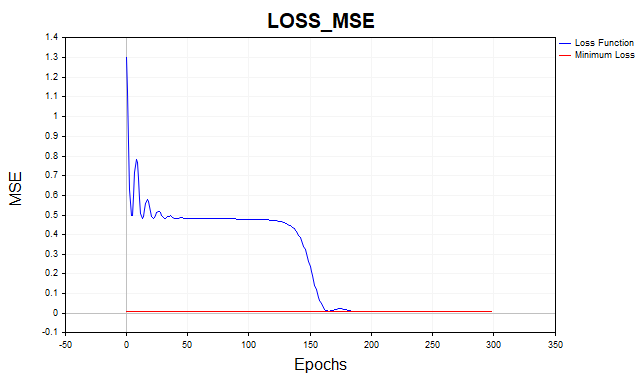
Abb. 5. MSE-Verlustfunktion, MLP(1-20-1) SD_Momentum

Stochastischer Gradientenabstieg

Momentum ist gut, aber wenn der Datensatz nicht 81 Datenpunkte umfasst, wie in unserem Beispiel, sondern Zehntausende von Dateninstanzen, dann ist es sinnvoll, über einen so bewährten (und einfachen) Algorithmus wie SGD zu sprechen. SGD ist derselbe Gradientenabstieg, aber der Gradient wird nicht über die gesamte Trainingsmenge berechnet, sondern nur über einen sehr kleinen Teil dieser Menge (Mini-Batch) oder sogar nur über einen Datenpunkt. Danach werden die Netzgewichte aktualisiert, ein neuer Datenpunkt wird nach dem Zufallsprinzip ausgewählt, und der Vorgang wird wiederholt, bis der Algorithmus konvergiert. Aus diesem Grund wird der Algorithmus stochastisch genannt. Beim konventionellen Gradientenabstieg werden die Netzgewichte erst nach der Berechnung des Gradienten für den gesamten Datensatz aktualisiert. Dies ist die so genannte Batch-Methode.

Wir implementieren eine Variante von SGD, bei der nur ein Datenpunkt als Mini-Batch verwendet wird.

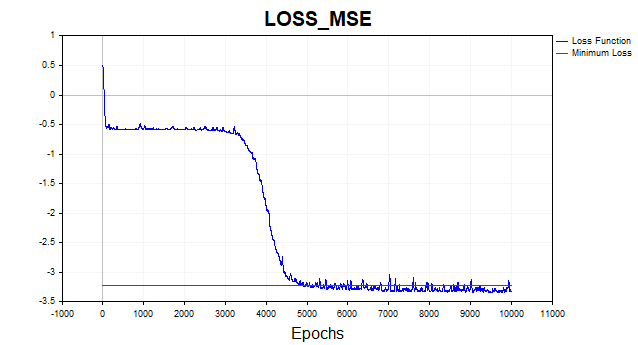
Abb. 6. Verlustfunktion im logarithmischen Maßstab, SGD

Der SGD-Algorithmus (batch_size = 1) konvergiert in 4-6 Tausend Iterationen zur minimalen Grenze, aber wir dürfen nicht vergessen, dass wir nur ein einziges von 81 Trainingsbeispielen zur Aktualisierung des Parametervektors verwenden. Daher konvergiert der Algorithmus bei diesem Datensatz in etwa 50-75 Epochen. Keine schlechte Verbesserung gegenüber dem vorherigen Algorithmus, oder? Auch hier habe ich Momentum verwendet, aber da nur ein Datenpunkt verwendet wird, hat dies keine großen Auswirkungen auf die Konvergenzgeschwindigkeit.

Levenberg-Marquardt-Algorithmus

Dieser gute alte Algorithmus ist aus irgendeinem Grund heutzutage völlig in Vergessenheit geraten, obwohl er bei Netzen mit bis zu einigen hundert Parametern zusammen mit L-BFGS einfach nicht zu übertreffen ist.

Aber es gibt einen wichtigen Punkt. Der LM-Algorithmus wurde entwickelt, um Funktionen zu minimieren, die Summen von Quadraten anderer nicht-linearer Funktionen sind. Daher beschränken wir uns bei dieser Methode auf eine quadratische Verlustfunktion oder eine Funktion mit quadratischem Mittelwert. Alles in allem erfüllt diese Verlustfunktion ihre Aufgabe perfekt, und es gibt hier kein großes Problem, aber wir müssen wissen, dass wir nicht in der Lage sein werden, das Netz mit diesem Algorithmus auf andere Funktionen zu trainieren.

Schauen wir uns nun im Detail an, wie dieser Algorithmus entstanden ist. Beginnen wir mit der Newtonschen Methode:

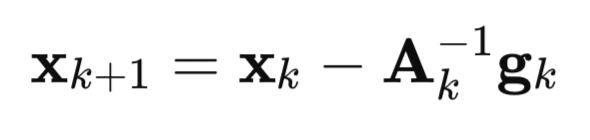
hier

A - inverse Hesse-Matrix der Verlustfunktion F(x),

g - F(x) Gradient der Verlustfunktion,

x - Vektor der Parameter

Betrachten wir nun unsere quadratische Verlustfunktion:

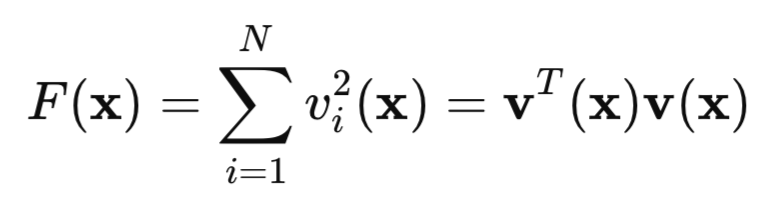
Hier ist v ein Netzwerkfehler (vorhergesagter Wert minus Ziel), während x ein Vektor von Netzwerkparametern ist, der alle Gewichte und Verzerrungen für jede Schicht enthält.

Bestimmen wir den Gradienten dieser Verlustfunktion:

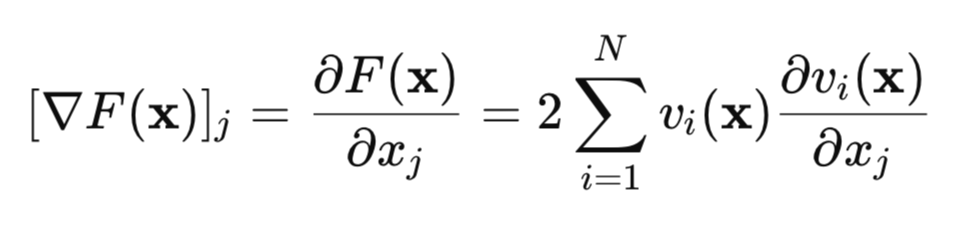
In Matrixform kann dies wie folgt geschrieben werden:

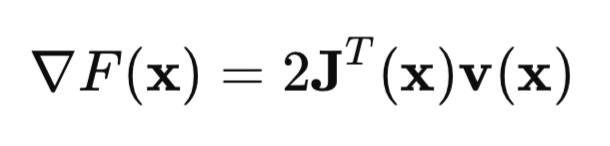
Der entscheidende Punkt ist die Jacobimatrix:

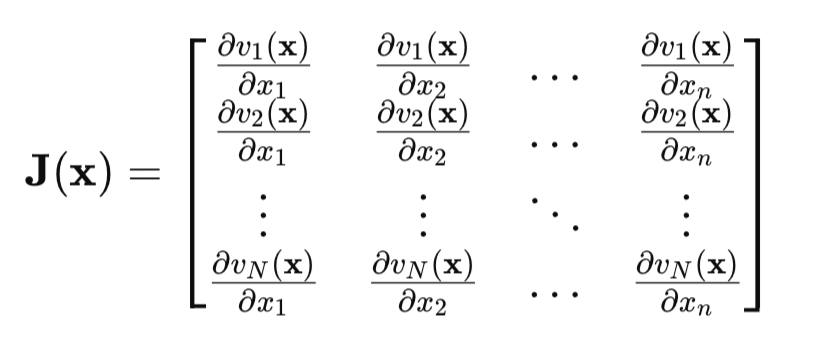
In der Jacobimatrix enthält jede Zeile alle partiellen Ableitungen des Netzfehlers in Bezug auf alle Parameter. Jede Zeile entspricht einem Beispiel aus der Trainingsmenge.

Betrachten wir nun die Hesse-Matrix. Dies ist die Matrix der zweiten partiellen Ableitungen der Verlustfunktion. Die Berechnung der Hesse-Matrix ist eine schwierige und aufwendige Aufgabe, daher wird eine Annäherung der Hesse- durch die Jacobimatrix verwendet:

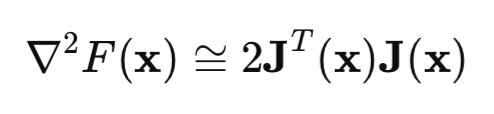
Setzt man die Hesse-Gleichung und die Gradientengleichung in die Gleichung der Newton-Methode ein, erhält man die Gauß-Newton-Methode:

Das Problem bei der Gauß-Newton-Methode ist jedoch, dass die Matrix [J'J] möglicherweise nicht umkehrbar ist. Um dieses Problem zu lösen, wird die Identitätsmatrix, multipliziert mit dem positiven Skalar mu*I, zur Matrix hinzugefügt. In diesem Fall erhalten wir den Levenberg-Marquardt-Algorithmus:

Die Besonderheit dieses Algorithmus besteht darin, dass der Algorithmus, wenn der Parameter mu große positive Werte annimmt, auf den üblichen Gradientenabstieg reduziert wird, den wir zu Beginn des Artikels besprochen haben. Wenn der Parameter mu gegen Null geht, kehren wir zum Gauß-Newton-Verfahren zurück.

Normalerweise beginnt das Training mit einem kleinen Wert von mu. Wenn der Wert der Verlustfunktion nicht kleiner wird, wird der Parameter mu erhöht (z. B. mit 10 multipliziert). Da wir uns damit der Methode des Gradientenabstiegs annähern, werden wir früher oder später eine Reduzierung der Verlustfunktion erreichen. Wenn die Verlustfunktion gesunken ist, verringern wir den Wert des Parameters mu, indem wir die Gauß-Newton-Methode anwenden, um schneller zum Minimalpunkt zu konvergieren. Dies ist der Grundgedanke der Levenberg-Marquardt-Methode, die ständig zwischen der Gradientenabstiegsmethode und der Gauß-Newton-Methode wechselt.

Die Implementierung der Backpropagation-Methode für den Levenberg-Marquardt-Algorithmus hat ihre eigenen Merkmale. Da es sich bei den Elementen der Jacobimatrix um partielle Ableitungen der Netzfehler und nicht um die Quadrate dieser Fehler handelt, wird die Gleichung zur Berechnung des Deltas der letzten Schicht des Netzes, die ich zu Beginn des Artikels angegeben habe, vereinfacht. Jetzt ist delta einfach gleich der Ableitung der Aktivierungsfunktion der letzten Schicht. Dieses Ergebnis erhält man, wenn man die Ableitung des Netzfehlers (y - Ziel) nach y findet, die offensichtlich gleich eins ist.

Hier ist der Code des neuronalen Netzes selbst mit ausführlichen Kommentaren.

//+------------------------------------------------------------------+
//|                                                           LM.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Graphics\Graphic.mqh>
#include <Math\Stat\Math.mqh>
#include <Math\Stat\Normal.mqh>
enum Plots
  {
   LossFunction_plot,
   mu_plot,
   gradient_plot,
   target_netpredict_plot
  };

matrix weights1,weights2,bias1,bias2;                    // network parameter matrices
matrix n1,n2,act1,act2,new_n1,new_n2,new_act1,new_act2;  // neural layer output matrices
input int    layer1     = 20;                            // neurons Layer 1
input int    Epochs     = 10;                            // Epochs
input double Initial_mu = 0.001;                         // mu
input double Incr_Rate  = 10;                            // increase mu
input double Decr_Rate  = 0.1;                           // decrease mu
input double Min_grad   = 0.000001;                      // min gradient norm
input double Loss_goal  = 0.001;                         // Loss goal
input double sigma_     = 0.1;                           // standard deviation synthetic data
input Plots  plot_      = LossFunction_plot;             // display graph
input bool   plot_log   = false;                         // logarithmic function graph 
input ENUM_ACTIVATION_FUNCTION ac_func      = AF_TANH;   // first layer activation function
input ENUM_ACTIVATION_FUNCTION ac_func_last = AF_LINEAR; // last layer activation function
input ENUM_LOSS_FUNCTION       loss_func    = LOSS_MSE;  // Loss function

double LossPlot[],NetOutput[],mu_Plot[],gradient_Plot[],target_Plot[];
matrix ones_;
double old_error,gradient_NormP2;
double mu_ = Initial_mu;
bool break_forloop = false;
int Sample_,Features;

//+------------------------------------------------------------------+
//| Script start function                                            |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- generate a training sample
   matrix data, target;
   Func(data,target);
   StandartScaler(data);
   Sample_= (int)data.Rows();
   Features = (int)data.Cols();
   ArrayResize(target_Plot,Sample_);
   for(int i=0; i< (int)target.Rows(); i++)
     {
      target_Plot[i] =target[i,0];
     }

   ones_ = matrix::Ones(1,Sample_);
//--- train the model
   ulong start=GetMicrosecondCount();
   Train(data, target, Epochs);
   ulong end = (GetMicrosecondCount()-start)/1000 ;
   Print("Learning time = " + (string)end + " msc");
   int NumberParameters = layer1*(Features+1) + 1*(layer1+1);
   Print("Number Parameters of NN = ",NumberParameters);

//--- generate a test sample
   Func(data,target);
   StandartScaler(data);
//--- test the model
   Test(data,target);
   
//--- display graphs
   PlotGraphic(15,plot_log);
  }
//+------------------------------------------------------------------+
//| Model training method                                            |
//+------------------------------------------------------------------+
bool Train(matrix &data, matrix &target, const int epochs)
  {
//--- create the model
   if(!CreateNet())
      return false;
//--- train the model
   for(int ep = 0; ep < epochs; ep++)
     {
      //--- feed forward
      if(!FeedForward(data))
         return false;
      PrintFormat("Epoch %d, loss %.5f", ep, act2.Loss(target, loss_func));
      //--- arrays for graphs
      ArrayResize(LossPlot,ep+1,10000);
      ArrayResize(mu_Plot,ep+1,10000);
      ArrayResize(gradient_Plot,ep+1,10000);
      LossPlot[ep]       = act2.Loss(target, loss_func);
      mu_Plot [ep]       = mu_;
      gradient_Plot[ep]  = gradient_NormP2;
      //--- Stop training if the target value of the loss function is reached
      if(break_forloop == true){break;}
      //--- backpropagation and update of weight matrix
      if(!Backprop(data, target))
         return false;
     }
//--- Euclidean norm of gradient, mu parameter, RMSE metric
   Print("gradient_normP2 =  ", gradient_NormP2);
   Print(" mu_ = ", mu_);
   double rmse=act2.RegressionMetric(target.Transpose(),REGRESSION_RMSE);
   PrintFormat("rmse %.3f / sigma %.2f ",rmse,sigma_);
//--- array of network output for graph
   ArrayResize(NetOutput,Sample_);
   for(int i=0; i< (int)act2.Transpose().Rows(); i++)
     {
      NetOutput[i]  = act2.Transpose()[i,0];
     }
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Model creation method                                            |
//+------------------------------------------------------------------+
bool CreateNet()
  {
//--- initialize weight matrices
   if(!weights1.Init(layer1,Features) || !weights2.Init(1,layer1))
      return false;
//--- initialize offset matrices
   if(!bias1.Init(layer1,1)  || !bias2.Init(1,1))
      return false;
//--- fill the weight matrices with random values
   weights1.Random(-0.1, 0.1);
   weights2.Random(-0.1, 0.1);
   bias1.Random(-0.1, 0.1);
   bias2.Random(-0.1, 0.1);   
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Feed-forward method                                              |
//+------------------------------------------------------------------+
bool FeedForward(matrix &data)
  {
//--- calculate the first neural layer
//--- n1 pre-activation of the first layer
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
//--- calculate the activation function of the act1 first layer
   n1.Activation(act1, ac_func);
//--- calculate the second neural layer
//--- n2 pre-activation of the second layer
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
//--- calculate the activation function of the act2 second layer
   n2.Activation(act2, ac_func_last);
//--- return result
   return true;
  }
//+------------------------------------------------------------------+
//| Backpropagation method                                           |
//+------------------------------------------------------------------+
bool Backprop(matrix &data, matrix &target)
  {
//--- current value of the loss function
   old_error = act2.Loss(target, loss_func);
//--- network error (quadratic loss function)
   matrix loss = act2.Transpose() - target ;
//--- derivative of the activation function of the last layer
   matrix D2;
   n2.Derivative(D2, ac_func_last);
//--- derivative of the first layer activation function
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func);
//--- first layer network error
   matrix D1 = weights2.Transpose().MatMul(D2);
   D1 = deriv_act1 * D1;
//--- first partial derivatives of network errors with respect to the first layer weights
   matrix jac1;
   partjacobian(data.Transpose(),D1,jac1);
//--- first partial derivatives of network errors with respect to the second layer weights
   matrix jac2;
   partjacobian(act1,D2,jac2);
//--- Jacobian
   matrix j1_D1 = Matrixconcatenate(jac1,D1.Transpose(),1);
   matrix j2_D2 = Matrixconcatenate(jac2,D2.Transpose(),1);
   matrix jac   = Matrixconcatenate(j1_D1,j2_D2,1);
// --- Loss function gradient
   matrix je = (jac.Transpose().MatMul(loss));
//--- Euclidean norm of gradient normalized to sample size
   gradient_NormP2 = je.Norm(MATRIX_NORM_FROBENIUS)/Sample_;
   if(gradient_NormP2 < Min_grad)
     {
      Print("Local minimum. The gradient is less than the specified value.");
      break_forloop = true; // stop training
      return true;
     }
//--- Hessian
   matrix Hessian = (jac.Transpose().MatMul(jac));
   matrix I=matrix::Eye(Hessian.Rows(), Hessian.Rows());
//---
   break_forloop = true;
   while(mu_ <= 1e10 && mu_ > 1e-20)
     {
      matrix H_I = (Hessian + mu_*I);
      //--- solution via Solve
      vector v_je = je.Col(0);
      vector Updatelinsolve = -1* H_I.Solve(v_je);
      matrix Update = matrix::Zeros(Hessian.Rows(),1);
      Update.Col(Updatelinsolve,0); // increment of the parameter vector
      
      //--- inefficient calculation of inverse matrix
      //   matrix Update = H_I.Inv();
      //   Update = -1*Update.MatMul(je);
      //---

      //--- save the current parameters
      matrix  Prev_weights1 = weights1;
      matrix  Prev_bias1    = bias1;
      matrix  Prev_weights2 = weights2;
      matrix  Prev_bias2    = bias2;
      //---

      //--- update the parameters
      //--- first layer
      matrix updWeight1 = matrix::Zeros(layer1,Features);
      int count =0;
      for(int j=0; j <Features; j++)
        {
         for(int i=0 ; i <layer1; i++)
           {
            updWeight1[i,j] = Update[count,0];
            count = count+1;
           }
        }

      matrix updbias1 = matrix::Zeros(layer1,1);
      for(int i =0 ; i <layer1; i++)
        {
         updbias1[i,0] = Update[count,0];
         count = count +1;
        }
        
      weights1 = weights1 + updWeight1;
      bias1 = bias1 + updbias1;

      //--- second layer
      matrix updWeight2 = matrix::Zeros(1,layer1);
      for(int i =0 ; i <layer1; i++)
        {
         updWeight2[0,i] = Update[count,0];
         count = count +1;
        }
      matrix updbias2 = matrix::Zeros(1,1);
      updbias2[0,0] = Update[count,0];

      weights2 = weights2 + updWeight2;
      bias2 = bias2 + updbias2;

      //--- calculate the loss function for the new parameters
      new_n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
      new_n1.Activation(new_act1, ac_func);
      new_n2 = weights2.MatMul(new_act1) + bias2.MatMul(ones_);
      new_n2.Activation(new_act2, ac_func_last);
      //--- loss function taking into account new parameters
      double new_error = new_act2.Loss(target, loss_func);
      //--- if the loss function is less than the specified threshold, terminate training
      if(new_error < Loss_goal)
        {
         break_forloop = true;
         Print("Training complete. The desired loss function value achieved");
         return true;
        }
      break_forloop = false;
      //--- correct the mu parameter
      if(new_error >= old_error)
        {
         weights1 = Prev_weights1;
         bias1    = Prev_bias1;
         weights2 = Prev_weights2;
         bias2    =  Prev_bias2;
         mu_ = mu_*Incr_Rate;
        }
      else
        {
         mu_ = mu_*Decr_Rate;
         break; 
        }

     }
//--- return result
   return true;
  }

Der Algorithmus konvergiert, wenn die Gradientennorm kleiner als eine vorgegebene Zahl ist oder wenn das gewünschte Niveau der Verlustfunktion erreicht ist. Der Algorithmus hält an, wenn der Parameter mu kleiner oder größer als eine vorgegebene Zahl ist, oder nachdem eine vorgegebene Anzahl von Epochen abgeschlossen wurde.

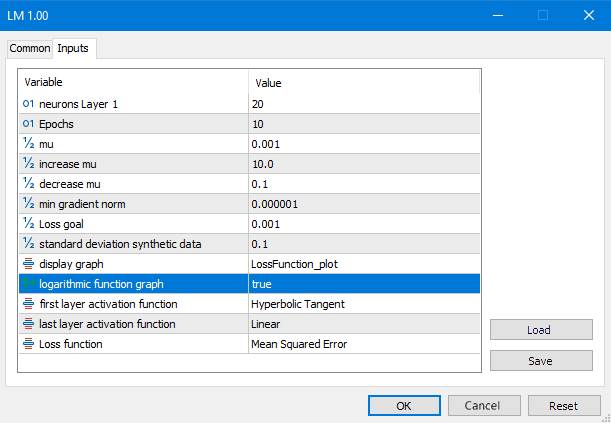
Abb. 7. LM-Skript-Parameter

Schauen wir uns das Ergebnis all dieser Berechnungen an:

Abb. 8. Verlustfunktion im logarithmischen Maßstab, LM

Es ist jetzt ein völlig anderes Bild. Der Algorithmus erreichte die minimale Grenze in 6 Iterationen. Was wäre, wenn wir das Netz mit eintausend Epochen trainieren würden? Wir würden eine typische Überanpassung erhalten. Das folgende Bild veranschaulicht dies gut. Das Netz beginnt einfach, sich Gaußsches Rauschen einzuprägen.

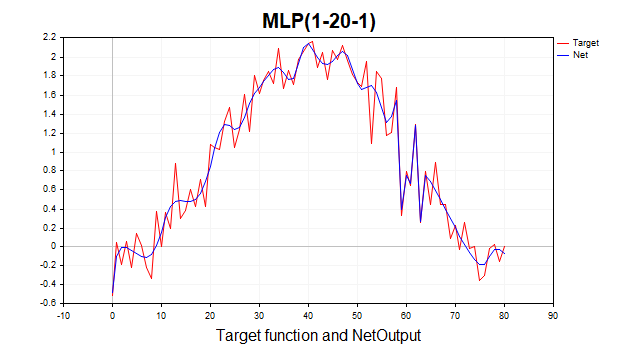
Abb. 9. Typische Überanpassung, LM, 1000 Epochen

Schauen wir uns die Metriken für die Trainings- und Testmengen an.

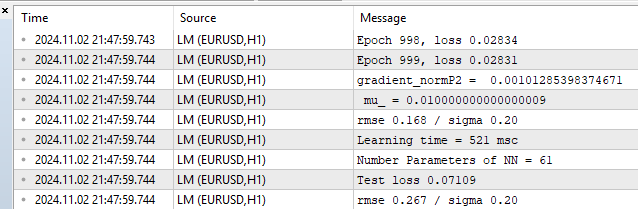
Abb. 10. Leistungsstatistik, LM, 1000 Epochen

Wir sehen einen RMSE von 0,168 mit einer Untergrenze von 0,20, und dann gibt es eine sofortige Vergeltung für die Überanpassung beim Test von 0,267.

Tests mit großen Daten und Vergleich mit der Python-Bibliothek sklearn

Nun ist es an der Zeit, unseren Algorithmus an einem realistischeren Beispiel zu testen. Jetzt habe ich zwei Merkmale mit 1000 Datenpunkten genommen. Sie können diese Daten zusammen mit dem Skript LM_BigData am Ende des Artikels herunterladen. LM wird mit Algorithmen aus der Python-Bibliothek konkurrieren: SGD, Adam und L-BFGS.

Hier ist ein Testskript in Python

# Eugene
# https://www.mql5.com

import numpy as np
import time 
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neural_network import MLPRegressor

# here is your path to the data
df = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Data.csv',delimiter=';')
X = df.to_numpy()
df1 = pd.read_csv(r'C:\Users\Evgeniy\AppData\Local\Programs\Python\Python39\Target.csv')
y = df1.to_numpy()
y = y.reshape(-1)

start = time.time() 

'''
clf = MLPRegressor(solver='sgd', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=700,batch_size=10,
                    learning_rate_init=0.01,momentum=0.9,
                    shuffle = False,n_iter_no_change = 2000, tol = 0.000001)
'''

'''
clf = MLPRegressor(solver='adam', alpha=0.0, 
                    hidden_layer_sizes=(20),
                    activation='tanh',
                    max_iter=3000,batch_size=100,                                    
                    learning_rate_init=0.01,
                    n_iter_no_change = 2000, tol = 0.000001)
'''

#'''
clf = MLPRegressor(solver='lbfgs', alpha=0.0, 
                    hidden_layer_sizes=(100),
                    activation='tanh',max_iter=300,
                    tol = 0.000001)
#'''                    
                       
clf.fit(X, y)
end = time.time() - start          # training time

print("learning time  =",end*1000) 
print("solver = ",clf.solver);      
print("loss = ",clf.loss_*2)
print("iter = ",clf.n_iter_)
#print("n_layers_ = ",clf.n_layers_)
#print("n_outputs_ = ",clf.n_outputs_)
#print("out_activation_ = ",clf.out_activation_)

coef = clf.coefs_
#print("coefs_ = ",coef)
inter = clf.intercepts_  
#print("intercepts_ = ",inter) 
plt.plot(np.log(pd.DataFrame(clf.loss_curve_)))
plt.title(clf.solver)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.show()  

Um die Algorithmen richtig vergleichen zu können, habe ich die Verlustfunktion in Python mit 2 multipliziert, da sie in dieser Bibliothek wie folgt berechnet wird:

return ((y_true - y_pred) ** 2).mean() / 2

Mit anderen Worten, die Entwickler dividieren MSE zusätzlich durch 2. Nachstehend finden Sie typische Ergebnisse von Optimierern. Ich habe versucht, die besten Hyperparametereinstellungen für diese Algorithmen zu finden. Leider bietet diese Bibliothek nicht die Möglichkeit, die Werte der Startparameter so zu initialisieren, dass alle Algorithmen von demselben Punkt im Parameterraum ausgehen. Es gibt auch keine Möglichkeit, eine Zielschwelle für die Verlustfunktion festzulegen. Für LM ist das Ziel der Verlustfunktion auf 0,01 gesetzt, für die Python-Algorithmen habe ich versucht, die Anzahl der Iterationen so festzulegen, dass annähernd das gleiche Niveau erreicht wird.

Testergebnisse des MLP mit einer versteckten Schicht, 20 Neuronen:

1) Stochastischer Gradientenabstieg

• MSE-Verlust – 0,00278
• Trainingszeit – 11459 msc

Fig. 11. SGD, 20 Neuronen, Verlust = 0,00278

2) Adam          

•  MSE-Verlust - 0,03363
•  Trainingszeit - 8581 msc

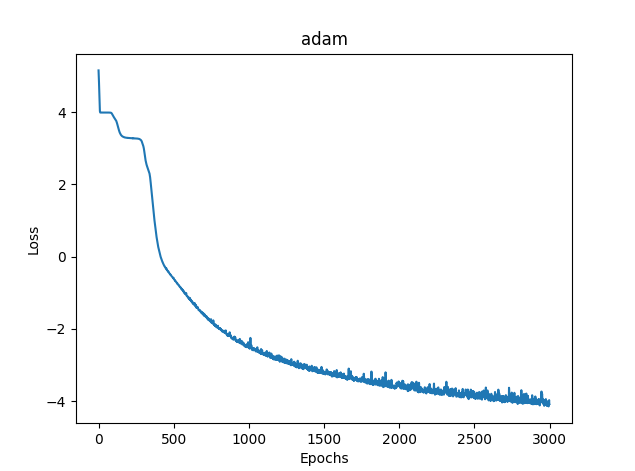
Abb. 12. Adam, 20 Neuronen, Verlust = 0,03363

3)L-BFGS

• MSE-Verlust - 0,02770
• Trainingszeit - 277 msc

Leider ist es nicht möglich, das Diagramm der Verlustfunktion für L-BFGS anzuzeigen.

4) LM MQL5

•  Verlust - 0,00846
•  Trainingszeit - 117 msc

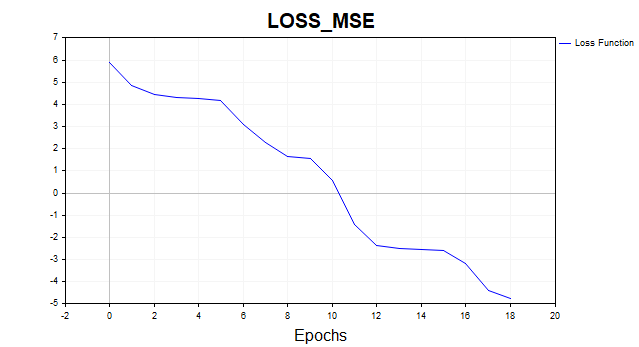
Abb. 13. LM, 20 Neuronen, Verlust = 0,00846

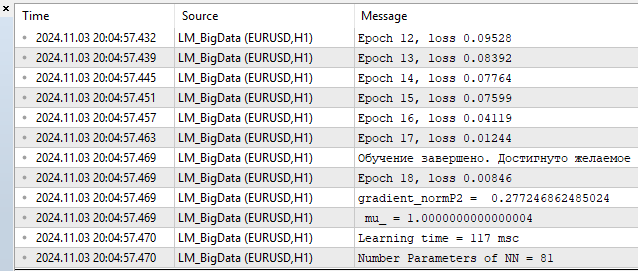
Was mich betrifft, so kann der Algorithmus problemlos mit L-BFGS konkurrieren und ihm sogar einen Vorteil verschaffen. Aber nichts ist perfekt. Mit zunehmender Anzahl von Parametern verliert die Levenberg-Marquardt-Methode gegenüber L-BFGS.

100 Neuronen L-BFGS:

• MSE-Verlust - 0,00847
• Trainingszeit - 671 msc

100 Neuronen LM:

• MSE-Verlust - 0,00206
• Trainingszeit - 1253 msc

100 Neuronen entsprechen 401 Netzparametern. Es liegt an Ihnen zu entscheiden, ob dies viel oder wenig ist, aber meiner bescheidenen Meinung nach ist dies ein Leistungsüberschuss. In Fällen mit bis zu 100 Neuronen ist LM eindeutig im Vorteil.

Schlussfolgerung

In diesem Artikel haben wir die grundlegenden und einfachsten Trainingsalgorithmen für neuronale Netze diskutiert und implementiert:

• Gradientenabstieg
• Gradientenabstieg mit Momentum
• stochastischer Gradientenabstieg

Gleichzeitig haben wir kurz die Fragen der Konvergenz und des Umlernens von neuronalen Netzen angesprochen.

Am wichtigsten ist jedoch, dass wir einen sehr schnellen Levenberg-Marquardt-Algorithmus entwickelt haben, der sich ideal für das Online-Training kleiner Netzwerke eignet.

Wir haben die Leistung von Trainingsalgorithmen für neuronale Netze verglichen, die in der scikit-learn-Bibliothek für maschinelles Lernen verwendet werden, und unser Algorithmus erwies sich als der schnellste, wenn die Anzahl der Parameter des neuronalen Netzes 400 oder 100 Neuronen in der verborgenen Schicht nicht übersteigt. Wenn die Anzahl der Neuronen zunimmt, beginnt L-BFGS zu dominieren.

Für jeden Algorithmus wurden eigene Skripte mit ausführlichen Kommentaren erstellt:

#	Name	Typ	Beschreibung
1	SD.mq5	Skript	Gradientenabstieg
2	Momentum_SD.mq5	Skript	Gradientenabstieg mit Momentum
3	SGD.mq5	Skript	Stochastischer Gradientenabstieg
4	LM.mq5	Skript	Levenberg-Marquardt-Algorithmus
5	LM_BigData.mq5	Skript	LM-Algorithmus, Test zweidimensionaler Merkmale
6	SklearnMLP.py	Skript	Skript zum Testen von Python-Algorithmen
7	FileCSV.mqh	Include	Lesen von Textdateien mit Daten
8	Data.csv, Target.csv	Csv	Merkmale und Zweck des Python-Skripts
9	X1.txt, X2.txt, Target.txt	Txt	Merkmale und Zweck des Skripts LM_BigData.mq5