
Neuronale Netze leicht gemacht (Teil 89): Transformer zur Frequenzzerlegung (FEDformer)
Einführung
Die Langzeitprognose von Zeitreihen ist ein seit langem bestehendes Problem bei der Lösung verschiedener angewandter Probleme. Die auf Transformer basierenden Modell zeigen vielversprechende Ergebnisse. Aufgrund der hohen Rechenkomplexität und des hohen Speicherbedarfs ist es jedoch schwierig, den Transformer für die Modellierung langer Sequenzen zu verwenden. Dies hat zu zahlreichen Studien geführt, die sich mit der Verringerung der Rechenkosten des Transformer-Algorithmus befassen.
Trotz der Fortschritte, die die auf Transformer basierenden Zeitreihenvorhersagemethoden gemacht haben, gelingt es ihnen in einigen Fällen nicht, die gemeinsamen Merkmale der Zeitreihenverteilung zu erfassen. Die Autoren des Artikels „FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting“ haben einen Versuch unternommen, dieses Problem zu lösen. Sie vergleichen die tatsächlichen Daten einer Zeitreihe mit den vorhergesagten Werten, die mit dem Vanilla Transformer ermittelt wurden. Nachstehend finden Sie einen Screenshot aus diesem Papier.
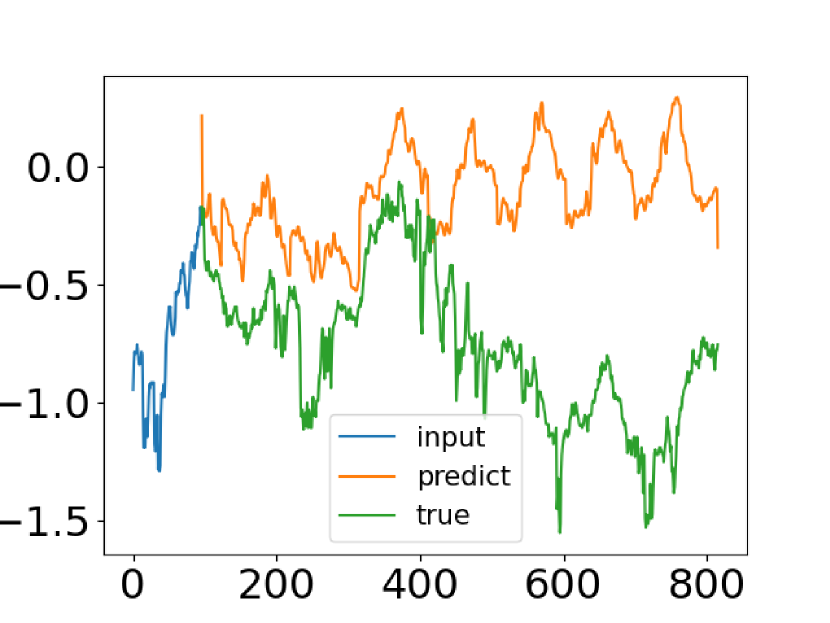
Sie können sehen, dass die Verteilung der prognostizierten Zeitreihe sich stark von der tatsächlichen unterscheidet. Die Diskrepanz zwischen erwarteten und vorhergesagten Werten lässt sich durch den Punkt Aufmerksamkeit (attention) im Transformer erklären. Da die Vorhersage für jeden Zeitschritt einzeln und unabhängig erfolgt, ist es wahrscheinlich, dass das Modell die globalen Eigenschaften und Statistiken der Zeitreihe als Ganzes nicht bewahren kann. Um dieses Problem zu lösen, machen sich die Autoren des Artikels zwei Ideen zunutze.
Die erste ist die Verwendung des Ansatzes der saisonalen Trendzerlegung, der in der Zeitreihenanalyse weit verbreitet ist. Die Autoren des Artikels stellen eine spezielle Modellarchitektur vor, die die Verteilung der Prognosen effektiv an die wahre Verteilung annähert.
Die zweite Idee besteht darin, die Fourier-Analyse in den Transformer-Algorithmus zu integrieren. Anstatt den Transformer auf die Zeitmessung der Sequenz anzuwenden, können wir ihre Frequenzmerkmale analysieren. Dadurch kann der Transformer die globalen Eigenschaften von Zeitreihen besser erfassen.
Die Kombination der vorgeschlagenen Ideen wird in dem Modell des Frequency Enhanced Decomposition Transformer, FEDformer, umgesetzt.
Eine der wichtigsten Fragen im Zusammenhang mit FEDformer ist, welche Untergruppe von Frequenzkomponenten in der Fourier-Analyse zur Darstellung der Zeitreihe verwendet werden soll. Bei solchen Analysen werden meist die niederfrequenten Komponenten beibehalten und die hochfrequenten Komponenten verworfen. Für die Zeitreihenprognose ist dies jedoch möglicherweise nicht geeignet, da einige Veränderungen in den Zeitreihentrends mit wichtigen Ereignissen verbunden sind. Dieser Teil der Information kann durch einfaches Entfernen aller hochfrequenten Komponenten des Signals verloren gehen. Die Autoren der Methode akzeptieren die Tatsache, dass Zeitreihen in der Regel unbekannte spärliche Darstellungen auf der Fourier-Basis haben. Ihre theoretische Analyse hat gezeigt, dass eine zufällig ausgewählte Untergruppe von Frequenzkomponenten, die sowohl niedrige als auch hohe Frequenzen enthält, eine bessere Darstellung der Zeitreihe ermöglicht. Diese Beobachtung wurde durch umfangreiche empirische Untersuchungen bestätigt.
Die Kombination des Transformers mit der Frequenzanalyse verbessert nicht nur die Effizienz der Langzeitprognose, sondern kann auch die Rechenaufwand von quadratischer auf lineare Komplexität reduzieren.
Die Autoren des Artikels fassen ihre Ergebnisse wie folgt zusammen:
1. Sie schlagen einen Transformer mit einer Signalzerlegungsarchitektur mit verbessertem Frequenzgang und den Einsatz von Experten für die Zerlegung von saisonalen Trends vor, um globale Eigenschaften von Zeitreihen besser zu erfassen.
2. Sie schlagen Fourier- und Wavelet-verstärkte Blöcke in der Transformer-Architektur vor, die die Erfassung wichtiger Strukturen in Zeitreihen durch die Untersuchung von Frequenzmerkmalen ermöglichen. Sie dienen als Ersatz für die Blöcke der Selbstaufmerksamkeit (self-attention) und der Fremdaufmerksamkeit (cross-attention).
3. Durch die zufällige Auswahl einer festen Anzahl von Fourier-Komponenten erreicht das vorgeschlagene Modell eine lineare Berechnungskomplexität und Speicherkosten. Die Wirksamkeit dieser Auswahlmethode wurde sowohl theoretisch als auch empirisch nachgewiesen.
4. Experimente, die mit sechs Basisdatensätzen in verschiedenen Bereichen durchgeführt wurden, zeigen, dass das vorgeschlagene Modell die Leistung von State-of-the-Art-Methoden um 14,8 % bzw. 22,6 % für multivariate und univariate Prognosen verbessert.
1. Der Algorithmus FEDformer
Die Autoren der Methode haben 2 Versionen des Modells FEDformer vorgestellt. Die Erste verwendet die Fourier-Basis, um die Frequenzmerkmale einer Zeitreihe zu analysieren. Die Zweite basiert auf der Verwendung von Wavelets, die eine kombinierte Analyse sowohl in Bezug auf die Zeit als auch im Bereich der Frequenzmerkmale ermöglichen.
Die Vorhersage langfristiger Zeitreihen ist ein Sequenz-zu-Sequenz-Problem. Bezeichnen wir die Größe der Folge von Ausgangsdaten als I und die vorhergesagte Sequenz als O. D sei die Größe des Vektors, der einen Zustand der Reihe beschreibt. Dann geben wir einen Tensor der Größe I*D in den Encoder ein, und der Decoder erhält die Matrix (I/2+O)*D.
Wie bereits erwähnt, haben die Autoren der Methode die Transformer-Architektur verbessert, indem sie die Analyse der Zerlegung und Verteilung der saisonalen Trends in die Methode aufgenommen haben. Der aktualisierte Transformer verfügt über eine tiefgehende Dekompositionsarchitektur und umfasst eine Frequenzganganalyseeinheit (FEB), einen Block für frequenzerweiterte Aufmerksamkeit (FEA) und Mixture Of Experts Dekompositionsblöcke(MOEDecomp).
Der Encoder FEDformer verwendet eine mehrstufige Struktur, ähnlich wie der Encoder Transformer. Ein einzelner Block davon kann durch die folgenden mathematischen Ausdrücke dargestellt werden:
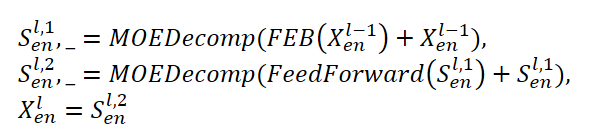
Hier steht Sen für die saisonale Komponente, die im Zerlegungsblock MOEDecomp aus den Originaldaten extrahiert wurde.
Für das FEB-Modul schlagen die Autoren der Methode zwei verschiedene Versionen vor (FEB-f und FEB-w), die unter Verwendung der diskreten Fourier-Transformation (DFT) bzw. der diskreten Wavelet-Transformation (DWT) implementiert werden. In dieser Implementierung ersetzen sie den Block der Selbstaufmerksamkeit.
Der Decoder verwendet ebenfalls eine mehrstufige Struktur, genau wie der Encoder. Die Architektur der einzelnen Bausteine ist jedoch viel umfassender und wird durch die Formeln beschrieben:
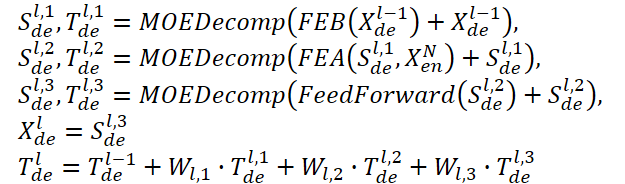
Sde und Tde stehen für die saisonale und die Trendkomponente nach dem Zerlegungsblock MOEDecomp. Wl dient als Projektion für den extrahierten Trend. Wie FEB hat auch FEA zwei verschiedene Versionen (FEA-f und FEA-w), die durch DFT- bzw. DWT-Projektion implementiert werden. FEA ist mit einer Aufmerksamkeisentwurf implementiert und ersetzt den Block der Kreuzaufmerksamkeit des Vanilla Transformer.
Die endgültige Prognose ist die Summe der beiden verfeinerten, zerlegten Komponenten. Die saisonale Komponente wird mit Hilfe der Matrix WS auf die Zielgröße projiziert.
![]()
Das vorgeschlagene Modell FEDformer verwendet die diskrete Fourier-Transformation (DFT), die es ermöglicht, die analysierte Sequenz in ihre einzelnen Schwingungen (Sinuskomponenten) zu zerlegen. Um die Effizienz des Modells zu verbessern, verwenden die Autoren von FEDformer die schnelle Fourier-Transformation (FFT).
Wie bereits erwähnt, verwendet die Methode eine zufällige Teilmenge der Fourier-Basis, und die Skala der Teilmenge wird durch einen Skalar begrenzt. Durch die Auswahl eines Modusindexes vor DFT- und inversen DFT-Operationen (IDFT) können Sie die Komplexität der Berechnungen weiter anpassen.
Der erweiterte Frequenzbereichsblock mit Fourier-Transformation (FEB-f) wird sowohl im Encoder als auch im Decoder verwendet. Die Quelldaten des Blocks FEB-f werden zunächst linear projiziert und dann vom Zeitbereich in den Frequenzbereich transformiert. Aus den erhaltenen Frequenzmerkmalen werden nach dem Zufallsprinzip die M-Harmonischen entnommen. Danach werden die ausgewählten Frequenzmerkmale mit der Matrix des parametrisierten Kernels multipliziert, der mit Zufallsparametern initialisiert und während des Modelltrainings angepasst wird. Das Ergebnis wird vor der Durchführung der inversen Fourier-Transformation, die die analysierte Sequenz in den Zeitbereich zurückführt, mit Nullen aufgefüllt, um den gesamten Frequenzgang zu erfassen. Die Originalvisualisierung des Blocks FEB-f, die von den Autoren des Artikels zur Verfügung gestellt wurde, ist unten dargestellt.
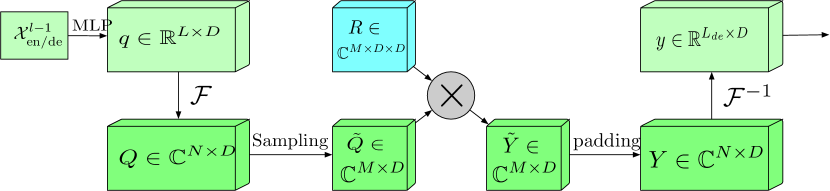
Der Frequenzgang-Aufmerksamkeitsblock mit diskreter Fourier-Transformation (FEA-f) verwendet den kanonischen Transformer-Ansatz mit einem kleinen Zusatz. Die Quelldaten werden in Werte für Query (Abfrage), Key (Schlüssel) und Values (Werte) umgewandelt. Bei Kreuzaufmerksamkeit kommt die Query vom Decoder, während Key und Value vom Encoder stammen. In FEA-f transformieren wir jedoch die Query, Key und Value mithilfe der Fourier-Transformation und führen einen ähnlichen kanonischen Aufmerksamkeitsmechanismus im Frequenzbereich durch. Wie im FEB-f-Block werden auch hier für die Analyse M-Schwingungen nach dem Zufallsprinzip ausgewählt. Das Ergebnis der Aufmerksamkeitsoperation wird mit Nullen in der Größe der ursprünglichen Sequenz aufgefüllt, und die inverse Fourier-Transformation wird durchgeführt. Die FEA-f-Struktur in der Visualisierung des Autors ist unten dargestellt.
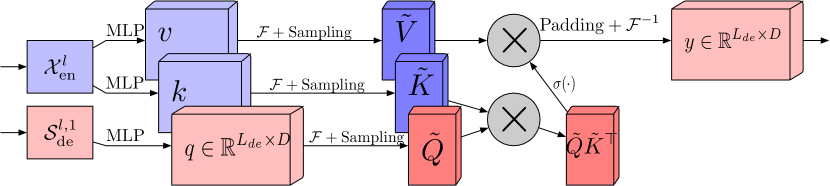
Während die Fourier-Transformation eine Darstellung eines Signals im Frequenzbereich erzeugt, ermöglicht die Wavelet-Transformation die Darstellung des Signals sowohl im Frequenz- als auch im Zeitbereich und bietet so einen effizienten Zugang zu lokalisierten Informationen über das ursprüngliche Signal. Die Multiwavelet-Transformation kombiniert die Vorteile von orthogonalen Polynomen und Wavelets. Eine Multiwavelet-Darstellung eines Signals kann durch das Tensorprodukt einer Multiskalen- und Multiwavelet-Basis erhalten werden. Beachten Sie, dass Basen auf verschiedenen Skalen durch ein Tensorprodukt miteinander verbunden sind. Die Autoren der FEDformer-Methode verwenden eine nicht standardisierte Wavelet-Darstellung, um die Komplexität des Modells zu verringern.
Die FEB-w-Architektur unterscheidet sich von der FEB-f-Architektur durch den rekursiven Mechanismus: Die ursprünglichen Daten werden rekursiv in drei Teile zerlegt, und jeder Teil wird einzeln verarbeitet. Für die Wavelet-Zerlegung schlagen die Autoren der Methode eine feste Matrix der Legendre-Wavelet-Basis-Zerlegung vor. Drei FEB-f-Module werden verwendet, um den resultierenden hochfrequenten Teil, den niederfrequenten Teil und den restlichen Teil der Wavelet-Zerlegung zu verarbeiten. Jede Iteration erzeugt einen verarbeiteten Hochfrequenz-Tensor, einen verarbeiteten Niederfrequenz-Tensor und einen rohen Niederfrequenz-Tensor. Dabei handelt es sich um einen Top-Down-Ansatz, bei dem der Zerlegungsschritt das Signal um den Faktor 1/2 vergrößert. Drei Sätze von FEB-f-Blöcken werden während verschiedener Zerlegungsiterationen zusammen verwendet. Bei der Wavelet-Rekonstruktion erstellen die Autoren der Methode auch den Ausgangstensor rekursiv.
FEA-w enthält eine Zerlegungs- und eine Rekonstruktionsphase, ähnlich wie FEB-w. Hier lassen die Autoren von FEDformer die Rekonstruktionsphase unverändert. Der einzige Unterschied besteht in der Zerlegungsphase. Sie verwenden dieselbe Matrix, um das Signal in die Entitäten Abfrage, Schlüssel und Wert zu zerlegen. Wie oben dargestellt, enthält der FEB-w-Block drei FEB-f-Blöcke zur Signalverarbeitung. FEB-f kann als Ersatz für den Mechanismus der Selbstaufmerksamkeit betrachtet werden. Die Autoren der Methode verwenden eine einfache Methode zur Erzeugung einer frequenzverstärkenden Kreuzaufmerksamkeit unter Verwendung der Wavelet-Zerlegung, wobei jedes FEB-f durch ein FEA-f-Modul ersetzt wird. Darüber hinaus wird ein weiteres FEA-f-Modul hinzugefügt, um die gröbsten Rückstände zu verarbeiten.
Aufgrund des häufig beobachteten komplexen periodischen Musters in Kombination mit einer Trendkomponente kann die Trendermittlung in realen Daten schwierig sein, wenn Durchschnittswerte mit festen Zeitfenstern zusammengeführt werden. Um dieses Problem zu überwinden, wurde der Zerlegungsblock der Mixture of Experts (MOEDecomp) entwickelt. Es enthält eine Reihe von Filtern mit unterschiedlichen Durchschnittsgrößen, um mehrere Trendkomponenten aus dem ursprünglichen Signal zu extrahieren, und eine Reihe von datenabhängigen Gewichten, um sie zu dem resultierenden Trend zu kombinieren.
Der vollständige Algorithmus der FEDformer-Methode ist in der folgenden Originalvisualisierung der Autoren dargestellt.
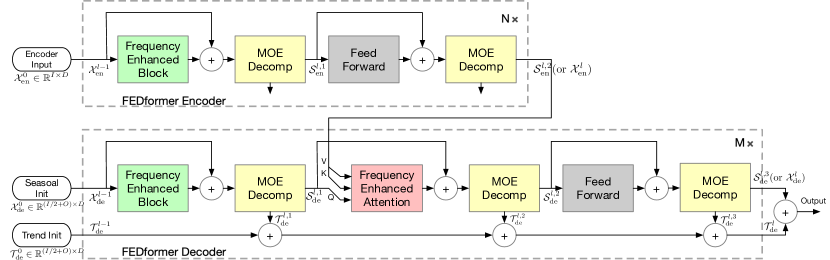
2. Implementierung in MQL5
Wir haben die theoretischen Aspekte der vorgeschlagenen FEDformer-Methode untersucht. Ich muss zugeben, dass unsere Umsetzung weit vom Original entfernt sein wird. Wir werden die vorgeschlagenen Ansätze verwenden, aber den vorgeschlagenen Algorithmus nicht vollständig umsetzen. Diesbezüglich gibt es mehrere persönliche Überzeugungen von mir.
Zunächst müssen wir uns entscheiden, welche Basis wir verwenden wollen: DFT oder DWT. Die Frage ist recht komplex und mehrdeutig. Aber wir werden es noch viel einfacher machen. Wenden wir uns nun den Ergebnissen der Methodentests zu, die in der Originalarbeit vorgestellt werden.

Achten Sie auf die Spalte „Exchange“. Wir werden nicht im Detail darauf eingehen, welche Daten genau das Modell getestet wurde, aber es gibt eine klare Überlegenheit des Modells, das DWT verwendet. Da die Eingabedaten keine eindeutige Periodizität aufweisen, ist DFT möglicherweise nicht in der Lage, den Zeitpunkt der Trendänderung zu bestimmen. Die Methode ignoriert nämlich die Zeitkomponente der Eingabedaten. DWT, die das Signal in beiden Dimensionen analysiert, ist in der Lage, genauere Vorhersagedaten zu liefern. Ich denke, in dieser Situation ist die Wahl von DWT offensichtlich.
2.1 Implementierung der DWT
Wir haben uns für eine Umsetzungsgrundlage entschieden. Beginnen wir nun mit der Implementierung der Wavelet-Zerlegung in unserer Bibliothek. Hierfür erstellen wir ein neues Objekt CNeuronLegendreWavelets.
Lassen Sie uns ein wenig über die Architektur des zu erstellenden Objekts nachdenken. Wie bereits oben erwähnt, schlagen die Autoren der Methode vor, für die Wavelet-Zerlegung eine feste Matrix der Legendre-Wavelet-Basiszerlegung zu verwenden. Mit anderen Worten: Um ein Signal zu zerlegen, müssen wir nur den Signalvektor mit der Wavelet-Basismatrix multiplizieren.
In unserer Eingangsdatensequenz müssen wir mehrere parallele Signale einer multimodalen Zeitreihe analysieren. Für jede unitäre Zeitreihe wird die gleiche Basismatrix verwendet.
Dieser Prozess ist der Faltung mit mehreren Filtern sehr ähnlich. In diesem Fall wird die Rolle der Filtermatrix jedoch von der Wavelet-Basismatrix übernommen. Logischerweise können wir ein neues Objekt als Nachfolger für unsere Faltungsschicht erstellen. Mit einem durchdachten Ansatz können wir das Beste aus den geerbten Methoden machen, indem wir nur ein paar von ihnen überschreiben.
class CNeuronLegendreWavelets : public CNeuronConvOCL { protected: virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } public: CNeuronLegendreWavelets(void) {}; ~CNeuronLegendreWavelets(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronLegendreWavelets; } };
In der obigen Struktur der neuen Klasse CNeuronLegendreWavelets sind nur 3 überschriebene Methoden zu sehen, von denen eine der Klassenbezeichner Type ist, der eine vordefinierte Konstante zurückgibt.
Der zweite Punkt, der bereits oben erwähnt wurde, ist, dass wir eine feste Matrix von Basis-Wavelets verwenden. Daher wird es in unserer Klasse keine trainierbaren Parameter geben, und die Methode updateInputWeights wird durch einen „Stummel“ neu definiert.
In der Tat müssen wir nur mit der Initialisierungsmethode Init des Klassenobjekts arbeiten. In der neuen Methode deklarieren wir keine lokalen Variablen oder Objekte. Bei der Initialisierungsmethode müssen wir nur die Matrix der Basis-Wavelets ausfüllen.
Die Autoren der Methode schlagen vor, Legendre-Polynome als Wavelets zu verwenden. Ich habe 9 solcher Polynome ausgewählt, deren Visualisierung unten dargestellt wird.

Wie Sie sehen, können wir mit den in der Grafik dargestellten Polynomen einen ziemlich großen Frequenzbereich beschreiben.
Beachten Sie auch, dass der Bereich der akzeptablen Werte der vorgestellten Polynome [0, 1] beträgt. Das ist sehr praktisch. Wir definieren die Fensterlänge der analysierten Sequenz als 1. Dann wird der Bereich durch die Anzahl der Elemente in der Folge geteilt. Auf diese Weise definieren wir den Zeitschritt zwischen zwei benachbarten Elementen der Sequenz, die wir zunächst mit einem festen Schritt bilden. In diesem Fall spielt der Zeitraum, in dem die ersten Daten erhoben wurden, keine Rolle. Wir analysieren die Frequenzmerkmale des Signals innerhalb des sichtbaren Fensters der Originalsequenz.
Und hier stehen wir vor dem Problem, die Anzahl der Elemente in einer Sequenz in der Phase des Modellentwurfs zu bestimmen. Bevor wir die Basismatrix erstellen, müssen wir ihre Dimensionen festlegen. In diesem Stadium haben wir nur die Anzahl der von uns ausgewählten Filter. Wir kennen die Fenstergröße der analysierten Sequenz nur bei der Initialisierung des Modells. In der Tat haben wir 2 Möglichkeiten, aus dieser Situation herauszukommen:
- Wir können die strengen Dimensionen der Matrix der Basis-Wavelets bestimmen und ihre Werte sofort ausfüllen. Durch die Verwendung einer trainierbaren Faltungsschicht vor der Matrix können wir mit jeder Größe der ursprünglichen Sequenz arbeiten.
- Entwicklung eines universellen Algorithmus zum Füllen der Matrix der Basis-Wavelets in der Phase der Modellinitialisierung für jede Größe der Ausgangsdaten.
Die erste Option erlaubt es uns, die Matrix auf beliebige Weise mit festen Werten zu füllen. Wir können sogar die Koeffizienten der grundlegenden Wavelets, an denen wir interessiert sind, im Internet finden. Doch wie lässt sich diese „goldene Mitte“ zwischen Genauigkeit und Leistung bestimmen? Außerdem können die Anforderungen an die Vorhersagegenauigkeit bei verschiedenen Aufgaben sehr unterschiedlich sein.
Meiner Meinung nach scheint die zweite Option für unsere Zwecke besser geeignet zu sein. Zur Umsetzung werden wir Formeln für die ausgewählten Polynome als Makrosubstitutionen erstellen. Nachfolgend sind einige von ihnen aufgeführt (die vollständige Liste finden Sie im Anhang):
#define Legendre4(x) (70*pow(x,4) - 140*pow(x,3) + 90*pow(x,2) - 20*x + 1) #define Legendre6(x) (924*pow(x,6) - 2772*pow(x,5) + 3150*pow(x,4) - 1680*pow(x,3) + \ 420*pow(x,2) - 42*x + 1) #define Legendre8(x) (12870*pow(x,8) - 51480*pow(x,7) + 84084*pow(x,6) - 72072*pow(x,5) + \ 34650*pow(x,4) - 9240*pow(x,3) + 1260*pow(x,2) - 72*x + 1)
Mit Hilfe dieser Makrosubstitutionen können wir den Wert des Polynoms für jeden beliebigen diskreten Wert ermitteln. Nach Abschluss der vorbereitenden Arbeiten können wir mit der Beschreibung des Algorithmus zur Initialisierung eines Objekts unserer neuen Klasse CNeuronLegendreWavelets::Init fortfahren.
In den Parametern der Methode übergeben wir die Schlüsselparameter der Objektarchitektur:
bool CNeuronLegendreWavelets::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 9, units_count, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir zunächst die gleiche Methode der übergeordneten Klasse auf.
Beachten Sie, dass wir in den Parametern der Initialisierungsmethode der neuen Klasse nur die Fenstergröße der zu analysierenden Sequenz und die Anzahl der Elemente in der Sequenz erhalten. Beim Aufruf der entsprechenden Methode der übergeordneten Klasse müssen wir den Fensterschritt und die Anzahl der Filter hinzufügen. Da wir uns bereits für die Anzahl der Filter entschieden haben, werden wir 9 Stück haben. Der Schritt des analysierten Fensters ist gleich dem analysierten Fenster.
Nachdem die Methode der Elternklasse erfolgreich initialisiert wurde, wird unsere Faltungsparametermatrix mit Zufallswerten gefüllt. Aber wir müssen sie mit den grundlegenden Parametern des Wavelets füllen. Wir füllen also zunächst die Gewichtsmatrix mit Nullwerten. Dies ist ein sehr wichtiger Punkt, da wir die angegebenen Bias-Parameter zurücksetzen müssen.
WeightsConv.BufferInit(WeightsConv.Total(), 0);
In der Schleife füllen wir dann die Matrix mit den Werten der Basis-Wavelets:
for(uint i = 0; i < iWindow; i++) { uint shift = i; float k = float(i) / iWindow; if(!WeightsConv.Update(shift, Legendre4(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre6(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre8(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre10(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre12(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre16(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre18(k))) return false; shift += iWindow + 1; if(!WeightsConv.Update(shift, Legendre20(k))) return false; }
Übertragen wir die gefüllte Matrix in den OpenCL-Kontextspeicher:
if(!!OpenCL) if(!WeightsConv.BufferWrite()) return false; //--- return true; }
Ende der Methode.
In dieser Implementierung haben wir alle übrigen Funktionen, die für den korrekten Betrieb des Objekts erforderlich sind, von der übergeordneten Klasse geerbt. Deshalb beenden wir die Arbeit an dieser Klasse und gehen weiter.
2.2 Der Block FED-w
Die nächste Stufe kann als Aufwärtsbewegung betrachtet werden. Wir werden unsere eigene Vision des FED-w-Blocks entwerfen. Seine Funktionalität ist in der Klasse CNeuronFEDW implementiert. Die Struktur dieser Klasse wird im Folgenden dargestellt.
class CNeuronFEDW : public CNeuronBaseOCL { protected: //--- uint iWindow; uint iCount; //--- CNeuronLegendreWavelets cWavlets; CNeuronBatchNormOCL cNorm; CNeuronSoftMaxOCL cSoftMax; CNeuronConvOCL cFF[2]; CNeuronBaseOCL cReconstruct; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Reconsruct(CBufferFloat* inputs, CBufferFloat *outputs); public: CNeuronFEDW(void) {}; ~CNeuronFEDW(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual int Type(void) const { return defNeuronFEDW; } virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
Sie können sehen, dass diese Klasse eine komplexere Architektur hat als die vorherige. Sie deklariert 2 lokale Variablen, um Schlüsselparameter zu speichern. Auch wir deklarieren hier eine ganze Reihe von internen Objekten. Wir werden ihren Zweck während des Umsetzungsprozesses erkennen. Alle Objekte werden statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse „leer“ lassen.
Die Initialisierung aller verschachtelten Objekte wird in der Methode CNeuronFEDW::Init durchgeführt. Parameter der Objektarchitektur werden an die Methode übergeben. Dazu gehören unter anderem die grundlegenden Parameter der Größe des sichtbaren Datenfensters (Window) und der Anzahl der analysierten Einzelsequenzen (Count).
bool CNeuronFEDW::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * count, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir zunächst die entsprechende Methode der übergeordneten Klasse auf. Danach speichern wir die Architekturparameter des initialisierten Objekts in lokalen Variablen:
iWindow = window; iCount = count;
Dann initialisieren wir die internen Objekte in der gleichen Reihenfolge, in der sie verwendet werden sollen.
Zunächst wollen wir aus den empfangenen Rohdaten Frequenzmerkmale extrahieren. Hierfür verwenden wir eine Instanz der oben erstellten Klasse CNeuronLegendreWavelets:
if(!cWavlets.Init(0, 0, OpenCL, iWindow, iWindow, iCount, optimization, iBatch)) return false; cWavlets.SetActivationFunction(None);
Der Block FED-w, den wir erstellen, ist im Vergleich zu der von den Autoren vorgeschlagenen Methode stark vereinfacht. Ich habe beschlossen, keine DFT-Blöcke zu verwenden. Ich habe den Eindruck, dass eine von der Zeitkomponente losgelöste Frequenzanalyse sich nachteilig auswirken und die Qualität der Prognosen verringern kann. Daher stellt sich die Frage nach der Zweckmäßigkeit des Einsatzes von DFT. Aber das ist meine persönliche Meinung, und sie könnte falsch sein.
Darüber hinaus werden durch den Wegfall eines recht arbeitsintensiven FFT-Prozesses den Aufwand für Rechenressourcen während des Trainings und des Betriebs des Modells erheblich reduziert.
Vor diesem Hintergrund habe ich beschlossen, die Leistung des Modells zu verbessern und dabei die Risiken einer möglichen Verschlechterung der Prognosequalität in Kauf zu nehmen.
Zunächst normalisiere ich die nach der Wavelet-Zerlegung erhaltenen Daten mit einer Batch-Normalisierungsschicht:
if(!cNorm.Init(0, 1, OpenCL, 9 * iCount, 1000,optimization)) return false; cNorm.SetActivationFunction(None);
Und dann bewerte ich den Anteil jedes der verwendeten Filter. Zu diesem Zweck übersetze ich die erhaltenen Daten mit der Funktion SoftMax in den Wahrscheinlichkeitsunterraum.
if(!cSoftMax.Init(0, 1, OpenCL, 9 * iCount, optimization, iBatch)) return false; cSoftMax.SetHeads(iCount); cSoftMax.SetActivationFunction(None);
Bitte beachten Sie, dass wir jeden Einheitskanal separat bewerten.
Danach werden wir die ursprüngliche Zeitreihe aus der wahrscheinlichen Darstellung durch inverse Faltung mit unserer Matrix aus Wavelet-Basen wiederherstellen. Das Ergebnis wird in der erstellten verschachtelten Basisebene gespeichert:
if(!cReconstruct.Init(0, 2, OpenCL, iWindow, optimization, iBatch)) return false; cReconstruct.SetActivationFunction(None);
Es ist ersichtlich, dass die oben genannten Operationen eine Art Kreis bilden: Zeitreihe → Wavelet-Zerlegung → Normalisierung → Wahrscheinlichkeitsdarstellung → Zeitreihe. Aber was wir am Ausgang erhalten, ist eine ziemlich geglättete Darstellung der Eingangszeitreihe, die wir durch eine Art digitalen Filter geschickt haben. Als Ergebnis erhalten wir eine recht effiziente Datenfilterung mit einem Minimum an trainierbaren Parametern, die nur in der Batch-Normalisierungsschicht vorhanden sind. Dieser Block ersetzt in unserer Implementierung die Selbstaufmerksamkeit.
Wichtig ist dabei, dass wir die trainierbaren Parameter des Modells durch vordefinierte Wavelets ersetzen. Das macht unser Modell verständlicher als die „Black Box“ der trainierbaren Parameter, aber weniger flexibel. Dies bedeutet auch eine zusätzliche Belastung für den Modellarchitekten, da er optimale Wavelets zur Lösung des gegebenen Problems finden muss. Aus diesem Grund habe ich Wavelet-Polynome in einen separaten Block von Makrosubstitutionen aufgenommen. Dieser Ansatz ermöglicht es uns, mit verschiedenen Wavelets zu experimentieren und die optimalen zu finden.
Aber kehren wir zu unserer Klasseninitialisierungsmethode zurück. Auf den digitalen Filterblock folgt der FeedForward-Block, der für die Transformer-Architektur üblich ist. Hier verwenden wir einen unveränderten zweischichtigen MLP mit LReLU zwischen den Schichten. Wie zuvor verwenden wir zur Implementierung der unabhängigen Kanalverarbeitung Faltungsschichtobjekte:
if(!cFF[0].Init(0, 3, OpenCL, iWindow, iWindow, 4 * iWindow, iCount, optimization, iBatch)) return false; cFF[0].SetActivationFunction(LReLU); if(!cFF[1].Init(0, 4, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iCount, optimization, iBatch)) return false; SetActivationFunction(None);
Am Ende der Initialisierungsmethode organisieren wir das Ersetzen des Fehlergradientenpuffers, um unnötige Datenkopiervorgänge zu minimieren:
if(Gradient != cFF[1].getGradient()) SetGradient(cFF[1].getGradient()); //--- return true; }
Nach Abschluss der Arbeiten zur Initialisierung unseres Objekts gehen wir dazu über, einen Feed-Forward-Durchgang des vorgeschlagenen Modells zu implementieren. Aus der obigen Beschreibung des geplanten Prozesses ist die inverse Faltung der erhaltenen Wahrscheinlichkeiten zu einer Zeitreihe hervorzuheben.
„Inverse Faltung“ klingt nach etwas Neuem in unserer Implementierung. Wir haben dieses Verfahren jedoch schon vor langer Zeit eingeführt. Mittels inverser Faltung propagieren wir den Fehlergradienten in der Faltungsschicht. Nun müssen wir aber den angegebenen Prozess im Rahmen des Feedforward-Passes implementieren.
Die Schwierigkeit besteht darin, dass alle Methoden unserer Klassen mit einer festen Liste von Datenpuffern arbeiten. Auf diese Weise müssen wir uns bei der Erstellung von Modellen keine Gedanken über die verwendeten Datenpuffer machen. Wir müssen lediglich einen Zeiger auf das Objekt angeben, während alle Datenpuffer bereits in die Methode geschrieben werden. Der „Nachteil“ ist, dass wir die Backpropagation-Methode nicht verwenden können, um den Algorithmus innerhalb des Feedforward-Durchgangs zu implementieren. Wir können jedoch eine neue Methode erstellen, in der wir den zuvor erstellten Kernel verwenden und ihm die richtigen Puffer und Parameter übergeben.
Genau das werden wir tun. Erstellen wir die Methode CNeuronFEDW::Reconstruction, in deren Parametern wir Zeiger auf die Puffer für die ermittelten Wahrscheinlichkeiten und die rekonstruierte Sequenz übergeben werden:
bool CNeuronFEDW::Reconsruct(CBufferFloat *sequence, CBufferFloat *probability) { uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = sequence.Total();
Im Methodenkörper definieren wir den Aufgabenbereich und übergeben dem Kernel alle notwendigen Parameter:
if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_w, cWavlets.GetWeightsConv().GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_g, probability.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_o, probability.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CalcHiddenGradientConv, def_k_chgc_matrix_ig, sequence.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_outputs, probability.Total())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_step, (int)iWindow)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_in, (int)iWindow)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_window_out, (int)9)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_activation, (int)None)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CalcHiddenGradientConv, def_k_chgc_shift_out, (int)0)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Danach stellen wir den Kernel in die Ausführungswarteschlange:
if(!OpenCL.Execute(def_k_CalcHiddenGradientConv, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
An dieser Stelle ist die Vorarbeit abgeschlossen, und wir können mit der Beschreibung der Feedforward-Pass-Methode unserer Klasse CNeuronFEDW::feedForward fortfahren. Wie immer übergeben wir in den Parametern der Feed-Forward-Methode einen Zeiger auf das Objekt der vorherigen Schicht unseres Modells, das die erforderlichen Eingabedaten enthält:
bool CNeuronFEDW::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cWavlets.FeedForward(NeuronOCL.AsObject())) return false;
Im Hauptteil der Methode zerlegen wir zunächst die erhaltene Sequenz in ihre einzelnen Frequenzmerkmale. Zu diesem Zweck rufen wir die Feed-Forward-Pass-Methode des verschachtelten cWavlets-Objekts auf.
Als Nächstes normalisieren wir die erhaltenen Daten nach dem vorgeschlagenen Algorithmus und übersetzen sie in einen probabilistischen Unterraum:
if(!cNorm.FeedForward(cWavlets.AsObject())) return false; if(!cSoftMax.FeedForward(cNorm.AsObject())) return false;
Dann stellen wir die zeitliche Abfolge wieder her:
if(!Reconsruct(cReconstruct.getOutput(), cSoftMax.getOutput())) return false;
Der weitere Algorithmus ähnelt dem des klassischen Transformers. Wir addieren und normalisieren die eingegebenen und rekonstruierten Zeitsequenzen:
if(!SumAndNormilize(NeuronOCL.getOutput(), cReconstruct.getOutput(), cReconstruct.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Wir verbreiten die Daten durch den FeedForward-Block:
if(!cFF[0].FeedForward(cReconstruct.AsObject())) return false; if(!cFF[1].FeedForward(cFF[0].AsObject())) return false;
Danach werden die Zeitsequenzen der beiden Datenströme neu summiert und normalisiert:
if(!SumAndNormilize(cFF[1].getOutput(), cReconstruct.getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Der Vorwärtsdurchgang ist fertig, und wir fahren mit der Erstellung der Rückwärtsdurchgangs fort. Beginnen wir mit der Erstellung einer Gradientenfehlerverteilungsmethode CNeuronFEDW::calcInputGradients:
bool CNeuronFEDW::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird zunächst geprüft, ob der in den Parametern enthaltene Zeiger auf das Objekt der vorherigen Schicht korrekt ist. Wenn es keinen korrekten Zeiger gibt, ist es sinnlos, die Operationen der Methode auszuführen.
Wie Sie sich erinnern, haben wir in der Initialisierungsmethode der Klasse die Datenpuffer für den Fehlergradienten ersetzt. Jetzt können wir sofort mit dem FeedForward-Block weiterarbeiten.
if(!cFF[0].calcHiddenGradients(cFF[1].AsObject())) return false; if(!cReconstruct.calcHiddenGradients(cFF[0].AsObject())) return false;
Ähnlich wie beim Datenfluss im Feed-Forward-Durchgang wird auch beim Backpropagation-Durchgang der Fehlergradient auf zwei parallele Datenflüsse verteilt. In diesem Stadium summieren wir den Fehlergradienten aus beiden Strömen.
if(!SumAndNormilize(Gradient, cReconstruct.getGradient(), cReconstruct.getGradient(), iWindow, false)) return false;
Als Nächstes müssen wir den Fehlergradienten durch die umgekehrte Faltungsoperation weitergeben. Offensichtlich handelt es sich um eine einfache Faltungsoperation. Allerdings gibt es ein Problem. Die Methode des Vorwärtsdurchgangs einer Faltungsschicht funktioniert nicht mit Fehlergradientenpuffern. Diesmal wenden wir einen kleinen Trick an: Wir ersetzen die Ergebnispuffer der Ebenen vorübergehend durch die Puffer ihrer Farbverläufe. In diesem Fall speichern wir zunächst die Zeiger auf die ersetzten Datenpuffer:
CBufferFloat *temp_r = cReconstruct.getOutput(); if(!cReconstruct.SetOutput(cReconstruct.getGradient(), false)) return false; CBufferFloat *temp_w = cWavlets.getOutput(); if(!cWavlets.SetOutput(cSoftMax.getGradient(), false)) return false;
Führen wir einen Vorwärtsdurchgang der Faltungsschicht durch:
if(!cWavlets.FeedForward(cReconstruct.AsObject())) return false;
und bringen die Datenpuffer an ihre ursprüngliche Position zurück:
if(!cWavlets.SetOutput(temp_w, false)) return false; if(!cReconstruct.SetOutput(temp_r, false)) return false;
Als Nächstes wird der Fehlergradient zurück zur vorherigen Schicht propagiert:
if(!cNorm.calcHiddenGradients(cSoftMax.AsObject())) return false; if(!cWavlets.calcHiddenGradients(cNorm.AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cWavlets.AsObject())) return false;
und fassen den Fehlergradienten aus den beiden Datenströmen zusammen:
if(!SumAndNormilize(NeuronOCL.getGradient(), cReconstruct.getGradient(), NeuronOCL.getGradient(), iWindow, false)) return false; //--- return true; }
Vergessen wir nicht, die Ausführung von Vorgängen zu kontrollieren. Dann schließen wir die Methode ab.
Nach der Fehlergradientenübertragung auf alle Elemente unseres Modells folgt die Optimierung der trainierbaren Parameter des Modells. Die Funktion zur Optimierung der Objektparameter ist in der Methode CNeuronFEDW::updateInputWeights implementiert. Der Algorithmus der Methode ist recht einfach, sodass wir nur die gleichnamigen Methoden der verschachtelten Objekte aufrufen und die Ergebnisse anhand des logischen Ergebnisses der aufgerufenen Methoden überprüfen.
bool CNeuronFEDW::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cFF[0].UpdateInputWeights(cReconstruct.AsObject())) return false; if(!cFF[1].UpdateInputWeights(cFF[0].AsObject())) return false; if(!cNorm.UpdateInputWeights(cWavlets.AsObject())) return false; //--- return true; }
Bitte beachten Sie, dass wir bei dieser Methode nur mit den Objekten arbeiten, die trainierbare Parameter enthalten.
Damit sind unsere Überlegungen zu Algorithmen für die Konstruktion neuer Klassenmethoden abgeschlossen. Den vollständigen Code der besprochenen Klassen und alle ihre Methoden finden Sie im Anhang. Der Anhang enthält auch den vollständigen Code für alle im Artikel verwendeten Programme.
Bitte beachten Sie, dass wir nur unsere eigene Vision des State Encoders des vorgeschlagenen FEDformer-Algorithmus erstellt haben. Aber wir haben den Decoder komplett weggelassen. Wir tun dies absichtlich, weil wir unsere Aufgabe, eine gewinnbringende Handelsstrategie zu entwickeln, prinzipiell angehen. So seltsam es auch klingen mag, wir streben nicht danach, die späteren Zustände der Umwelt so genau wie möglich vorherzusagen. Diese Zustände beeinflussen die Arbeit unseres Agenten nur indirekt. Wenn wir einen eindeutigen Algorithmus mit Regeln für den nachfolgenden Zustand erstellen würden, bräuchten wir die genaueste Vorhersage der kommenden Preisbewegung. Wir gestalten unsere Agentenpolitik jedoch anders.
Wir trainieren den Encoder, um zukünftige Zustände der Umgebung vorherzusagen, um den informativsten versteckten Zustand des Encoders zu erhalten. Der Akteur wiederum extrahiert den verborgenen Zustand des Encoders, der im Wesentlichen ein integraler Bestandteil des Akteurs ist, und analysiert den aktuellen Zustand der Umgebung. Auf der Grundlage der Analyse des aktuellen Zustands des Umfelds des Akteurs erstellt er dann seine eigene Strategie.
Hier gibt es einen schmalen Grat, den wir verstehen müssen. Daher verwenden wir keine übermäßigen Ressourcen auf die Zerlegung des verborgenen Zustands des Encoders, um eine möglichst genaue Vorhersage der zukünftigen Zustände der Umgebung zu erhalten.
2.3 Modellarchitektur
Nachdem wir die Objekte konstruiert haben, die die Bausteine unseres Modells sind, gehen wir zur Beschreibung der Gesamtarchitektur der Modelle über. In dieser Arbeit habe ich beschlossen, scheinbar völlig unterschiedliche Ansätze zu kombinieren. Man könnte sogar sagen, dass sie miteinander konkurrieren. Ich habe mich entschieden, den vorgeschlagenen Ansatz mit Wavelet-Zerlegung der Zeitreihe als primäre Verarbeitung der Quelldaten vor der im vorherigen Artikel besprochenen Methode TiDE zu verwenden. Folglich wirkten sich die Änderungen auf die Architektur des Environmental State Encoder aus, der in der Methode CreateEncoderDescriptions dargestellt wird.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Im Hauptteil der Methode wird wie üblich zunächst die Relevanz des empfangenen Zeigers auf das dynamische Array für die Aufzeichnung der Modellarchitektur geprüft und ggf. eine Instanz eines neuen Objekts erzeugt.
Um die Eingabedaten zu erhalten, verwenden wir das grundlegende Objekt der vollständig verbundenen neuronalen Schicht.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Das Modell erhält, wie immer, „rohe“ Eingabedaten. Die Daten werden in der Batch-Daten-Normalisierungsschicht vorverarbeitet:
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 10000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Anschließend transponieren wir die Eingabedaten, sodass die nachfolgenden Operationen eine unabhängige Analyse der unitären Sequenzen der verwendeten Indikatoren durchführen:
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
Als Nächstes verwenden wir einen Block von 10 FED-w-Schichten:
//--- layer 3-12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFEDW; descr.count = BarDescr; descr.window = HistoryBars; descr.activation = None; for(int i = 0; i < 10; i++) if(!encoder.Add(descr)) { delete descr; return false; }
Unmittelbar danach fügen wir einen vollständig angeschlossenen Time Series Encoder hinzu:
//--- layer 13 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTiDEOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.window_out = NForecast; descr.step = 4; { int windows[] = {HistoryBars, 2 * EmbeddingSize, EmbeddingSize, 2 * EmbeddingSize, NForecast}; if(ArrayCopy(descr.windows, windows) <= 0) return false; } descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Als Nächstes verwenden wir wie zuvor eine Faltungsschicht, um die Verzerrung der vorhergesagten Werte zu korrigieren:
//--- layer 14 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = NForecast; descr.step = NForecast; descr.window_out = NForecast; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Wir transponieren die vorhergesagten Werte in die Darstellung der Eingabedaten:
//--- layer 15 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; if(!encoder.Add(descr)) { delete descr; return false; }
Wir geben die statistischen Parameter der Eingabezeitsequenz zurück:
//--- layer 16 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Wie Sie sehen können, betreffen die Änderungen nur die interne Architektur des Encoders. Daher müssen wir nur den Zeiger auf die latente Zustandsschicht des Encoders ändern, um Daten zu extrahieren. Die Architekturen Actor und Critic bleiben unverändert.
#define LatentLayer 14
Außerdem müssen wir keine Änderungen an der Umweltinteraktions-EA oder den Modellschulungs-EAs vornehmen. Den vollständigen Code finden Sie in der Anlage. Die Beschreibungen der Algorithmen finden Sie im vorherigen Artikel.
3. Tests
In diesem Artikel haben wir uns mit der FEDformer-Methode vertraut gemacht, die die Zeitreihenanalyse in die Domäne der Frequenzmerkmale überträgt. Dies ist eine sehr interessante und vielversprechende Methode. Wir haben uns viel Mühe gegeben, die vorgeschlagenen Ansätze mit MQL5 zu implementieren.
Ich möchte noch einmal darauf hinweisen, dass der Artikel meine eigene Vorstellung von den vorgeschlagenen Ansätzen darstellt, die sich von der Beschreibung der Methode im Quellenpapier deutlich unterscheidet. Dementsprechend gelten die Schlussfolgerungen aus den Modelltestergebnissen nur für diese Implementierung und können nicht vollständig auf die ursprüngliche Methode extrapoliert werden.
Wie bereits erwähnt, betrafen die Änderungen nur die interne Architektur des Encoders. Das bedeutet, dass wir bereits gesammelte Trainingsdatensätze verwenden können, um Modelle zu trainieren.
Ich möchte Sie daran erinnern, dass wir für das Offline-Modelltraining vorab gesammelte Trajektorien der Interaktion mit der Umwelt verwenden. Dieser Datensatz basiert auf realen historischen Daten für das gesamte Jahr 2023. Trainingssymbol: EURUSD mit dem Zeitrahmen H1. Um das trainierte Modell im MetaTrader 5 Strategy Tester zu testen, verwende ich historische Daten vom Januar 2023.
Im ersten Schritt trainieren wir den Environment State Encoder, indem wir den Fehler zwischen den tatsächlichen Metriken, die die nachfolgenden Umweltzustände beschreiben, und ihren vorhergesagten Werten minimieren. Im Encoder werden nur Umweltzustände analysiert und vorhergesagt, die nicht von den Aktionen des Agenten abhängen. Daher führen wir ein vollständiges Training des Encoders durch, ohne den Trainingsdatensatz zu aktualisieren.
Meiner subjektiven Meinung nach hat sich in dieser Phase die Qualität der Vorhersage der nachfolgenden Umweltzustände verbessert. Dies zeigt sich an der geringeren Fehlerquote im Lernprozess. Ich habe jedoch keinen grafischen Vergleich von Ist- und Prognosewerten durchgeführt, um deren Qualität im Detail zu analysieren.
In der zweiten Iterationsstufe trainieren wir die Politik des Akteurs parallel zum Training des kritischen Modells. Dies ergibt die wahrscheinlichste Bewertung der Handlungen des Akteurs. In diesem Stadium ist die Genauigkeit der Bewertung der Handlungen des Akteurs für uns von entscheidender Bedeutung. Daher wechseln wir den Prozess des Trainings der Modelle und der Aktualisierung des Trainingsdatensatzes unter Berücksichtigung der aktuellen Politik des Akteurs ab.
Nach einer Reihe der oben genannten Iterationen gelang es mir, eine Verhaltenspolitik für den Akteur zu trainieren, die sowohl in der Trainings- als auch in der Testphase Gewinne abwirft. Die Testergebnisse werden im Folgenden vorgestellt.

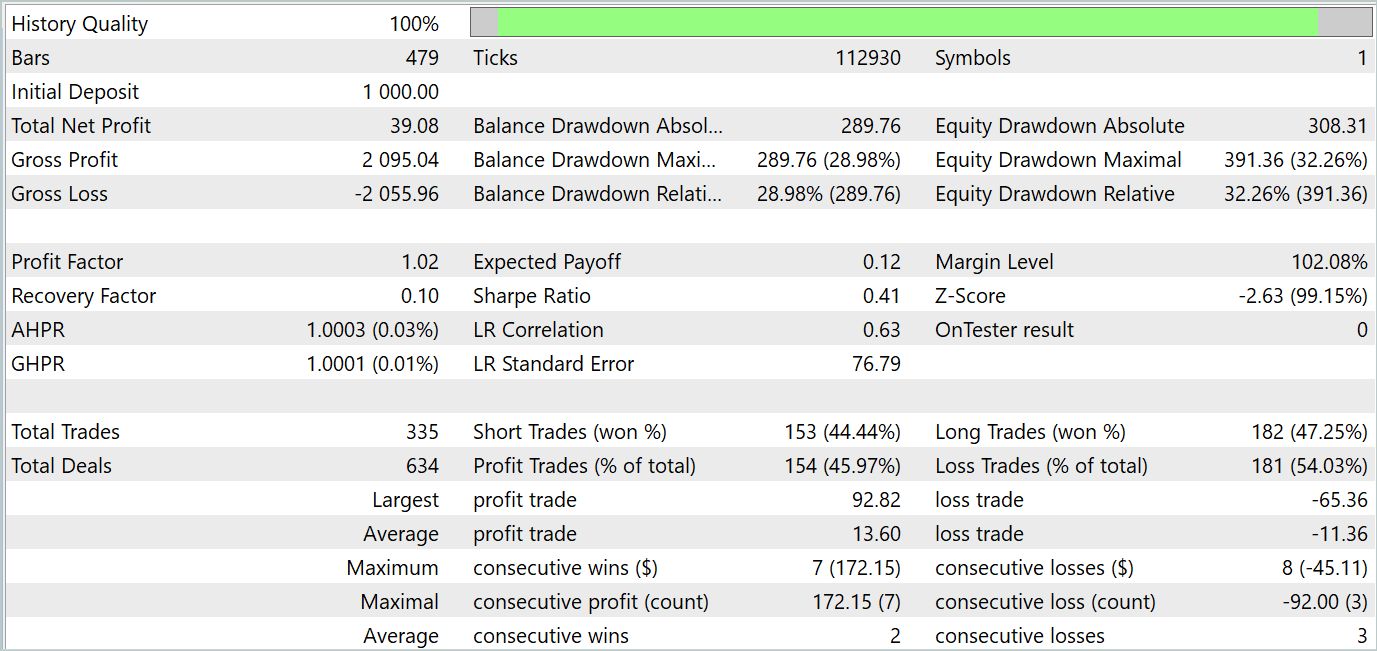
Wie Sie sehen können, zeigt die Saldenkurve einen allgemeinen Aufwärtstrend. Gleichzeitig lassen sich auf dem Chart 4 Trends klar erkennen: 2 rentable und 2 unrentable. Das Positive daran ist, dass profitable Trends mehr Potenzial haben. Auf diese Weise können Sie genügend Gewinn anhäufen, um zu vermeiden, dass Sie Ihre Einlage während einer Verlustphase verlieren. Der Ausgleich ist jedoch sehr subtil. Während des Testzeitraums lag der Gewinnfaktor bei nur 1,02, und der Anteil der gewinnbringenden Geschäfte lag bei knapp 46 %.
Insgesamt zeigt das Modell Potenzial, aber es ist noch mehr Arbeit nötig, um die Verlustzonen zu minimieren.
Schlussfolgerung
In diesem Artikel haben wir die FEDformer-Methode erörtert, die für langfristige Zeitreihenprognosen vorgeschlagen wurde. Es beinhaltet einen Aufmerksamkeitsmechanismus mit Frequenzannäherung mit niedrigem Rang und Mischungszerlegung zur Kontrolle der Verteilungsverschiebung.
Im praktischen Teil haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt und das Modell auf realen historischen Daten trainiert und getestet. Die Testergebnisse zeigen das Potenzial des betrachteten Modells. Gleichzeitig gibt es aber auch Punkte, die zusätzliche Aufmerksamkeit erfordern.
Referenzen
- FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14858
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronales Netz in der Praxis: Geradenfunktion
Neuronales Netz in der Praxis: Geradenfunktion
 Entwicklung eines Replay Systems (Teil 50): Die Dinge werden kompliziert (II)
Entwicklung eines Replay Systems (Teil 50): Die Dinge werden kompliziert (II)
 Entwicklung eines Expertenberaters für mehrere Währungen (Teil 12): Entwicklung eines Risikomanagers auf der Ebene des Eigenhandels
Entwicklung eines Expertenberaters für mehrere Währungen (Teil 12): Entwicklung eines Risikomanagers auf der Ebene des Eigenhandels
 Neuronales Netz in der Praxis: Kleinste Quadrate
Neuronales Netz in der Praxis: Kleinste Quadrate
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.