
交易中的神经网络:免掩码注意力方式预测价格走势
概述
我们继续运用点云处理方法的探索。在上一篇文章中,我们介绍了 SPFormer 方法。它的作者开发了一种基于 变换器 架构的综合算法。变换器解码器的多个层利用固定数量的对象查询,从而实现全局特征的迭代处理,及直接对象预测。SPFormer 不需要后期处理来剔除重复项,在于训练期间采用了一对一的双分匹配策略。甚至,在最后一层生成的对象掩码,可用于引导交叉注意力。
然而,论文《免掩码注意力的 3D 实例分段转换器》的作者指出,当前基于 变换器 的方法收敛缓慢。通过对基线方法的分析,他们发现这个问题可能源于初始掩码的低品质。具体来说,初始对象掩码是通过映射初始对象查询、和每点的掩码特征之间的相似性来生成的。初始掩码品质太差会增加训练的复杂性,从而减慢收敛速度。
为了解决初始掩码完整性较低的问题,作者提出了一种新型算法,即 免掩码注意力变换器(MATF),它放弃了掩码注意力设计,取而代之引入了一个辅助中心回归任务来引导交叉注意力。为了实现中心回归,作者开发了一系列组件,均会参考点位置。首先,他们添加一组可学习的位置查询,每个代表相应内容查询的位置。这些查询位置贯穿学习空间密集分布。此外,还引入了一个约束,从而确保每个查询都专注于其局部区域。如是结果,查询可以有效地捕获场景中具有更高独特性的物体,其对于降低训练复杂性、及加速收敛至关重要。
此外,MATF 的作者提出了交叉注意力的上下文相对位置编码。与之前工作中所用的注意力掩码相比,这种解决方案更加灵活,在于注意力权重的调整是基于相对位置,而非刚性掩码。查询位置将迭代更新,以便达成更准确的表示。
论文中展示的实验结果表明,MATF 在各种数据集中都提供了卓越的性能。
1. MATF 算法
SPFormer 算法表示一个完全端到端的管线,允许对象查询直接生成实例预测。使用 变换器 解码器,固定数量的对象查询从所分析点云中聚合全局对象信息。此外,SPFormer 利用对象掩码来引导交叉注意力,要求查询仅关注已掩码特征。然而,在训练的早期阶段,这些掩码的品质很低。这会阻碍后续层的性能,并提升整体训练复杂性。
为了解决这一点,MAFT 方法作者引入了一个辅助性中心回归任务来引导实例分段。最初,从原始点云中选择全局位置 𝒫,并通过主干网络提取全局对象特征 ℱ。这些可以是体素或超点。除了内容查询 𝒬0c 之外,MAFT 的作者还引入了固定数量的位置查询 𝒬0p,表示归一化的物体中心。而 𝒬0p 是随机初始化的,而 𝒬0c 是从零值开始。核心意图是允许位置查询在交叉注意力中引导相应的上下文查询,随后两个查询集进行迭代细化,从而预测物体中心、分类、和掩码。
为了有效地解决物体中心回归任务,并改进初始物体掩码的生成,MAFT 的作者提出了一系列参控点位置的架构组件。
与之前的方式不同,引入了一组额外的位置查询 𝒬0p。跨场景的点范围差异明显,初始位置查询以归一化形式存储,作为可学习参数,后随 sigmoid 激活函数。
值得注意的是,这些初始位置查询贯穿目标空间密集分布。甚至,每个查询都会聚合来自其相应局部区域的物体。该设计利用初始查询的能力,来捕获具有高召回率的场景物体。它解决了初始实例掩码品质太差导致的低记忆性问题,并降低了后续层的训练复杂性。
除了绝对位置编码外,MAFT 还在交叉注意力机制中采用了上下文相对位置编码。为了达成这一点,首先计算位置查询 𝒬tp 和全局位置 𝒫 之间的相对位置 𝐫,然后量化为离散整数 𝐫'。这些离散的相对位置当作索引,从位置编码表中提取相应的数值。
接下来,将相对位置编码 𝐟pos 与交叉注意力模块中的 查询 𝐟q、或 键 特征 𝐟k 相乘。然后把结果添加到交叉注意力权重之中,然后是 Softmax 函数。
值得注意的是,比之掩码注意力,相对位置编码提供了更大的灵活性,以及对错误的健壮性。本质上,它的功能是一个软性掩码,可以灵活地调整注意力权重,超过应用严格的掩码。另一个优点是它集成了语义信息,且可选择性地捕获局部上下文。这是经由相对位置和语义特征之间的互动来达成的。
由于解码器层中的上下文查询不断更新,故在贯穿解码过程中维护固定的位置查询并不理想。由于初始位置查询是静态的,故在后续层中适配特定的输入场景是有益的。为达此目的,作者基于内容查询迭代优化位置查询。具体地,用 MLP 来预测据更新的上下文查询 𝒬t+1c 的中心偏移量 Δpt。然后将该偏移量添加到前面的位置查询 𝒬tp 中。
上述论文中 MAFT 方法的原始可视化如下所示。

2. 利用 MQL5 实现
在探索了免掩码注意力变换器方法的理论基础之后,我们现在进入本文的实践部分,在那里我们利用 MQL5 实现对所提出方法的解释。我们首先扩展 OpenCL 程序。
2.1扩展 OpenCL 程序
我们首先构造相对位置编码算法。一方面,算法相对简单。我们只需计算两点之间的距离。甚至,作者还分别计算沿每个坐标轴的距离。另一方面,MAFT 作者对生成的偏移量执行量化,用其索引到可学习的参数表之中。我们选择轻微优化原始解决方案。我们的实现基于以下假设:最大的影响来自位于所分析查询附近的点。照该逻辑,我们首先计算 N-维空间中两点之间的距离 S。然后用以下公式计算位置偏置系数 kpb:

很明显,任意两点之间的距离总是大于或等于 0。如果点重合,则系数等于 1。随着距离的增加,相对位置编码系数接近 0。
所提算法的实现在 CalcPositionBias 内核中提供。内核参数包括指向三个全局数据缓冲区的指针:其中 2 个包含输入数据。第三个存储结果。此外,我们还指定了单个元素的特征向量的维数。
注意,为了正确计算两个向量之间的距离,必须将它们投影到同一个子空间上。这意味着两个输入张量中的特征向量必须具有相同的维度。
__kernel void CalcPositionBias(__global const float *data1, __global const float *data2, __global float *result, const int dimension ) { const size_t idx1 = get_global_id(0); const size_t idx2 = get_global_id(1); const size_t total1 = get_global_size(0); const size_t total2 = get_global_size(1);
我们计划在二维任务空间中启动内核,每个都等于原始数据相应张量中的元素数量。在内核主体中,我们立即在任务空间的两个维度中标识当前线程。
在下一步中,我们判定数据缓冲区的偏移量。
const int shift1 = idx1 * dimension; const int shift2 = idx2 * dimension; const int shift_out = idx1 * total2 + idx2;
准备阶段完结后,我们继续计算的执行。在这里,我们首先组织一个循环来计算分析向量之间的距离。
float res = 0; for(int i = 0; i < dimension; i++) res = pow(data1[shift1 + i] - data2[shift2 + i], 2.0f); res = sqrt(res);
然后我们计算相对偏差系数。
res = 1.0f / exp(res); if(isnan(res) || isinf(res)) res = 0; //--- result[shift_out] = res; }
然后,我们将计算出的数值写入结果缓冲区中的相应元素。
注意,得到的任何系数都非负数。这意味着我们不会掩盖输入序列中的任何元素。相较之,我们的实现强调在空间上最接近查询的元素。
在该阶段,我们已计算出相对位置偏置系数。下一步是将它们集成到我们的交叉注意力机制当中。不过,在我们继续实现之前,我想提请您注意一个重要的细节。细看上面显示的作者对 MAFT 方法的可视化。特别注意场景表示信息的流向。作者的方法立足于场景表示内的位置编码。具体而言,位置编码仅应用于 j键 实体。值 实体不受位置编码的影响。这体现了一个经过深思熟虑的选择,以确保在计算注意力权重时会参考位置编码。但与此同时,它们不会扭曲场景元素的实际特征描述符。故此,必须从不同的来源生成 键 和 值 张量。实际上,我们必须首先自原始输入表示中生成 值 张量。然后,我们将位置编码添加到原始数据之中。只有这样,我们才能获得 键 张量。
为什么我现在要强调这一点?上述推理意味着我们必须将 键 和 值 实体分离成不同的张量。我们可以设计一个新的注意力内核,来解释这种架构上的细微差别。这种方式还可令我们避免级联两个张量,而我们以前必须这样做。
为了实现注意力算法,我们将创建一个名为 MHPosBiasAttentionOut 的内核。这个内核接受后续的全局数据缓冲区,其中许多已在我们之前实现的注意力机制中领略。此外,我们传递一个指向相对位置偏差缓冲区中 pos_bias 的索引。我们在设计该内核时,还可选择性地支持无需位置偏差的标准注意力计算。该功能可用 use_pos_bias 参数启用和禁用。
__kernel void MHPosBiasAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global float *score, ///<[out] Matrix of Scores __global const float *pos_bias, ///<[in] Position Bias __global float *out, ///<[out] Matrix of attention const int dimension, ///< Dimension of Key const int heads_kv, const int use_pos_bias ) { //--- const int q_id = get_global_id(0); const int k_id = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
如前,我们计划在三维任务空间中运行这个内核。前两个示意正分析序列中的元素数量,任务空间的第三个维度示意用到的注意力头数量。内核算法首先在任务空间的所有三个维度中标识当前线程。
接下来,我们定义所有必要的常量。
const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads_kv * k_id + h_kv); const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
然后我们在局部内存中创建一个数据数组,用来在局部组的线程之间交换数据。
__local float temp[LOCAL_ARRAY_SIZE];
准备工作阶段就这样完成了,我们转入直接计算。计算过程在很大程度上重复了经典算法。我们只在必要时添加相对位置偏差。使用它们的必要性由 use_pos_bias 参数值控制。
首先,我们计算注意力系数的指数值之和。在第一阶段,局部组的每个线程计算其一部分。然后,它将结果保存在局部数据数组的相应元素之中。
//--- sum of exp uint count = 0; if(k_id < ls) { temp[k_id] = 0; do { if(q_id >= (count * ls + k_id)) if((count * ls) < (kunits - k_id)) { float sum = 0; int sh_k = dimension * heads_kv * count * ls; for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * k[shift_kv + d + sh_k]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; temp[k_id] = temp[k_id] + sum + (use_pos_bias > 0 ? pos_bias[shift_pb + count * ls] : 0); } count++; } while((count * ls + k_id) < kunits); } barrier(CLK_LOCAL_MEM_FENCE);
请注意,我们计算出的总和,必须包括位置偏差系数的总和。
接下来,我们汇总局部数组的元素值。
count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
在计算总和之后,我们判定并存储依赖系数的归一化值,同时参考位置偏差系数。
//--- score float sum = temp[0]; float sc = 0; if(q_id >= (count * ls + k_id)) if(sum != 0) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * k[shift_kv + d]; sc = (exp(sc / koef) + (use_pos_bias > 0 ? pos_bias[shift_pb] : 0)) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
得到的注意力系数,令我们能计算所分析序列中每个元素的多头注意力的最终值。
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k_id < ls) do { if((count * ls) < (kunits - k_id)) { int sh_v = 2 * dimension * heads_kv * count * ls; float sum = v[shift_kv + d + sh_v] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; temp[k_id] = (count > 0 ? temp[k_id] : 0) + sum; } count++; } while((count * ls + k_id) < kunits); barrier(CLK_LOCAL_MEM_FENCE); //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
接下来,我们继续在 MHPosBiasAttentionInsideGradients 内核中实现反向传播算法。值得一提的是,当经由求和运算分派误差梯度时,该梯度典型情况下会全部传播到两个合计值。采用明显小于一的学习率,给予潜在的错误过度计算更多补偿。另一个需要考虑的关键点是,相对位置偏差系数的计算完全基于点的实际空间布局。这些实际上表示原始输入数据。故此,这些计算不受模型参数的影响。计算过程本身不包含可学习的参数。相较之,将梯度传播到相对位置偏差系数的张量是不合逻辑的。因此,我们将该步骤从反向传播过程中排除。
考虑到这些因素,我们得出了注意力模块的经典梯度分派方法。不过,我们开发了一个新的内核,正如早前所述,我们已将 键 和 值 实体分离到不同的数据缓冲区当中。您可在附件中查看 MHPosBiasAttentionInsideGradients 反向传播内核的实现。至此,我们结束 OpenCL 组件的工作。
2.2创建 MAFT 类
下一阶段我们的工作涉及创建一个新对象,该对象封装了我们免掩码变换器方法作者提出的技术解释。为此目的,我们引入了一个名为 CNeuronMAFT 的新类。
MAFT 算法基于前面讨论的 SPFormer 架构搭建。类似地,我们的实现将利用 CNeuronSPFormer 类中奠定的基础。不过,修改的规模和范围令继承该类不切实际。如是结果,我们的新对象将直接继承自基本全连接层类 CNeuronBaseOCL。新类结构如下所示。
class CNeuronMAFT : public CNeuronBaseOCL { protected: uint iWindow; uint iUnits; uint iHeads; uint iSPWindow; uint iSPUnits; uint iSPHeads; uint iWindowKey; uint iLayers; uint iLayersSP; //--- CLayer cSuperPoints; CLayer cQuery; CLayer cQPosition; CLayer cQKey; CLayer cQValue; CLayer cMHSelfAttentionOut; CLayer cSelfAttentionOut; CLayer cSPKey; CLayer cSPValue; CArrayInt cScores; CArrayInt cPositionBias; CLayer cMHCrossAttentionOut; CLayer cCrossAttentionOut; CLayer cResidual; CLayer cFeedForward; CBufferFloat cTempSP; CBufferFloat cTempQ; CBufferFloat cTempCrossK; CBufferFloat cTempCrossV; //--- virtual bool CreateBuffers(void); virtual bool CalcPositionBias(CBufferFloat *pos_q, CBufferFloat *pos_k, const int pos_bias, const int units, const int units_kv, const int dimension); virtual bool AttentionOut(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v, const int scores, CNeuronBaseOCL *out, const int pos_bias, const int units, const int heads, const int units_kv, const int heads_kv, const int dimension, const bool use_pos_bias); virtual bool AttentionInsideGradients(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v, const int scores, CNeuronBaseOCL *out, const int units, const int heads, const int units_kv, const int heads_kv, const int dimension); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMAFT(void) {}; ~CNeuronMAFT(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMAFT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
在所呈现结构中,我们观察到熟悉的可覆盖虚拟方法集,以及大量内部对象。其中一些内部组件重复了以前用到的组件,而另一些则是全新的。随着我们继续实现 CNeuronMAFT 类方法,我们将熟悉每个类方法的功能。
如前,所有内部对象都声明为静态,允许我们将类构造函数和析构函数留空。继承的组件和新声明的组件的初始化都在 Init 方法中处理。
bool CNeuronMAFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
该方法的参数包括定义正在创建的对象架构的主要常量。此处可注意到,该方法的参数完全借鉴了 CNeuronSPFormer 类的相关方法。这与我们遵循的基于继承的设计理念是一致的。不过,该方法的实际逻辑并未发生重大变化。
在方法主体中,我们首先调用父类的同名方法,该方法针对接收到的参数实现了主要控制,并初始化继承的对象。之后,我们将结果常量保存在类的内部变量之中。
iWindow = window; iUnits = units_count; iHeads = heads; iSPUnits = units_sp; iSPWindow = window_sp; iSPHeads = heads_sp; iWindowKey = window_key; iLayers = MathMax(layers, 1); iLayersSP = MathMax(layers_to_sp, 1);
下一步是初始化对象,以便生成对象的可学习查询,及其位置编码。MAFT 方法作者建议按零值初始化查询。我们也可这样做。为此,我们重置查询生成参数。
CNeuronBaseOCL *base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(iWindow * iUnits, 0, OpenCL, 1, optimization, iBatch)) return false; CBufferFloat *buf = base.getOutput(); if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite()) return false; buf = base.getWeights(); if(!buf || !buf.BufferInit(buf.Total(), 0) || !buf.BufferWrite()) return false; if(!cQuery.Add(base)) return false; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, 1, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cQuery.Add(base)) return false;
我们还添加了一个用随机值初始化可学习位置编码。
CNeuronLearnabledPE *pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, 2, OpenCL, base.Neurons(), optimization, iBatch)) return false; if(!cQuery.Add(pe)) return false;
应当说,位置编码作为单独的信息流,贯穿整个 MAFT 算法。因此,我们将它作为单独的对象提供。
if(!base || !base.Init(0, 3, OpenCL, pe.Neurons(), optimization, iBatch)) return false; if(!base.SetOutput(pe.getOutput())) return false; if(!cQPosition.Add(base)) return false;
下一阶段是主要的数据处理。在此,我们借鉴 SPFormer 方法中讲述的超点方式。
//--- Init SuperPoints int layer_id = 4; for(int r = 0; r < 4; r++) { if(iSPUnits % 2 == 0) { iSPUnits /= 2; CResidualConv *residual = new CResidualConv(); if(!residual) return false; if(!residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch)) return false; if(!cSuperPoints.Add(residual)) return false; } else { iSPUnits--; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, iBatch)) return false; if(!cSuperPoints.Add(conv)) return false; } layer_id++; }
请注意,此处提供的实现允许使用不同维度的张量进行交叉注意力。然而,这对于所提议相对位置偏差系数算法来说是不可接受的。因此,我们在可学习查询空间中添加了一个超点投影层。
CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch)) return false; if(!cSuperPoints.Add(conv)) return false; layer_id++;
我们添加了一个位置编码层。
pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch)) return false; if(!cSuperPoints.Add(pe)) return false; layer_id++;
请注意,在这一点上,我们与 MAFT 方法作者提出的原始算法略有不同。在他们的工作中,用到了基于原始坐标的点云体素化。取而代之,我们使用了完全可学习位置编码,从而允许模型学习输入序列每个元素的最优位置。
在完成源数据的初级处理工作后,我们组织一个遍历解码器内层的循环。
//--- Inside layers for(uint l = 0; l < iLayers; l++) { //--- Self-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false; layer_id++;
注意,MAFT 的作者在此处使用了经典布局:自注意力 -> 交叉注意力 -> 前馈。不过,SPFormer 方法的作者互换了 自注意力 和 交叉注意力。
首先,我们生成查询实体。然后我们添加 键 和 值。
//--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQValue.Add(conv)) return false; layer_id++;
在这种情况下,我们期待使用少量的可学习查询。因此,我们不会减少处置 键-值 的头数量,而是在每个内层生成新实体。
我们将生成的实体传递至多头注意力模块,无需使用位置偏差系数。
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch)) return false; if(!cMHSelfAttentionOut.Add(base)) return false; layer_id++;
我们增加了一个多头注意力结果的伸缩层。
//--- Self-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cSelfAttentionOut.Add(conv)) return false; layer_id++;
在 自注意力 模块的末尾,我们遵循经典的 变换器 算法,添加一个残差连接层。
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false; layer_id++;
接下来,我们构建交叉注意力模块的对象。我们从 查询 实体张量开始。
//--- Cross-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; if(!cQuery.Add(conv)) return false; layer_id++;
然后,我们为 键 和 值 实体添加张量。这一次,我们按照用户的指令来降低注意力头和交替层。
if(l % iLayersSP == 0) { //--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch)) return false; if(!cSPKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch)) return false; if(!cSPValue.Add(conv)) return false; layer_id++; }
我们添加了一个来自多头关注的结果层。
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch)) return false; if(!cMHCrossAttentionOut.Add(base)) return false; layer_id++;
然后,通过添加残差连接来伸缩它。
//--- Cross-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cCrossAttentionOut.Add(conv)) return false; layer_id++; //--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false; layer_id++;
解码器由 FeedForward 模块完成,我们还向该模块添加残差连接。
//--- Feed Forward conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; layer_id++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false; layer_id++; //--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cResidual.Add(base)) return false; layer_id++;
现在,我们只需添加 MLP 校正即可处置可学习查询的位置编码。
//--- Delta position conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(SIGMOID); if(!cQPosition.Add(conv)) return false; layer_id++; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cQPosition.Add(base)) return false; layer_id++; }
然后我们转到循环的下一次迭代,创建解码器的新内层对象。
解码器所有内层的对象初始化成功后,我们替换指向误差梯度缓冲区的指针,并返回调用程序示意成功的布尔结果。
base = cResidual[iLayers * 3 - 1]; if(!SetGradient(base.getGradient())) return false; //--- SetOpenCL(OpenCL); //--- return true; }
应当补充的是,辅助数据缓冲区的初始化已移至单独的方法 CreateBuffers,我建议您自行研究。
该类及其所有方法的完整实现均可在附件中找到。
初始化内部对象之后,我们转到 feedForward 方法构造前馈通验算法。在该方法参数中,我们接收指向源数据对象的指针。
bool CNeuronMAFT::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Superpoints CNeuronBaseOCL *superpoints = NeuronOCL; int total_sp = cSuperPoints.Total(); for(int i = 0; i < total_sp; i++) { if(!cSuperPoints[i] || !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints)) return false; superpoints = cSuperPoints[i]; }
我们在生成超点特征时立即使用生成的对象。为此,我们将用到嵌套模型 cSuperPoints。
该模型的最后一层是位置编码层。
接下来,我们配以位置编码生成可学习查询。
//--- Query CNeuronBaseOCL *inputs = NULL; for(int i = 0; i < 2; i++) { inputs = cQuery[i + 1]; if(!inputs || !inputs.FeedForward(cQuery[i])) return false; }
然后,我们创建局部变量来临时存储指向对象的指针。
CNeuronBaseOCL *query = NULL, *key = NULL, *value = NULL, *base = NULL;
我们组织一个遍历解码器内层的循环。
//--- Inside layers for(uint l = 0; l < iLayers; l++) { //--- Self-Atention query = cQuery[l * 2 + 3]; if(!query || !query.FeedForward(inputs)) return false; key = cQKey[l]; if(!key || !key.FeedForward(inputs)) return false; value = cQValue[l]; if(!value || !value.FeedForward(inputs)) return false;
在此,我们首先为所用位置编码的可学习查询组织 自注意力 模块的操作。为此,我们首先生成必要的实体,并将其传递至多头注意力模块。
if(!AttentionOut(query, key, value, cScores[l * 2], cMHSelfAttentionOut[l], -1, iUnits, iHeads, iUnits, iHeads, iWindowKey, false)) return false;
然后,我们伸缩获得的结果,并添加残差连接。
base = cSelfAttentionOut[l]; if(!base || !base.FeedForward(cMHSelfAttentionOut[l])) return false; value = cResidual[l * 3]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
作为单独的线程,我们加入位置编码。
value = cQPosition[l * 2]; if(!value || !SumAndNormilize(inputs.getOutput(), value.getOutput(),inputs.getOutput(), iWindow, false, 0, 0, 0, 1)) return false;
之后,我们转到交叉注意力模块。但首先,我们定义相对位置偏差系数。
//--- Calc Position bias if(!CalcPositionBias(value.getOutput(), ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l], iUnits, iSPUnits, iWindow)) return false;
接下来,我们据位置查询张量生成一个查询实体,同时参考位置编码。
//--- Cross-Attention query = cQuery[l * 2 + 4]; if(!query || !query.FeedForward(inputs)) return false;
至于 键 和 值 实体的操作,则充满了细微差别。首先,新张量仅在必要时生成。
key = cSPKey[l / iLayersSP]; value = cSPValue[l / iLayersSP]; if(l % iLayersSP == 0) { if(!key || !key.FeedForward(superpoints)) return false; if(!value || !value.FeedForward(cSuperPoints[total_sp - 2])) return false; }
其二,键实体是依据最后一个 cSuperPoints 层的数据生成的,其包含位置编码。为了生成 值,我们用到没有位置编码的倒数第二层。
我们将结果实体传递给多头注意力模块,无需用到位置偏差系数。
if(!AttentionOut(query, key, value, cScores[l * 2 + 1], cMHCrossAttentionOut[l], cPositionBias[l], iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true)) return false;
之后,我们伸缩获得的数据,并添加残差连接。
base = cCrossAttentionOut[l]; if(!base || !base.FeedForward(cMHCrossAttentionOut[l])) return false; value = cResidual[l * 3 + 1]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
在解码器的末尾,我们经由前馈模块传递数据,后随残差连接。
//--- Feed Forward base = cFeedForward[l * 2]; if(!base || !base.FeedForward(inputs)) return false; base = cFeedForward[l * 2 + 1]; if(!base || !base.FeedForward(cFeedForward[l * 2])) return false; value = cResidual[l * 3 + 2]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
在该阶段,我们已完成了一个解码器层的操作,但我们仍要调整可学习查询的位置编码数据。为此,我们将基于得到的数据生成位置偏差,并将其添加到现有数值之中。
//--- Delta Query position base = cQPosition[l * 2 + 1]; if(!base || !base.FeedForward(inputs)) return false; value = cQPosition[(l + 1) * 2]; query = cQPosition[l * 2]; if(!value || !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0,0,0,0.5f)) return false; }
现在我们可转去执行解码器下一个内层操作。
在成功执行解码器的所有内层操作之后,我们得到的结果,会是丰富的查询配上其细化位置的形式。我们将 2 个结果张量相加,并将它们传递至预测头。
value = cQPosition[iLayers * 2]; if(!value || !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
该方法返回一个布尔值,该值指示初始化过程的成功或失败。
据此,我们就完成了前馈通验的实现。现在我们继续开发反向传播算法,在 calcInputGradients 和 updateInputWeights 方法中实现。前者负责根据误差梯度对最终输出的贡献,在所有内部组件之间分派误差梯度。后者更新模型参数。
如您所知,梯度分派是相对于前馈通验的信息流,严格按照相反的顺序执行的。我鼓励您自行探索这些方法的实现。
该类及其所有方法的完整实现均可在附件中找到。
本文所用的模型架构,以及用来训练和与环境互动的所有程序,完全借鉴了我们以前的工作。事实上,我们针对环境状态编码器所做的唯一更改,只是修改了单个层的标识符。因此,我们不会在此详究它们。附件中还包含准备本文时所有程序类的完整代码。
3. 测试
在本文中,我们领略了 MAFT 方法,并利用 MQL5 实现了我们对所提议方式的愿景。现在,我们开始评估我们的工作成果。该模型将采用 MAFT 框架据真实历史数据上进行训练,随后测试经过训练的参与者政策。
如常,为了训练模型,我们采用 EURUSD 金融产品整个 2023 年的真实历史数据,以及 H1 时间帧。所有指标参数均按其默认值设置。
模型训练过程和相关工具,是从我们之前的文章中继承而来的。
训练后的参与者政策在 MetaTrader 5 策略测试器中依据 2024 年 1 月的历史数据进行了测试。所有其它参数保持不变。测试结果呈现如下。
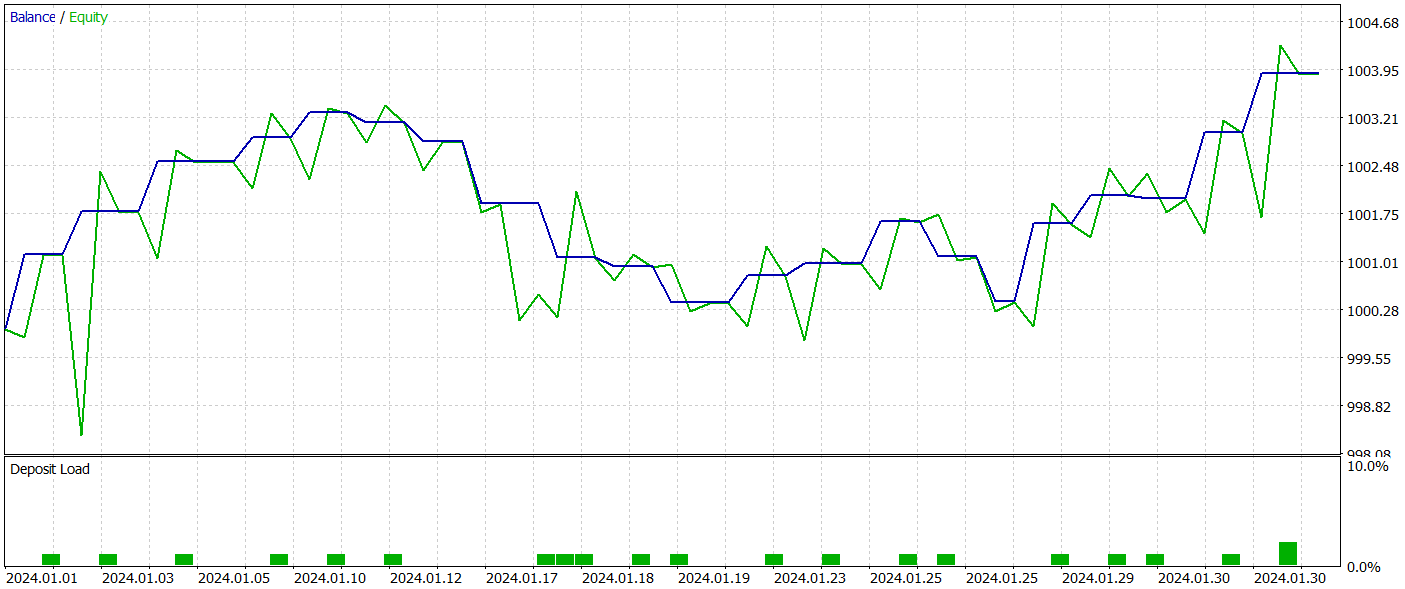
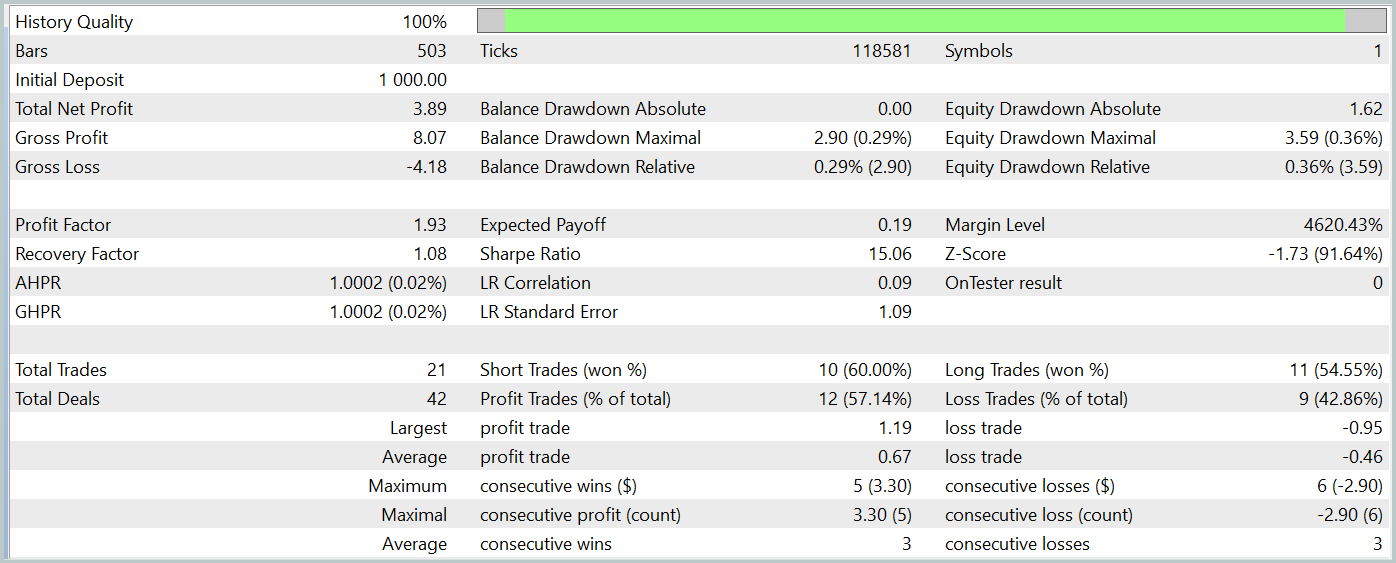
测试期间的余额图显示出上升趋势,这显然是一个积极的结果。然而,该模型在整个测试期间只执行了 21 笔交易,其中 12 笔盈利。不幸的是,有限的交易数量无法给出模型在较长时间内有效的结论性评估。
结束语
在本文中,我们讨论了 免掩码变换器(MAFT)方法及其在算法交易中的应用。与传统的 Transformer 架构不同,MAFT 通过消除数据屏蔽和加速序列处理的需求来提供更高的计算效率。
测试结果确认,MAFT 能提升预测准确性,同时还降低了模型训练时间。
参考
文章中所用程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | 智能系统 | 收集样本的 EA |
| 2 | ResearchRealORL.mq5 | 智能系统 | 利用 Real ORL方法收集样本的 EA |
| 3 | Study.mq5 | 智能系统 | 模型训练 EA |
| 4 | Test.mq5 | 智能系统 | 模型测试 EA |
| 5 | Trajectory.mqh | 类库 | 系统状态描述结构 |
| 6 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 7 | NeuroNet.cl | 函数库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/15973
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 从基础到中级:FOR 语句
从基础到中级:FOR 语句
 价格行为分析工具包开发(第一部分):图表投影仪
价格行为分析工具包开发(第一部分):图表投影仪
 Connexus请求解析(第六部分):创建HTTP请求与响应
Connexus请求解析(第六部分):创建HTTP请求与响应
 从基础到中级:按值传递还是按引用传递
从基础到中级:按值传递还是按引用传递
你好,德米特里、
看来您的压缩文件制作有误。 我本以为您的压缩包里会列出源代码,但压缩包里却只有这些。 看来列出的每个目录都包含您在不同文章中使用过的文件。 您能否提供每个目录的说明,或者最好在每个目录后附上相应的文章编号。
谢谢
科达角
你好,德米特里、
看来您的压缩文件制作有误。 我本以为您的压缩包里会列出源代码,但压缩包里却只有这些。 看来列出的每个目录都包含您在不同文章中使用过的文件。 您能否提供每个目录的说明,或者最好在每个目录后附上相应的文章编号。
谢谢
科达角
你好,CapeCoddah、
压缩文件包含所有系列的文件。保存在 "MQL5\Experts\NeuroNet_DNG\NeuroNet.cl "中的 OpenCL 程序。您可以在 "MQL5\Experts\NeuroNet_DNG\NeuroNet.mqh "中找到包含所有类的库。本文引用的模型和专家位于目录 "MQL5\Experts\MAFT\" 中。
Regards,
Dmitriy.
你好,科达角
压缩文件包含所有系列的文件。保存在 "MQL5\Experts\NeuroNet_DNG\NeuroNet.cl "中的 OpenCL 程序。您可以在 "MQL5\Experts\NeuroNet_DNG\NeuroNet.mqh "中找到包含所有类的库。本文引用的模型和专家位于目录 "MQL5\Experts\MAFT\" 中。
Regards,
Dmitriy.
你好,德米特里、
感谢您的及时回复。 我明白您的意思,但我认为您误解了我的意思。 我如何将子目录名称与相应的文章关联起来,可以通过名称或文章编号来搜索文章。
谢谢
科达角
你好,德米特里、
感谢您的及时回复。 我明白您的意思,但我认为您误解了我的意思。 我如何将子目录名称与相应的文章关联起来,可以通过名称或文章编号来搜索文章。
谢谢
科达角
框架名称