Vorhersage von Wechselkursen mit klassischen Methoden des maschinellen Lernens: Logit- und Probit-Modelle

Einführung

Finanzmarktforscher stehen immer vor der schwierigen Aufgabe, ein mathematisches Modell auszuwählen, um das zukünftige Verhalten von Handelsinstrumenten vorherzusagen. Bis heute wurde eine große Anzahl solcher Modelle entwickelt. Es stellt sich also die Frage, wie man in dieser Vielfalt von Methoden und Ansätzen nicht untergeht, wo man anfängt und auf welche Modelle man sich am besten konzentriert, vor allem, wenn man gerade erst beginnt, Prognosen mit Hilfe von Modellen des maschinellen Lernens zu erstellen. Wenn wir versuchen, die Aufgabe der Vorhersage auf eine einfache Antwort auf die Frage zu reduzieren: „Wird der morgige Schlusskurs höher sein als der von heute?“, dann wären binäre Klassifizierungsmodelle die logische Wahl. Einige der einfachsten und am weitesten verbreiteten Methoden sind die Logit- und Probit-Regression. Diese Modelle gehören zu der am weitesten verbreiteten Form des maschinellen Lernens, dem so genannten überwachten Lernen.

Die Aufgabe des überwachten Lernens wiederum besteht darin, unserem Modell beizubringen, eine Reihe von Eingaben {x} (Prädiktoren oder Eigenschaften) in eine Reihe von Ausgaben {y} (Ziele oder Kennzeichnungen) umzuwandeln. Hier werden wir nur zwei Marktbedingungen vorhersagen - den Anstieg oder Fall des Preises des Währungspaares. Daher gibt es nur zwei Klassen von Kennzeichnungen y ∊ {1,0}. Preismuster, d. h. standardisierte Preiserhöhungen mit einer gewissen Verzögerung, werden als Prädiktoren dienen. Diese Daten bilden unseren {x, y} Trainingssatz, der zur Schätzung der Parameter unserer Modelle verwendet wird. Das auf trainierten Klassifikatoren basierende Vorhersagemodell ist als LogitExpert EA implementiert.

Binäre Logit- und Probit-Regression

Lassen Sie uns kurz auf den theoretischen Teil eingehen. Das einfachste Modell einer binären Wahl ist ein lineares Wahrscheinlichkeitsmodell, bei dem die Wahrscheinlichkeit eines erfolgreichen Ereignisses von P(yn=1|xn) eine lineare Funktion der erklärenden Variablen ist:

P(yn=1|xn) = w0*1 + w1x1 + w2x2 + … + wkxk

Leider hat ein solches Modell einen schwerwiegenden Nachteil - der vorhergesagte Wert kann größer als eins oder kleiner als null sein, und das wiederum erlaubt es nicht, den vorhergesagten Wert als Wahrscheinlichkeit zu interpretieren. Daher wurde zur Lösung dieses Problems vorgeschlagen, bekannte Wahrscheinlichkeitsverteilungsfunktionen zu verwenden, in die die Werte der linearen Funktion eingesetzt werden.

Das Probit-Modell basiert auf dem Gesetz der Standardnormalverteilung N(0,1):

P(yn=1|xn) = F(xnw)=μn

• n – niedriger Index, der die Nummer der Beobachtung (Beispiel) angibt,

• yn – Klassenkennzeichnung,

• F( ) – Normalverteilungsfunktion (Aktivierungsfunktion),

• xn – Eigenschaftssvektor,

• w – Vektor der Modellparameter,

• xnw – Logit oder Voraktivierung (stellt das Skalarprodukt aus dem Eigenschaftssvektor und dem Parametervektor dar)

xnw = w0*1 + w1x1 + w2x2 + … + wkxk

Das Logit-Modell wiederum basiert auf dem logistischen Gesetz der Wahrscheinlichkeitsverteilung:

                                                      P(yn=1|xn) = L(xnw) = exp(xnw)/(1 + exp(xnw)) = μn

Die Verteilungsfunktionen der logistischen Verteilung und der Normalverteilung liegen recht nahe beieinander und sind im Intervall [-1,2;1,2] fast identisch. Daher führen Logit- und Probit-Modelle häufig zu ähnlichen Ergebnissen, es sei denn, die Wahrscheinlichkeit liegt nahe bei Null oder Eins. Wenn diese Modelle also durch einen Eigenschaftssvektor ersetzt werden, können wir die Wahrscheinlichkeiten der Klassenbezeichnungen und damit die Wahrscheinlichkeit der zukünftigen Kursbewegungsrichtung berechnen.

Vorbereitung der Daten

Bevor wir die Parameter des Modells schätzen, müssen wir die Eigenschaften definieren, sie dann standardisieren und sie in der richtigen Form für die Funktion darstellen, die die optimalen Parameter (im Sinne der Minimierung der Verlustfunktion) findet. Die zuständige Funktion ist GetDataset:

• InpCount_ – legt die Anzahl der Beispiele für das Training fest

• lag_ – Anzahl der analysierten Eigenschaften (Preiserhöhungen mit Verzögerung)

• string X – Währungspaar, für das die Eigenschaften berechnet werden

• string y – Währungspaar, für das die Kennzeichnungen berechnet werden

• int start – Nummer eines Balkens, ab dem wir mit den Trainingsbeispielen beginnen

Als anschauliches Beispiel werden wir die Verzögerungsschritte des Preises eines Währungspaares als Zeichen verwenden. Wenn wir zum Beispiel das Funktionsargument lag_ = 4 setzen, dann sind die Features x{return-4,return-3,return-2,return-1} und wir haben genau (InpCount_- lag_) Beispiele für das Training.

//+------------------------------------------------------------------+
//|Get data for analysis: features and corresponding labels          |
//+------------------------------------------------------------------+
bool GetDataset(int InpCount_,int lag_,int start,matrix &Input_X,vector & Target_y,string X,string y)
  {

   matrix rates;
   matrix target;
   target.CopyRates(y, PERIOD_CURRENT, COPY_RATES_OHLC, start+1, InpCount_);
   rates.CopyRates(X, PERIOD_CURRENT, COPY_RATES_OHLC, start+2, InpCount_-1);
   rates = rates.Transpose();
   target = target.Transpose();
   int Class_ [];
   ArrayResize(Class_,InpCount_);
   for(int i=0; i<InpCount_; i++)
     {
      if(target[i,3] >  target[i,0])
         Class_[i] = 1;
      else
         Class_[i] = 0;
     }

   vector label=vector::Zeros(InpCount_-lag_);
   for(int i=0; i<InpCount_-lag_; i++)
     {
      label[i] = Class_[i+lag_]; // class label
     }

   matrix returns=matrix::Zeros(InpCount_-lag_, lag_);
   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] =rates[i+j,3] - rates[i+j,0]  ; // Input Data
        }
     }

   vector cols_mean=returns.Mean(0);
   vector cols_std=returns.Std(0);

   mean_ = cols_mean[lag_-1];
   std_ = cols_std[lag_-1];

   for(int j=0; j<lag_; j++)
     {
      for(int i=0; i<InpCount_-lag_; i++)
        {
         returns[i,j] = (returns[i,j] - cols_mean[lag_-1])/cols_std[lag_-1];
        }
     }
   Input_X = returns;
   Target_y = label;

   return true;
  }

Am Ausgang erhalten wir die Eigenschaftssmatrix Input_X und den Kennzeichnungsvektor Target_y. Nachdem der Trainingssatz gebildet wurde, gehen wir zur Schätzung der Parameter über.

Schätzung der Modellparameter

Meistens werden die Parameterschätzungen mit der Maximum-Likelihood-Methode ermittelt. Im binären Fall gehen die Logit- und Probit-Modelle davon aus, dass die abhängige Variable y eine Bernoulli-Verteilung hat. Wenn ja, dann ist die logarithmische Wahrscheinlichkeitsfunktion gleich:

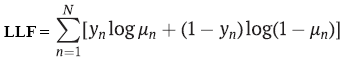
• yn – Kennzeichnung der Klasse,

• μn – Wahrscheinlichkeit der Vorhersage einer Klasse mittels Logit- oder Probit-Regression,

• N – Anzahl der Trainingsbeispiele

Um die Parameter zu schätzen, müssen wir das Maximum dieser Funktion finden, aber da es beim maschinellen Lernen üblich ist, die Verlustfunktion zu minimieren, und alle Optimierer hauptsächlich so konfiguriert sind, dass sie die Zielfunktionen minimieren, wird der Likelihood-Funktion einfach ein Minuszeichen hinzugefügt. Das Ergebnis ist die so genannte negative Log-Likelihood (NLL). Wir werden diese Verlustfunktion mit Hilfe devon L-BFGS, die Quasi-Newtonschen Optimierungsmethode zweiter Ordnung, minimieren, die in der Bibliothek Alglib implementiert ist. Diese numerische Methode wird in der Regel zur Ermittlung der Parameter von Logit- und Probit-Modellen verwendet. Eine weitere beliebte Optimierungsmethode ist die Methode der iterativen kleinsten Quadrate (IRLS).

//+------------------------------------------------------------------+
//| Derived class from CNDimensional_Func                            |
//+------------------------------------------------------------------+
class CNDimensional_Logit : public CNDimensional_Func
  {
public:
                     CNDimensional_Logit(void) {}
                    ~CNDimensional_Logit(void) {}
   virtual void      Func(CRowDouble &w,double &func,CObject &obj);
  };

//+------------------------------------------------------------------+
//| Objective Function: Logit Negative loglikelihood                 |
//+------------------------------------------------------------------+
void CNDimensional_Logit::Func(CRowDouble &w,double &func,CObject &obj)
  {

   double LLF[],probit[],probitact[];
   vector logitact;
   ArrayResize(LLF,Rows_);
   ArrayResize(probit,Rows_);
   vector params=vector::Zeros(Cols_);

   for(int i = 0; i<Cols_; i++)
     {
      params[i] =  w[i]; // vector of parameters
     }

   vector logit=vector::Zeros(Rows_);
   logit = Input_X_gl.MatMul(params);

   for(int i=0; i <Rows_; i++)
     {
      probit[i] = logit[i];
     }

   if(probit_)
      MathCumulativeDistributionNormal(probit,0,1,probitact); // Probit activation
   else
      logit.Activation(logitact,AF_SIGMOID); // Logit activation

//--------------------to avoid NAN error when calculating logarithm ------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(probitact[i]==1)
            probitact[i]= 0.999;
         if(probitact[i]==0)
            probitact[i]= 0.001;
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {
         if(logitact[i]==1)
            logitact[i]= 0.999;
         if(logitact[i]==0)
            logitact[i]= 0.001;
        }
     }
//-------------------------------------------------------------------------------------------------
   double L2_reg;
   if(L2_)
      L2_reg = 0.5 * params.Dot(params); //  L2_regularization
   else
      L2_reg =0;

//------------------ calculate loss function-------------------------------------------------------------
   if(probit_)
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(probitact[i]) + (1-target_y_gl[i])*MathLog(1-probitact[i]) ;

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }
   else
     {
      for(int i = 0; i<Rows_; i++)
        {

         LLF[i]=target_y_gl[i]*MathLog(logitact[i]) + (1-target_y_gl[i])*MathLog(1-logitact[i]);

         if(!MathIsValidNumber(LLF[i]))
           {
            break;
           }
        }
     }

   func = -MathSum(LLF) + L2_reg/(Rows_*C_); // Negative Loglikelihood + L2_regularization
//------------------------------------------------------------------------------------------------------
   func_ = func;
  }

Die Berechnung von Parameterschätzungen allein reicht jedoch nicht aus; wir möchten auch die Standardfehler dieser Schätzungen erhalten, um zu verstehen, wie signifikant unsere Eigenschaften sind.

Die beliebte Bibliothek für maschinelles Lernen scikit-learn beispielsweise berechnet diese Informationen aus irgendeinem Grund nicht für das Logit-Modell. Ich habe die Berechnung von Standardfehlern sowohl für das Logit- als auch für das Probit-Modell implementiert, sodass Sie jetzt sehen können, ob bestimmte Eigenschaften einen statistisch signifikanten Einfluss auf die Prognose haben oder nicht. Dies ist einer der Gründe, warum ich es vorziehe, den Code für das Logit-Modell selbst in MQL zu schreiben, anstatt ONNX zur Konvertierung fertiger Modelle aus gängigen Machine-Learning-Paketen zu verwenden. Ein weiterer Grund ist, dass ich ein dynamisches Modell benötige, das die Klassifizierungsparameter bei jedem Balken oder in einer bestimmten Häufigkeit neu optimieren kann.

Aber kommen wir zurück zu unserer Verlustfunktion. Es sollte gesagt werden, dass es einer gewissen Überarbeitung bedarf. Der springende Punkt ist, dass unsere Klassifikatoren, genau wie fortgeschrittene neuronale Netzwerkmethoden, anfällig für eine Überanpassung sind. Dies äußert sich in abnorm großen Werten der Parameterschätzungen, und um dieses negative Phänomen zu verhindern, brauchen wir eine Methode, die solche Schätzungen begrenzt. Diese Methode wird als L2-Regularisierung bezeichnet:

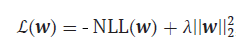
• λ = 1/С , С = (0,1]

Hier fügen wir einfach das Quadrat der Norm des Parametervektors multipliziert mit dem Hyperparameter λ lambda zu unserer bestehenden Verlustfunktion hinzu. Je größer Lambda ist, desto stärker werden die Parameter für große Werte bestraft und desto stärker ist die Regularisierung.

Die Funktion, die für die Auswertung der Klassifikatorparameter zuständig ist, heißt FitLogitRegression:

• bool L2 = false – standardmäßig ist die L2-Regularisierung deaktiviert,
• double C=1.0 – Regularisierungsstärke Hyperparameter, je kleiner er ist, desto mehr werden die Werte der optimierten Parameter begrenzt,
• bool probit = false – das Logit-Modell ist standardmäßig aktiviert,
• double alpha – Alpha-Signifikanzniveau Chi-Quadrat-Verteilung der LR-Statistik

Diese Funktion nimmt eine Eigenschaftssmatrix als Argument und fügt ihr eine so genannte bedingte oder Dummy-Variable hinzu, die in allen Beobachtungen den Wert eins annimmt. Dies ist notwendig, damit wir den Parameter w0(bias) in unserem Modell schätzen können. Zusätzlich zu den Parameterschätzungen berechnet diese Funktion auch deren Kovarianzmatrizen zur Berechnung der Standardfehler.

//+------------------------------------------------------------------+
//| Finding the optimal parameters for the Logit or Probit model     |
//+------------------------------------------------------------------+
vector FitLogitRegression(matrix &input_X, vector &target_y,bool L2 = false, double C=1.0,bool probit = false,double alpha = 0.05)
  {
   L2_=L2;
   probit_ = probit;
   C_ = C;
   double              w[],s[];
   CObject             obj;
   CNDimensional_Logit ffunc;
   CNDimensional_Rep   frep;
   ulong Rows = input_X.Rows();
   ulong Cols = input_X.Cols();
   matrix One=matrix::Ones(int(Rows),int(Cols+1));
   for(int i=0;i<int(Cols); i++)
     {
      One.Col(input_X.Col(i),i+1);  // design matrix
     }
   input_X = One;
   Cols = input_X.Cols();
   Rows_ = int(Rows);
   Cols_ = int(Cols);
   Input_X_gl = input_X;
   target_y_gl = target_y;
   ArrayResize(w,int(Cols));
   ArrayResize(s,int(Cols));
//--- initialization
   ArrayInitialize(w,0.0);
   ArrayInitialize(s,1.0);
//--- optimization stop conditions
   double epsg=0.000001;
   double epsf=0.000001;
   double epsx=0.000001;
   double diffstep=0.000001;
   int maxits=0;
//------------------------------
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CAlglib::MinLBFGSCreateF(1,w,diffstep,state);
   CAlglib::MinLBFGSSetCond(state,epsg,epsf,epsx,maxits);
   CAlglib::MinLBFGSSetScale(state,s);
   CAlglib::MinLBFGSOptimize(state,ffunc,frep,0,obj);
   CAlglib::MinLBFGSResults(state,w,rep);
   Print("TerminationType ="," ",rep.GetTerminationType());
   Print("IterationsCount ="," ",rep.GetIterationsCount());

   vector parameters=vector::Zeros(Cols);
   for(int i = 0; i<int(Cols); i++)
     {
      parameters[i]= w[i];
     }
   Print("Parameters = "," ",parameters);

//-------Likelihood Ratio Test LR-----------------------------------------
   double S = target_y.Sum();   // number of "success"
   ulong All = target_y.Size(); // all data
   double L0 = S*MathLog(S/All) + (All-S)*MathLog((All-S)/All); // Log-likelihood for the trivial model
 //  Print("L0 = ",L0);
 //  Print("LLF = ",func_);
   double LR;
   LR = 2*(-func_ - L0); // Likelihood Ratio Test LR
   int err;
   double Chi2 = MathQuantileChiSquare(1-alpha,Cols-1,err); // If H0 true ---> Chi2Distribution(alpha,v)
   Print("LR ",LR," ","Chi2 = ",Chi2);
//--------------------------------------------------------------------------------
//-------------- calculate if model significant or not
   if(LR > Chi2)
      ModelSignificant = true;
   else
      ModelSignificant = false;
//----------------------------------------------------

//-------------Estimation of the covariance matrix of parameters for the Probit model------------
   vector logit = input_X.MatMul(parameters);  //
   vector activation;
   logit.Activation(activation,AF_SIGMOID); // Logit activation
   double probit_SE[],probitact[];
   ArrayResize(probit_SE,Rows_);

   for(int i=0; i <Rows_; i++)
     {
      probit_SE[i] = logit[i];
     }

   if(probit_)
     {
      ulong size_parameters = parameters.Size();
      matrix CovProbit=matrix::Zeros(int(size_parameters),int(size_parameters));
      int err;
      vector a_=vector::Zeros(Rows_);
      vector b=vector::Zeros(Rows_);
      vector c=vector::Zeros(Rows_);
      vector xt=vector::Zeros(int(size_parameters));

      for(int i = 0; i<Rows_; i++)
        {
         a_[i] = MathPow((MathProbabilityDensityNormal(probit_SE[i],0,1,err)),2);
         b[i] = MathCumulativeDistributionNormal(probit_SE[i],0,1,err);
         c[i] = a_[i]/(b[i]*(1-b[i]));
         xt = input_X.Row(i);
         CovProbit = CovProbit + c[i]*xt.Outer(xt);
        }
      CovProbit = CovProbit.Inv();
      vector SE;
      SE = CovProbit.Diag(0);
      SE = MathSqrt(SE);  // standard errors of parameters
      Print("Probit_SE = ", SE);
     }
   else
     {
      //-------------Estimation of the covariance matrix of parameters for the Logit model------------
      vector v = vector::Zeros(Rows_);

      for(int i = 0; i<Rows_; i++)
        {
         v[i] = activation[i]*(1-activation[i]);
        }

      matrix R,Hesse,X,a,CovLogit;
      R.Diag(v,0);
      X = input_X.Transpose();
      a = X.MatMul(R);
      Hesse = a.MatMul(input_X);
      CovLogit = Hesse.Inv();
      vector SE;
      SE = CovLogit.Diag(0);
      SE = MathSqrt(SE); // standard errors of parameters
      Print("Logit_SE = ", SE);
      //-----------------------------------------------
     }
   return parameters;
  }

Sobald die Parameter gefunden und ihre Kovarianzmatrizen berechnet sind, können wir zur Vorhersage übergehen.

Vorhersage

Die Funktion, die für die Vorhersage von Klassenkennzeichnungen und damit von Kauf- oder Verkaufssignalen verantwortlich ist, heißt Trade_PredictedTarget. Es erhält die zu optimierenden Parameter als Eingaben und gibt die vorhergesagte Klassenkennzeichnung aus. Danach bildet der EA LogitExpert die Regeln für die Eröffnung von Positionen. Sie sind ganz einfach. Wenn wir ein Kaufsignal erhalten (Signal = 1), eröffnen wir eine Kaufposition. Wenn bereits eine Kaufposition besteht, halten wir sie weiterhin. Wenn ein Verkaufssignal empfangen wird, wird die Kaufposition geschlossen und sofort eine Verkaufsposition eröffnet.

Der eigentliche Code des EAS LogitExpert

//+------------------------------------------------------------------+
//|                                                  LogitExpert.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include <\LogitReg.mqh>
#include <Trade\Trade.mqh>
#include <Trade\PositionInfo.mqh>
CTrade m_trade;
CPositionInfo m_position;

sinput string   symbol_X       = "EURUSD";    // Input symbol
sinput string   symbol_y       = "EURUSD";    // Target symbol
input bool     _probit_        = false;       // Probit model
input  int      InpCount       = 20;          // Depth of history
input  int     _lag_           = 4;           // Number of features
input bool     _L2_            = false;       // L2_regularization
input double   _C_             = 1;           // C(0,1) inverse of regularization strength
input double   alpha_          = 0.05;        // Significance level Alpha (0,1)
input int      reoptimize_step = 2;           // Reoptimize step

#define MAGIC_NUMBER 23092024

int prev_bars = 0;
MqlTick ticks;
double min_lot;
vector params_;
matrix _Input_X;
vector _Target_y;
static int count_ = 0;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   m_trade.SetExpertMagicNumber(MAGIC_NUMBER);
   m_trade.SetTypeFillingBySymbol(Symbol());
   m_trade.SetMarginMode();
   min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Print(__FUNCTION__," Deinitialization reason code = ",reason);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(!isnewBar(PERIOD_CURRENT))
      return;

   double step;
   step = count_ % reoptimize_step;
//------------------------------------Train Dataset-------------------------------------------------
   int start = 0;
   if(step == 0)
     {
      GetDataset(InpCount,_lag_,start,_Input_X,_Target_y,symbol_X,symbol_y);
      params_ = FitLogitRegression(_Input_X,_Target_y,_L2_,_C_,_probit_,alpha_);
     }
   count_ = count_+1;
//--------------------------------------------------------------------------------------------------

//--- Get trade signal
   int signal = Trade_PredictedTarget(params_,start,_lag_,InpCount,symbol_X);
   Comment("Trade signal: ",signal,"  ","ModelSignificant: ",ModelSignificant);  
//---------------------------------------------

//--- Open trades based on Signals
   SymbolInfoTick(Symbol(), ticks);
   if(signal==1)
     {
      if(!PosExists(POSITION_TYPE_BUY) && ModelSignificant)
        {
         m_trade.Buy(min_lot,Symbol(), ticks.ask);
         PosClose(POSITION_TYPE_SELL);
        }
      else
        {
         PosClose(POSITION_TYPE_SELL);
        }
     }
   else
     {
      if(!PosExists(POSITION_TYPE_SELL) && ModelSignificant)
        {
         m_trade.Sell(min_lot,Symbol(), ticks.bid);
         PosClose(POSITION_TYPE_BUY);
        }
      else
        {
         PosClose(POSITION_TYPE_BUY);
        }
     }
  }
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//|   Function tracks the occurrence of a new bar event              |
//+------------------------------------------------------------------+
bool isnewBar(ENUM_TIMEFRAMES TF)
  {
   if(prev_bars == 0)
      prev_bars = Bars(Symbol(), TF);

   if(prev_bars != Bars(Symbol(), TF))
     {
      prev_bars = Bars(Symbol(), TF);
      return true;
     }

   return false;
  }

//+------------------------------------------------------------------+
//|Function determines whether there is an open buy or sell position |
//+------------------------------------------------------------------+
bool PosExists(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            return true;

   return false;
  }
//+------------------------------------------------------------------+
//|The function closes a long or short trade                         |
//+------------------------------------------------------------------+
void PosClose(ENUM_POSITION_TYPE type)
  {
   for(int i=PositionsTotal()-1; i>=0; i--)
      if(m_position.SelectByIndex(i))
         if(m_position.Symbol()==Symbol() && m_position.Magic() == MAGIC_NUMBER && m_position.PositionType()==type)
            if(!m_trade.PositionClose(m_position.Ticket()))
               printf("Failed to close position %d Err=%s",m_position.Ticket(),m_trade.ResultRetcodeDescription());
  }

Was unterscheidet diesen EA von einer Reihe anderer Ansätze? Erstens ermöglicht es eine erneute Optimierung der Klassifikatorparameter in jedem (reoptimize_step) Balken. Zweitens werden nicht nur die Parameter des Modells geschätzt, sondern auch die Standardfehler dieser Schätzungen berücksichtigt, was oft übersehen wird. Es reicht nicht aus, die „optimalen“ Parameter für eine Probe zu finden. Außerdem muss geprüft werden, wie aussagekräftig diese Parameter oder das Modell als Ganzes sind. Denn wenn die Parameter nicht signifikant sind, wäre es logischer, ein solches Handelssignal zu ignorieren.

Daher umfasst dieser EA auch ein Verfahren zur Prüfung der Modellhypothese auf Signifikanz. In diesem Fall besagt die Nullhypothese, dass alle Modellparameter gleich Null sind (H0:w1=0,w2=0,w3=0,..., wk=0), während die alternative H1-Hypothese besagt, dass einige Parameter nicht gleich Null sind und das Modell daher für die Vorhersage nützlich ist. Um eine solche Hypothese zu testen, wird das Likelihood-Ratio-Kriterium (LR) verwendet, das den Unterschied zwischen dem angenommenen und dem trivialen Modell bewertet:

LR = 2(LLF – LLF0)

• LLF – der gefundene Wert des Logarithmus der Likelihood-Funktion,

• LLF0 – der Likelihood-Logarithmus unter der Nullhypothese, d. h. für das triviale Modell

p0 = ∑(yn =1)/N – Erfolgsquote der Stichprobe,

LLF0 = N(p0*Ln(p0) + (1- p0)*Ln(1 – p0))

Je größer der Unterschied ist, desto besser ist das vollständige Modell im Vergleich zum trivialen Modell. Wenn die Nullhypothese erfüllt ist, hat die LR-Statistik eine Chi-Quadrat-Verteilung mit v Freiheitsgraden (v ist gleich der Anzahl der Eigenschaften). Wenn der berechnete Wert der LR-Statistik in den kritischen Bereich fällt, d.h. LR > X²crit (alpha; v=lag_), dann wird die H0-Hypothese abgelehnt, und somit wird das Handelssignal nicht ignoriert und eine Handelsposition wird eröffnet.

Eines der möglichen Szenarien. GBPUSD, Täglich

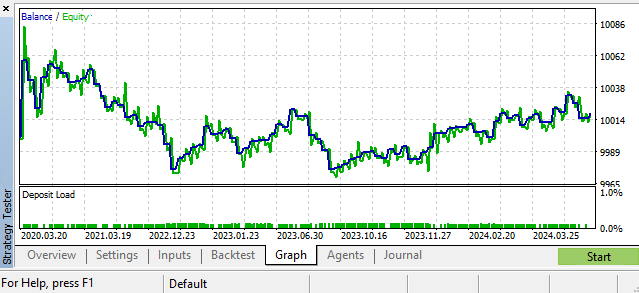
Hyperparameter

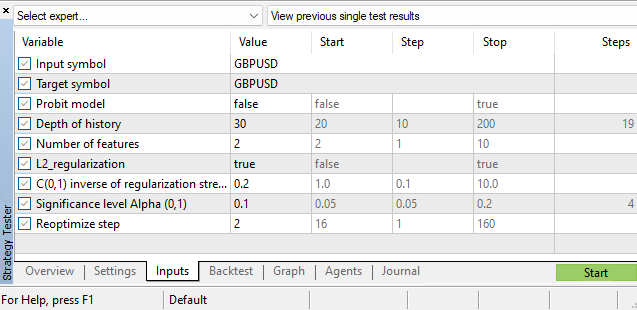
Neben der Bewertung der Parameter der Klassifizierungsmodelle selbst haben wir auch eine große Anzahl von Hyperparametern:

• Umfang der Geschichte
• Die Anzahl der Features,
• Alpha-Signifikanzniveau
• Re-Optimierungsschritt

Die Hyperparameter werden im MetaTrader 5 Strategie-Tester ausgewählt. Eine der Aufgaben, die die Leistung des EA verbessern können, besteht darin, eine Funktion für die Abhängigkeit des Parameters für die Tiefe der Historie vom aktuellen Marktzustand zu erstellen, d. h. ihn auf die gleiche Weise dynamisch zu machen, wie wir es mit den Parametern der Logit- und Probit-Modelle getan haben. Aber das ist eine andere Geschichte. Einen Hinweis finden Sie in meinem Artikel „Kolmogorov-Smirnov-Test bei zwei Stichproben als Indikator für die Nicht-Stationarität von Zeitreihen“, der sich mit der Konstruktion eines Störungsindikators befasst.

Schlussfolgerung

In diesem Artikel haben wir uns mit Regressionsmodellen mit binären Leistungsindikatoren befasst, gelernt, wie man die Parameter dieser Modelle auswertet, und auch den LogitExpert Trading EA zum Testen und Einrichten dieser Modelle implementiert. Sein einzigartiges Eigenschafts besteht darin, dass er es uns ermöglicht, die Parameter des Klassifikators auf der Grundlage der neuesten und relevantesten Daten im laufenden Betrieb neu zu trainieren.

Besonderes Augenmerk wurde auf die Schätzung der Standardfehler der Parameter gelegt, was die Schätzung von Kovarianzmatrizen für Logit- und Probit-Modelle erforderte.

Das Likelihood-Ratio-Kriterium wird verwendet, um die Signifikanz der Gleichung des Klassifizierungsmodells als Ganzes zu testen. Diese Statistik wird verwendet, um statistisch unzuverlässige Handelssignale auszusortieren.