MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 35): Support-Vektor-Regression

Einführung

Support Vector Regression (SVR) ist eine Form der Regression, die von Support Vector Machinen abgeleitet ist. SVR verwendet im Kern Kernel-Methoden, um Eingabedaten in höherdimensionalen Räumen abzubilden, wodurch komplexere Beziehungen erfasst werden können, was im Gegensatz zur Dimensionalitätsreduktion steht. In diesem Artikel untersuchen wir jedoch ausschließlich die Rolle der Verlustfunktion bei der Verwendung mit einem mehrschichtigen Perzeptron. Eine verwandte, aber andere Form der Regression, die wir in einem früheren Artikel behandelt haben, ist die Gaußsche Prozessregression (GPR). Vielleicht ist es daher wichtig, zunächst einmal zwischen beiden zu unterscheiden.

Unterschiede zwischen SVR und GPR

Um die Unterschiede zwischen diesen beiden zu verdeutlichen, wollen wir uns vom Machine-Learning-Lingo lösen und anhand von Fallbeispielen aus dem Alltag zeigen, warum beide wichtig sind. Stellen Sie sich also ein Szenario vor, in dem Sie ein Start-up-Unternehmen leiten, das ein sehr gesundes, zuckerarmes Eis entwickelt hat, das in Ihrer Heimatstadt eine große Nachfrage hat. Da Sie noch ganz am Anfang stehen und das Eis nur in Ihrer Heimatstadt verkauft haben, führen Sie den größten Teil der Produktion noch manuell durch. Sie müssen daher damit beginnen, Ihre Produktivität zu steigern, da dies neben der Kostenkontrolle auch Vorteile wie Qualitätskontrolle und die Einführung bestimmter Produktionsstandards mit sich bringt.

Eine solche Expansion würde Kapital erfordern, das Sie auf institutionellem Wege nicht aufnehmen können, weil Ihnen die notwendigen Sicherheiten (oder die Mittel) fehlen, um dies bei den Banken durchzusetzen; oder Sie könnten eine Partnerschaft mit einer großen, etablierten Eismarke eingehen, doch die Angestellten großer, etablierter Marken sind oft Bürokraten und werden ablehnen, egal was sie von Ihrem Produkt halten.

Es bleibt Ihnen also nur die Möglichkeit, Kapital über einen privaten, halbformellen Weg zu beschaffen, und zwar unter dem Vorbehalt, dass Sie Ihr Produkt skalieren oder erweitern müssen. Wenn Sie jedoch außerhalb Ihrer Heimatstadt expandieren, welche Kunden werden sich Ihr Produkt im Vergleich zu den etablierten Marken ansehen oder sogar in Betracht ziehen? Da es sich um Neuland handelt, können Sie nicht so vorgehen wie in Ihrer Heimatstadt. Dies wirft die Frage auf, die Sie in Ihrem anfänglichen Bestreben, die Nachfrage zu befriedigen, vielleicht übersehen haben: Welches ist Ihr primäres Kundensegment?

Bei der Kundensegmentierung, einem Geschäftsaspekt, den einige vielleicht ignorieren, gibt es verschiedene Arten. Dazu gehören (aber nicht nur) Segmente nach Postleitzahl (oder Adresse), Segmente nach Alter, Bildungsniveau, Beruf und Einkommensniveau; ein weiteres „neues“ und dank der sozialen Medien wachsendes Segment könnte das Segment der Lebensstil- und Interessengruppen sein. Indem wir die Verkaufsdaten um diese Segmente erweitern, können wir einige interessante Datensätze erstellen, die, wenn sie auch über unseren Heimatort hinaus gesammelt werden, einen Einblick in die Geschehnisse außerhalb unseres Hauptstandortes geben können.

Die Gaußsche Prozessregression, die in einem früheren Artikel vorgestellt wurde, liefert nicht nur eine Mittelwertprojektion, sondern ordnet diesem Mittelwert auch einen indikativen Bereich zusammen mit einem Vertrauensniveau zu. Dies bedeutet in der Regel, dass sie für die Erstellung von Prognosen in Situationen geeignet ist, in denen die Nachfrage nach einem Produkt stark von externen Faktoren beeinflusst wird (nicht konsistent ist) und es sich daher um ein Luxus- oder teures Produkt handelt, um die unbeständige Nachfrage auszugleichen. Wenn es sich nicht um ein Luxusprodukt handelt, könnte es stark saisonabhängig sein oder es könnte sich um ein Nischenprodukt mit einem hohen Preispunkt und schwankender Nachfrage handeln. Das würde bedeuten, dass unser Eis einen höheren Preis haben müsste als die Konkurrenz, um als Nischen-/Luxusprodukt für die Verwendung mit GPR geeignet zu sein.

Darüber hinaus stellen die Art des Produkts und die Kundensegmentierung eine Reihe von Faktoren dar, die bei der Auswahl eines Datensatzes für die Prognose der künftigen Nachfrage sorgfältig zu berücksichtigen sind, wie in der nachstehenden Tabelle dargestellt.

Segmentierung Typ	Am besten mit SVR	Am besten mit GPR
Postleitzahl	Alltägliche Konsumgüter	Nicht ideal, wenn nicht mit anderen dynamischen Daten kombiniert
Alter	Bekleidung, Konsumgüter, Lehrmittel	Nicht ideal, wenn nicht mit anderen dynamischen Daten kombiniert
Bildungsstand	Bildungsprodukte, technische Produkte	Nicht ideal, es sei denn, es sind komplexe Faktoren im Spiel
Einkommensniveau	Basisprodukte auf stabilen Märkten	Luxusgüter, High-End-Elektronik, Premiumartikel
Beruf	Produkte in Verbindung mit stabilen Arbeitsplätzen	Saisonale Produkte, Artikel, die von externen Faktoren (z. B. Wetter) beeinflusst werden
Lebensstil/Interessengruppen	Vorhersehbare Interessengruppen (z. B. Fitnessbekleidung)	Spezialitäten- oder Nischenprodukte, stark schwankende Nachfrage

Auch wenn unsere obige Tabelle nicht unbedingt eine faktische Darstellung der Beziehung zwischen Kundensegmenten und Produkttypen ist, unterstreicht sie doch den wichtigen Punkt, diese zu berücksichtigen, bevor ein geeigneter Datensatz für die Erstellung von Prognosen ausgewählt wird. Zusammenfassend lässt sich sagen, dass GPR besser für Unternehmen geeignet ist, die häufig mit Unsicherheiten und komplexen Wachstumsmustern konfrontiert sind, die Vorhersagen mit Konfidenzintervallen erforderlich machen.

Support Vector Regressions hingegen eignen sich gut für Projektionen, bei denen Sicherheit und stabiles Wachstum im Spiel sind. Sie sind ideal, wenn Entscheidungen auf linearen oder mäßig linearen Trends beruhen können. Warum? Denn SVR ist robust gegenüber Rauschen. Sie konzentriert sich darauf, die Entscheidungsgrenze zu finden, die die Fehlermarge maximiert und gleichzeitig den Einfluss von Ausreißern minimiert. Dadurch, dass die Fehlerspanne (Epsilon) als Klassifikator fungiert, sollte SVR bei Datensätzen, die nicht viele Ausreißer enthalten, effektiv sein.

Wie aus der obigen Kreuztabelle hervorgeht, eignet sich der SVR am besten für Prognosen zu Grundnahrungsmitteln oder alltäglichen Konsumgütern, bei denen die Nachfrage nahezu konstant ist und - abgesehen von einem COVID-Ausbruch (der die Nachfrage in die Höhe treiben und zum Absturz bringen kann) - kaum oder gar nicht schwanken dürfte. Für unsere Situation, den Verkauf von Speiseeis außerhalb der Heimatstadt auszuweiten, wäre SVR ein geeignetes Instrument, wenn es nicht zu vordergründig bepreist wird (wie es oben für GPR empfohlen wurde), sondern in den Geschäften an den Regalstellen angeboten wird, an denen die Verbraucher ihre täglichen Lebensmittel und Grundnahrungsmittel für die Woche abholen.

Wenn wir also die Kreuztabelle als Anhaltspunkt nehmen, wenn unser Speiseeis ein Premium-Produkt ist, das wir hauptsächlich an wichtigen Feiertagen oder nur im Sommer verkaufen oder das beispielsweise in bestimmten gehobenen Restaurants angeboten wird, dann sollten wir die SVR mit Verkaufsdaten verwenden, die nach Einkommensniveau aggregiert sind. Darüber hinaus werden in der Kreuztabelle Berufs- und Lifestyle-/Spezialinteressengruppen empfohlen, die ebenfalls berücksichtigt werden könnten. Auf der anderen Seite würde SVR am besten funktionieren, wenn unser Produkt überwiegend in großen Geschäften verkauft würde, in denen niedrige Preise wichtig sind, wie oben dargelegt, und das Verbrauchersegment, für das dies relevant ist, die Adresse (oder Postleitzahl) ist. Aggregierte Umsatzdaten nach Adressen wären daher besser geeignet, um mit dem SVR Prognosen darüber zu erstellen, wie schnell oder langsam wir unsere Eiscreme-Expansion vorantreiben sollten, da dies etwas ist, das wir richtig machen müssen, da wir jetzt das Geld anderer Leute verwenden.

SVR eignet sich also am besten für Vorhersagesituationen, in denen ein hohes Maß an Unsicherheit akzeptabel ist, während SVR, auf das wir uns in diesem Artikel konzentrieren, fast am anderen Ende des Spektrums liegt, da es Ausreißer ignoriert, die bei der Definition der Hyperebene des Datensatzes außerhalb eines festgelegten Schwellenwerts liegen.

SVR-Definition

SVR kann als Zielfunktion und als Entscheidungsfunktion formuliert werden. Wenn wir mit der Formel für die Zielfunktion beginnen, lautet sie wie folgt:

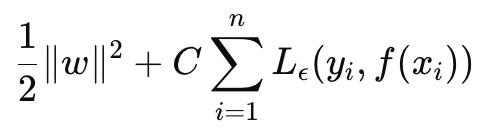
Wobei

• w ist der Gewichtsvektor (Parameter des Modells). In unserem Fall sind wir an der L2-Norm der Gewichtsmatrizen interessiert,
• C ist der Regularisierungsparameter, der den Kompromiss zwischen Modellkomplexität und Toleranz gegenüber Fehlklassifizierungen steuert,
• L ϵ ist die ϵ-unempfindliche Verlustfunktion, definiert durch:

Wobei

• f(xxi) ist der vorhergesagte Wert,
• yi ist der wahre Wert,
• ϵ legt eine Toleranzspanne fest, innerhalb derer keine Strafe für Fehler verhängt wird.

Die Entscheidungsfunktion hingegen, die vor allem bei Prognosen verwendet wird, hat folgende Formel:

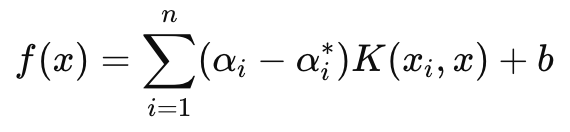
Wobei

• αi und αi^∗ sind die Lagrange-Multiplikatoren,
• K (xi, x) ist die Kernel-Funktion (z. B. linear, polynomial, RBF),
• b ist der Bias-Term.

Wie bereits erwähnt, führt SVR einen verlustunempfindlichen Parameter epsilon ein, der dafür sorgt, dass Fehler, die kleiner als epsilon sind, ignoriert werden und nicht zu einer Anpassung der Gewichte oder Parameter des trainierten Modells führen. Dies macht den SVR robuster im Umgang mit kleinen Störungen und Schwankungen in den Daten, sodass er sich auf das Gesamtbild oder wichtige Trends konzentrieren kann.

Darüber hinaus sorgt der Parameter C in unserer Zielfunktion für einen Kompromiss zwischen der Minimierung des Trainingsfehlers und der Minimierung der Komplexität des Modells. Ein höherer C-Wert minimiert den Trainingsfehler, birgt aber die Gefahr einer Überanpassung, während ein niedrigerer C-Wert auf dem Papier zu mehr Generalisierung und besserer Flexibilität bei der Erstellung von Prognosen in verschiedenen Szenarien führen würde.

Wir werden uns ausschließlich auf die Verwendung der Verlustfunktion von SVR konzentrieren, wenn wir ein einfaches MLP für dieses Netz trainieren. Wir werden keine Projektionen mit ihren Kernen vornehmen, wie es bei der Entscheidungsfunktion der Fall wäre. Es ist jedoch erwähnenswert, dass SVR Kernel-Funktionen verwendet, um die Eingabedaten in einen höherdimensionalen Raum zu transformieren, in dem Beziehungen, die im ursprünglichen Raum möglicherweise nicht linear sind, genau bestimmt werden können. Zu den gebräuchlichen Kerneln gehören: der lineare Kernel, der polynomiale Kernel und der RBF-Kernel.

Die SVR-Verlustfunktion kann in MQL5 wie folgt implementiert werden:

//+------------------------------------------------------------------+
//| SVR Loss                                                         |
//+------------------------------------------------------------------+
vector Cmlp::SVR_Loss()
{  vector _loss = fabs(output - label);
   for(int i = 0; i < int(_loss.Size()); i++)
   {  if(_loss[i] <= THIS.svr_epsilon)
      {  _loss[i] = 0.0;
      }
   }
   vector _l = THIS.svr_c*_loss;
   double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2);
   vector _weight_norms;
   _weight_norms.Init(_loss.Size());
   _weight_norms.Fill(_w);
   return(_weight_norms + _l);
}

Normalerweise ist dieser Verlustwert ein Skalar, aber da diese Verlustfunktion jetzt in der Rückwärtsfortpflanzung verwendet wird und bestimmte Netze mehr als einen Endausgang haben, war es wichtig, die Verluststruktur in einer Vektorform beizubehalten, obwohl SVR sie zu einem Skalar kondensiert. Und genau das haben wir getan. Außerdem überprüfen wir innerhalb der Backpropagation-Funktion, ob der SVR-Verlust verwendet wird. Dies ist wie unten angegeben:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
   
   ...


   if(EpochIndex < 0)
   {  printf(__FUNCSIG__ + " Epoch Index Should start from 1. ");
      return;
   }


    ...


   vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss));

    ....
}

Wir sind in der Lage, diese einzeilige Änderung hinzuzufügen, weil unsere Konstruktorparameter in einer Struktur enthalten sind und wir diese Struktur (da diese Klasse in früheren Artikeln eingeführt wurde) wie folgt ändern können:

//+------------------------------------------------------------------+
//| Multi-Layer-Perceptron Struct for Constructor Parameters         |
//+------------------------------------------------------------------+
struct Smlp
{  //arch array must be defined with at least 2 non zero values
   //that represent the size of the input layer and output layer
   //If more values than this are provided in the array then the
   //middle values will define the size(s) of the hidden layer(s)
   //first value (index zero) is size of input layer
   //last value (index size-1) is size of output layer
   int               arch[];


  ...


   bool              svr_loss;
   double            svr_c;
   double            svr_epsilon;

                     Smlp()
   {                 ArrayFree(arch);

     ...

      svr_loss = false;
      svr_c = 1.0;
      svr_epsilon = __EPSILON * 5.0;
   };
                    ~Smlp() {};
};

Implementieren einer Signalklasse

Um eine Signalklasse mit einem MLP zu haben, dessen Verlustfunktion den SVR verwendet, würden wir unsere bereits kodierte Klasse für einen MLP verwenden, die in früheren Artikeln geteilt wurde. Die Änderungen, die an dieser Klasse vorgenommen werden müssen, damit wir den SVR-Verlust verwenden können, wurden bereits oben erläutert, sodass nur noch zu klären ist, wie diese Klasse innerhalb einer nutzerdefinierten Instanz einer Signalklasse aufgerufen und verwendet wird. Unsere MLP, die wir kürzlich in dieser Serie behandelt haben, versuchen alle, die nächste Veränderung des Schlusskurses auf jedem neuen Balken vorherzusagen. Das bedeutet, dass auf einer zeitlichen Basis (jeder neue Balken) neue Berechnungen für die nächste Änderung des Schlusskurses vorgenommen werden.

Die Inputs für die Berechnung dieses Wertes sind ebenfalls Preisänderungen vor dem Börsenschluss, wobei die wichtigste Variable die Anzahl dieser Änderungen ist. (Diese Variable legt die Größe der Eingabeschicht fest). Es gibt verschiedene Möglichkeiten, nicht nur festzulegen, welche Inputs in den MLP eingespeist werden sollen, wenn es um die Projektion der nächsten Bar-Close-Preisänderung geht, sondern auch, wie vorausschauend die Prognose sein soll. Der letzte Punkt ist wichtig, da wir zu Testzwecken einen einzelnen Preisbalken für den Ausblick verwenden. Außerdem führen wir vor jeder Vorhersage eine Backpropagation für jeden neuen Balken durch, um unser Netzwerk über eine bestimmte Größe der Trainingsmenge für eine bestimmte Anzahl von Epochen zu trainieren.

Diese beiden Eingabeparameter „Größe der Trainingsmenge“ und „Epochen“ sind ebenfalls optimierbar, und dies erfordert ein Gleichgewicht zwischen den idealen Gewichten des Netzes und der Generalisierung. Denn während ein größerer Trainingssatz und mehr Epochen auf eine gute Leistung bei den Stichprobendaten hindeuten können, ist eine Kreuzvalidierung zwangsläufig nicht so rosig, es sei denn, das Netz verfügt über eine gewisse Generalisierung und ist nicht übermäßig an seine Trainingsdaten angepasst. Die Funktion „GetOutput“ übernimmt die Vorhersage durch den MLP, und ihr Quellcode ist unten angegeben:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old;
         if
         (
            _in_new.Init(__MLP_SIGN_INPUTS) &&
            _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_new.Size() == __MLP_SIGN_INPUTS &&
            _in_old.Init(__MLP_SIGN_INPUTS) &&
            _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_old.Size() == __MLP_SIGN_INPUTS
         )
         {  _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new, _target_old;
               if
               (
                  _target_new.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) &&
                  _target_new.Size() == __MLP_SIGN_OUTPUTS &&
                  _target_old.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) &&
                  _target_old.Size() == __MLP_SIGN_OUTPUTS
               )
               {  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Sie unterscheidet sich nicht wesentlich von den Implementierungen, die wir in früheren Artikeln hatten. Die Backpropagation wird für jeden Datenpunkt des Trainingssatzes durchgeführt, der ein Label (oder einen Zielwert) hat. Normalerweise haben alle Trainingsdaten einen Zielwert, aber da es sich in unserem Fall um eine Zusammenführung mit Prognosen handelt, ist der endgültige „Trainingsdatenpunkt“ aktuell und seine eventuelle Schlusskursänderung ist das, was wir suchen. Wenn wir also zu den aktuellen Eingabedaten kommen, die uns unsere Prognose liefern sollen, führen wir kein Training durch. Das ist auch der Grund, warum wir in jedem Trainingssatz abwärts zählen, d.h. wir trainieren zuerst mit sehr alten Daten und arbeiten uns dann abwärts zu den aktuellen Daten vor.

Implementieren einer Trailing-Stop-Klasse

Es ist schon eine Weile her, dass wir in dieser Serie etwas anderes als eine nutzerdefinierte Signalklasse besprochen haben, und dennoch werden sich Leser, die meine früheren Artikel gelesen haben, daran erinnern, dass ich Handelsideen oft nicht nur in die Signalklasse, sondern auch in Trailing-Stop-Klassen und sogar in Geldmanagement-Klassen aufgeteilt habe. Wir kehren also zu dieser Situation zurück, indem wir eine nutzerdefinierte Trailing-Stop-Klasse in Betracht ziehen, die über den MQL5-Assistenten an einen Expert Advisor angehängt werden kann. Eine Anleitung für neue Leser, wie der unten gezeigte Code im MQL5-Assistenten zur Erstellung eines Expert Advisors verwendet werden kann, finden Sie hier und hier.

Um also eine nutzerdefinierte Trailing-Klasse zu implementieren, müssen wir prüfen, ob für eine offene Position entweder kein Stop-Loss vorhanden ist und ein solcher eingeführt werden muss oder ob bereits ein Stop-Loss vorhanden ist, der jedoch angepasst werden muss, um die Gewinne besser zu sichern. Stop-Losses sind etwas umstritten, weil sie nie garantiert sind. Nur die Preise für Limitaufträge sind es. Wenn sich der Markt, aus welchen Gründen auch immer, stärker bewegt als von den meisten erwartet, kann der Broker Ihren Auftrag nur zum nächsten „verfügbaren Kurs“ schließen, nicht aber zu Ihrem Stop-Loss. Dessen ungeachtet werden wir die Entscheidung, den Stop-Loss zu setzen oder zu verschieben, auf der Grundlage der prognostizierten Größenordnung der Kurs-Bar-Spanne treffen. Wir implementieren dies in einer weiteren Get-Output-Funktion, die der nutzerdefinierten Signalklasse ähnelt, sich aber von dieser unterscheidet. Dies wird unten mitgeteilt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo;
         if
         (
            _in_new_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_hi.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_hi.Size() == __MLP_TRAIL_INPUTS
            &&
            _in_new_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_lo.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_lo.Size() == __MLP_TRAIL_INPUTS
         )
         {  vector _in_new = _in_new_hi - _in_new_lo;
            vector _in_old = _in_old_hi - _in_old_lo;
            _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo;
               if
               (
                  _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS
                  &&
                  _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS
               )
               {  vector _target_new = _target_new_hi - _target_new_lo;
                  vector _target_old = _target_old_hi - _target_old_lo;
                  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Unser obiger Code ist zwar fast identisch mit dem des Signals, unterscheidet sich aber hauptsächlich durch die Art der Eingabedaten, die er empfängt, und die erwartete Ausgabe. Wir versuchen zu bestimmen, ob wir unseren Stop-Loss verschieben müssen, und unsere Voraussetzung dafür ist ein Anstieg der Volatilität. Daher müssen wir herausfinden, was die nächste Änderung der Preisspanne sein wird. Diese Art von Daten ist zwangsläufig selbst sehr volatil (oder verrauscht), weshalb es umsichtiger gewesen wäre, wenn wir gleitende Durchschnittspuffer als Eingangsdaten und Zielwerte verwendet hätten. Dies kann geändert werden, die vollständige Quelle ist unten angehängt, jedoch sind wir mit Änderungen in der Hochs minus Tiefs von jedem Preis bar als Eingaben und wir sind für die Ausgabe suchen, um die nächste Änderung in diesen Input-Werte genau wie wir mit Close-Preise für das Signal oben hatte.

Wenn also die prognostizierte Veränderung der Preisspanne positiv ist, was bedeutet, dass die Volatilität zunimmt, verschieben wir unseren Stop-Loss im Verhältnis zu unserem prognostizierten Anstieg. Dies mag leichtsinnig erscheinen, da, wie bereits erwähnt, Broker nie einen Stop-Loss-Kurs garantieren, weshalb die Gegenoption, einen Stop-Loss nur bei einem prognostizierten Rückgang der Volatilität zu verschieben, „sicherer“ sein könnte, da Broker in weniger volatilen Zeiten eher Stop-Loss-Kurse einhalten als bei hoher Volatilität. Ja, es ist also ein bisschen eine Debatte, und ich überlasse es dem Leser, dies zu erforschen und je nach seinen Erkenntnissen entsprechende Anpassungen am Code vorzunehmen.

Strategie-Testergebnisse

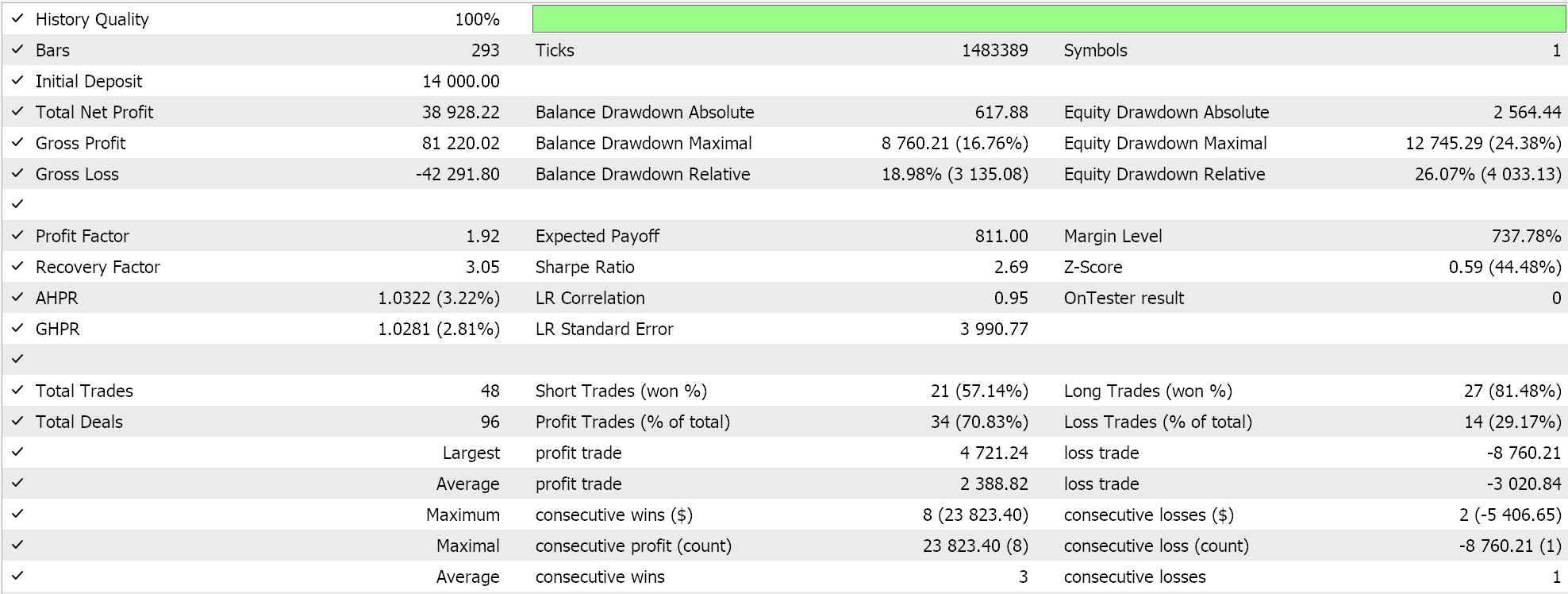
Wir testen das Paar USDJPY auf dem täglichen Zeitrahmen von 2023.01.01 bis 2024.01.01. Diese Testläufe werden mit einigen der besten Einstellungen durchgeführt, die sich aus sehr schnellen Optimierungen ergeben haben, für die keine Forward Walks oder Kreuzvalidierungen durchgeführt wurden. Sie werden hier ausgestellt, um einfach die Fähigkeit zu demonstrieren, Handelsgeschäfte zu platzieren und den vom Assistenten zusammengestellten Expert Advisor zu verwenden. Die zusätzliche Sorgfalt beim Testen über längere Zeiträume hinweg und beim Vorwärtsgehen, wenn es um Optimierung geht, bleibt dem Leser überlassen. Erwähnenswert ist auch, dass die vom Assistenten zusammengestellten Expert Advisors bei der Entwicklung eines Handelssystems mehrere Signale kombinieren können, sodass das Testen oder die Optimierung nicht nur mit den hier verwendeten nutzerdefinierten Signalen erfolgen muss.

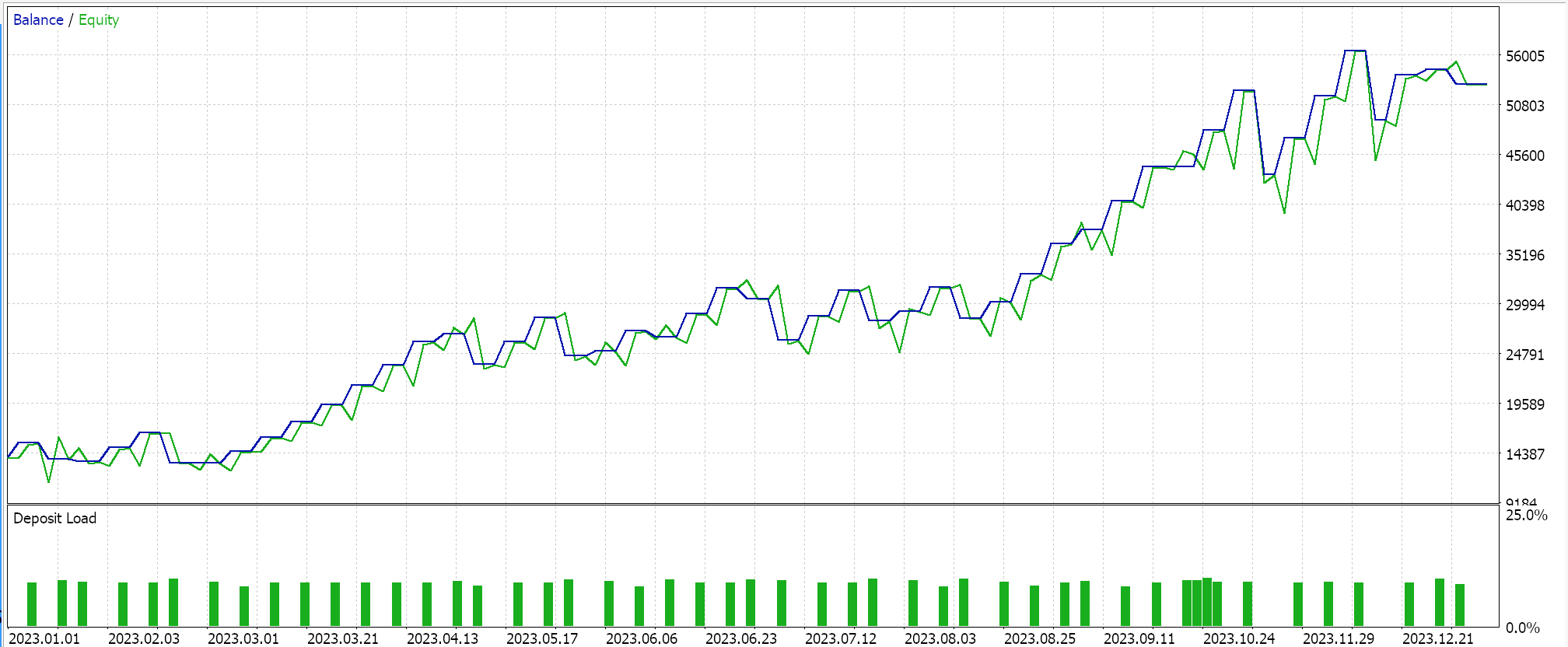
Wir haben ein nutzerdefiniertes Signal mit SVR und eine nutzerdefinierte Trailing-Klasse mit einem ähnlichen MLP entwickelt. Die im Folgenden vorgestellten Testläufe beziehen sich daher auf zwei Expert Advisors, deren Schnittstellencode unten beigefügt ist. Die erste verwendet nur das nutzerdefinierte Signal ohne Trailing-Stop. Die Ergebnisse werden im Folgenden vorgestellt:

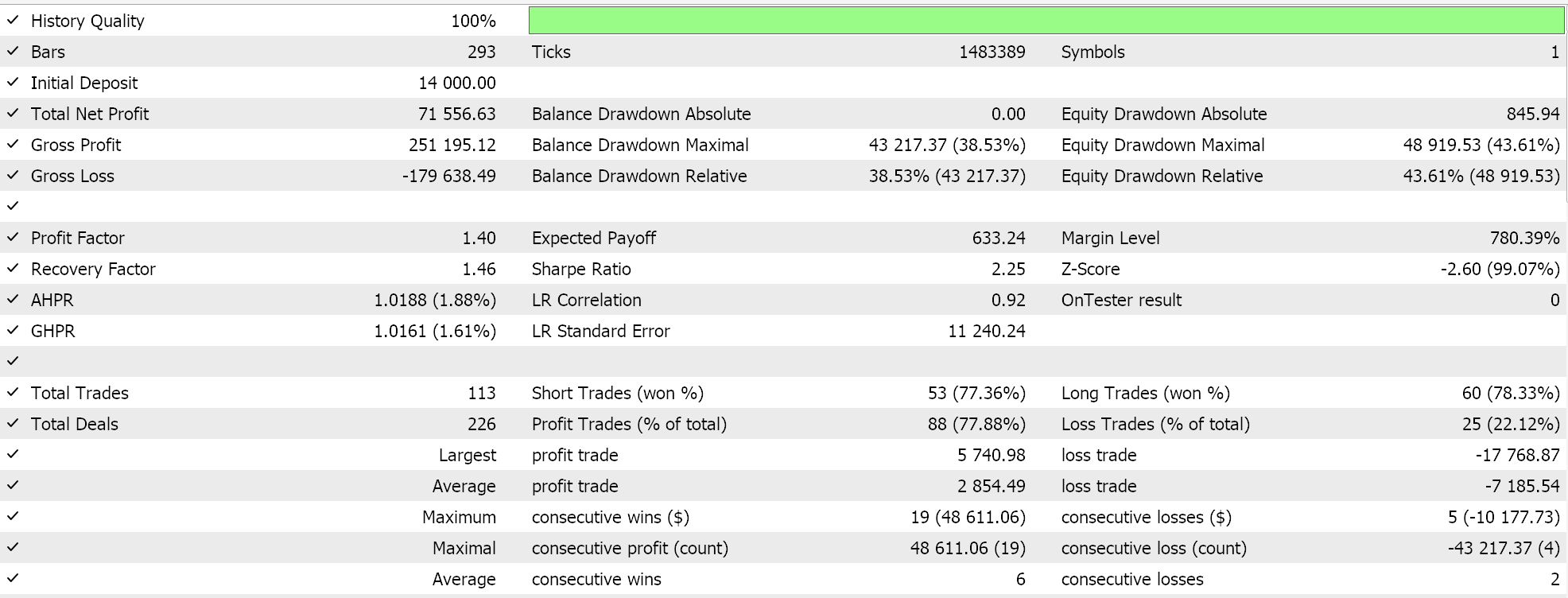
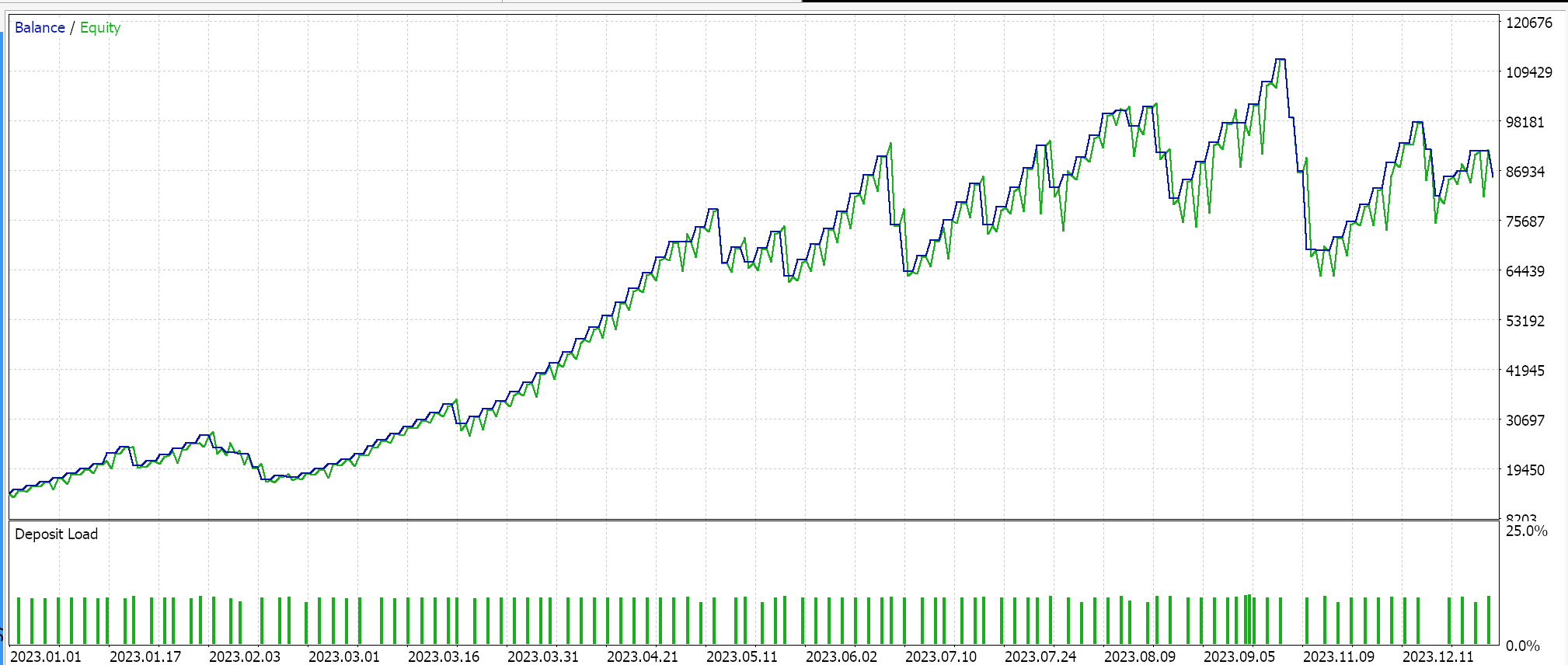
Die zweite verwendet das nutzerdefinierte Signal und die nutzerdefinierte Trailing-Klasse, die wir oben implementiert haben. Die Ergebnisse sind ebenfalls unten aufgeführt.

Schlussfolgerung

Abschließend haben wir uns mit der Support Vector Regression befasst, die einer anderen Form der Regression folgt, die wir bei der Betrachtung der Gaußschen Prozesskerne betrachtet haben. Diese beiden Regressionen, die Support Vector Regression und die Gaussian Process Regression, sind in ihrer Anwendung nahezu gegensätzlich, da SVR eher für weniger volatile und tendenzielle Datensätze geeignet ist, während GPR in volatileren und weniger sicheren Umgebungen gedeiht. Die Support-Vektor-Regression verfügt über eine Zielfunktion und eine Entscheidungsfunktion. Wir haben versucht, die erste, die Zielfunktion, als Verlustfunktion für ein mehrschichtiges Perzeptron in einer Signalklasse und einer nutzerdefinierten Trailing-Stop-Klasse zu nutzen.

Die Verwendung der Entscheidungsfunktion als Prognosemodell würde die zusätzliche Verwendung von Kerneln erfordern, die wir in dem Artikel über Gaußsche Prozesskerne untersucht haben, aber in diesem Artikel nicht verwenden, da unser Prognosemodell ein reines MLP ist. In einem oder mehreren künftigen Artikeln könnten wir uns damit befassen, da es verschiedene Formen von Kerneln gibt, die für diese Aufgabe verwendet werden können, doch war die SVR-Verlustfunktion unser Ziel für diesen Artikel. Durch die Verwendung eines verlustunempfindlichen Parameters epsilon kann auch sie, zusammen mit einer wachsenden Liste von Verlustfunktionsimplementierungen, von denen wir einige hier behandelt haben, eine andere Art des Trainings neuronaler Netze einführen.

Dieser verlustunempfindliche Parameter epsilon verhält sich eher wie ein Klassifikator als ein Regressor, und man könnte argumentieren, dass dies dafür spricht, diese Verlustfunktion eher in Klassifikator-Netzwerken als in Regressor-Netzwerken zu verwenden, wie wir es für diesen Artikel getan haben, und das könnte auch stimmen. SVR befasst sich jedoch nach wie vor mit kontinuierlichen Ausgaben (dezimale Datensätze) und sagt numerische Werte in einem ähnlichen Format voraus. Es verwendet einfach die Epsilon-Marge, um zu entscheiden, ob ein Fehler bestraft werden sollte, aber sein Ziel bleibt die Regression und nicht die Klassifizierung.