知っておくべきMQL5ウィザードのテクニック（第35回）：サポートベクトル回帰

はじめに

サポートベクトル回帰(SVR: Suppor Vector Regression)（英語）は、サポートベクターマシンから派生した回帰分析の形式です。SVRの核心は、カーネル法を用いて入力データを高次元空間にマッピングすることであり、次元削減とは対照的に、より複雑な関係を捉えることが可能です。この記事では、多層パーセプトロンを用いる際の損失関数の役割について詳しく探求します。以前の記事で触れた、関連性はあるが異なる回帰手法としてガウス過程回帰(GPR)があり、まずはこの2つの違いを明確にすることが重要です。

SVRとGPRの違い

この2つの違いを強調するために、機械学習の専門用語から離れ、日常的な事例を用いて、それぞれの重要性を説明します。例えば、あなたがスタートアップ企業を経営していて、非常にヘルシーな低糖質のアイスクリームを開発したとします。地元には健全な需要があるものの、あなたはまだ起業したばかりで、アイスクリームは地元でのみ販売しているため、製造のほとんどを手作業でおこなっています。そのため、生産性の向上が求められています。生産性を高めることは、コスト管理に加え、品質管理や生産基準の導入といった他のメリットももたらします。

このように事業を拡大するには、銀行に提案するための担保（または資金）が不足しているため、機関から借り入れができません。また、大手の確立されたアイスクリームブランドとの提携を試みることもできますが、大手ブランドの従業員は官僚的な体質を持つことが多く、製品についての評価にかかわらず、提携を断られる可能性があります。

そのため、民間の半公式なルートで資本を調達する選択肢しか残されておらず、それには製品の規模を拡大する必要があるという注意点があります。しかし、地元以外の地域に進出する際には、どのような顧客が既存のブランドと比較して、あなたの製品を選ぶのかを考慮しなければなりません。未知の領域に進むため、地元と同様のアプローチではうまくいかないことが多いです。このことは、家庭の需要に応えようとする初期の努力の中で見落とされがちな疑問を提起します。

顧客セグメンテーションは、時には無視されることもあるビジネスの側面ですが、様々な手法があります。例えば、郵便番号や住所、年齢、教育レベル、職業、所得レベルなどによるセグメントがあります（これらに限定されるわけではありません）。これらのセグメント別に売上データを分析することで、興味深いデータセットを作成できます。これらのデータを地元全体で収集することで、主要な市場の外で次に何が起こるかについての手がかりを得ることができます。

以前の記事で紹介したガウス過程回帰(GPR)は、単なる平均値の予測を提供するだけでなく、その平均値に信頼区間を付与します。これは、ある製品の需要が外的要因に大きく影響され、一貫性がないために、一貫性のない需要を補うために高級品や贅沢品に適した状況を意味します。高級品でなければ、季節性が高い商品や高価格帯で需要が変動するニッチな商品かもしれません。つまり、GPRの使用に最適なニッチで高級な製品に位置づけるためには、あなたのアイスクリームは競合他社よりも高価格帯でなければならないということです。

さらに、製品の種類と顧客セグメンテーションは、今後の需要を予測するためのデータセットを選ぶ際に、慎重な検討が必要な選択肢の組み合わせを提示します。以下の表に示すように、これらの要素が相互に関連しています。

セグメンテーションタイプ	SVRに最適	GPRに最適
郵便番号	日常消費財	他のダイナミックデータと組み合わせない限り理想的ではない
年齢	アパレル、消費財、教育ツール	他のダイナミックデータと組み合わせない限り理想的ではない
教育レベル	教育製品、ハイテク製品	複雑な要因が絡まない限り理想的ではない
所得水準	安定した市場における基本製品	高級品、高級電化製品、プレミアム商品
職業	安定した職業につながる商品	季節商品、外的要因（天候など）に左右される商品
ライフスタイル/趣味グループ	予測可能な利益集団（フィットネスアパレルなど）	特殊またはニッチ製品、需要の変動が激しい

上記の表は、顧客セグメントと商品タイプの関係を必ずしも事実に基づいて描写したものではありませんが、予測をおこなうために適切なデータセットを選択する前に考慮すべき重要な要点を強調しています。要約すると、GPRは不確実性や複雑な成長パターンに直面するケースにおいて、信頼区間を伴う予測が必要なビジネスに最適です。

一方で、サポートベクトル回帰(SVR)は、安定した成長が期待できる予測に適しており、線形または中程度の線形トレンドに基づく意思決定に最適です。なぜなら、SVRはノイズに強く、異常値の影響を最小限に抑えながら、誤差(ε)を最大限に小さくする決定境界を重視しているからです。これは、誤差を分類器として機能させることで、SVRが外れ値の少ないデータセットで最大の効果を発揮することを意味します。

また、クロステーブルの推奨事項に基づけば、SVRは需要がほぼ一定であり、COVIDのような急激な需要変動のイベントがない限り、製品の需要が大きく変動しない主食や日常消費財の予測に適しています。したがって、地元以外でのアイスクリーム販売を拡大する現状を考慮すると、SVRは、価格があまり高額でなく、消費者が日用品や1週間分の必需品を購入するような棚に並んでいる場合に、適したツールとなります。

つまり、クロステーブルを目安にすれば、アイスクリームが大型連休向けのプレミアム商品、夏季限定商品、または特定の高級レストラン向けの製品である場合、所得階層別に集計された販売データを持つGPRの利用が望ましいと考えられます。また、クロステーブルでは消費者の職業、ライフスタイル、特別な興味を持つグループの要素も推奨しており、これらも考慮することができます。逆に、SVRが最も効果的なのは、製品が主に大型店で販売され、低価格が重視される場合です。この場合、適切な消費者セグメントは住所（または郵便番号）に基づいて決定されるため、住所別に集計された売上データは、SVRを活用してアイスクリームの市場拡大の速度を予測する際に役立ちます。この予測は、他人の資金を使って事業拡大をおこなうため、特に正確さが求められます。

総じて、GPRは不確実性が高い予測シナリオで特に役立つのに対し、今回注目するSVRは、指定されたしきい値から外れる異常値を無視することでデータセットの超平面を定義するため、両者は予測手法のスペクトルでほぼ対極に位置しています。

SVRの定義

SVRは目的関数としても決定関数としても定式化できます。目的関数の式から始めると、次のようになります。

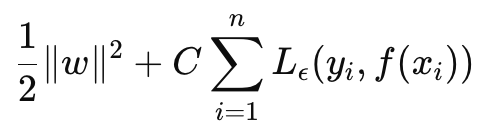
ここで

• wは重みベクトル（モデルのパラメータ）であり、私たちの場合は重み行列のL2-Normに興味がある
• Cは、モデルの複雑さと誤分類に対する耐性の取引オフを制御する正則化パラメータ
• L ϵは次式で定義されるϵ感受性損失関数

ここで

• f(xi)は予測値
• yiは真の値
• ϵは、誤差に対してペナルティが与えられない許容誤差を定義する

一方、予測で主に使われる決定関数は以下の式で表されます。

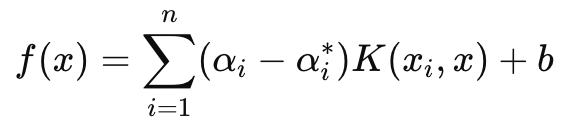
ここで

• αiとαi ^∗はラグランジュ乗数
• K (xi , x)は、カーネル関数（例えば、線形、多項式、RBF）
• bはバイアス項

述べたように、SVRでは損失非感受性パラメータεを導入することで、誤差がε以下の範囲であれば無視され、学習中のモデルの重み付けやパラメータ調整に影響を与えないようにしています。これにより、SVRはデータの小さなノイズや変動に対して強くなり、全体の傾向や主要なトレンドに焦点を合わせることが可能になります。

また、目的関数では、パラメータCが学習誤差の最小化とモデルの複雑さのバランスを制御します。Cの値が高いほど、学習誤差が小さくなる一方で、過剰適合のリスクが高まります。逆に、Cの値が低いほどモデルは一般化され、異なるシナリオに対応できる柔軟性が向上します。

ここでは、シンプルなMLP（多層パーセプトロン）を訓練する際にSVRの損失関数を用いることに焦点を当てます。この場合、決定関数のようにカーネルでの投影はおこないませんが、SVRがカーネル関数を用いて入力データを高次元空間にマッピングし、元の空間では線形的でない可能性のある関係を特定できる点は注目に値します。代表的なカーネルとしては、線形カーネル、多項式カーネル、RBFカーネルなどが挙げられます。

SVR損失関数はMQL5で次のように実装できます。

//+------------------------------------------------------------------+
//| SVR Loss                                                         |
//+------------------------------------------------------------------+
vector Cmlp::SVR_Loss()
{  vector _loss = fabs(output - label);
   for(int i = 0; i < int(_loss.Size()); i++)
   {  if(_loss[i] <= THIS.svr_epsilon)
      {  _loss[i] = 0.0;
      }
   }
   vector _l = THIS.svr_c*_loss;
   double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2);
   vector _weight_norms;
   _weight_norms.Init(_loss.Size());
   _weight_norms.Fill(_w);
   return(_weight_norms + _l);
}

通常、損失値はスカラーですが、バックプロパゲーションで使用されるため、ネットワークによっては複数の最終出力を持つ場合があります。そのため、SVRでは最終的に損失がスカラーに凝縮されるとしても、損失構造をベクトル形式で維持することが重要でした。これは、私たちが取り組んできた要点です。また、バックプロパゲーション関数内でSVR損失が使用されているかどうかを確認します。これは以下の通りです。

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
   
   ...


   if(EpochIndex < 0)
   {  printf(__FUNCSIG__ + " Epoch Index Should start from 1. ");
      return;
   }


    ...


   vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss));

    ....
}

コンストラクタパラメータが構造体内にあり、この構造体を次のように簡単に変更できるため、この1行の変更を追加できます（このクラスは以前の記事で紹介されているため）。

//+------------------------------------------------------------------+
//| Multi-Layer-Perceptron Struct for Constructor Parameters         |
//+------------------------------------------------------------------+
struct Smlp
{  //arch array must be defined with at least 2 non zero values
   //that represent the size of the input layer and output layer
   //If more values than this are provided in the array then the
   //middle values will define the size(s) of the hidden layer(s)
   //first value (index zero) is size of input layer
   //last value (index size-1) is size of output layer
   int               arch[];


  ...


   bool              svr_loss;
   double            svr_c;
   double            svr_epsilon;

                     Smlp()
   {                 ArrayFree(arch);

     ...

      svr_loss = false;
      svr_c = 1.0;
      svr_epsilon = __EPSILON * 5.0;
   };
                    ~Smlp() {};
};

シグナルクラスの実装

MLPでSVRを損失関数として用いるシグナルクラスを実装するには、以前の記事で共有したMLP用にすでにコーディング済みのクラスを活用します。このクラスにSVR損失を使用するための変更点についてはすでに述べたので、ここでは、このクラスがどのように呼び出され、シグナルクラスのカスタムインスタンス内で使用されるかについて説明します。本連載で最近取り上げたMLPはすべて、新しいバーごとに終値の次の変化を予測することを目的としています。つまり、時間単位で（新しいバーごとに）、次の終値の変化がどうなるかを計算しています。

この予測をおこなうための入力もまた、前日終値の変化であり、その主要な変数は変化回数です（この変数は入力層のサイズを決定します）。次のバー終了時の価格変動を予測する際、MLPにどのような入力データを与えるべきか、さらに予測をどの程度先読みすべきかについても、複数のアプローチが考えられます。この点は重要です。なぜなら、テスト目的では1本の価格バーごとにフォワード予測をおこなっているからです。また、各予測前に、各新しいバーに対してバックプロパゲーションを実行し、定義したエポック数に基づいて、指定された訓練セットサイズでネットワークを訓練します。

このときの「訓練セットのサイズ」と「エポック数」の2つの入力パラメータも最適化可能であり、ネットワークが理想的な重みを取得しつつ、汎化性能とのバランスが求められます。なぜなら、大規模な訓練セットやエポック数を増やすことで、サンプリングしたデータ上でのパフォーマンスは向上しますが、交差検証によってネットワークが過度に訓練データに適合せず、一定の汎化能力を保っていることを確認しなければならないからです。MLPを用いた予測を実行するためのGetOutput関数のソースコードを以下に示します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old;
         if
         (
            _in_new.Init(__MLP_SIGN_INPUTS) &&
            _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_new.Size() == __MLP_SIGN_INPUTS &&
            _in_old.Init(__MLP_SIGN_INPUTS) &&
            _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_old.Size() == __MLP_SIGN_INPUTS
         )
         {  _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new, _target_old;
               if
               (
                  _target_new.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) &&
                  _target_new.Size() == __MLP_SIGN_OUTPUTS &&
                  _target_old.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) &&
                  _target_old.Size() == __MLP_SIGN_OUTPUTS
               )
               {  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

以前の記事で紹介した実装と大きな違いはありません。バックプロパゲーションは、各訓練セットのデータポイントに対してラベル（または目標値）を使用して実行されます。一般的にはすべての訓練データに目標値がありますが、今回のケースでは予測との結びつきがあるため、最終的な「訓練データポイント」は現在のデータです。つまり、私たちが求めているのは、現在の終値変化です。そのため、予測を得るための現在の入力データに到達した時点では訓練をおこなわず、また各訓練セットでカウントダウンをおこなうのもこの理由からです。最も古いデータから訓練を始め、次第に現在のデータへと近づいていく方法をとっています。

トレーリングストップクラスの実装

この連載でカスタムシグナルクラス以外を検討するのは久しぶりですが、過去の記事をご覧になった読者の方は、シグナルクラスに加え、トレーリングストップクラスやマネーマネジメントクラスも頻繁に取り上げ、取引アイデアを共有していたことを思い出すでしょう。今回はその例に戻り、MQL5ウィザードを介してEAに組み込むことが可能なカスタムトレーリングストップクラスについて考察します。MQL5ウィザードでこのコードを活用してEAを作成する方法については、こちらとこちらをご覧ください。

そこで、カスタムトレーリングクラスを実装するために、ストップロスがなく、導入する必要があるポジションか、すでにストップロスがあるが、より利益を確定するために調整する必要があるポジションかを確認することになります。ストップロスは決して保証されるものではないので、少し議論の余地があります。指値注文の価格のみです。何らかの理由で市場が多くの人の予想以上に動いた場合、ブローカーはストップロスではなく、次の「利用可能価格」でしか注文を決済できません。それにもかかわらず、私たちは、予想される値幅の変化に基づいて、ストップロスを設定するか移動するかを決定するつもりです。カスタムシグナルクラスで持っていたものと似ているが異なる、別の出力取得関数でこれを実装します。以下、これを紹介します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo;
         if
         (
            _in_new_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_hi.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_hi.Size() == __MLP_TRAIL_INPUTS
            &&
            _in_new_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_lo.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_lo.Size() == __MLP_TRAIL_INPUTS
         )
         {  vector _in_new = _in_new_hi - _in_new_lo;
            vector _in_old = _in_old_hi - _in_old_lo;
            _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo;
               if
               (
                  _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS
                  &&
                  _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS
               )
               {  vector _target_new = _target_new_hi - _target_new_lo;
                  vector _target_old = _target_old_hi - _target_old_lo;
                  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

上記のコードは、シグナルクラスで使用していたものとほぼ同じですが、主に受け取るデータの種類や期待される出力が異なっています。ここでの目的は、ストップロスを移動させる必要があるかどうかを判断することです。その前提条件としてボラティリティの上昇を考慮しているため、次に予想される価格帯の変化を見極める必要があります。この種のデータは非常に不安定（あるいはノイジー）である可能性が高いので、もし移動平均のバッファを入力データおよび目標値として使えば、より慎重な判断が可能かもしれません。コードの完全なソースは下記に添付されていますので、適宜変更が可能です。現在は、各価格バーの高値から安値を差し引いた値を入力データとして使用しており、シグナルクラスで終値を使った場合と同様に、次の変化を出力として予測する形式になっています。

したがって、価格帯の変化予測がプラスであり、ボラティリティの上昇が示唆される場合には、予測される上昇に応じてストップロスを調整する措置を取ります。この手法は一見リスクがあるように思われるかもしれません。というのも、前述のとおりブローカーがストップロス価格を確実に保証するわけではないからです。そのため、ボラティリティが低下すると予測される際にのみストップロスを移動するという方策は「より安全」かもしれません。なぜなら、ボラティリティが低いときの方が、ボラティリティが高いときよりもブローカーがストップロスを尊重する傾向があるためです。この方法については賛否が分かれるかもしれません。最終的には、読者の皆さんが調査や検証を通じて、ご自身の戦略に適したコードへ調整していただくことをお勧めします。

ストラテジーテスターの結果

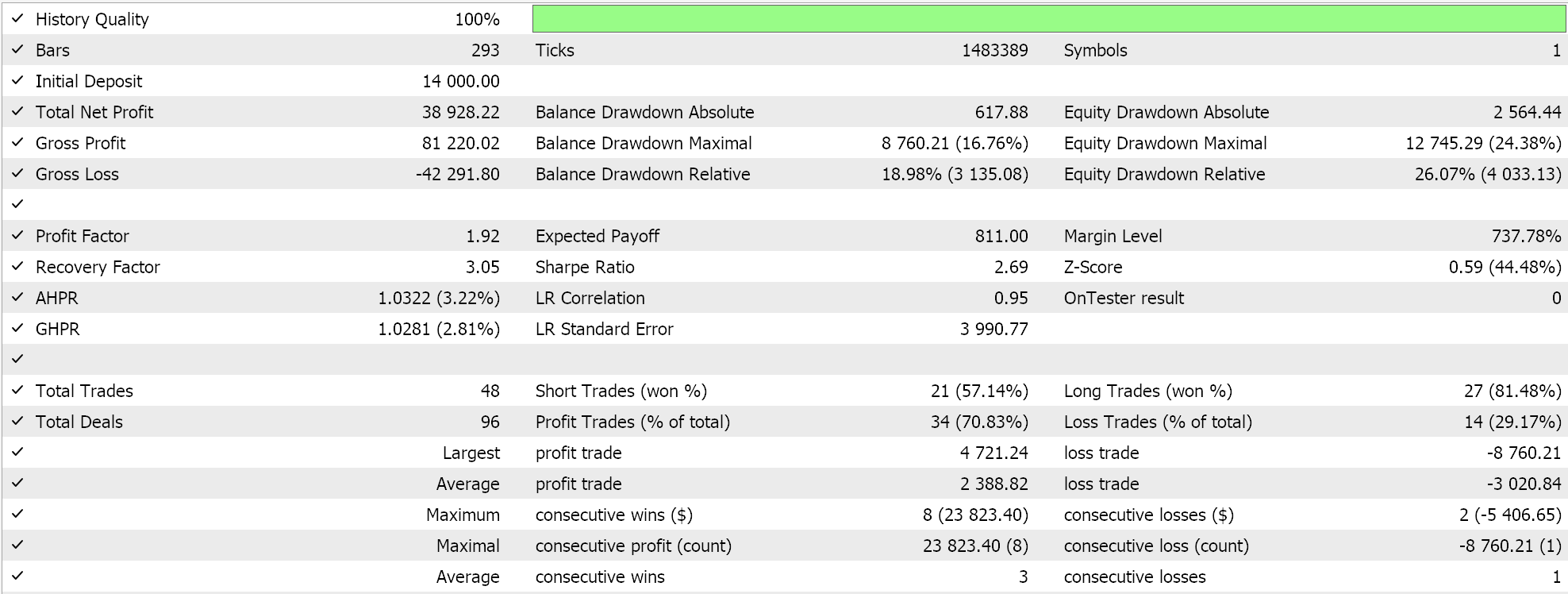
このテストでは、2023年1月1日から2024年1月1日までの期間において、日足の時間枠でUSD/JPYペアのシミュレーションを実施しました。以下の内容は、フォワードウォーク法や交差検証などのテスト精度の向上を目的としたプロセスを経ずに、迅速に実行された結果です。このテストは、あくまで取引の実行力や、MQL5ウィザードを使用して構築したEAの動作確認をおこなうためのもので、最適な取引戦略を見つけ出すためのものではありません。より詳細な最適化や、より長期間にわたるデータでのフォワードウォーク検証をおこなう場合は、読者ご自身で設定することをおすすめします。また、ウィザードで開発されたEAは、複数のシグナルを組み合わせたシステム設計が可能なため、今回テストに使用するカスタムシグナルのみを前提とせず、柔軟な設定ができる点も注目に値します。

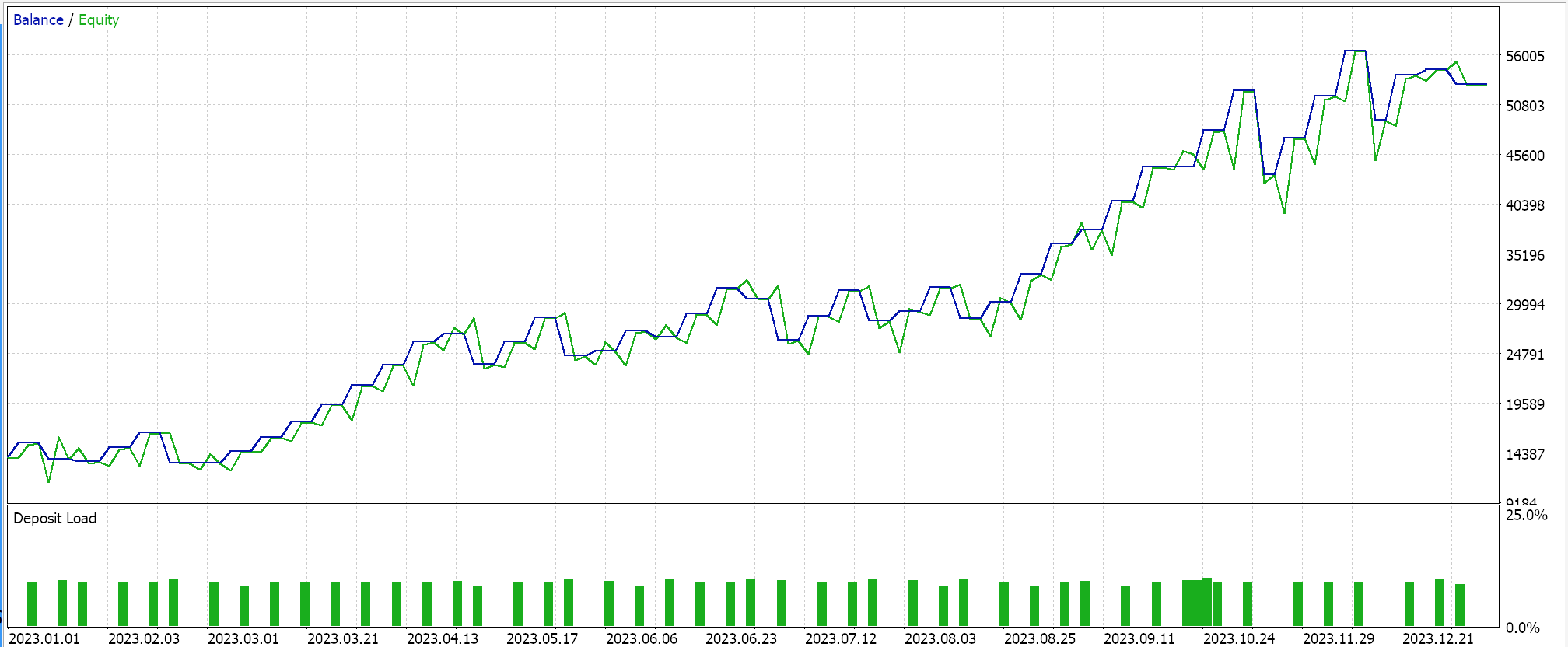
今回、SVRを活用したカスタムシグナルと、MLPを利用したトレーリングストップ機能付きのカスタムクラスを開発しました。これに基づき、以下の結果は2つの異なるEA（インターフェイスコードも含む）を用いたテスト実行に対するものです。最初のテストでは、トレーリングストップなしでカスタムシグナルのみを使用した場合の結果を示しています。

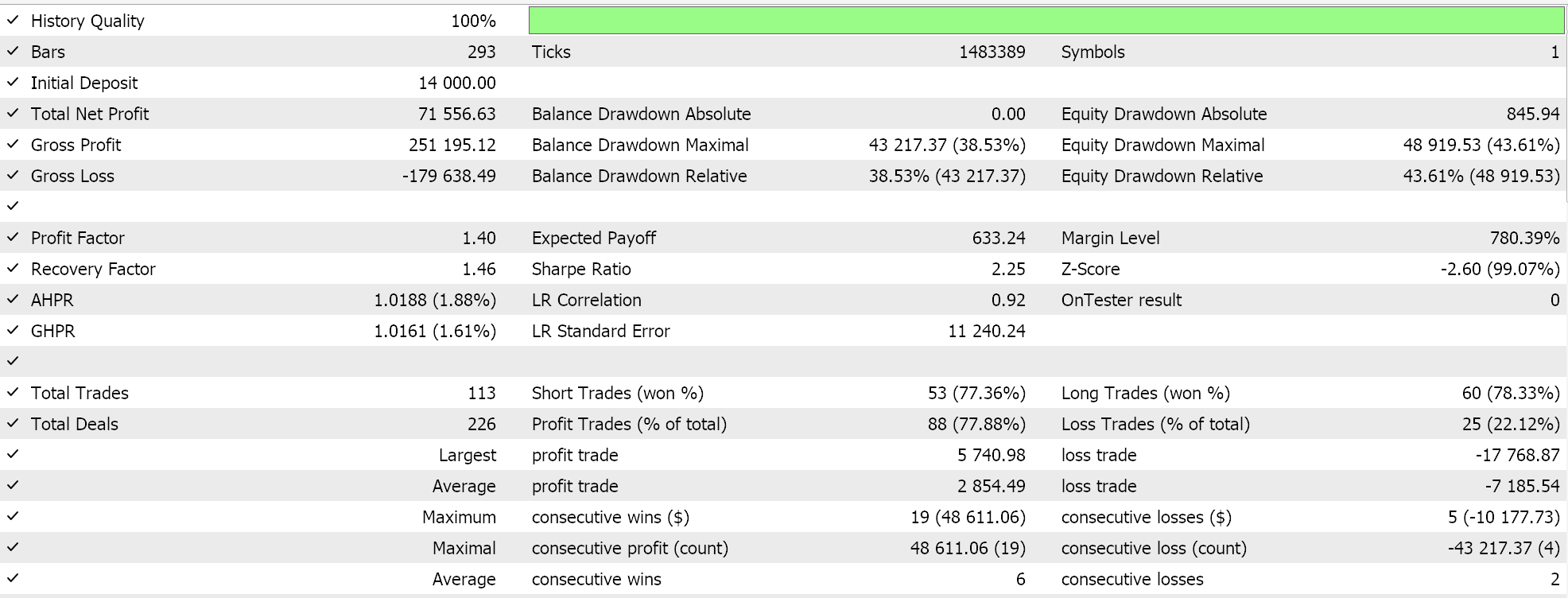
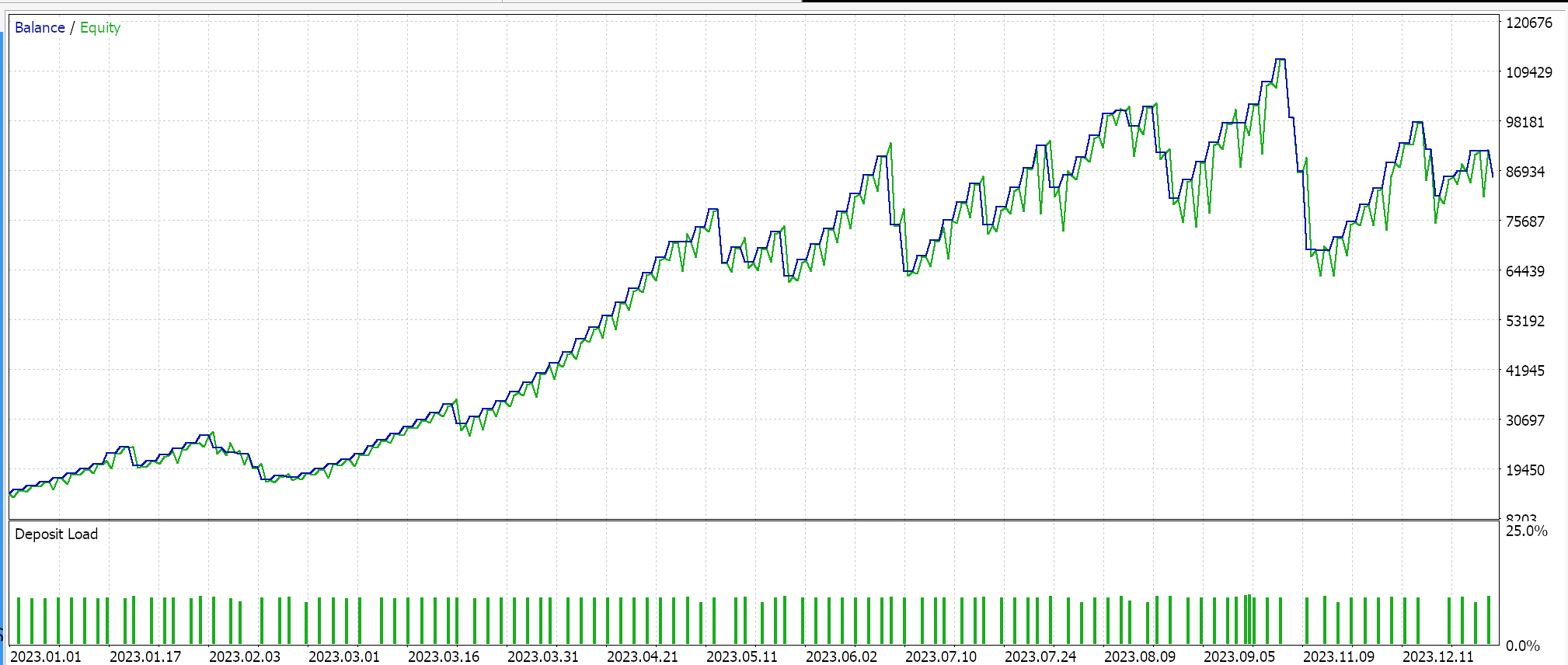
2つ目は、上で実装したカスタムシグナルとカスタムトレーリングクラスを使います。その結果も以下に示します。

結論

本稿では、サポートベクトル回帰(SVR)について考察し、これはガウス過程回帰(GPR)という別の回帰手法と対比して取り上げました。これら2つの回帰手法は、その適用分野においてほぼ正反対の特性を持っています。SVRは、変動が少なくトレンドのあるデータセットに適しているのに対し、GPRは変動が激しく不確実性の高い環境での適用に向いています。サポートベクトル回帰は、目的関数と決定関数を特徴とします。私たちは、シグナルクラスとカスタムトレーリングストップクラスにおいて、SVRの目的関数を利用した多層パーセプトロンの損失関数を導入しました。

決定関数を予測器として活用するためには、カーネル関数を追加で使用する必要があります。カーネルに関しては、前回のガウスプロセスカーネルの記事で詳しく検討しましたが、私たちの予測器は純粋にMLPに基づいているため、この記事ではカーネルの使用を省略しました。将来的には、様々な形状のカーネルを用いてこの手法を実行する可能性を考慮し、詳細に検討する予定です。ただし、SVRの損失関数に焦点を当てた本稿では、損失に影響されないパラメータεを使用することで、ニューラルネットワークの訓練に新たなアプローチをもたらすことができます。

このような損失感受性の高いパラメータεは、回帰というよりも分類器に近い動作を示すため、従来の回帰ネットワークよりも分類器ネットワークでの使用が適していると考えられます。しかしながら、SVRは依然として連続的な出力（10進数データセット）を処理し、類似の形式で数値予測をおこないます。これは単にεマージンを用いて、誤差に対してペナルティを科すべきかどうかを判断しますが、最終的な目的はあくまで回帰であり、分類ではないのです。