Beispiel einer Kausalitätsnetzwerkanalyse (CNA) und eines Vektor-Autoregressionsmodells zur Vorhersage von Marktereignissen

Einführung

Die Kausalitätsnetzwerkanalyse (Causality Network Analysis, CNA) ist eine Methode zum Verständnis und zur Modellierung komplexer kausaler Beziehungen zwischen Variablen in einem System. Bei der Anwendung auf die Finanzmärkte kann sie helfen zu erkennen, wie sich verschiedene Marktereignisse und Faktoren gegenseitig beeinflussen, was zu genaueren Vorhersagen führen kann.

Kausale Entdeckung: Bei der Kausalitätsermittlung werden kausale Beziehungen aus Beobachtungsdaten abgeleitet. Im Zusammenhang mit den Finanzmärkten bedeutet dies, zu ermitteln, welche Variablen (wie Wirtschaftsindikatoren, Marktpreise oder externe Ereignisse) kausale Auswirkungen auf andere haben. Es gibt mehrere Algorithmen für die Kausalerkennung, aber einer der beliebtesten ist der PC-Algorithmus (Peter-Clark-Algorithmus).

Dieser Trading Bot implementiert nicht explizit ein System namens „Causality Network Analysis for Market Event Prediction“ als benannte Komponente. Der Bot enthält jedoch Elemente der Kausalanalyse und netzwerkbasierter Ansätze, die konzeptionell ähnlich sind. Schauen wir uns das mal genauer an:

Kausalanalyse: Der Bot verwendet einen Kausalerkennungsalgorithmus, insbesondere den FCI-Algorithmus (Fast Causal Inference) (anstelle des PC-Algorithmus). Dies ist in der Funktion FCIAlgorithm() implementiert.

Netzwerkanalyse: Der Bot verwendet eine Netzwerkstruktur, um Beziehungen zwischen verschiedenen Finanzinstrumenten oder Indikatoren darzustellen. Dies ist aus der Node-Struktur und der Funktion SetupNetwork() ersichtlich.

Vorhersage des Ereignisses: Auch wenn der Bot nicht ausdrücklich als „Ereignisprognose“ bezeichnet wird, verwendet er ein Vektor-Autoregressions-Modell (VAR), um Vorhersagen über künftige Marktzustände zu treffen. Dies wird in Funktionen wie TrainVARModel() und PredictVARValue() umgesetzt.

Kausalitätsnetzanalyse: Eine neue Grenze für die Vorhersage von Marktereignissen

In der Welt des algorithmischen Handels gewinnt ein neuer Ansatz bei Quants und Händlern gleichermaßen an Bedeutung: Kausalitätsnetzwerkanalyse für die Vorhersage von Marktereignissen. Diese ausgefeilte Methode kombiniert die Leistungsfähigkeit von Kausalschlüssen, Netzwerktheorie und prädiktiver Analytik, um wichtige Marktereignisse mit bisher unerreichter Genauigkeit vorherzusagen.

Stellen Sie sich den Finanzmarkt als ein riesiges, zusammenhängendes Netz vor. Jedes Konzept stellt eine Beziehung zwischen verschiedenen Marktvariablen dar - Aktienkurse, Wirtschaftsindikatoren, geopolitische Ereignisse und mehr. Die traditionelle Analyse konzentriert sich oft auf Korrelationen, aber wie jeder erfahrene Händler weiß, bedeutet Korrelation nicht immer Kausalität.

Hier kommt die Kausalitätsnetzanalyse ins Spiel. Sie zielt darauf ab, die wahren Ursache-Wirkungs-Beziehungen innerhalb dieses komplexen Netzes aufzudecken. Auf diese Weise erhalten die Händler ein tieferes Verständnis der Marktdynamik und können Ereignisse vorhersehen, die für die herkömmliche Analyse unsichtbar sind.

Die Analyse des Kausalitätsnetzes umfasst im Wesentlichen drei Schritte:

1. Aufbau des Netzwerks: Zunächst konstruieren wir ein Netzwerk, in dem jeder Knoten eine Marktvariable darstellt. Diese können von den Preisen der Kapitalanlagen und Handelsvolumina bis hin zu Wirtschaftsindikatoren und Stimmungswerten reichen.

2. Entdeckung kausaler Zusammenhänge: Anschließend verwenden wir fortschrittliche Algorithmen, um die kausalen Beziehungen zwischen diesen Knoten zu ermitteln. Das ist der Punkt, an dem sich die Magie entfaltet - wir untersuchen nicht nur, welche Variablen sich gemeinsam bewegen, sondern auch, welche davon tatsächlich Veränderungen bei anderen bewirken.

3. Ereignisse vorhersagen: Schließlich nutzen wir dieses kausale Netzwerk, um wichtige Marktereignisse vorherzusagen. Wenn wir die wahren Triebkräfte der Marktbewegungen verstehen, können wir größere Umschwünge, Crashs oder Erholungen besser vorhersehen.

Die Vorteile für Trader

Für MQL5-Händler kann die Implementierung der Kausalitätsnetzwerkanalyse ein entscheidender Faktor sein. Hier ist der Grund dafür:

• Verbessertes Risikomanagement: Wenn Sie die Ursachen der Marktvolatilität erkennen, können Sie sich besser auf mögliche Abschwünge vorbereiten.
• Präzisere Vorhersagen: Das Verständnis der kausalen Zusammenhänge führt zu zuverlässigeren Prognosen als solche, die auf bloßen Korrelationen beruhen.
• Verborgene Möglichkeiten aufdecken: Das Kausalitätsnetzwerk kann Verbindungen aufzeigen, die auf den ersten Blick nicht offensichtlich sind und zu einzigartigen Handelsmöglichkeiten führen.
• Anpassungsfähige Strategien: Wenn sich der Markt entwickelt, tut dies auch das kausale Netzwerk, sodass sich Ihre Strategien in Echtzeit anpassen können.

Implementierung in MQL5

Die Implementierung eines vollständigen Systems zur Analyse von Kausalitätsnetzwerken ist zwar komplex, aber MQL5 bietet eine robuste Plattform für diese Art von fortgeschrittener Analyse. Sie könnten damit beginnen:

1. Verwendung der Funktion „iCustom()“ zur Erstellung von Indikatoren für jeden Knoten in Ihrem Netz.
2. Implementierung von Algorithmen zur Kausalitätserkennung wie dem PC-Algorithmus oder Granger-Kausalitätstests (in diesem Fall wurden FCI-Algorithmen verwendet).
3. Nutzung der neuronalen Netzwerkfähigkeiten von MQL5 zur Erstellung von Prognosemodellen auf der Grundlage Ihres Kausalnetzwerks.

Warum haben wir FCI und nicht PC verwendet?

FCI (Fast Causal Inference) und PC (Peter-Clark) sind beides Algorithmen zur Entdeckung kausaler Zusammenhänge, die auf dem Gebiet der kausalen Inferenz eingesetzt werden. Sie dienen dazu, aus Beobachtungsdaten kausale Zusammenhänge abzuleiten. Hier ist der Grund, warum man die FCI dem PC vorziehen könnte:

1. Latente Störfaktoren: Der Hauptvorteil der FCI gegenüber der PC ist ihre Fähigkeit, latente Störfaktoren zu berücksichtigen. Die FCI kann auf das Vorhandensein verborgener gemeinsamer Ursachen schließen, während die PC von kausaler Suffizienz ausgeht (keine latenten Störfaktoren).
2. Auswahlverzerrung: FCI kann auch Selektionsverzerrungen in den Daten berücksichtigen, was PC nicht kann.
3. Ein allgemeineres Modell: FCI erzeugt ein allgemeineres grafisches Modell, das als Partial Ancestral Graph (PAG) bezeichnet wird und eine breitere Klasse von Kausalstrukturen darstellen kann als die von PC erzeugten Directed Acyclic Graphs (DAGs).
4. Solidität und Vollständigkeit: FCI ist solide und vollständig für die Klasse der kausal unzureichenden Systeme, d.h. es kann alle möglichen kausalen Beziehungen bei unendlicher Stichprobengröße korrekt identifizieren.
5. Robustheit: Aufgrund seiner Fähigkeit, latente Störfaktoren und Selektionsverzerrungen zu behandeln, ist FCI im Allgemeinen robuster, wenn es um reale Daten geht, bei denen versteckte Variablen häufig vorkommen.

Es ist jedoch anzumerken, dass die FCI im Vergleich zum PC einige Nachteile hat:

1. Berechnungskomplexität: FCI ist im Allgemeinen rechenintensiver als PC, insbesondere bei großen Datensätzen.
2. Weniger endgültige Ergebnisse: Die von FCI erzeugten PAGs enthalten oft mehr unbestimmte Kantenrichtungen als die DAGs von PC, was die zusätzliche Unsicherheit durch potenzielle latente Confounder widerspiegelt.
3. Interpretation: PAGs können für Nicht-Experten schwieriger zu interpretieren sein als DAGs.

In der Praxis hängt die Wahl zwischen FCI und PC oft von den spezifischen Anforderungen Ihrer Kausalschlussaufgabe, der Art Ihrer Daten und Ihren Annahmen über das Kausalsystem ab. Wenn Sie sicher sind, dass es keine versteckten Störfaktoren und keine Selektionsverzerrungen gibt, könnte PC ausreichend und effizienter sein. Wenn Sie latente Variablen oder Selektionsverzerrungen vermuten, wäre die FCI die geeignetere Wahl.

Vektorautoregressionsmodell (VAR)

VAR ist ein multivariater Prognosealgorithmus, der verwendet wird, wenn sich zwei oder mehr Zeitreihen gegenseitig beeinflussen. In diesem Handelssystem wird es wahrscheinlich verwendet, um die Beziehungen zwischen verschiedenen Finanzinstrumenten oder Wirtschaftsindikatoren zu modellieren.

Hauptmerkmale von VAR:

1. Es erfasst lineare Abhängigkeiten zwischen mehreren Zeitreihen.
2. Jede Variable ist eine lineare Funktion vergangener Verzögerungen ihrer selbst und vergangener Verzögerungen der anderen Variablen.
3. Es ermöglicht eine reichhaltige Dynamik in einem System mit mehreren Zeitreihen.

Im Rahmen dieses Handelssystems:

• Das VAR-Modell wird mit der Funktion „TrainVARModel“ trainiert.
• Die Funktion „PredictVARValue“ verwendet das trainierte Modell, um Vorhersagen zu treffen.
• Das System optimiert das VAR-Modell, indem es die optimale Verzögerung und die signifikanten Variablen mit Hilfe der Funktion „OptimizeVARModel“ auswählt.

Mathematische Darstellung:

Für ein Zwei-Variablen-VAR-Modell mit Verzögerung 1:

y1,t = c1 + φ11y1,t-1 + φ12y2,t-1 + ε1,t

y2,t = c2 + φ21y1,t-1 + φ22y2,t-1 + ε2,t

wobei:

• y1,t und y2,t sind die Werte der beiden Variablen zum Zeitpunkt t
• c1 und c2 sind Konstanten
• φij sind die Koeffizienten
• ε1,t und ε2,t sind die Terme der Fehler

Das System schätzt diese Koeffizienten, um Vorhersagen zu treffen.

Stellen Sie sich vor, Sie sagen nicht nur den künftigen Preis eines einzelnen Vermögenswerts voraus, sondern prognostizieren gleichzeitig mehrere miteinander verknüpfte Finanzvariablen. Hier kommt VAR ins Spiel. Es ist, als hätte man eine Kristallkugel, die einem nicht nur eine Zukunft zeigt, sondern gleich mehrere miteinander verknüpfte Zukünfte.

Im Kern ist VAR ein multivariater Prognosealgorithmus, der verwendet wird, wenn sich zwei oder mehr Zeitreihen gegenseitig beeinflussen. Einfacher ausgedrückt: Es ist eine Möglichkeit, die linearen Abhängigkeiten zwischen mehreren Zeitreihen zu erfassen.

Wie funktioniert die VAR-Magie?

Schauen wir uns das mal an:

1. Datenerhebung: Wir beginnen damit, historische Daten für alle Variablen zu sammeln, die wir in unser Modell einbeziehen wollen. Dabei kann es sich um Preisdaten für mehrere Währungspaare, Rohstoffe oder sogar Wirtschaftsindikatoren handeln.
2. Spezifikation des Modells: Wir entscheiden, wie viele Verzögerungen (vergangene Zeiträume) wir einbeziehen möchten. Hier kommt die Handelserfahrung ins Spiel!
3. Schätzung: Das Modell schätzt, wie jede Variable von ihren eigenen Vergangenheitswerten und den Vergangenheitswerten der anderen Variablen beeinflusst wird.
4. Vorhersage: Einmal geschätzt, kann das VAR-Modell Prognosen für alle einbezogenen Variablen gleichzeitig erstellen.

Implementierung von VAR in MQL5

MQL5 verfügt zwar nicht über eine eingebaute VAR-Funktion, aber Sie können sie selbst implementieren. Hier ein vereinfachtes Beispiel dafür, wie Sie Ihren Code strukturieren könnten:

// Define your VAR model
struct VARModel {
    int lag;
    int variables;
    double[][] coefficients;
};

// Estimate VAR model
VARModel EstimateVAR(double[][] data, int lag) {
    // Implement estimation logic here
    // You might use matrix operations for efficiency
}

// Make predictions
double[] Forecast(VARModel model, double[][] history) {
    // Implement forecasting logic here
}

// In your EA or indicator
void OnTick() {
    // Collect your multivariate data
    double[][] data = CollectData();
    
    // Estimate model
    VARModel model = EstimateVAR(data, 5); // Using 5 lags
    
    // Make forecast
    double[] forecast = Forecast(model, data);
    
    // Use forecast in your trading logic
    // ...
}

Der VAR-Vorteil in Aktion

Stellen Sie sich vor, Sie handeln mit EUR/USD. Ein traditioneller Ansatz könnte sich auf die vergangenen EUR/USD-Kurse beschränken. Aber mit VAR könnten Sie es einbeziehen:

• EUR/USD-Preise
• USD/JPY-Kurse (zur Erfassung der allgemeinen USD-Stärke)
• Ölpreise (ein wichtiger Faktor für viele Währungen)
• S&P 500-Index (zur Messung der allgemeinen Marktstimmung)
• US-EU-Zinsdifferenz

Das Modell zeichnet nun ein viel umfassenderes Bild der Devisenlandschaft, was zu fundierteren Handelsentscheidungen führen kann.

Herausforderungen und Überlegungen

Wie jedes leistungsfähige Instrument birgt auch VAR seine Herausforderungen:

1. Datenanforderungen: VAR-Modelle können sehr datenintensiv sein. Stellen Sie sicher, dass Sie über genügend historische Daten verfügen, um zuverlässige Schätzungen vornehmen zu können.
2. Berechnungsintensität: Mit zunehmender Anzahl von Variablen und Verzögerungen steigen auch die Rechenanforderungen. Optimieren Sie Ihren Code auf Effizienz.
3. Stationarität: VAR geht von stationären Zeitreihen aus. Möglicherweise müssen Sie Ihre Daten vorverarbeiten (z. B. durch Differenzierung), um diese Annahme zu erfüllen.
4. Interpretation: Bei mehreren Variablen und Verzögerungen kann die Interpretation der VAR-Ergebnisse komplex sein. Vergessen Sie nicht, statistische Erkenntnisse mit Ihrem Handelswissen zu kombinieren.

Netzwerkanalyse im CNA-Handelssystem

Die in diesem Expert Advisor (EA) implementierte Netzwerkanalyse ist ein wesentlicher Bestandteil seiner Marktanalyse- und Prognosestrategie. Es wurde entwickelt, um die komplexen Beziehungen zwischen verschiedenen Finanzinstrumenten oder Marktvariablen darzustellen und zu analysieren.

Um die wichtigsten Punkte der in dieser EA verwendeten Netzwerkanalyse zusammenzufassen:

1. Struktur: Das Netz besteht aus Knoten, die jeweils ein Finanzinstrument (in der Regel ein Währungspaar) darstellen.
2. Zweck: Es wurde entwickelt, um die Beziehungen und Abhängigkeiten zwischen verschiedenen Finanzinstrumenten auf dem Markt zu modellieren.
3. Kausale Entdeckung: Die EA verwendet den Algorithmus Fast Causal Inference (FCI), um potenzielle kausale Beziehungen zwischen diesen Instrumenten aufzudecken.
4. Vertretung: Diese Beziehungen werden in einer Adjazenzmatrix dargestellt, aus der hervorgeht, welche Instrumente im Hinblick auf den kausalen Einfluss direkt miteinander verbunden sind.
5. Analyse: Der EA führt verschiedene Analysen an diesem Netzwerk durch, einschließlich der Identifizierung von V-Strukturen (ein spezifisches Muster in Kausaldiagrammen) und der Anwendung von Orientierungsregeln, um das Verständnis der kausalen Beziehungen weiter zu verfeinern.
6. Integration mit Vorhersage: Die Netzwerkstruktur und die durch diese Analyse entdeckten Beziehungen dienen als Input für das Vektor-Autoregressions-Modell (VAR), das für die Erstellung von Prognosen verwendet wird.
7. Anpassungsfähige Natur: Die Netzwerkanalyse ist nicht statisch. Sie kann im Laufe der Zeit aktualisiert werden, sodass sich der EA an veränderte Marktbedingungen und Beziehungen zwischen Instrumenten anpassen kann.

Der Grundgedanke hinter diesem Ansatz ist, dass sich Finanzinstrumente nicht isoliert bewegen. Durch die Modellierung und Analyse des Beziehungsgeflechts zwischen verschiedenen Instrumenten will die EA ein umfassenderes Verständnis der Marktdynamik gewinnen. Theoretisch sollte dies zu genaueren Vorhersagen und besser informierten Handelsentscheidungen führen.

Es ist jedoch wichtig zu wissen, dass dieser Ansatz zwar ausgeklügelt ist, die Finanzmärkte jedoch äußerst komplex sind und von vielen Faktoren beeinflusst werden. Die Wirksamkeit dieser Netzwerkanalyse hängt davon ab, wie gut sie die reale Marktdynamik erfasst und wie sie in andere Komponenten der Handelsstrategie integriert wird.

Struktur des Netzes

Das Netz wird durch die folgenden Strukturen dargestellt:

struct Node
{
    string name;
    double value;
};

Node g_network[];
int g_node_count = 0;

Jeder Knoten im Netz steht für ein bestimmtes Finanzinstrument oder eine Marktvariable. Das Namensfeld identifiziert das Instrument (z. B. „EURUSD“, „GBPUSD“), und das Wertfeld kann relevante Daten für diesen Knoten speichern.

Einrichten des Netzwerks

Das Netzwerk wird mit der Funktion SetupNetwork() initialisiert:

void SetupNetwork()
{
    string symbols[] = {"EURUSD", "GBPUSD", "USDCAD", "USDCHF", "USDJPY", "AUDUSD"};
    for(int i = 0; i < ArraySize(symbols); i++)
    {
        AddNode(symbols[i]);
    }
}

void AddNode(string name)
{
    ArrayResize(g_network, g_node_count + 1);
    g_network[g_node_count].name = name;
    g_network[g_node_count].value = 0; // Initialize with default value
    g_node_count++;
}

Auf diese Weise entsteht ein Netzwerk, in dem jeder Knoten ein anderes Währungspaar repräsentiert.

Zweck des Netzes

Das Netz dient in diesem EA mehreren wichtigen Zwecken:

1. Darstellung der Marktstruktur: Er modelliert die Zusammenhänge zwischen verschiedenen Währungspaaren, sodass der EA berücksichtigen kann, wie sich Bewegungen in einem Paar auf andere auswirken könnten.
2. Grundlage für die Kausalanalyse: Die Netzwerkstruktur wird als Grundlage für den Algorithmus Fast Causal Inference (FCI) verwendet, der versucht, kausale Beziehungen zwischen den Knoten zu entdecken.
3. Input für prädiktive Modellierung: Die Netzwerkstruktur und die durch die Kausalanalyse ermittelten Beziehungen dienen als Input für das Vektor-Autoregressionsmodell (VAR), das für die Vorhersagen verwendet wird.

Netzwerkanalyse in Aktion

Der EA führt mehrere Arten von Analysen in diesem Netzwerk durch:

1. Kausale Entdeckung: Die Funktion FCIAlgorithm() wendet den Algorithmus Fast Causal Inference an, um mögliche kausale Beziehungen zwischen den Knoten aufzudecken.
2. Adjazenzmatrix: Die kausalen Beziehungen werden in einer Adjazenzmatrix dargestellt, wobei jeder Eintrag angibt, ob eine direkte kausale Verbindung zwischen zwei Knoten besteht.
3. Ausrichtung der V-Struktur: Die Funktion OrientVStructures() identifiziert und orientiert v-Strukturen im Netz, die wichtige Muster in Kausaldiagrammen darstellen.
4. Graphische Analyse: Die endgültige Graphenstruktur wird analysiert, um Handelsentscheidungen zu treffen, wobei davon ausgegangen wird, dass kausal verknüpfte Instrumente einander vorhersagende Informationen liefern können.

Auswirkungen auf den Handel

Dieser netzwerkbasierte Ansatz ermöglicht es der EA,:

1. Berücksichtigen Sie komplexe Marktdynamiken, die bei einer isolierten Betrachtung der Instrumente möglicherweise nicht erkennbar sind.
2. Mögliche Identifizierung von Frühindikatoren unter den analysierten Instrumenten.
3. Treffen Sie fundiertere Vorhersagen, indem Sie den breiteren Marktkontext berücksichtigen.
4. Anpassung an sich ändernde Marktbedingungen, da die Kausalstruktur regelmäßig neu bewertet wird.

Durch die Nutzung dieser Netzwerkanalyse will der EA ein tieferes Verständnis der Marktdynamik gewinnen, was zu genaueren Vorhersagen und besser informierten Handelsentscheidungen führen kann.

Beispiel Code

Dieser Code folgt diesen beiden Flussdiagrammen:

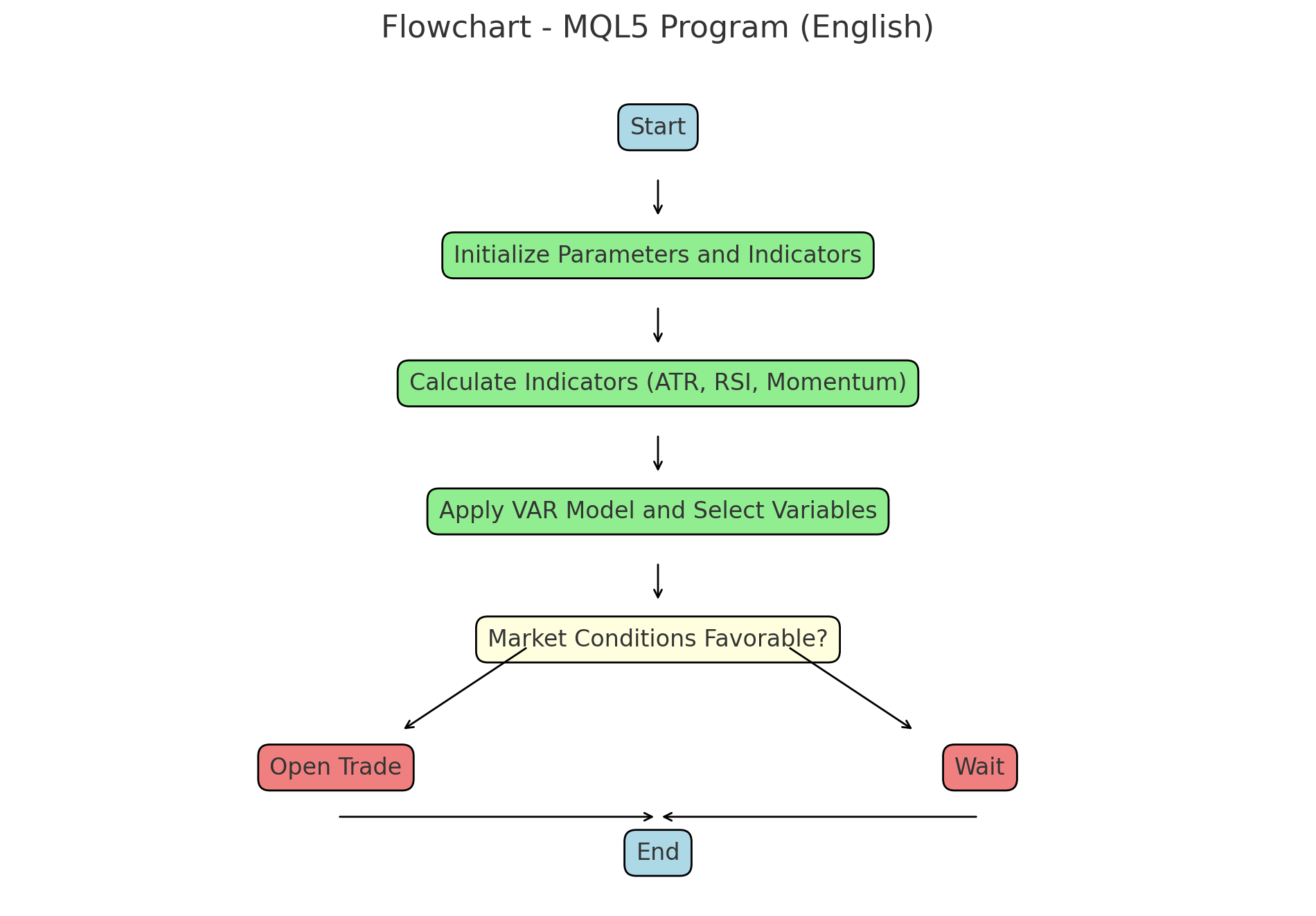
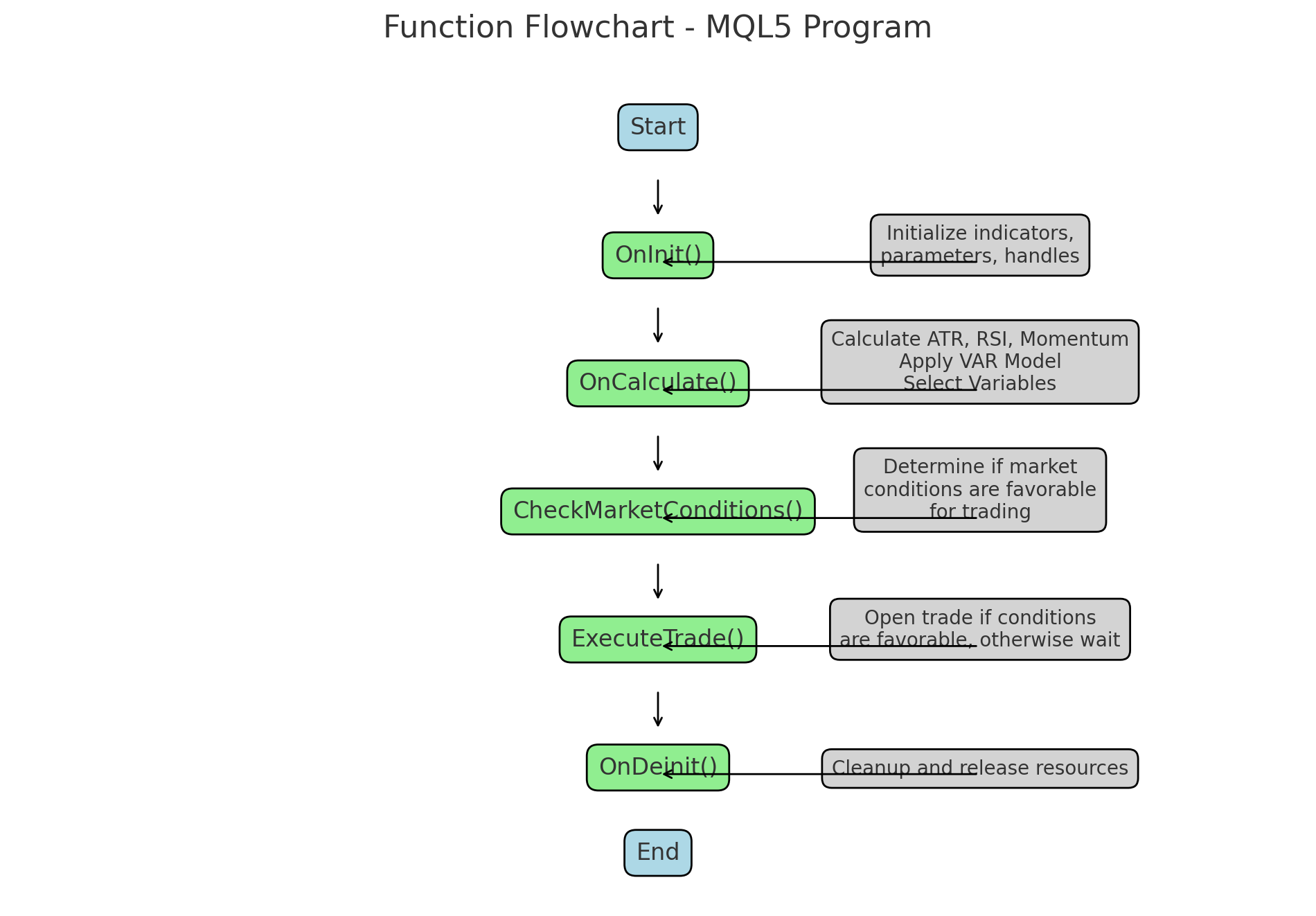
Detaillierte Erläuterung der wichtigsten Funktionen im MQL5-Handelsprogramm

Dieser Handels-EA ist ziemlich anspruchsvoll und kombiniert mehrere fortschrittliche Ansätze:

1. Es verwendet ein Vektor-Autoregressions-Modell (VAR) für Vorhersagen.
2. Es implementiert einen Kausalerkennungsalgorithmus (FCI - Fast Causal Inference), um Beziehungen zwischen verschiedenen Marktvariablen zu verstehen.
3. Es nutzt eine Netzwerkstruktur, um mehrere Finanzinstrumente gleichzeitig darzustellen und zu analysieren.
4. Er enthält verschiedene technische Filter wie Volatilität, RSI und Trendstärke.
5. Es nutzt adaptives Risikomanagement und Positionsgrößenbestimmung.
6. Es setzt eine gleitende Fenster-Strategie ein, um das Modell kontinuierlich zu aktualisieren und neu zu trainieren.
7. Es umfasst Techniken zur Kreuzvalidierung und Modelloptimierung.

Die Struktur des EA ermöglicht eine komplexe Analyse und Entscheidungsfindung, wobei die Flexibilität für künftige Verbesserungen oder Anpassungen an unterschiedliche Marktbedingungen erhalten bleibt.

Detaillierte Erläuterung der wichtigsten Funktionen im Handels-EA

1. OnInit()

int OnInit()
  {
// Step 1: Set up your network structure
   SetupNetwork();

// Step 2: Run the causal discovery algorithm (e.g., PC or FCI)
   FCIAlgorithm();

// Step 3: Train the optimized causal model
   TrainOptimizedVARModel();

   ArrayResize(g_previous_predictions, g_node_count);
   ArrayInitialize(g_previous_predictions, 0);  // Initialize with zeros

   return(INIT_SUCCEEDED);
  }

Dies ist die Initialisierungsfunktion, die ausgeführt wird, wenn der EA zum ersten Mal in einem Chart geladen oder neu geladen wird.

Hauptaufgaben:

• Einrichten der Netzwerkstruktur durch den Aufruf von SetupNetwork()
• Ausführen des Kausalerkennungsalgorithmus (FCI) mit FCIAlgorithm()
• Trainieren des optimierten Kausalmodells mit TrainOptimizedVARModel()
• Initialisieren des Arrays der vorherigen Vorhersagen

Diese Funktion bildet die Grundlage für alle Analysen und Vorhersagen, die der EA durchführen wird.

2. OnTick()

void OnTick()
  {
   ENUM_TIMEFRAMES tf = ConvertTimeframe(InputTimeframe);

   static datetime lastBarTime = 0;
   datetime currentBarTime = iTime(Symbol(), tf, 0);

   if(currentBarTime == lastBarTime)
      return;

   lastBarTime = currentBarTime;

   Print("--- New bar on timeframe ", EnumToString(tf), " ---");

   UpdateModelSlidingWindow();

   for(int i = 0; i < g_node_count; i++)
     {
      string symbol = g_network[i].name;
      Print("Processing symbol: ", symbol);

      double prediction = PredictVARValue(i);
      Print("Prediction for ", symbol, ": ", prediction);

      int signal = GenerateSignal(symbol, prediction);
      Print("Signal for ", symbol, ": ", signal);

      // Imprimir más detalles sobre las condiciones
      Print("RSI: ", CustomRSI(symbol, ConvertTimeframe(InputTimeframe), 14, PRICE_CLOSE, 0));
      Print("Trend: ", DetermineTrend(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Trend Strong: ", IsTrendStrong(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Volatility OK: ", VolatilityFilter(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Fast MA > Slow MA: ", (iMA(symbol, PERIOD_CURRENT, 14, 0, MODE_EMA, PRICE_CLOSE) > iMA(symbol, PERIOD_CURRENT, 24, 0, MODE_EMA, PRICE_CLOSE)));

      if(signal != 0)
        {
         Print("Attempting to execute trade for ", symbol);
         ExecuteTrade(symbol, signal);
        }
      else
        {
         g_debug_no_signal_count++;
         Print("No trade signal generated for ", symbol, ". Total no-signal count: ", g_debug_no_signal_count);
        }
      ManageOpenPositions();
      ManageExistingOrders(symbol);


      Print("Current open positions for ", symbol, ": ", PositionsTotal());
      Print("Current pending orders for ", symbol, ": ", OrdersTotal());
     }

   Print("--- Bar processing complete ---");
   Print("Total no-signal count: ", g_debug_no_signal_count);
   Print("Total failed trade count: ", g_debug_failed_trade_count);
  }

Diese Funktion wird bei jedem Markttick aufgerufen.

Hauptaufgaben:

• Konvertiert den eingegebenen Zeitrahmen
• Aktualisiert das Modell unter Verwendung eines Schiebefensters mit UpdateModelSlidingWindow()
• Für jedes Symbol im Netz:
  • Sagt Werte mit PredictVARValue() voraus
  • Erzeugt Handelssignale mit GenerateSignal()
  • Führt Trades aus, wenn Signale generiert werden
  • Verwaltet offene Positionen
  • Verwaltet bestehende Aufträge

Dies ist das operative Herzstück des EA, in dem die Handelsentscheidungen getroffen werden.

3. OnCalculate()

Diese Funktion wird zwar nicht explizit im bereitgestellten Code gezeigt, wird aber normalerweise zur Berechnung von nutzerdefinierten Indikatorwerten verwendet. In diesem EA scheint ein Teil dieser Funktionalität in OnTick() integriert zu sein.

4. CheckMarketConditions()

int GenerateSignal(string symbol, double prediction)
  {
   int node_index = FindNodeIndex(symbol);
   if(node_index == -1)
      return 0;

   static bool first_prediction = true;
   if(first_prediction)
     {
      first_prediction = false;
      return 0; // No generar señal en la primera predicción
     }

   double current_price = SymbolInfoDouble(symbol, SYMBOL_BID);

// Calculate predicted change as a percentage
   double predicted_change = (prediction - current_price) / current_price * 100;

   bool volatility_ok = VolatilityFilter(symbol, ConvertTimeframe(InputTimeframe));
   double rsi = CustomRSI(symbol, ConvertTimeframe(InputTimeframe), 14, PRICE_CLOSE, 0);
   bool trend_strong = IsTrendStrong(symbol, ConvertTimeframe(InputTimeframe));
   int trend = DetermineTrend(symbol, ConvertTimeframe(InputTimeframe));

   double fastMA = iMA(symbol, PERIOD_CURRENT, 8, 0, MODE_EMA, PRICE_CLOSE);
   double slowMA = iMA(symbol, PERIOD_CURRENT, 24, 0, MODE_EMA, PRICE_CLOSE);

   Print("Debugging GenerateSignal for ", symbol);
   Print("Current price: ", current_price);
   Print("Prediction diff: ", prediction);
   Print("predicted_change: ", predicted_change);
   Print("RSI: ", rsi);
   Print("Trend: ", trend);
   Print("Trend Strong: ", trend_strong);
   Print("Volatility OK: ", volatility_ok);
   Print("Fast MA: ", fastMA, ", Slow MA: ", slowMA);

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA;

   Print("Buy condition met: ", buy_condition);
   Print("Sell condition met: ", sell_condition);

// Buy conditions
   if(buy_condition)
     {
      Print("Buy signal generated for ", symbol);
      int signal = 1;
      return signal;  // Buy signal
     }
// Sell conditions
   else
      if(sell_condition)
        {
         Print("Sell signal generated for ", symbol);
         int signal = -1;
         return signal; // Sell signal
        }
      else
        {
         Print("No signal generated for ", symbol);
         int signal = 0;
         return signal; // No signal
        }


  }

Diese Funktion ist im Code nicht explizit definiert, aber ihre Funktionalität ist über mehrere Teile verteilt, hauptsächlich in GenerateSignal():

• Prüfen der Volatilität mit VolatilityFilter()
• Prüfen des RSI
• Prüfen der Trendstärke mit IsTrendStrong()
• Bestimmen der Trendrichtung mit DetermineTrend()
• Vergleichen von schnellen und langsamen, gleitende Durchschnitte

Dabei wird geprüft, ob die Marktbedingungen für den Handel günstig sind.

5. ExecuteTrade()

void ExecuteTrade(string symbol, int signal)
  {
   if(!IsMarketOpen(symbol) || !IsTradingAllowed())
     {
      Print("Market is closed or trading is not allowed for ", symbol);
      return;
     }

   double price = (signal == 1) ? SymbolInfoDouble(symbol, SYMBOL_ASK) : SymbolInfoDouble(symbol, SYMBOL_BID);

   double stopLoss, takeProfit;
   CalculateAdaptiveLevels(symbol, signal, stopLoss, takeProfit);

   double lotSize = CalculateDynamicLotSize(symbol, stopLoss);

   if(lotSize <= 0)
     {
      Print("Invalid lot size for symbol: ", symbol);
      return;
     }

   trade.SetExpertMagicNumber(123456);
   trade.SetTypeFilling(ORDER_FILLING_FOK);

   bool result = false;
   int attempts = 3;

   for(int i = 0; i < attempts; i++)
     {
      if(signal == 1)
        {
         result = trade.Buy(lotSize, symbol, price, stopLoss, takeProfit, "CNA Buy");
         Print("Attempting Buy order: Symbol=", symbol, ", Lot Size=", lotSize, ", Price=", price, ", SL=", stopLoss, ", TP=", takeProfit);
        }
      else
         if(signal == -1)
           {
            result = trade.Sell(lotSize, symbol, price, stopLoss, takeProfit, "CNA Sell");
            Print("Attempting Sell order: Symbol=", symbol, ", Lot Size=", lotSize, ", Price=", price, ", SL=", stopLoss, ", TP=", takeProfit);
           }

      if(result)
        {
         Print("Order executed successfully for ", symbol, ", Type: ", (signal == 1 ? "Buy" : "Sell"), ", Lot size: ", lotSize);
         break;
        }
      else
        {
         int lastError = GetLastError();
         Print("Attempt ", i+1, " failed for ", symbol, ". Error: ", lastError, " - ", GetErrorDescription(lastError));

         if(lastError == TRADE_RETCODE_REQUOTE || lastError == TRADE_RETCODE_PRICE_CHANGED || lastError == TRADE_RETCODE_INVALID_PRICE)
           {
            price = (signal == 1) ? SymbolInfoDouble(symbol, SYMBOL_ASK) : SymbolInfoDouble(symbol, SYMBOL_BID);
            CalculateAdaptiveLevels(symbol, signal, stopLoss, takeProfit);
           }
         else
            break;
        }
     }

   if(!result)
     {
      Print("All attempts failed for ", symbol, ". Last error: ", GetLastError(), " - ", GetErrorDescription(GetLastError()));
     }
  }

Diese Funktion übernimmt die eigentliche Ausführung der Handelsgeschäfte.

Wichtige Aspekte:

• Prüfen, ob der Markt geöffnet und der Handel erlaubt ist
• Berechnen von adaptiven Stop-Loss- und Take-Profit-Levels
• Bestimmen der Losgröße auf der Grundlage des Risikomanagements
• Versuch der Durchführung des Auftrags, mit Wiederholungsversuchen bei Misserfolg
• Fehlerbehandlung mit detaillierter Rückmeldung

6. OnDeinit()

void OnDeinit(const int reason)
  {
   if(atr_handle != INVALID_HANDLE)
      IndicatorRelease(atr_handle);
   if(rsi_handle != INVALID_HANDLE)
      IndicatorRelease(rsi_handle);
   if(momentum_handle != INVALID_HANDLE)
      IndicatorRelease(momentum_handle);
   GenerateFinalSummary();
  }

Diese Funktion wird aufgerufen, wenn der EA aus dem Chart entfernt wird oder wenn das Terminal geschlossen wird.

Hauptaufgaben:

• Gibt die Handles der Indikatoren frei
• Erzeugt eine endgültige Zusammenfassung der EA-Leistung durch den Aufruf von GenerateFinalSummary()

Weitere wichtige Funktionen

UpdateModelSlidingWindow()

void UpdateModelSlidingWindow()
  {
   static int bars_since_update = 0;
   ENUM_TIMEFRAMES tf = ConvertTimeframe(InputTimeframe);

// Check if it's time to update
   if(bars_since_update >= g_update_frequency)
     {
      // Collect new data
      double training_data[];
      CollectTrainingData(training_data, g_window_size, tf);

      // Retrain model
      TrainModel(training_data);

      // Validate model
      double validation_score = ValidateModel();
      Print("Model updated. Validation score: ", validation_score);

      bars_since_update = 0;
     }
   else
     {
      bars_since_update++;
     }
  }

Aktualisiert das VAR-Modell unter Verwendung eines gleitenden Datenfensters, sodass sich das Modell an veränderte Marktbedingungen anpassen kann.

TrainOptimizedVARModel()

void TrainOptimizedVARModel()
  {
   OptimizationResult opt_result = OptimizeVARModel();

   Print("Lag óptimo encontrado: ", opt_result.optimal_lag);
   Print("AIC: ", opt_result.aic);
   Print("Variables seleccionadas: ", ArraySize(opt_result.selected_variables));

// Usar opt_result.optimal_lag y opt_result.selected_variables para entrenar el modelo final
   TrainVARModel(opt_result.optimal_lag, opt_result.selected_variables);
  }

Optimiert und trainiert das VAR-Modell und wählt die optimale Anzahl von Verzögerungen und signifikanten Variablen.

VorhersageVARValue()

double PredictVARValue(int node_index)
{
   if(node_index < 0 || node_index >= g_node_count)
   {
      Print("Error: Invalid node index: ", node_index);
      return 0;
   }

   double prediction = 0;
   int lag = g_var_params[node_index].lag;

   Print("Predicting for node: ", g_network[node_index].name, ", Lag: ", lag);

   // Retrieve the previous prediction
   double previous_prediction = g_previous_predictions[node_index];

   // Verify if there are enough coefficients
   int expected_coefficients = g_node_count * lag + 1; // +1 for the intercept
   if(ArraySize(g_var_params[node_index].coefficients) < expected_coefficients)
   {
      Print("Error: Not enough coefficients for node ", node_index, ". Expected: ", expected_coefficients, ", Actual: ", ArraySize(g_var_params[node_index].coefficients));
      return 0;
   }

   prediction = g_var_params[node_index].coefficients[0]; // Intercept
   Print("Intercept: ", prediction);

   double sum_predictions = 0;
   double sum_weights = 0;
   double current_price = iClose(g_network[node_index].name, PERIOD_CURRENT, 0);

   for(int l = 1; l <= lag; l++)
   {
      double time_weight = 1.0 - (double)(l-1) / lag; // Time-based weighting
      sum_weights += time_weight;

      double lag_prediction = 0;
      for(int j = 0; j < g_node_count; j++)
      {
         int coeff_index = (l - 1) * g_node_count + j + 1;
         if(coeff_index >= ArraySize(g_var_params[node_index].coefficients))
         {
            Print("Warning: Coefficient index out of range. Skipping. Index: ", coeff_index, ", Array size: ", ArraySize(g_var_params[node_index].coefficients));
            continue;
         }

         double coeff = g_var_params[node_index].coefficients[coeff_index];
         double raw_value = iClose(g_network[j].name, PERIOD_CURRENT, l);

         if(raw_value == 0 || !MathIsValidNumber(raw_value))
         {
            Print("Warning: Invalid raw value for ", g_network[j].name, " at lag ", l);
            continue;
         }

         // Normalize the value as a percentage change
         double normalized_value = (raw_value - current_price) / current_price;

         double partial_prediction = coeff * normalized_value;
         lag_prediction += partial_prediction;

         Print("Lag ", l, ", Node ", j, ": Coeff = ", coeff, ", Raw Value = ", raw_value,
               ", Normalized Value = ", normalized_value, ", Partial prediction: ", partial_prediction);
      }

      sum_predictions += lag_prediction * time_weight;
      Print("Lag ", l, " prediction: ", lag_prediction, ", Weighted: ", lag_prediction * time_weight);
   }

   Print("Sum of weights: ", sum_weights);

   // Calculate the final prediction
   if(sum_weights > 1e-10)
   {
      prediction = sum_predictions / sum_weights;
   }
   else
   {
      Print("Warning: sum_weights is too small (", sum_weights, "). Using raw sum of predictions.");
      prediction = sum_predictions;
   }

   // Calculate the difference between the current prediction and the previous prediction
   double prediction_change = prediction - previous_prediction;

   Print("Previous prediction: ", previous_prediction);
   Print("Current prediction: ", prediction);
   Print("Prediction change: ", prediction_change);

   // Convert the prediction to a percentage change
   double predicted_change_percent = (prediction - current_price) / current_price * 100;

   Print("Final prediction (as percentage change): ", predicted_change_percent, "%");

   // Update the current prediction for the next iteration
   g_previous_predictions[node_index] = prediction;

   // Return the difference in basis points
   return prediction_change * 10000; // Multiply by 10000 to convert to basis points
}

Erstellt Vorhersagen unter Verwendung des trainierten VAR-Modells und berücksichtigt dabei historische Werte und Modellkoeffizienten.

ManageOpenPositions() und ManageExistingOrders()

void ManageOpenPositions()
  {
   for(int i = PositionsTotal() - 1; i >= 0; i--)
     {
      ulong ticket = PositionGetTicket(i);
      if(PositionSelectByTicket(ticket))
        {
         string symbol = PositionGetString(POSITION_SYMBOL);
         double openPrice = PositionGetDouble(POSITION_PRICE_OPEN);
         double currentPrice = PositionGetDouble(POSITION_PRICE_CURRENT);
         double stopLoss = PositionGetDouble(POSITION_SL);
         ENUM_POSITION_TYPE positionType = (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE);

         // Implement trailing stop
         if(positionType == POSITION_TYPE_BUY && currentPrice - openPrice > 2 * CustomATR(symbol, PERIOD_CURRENT, 14, 0))
           {
            double newStopLoss = NormalizeDouble(currentPrice - CustomATR(symbol, PERIOD_CURRENT, 14, 0), SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            if(newStopLoss > stopLoss)
              {
               trade.PositionModify(ticket, newStopLoss, 0);
              }
           }
         else
            if(positionType == POSITION_TYPE_SELL && openPrice - currentPrice > 2 * CustomATR(symbol, PERIOD_CURRENT, 14, 0))
              {
               double newStopLoss = NormalizeDouble(currentPrice + CustomATR(symbol, PERIOD_CURRENT, 14, 0), SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               if(newStopLoss < stopLoss || stopLoss == 0)
                 {
                  trade.PositionModify(ticket, newStopLoss, 0);
                 }
              }
        }
     }
  }

void ManageExistingOrders(string symbol)
  {
   for(int i = PositionsTotal() - 1; i >= 0; i--)
     {
      ulong ticket = PositionGetTicket(i);
      if(PositionSelectByTicket(ticket) && PositionGetString(POSITION_SYMBOL) == symbol)
        {
         double stopLoss = PositionGetDouble(POSITION_SL);
         double takeProfit = PositionGetDouble(POSITION_TP);
         double openPrice = PositionGetDouble(POSITION_PRICE_OPEN);
         double currentPrice = PositionGetDouble(POSITION_PRICE_CURRENT);
         ENUM_POSITION_TYPE positionType = (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE);

         double atr = CustomATR(symbol, PERIOD_CURRENT, 14, 0);
         double newStopLoss, newTakeProfit;

         if(positionType == POSITION_TYPE_BUY)
           {
            newStopLoss = NormalizeDouble(currentPrice - 2 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            newTakeProfit = NormalizeDouble(currentPrice + 3 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            if(newStopLoss > stopLoss && currentPrice - openPrice > atr)
              {
               trade.PositionModify(ticket, newStopLoss, newTakeProfit);
              }
           }
         else
            if(positionType == POSITION_TYPE_SELL)
              {
               newStopLoss = NormalizeDouble(currentPrice + 2 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               newTakeProfit = NormalizeDouble(currentPrice - 3 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               if(newStopLoss < stopLoss && openPrice - currentPrice > atr)
                 {
                  trade.PositionModify(ticket, newStopLoss, newTakeProfit);
                 }
              }

         // Implementar cierre parcial
         double profit = PositionGetDouble(POSITION_PROFIT);
         double volume = PositionGetDouble(POSITION_VOLUME);
         if(profit > 0 && MathAbs(currentPrice - openPrice) > 2 * atr)
           {
            double closeVolume = volume * 0.5;
            if(IsValidVolume(symbol, closeVolume))
              {
               ClosePosition(ticket, closeVolume);
              }
           }
        }
     }
  }

Sie verwalten die offene Positionen und bestehende Aufträge, indem sie die Strategien wie Trailing-Stops und Teilschließungen umsetzen.

Dieser EA kombiniert die traditionelle technische Analyse mit fortschrittlicher statistischer Modellierung (VAR) und maschinellen Lerntechniken (Kausalerkennung), um Handelsentscheidungen zu treffen. Der modulare Aufbau ermöglicht eine einfache Modifikation und Verbesserung der einzelnen Komponenten.

Ergebnisse

Dies sind die Ergebnisse für einige Symbole, die Einstellungen und Eingaben bleiben für alle untersuchten Symbole gleich:

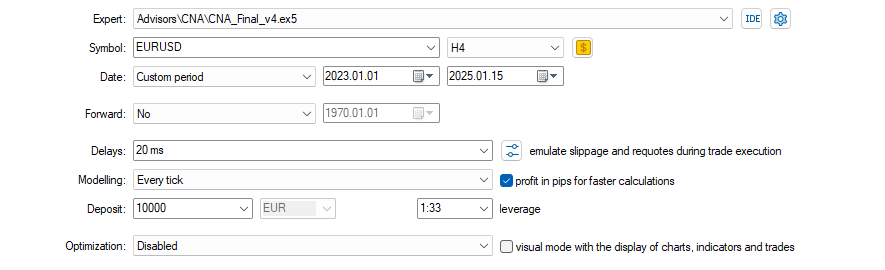
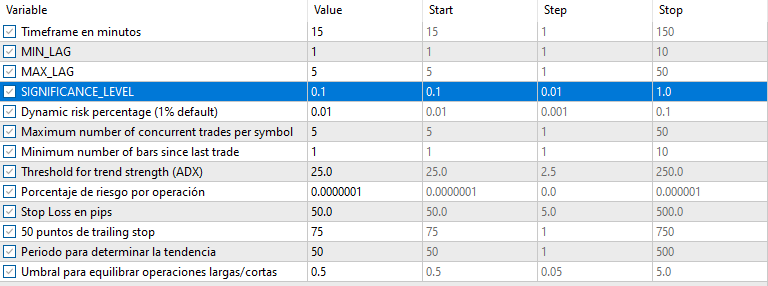
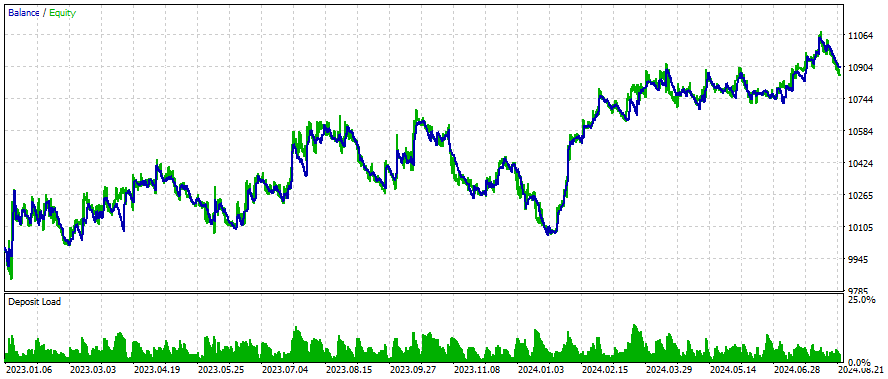
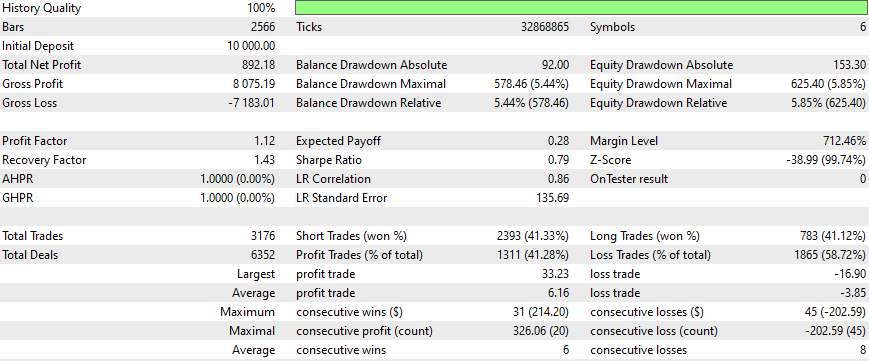
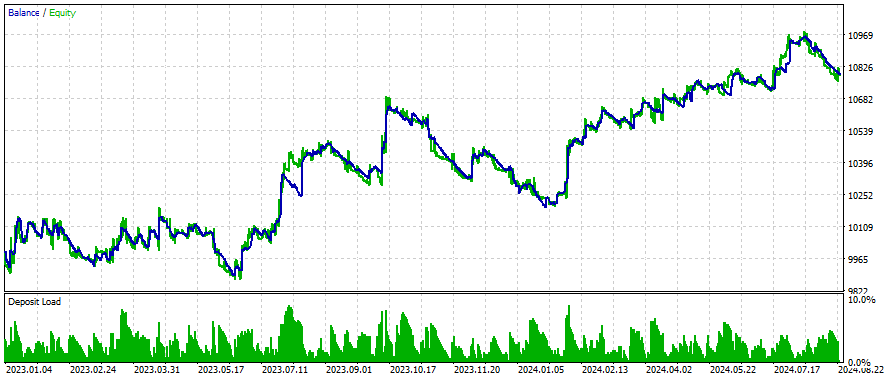
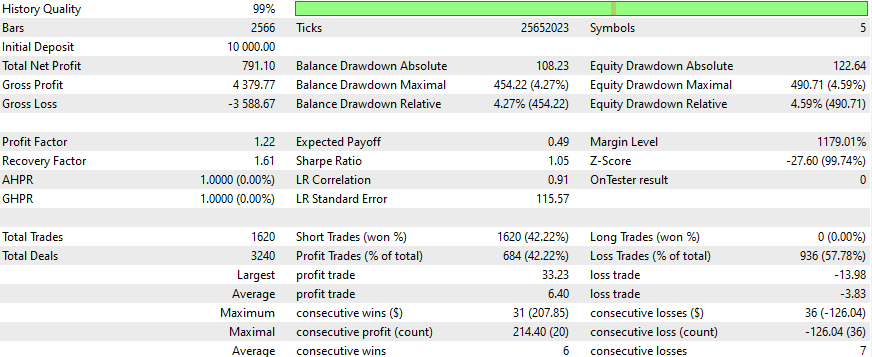
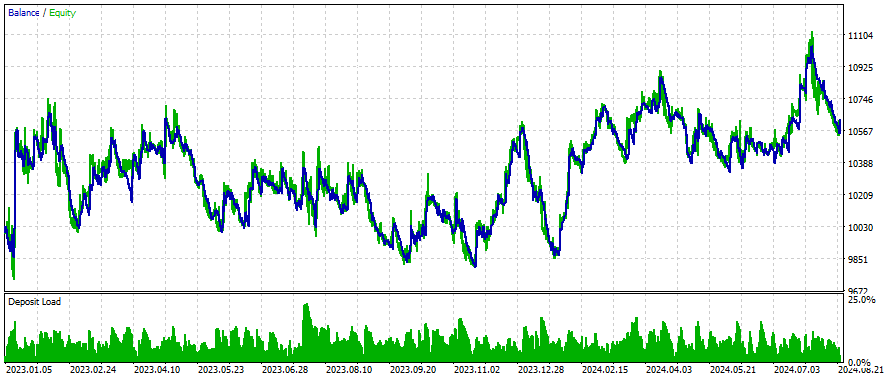
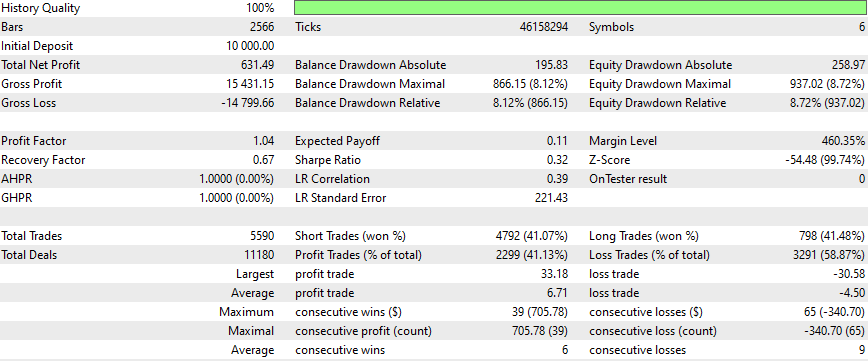
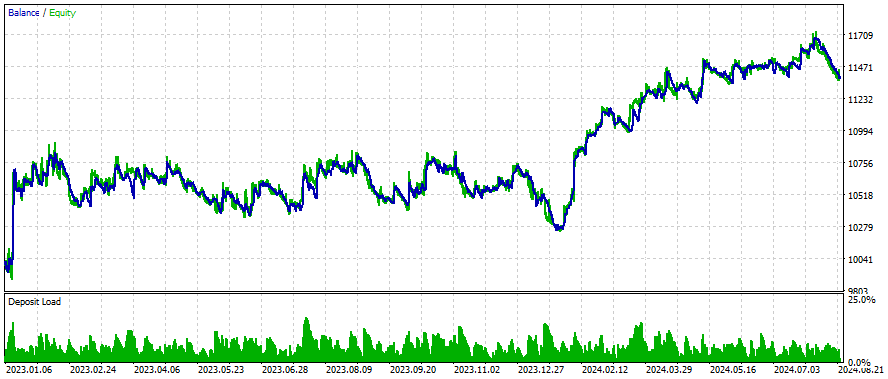
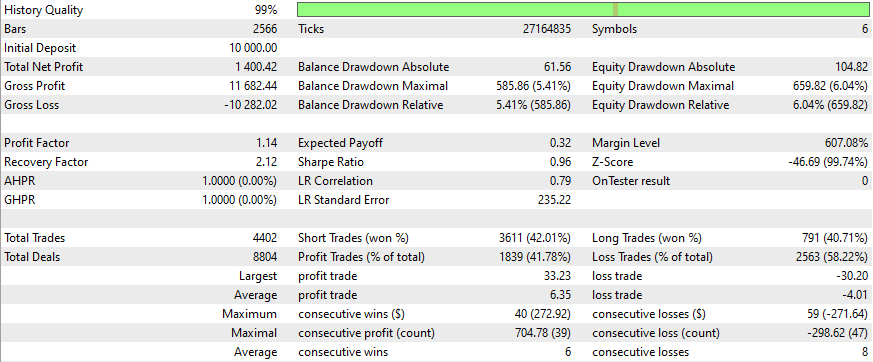
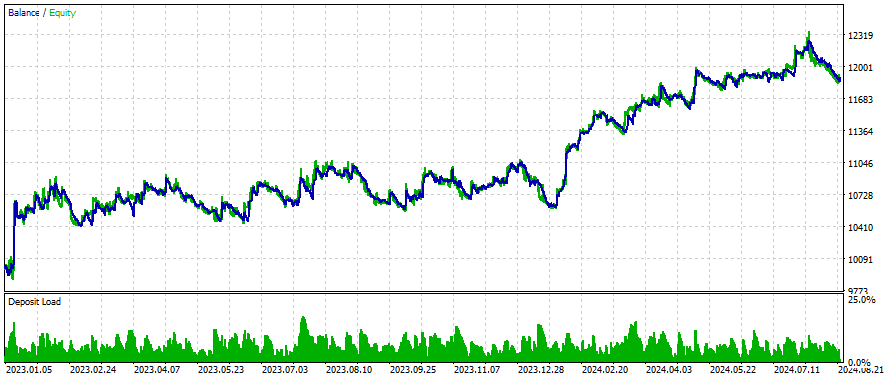
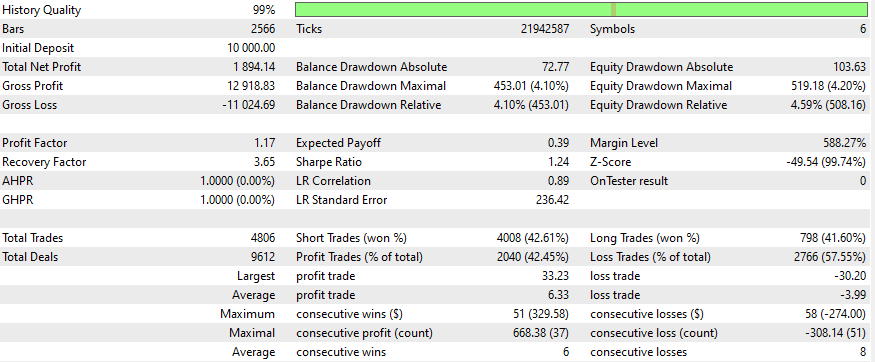
Wie kann man bessere Ergebnisse erzielen?

Bessere Ergebnisse lassen sich erzielen, wenn Sie im Symbolknoten mehr Symbole hinzufügen und auch kointegrierte und korrelierte Symbole verwenden. Um zu wissen, welches diese Symbole sind, können Sie mein Python-Skript aus diesem Artikel verwenden:  Anwendung der Nash'schen Spieltheorie mit HMM-Filterung im Handel - MQL5-Artikel.

Bessere Ergebnisse lassen sich auch erzielen, wenn man die Strategie durch Deep Learning ergänzt. Einige Beispiele dafür finden sich in Artikeln wie diesem:  Sentiment-Analyse und Deep Learning für den Handel mit EA und Backtesting mit Python - MQL5 Artikel 

Außerdem wurden die Filter nicht optimiert, und Sie könnten auch versuchen, weitere Filter hinzuzufügen.

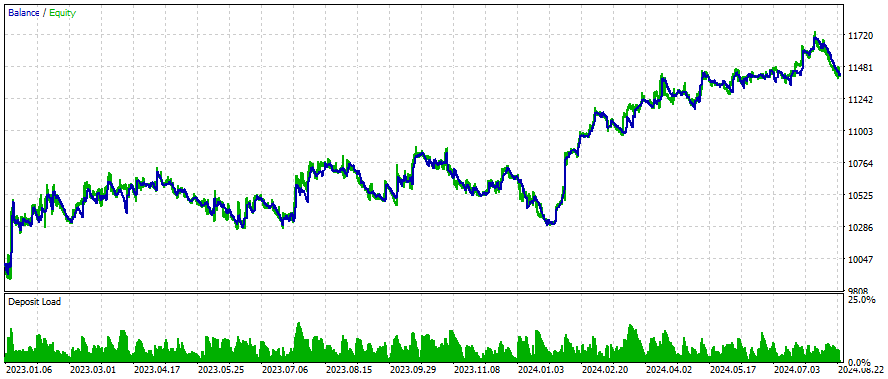
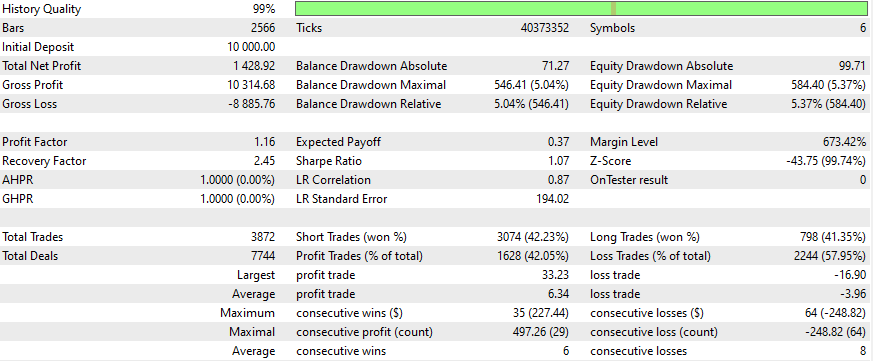
Beispiel dafür, wie sich der Graph verändert, wenn dem Netz weitere Symbole hinzugefügt werden

void SetupNetwork()
  {
   string symbols[] = {"EURUSD", "GBPUSD", "USDCAD", "USDCHF", "USDJPY", "AUDUSD", "XAUUSD", "SP500m", "ND100m"};
   for(int i = 0; i < ArraySize(symbols); i++)
     {
      AddNode(symbols[i]);
     }
  }

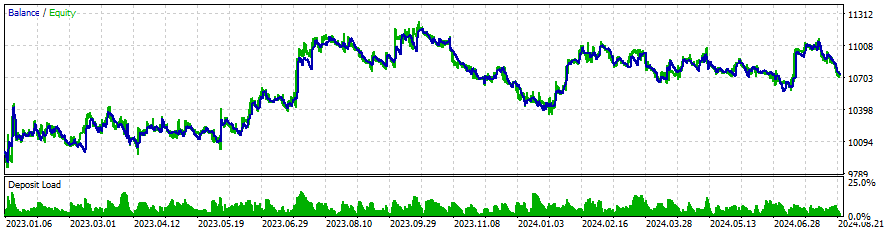
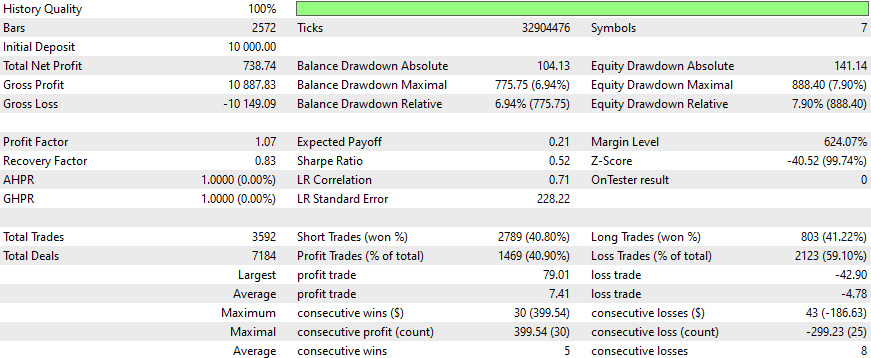
Durch das Hinzufügen weiterer Symbole zum Netz konnten wir uns verbessern:

1. Handelsaktivität (mehr Handelsgeschäfte insgesamt)
2. Gewinnrate im Kurzhandel
3. Prozentsatz der gewinnbringenden Abschlüsse
4. Umfang des größten profitablen Handels
5. Durchschnittlicher Gewinn pro gewonnenem Handel
6. Geringerer Anteil an Verlustgeschäften
7. Geringerer durchschnittlicher Verlust pro Verlustgeschäft

Diese Verbesserungen deuten auf ein insgesamt besseres Handelsmanagement und eine bessere Risikokontrolle hin, auch wenn einige wichtige Leistungskennzahlen (wie der Gewinnfaktor und der Erholungsfaktor) niedriger sind.

Schlussfolgerung

In diesem Artikel wird ein fortschrittliches Handelssystem erörtert, das die Kausalitätsnetzwerkanalyse (CNA) und die Vektor-Autoregression (VAR) zur Vorhersage von Marktereignissen und für Handelsentscheidungen integriert. Das System verwendet ausgefeilte statistische und maschinelle Lerntechniken, um Beziehungen zwischen Finanzinstrumenten zu modellieren. Er ist zwar vielversprechend, unterstreicht aber, wie wichtig es ist, diesen Ansatz mit einem soliden Risikomanagement und einem tiefen Verständnis der Märkte zu kombinieren.

Für Händler, die bessere Ergebnisse erzielen möchten, schlägt der Artikel vor, das Netzwerk mit mehr korrelierten Symbolen zu erweitern, Deep Learning einzubeziehen und die Filtermethoden zu optimieren. Kontinuierliches Lernen und Anpassung sind für den langfristigen Erfolg im Handel entscheidend.

Viel Spaß beim Handeln, und mögen Ihre Algorithmen dem Markt immer einen Schritt voraus sein!