MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 60): Inferenzlernen (Wasserstein-VAE) mit gleitendem Durchschnitt und stochastischen Oszillatormustern

Einführung

Bei der Untersuchung der Muster, die sich aus der Paarung von MA und stochastischem Oszillator ergeben, haben wir das maschinelle Lernen als Mittel zur Systematisierung unseres Ansatzes herangezogen. Beim maschinellen Lernen gibt es hauptsächlich drei Methoden für das Training von Netzwerken: überwachtes Lernen, Verstärkungslernen und Inferenz. Da wir davon ausgehen, dass jede dieser Lernmethoden in verschiedenen Stadien der Modell-/Netzwerkentwicklung eingesetzt werden kann, haben wir den Beweis angetreten, dass ein Modell durch die Einbeziehung aller dieser Methoden bereichert werden kann.

Kurze Rekapitulation

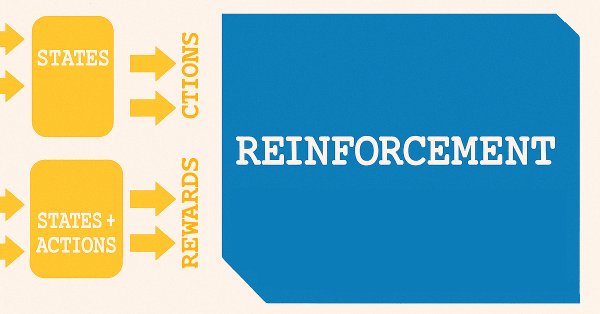
Um kurz zu rekapitulieren: In unserem früheren Artikel über Supervision-Learning ging es um die Modellierung von Merkmalen für Zustände. Merkmale sind die Indikatormuster sowohl des MA als auch des Stochastik-Oszillators. Bei den Staaten handelt es sich um prognostizierte Preisveränderungen, die unseren Indikatormustern hinterherhinken und von unserem Modell/Netzwerk vorhergesagt werden. Das folgende einfache Diagramm verdeutlicht dies.

 

Die Verwendung der Bezeichnung „Zustände“ für die Vorhersage von Preisänderungen ist zufällig, weil wir vom überwachten Lernen zum verstärkten Lernen übergehen. Im Rahmen des Verstärkungslernens sind Zustände ein wichtiger Ausgangspunkt für den Trainingsprozess, der dem nachstehenden Diagramm sehr ähnlich ist.

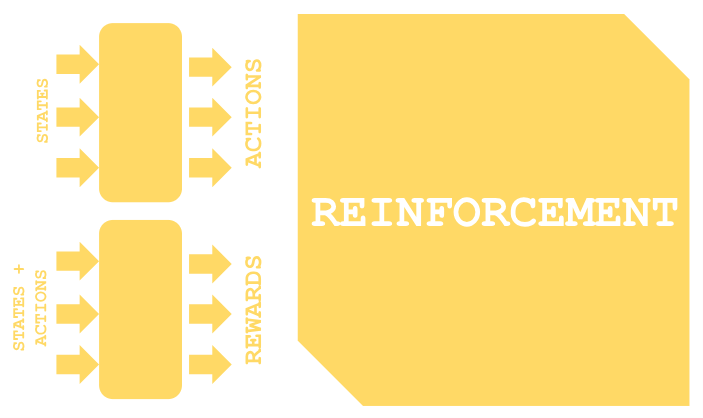
Es gibt eine Reihe von Variationen des Verstärkungslernens, je nach verwendetem Algorithmus, aber bei den meisten werden im Prinzip zwei Netze verwendet. Das eine ist eine Politik, die als oberes der beiden Netze im obigen Diagramm dargestellt ist, das andere ist das Wertnetz, das als unteres dargestellt ist.

Verstärkung kann eine alleinige Trainingsmethode für ein Modell oder ein System sein, aber wir haben im letzten Artikel argumentiert, dass sie mehr auf live eingesetzte Modelle angewendet werden könnte. In diesem Fall wäre das Gleichgewicht zwischen Erkundung und Nutzung wichtiger, um sicherzustellen, dass sich ein bereits trainiertes Modell an ein sich veränderndes Marktumfeld anpassen kann. Darüber hinaus haben wir aber auch gesehen, wie Entscheidungen, zu kaufen oder zu verkaufen, weiterverarbeitet werden können, um die Art von Aktion auszuwählen, die für einen Prognosezustand notwendig ist.

Inferenz

Dies führt uns dann zur Inferenz, oder was auch als unüberwachtes Lernen bezeichnet wird. Was ist das Ziel der Inferenz? Als ich anfing, darüber nachzudenken, war ich der Ansicht, dass man trainierte Netze/Modelle für eine bestimmte Situation nehmen und sie mit einigen geringfügigen Anpassungen und Abstimmungen in einer anderen Umgebung anwenden kann. Für Händler bedeutet dies, dass sie ein Modell für EUR USD trainieren und dann, mit leichten Anpassungen, dieses Wissen auf EUR JPY übertragen können. Wie die meisten Händler jedoch bestätigen werden, ist selbst die Entwicklung eines Expert Advisors ohne Arbitrage, der mehr als ein Symbol gleichzeitig handeln kann, ein schwieriger Prozess mit einem problematischen Risiko-Ertrags-Profil.

Darüber hinaus sind die Rechenkosten für das Training verschiedener Modelle für mehrere Währungspaare nicht mehr so hoch wie früher. Dies ist zum großen Teil den schnelleren Grafikprozessoren und der weit verbreiteten Cloud-Infrastruktur zu verdanken, die dies für viele Nutzer ermöglicht. Auf dem Papier sollte diese Situation also zur Schaffung vieler Modelle führen. Zwar sinken auch die Speicherkosten, vor allem wenn man bedenkt, dass große Modelle mit mehreren Millionen Parametern jetzt wie normale Computerdateien gespeichert werden, aber ich denke, dass die Inferenz über Encoder dafür spricht, dass dieses Wissen komprimiert und „besser speicherbar“ ist.

Da der Bedarf an mehr oder besonderem Speicherplatz angesichts des geringen Preises kaum ins Gewicht fällt, könnte man dies leicht abtun. Dies gilt insbesondere, wenn man bedenkt, dass ein bereits trainiertes Modell mit überwachtem Lernen und ein Verstärkungs-Lernsystem, das es auf dem Laufenden hält, was würde die Inferenz mit sich bringen? Nun, wir argumentieren, dass nicht alle Daten in Form kontinuierlicher Zeitreihen vorliegen. 

Wenn man alte historische Daten in Betracht zieht, die in irgendeiner Weise mit aktuellen oder sich anbahnenden Ereignissen übereinstimmen könnten, kann die Inferenz bei der Abbildung dieser Daten helfen und gleichzeitig das weiße Rauschen minimieren. Mit „Mapping“ ist die in der nachstehenden Abbildung dargestellte Anordnung gemeint:

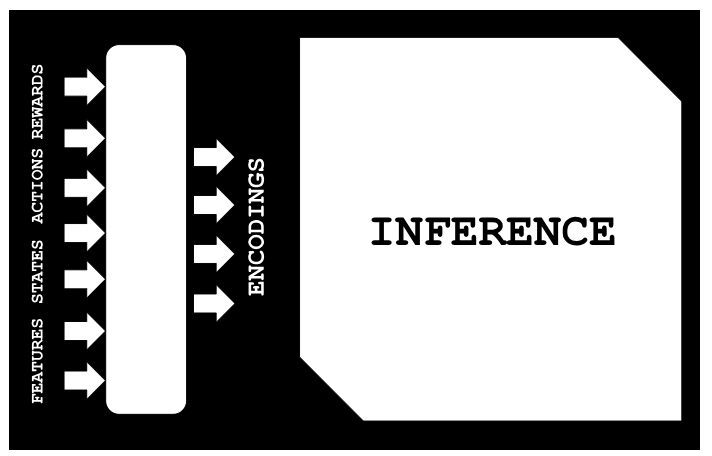
In einer Situation, in der Merkmale für historische Daten verfügbar sind, zeigen wir im Folgenden, wie wir ohne Überwachung (in diesem Fall durch lineare Regression) auf die jeweiligen Zustände, Handlungen und Belohnungen schließen können. Das liegt daran, dass wir ein Variations-Auto-Encoder-Modell trainiert haben, um Merkmale-Zustände-Handlungen-Belohnungen (FSAR) mit einer versteckten Schicht zu verbinden, die wir als Kodierungen bezeichnen. Mit Datensätzen von FSAR und Kodierungen passen wir also ein lineares Regressionsmodell an, das uns dann hilft, fehlende Lücken in einem FSAR-Datensatz zu füllen. Dies ist die wichtigste Anwendung, die wir in diesem Artikel untersuchen werden.

Wenn man jedoch einen Schritt zurücktritt und den Prozess des überwachten Lernens und des verstärkten Lernens betrachtet, wird deutlich, dass mit der Zeit die Notwendigkeit wächst, das gesammelte Wissen ganzheitlicher zu integrieren. Und während die Durchführung einer weiteren überwachten Lernphase über diesen längeren Zeitraum und die anschließende Durchführung von Reinforcement-Learning eine Option sein kann, sollte Inferenz-Learning eine skalierbarere und ganzheitlichere Alternative darstellen.

Um unsere Einführung abzurunden: Inferenz ist die Schätzung verborgener Variablen aus beobachteten Daten. Bei Bayes'schen Modellen ist die Inferenz (Schlussfolgerung) in der Regel der Prozess der Berechnung der Posterior-Verteilung der verborgenen Variablen, wenn die Datensätze der sichtbaren Schichten vorliegen. Mathematisch lässt sie sich daher wie folgt definieren:

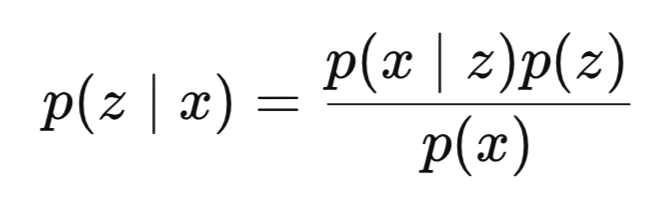
wobei:

• z ist die latente Variable oder Kodierungen,
  
  
• x sind die beobachteten Daten, die in unserem Fall FSAR sind,
  
  
• p(z∣x) ist das Posterior (das, was wir lernen wollen) oder die Wahrscheinlichkeit, z zu beobachten, wenn x gesehen wurde,
  
  
• p(x∣z) ist die Wahrscheinlichkeit, dass man x sieht, wenn z erscheint,
  
  
• p(z) ist die Priorität,
  
  
• p(x) ist der Hinweis.

P(x) ist oft nicht oder nur schwer zu berechnen.

Warum ist es schwer? Der Nenner, p(x), beinhaltet die Integration über alle möglichen latenten Variablen:

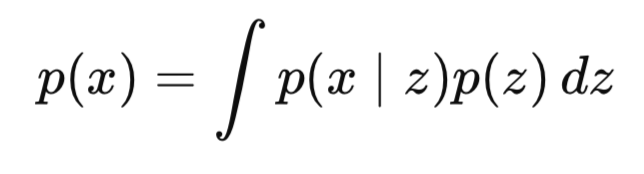
Dies ist in der Regel in hohen Dimensionen, d. h. mit zunehmender Größe der latenten Variable, rechnerisch nicht zu bewältigen.

Wie können VAEs also helfen? VAEs wandeln das Problem der approximativen Inferenz in eine Optimierungsaufgabe um. Dies wird durch die Einführung eines Encoders/Inferenznetzes und eines Decoders/generativen Netzes erreicht. Der Encoder beantwortet die Frage nach q(z|x), einer gelernten Approximation des Exterieurs, während das Decoder-Netzwerk p(x|z) anspricht, das eine Rekonstruktion der Daten (in unserem Fall FSAR) aus dem latenten Code (Kodierungen) ist.

Die wichtigste Neuerung der VAE besteht jedoch darin, dass die VAE anstelle einer exakten Berechnung des Posteriorwerts eine Optimierung für die Optimierung der unteren Schranke der Evidenz (ELBO). Die ELBO ist die Zielfunktion, die zum Trainieren von VAEs verwendet wird, indem sie die wahre Datenverteilung annähert und gleichzeitig sicherstellt, dass das Modell sinnvolle latente Repräsentationen und weniger Rauschen lernt. Hier ist die Schlüssel-Intuition:

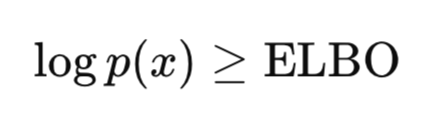
Wie bereits erwähnt, ist die Berechnung von p(x) sehr schwierig und schwer lösbar; der Nachweis, dass p(x) und damit auch log p(x) größer als ein bestimmter Wert ist, ist jedoch machbar und lösbar. Da unser Ziel die Maximierung von p(x) ist, erhöhen wir durch die Maximierung oder Anhebung der unteren Schranke letztendlich auch p(x). VAE lernt, latente Strukturen aus den Daten abzuleiten und wird durchgängig mit Gradientenabstieg trainiert. Sie demonstriert somit sowohl Amortisierte Inferenz und generative Modellierung in einem Rahmen.

Warum ist VAE das Herzstück der Inferenzphilosophie? Denn die VAE lernt, über den Encoder Inferenzen durchzuführen. Das bedeutet, dass das Inferenzproblem nicht jedes Mal gelöst werden muss, wenn ein neuer Datensatz vorliegt, sondern dass ein gemeinsamer Kodierer verwendet wird. Dies wird auch als „amortisierte Schlussfolgerung“ bezeichnet. Dies ist ein hervorragendes Instrument, um den Kompromiss zwischen Treue und Regelmäßigkeit abzuwägen, aber auch um allgemein zu verstehen, wie latente Variablen die generative Struktur darstellen.

Wir setzen die VAE für diesen Artikel um, indem wir die Wasserstein-Distanz anstelle der traditionellen KL-Divergenz beim Vergleich von Verteilungen untersuchen. Die Gründe dafür sind hauptsächlich explorativ, da wir in zukünftigen Artikeln die KL-Divergenz berücksichtigen könnten. Es wurde jedoch argumentiert, dass die KL-Divergenz den latenten Raum zu stark einschränkt, was wiederum zu einem Zusammenbruch des posterioren Bereichs führen kann. Zweitens sei der Wasserstein-Abstand ein flexibleres Maß für den Vergleich von Verteilungen, insbesondere in Situationen, in denen sich die fraglichen Verteilungen wenig oder gar nicht überschneiden.

Der Kerngedanke der Wasserstein-Distanz ist es, die „Kosten“ der Umwandlung einer Wahrscheinlichkeitsverteilung in eine andere zu messen. Aus diesem Grund wird sie manchmal auch als Entfernung des Earth-Movers bezeichnet. Sie wird durch die folgende Gleichung erfasst:

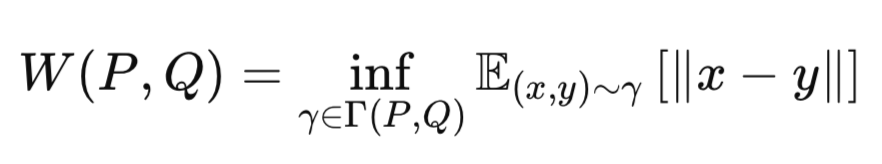
wobei:

• P: Wahre Datenverteilung (z. B. Gaußscher Prior p(z)).

• Q Näherungsweise Verteilung (z. B. Ausgang des Encoders q(z∣x)).

• γ: Eine gemeinsame Verteilung (Kopplung) über P und Q.

• Γ(P,Q): Menge aller möglichen Kopplungen zwischen P und Q.

• ∥x-y∥: Abstandsmetrik (z. B. Euklidischer Abstand).

• inf: Infimum (größte untere Grenze, d. h. die kleinstmöglichen Transportkosten).

Wasserstein berechnet daher die geringste Menge an „Arbeit“, die erforderlich ist, um die Masse Q so zu verschieben, dass sie mit P übereinstimmt. Wasserstein VAE ist wichtig, weil es schärfere Muster erzeugt und aussagekräftigere latente Darstellungen hat. Es gilt allgemein als stabiler, wenn unter bestimmten Bedingungen trainiert wird.

Es gibt im Wesentlichen zwei gängige Umsetzungen der Wasserstein-VAE. WVAE-MMD, und WVAE-GAN. Erstere verwendet die Maximum-Mean-Discrepancy, um p(z) und q(z) zu vergleichen. Das werden wir in diesem Artikel verwenden. Nebenbei bemerkt, verwendet WVAE-GAN einen adversen Verlust, um latente Verteilungen anzugleichen. Wir werden uns in künftigen Artikeln auch mit dieser Umsetzung befassen. Die Maximum-Mean-Discrepancy wird durch die folgende Gleichung erfasst:

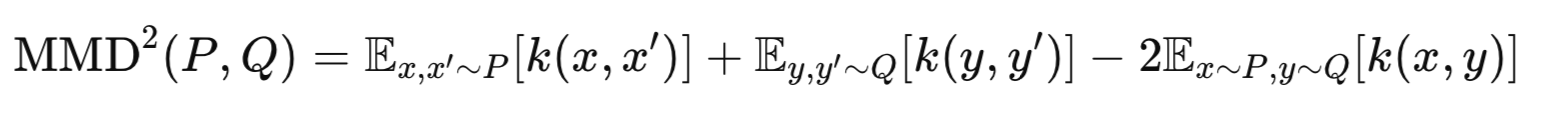
wobei:

• P: Wahrer Prior (z. B. p(z)=N(0,I)).

• Q Verteilung des Encoders (z. B. q(z∣x)).

• k(⋅,⋅): Kernel-Funktion (z. B. Gauß-RBF).

• x,x′: Zwei unabhängige Proben von P.

• y,y′: Zwei unabhängige Proben von Q.

MMD vergleicht Mittelwerteinbettungen von P und Q in einem hochdimensionalen Raum (Reproducing Kernel Hilbert Space). Je näher diese Mittelwerte beieinander liegen, desto ähnlicher sind die Verteilungen.

VAE-Implementierung

Beginnen wir damit, unsere Modelle/Netzwerke in Python zu implementieren, vor allem weil es sinnvoller ist, sie hier zu trainieren als in MQL5. Es gibt Workarounds in MQL5, die die Verwendung von OpenCL beinhalten, die den Leistungsunterschied verringern können, aber wir müssen uns diese in dieser Serie noch ansehen. Wir implementieren eine Wasserstein-VAE-Klasse wie folgt in Python:

class WassersteinVAEUnsupervised(nn.Module):
    def __init__(self, feature_dim, encoding_dim, k_neighbors=5):
        super().__init__()
        self.encoding_dim = encoding_dim
        self.k_neighbors = k_neighbors
        
        # Feature encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, encoding_dim * 2)  # mean and logvar
        )
        
        # Buffer for storing training references
        self.register_buffer('ref_encoding', torch.zeros(1, encoding_dim))
        self.register_buffer('ref_states', torch.zeros(1, 1))
        self.register_buffer('ref_actions', torch.zeros(1, 1))
        self.register_buffer('ref_rewards', torch.zeros(1, 1))
        self._references_loaded = False
    
    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar
    
    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std
    
    def update_references(self, encoding_vectors, states, actions, rewards):
        """Store reference data for unsupervised prediction"""
        self.ref_encoding = encoding_vectors.detach().clone()
        self.ref_states = states.detach().clone().unsqueeze(-1)
        self.ref_actions = actions.detach().clone().unsqueeze(-1)
        self.ref_rewards = rewards.detach().clone().unsqueeze(-1)
        self._references_loaded = True
    
    def knn_predict(self, z, ref_values):
        # z shape: [batch_size, encoding_dim]
        # ref_values shape: [ref_size, 1] or [ref_size]
        
        # Ensure ref_values is properly shaped
        ref_values = ref_values.view(-1)  # Flatten to [ref_size]
        
        # Calculate distances between z and reference encodings
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, ref_size]
        
        # Get top-k nearest neighbors
        _, indices = torch.topk(distances, k=self.k_neighbors, largest=False)  # [batch_size, k]
        
        # Gather corresponding reference values
        neighbor_values = torch.gather(
            ref_values.unsqueeze(0).expand(indices.size(0), -1),  # [batch_size, ref_size]
            1,
            indices
        )  # [batch_size, k]
        
        # Average the nearest values
        predictions = neighbor_values.mean(dim=1, keepdim=True)  # [batch_size, 1]
        
        return predictions
    
    def gaussian_predict(self, z, ref_values):
        # Input validation
        assert z.dim() == 2, "z must be 2D [batch, encoding]"
        assert ref_values.dim() == 2, "ref_values must be 2D"
        
        # Calculate distances (Euclidean)
        distances = torch.cdist(z, self.ref_encoding)  # [batch, ref_size]
        
        # Convert to similarities (Gaussian weights)
        weights = torch.softmax(-distances, dim=1)  # [batch, ref_size]
        
        # Prepare reference values
        ref_values = ref_values.squeeze(-1) if ref_values.size(1) == 1 else ref_values
        ref_values = ref_values.unsqueeze(0) if ref_values.dim() == 1 else ref_values
        
        # Ensure proper shapes
        ref_values = ref_values.view(-1, 1)  # Force [792, 1] shape
        
        # Calculate distances
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, 792]
        
        # Convert to weights
        weights = torch.softmax(-distances, dim=1)  # [batch_size, 792]
        
        # Matrix multiplication Weighted combination
        predictions = torch.matmul(weights, ref_values)  # [batch, 1]
        
        return predictions.unsqueeze(-1) if predictions.dim() == 1 else predictions
    
    def linear_predict(self, z, ref_values):
        """Linear regression prediction using normal equations"""
        # Add bias term
        X = torch.cat([self.ref_encoding, torch.ones_like(self.ref_encoding[:, :1])], dim=1)
        y = ref_values
        
        # Compute closed-form solution
        XtX = torch.matmul(X.T, X)
        Xty = torch.matmul(X.T, y)
        theta = torch.linalg.solve(XtX, Xty)
        
        # Predict with new z values
        X_new = torch.cat([z, torch.ones_like(z[:, :1])], dim=1)
        return torch.matmul(X_new, theta)

    def predict_from_encoding(self, z):
        if not self._references_loaded:
            raise RuntimeError("Reference data not loaded")
            
        # Validate reference shapes
        self.ref_states = self.ref_states.view(-1, 1)
        self.ref_actions = self.ref_actions.view(-1, 1)
        self.ref_rewards = self.ref_rewards.view(-1, 1)
        
        states = self.knn_predict(z, self.ref_states)
        actions = self.gaussian_predict(z, self.ref_actions)
        rewards = self.linear_predict(z, self.ref_rewards)
        
        return states, actions, rewards
    
    def forward(self, features, states=None, actions=None, rewards=None):
        z_mean, z_logvar = self.encode(features)
        z = self.reparameterize(z_mean, z_logvar)
        
        if states is not None and actions is not None and rewards is not None:
            return {
                'z': z,
                'z_mean': z_mean,
                'z_logvar': z_logvar
            }
        else:
            pred_states, pred_actions, pred_rewards = self.predict_from_encoding(z)
            return {
                'states': pred_states,
                'actions': pred_actions,
                'rewards': pred_rewards
            }

Unsere obige Wasserstein-VAE-Implementierung besteht hauptsächlich aus vier Dingen. Ein Merkmalscodierer, Referenzpuffer, Vorhersagemethoden und ein Dual-Mode-Vorwärtspass. Der Merkmalscodierer ist ein 3-Schichten-MLP, dessen Aufgabe es ist, die Eingaben zu latenten Raumparametern (von z, z-Mittelwert und z-Logvar) zu komprimieren. In den Referenzpuffern werden bereits trainierte Modelleingaben von Merkmalen, Zuständen, Aktionen und Belohnungen zusammen mit ihren jeweiligen Kodierungen gespeichert. Die aufgeführten Prognosemethoden dienen der Vorhersage von Zuständen, Aktionen und Belohnungen für einen unvollständigen Datensatz, der nur mit Merkmalen präsentiert wird. Diese Methoden sind K-NN, Gaußsche Gewichtung, lineare Regression. Sie arbeiten innerhalb des latenten Raums, indem sie Kodierungen auf die fehlenden Datenpunkte von Zuständen, Handlungen und Belohnungen abbilden. Der Dual-Mode-Forward-Pass übernimmt sowohl das Training als auch die Inferenz.

Die wichtigsten funktionalen Komponenten sind der Kodierungsprozess, das Referenzsystem, die Vorhersagemechanismen und der Inferenzfluss. Bei der Kodierung durchlaufen die eingegebenen Merkmale, Zustände, Aktionen und Belohnungen das Kodierungsnetz. Die Ausgabe zerlegt diese Eingaben in eine „Kodierung“ von z, z-Mittelwert und z-log-var. Der Trick der Reparametrisierung ermöglicht es uns außerdem, differenzierbare Stichproben zu nehmen. Das Referenzsystem speichert die „eingefrorenen“ Ausgaben mit den entsprechenden FSAR-Eingabepaaren. Sie erfordert eine explizite Initialisierung über die Funktion update_references().

Die 3 Vorhersagemechanismen zielen auf die Vorhersage von Zuständen, Aktionen oder Belohnungen ab. Unser Modell geht davon aus, dass die Merkmale immer als Teil des FSAR-Datensatzes verfügbar sind, es kann jedoch vorkommen, dass nur SARs (states-actions-rewards oder Zustände-Aktionen-Belohnungen) fehlen. KNN-Clustering bildet Zustände ab, Gaussian Process Regression bildet Aktionen ab und Lineare Regression bildet Belohnungen ab. Der Inferenzfluss kodiert daher unsere Eingabemerkmale in den latenten Raum, wählt die Vorhersagemethode für jeden Eingabetyp auf der Grundlage der soeben erwähnten Paarungen aus und gibt dann die jeweiligen Zustands-/Aktions-/Belohnungsschätzungen zurück.

Unser obiger Ansatz könnte jedoch noch in einigen Punkten verbessert werden. Diese lassen sich grob in 3 Kategorien einteilen. Architektonische Erweiterungen, Verbesserungen bei der Ausbildung oder einfach mehr Robustheit. Zu den Architekturverbesserungen könnten gehören: Hinzufügen einer Spektralnormierung zur Durchsetzung der Lipschitz-Kontinuität, Implementierung einer lernfähigen Temperatur für die Gaußsche Prozessgewichtung, Einbeziehung der Referenzspeicherverwaltung (FIFO/Pruning) und Hinzufügen von Monte-Carlo-Samples zur Unsicherheitsabschätzung. Der Trainingsprozess kann auch durch die Einführung einer Gradientenstrafe für Wasserstein-Beschränkungen, die Hinzufügung einer Regularisierung des latenten Raums (MMD/Coverage-Terme), die Implementierung einer adaptiven Auswahl von Vorhersagemethoden und die Hinzufügung einer Ensemble-Gewichtung von Vorhersagemethoden verbessert werden.

Verbesserungen der Robustheit sind ein wenig unklar, aber es könnten Anstrengungen unternommen werden in Bezug auf: die Fähigkeit zur Erkennung von Out-of-Distribution, ein Bewertungssystem für die Referenzqualität, eine dynamische Anpassung der Nachbarschaftsgröße und eine eingangsabhängige Rauschskalierung.

Implementierung des MMD-Verlusts

Die Form der Wasserstein-VAE, die wir implementieren, ist die MMD-Loss und ihre beiden Verlustfunktionen, die wir für die VAE verwenden, werden im Folgenden vorgestellt:

def mmd_loss(y_true, y_pred, kernel_mul=2.0, kernel_num=5):
    """
    MMD loss using Gaussian RBF kernel.
    Args:
        y_true: Ground truth samples (shape: [batch_size, dim])
        y_pred: Predicted samples (shape: [batch_size, dim])
        kernel_mul: Multiplier for kernel bandwidths
        kernel_num: Number of kernels to use
    Returns:
        MMD loss (scalar)
    """
    batch_size = y_true.size(0)
    
    # Combine real and predicted samples
    xx = y_true
    yy = y_pred
    xy = torch.cat([xx, yy], dim=0)
    
    # Compute pairwise distances
    distances = torch.cdist(xy, xy, p=2)
    
    # Compute MMD using multiple RBF kernels
    loss = 0.0
    for sigma in [kernel_mul ** k for k in range(-kernel_num, kernel_num + 1)]:
        if sigma == 0:
            continue
        kernel_val = torch.exp(-distances ** 2 / (2 * sigma ** 2))
        k_xx = kernel_val[:batch_size, :batch_size]
        k_yy = kernel_val[batch_size:, batch_size:]
        k_xy = kernel_val[:batch_size, batch_size:]
        
        # MMD formula: E[k(x,x)] + E[k(y,y)] - 2*E[k(x,y)]
        loss += (k_xx.mean() + k_yy.mean() - 2 * k_xy.mean())
    
    return loss / (2 * kernel_num)

def compute_loss(predictions, batch):
    # Ensure shapes match (squeeze if needed)
    pred_states = predictions['states'].squeeze(-1)  # [B, 1] → [B]
    pred_actions = predictions['actions'].squeeze(-1)
    pred_rewards = predictions['rewards'].squeeze(-1)
    
    # MMD Loss (distributional matching)
    mmd_state = mmd_loss(batch['states'], pred_states)
    mmd_action = mmd_loss(batch['actions'], pred_actions)
    mmd_reward = mmd_loss(batch['rewards'], pred_rewards)
    
    # Combine losses (adjust weights as needed)
    total_loss = mmd_state + mmd_action + mmd_reward
    
    return {
        'loss': total_loss,
        'mmd_state': mmd_state,
        'mmd_action': mmd_action,
        'mmd_reward': mmd_reward
    }

Die Eingabeparameter der Funktion MMD-Loss sind y_true und y_pred. Sie stellen einen Vergleich zwischen den echten und den erzeugten Proben dar. Ihre Ausrichtung nach Dimensionen ist wichtig, um einen Vergleich anstellen zu können. Die Eingaben kernel_mul/ kernel_num steuern die Bandbreiten des RBF-Kerns und wirken sich daher auf die Empfindlichkeit gegenüber verschiedenen Skalen der Verteilungsunterschiede aus.

Die Stichprobenkombination xy führt reale und generierte Stichproben zusammen, um alle paarweisen Abstände in einem Arbeitsgang zu berechnen. Dies ist speichereffizient und gewährleistet konsistente Entfernungsberechnungen. Bei der Berechnung des Abstands wird p=2 (euklidischer Abstand) verwendet, was der Standard für MMD ist. Diese Wahl hat einen direkten Einfluss auf die Empfindlichkeit gegenüber Verteilungsunterschieden. Die Operation „cdist“ ist mathematisch gesehen das A und O, da MMD auf paarweisen Vergleichen beruht.

Beim Multi-Kernel-Ansatz werden geometrisch beabstandete Bandbreiten (kernel_mul^k) verwendet, um ein Gefühl für die Eigenschaften der Multiskalenverteilung zu bekommen. Damit wird das Szenario sigma=0 vermieden, das zu Null-Teilungen führt. Jeder Kernel trägt durch Mittelwertbildung gleichermaßen zum endgültigen Verlust bei. Bei der MMD-Berechnung wird die Kernformel (k_xx + k_yy - 2k_xy) verwendet, die die Diskrepanzen zwischen den Verteilungen quantifiziert. Mittelwertoperationen liefern Erwartungsschätzungen aus endlichen Stichproben, und die Normalisierung durch die Kernelanzahl macht die Verlustskala über verschiedene Konfigurationen hinweg konsistent.

Verbesserungen an diesem MMD könnten mit der Kernelauswahl vorgenommen werden, wobei: eine zusätzliche adaptive Bandbreitenauswahl auf der Grundlage von Stichprobenstatistiken implementiert werden kann; Experimente mit Nicht-RBF-Kerneln durchgeführt werden können, um festzustellen, welche Kernel für welche Datentypen am besten geeignet sind; die Implementierung einer automatischen Relevanzbestimmung für die Bandbreiten erfolgen kann. Die numerische Stabilität kann auch durch folgende Maßnahmen erreicht werden: Hinzufügen eines kleinen Epsilons zum Nenner, um die Stabilität zu erhöhen; Implementierung von Berechnungen im logarithmischen Bereich für sehr kleine Kernel-Werte; und Begrenzung extremer Abstandswerte, um einen Überlauf zu verhindern. Andere Maßnahmen können die Berechnungseffizienz und die VAE-Integration betreffen. 

Es gibt eine Menge anderer Codes, die wir bei der Ausführung dieser Schlussfolgerung verwenden müssen und die wir hier nicht explizit hervorheben. Bemerkenswert ist jedoch, dass die Generierung der FASR-Eingabedaten durch die Ausführung des Codes aus den beiden früheren Artikeln über den MA und den stochastischen Oszillator erfolgt. Der Artikel „Überwachtes Lernen“ gibt uns die Merkmale und Zustandskomponenten unserer VAE-Eingabe, während der Artikel „Verstärkungslernen“ uns die Aktionen und Belohnungen liefert.

Implementierung der linearen Regression

Um unser Inferenzmodell zu verwenden, stützen wir uns ausschließlich auf die Regressionsfunktionen, die von der latenten Schicht auf die fehlenden Eingaben abgebildet werden, und nicht auf das VAE-Netzwerk. Dies steht im Gegensatz zu dem, was wir in den vergangenen Artikeln getan haben, wo wir das trainierte Netz als ONNX-Datei exportieren mussten. 

Der Grund hierfür ist, dass wir daran interessiert sind, den Eingabedatensatz für eine von uns trainierte VAE zu vervollständigen.

Für die Zukunft liegen uns nur Merkmalsdaten vor. Es stellt sich also die Frage, welche Zustände, Handlungen und Belohnungen für diese Merkmale vorgesehen sind. Um diese Frage zu beantworten, müssen wir bei der Initialisierung unseres Expert Advisors ein lineares Regressionsmodell mit Datensätzen von Paaren für Merkmalscodierungen, Zustandscodierungen, Aktionscodierungen und Belohnungscodierungen trainieren. Mit unserem trainierten (oder angepassten) linearen Regressionsmodell würden wir jeden neuen Merkmalsdatenpunkt neuer Daten einer Kodierung zuordnen und diese Kodierung dann innerhalb desselben Modells verwenden, um sie wieder Zuständen, Aktionen und Belohnungen zuzuordnen.

Dieser Anpassungsprozess zur Ermittlung der Kodierungsverbindungen erfolgt durch unüberwachtes Lernen. Unsere lineare Regression ist wie folgt in MQL5 implementiert:

//+------------------------------------------------------------------+
// Linear Regressor (unchanged from previous implementation)         |
//+------------------------------------------------------------------+
class LinearRegressor
{
private:
   vector m_coefficients;
   double m_intercept;

   matrix m_coefficients_2d;
   vector m_intercept_2d;

public:
   void Fit(const matrix &X, const vector &y)
   {  int n = (int)X.Rows();
      int p = (int)X.Cols();
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      vector y_col = y;
      y_col.Resize(n, 1);
      vector beta = XtX_inv.MatMul(Xt.MatMul(y_col));
      m_coefficients = beta;
      m_coefficients.Resize(p);
      m_intercept = beta[p];
   }

   void Fit2d(const matrix &X, const matrix &Y)
   {  int n = (int)X.Rows();    // Number of samples
      int p = (int)X.Cols();    // Number of input features
      int k = (int)Y.Cols();    // Number of output encodings
      // Add bias term (column of 1s) to X
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      // Calculate coefficients using normal equation: (X'X)^-1 X'Y
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      matrix beta = XtX_inv.MatMul(Xt.MatMul(Y));
      // Split coefficients and intercept
      m_coefficients_2d.Resize(p, k);  // Coefficients for each output encodings
      m_intercept_2d.Resize(k);        // Intercept for each input feature
      for(int j = 0; j < p; j++)
      {  for(int d = 0; d < k; d++)
         {  m_coefficients_2d[j][d] = beta[j][d];
         }
      }
      for(int d = 0; d < k; d++)
      {  m_intercept_2d[d] = beta[p][d];
      }
   }

   double Predict(const vector &x)
   {  return m_intercept + m_coefficients.Dot(x);
   }

   vector Predict2d(const vector &X) const
   {  int p = (int)X.Size();    // Number of input features
      int k = (int)m_intercept_2d.Size(); // Number of output encodings
      vector predictions(k);  // vector to store predictions
      for(int d = 0; d < k; d++)
      {  // Initialize with intercept for this output dimension
         predictions[d] = m_intercept_2d[d];
         // Add contribution from each feature
         for(int j = 0; j < p; j++)
         {  predictions[d] += m_coefficients_2d[j][d] * X[j];
         }
      }
      return predictions;
   }
};

Die Kernstruktur enthält getrennte Koeffizientenspeicher für 1D (für die Variablen m_coefficients/m_intercept) und 2D (für die Variablen m_coefficients_2d/m_intercept_2d). Die Matrixalgebra wird für eine gewisse Effizienz bei Stapeloperationen verwendet. Es implementiert sowohl Single-Output- als auch Multi-Output-Regressionsvarianten. Bei den Anpassungsmethoden wird die Normalengleichung verwendet, indem (X'X)^- 1X'y direkt gelöst wird. Es behandelt Verzerrungen, indem es eine Spalte von 1en zu den Eingangsmerkmalen hinzufügt. Die 2D-Spezialisierung durch die Klasse verarbeitet auch mehrere Ausgaben gleichzeitig über Matrixoperationen.

Die Vorhersagemethoden verwenden eine Punkt-Produkt-Implementierung, die als effiziente lineare Kombination von Eingaben und Gewichten dient. Die Handhabung von Dimensionen wird sowohl für Einzel- als auch für Mehrfachausgabeszenarien ordnungsgemäß verarbeitet, und die Speicherverwaltung ordnet den Ergebnisvektor im Voraus zu, um die Effizienz zu erhöhen. Wir verwenden eine Pseudo-Wasserstein-VAE-Klasse, um unsere Zustands-, Handlungs- und Belohnungsprognosen aufzurufen und zu implementieren. Dies ist in MQL5 wie folgt kodiert:

//+------------------------------------------------------------------+
// Wasserstein VAE Predictors Implementation (unchanged)             |
//+------------------------------------------------------------------+
class WassersteinVAEPredictors
{
private:
   LinearRegressor m_feature_predictor;
   LinearRegressor m_state_predictor;
   LinearRegressor m_action_predictor;
   LinearRegressor m_reward_predictor;
   bool m_predictors_trained;

public:
   WassersteinVAEPredictors() : m_predictors_trained(false) {}

   void FitPredictors(const matrix &features,
                      const vector &states,
                      const vector &actions,
                      const vector &rewards,
                      const matrix &encodings)
   {  m_feature_predictor.Fit2d(features, encodings);
      m_state_predictor.Fit(encodings, states);
      m_action_predictor.Fit(encodings, actions);
      m_reward_predictor.Fit(encodings, rewards);
      m_predictors_trained = true;
   }

   void PredictFromFeatures(const vector &y, vector &z)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      z = m_feature_predictor.Predict2d(y);
   }

   void PredictFromEncodings(const vector &z, double &state, double &action, double &reward)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      state = m_state_predictor.Predict(z);
      action = m_action_predictor.Predict(z);
      reward = m_reward_predictor.Predict(z);
   }
};

In unserer nutzerdefinierten Signalklasse stützen wir uns jetzt auch auf eine „Infer“-Funktion, um unsere Prognosen zu verarbeiten. Dies ist wie folgt:

//+------------------------------------------------------------------+
//| Inference Learning Forward Pass.                                 |
//+------------------------------------------------------------------+
vector CSignal_WVAE::Infer(int Index, ENUM_POSITION_TYPE T)
{  vectorf _f = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vector _features;
   _features.Init(_f.Size());
   _features.Fill(0.0);
   for(int i = 0; i < int(_f.Size()); i++)
   {  _features[i] = _f[i];
   }
// Make a prediction
   vector _encodings;
   _encodings.Init(__ENCODINGS);
   _encodings.Fill(0.0);
   double _state = 0.0, _action = 0.0, _reward = 0.0;
   if(Index == 1)
   {  m_vae_1.PredictFromFeatures(_features, _encodings);
      m_vae_1.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 2)
   {  m_vae_2.PredictFromFeatures(_features, _encodings);
      m_vae_2.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 5)
   {  m_vae_5.PredictFromFeatures(_features, _encodings);
      m_vae_5.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   vector _inference;
   _inference.Init(3);
   _inference[0] = _state;
   _inference[1] = _action;
   _inference[2] = _reward;
   //
   if(T == POSITION_TYPE_BUY)
   {  if(_state > 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= 2.0;
         if(_action < 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   else if(T == POSITION_TYPE_SELL)
   {  if(_state < 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= -2.0;
         if(_action > 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   return(_inference);
}

Für neue Leser gibt es hier und hier Anleitungen, wie man einen Expert Advisor mit dem MQL5-Assistenten zusammenstellt. Aus dem letzten Artikel geht hervor, dass von den 10 Mustern, mit denen wir begonnen haben, nur die Muster 1, 2 und 5 Vorwärtstest bestreiten konnten. Daher verarbeiten unsere Long Condition- und Short Condition-Funktionen für diesen Expert Advisor nur diese drei Muster. Wir prognostizieren 3 Werte. Zustände, Handlungen und Belohnungen. Die Zustände sind an den Bereich 0 bis 1 gebunden. Die Aktionen sind ebenfalls an einen ähnlichen Bereich gebunden, während die Belohnungen im Bereich von -1 bis +1 liegen. Jeder, der etwas Erfahrung mit dem Training und der Verwendung neuronaler Netze hat, weiß, dass die Test- oder Einsatzergebnisse neuronaler Netze nach dem Training mit Zielvorgaben, die festgelegte Grenzwerte einhalten, nicht immer innerhalb der erwarteten Grenzwerte liegen. Häufig ist eine Form der Normalisierung nach dem Vorwärtslauf erforderlich.

Wir führen hier keine Normalisierung durch, sondern weisen den Leser lediglich darauf hin, dass er dies berücksichtigen sollte, wenn er ein trainiertes Netzwerk in die Produktion einführt. Wir laden 2 Jahre täglicher Preisdaten für EUR USD in Python hoch, um eine VAE zu trainieren, die uns ein Datensatzpaar aus Merkmalen-Zuständen-Aktionen-Belohnungen mit Kodierungen liefert. Dieser Datensatz wird wiederum an lineare Regressionsmodelle angepasst, die wir dann verwenden, um Zustände, Handlungen und Belohnungen bei der Präsentation von Merkmalen darzustellen. Von diesen hochgeladenen Daten, die über das Python-Modul von Meta Trader 5 verarbeitet werden, werden 80 % für das Training und 20 % für die Tests verwendet.

Der Datenzeitraum erstreckt sich von 2023.01.01 bis 2025.01.01. Ein Vorwärtstest wäre also ungefähr die 5 Monate vor dem 2025.01.01. Wir führen Tests für einen etwas längeren Zeitraum durch, nämlich die 6 Monate davor, d.h. vom 2024.07.01 bis 2025.01.01, und erhalten die folgenden Berichte:

Für Muster 1:

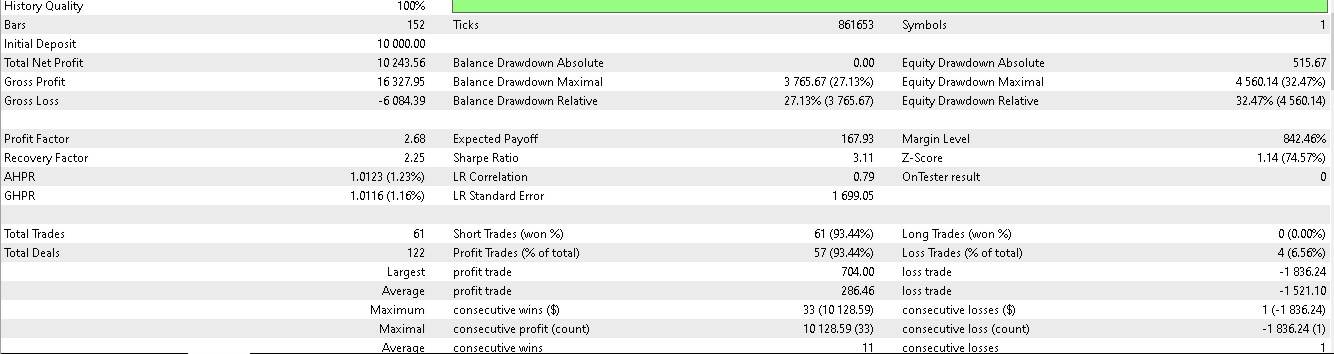
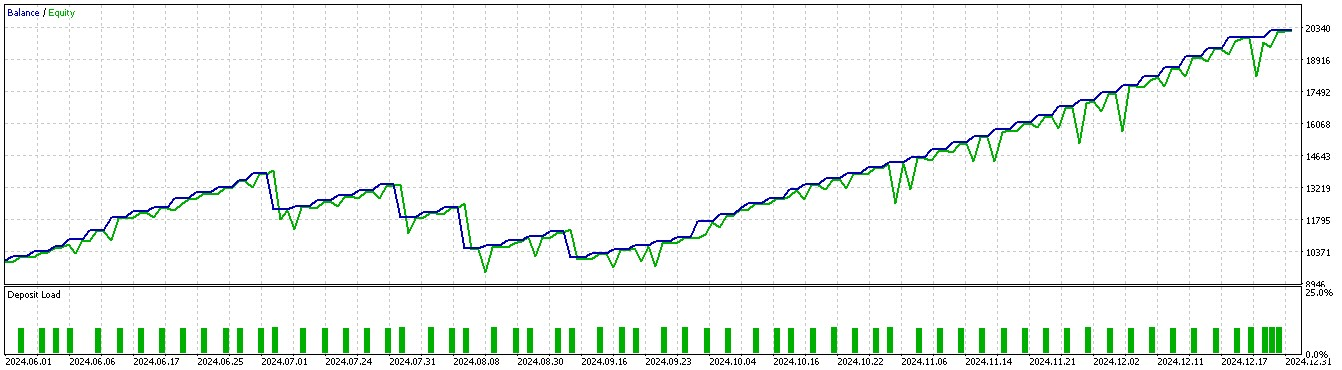
Für Muster 2:

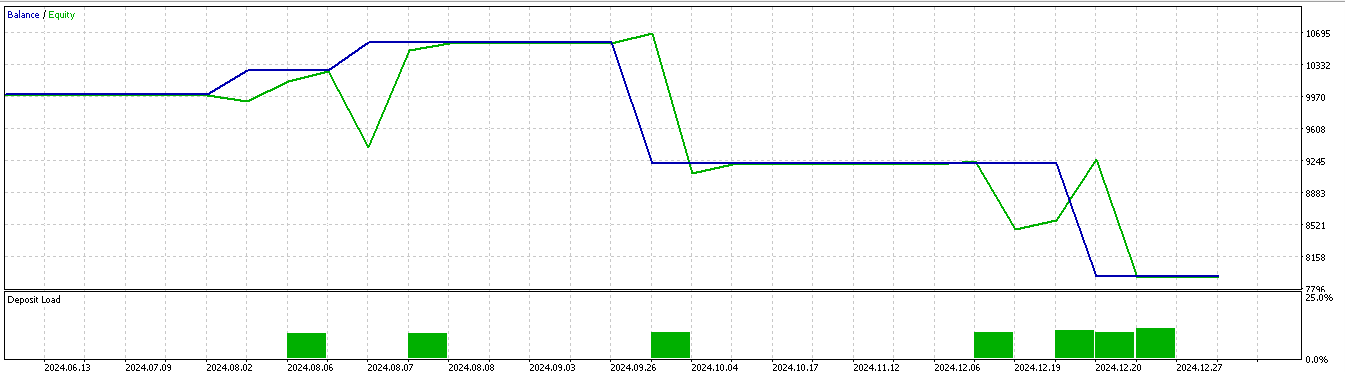
Für Muster 5:

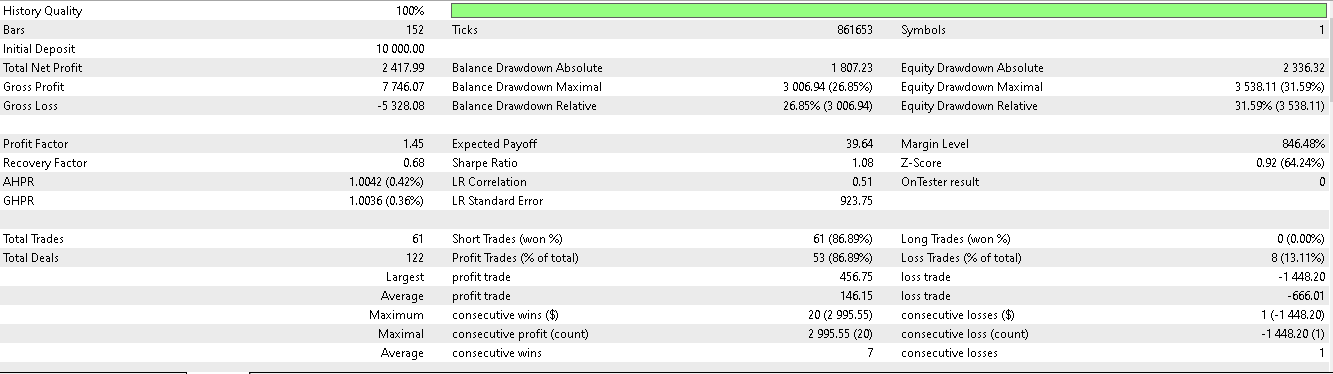
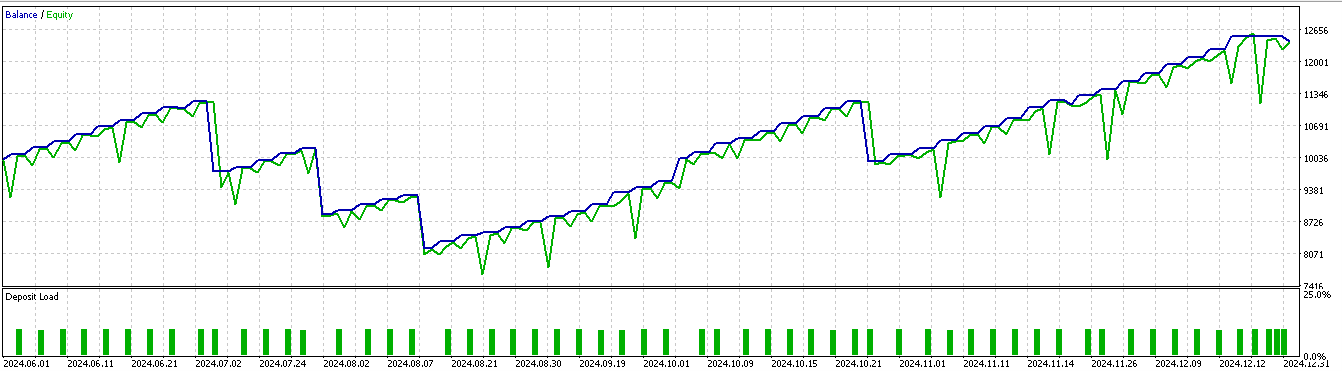
Es scheint, dass nur die Muster 1 und 5 in der Lage sind, auf der Grundlage eines kurzen 2-Jahresfensters für Training und Vorwärtstest aus den Schlussfolgerungen Kapital zu schlagen.

Schlussfolgerung

Wir schließen unseren Blick auf gleitende Durchschnitte und stochastische Oszillatormuster, die mit maschinellem Lernen genutzt werden, indem wir den Anwendungsfall des Inferenz-Lernens untersuchen. Wir haben einen möglichen Implementierungspfad für das Inferenzlernen vorgestellt, der auf dem Argument basiert, dass, sobald das überwachte Lernen abgeschlossen und das Verstärkungslernen in einer Live-Testumgebung eingeführt ist, ein ganzheitlicherer Ansatz erforderlich ist, um das gesamte Wissen aus dem überwachten Lernen und dem Verstärkungslernen zu sammeln und zu „speichern“. Ich bin der Meinung, dass das Inferenzlernen für diese Aufgabe geeignet ist, zumal seine Lernmethode keine Duplizität zu dem aufweist, was wir bereits beim überwachten Lernen und beim Verstärkungslernen verwendet haben.

Name	Beschreibung
wz_60.mq5	Vom Assistenten erstellter Expert Advisor für die Kopfzeile zur Anzeige der erforderlichen Assembly-Dateien enthalten
SignalWZ_60.mqh	Datei der Signal-Klasse
60_vae_1.onnx	VAE ONNX-Modell für Muster 1, nicht erforderlich für Expert Advisor.
60_vae_2.onnx	VAE ONNX-Modell für Muster 2, dito
60_vae_5.onnx	VAE ONNX-Modell für Muster 5, dito