MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 58): Reinforcement Learning (DDPG) mit gleitendem Durchschnitt und stochastischen Oszillatormustern

Einführung

In unserem letzten Artikel haben wir 10 Signalmuster aus unseren 2 Indikatoren (MA & Stochastik Oszillator) getestet.  Sieben waren in der Lage, auf der Grundlage eines 1-Jahres-Testfensters einen Vorwärtstest zu machen. Von diesen haben jedoch nur 2 sowohl Kauf- als auch Verkaufs-Handelsgeschäfte getätigt. Das lag an unserem kleinen Testfenster, weshalb wir den Lesern dringend empfehlen, das Programm mit mehr Daten zu testen, bevor sie es weiter verwenden. 

Wir verfolgen hier die These, dass die drei Hauptarten des maschinellen Lernens zusammen verwendet werden können, jede in ihrer eigenen „Phase“. Diese Modi sind, um es kurz zu machen, überwachtes Lernen (SL), Verstärkungslernen (RL) und Inferenzlernen (IL). Wir haben uns im letzten Artikel mit SL beschäftigt, wo kombinierte Muster des gleitenden Durchschnitts und des stochastischen Oszillators zu einem binären Merkmalsvektor normalisiert wurden. Diese Daten wurden dann in ein einfaches neuronales Netz eingespeist, das wir für das Paar EUR/USD für das Jahr 2023 trainierten und anschließend Vorwärtstests für das Jahr 2024 durchführten. 

Da unser Ansatz auf der These basiert, dass RL zum Trainieren von Modellen im laufenden Betrieb verwendet werden kann, wollen wir dies in diesem Artikel anhand unserer früheren Ergebnisse und des Netzwerks von SL demonstrieren. RL, so unsere These, ist eine Form der Rückvermehrung im Einsatz, die unsere Kauf-Verkaufs-Entscheidungen sorgfältig abstimmt, sodass sie nicht allein auf prognostizierten Preisänderungen beruhen, wie es im SL-Modell der Fall war. 

Bei dieser „Feinabstimmung“ werden, wie wir in früheren RL-Artikeln gesehen haben, Erkundung und Ausbeutung miteinander verbunden. Auf diese Weise würde unser Politiknetzwerk durch Training in einer realen Marktumgebung bestimmen, welche Zustände zu Kauf- oder Verkaufsaktionen führen sollten. Es kann vorkommen, dass ein Aufwärtstrend nicht unbedingt eine Kaufgelegenheit bedeutet und umgekehrt. Das bedeutet, dass unser RL-Modell als zusätzlicher Filter für die vom SL-Modell getroffenen Entscheidungen fungiert. Die Zustände aus unserem SL-Modell verwendeten eindimensionale kontinuierliche Werte, und dies wird dem Aktionsraum, den wir verwenden werden, sehr ähnlich sein.

DDPG

Wir haben bereits eine Reihe verschiedener RL-Algorithmen betrachtet, und in diesem Artikel befassen wir uns mit Deep Deterministic Policy Gradient (DDPG). Dieser spezielle Algorithmus dient, ähnlich wie DQN, den wir in einem früheren Artikel betrachtet haben, dazu, Vorhersagen in kontinuierlichen Handlungsräumen zu treffen. Bei den meisten Algorithmen, die wir uns in letzter Zeit angesehen haben, handelte es sich um Klassifizierer, die Wahrscheinlichkeitsverteilungen darüber ausgeben, ob die nächste Aktion (zum Beispiel) Kaufen, Verkaufen oder Halten sein sollte. 

Dieser ist kein Klassifikator, sondern ein Regressor. Wir definieren einen Aktionsraum als einen Fließkommawert im Bereich von 0,0 bis 1,0. Mit diesem Ansatz lassen sich weitaus mehr Optionen bestimmen als einfach nur:

• Kaufen (immer wenn über 0,5);
• Verkaufen (immer wenn unter 0,5);
• oder Halten (immer wenn in der Nähe von 0,5)

Dies könnte durch die Einführung von schwebenden Aufträgen oder sogar Positionsgrößen erreicht werden. Es bleibt dem Leser überlassen, diese Maßnahmen zu erforschen, da wir uns auf die einfache Implementierung beschränken, bei der 0,5 als Schlüsselschwelle dient. 

Im Prinzip verwendet DDPG neuronale Netze, um Q-Werte (Belohnungen von Aktionen) zu approximieren und optimiert direkt die Strategie (das Netz, das die nächstbeste Aktion wählt, wenn es mit Umgebungszuständen konfrontiert wird); anstatt nur Q-Werte zu schätzen. Im Gegensatz zu DQN, das auch für diskrete/klassifizierende Aktionen wie links oder rechts verwendet werden kann, ist DDPG rein für kontinuierliche Aktionsräume. (Denken Sie an Lenkwinkel oder Motordrehmomente, z. B. beim Robotikunterricht). Wie funktioniert das?

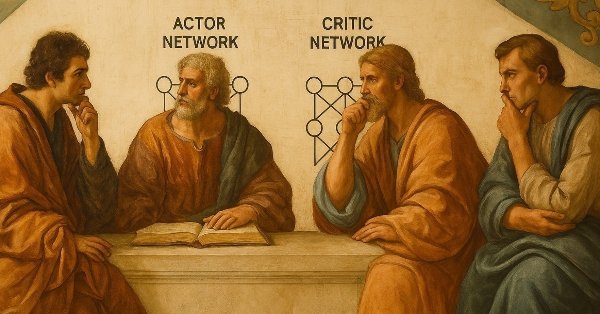
In erster Linie werden zwei neuronale Netze verwendet. 

• Das eine ist das Akteursnetzwerk, dessen Aufgabe es ist, die beste Aktion für einen bestimmten Zustand der Umgebung zu entscheiden. 
• Das andere ist das Kritikernetz, dessen Aufgabe es ist, zu bewerten, wie gut die vom Akteur gewählte Handlung ist, indem es die potenziellen Belohnungen abschätzt, die für die Durchführung dieser Handlung erzielt werden können. 

Diese Schätzung wird auch als Q-Wert bezeichnet. Ein weiterer wichtiger Bestandteil der DDPG ist der Erfahrungswiedergabepuffer. Dieser speichert vergangene Erfahrungen (ein Sammelbegriff für Zustände, Aktionen, Belohnungen und nächste Zustände) in einem Puffer. Zufallsstichproben aus diesem Puffer werden zum Trainieren der Netze verwendet und verringern die Korrelation zwischen den Aktualisierungen.

Neben den beiden oben erwähnten Netzen werden auch ihre gleichwertigen Kopien, die als „Ziele“ bezeichnet werden, eingesetzt. Die Gewichte dieser separaten Kopien des Akteurs- und des Kritikernetzes werden langsamer aktualisiert, was zur Stabilisierung des Trainingsprozesses beiträgt, indem konsistente Ziele vorgegeben werden. Schließlich wird die Erkundung, ein Schlüsselmerkmal des Verstärkungslernens, in der DDPG noch einen Schritt weitergeführt, indem durch Algorithmen eine Rauschkomponente in die Aktionen eingebracht wird, von denen das Ornstein-Uhlenbeck-Rauschen die häufigste ist.

Die Ausbildung der DDPG umfasst im Wesentlichen 3 Dinge. Erstens geht es um die Verbesserung des Akteursnetzwerks, wobei das Kritikernetzwerk das Akteursnetzwerk bei der Festlegung, welche Aktion gut/schlecht ist, anleitet, sodass das Akteursnetzwerk seine Gewichtung bei der Auswahl von Aktionen, die die Belohnung maximieren, besser anpasst. Zweitens, die Verbesserung des Kritiker-Netzwerks, indem es lernt, Belohnungen/Q-Werte mit Hilfe von Bellman-Updates besser abzuschätzen, wie in der folgenden Gleichung dargestellt:

wobei:

• Q(s,a): Der vorhergesagte Q-Wert (Schätzung des Kritikers) für die Durchführung von Aktion a im Zustand s.

• r: Unmittelbarer Erhalt einer Belohnung nach Durchführung einer Aktion a im Zustand s.

• γ: Abzinsungsfaktor (0≤γ<1), der bestimmt, wie sehr zukünftige Belohnungen bewertet werden (näher an 0 = kurzfristige Ausrichtung, näher an 1 = langfristige Ausrichtung).

• s′: Nächster beobachteter Zustand nach Durchführung der Aktion a im Zustand s.

• Qtarget(s′,⋅): Die Schätzung des Q-Wertes des Ziel-Q-Netzes für den nächsten Zustand s′(wird zur Stabilisierung des Trainings verwendet).

• Actortarget(s′): Die empfohlene Aktion des Zielakteurs für den nächsten Zustand s′(deterministische Politik).

Schließlich gibt es weiche Aktualisierungen für das Akteur-Ziel und das Kritiker-Ziel, bei denen die Aktualisierungen langsam durchgeführt werden, um die Hauptnetze gemäß der folgenden Gleichung anzupassen:

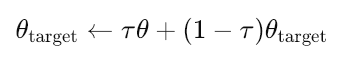
wobei:

• θtarget: Parameter (Gewichte) des Zielnetzes (entweder Akteur oder Kritiker).
• θ: Parameter des wichtigsten (Online-) Netzwerks (entweder Akteur oder Kritiker).
• τ: Sanfte Aktualisierungsrate (0≪τ≪1, z. B. 0,001). Steuert, wie langsam die Zielnetze aktualisiert werden.
• Kleines τ = Zielnetze ändern sich sehr langsam (stabileres Training).
• Großes τ = Zielnetze werden schneller aktualisiert (weniger stabil, aber möglicherweise schneller angepasst).

Warum DDPG? Es ist beliebt, weil es in hochdimensionalen, kontinuierlichen Aktionsräumen gut funktioniert und die Stabilität von Q-Learning mit der Flexibilität von Policy-Gradienten kombiniert. Wie das obige Beispiel des kontinuierlichen Aktionsraums in der Robotik zeigt, ist es in der Robotik, der physikalischen Steuerung und anderen ähnlich komplexen Aufgaben sehr beliebt. Das bedeutet jedoch nicht, dass wir sie nicht auch für finanzielle Zeitreihen verwenden können, und genau das werden wir untersuchen. 

Wir implementieren den größten Teil unseres Codes in Python 3.10, weil dies beim Training sehr tiefer Netze effizienter ist. Aber in diesem Bereich lernt man immer wieder etwas Neues. In meinem Fall war es die Tatsache, dass Python dank Ankercode und Klassen in C/C++ sowie CUDA in der Lage ist, so schnelle Berechnungen in Trainingsnetzwerken (PyTorch & TensorFlow) durchzuführen. Jetzt ist MQL5 C sehr ähnlich und die Implementierung von OpenCL wird schon seit einiger Zeit unterstützt. Ich denke, dass einfach eine grundlegende Multiplikation Matrix-Code-Bibliothek (teilweise in OpenCL) fehlt, um ähnliche Leistung in MQL5 zu erhalten? Dies könnte eine Untersuchung wert sein.

Replay Buffer

Der Replay-Buffer ist eine sehr wichtige Komponente in DDPG und anderen Off-Policy Algorithmen des Verstärkungslernens (Reinforcement Learning). Es wird hauptsächlich verwendet, um zeitliche Korrelationen zwischen aufeinanderfolgenden Stichproben aufzubrechen, die Wiederverwendung von Erfahrungen zu ermöglichen, sodass das Lernen effizienter wird, einen vielfältigen Satz von Übergängen für ein stabiles Training bereitzustellen und vergangene Erfahrungen (Zustand, Aktion, Belohnung, nächster Zustand, erledigte Tupel) für die Verwendung im Trainings-/Netzgewicht-Aktualisierungsprozess zu speichern.

Die Kernimplementierung beginnt in erster Linie mit der Initialisierungsfunktion:

def __init__(self, capacity):

    self.buffer = deque(maxlen=capacity)

Wir verwenden collections.deque mit einer festen Maximalkapazität und verwerfen automatisch alte Erfahrungen, wenn sie voll sind, durch ein First-In-First-Out-Verhalten. Sie ist sehr einfach und speichereffizient. Als Nächstes folgt die Push-Operation, bei der der Puffer vollständige Übergangstupel speichert und sowohl erfolgreiche als auch abgeschlossene Übergänge behandelt (durch Verwendung des Flags done). Es sorgt für einen minimalen Overhead beim Hinzufügen neuer Erfahrungen.

def push(self, state, action, reward, next_state, done):

    self.buffer.append((state, action, reward, next_state, done))

Der verwendete Stichprobenmechanismus ist eine gleichmäßige Zufallsstichprobe, die sehr wichtig ist, um Korrelationen zu brechen. Es ist insofern effizient, als es eine Stapelverarbeitung über zip(*batch) verwendet, die bei der Trennung der Umweltkomponenten hilft. Sie liefert alle notwendigen Komponenten für die Aktualisierung des Q-Learnings.

def sample(self, batch_size):

    batch = random.sample(self.buffer, batch_size)

    states, actions, rewards, next_states, dones = zip(*batch)

Als Nächstes folgt in der Replay-Buffer-Klasse die Tensor-Konvertierung und die Gerätebehandlung für jede der Umgebungskomponenten. Diese sind, wie bereits oben gezeigt, Zustände, Aktionen, Belohnungen, nächste Zustände und Ausgaben. Der Umbau ist sehr robust. Es verarbeitet sowohl NumPy-Arrays als auch PyTorch-Tensoren als Eingabe. Dadurch wird sichergestellt, dass Tensoren (die als Arrays mit angehängten Gradienteninformationen aufgefasst werden können) von den Berechnungsgraphen losgelöst sind.

Wir verlagern die Daten in die CPU, um Gerätekonflikte zu vermeiden. Wir führen eine explizite Umwandlung in Float Tensor (float-32) durch, die eine übliche Voraussetzung für neuronale Netze ist. Dieser Datentyp, der kleiner ist als der in MQL5 häufig verwendete Double, der wesentlich rechenintensiver ist. Schließlich können wir dank PyTorch (im Gegensatz zu TensorFlow) die Daten auf ein bestimmtes Rechengerät, wie z. B. einen Grafikprozessor, verschieben, wenn dieser verfügbar ist.

states = torch.FloatTensor(

    np.array([s.detach().cpu().numpy() if torch.is_tensor(s) else s for s in states])

).to(device)

Unsere Replay-Buffer-Klasse funktioniert gut mit DDPG, da sie erstens das Off-Policy-Lernen erleichtert, da DDPG einen Replay-Buffer benötigt, um aus historischen Daten zu lernen. Die kontinuierlichen Aktionsräume von DDPG werden mit der Float-Tensor-Konvertierung gut behandelt. Das verleiht der DDPG eine gewisse Stabilität durch Zufallsstichproben, die dazu beitragen, korrelierte Aktualisierungen zu verhindern, die das Training destabilisieren könnten. Außerdem bietet es eine gewisse Flexibilität, da es sowohl mit NumPy- als auch mit Torch-Inputs, den üblichen Reinforcement-Learning-Pipelines, arbeiten kann.

Mögliche Verbesserungen sind der Wechsel zu priorisierten Erfahrungswiedergabepuffern, um wichtige Übergänge zu behandeln, die Verwendung von mehrstufigen Rückgaben oder n-stufigem Lernen, die Trennung/Klassifizierung verschiedener Erfahrungstypen und effizientere Tensorkonvertierungen, die das NumPy-Zwischenprodukt vermeiden.

Im Großen und Ganzen ist unsere Wiedergabepufferklasse jedoch robust, da die Typüberprüfung mit torch.is_tensor(), die Gerätebehandlung zur Gewährleistung der CPU/GPU-Kompatibilität und die saubere Trennung der Umgebungskomponenten zum Einsatz kommen. Auch die Leistung wird nicht beeinträchtigt, da deque O(1) Append- und Pop-Operationen anbietet, die Stapelverarbeitung zur Minimierung des Overheads verwendet und Zufallsstichproben implementiert, die bei Puffern mittlerer Größe effizient sind. Es ist auch wartbar, da der Code eine klare und präzise Implementierung hat, einfach zu erweitern oder zu ändern ist und eine gute Typ-Konsistenz in der Ausgabe bietet.

Die wichtigsten Einschränkungen und Überlegungen könnten sich aus der Speichernutzung ergeben. Die Speicherung vollständiger Übergänge kann bei einer hohen Anzahl von Übergangszuständen sehr umfangreich sein. Außerdem muss die festgelegte Kapazität möglicherweise für verschiedene Umgebungen angepasst werden. Eine weitere Einschränkung ergibt sich aus der Effizienz der Stichproben. Bei einer einheitlichen Stichprobe werden wichtige Erfahrungen nicht priorisiert, da alle gleich gewichtet werden. Es gibt auch keine Behandlung von Episodengrenzen beim Sampling.

Mögliche Alternativen, die einige dieser Probleme lösen, könnten die Verwendung von plattenbasiertem Speicher für sehr große Puffer, bildbasierte Zustände für die Speicherung komprimierter Darstellungen und die zusätzliche Unterstützung für die Speicherung zusätzlicher Informationen wie Protokollwahrscheinlichkeiten sein. Solche Änderungen könnten eine solide Grundlage für die DDPG bilden, die es ermöglicht, sie auf der Grundlage spezifischer Anwendungsbedürfnisse zu erweitern, während ihre Kernfunktionalität erhalten bleibt.

Kritiker- und Akteursnetzwerke

Beide Netze folgen einer ähnlichen Multi-Layer-Perceptron-Struktur, aber wie man es beim Verstärkungslernen erwarten würde, dienen sie beim DDPG unterschiedlichen Zwecken. Das Kritikernetz, das auch als Q-Funktion bezeichnet wird, schätzt den Wert von Zustands-Aktions-Paaren (Q-Werte oder Belohnungen), während das Akteursnetz, das auch als Politiknetz bezeichnet wird, die optimale Aktion für einen bestimmten Zustand bestimmt.

Die Initialisierung und Schichtstruktur des kritischen Netzes sieht folgendermaßen aus:

def __init__(self, state_dim, action_dim, hidden_dim):

    super(Critic, self).__init__()

    self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)

    self.fc2 = nn.Linear(hidden_dim, hidden_dim)

    self.fc3 = nn.Linear(hidden_dim, 1)

Die wichtigsten Punkte hier sind, dass: es sowohl Zustände als auch Aktionen (wie wir sie in früheren RL-Algorithmen gesehen haben) als Eingabe akzeptiert, im Gegensatz zu Wertfunktionen in anderen Methoden; wir implementieren dieses Netzwerk mit drei vollständig verbundenen Schichten mit versteckten Dim-Neuronen in den ersten beiden Schichten; die letzte Ausgabeschicht gibt nur einen Q-Wert-Skalar aus; und die Architektur ist dazu gedacht, Q(s,a) für kontinuierliche Aktionsräume zu schätzen.

Die Mechanik des Vorwärtsdurchgangs ist wie folgt:

def forward(self, state, action):

    x = torch.cat([state, action], dim=1)

    x = self.relu(self.fc1(x))

    x = self.relu(self.fc2(x))

    q_value = self.fc3(x)

Zu den „kritischen“ Komponenten dieser Implementierung gehört torch.cat, die für die DDPG-Schätzung des Aktionswerts unerlässlich ist. Es kombiniert Zustands- und Aktions-Eingangsvektoren vor der Verarbeitung. Die Größenbestimmung dim=1 gewährleistet eine ordnungsgemäße Verkettung bei der Stapelverarbeitung. Ein weiterer bemerkenswerter Teil unseres Codes könnten die Aktivierungsfunktionen sein. ReLU wird für die versteckten Schichten verwendet, da es das Problem des verschwindenden Gradienten entschärft. In der letzten Schicht wird keine Aktivierung durchgeführt, da die Q-Werte eine beliebige reelle Zahl sein können.

Der Informationsfluss erfolgt vom Zustands-Aktionspaar über die verborgenen Schichten bis hin zur Q-Wert-Schätzung. Sie stellt den Kern der Q-Learning-Funktion dar. Das Akteursnetzwerk hat außerdem die folgende Initialisierung und Struktur:

def __init__(self, state_dim, action_dim, hidden_dim):

    super(Actor, self).__init__()

    self.fc1 = nn.Linear(state_dim, hidden_dim)

    self.fc2 = nn.Linear(hidden_dim, hidden_dim)

    self.fc3 = nn.Linear(hidden_dim, action_dim)

    self.tanh = nn.Tanh()

Die wichtigsten Aspekte, die hier zu erwähnen sind, sind, dass es nur state-dim als Eingabe benötigt, da die Politik zustandsabhängig ist. Für unsere Zwecke folgt es einer ähnlichen Drei-Schichten-Struktur wie das obige kritische Netz, jedoch mit einer anderen Handhabung der Ausgabe. Die endgültige Schichtgröße entspricht der Dimensionalität des Aktionsraums. Die für die Ausgabeschicht verwendete Tanh-Aktivierung ist wichtig für begrenzte Aktionen. Die Mechanik des Vorwärtsdurchgangs wird durch die folgende Auflistung definiert:

def forward(self, state):

    x = self.relu(self.fc1(state))

    x = self.relu(self.fc2(x))

    action = self.tanh(self.fc3(x))

Es ist viel einfacher und geradliniger als das kritische Netz, bei dem die Zustandsverarbeitung nur den Zustand als Input nimmt (im Gegensatz zum kritischen Netz) und dann die Zustandsrepräsentation durch die verborgenen Schichten aufbaut. Die Aktionsgenerierung wird durch die Tanh-Aktivierung ermöglicht, die die Ausgaben auf [-1, 1] beschränkt. Dies ist für kontinuierliche Aktionsräume der DDPG unerlässlich. Dieser feste Bereich kann auf den Aktionsbereich der Umgebung umskaliert werden, z. B. [0, 1], usw. Bemerkenswert ist hier auch, dass die Politik von Natur aus deterministisch ist. Es wird eine spezifische Aktion ausgegeben und nicht eine Wahrscheinlichkeitsverteilung über eine diskrete Menge von Aktionen, wie es bei stochastischen Methoden oft der Fall ist.

Die DDPG-spezifischen Design-Entscheidungen, die für das kritische Netz getroffen wurden, stimmen ein wenig mit anderen Reinforcement-Learning-Algorithmen überein, und zwar: die gemeinsame Handhabung von Eingaben, da Zustand und Aktion miteinander verkettet sind; eine skalare Ausgabe, die gut in kontinuierlichen Aktionsräumen funktioniert; und keine Aktivierung, die die gesamte Bandbreite der Q-Wert-Schätzungen bewahrt. Für das DDPG-Design des Akteursnetzwerks werden begrenzte Outputs durch die Verwendung von Tanh, das sicherstellt, dass die Aktionen innerhalb eines erlernbaren Bereichs liegen, deterministischer Charakter, da eine spezifischere Aktionsgewichtung anstelle einer stochastischen Politik angestrebt wird, und Action-Space-Matching, bei dem die endgültige Schichtgröße direkt auf die Aktionsdimensionen der Umgebung abgestimmt wird, gewählt.

Unser DDPG-Beispiel verwendet einen eindimensionalen Aktionsraum. Der Zustandsraum ist ebenfalls ein eindimensionaler Raum, da dies die Ausgabe des im letzten Artikel verwendeten überwachten Lernnetzes war. Gemeinsame architektonische Merkmale sind ReLU-Aktivierungen, die häufig für versteckte Schichten beim tiefen Reinforcement-Learning gewählt werden. Durch eine einheitliche Dimensionalität haben wir eine konsistente versteckte Größe beibehalten und eine MLP-Struktur gewählt, die für niedrigdimensionale Zustandsräume geeignet ist.

Die Stärken der Implementierung von PyTorch-Netzen sind nicht besonders hervorzuheben, aber sie sind: Robustheit bei der Handhabung von Dimensionen und klare Spezifikation von Eingabe- und Ausgabedimensionen; Aktivierungsmanagement, bei dem es eine ordnungsgemäße Trennung von versteckten und Ausgabeaktivierungen gibt; und Unterstützung der Stapelverarbeitung, da alle Operationen (in ihren Tensoren) eine Stapeldimension beibehalten. Darüber hinaus gibt es einige Überlegungen, die die Leistung dieser Netze steigern: die ReLU-Effizienz, da diese Aktivierung im Vergleich zu anderen Aktivierungsarten schneller ist, die Einfachheit der linearen Schichten (ohne Faltungen oder Rekursionen) und die minimalen Operationen angesichts der rationalisierten Vorwärtsdurchgängen.

Potenzielle Verbesserungen für das kritische Netzwerk sind: Layer-Normalisierung, die das Lernen stabilisieren könnte; Duelling-Architektur, bei der Zustandswerte und mehrere Q-Ausgänge wie in TD3 für Clipped Double Q-Learning. Für das Akteursnetzwerk könnten Verbesserungen in der Rauschinjektion für die Exploration (obwohl DDPG externes Rauschen verwendet), in der Stapelnormalisierung für unterschiedliche Zustandsgrößen und in der Spektralnormalisierung für ein stabileres Training bestehen. 

Für die Integration dieser beiden im DDPG-Kontext: Die Rolle des Kritikernetzes beim Training besteht darin, Q-Wert-Schätzungen für Politikaktualisierungen zu liefern, die dann verwendet werden, um die zeitlichen Differenzziele für sich selbst zu berechnen. Sie muss ihre Inputs, d. h. die Werte der staatlichen Maßnahmen, genau bewerten, um zu bestimmen, um wie viel die Politik (Gewichte und Verzerrungen des Akteursnetzes) angepasst werden muss. Die Rolle des Akteurs beim Training besteht darin, Aktionen für das Funktionieren der Umgebung und die Berechnung des Q-Wertes bereitzustellen, den Gradientenanstieg an den Q-Werten der Kritiker zu aktualisieren und glatte deterministische Strategien für die kontinuierliche Kontrolle zu erlernen.

Schlussfolgerung

Wir sollten uns die DDPG-Agentenklasse und die Umgebungsdatenklasse ansehen, bevor wir die Berichte der Strategietester für unsere 7 Muster überprüfen, die aus dem letzten Artikel übernommen werden konnten. Wir werden diese jedoch im nächsten Teil behandeln, da dieser bereits sehr umfangreich ist. Ein großer Teil des hier behandelten Materials ist in Python, mit der Absicht, ONNX-Netzwerke zu exportieren, um sie in MQL5 als Ressource zu integrieren.

Python ist im Moment wichtig, weil es beim Training effizienter ist als das reine MQL5, aber es könnte Umgehungen geben, die OpenCL verwenden, die wir in zukünftigen Artikeln ebenfalls untersuchen könnten. Der typische angehängte Code, den wir in der Assistentenbaugruppe von Signalklassen verwenden, wird auch im folgenden Teil betrachtet, und daher haben wir keine Anhänge für diesen Artikel.

Name	Beschreibung
wz_58_ddpg.py	Skriptdatei für die Implementierung von Reinforcement-Learning DDPG in Python