Características del Wizard MQL5 que debe conocer (Parte 35): Regresión de vectores de soporte

Introducción

La Regresión por vectores de soporte (Support Vector Regression, SVR) es una forma de regresión derivada de Máquina de vectores de soporte (Support Vector Machine, SVM). En esencia, SVR utiliza métodos kernel para mapear datos de entrada en espacios de mayor dimensión, lo que permite capturar relaciones más complejas, lo que contrasta con la reducción de dimensionalidad. Sin embargo, en este artículo exploraremos estrictamente su papel como función de pérdida cuando se utiliza con un perceptrón multicapa. Una forma de regresión relacionada pero diferente que analizamos en un artículo anterior fue la regresión de procesos gaussianos. Por ello, quizá sea clave que empecemos por distinguir entre ambos.

Diferencias entre SVR (Support Vector Regression) y GPR (Gaussian Process Regression)

Para poner de relieve las diferencias entre estos dos conceptos, nos alejaremos un poco de la jerga del aprendizaje automático y utilizaremos ejemplos de casos cotidianos para mostrar por qué cada uno de ellos es importante. Imaginemos que usted dirige una empresa emergente que ha desarrollado un helado muy saludable y bajo en azúcar que tiene una gran demanda en su ciudad natal. Como acaba de empezar y sólo ha vendido el helado en su ciudad natal, sigue realizando la mayor parte de la fabricación manualmente. Por tanto, tiene que empezar a aumentar su productividad, ya que, además de controlar los costes, le aportará ventajas como el control de la calidad y la aplicación de algunas normas de producción.

Una expansión de este tipo requeriría un capital que no se puede pedir prestado institucionalmente porque no se tienen las garantías (o los medios) necesarios para presentarlo a los bancos; o se podría asociar con una gran marca de helados establecida; sin embargo, los empleados de estas grandes marcas a menudo son burócratas y van a decir que no, independientemente de lo que piensen de su producto.

Por lo tanto, solo le queda la opción de recaudar capital a través de una vía privada y semiformal, con la salvedad de que debe escalar o expandir su producto. Sin embargo, a medida que usted se expande fuera de su ciudad natal, ¿qué clientes mirarán o incluso considerarán su producto frente a las marcas establecidas? Al ser un territorio desconocido, no puedes abordarlo de la misma manera que lo hiciste en tu ciudad natal. Esto, entonces, plantea la pregunta que quizás haya pasado por alto en sus inicios para satisfacer la demanda de viviendas: ¿cuál es su segmento principal de clientes?

La segmentación de clientes, un aspecto comercial que algunos pueden optar por ignorar, tiene varios tipos. Incluye (pero no se limita a) segmento por código postal (o dirección), segmento por edad, nivel educativo, ocupación/profesión y segmento por nivel de ingresos; y otro segmento "nuevo" y en crecimiento gracias a las redes sociales podría ser el segmento de estilos de vida/grupos de interés. Al aumentar los datos de ventas con estos segmentos, podemos crear algunos conjuntos de datos interesantes que, al recopilarse incluso en nuestra ciudad natal, podrían brindar una ventana a lo que sucederá fuera de nuestra ubicación principal.

La regresión del proceso gaussiano, como se presentó en un artículo anterior, no solo proporciona una proyección media, sino que también asigna un rango indicativo a esta media junto con un nivel de confianza. Esto tiende a significar que es adecuado para hacer proyecciones en situaciones donde la demanda de un producto está enormemente influenciada por factores externos (no es consistente) y, por lo tanto, es un producto de lujo o costoso para compensar las series de demanda inconsistentes. Si no se trata de un producto de lujo, podría ser muy estacional o podría ser un producto de nicho con un precio elevado y una demanda fluctuante. Esto significaría que nuestro helado tendría que tener un precio más alto que el de la competencia para poder adaptarse al producto de nicho/lujo más adecuado para su uso con GPR.

Además, el tipo de producto y la segmentación del cliente presentan una confluencia de opciones a la hora de seleccionar un conjunto de datos para proyectar la demanda futura, lo que requiere una consideración cuidadosa como se ilustra en la siguiente tabla.

Tipo de segmentación	Mejor con SVR	Mejor con GPR
Código postal	Bienes de consumo cotidianos	No es ideal a menos que se combine con otros datos dinámicos
Edad	Ropa, bienes de consumo, herramientas educativas	No es ideal a menos que se combine con otros datos dinámicos
Nivel educativo	Productos educativos, productos tecnológicos.	No es ideal a menos que intervengan factores complejos
Nivel de ingresos	Productos básicos en mercados estables	Artículos de lujo, electrónica de alta gama, artículos premium.
Ocupación	Productos vinculados a ocupaciones estables	Productos de temporada, artículos influenciados por factores externos (por ejemplo, el clima)
Estilo de vida/Grupos de interés	Grupos de interés predecibles (por ejemplo, ropa deportiva)	Productos especializados o de nicho, demanda muy variable

Si bien la tabla anterior no es necesariamente una representación factual de la relación entre los segmentos de clientes y los tipos de productos, sí enfatiza el punto importante de considerarlos antes de seleccionar un conjunto de datos apropiado para hacer pronósticos. En resumen, el GPR es más adecuado para empresas que a menudo enfrentan incertidumbre y patrones de crecimiento complejos que requieren realizar predicciones con intervalos de confianza.

Por otro lado, las regresiones de vectores de soporte son buenas para hacer proyecciones donde la certeza y el crecimiento estable están en juego. Son ideales para cuando las decisiones pueden basarse en tendencias lineales o moderadamente lineales. ¿Por qué? Porque SVR es robusto al ruido. Se centra en obtener el límite de decisión que maximiza el margen de error y minimiza la influencia de valores atípicos. Al hacer que el margen de error (épsilon) actúe como clasificador, la SVR debería ser eficaz con conjuntos de datos que no tienen muchos valores atípicos.

Y como podemos ver en la recomendación de la tabla cruzada anterior, SVR es el más adecuado para hacer proyecciones de productos básicos o bienes de consumo cotidianos para los cuales la demanda es casi constante y, salvo que se produzca un brote de COVID (que puede dispararse y desplomarse la demanda), el nivel de demanda del producto no debería fluctuar mucho, si es que lo hace. Entonces, para considerar nuestra situación de expandir nuestras ventas de helados fuera de nuestra ciudad natal, SVR sería una herramienta adecuada si no tiene un precio demasiado ostensible (como se había recomendado para GPR anteriormente) pero tiene un precio y se coloca en los estantes de las tiendas en los puntos donde los consumidores recogen sus alimentos diarios y productos básicos que pueden necesitar para la semana.

Entonces, si utilizamos la tabla cruzada como guía, si nuestro helado es un producto premium que vendemos principalmente en los días festivos principales, o solo en verano, o se ofrece a determinados restaurantes de alta gama, por ejemplo, entonces buscamos utilizar GPR con datos de ventas agregados por nivel de ingresos. Además, la tabla cruzada recomienda grupos de ocupación y estilo de vida del consumidor/intereses especiales y estos también podrían considerarse. Por otro lado, SVR funcionaría mejor si nuestro producto se vendiera predominantemente en grandes tiendas donde los precios bajos son importantes, como se argumentó anteriormente, y el segmento de consumidores al que esto es pertinente es la dirección (o el código postal). Por lo tanto, los datos de ventas agregados por dirección serían más útiles para hacer proyecciones con SVR sobre qué tan rápido o lento deberíamos implementar nuestra expansión de helados, ya que esto es algo que tendríamos que hacer correctamente ya que ahora estamos usando el dinero de otras personas.

Entonces, GPR funciona mejor en situaciones de pronóstico donde un alto grado de incertidumbre es aceptable, mientras que SVR, en el que nos centramos en este artículo, está casi en el otro extremo del espectro, ya que ignora los valores atípicos que quedan fuera de un umbral designado al definir el hiperplano de los conjuntos de datos.

Definición de SVR

La SVR puede formularse como una función objetivo y como una función de decisión. Si comenzamos con la fórmula de la función objetivo es la siguiente:

Donde:

• w es el vector de pesos (parámetros del modelo) en nuestro caso nos interesa la norma L2 de las matrices de pesos,
• C es el parámetro de regularización que controla el equilibrio entre la complejidad del modelo y la tolerancia a los errores de clasificación,
• L ϵ es la función de pérdida insensible a ϵ definida por:

Donde:

• f(xi ) es el valor predicho,
• yi es el valor verdadero,
• ϵ define un margen de tolerancia dentro del cual no se penalizan los errores.

Por otra parte, la función de decisión, que se utiliza principalmente en la previsión, tiene la siguiente fórmula:

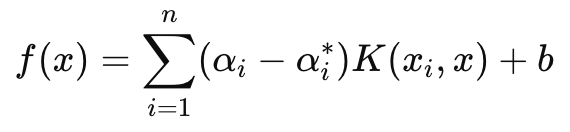
Donde:

• αi y αi^∗ son los multiplicadores de Lagrange,
• K (xi , x) es la función del núcleo (por ejemplo, lineal, polinómica, RBF),
• b es el término de sesgo.

Como se ha mencionado anteriormente, SVR introduce un parámetro epsilon insensible a las pérdidas que se encarga de que los errores con una magnitud inferior a epsilon se ignoren y no den lugar a ajustes de pesos o parámetros para el modelo que se está entrenando. Esto hace que el SVR sea más robusto a la hora de manejar pequeños ruidos y variaciones en los datos, de modo que puede centrarse en el panorama general o en las tendencias principales.

Además, en nuestra función objetivo el parámetro C gestiona el compromiso entre minimizar el error de entrenamiento y minimizar la complejidad del modelo. Una C más alta minimiza el error de entrenamiento pero corre el riesgo de sobreajustarse, mientras que una C más baja, sobre el papel, conduciría a una mayor generalización y una mejor flexibilidad a la hora de hacer previsiones en diferentes escenarios.

Nos vamos a centrar estrictamente en utilizar la función de pérdida de SVR al entrenar un MLP simple para esta red. No haremos proyecciones con sus núcleos como sería el caso de la función de decisión. Sin embargo, cabe mencionar que SVR utiliza funciones de núcleo para transformar los datos de entrada en un espacio de mayor dimensión en el que se pueden señalar relaciones que pueden no ser lineales en el espacio original. Los kernels más comunes son: el kernel lineal, el kernel polinómico y el RBF.

La función de pérdida SVR se puede implementar en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| SVR Loss                                                         |
//+------------------------------------------------------------------+
vector Cmlp::SVR_Loss()
{  vector _loss = fabs(output - label);
   for(int i = 0; i < int(_loss.Size()); i++)
   {  if(_loss[i] <= THIS.svr_epsilon)
      {  _loss[i] = 0.0;
      }
   }
   vector _l = THIS.svr_c*_loss;
   double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2);
   vector _weight_norms;
   _weight_norms.Init(_loss.Size());
   _weight_norms.Fill(_w);
   return(_weight_norms + _l);
}

Normalmente, este valor de pérdida es un escalar, sin embargo, debido a que esta función de pérdida ahora se utiliza en la retropropagación y ciertas redes tienen más de una salida final, era importante mantener la estructura de pérdida en forma vectorial aunque SVR la condensa en un escalar. Y eso es lo que hemos hecho. Además, dentro de la función de retropropagación, verificamos y vemos si se está utilizando la pérdida SVR. Esto es como se indica a continuación:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
   
   ...


   if(EpochIndex < 0)
   {  printf(__FUNCSIG__ + " Epoch Index Should start from 1. ");
      return;
   }


    ...


   vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss));

    ....
}

Podemos agregar esta modificación de una línea porque nuestros parámetros de constructor están en una estructura y modificamos fácilmente esta estructura (ya que esta clase se presentó en artículos anteriores) de la siguiente manera:

//+------------------------------------------------------------------+
//| Multi-Layer-Perceptron Struct for Constructor Parameters         |
//+------------------------------------------------------------------+
struct Smlp
{  //arch array must be defined with at least 2 non zero values
   //that represent the size of the input layer and output layer
   //If more values than this are provided in the array then the
   //middle values will define the size(s) of the hidden layer(s)
   //first value (index zero) is size of input layer
   //last value (index size-1) is size of output layer
   int               arch[];


  ...


   bool              svr_loss;
   double            svr_c;
   double            svr_epsilon;

                     Smlp()
   {                 ArrayFree(arch);

     ...

      svr_loss = false;
      svr_c = 1.0;
      svr_epsilon = __EPSILON * 5.0;
   };
                    ~Smlp() {};
};

Implementación de una clase de señal

Para tener una clase de señal con un MLP cuya función de pérdida utilice la SVR, estaríamos usando nuestra clase ya codificada para un MLP que se compartió en artículos anteriores. Los cambios necesarios para que podamos usar la pérdida SVR ya están resaltados arriba, por lo que lo que queda es cómo se llama y se usa esta clase dentro de una instancia personalizada de una clase de señal. Todos nuestros MLP cubiertos recientemente en esta serie están intentando pronosticar el próximo cambio en el precio de cierre en cada nueva barra. Esto significa que, periódicamente (cada nueva barra), se realizan nuevos cálculos para determinar cuál será el próximo cambio en el precio de cierre.

Las entradas para calcular esto también son cambios en el precio de cierre previo, siendo la variable principal la cantidad de estos cambios. (Esta variable establece el tamaño de la capa de entrada). Existen alternativas para definir no sólo los datos que deben introducirse en el MLP cuando se proyecta el cambio de precio de cierre de la siguiente barra, sino también el grado de previsión que debe tener la previsión. El último punto es importante porque para nuestros propósitos de prueba estamos utilizando una perspectiva a futuro con una única barra de precios. Además, antes de realizar cada pronóstico, realizamos una retropropagación en cada nueva barra para entrenar nuestra red en un tamaño de conjunto de entrenamiento determinado para un número de épocas definido en la entrada.

Estos dos parámetros de entrada, "training set size" y "epochs", también son optimizables y esto requiere un equilibrio entre obtener los pesos ideales de la red y la generalización. Esto se debe a que, si bien un conjunto de entrenamiento más grande y más épocas pueden indicar un buen desempeño en los datos muestreados, una validación cruzada seguramente no será tan optimista a menos que la red tenga cierta generalización y no se ajuste demasiado a sus datos de entrenamiento. La función Obtener salida maneja la previsión a través de MLP y su código fuente se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old;
         if
         (
            _in_new.Init(__MLP_SIGN_INPUTS) &&
            _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_new.Size() == __MLP_SIGN_INPUTS &&
            _in_old.Init(__MLP_SIGN_INPUTS) &&
            _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_old.Size() == __MLP_SIGN_INPUTS
         )
         {  _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new, _target_old;
               if
               (
                  _target_new.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) &&
                  _target_new.Size() == __MLP_SIGN_OUTPUTS &&
                  _target_old.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) &&
                  _target_old.Size() == __MLP_SIGN_OUTPUTS
               )
               {  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

No difiere significativamente de las implementaciones que hemos tenido en artículos anteriores. La retropropagación se realiza para cada punto de datos del conjunto de entrenamiento que tiene una etiqueta (o valor objetivo). Generalmente, todos los datos de entrenamiento tienen un valor objetivo, pero como en nuestro caso estamos fusionando con pronósticos, el "punto de datos de entrenamiento" final es actual y su eventual cambio de precio de cierre es lo que estamos buscando. Entonces, cuando llegamos a los datos de entrada actuales que se supone que nos darán nuestro pronóstico, no realizamos ningún entrenamiento. Además, este es el motivo por el que realizamos una cuenta regresiva en cada conjunto de entrenamiento, es decir, primero entrenamos con datos muy antiguos y luego avanzamos hacia abajo hasta llegar a los datos actuales.

Implementación de una clase de Trailing Stop

Ha pasado un tiempo en estas series desde que consideramos algo más que una clase de señal personalizada y, sin embargo, los lectores que vieron mis artículos anteriores recordarán que a menudo compartí ideas comerciales no solo como una clase de señal sino también clases de trailing stop e incluso clases de administración de dinero. Por lo tanto, volvemos a estas dificultades al considerar una clase de stop dinámico personalizada que se puede adjuntar a un Asesor Experto a través del asistente MQL5. Se puede encontrar orientación, para nuevos lectores, sobre cómo se puede utilizar el código que se comparte a continuación en el asistente MQL5 para crear un Asesor Experto aquí y aquí.

Entonces, para implementar una clase de seguimiento personalizada, buscaremos verificar si hay alguna posición abierta que no tenga un stop loss y necesite que se introduzca uno o una que ya tenga un stop loss pero necesite que se ajuste para fijar mejor las ganancias. Los stop loss son un poco controvertidos porque nunca están garantizados. Solamente se aplican precios de órdenes limitadas. Si por alguna razón el mercado se mueve más de lo que la mayoría de la gente anticipó, entonces el bróker sólo podrá cerrar su orden al próximo "precio disponible", no a su Stop Loss. No obstante, tomaremos la decisión de establecer o mover el stop loss en función del cambio de magnitud previsto en el rango de la barra de precios. Implementamos esto en otra función Obtener salida, similar pero diferente a lo que teníamos con la clase de señal personalizada. Esto se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo;
         if
         (
            _in_new_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_hi.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_hi.Size() == __MLP_TRAIL_INPUTS
            &&
            _in_new_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_lo.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_lo.Size() == __MLP_TRAIL_INPUTS
         )
         {  vector _in_new = _in_new_hi - _in_new_lo;
            vector _in_old = _in_old_hi - _in_old_lo;
            _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo;
               if
               (
                  _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS
                  &&
                  _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS
               )
               {  vector _target_new = _target_new_hi - _target_new_lo;
                  vector _target_old = _target_old_hi - _target_old_lo;
                  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Nuestro código anterior, aunque es casi idéntico a lo que teníamos en la señal, se diferencia principalmente por el tipo de datos de entrada que recibe y su salida esperada. Estamos tratando de determinar si necesitamos mover nuestro Stop Loss y nuestro supuesto previo para esto es un aumento en la volatilidad. Por lo tanto, necesitamos averiguar cuál será el próximo cambio en el rango de la barra de precios. Este tipo de datos seguramente serán muy volátiles (o ruidosos), por lo que si hubiéramos utilizado buffers de promedio móvil como nuestros datos de entrada y valores objetivo, podría haber sido más prudente. Esto se puede modificar ya que la fuente completa se adjunta a continuación, sin embargo, estamos usando cambios en los máximos menos mínimos de cada barra de precios como entradas y estamos buscando que la salida sea el próximo cambio en estos valores de entrada tal como lo hicimos con los precios de cierre para la señal anterior.

Entonces, si el cambio proyectado en el rango de la barra de precios es positivo, lo que implica que la volatilidad está aumentando, tomamos medidas para mover nuestro Stop Loss en proporción a nuestro aumento proyectado. Esto puede parecer temerario porque, como se mencionó anteriormente, los corredores nunca garantizan un precio de Stop Loss, por lo que la contraopción de solo mover un Stop Loss en una disminución proyectada en la volatilidad podría ser "más segura", ya que en tiempos menos volátiles los corredores tienen más probabilidades de honrar los stop loss que cuando hay volatilidad. Sí, es un poco de debate y dejo que el lector lo explore y haga los ajustes apropiados al código dependiendo de sus hallazgos.

Resultados del Probador de estrategias

Realizamos pruebas en el par USDJPY, en el marco temporal diario de 2023.01.01 a 2024.01.01. Estas ejecuciones de prueba se llevan a cabo con algunas de las mejores configuraciones obtenidas de manera muy rápida y con optimizaciones para las que no se han realizado recorridos hacia adelante ni validaciones cruzadas. Se exhiben aquí simplemente para demostrar la capacidad de realizar operaciones y utilizar el Asesor Experto ensamblado por el asistente. La diligencia adicional en la realización de pruebas durante períodos extensos de historia mientras también se hacen recorridos hacia adelante si se trata de optimización se deja al lector. También es importante destacar que los Asesores Expertos ensamblados por el asistente pueden combinar múltiples señales al desarrollar un sistema comercial, de modo que las pruebas u optimización no tienen que realizarse solo con las señales personalizadas que se usan aquí.

Hemos desarrollado una señal personalizada con SVR y una clase de seguimiento personalizada con un MLP similar. Por lo tanto, las ejecuciones de prueba que se presentan a continuación son para dos Asesores Expertos cuyo código de interfaz se adjunta a continuación. El primero utiliza únicamente la señal personalizada sin stop dinámico. Sus resultados se presentan a continuación:

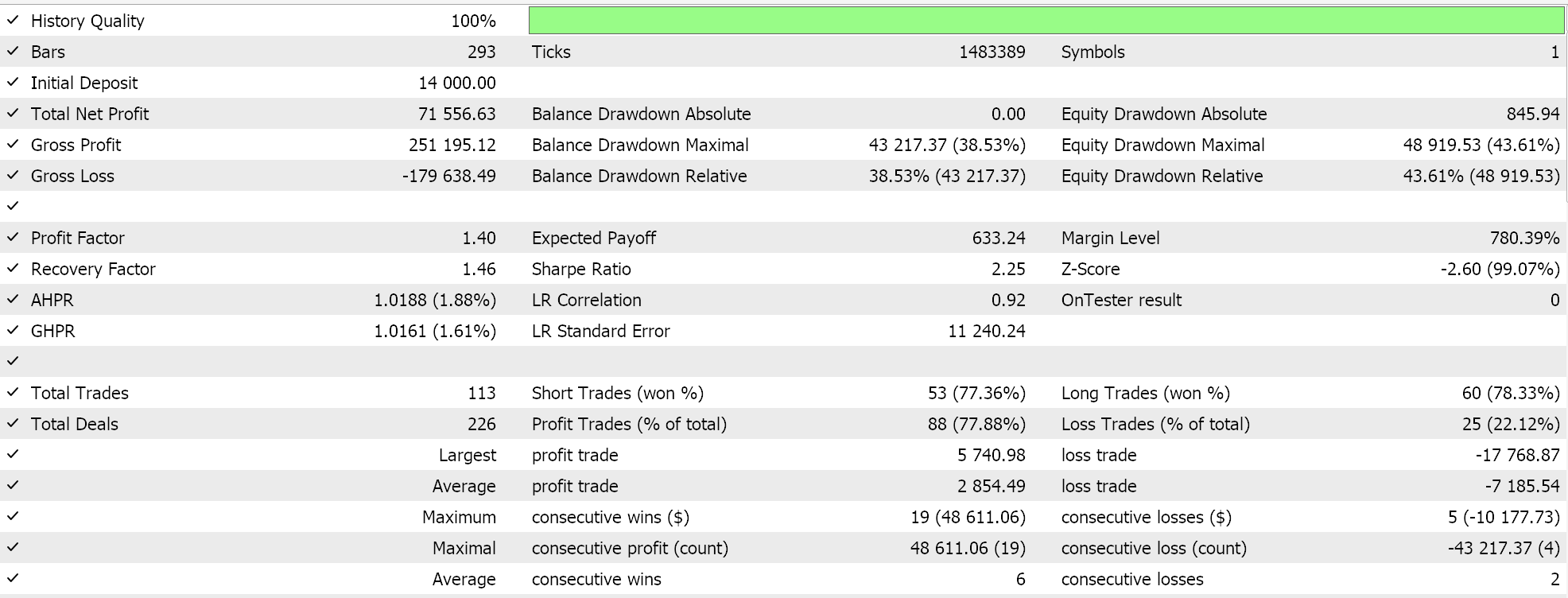
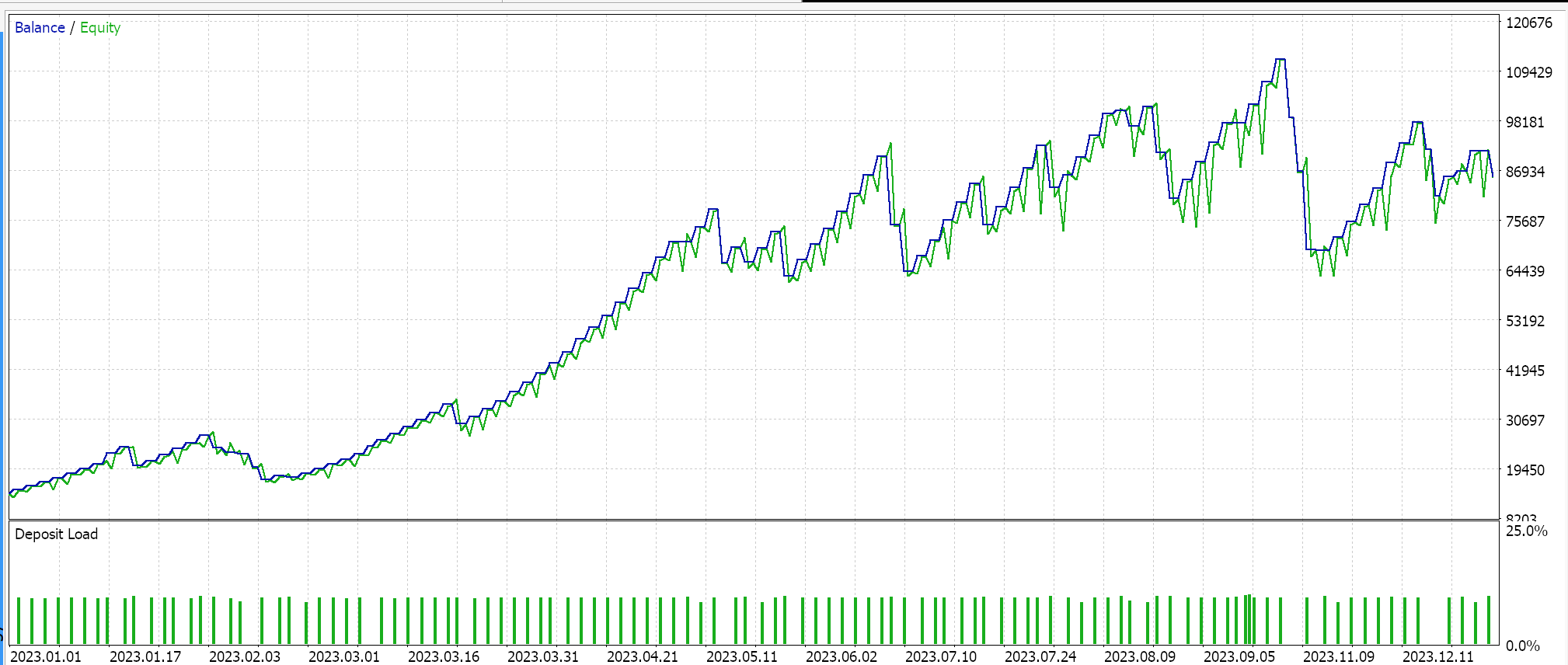
El segundo utiliza la señal personalizada y la clase de seguimiento personalizada que implementamos anteriormente. Sus resultados también se muestran a continuación.

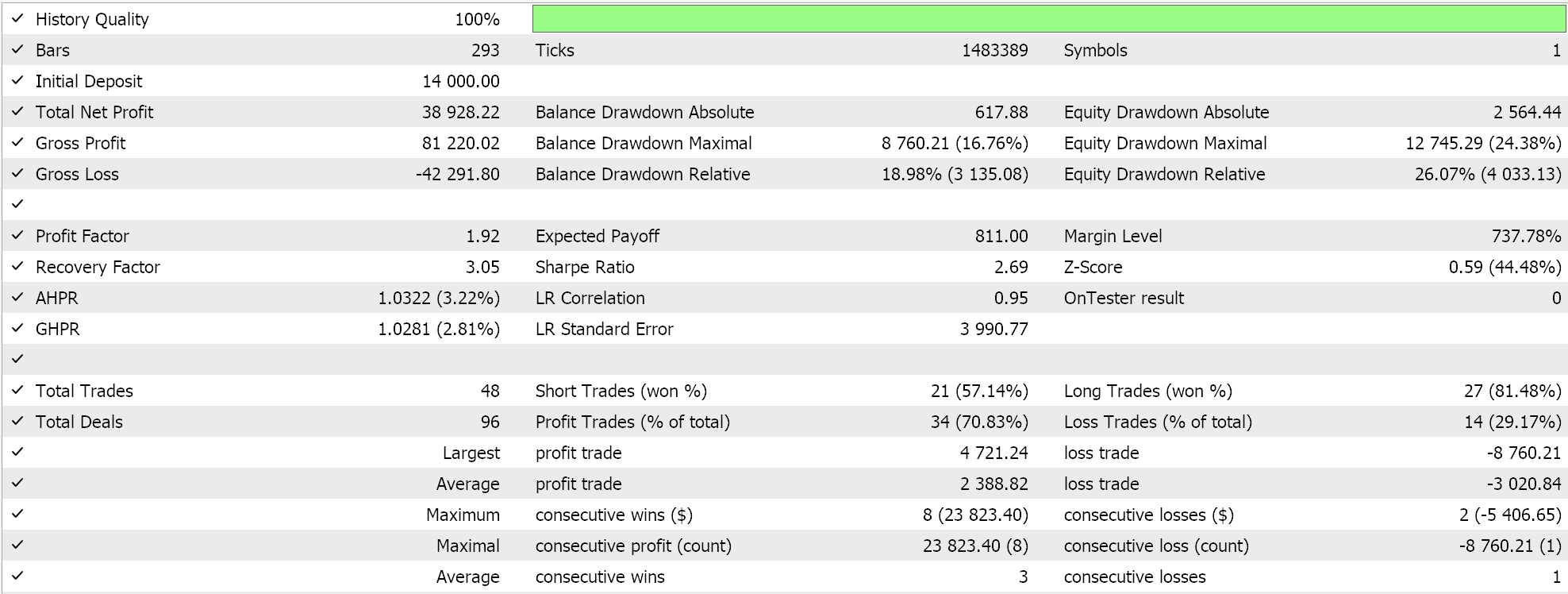
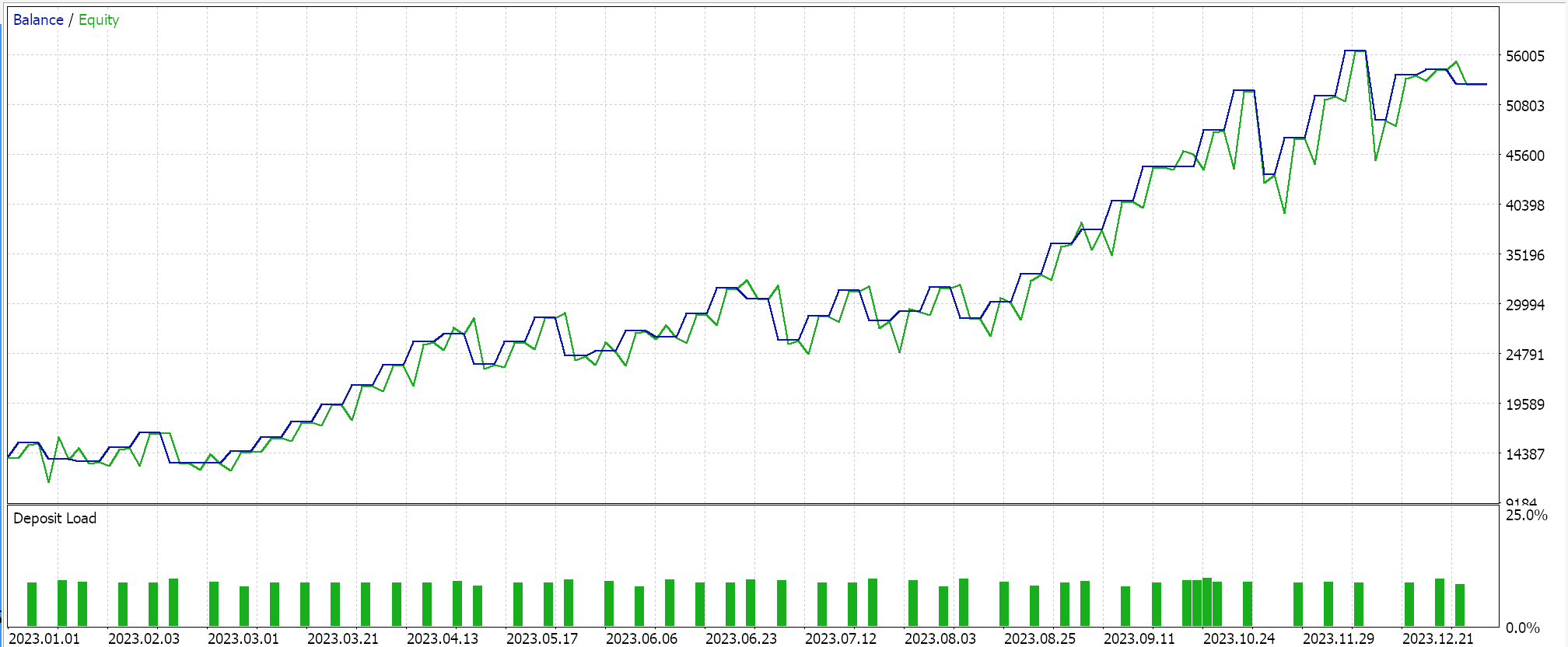
Conclusión

Para concluir, hemos analizado la regresión de vectores de soporte, que sigue otra forma de regresión que consideramos cuando analizamos los núcleos de procesos gaussianos. Estas dos regresiones, la regresión de vectores de soporte y la regresión de proceso gaussiano, son casi polos opuestos en su aplicación, ya que la SVR tiende a ser más adecuada para conjuntos de datos menos volátiles y con tendencias, mientras que la GPR prospera en entornos más volátiles y menos certeros. La regresión de vectores de soporte presenta una función objetivo y una función de decisión. Hemos buscado explotar la primera, la función objetivo, como una función de pérdida para un perceptrón multicapa en una clase de señal y una clase de Trailing Stop personalizada.

El uso de la función de decisión, para actuar como pronosticador, requeriría el uso adicional de kernels, algo que exploramos en el artículo sobre kernels de procesos gaussianos, pero de lo que nos hemos abstenido en este artículo ya que nuestro pronosticador era puramente un MLP. En un futuro artículo(s) podríamos considerar esto dado que hay diferentes formas de núcleos que se pueden utilizar en la realización de esto sin embargo la función de pérdida SVR era nuestro objetivo para este artículo. Mediante el uso de un parámetro epsilon insensible a las pérdidas, también, junto con una creciente lista de implementaciones de funciones de pérdida algunas de las cuales cubrimos aquí, puede introducir una forma diferente de entrenar redes neuronales.

Este parámetro epsilon, insensible a las pérdidas, actúa más como un clasificador que como un regresor y se podría argumentar que esto justifica que esta función de pérdida se utilice más en redes de clasificadores que en redes de regresores, como hemos hecho en este artículo, y podría ser cierto. Sin embargo, SVR sigue tratando con salidas continuas (conjuntos de datos decimales) y predice valores numéricos en un formato similar. Simplemente utiliza el margen épsilon para decidir si un error debe penalizarse, pero su objetivo sigue siendo la regresión, y no la clasificación.