MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 33): Gauß-Prozess-Kerne

Einführung

Die Kernel der Gauß- Prozesse sind Kovarianzfunktionen, die in Gauß-Prozessen verwendet werden, um die Beziehungen zwischen Datenpunkten zu messen, z. B. in einer Zeitreihe. Diese Kernel erzeugen Matrizen, die die Beziehung zwischen den Daten erfassen und es dem Gauß-Prozess ermöglichen, Projektionen oder Vorhersagen unter der Annahme zu erstellen, dass die Daten einer Normalverteilung folgen. Da diese Serien neue Ideen erforschen und gleichzeitig untersuchen, wie diese Ideen genutzt werden können, dienen Gaußsche Prozesskerne (GP) als unser Thema beim Aufbau eines nutzerdefinierten Signals.

In den letzten fünf Artikeln haben wir viel über maschinelles Lernen berichtet. In diesem Artikel machen wir eine Pause und schauen uns die gute alte Statistik an. Es liegt in der Natur der Sache, dass bei der Entwicklung von Systemen oft beides zusammenkommt. Bei der Entwicklung dieses speziellen, nutzerdefinierten Signals werden wir jedoch keine Algorithmen des maschinellen Lernens ergänzen oder berücksichtigen. GP-Kerne zeichnen sich durch ihre Flexibilität aus.

Sie können zur Modellierung einer Vielzahl von Datenmustern verwendet werden, die von Periodizität über Trends bis hin zu nicht-linearen Beziehungen reichen. Noch wichtiger ist jedoch, dass sie bei der Vorhersage mehr als nur einen einzigen Wert liefern. Stattdessen liefern sie eine Unsicherheitsschätzung, die den gewünschten Wert sowie eine obere und untere Grenze enthält. Diese Bandbreiten werden häufig mit einer Konfidenzeinstufung versehen, was die Entscheidungsfindung des Händlers bei der Vorlage eines Prognosewertes weiter erleichtert. Diese Konfidenzraten können auch aufschlussreich sein und zu einem besseren Verständnis der gehandelten Wertpapiere beitragen, wenn man verschiedene Prognosebänder vergleicht, die mit unterschiedlichen Konfidenzniveaus gekennzeichnet sind.

Darüber hinaus können sie gut mit verrauschten Daten umgehen, da sie es erlauben, einen Wert für das Rauschen zur erstellten K-Matrix hinzuzufügen (siehe unten), und sie können auch unter Einbeziehung von Vorwissen verwendet werden, außerdem sind sie sehr skalierbar. Es gibt eine ganze Reihe verschiedener Kernel, aus denen man wählen kann. Die Liste umfasst (aber nicht nur): Quadratischer Exponentialkern (RBF), linearer Kernel, periodischer Kernel, rationaler quadratischer Kern, Matern-Kernel, Exponential-Kernel, Polynom-Kernel, Kernel des weißen Rauschens, Punktprodukt-Kernel, spektraler Mischungskernel, konstanter Kernel, Kosinus-Kernel, Kernel des neuronalen Netzes (Arkosinus) sowie Produkt- und Summen-Kernels.

In diesem Artikel werden wir uns nur mit dem RBF-Kernel (Radial Basis Function) beschäftigen. Wie die meisten Kernel misst er die Ähnlichkeit zwischen zwei beliebigen Datenpunkten, indem er sich auf deren Abstand konzentriert, wobei die Grundannahme gilt, dass die Punkte umso weniger ähnlich sind, je weiter sie voneinander entfernt sind und umgekehrt. Dies wird durch die folgende Gleichung geregelt:

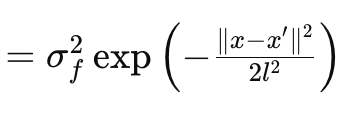
Wobei

• x und x′: Dies sind die Eingabevektoren oder Punkte im Eingaberaum.
• σ f ²: Dies ist der Varianzparameter des Kernels, der als vorbestimmter oder optimierbarer Parameter dient.
• l: wird häufig als Längenskalenparameter bezeichnet. Er steuert die Glätte der resultierenden Funktion. Ein kleineres l (oder eine kürzere Längenskala) führt zu einer sich schnell verändernden Funktion, während ein größeres l (eine längere Längenskala) zu einer glatteren Funktion führt.
• exp: Dies ist die Exponentialfunktion.

Dieser Kernel kann in MQL5 leicht als kodiert werden:

//+------------------------------------------------------------------+
// RBF Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::RBF_Kernel(vector &Rows, vector &Cols)
{  matrix _rbf;
   _rbf.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _rbf[i][ii] = m_variance * exp(-0.5 * pow(Rows[i] - Cols[ii], 2.0) / pow(m_next, 2.0));
      }
   }
   return(_rbf);
}

Gaußsche Prozesse in finanziellen Zeitreihen

Gaußsche Prozesse sind ein probabilistischer Rahmen, in dem Prognosen in Form von Verteilungen und nicht in Form von festen Werten erstellt werden. Aus diesem Grund wird sie auch als nicht-parametrisiertes Framework bezeichnet. Die Ausgabeprognosen enthalten eine mittlere Vorhersage und eine Varianz (oder Unsicherheit) um diese Vorhersage. Die Varianz der GPs stellt die Unsicherheit oder das Vertrauen in die gemachte Prognose dar. Diese Unsicherheit ist im Prinzip zufällig, da sie auf der Normalverteilung der GP beruht. Da sie jedoch ein Intervall und einen Konfidenzwert (in der Regel auf der Grundlage von 95 %) impliziert, müssen nicht alle Vorhersagen eingehalten werden. Im Vergleich zu anderen statistischen Prognosemethoden wie ARIMA ist GP sehr flexibel und in der Lage, komplexe nichtlineare Beziehungen mit quantifizierter Unsicherheit zu modellieren, während ARIMA am besten mit stationären Zeitreihen mit festen Strukturen funktioniert. Der Hauptnachteil von GP ist, dass es rechenintensiv ist, während Methoden wie ARIMA dies nicht sind.

Der RBF-Kernel

Die Berechnung des GP-Kerns umfasst im Wesentlichen 6 Matrizen und 2 Vektoren. Diese Matrizen und Vektoren werden alle in unserer Funktion „GetOutput“ verwendet, deren Code im Folgenden kurz dargestellt wird:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalGauss::GetOutput(double BasisMean, vector &Output)
{  
   ...

   matrix _k = RBF_Kernel(_past_time, _past_time);
   matrix _noise;
   _noise.Init(_k.Rows(), _k.Cols());
   _noise.Fill(fabs(0.05 * _k.Min()));
   _k += _noise;
   matrix _norm;
   _norm.Init(_k.Rows(), _k.Cols());
   _norm.Identity();
   _norm *= 0.0005;
   _k += _norm;
   vector _next_time;
   _next_time.Init(m_next);
   for(int i = 0; i < m_next; i++)
   {  _next_time[i] = _past_time[_past_time.Size() - 1] + i + 1;
   }
   matrix _k_s = RBF_Kernel(_next_time, _past_time);
   matrix _k_ss = RBF_Kernel(_next_time, _next_time);
// Compute K^-1 * y
   matrix _k_inv = _k.Inv();
   if(_k_inv.Rows() > 0 && _k_inv.Cols() > 0)
   {  vector _alpha = _k_inv.MatMul(_past);
      // Compute mean predictions: mu_* = K_s * alpha
      vector _mu_star = _k_s.MatMul(_alpha);
      vector _mean;
      _mean.Init(_mu_star.Size());
      _mean.Fill(BasisMean);
      _mu_star += _mean;
   // Compute covariance: Sigma_* = K_ss - K_s * K_inv * K_s^T
      matrix _v = _k_s.MatMul(_k_inv);
      matrix _sigma_star = _k_ss - (_v.MatMul(_k_s.Transpose()));
      vector _variances = _sigma_star.Diag();
      //Print(" sigma star: ",_sigma_star);
      Print(" pre variances: ",_variances);
      Output = _mu_star;
      SetOutput(Output);
      SetOutput(_variances);
      Print(" variances: ",_variances);
   }
}

Diese sind im Einzelnen:

• _k
• _k_s
• _k_ss
• _k_inv
• _v
• und _sigma_star

_k ist die Anker- und Hauptkovarianzmatrix. Sie erfasst die Beziehungen zwischen dem Paar von Eingangsvektoren und der verwendeten Kernel-Funktion. Wir verwenden den RBF-Kernel (Radial Basis Function), dessen Quelle bereits oben genannt wurde. Da wir eine Vorhersage für eine Zeitreihe machen, wären die Eingaben für unseren RBF-Kernel zwei ähnliche Zeitvektoren, die die Zeitindizes der Datenreihe protokollieren, die wir vorhersagen wollen. Durch die Kodierung von Ähnlichkeiten zwischen protokollierten Zeitpunkten dient dies als Grundlage für die Bestimmung der Gesamtstruktur. Denken Sie daran, dass es eine Menge anderer Kernelformate gibt, wie aus den vierzehn oben aufgeführten ersichtlich ist, und dass wir in zukünftigen Artikeln diese Alternativen als nutzerdefinierte Signalklasse berücksichtigen könnten.

Dies führt uns zur Kovarianzmatrix _k_s. Diese Matrix dient als Brücke zu den nächsten Zeitindizes, ebenfalls über einen RBF-Kernel wie der Matrix _k. Die Länge oder Anzahl dieser Zeitindizes bestimmt die Anzahl der durchzuführenden Projektionen und wird durch den Eingabeparameter Längenskala definiert. Wir bezeichnen diesen Parameter in der nutzerdefinierten Signalklasse als m_next. Die Verknüpfung der Indizes der Vergangenheit mit den Indizes der nächsten Zeit _k_s dient dazu, eine Beziehung zwischen bekannten Daten und den nächsten unbekannten Daten zu projizieren, und dies ist, wie zu erwarten, für Vorhersagen ziemlich nützlich. Diese spezielle Matrix ist sehr empfindlich gegenüber der vorgenommenen Projektion, sodass die Präzision auf den Punkt genau sein muss. Unser Code und die RBF-Kernel-Funktion können dies problemlos bewältigen. Dennoch müssen die beiden einstellbaren Parameter Varianz und Längenskala sorgfältig aufeinander abgestimmt werden, um die Genauigkeit der Projektion zu maximieren.

Diese Matrix kann wie folgt definiert werden:

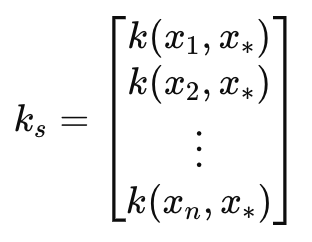
Wobei

• k(x i , y i ) ist eine Radialbasisfunktion zwischen zwei Werten in den Vektoren x und y bei Index i. In unserem Fall sind x und y derselbe Eingabezeitvektor, sodass beide Vektoren mit x bezeichnet werden. x ist in der Regel die Trainingsdaten, während y ein Platzhalter für die Testdaten ist.
• k s ist der Kovarianzvektor (oder die Kovarianzmatrix bei gerader Längenskala oder einer Anzahl von Projektionen über 1) zwischen den Trainingsdaten und dem Testpunkt x∗.
• x 1 , x 2 ,..., xn, sind die eingegebenen Trainingsdatenpunkte.
• x∗ ist der Eingangstestdatenpunkt, für den Vorhersagen getroffen werden sollen.

Daraus ergibt sich die Matrix _k_ss, die im Wesentlichen ein Spiegelbild der Matrix_k ist, wobei der Hauptunterschied darin besteht, dass es sich um eine Kovarianz der Prognosezeitindizes handelt. Ihre Dimensionen entsprechen daher dem Eingangsparameter Längenskala. Sie ist für die Berechnung des Unsicherheitsschätzungsanteils der Prognose von Bedeutung. Sie misst die Varianz über die prognostizierten Zeitindizes, bevor die Daten einbezogen werden. Dies kann in eine Formel gefasst werden als:

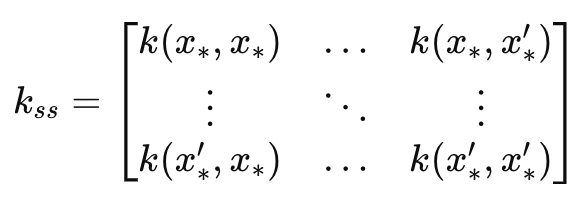
Wobei

• k ss ist die Kovarianzmatrix der Testdatenpunkte.
• x∗, x∗′ sind die eingegebenen Testdatenpunkte, für die Vorhersagen gemacht werden sollen.
• k(x∗,x∗′) ist die Kernel-Funktion, die auf das Paar von Testpunkten 𝑥∗ und 𝑥∗′ angewendet wird.

Die Matrix _k_inv ist, wie der Name schon sagt, die Inverse der Matrix k. Die Inversion von Matrizen wird durch integrierte Funktionen gehandhabt, ist jedoch nicht fehlerfrei, da die Inversion oft nicht möglich ist. Deshalb prüfen wir in unserem Code, ob die invertierte Matrix irgendwelche Zeilen oder Spalten hat. Wenn keine vorhanden sind, bedeutet dies, dass die Inversion fehlgeschlagen ist. Diese Inversion ist wichtig für die Berechnung der Gewichtungen, die bei der Vorhersage auf die Trainingsdaten angewendet werden. Alternative nutzerdefinierte Methoden zur Durchführung dieser Inversion, wie z. B. Cholesky, könnten in Betracht gezogen werden (vorausgesetzt, es handelt sich nicht um den eingebauten Ansatz), wobei die Kodierung dieser Optionen dem Leser überlassen bleibt.

Der Gewichtsvektor wird verwendet, um die Ergebnisse des Trainings auf der Grundlage ihrer Kovarianzstruktur zu kombinieren. Der Gewichtungsvektor bestimmt, wie viel Einfluss neue Datenpunkte auf die Vorhersage über die Test-/Längenskalenpunkte haben. Wir erhalten Alpha aus dem Matrixprodukt der invertierten Matrix k und den alten Rohdaten, für die wir eine Prognose suchen. Dies bringt uns zu unserem Ziel, dem Vektor _mu_star. Dies protokolliert schließlich die Prognosen über den eingegebenen Längenskalenzeitraum auf der Grundlage der vorherigen Daten, deren Größe durch den Eingabeparameter m_past in der nutzerdefinierten Signalklasse definiert ist. Die Anzahl der projizierten Mittelwerte wird also durch die Längenskala bestimmt, die wir in der Klasse als m_next bezeichnen, und da die Vektoren in MQL5 nicht als Reihen sortiert werden (beim Kopieren und bei der Behandlung von Raten), wird der höchste Index dieses Prognosevektors als letzter projiziert, während der Null-Index als unmittelbar bevorstehend angesehen wird. Dies bedeutet, dass wir nicht nur abschätzen können, welche Werte als Nächstes in der Reihe auftreten werden, sondern auch den Trend projizieren können, der in Abhängigkeit von der Größe des Längenskalenparameters folgen wird. Diese hochgerechneten Werte werden auch als Prüfpunkte bezeichnet.

Sobald wir indikative Mittelwerte haben, liefert der GP-Prozess über die Matrix _sigma_star auch ein Gefühl für die Unsicherheit um diese Werte. Was sie erfasst, ist die Kovarianz zwischen verschiedenen Vorhersagen zu verschiedenen Zeitpunkten in der Zukunft oder über die Testzeitpunkte hinweg. Da wir eine bestimmte Anzahl von Vorhersagen machen, eine für jeden Testpunkt, sind wir nur an den Diagonalwerten dieser Matrix interessiert. Wir sind nicht an der Kovarianz zwischen den Vorhersagen interessiert. Die Formel für diese Matrix lautet wie folgt:

Wobei

• k ss ist die Kovarianzmatrix der neuen Datenpunkte wie oben als _k_ss beschrieben.
• k s ist die Kovarianzmatrix zwischen den neuen Datenpunkten und den Trainingsdaten, ebenfalls wie bereits oben als _k_s erwähnt.
• K ist die Kovarianzmatrix der Trainingsdaten, die erste Matrix, die wir definiert haben.

Aus unserer obigen Gleichung geht hervor, dass Matrix _v das Produkt aus _k_s und der Inversen K^-1 ist. Wir testen mit einem Konfidenzintervall von 95 %, und dank der Normalverteilungstabellen bedeutet dies, dass der obere Grenzwert für jeden Testpunkt der prognostizierte Mittelwert plus das 1,96-fache des jeweiligen Varianzwerts in der Matrix ist. Umgekehrt ist der untere Grenzwert der vorhergesagte Mittelwert minus das 1,96-fache des Varianzwertes aus unserer Matrix _sigma_star. Diese Varianz hilft, unser Vertrauen in die mittleren Vorhersagen zu quantifizieren, wobei - und das ist wichtig - größere Werte eine größere Unsicherheit anzeigen. Je breiter also der Vertrauensbereich (von der oberen Grenze bis zur unteren Grenze) ist, desto weniger Vertrauen sollte man haben!

Eine Randbemerkung, aber dennoch ein wichtiger Punkt: GP-Kernel-Berechnungen beinhalten die Inversion von Matrizen, und wie bereits oben erwähnt, kann dies vom Leser weiter angepasst werden, indem er Ansätze wie die Cholesky-Zerlegung in Betracht zieht, um Fehler und NaNs zu minimieren. Darüber hinaus ist eine gängige Normalisierungstechnik, die zu einem frühen Zeitpunkt im GP-Kernelprozess auf die Matrix _k angewendet wird, das Hinzufügen eines kleinen Nicht-Null-Werts auf der Diagonalen, um zu verhindern, dass negative Werte in der Matrix _sigma_star auftauchen. Erinnern Sie sich daran, dass diese Matrix quadrierte Standardabweichungswerte oder Varianzwerte hat und daher alle Werte positiv sein müssen. Und bizarrerweise kann ein Weglassen dieser kleinen Addition über die Matrixdiagonale _k dazu führen, dass diese Matrix negative Werte hat! Es handelt sich also um einen wichtigen Schritt, der in der obigen Auflistung der Funktion, um das Ergebnis zu erhalten, angegeben ist.

Unsere Prognosen geben uns also zwei Dinge vor: die Vorhersage und die Zuversicht, die wir in Bezug auf diese Vorhersage haben sollten. In diesem Artikel führen wir, wie unten zu sehen ist, Tests durch, die sich ausschließlich auf die Rohprojektion stützen, ohne die Konfidenzniveaus zu berücksichtigen, die durch die Matrix _sigma_star impliziert werden. Dies ist in vielerlei Hinsicht eine enorme Unterrepräsentation von GP-Kerneln. Wie könnten wir also das implizite Vertrauen in eine Prognose in unser nutzerdefiniertes Signal einbeziehen? Es gibt eine Vielzahl von Möglichkeiten, dies zu erreichen, aber noch bevor diese in Betracht gezogen werden, würde eine schnelle Lösung normalerweise außerhalb der nutzerdefinierten Signalklasse liegen, indem die Größe des Konfidenzniveaus verwendet wird, um die Positionsgröße zu bestimmen.

Dies würde bedeuten, dass wir nicht nur einen GP-Kernel in einer nutzerdefinierten Signalklasse haben, sondern auch einen weiteren GP-Kernel in einer nutzerdefinierten Geldmanagementklasse. Und in diesem Fall müssten sowohl die Signalklasse als auch die Geldmanagementklassen ähnliche Eingangsdatensätze und Varianz- sowie Längenskalenparameter verwenden. Innerhalb der nutzerdefinierten Signalklasse wäre es jedoch einfach, einen Varianzvektor zu erstellen, der die Diagonale der _sigma_star-Matrix kopiert, ihn mit unserer Funktion „SetOutput“ zu normalisieren und dann den Index mit dem niedrigsten Wert zu bestimmen. Dieser Index würde dann im Vektor _mu_star verwendet werden, um den Zustand des nutzerdefinierten Signals zu bestimmen. Da _mu_star ebenfalls mit der gleichen Funktion normalisiert wird, würden alle Werte unter 0,5 negativen Veränderungen entsprechen, was auf einen Abwärtstrend deutet, während alle Werte über 0,5 auf einen Abwärtstrend implizieren würde.

Eine andere Methode zur Verwendung der quantifizierten Unsicherheit einer Prognose innerhalb einer nutzerdefinierten Signalklasse könnte darin bestehen, den gewichteten Mittelwert aller Prognosen oder Projektionen über alle Testpunkte hinweg zu nehmen, aber den normalisierten Varianzwert als inverse Gewichtung zu verwenden. Er wäre invers, d. h. wir subtrahieren ihn von eins oder invertieren ihn und addieren einen kleinen Wert zum Nenner. Diese Umkehrung ist wichtig, weil, wie oben betont, eine größere Varianz eine größere Unsicherheit bedeutet. Diese Ansätze zur Nutzung von Unsicherheit werden hier nur erwähnt, aber nicht im Code oder während unseres Testlaufs implementiert. Der Leser ist eingeladen, einen Schritt weiter zu gehen und eigene, unabhängige Tests durchzuführen.

Daten-Vorverarbeitung und Normalisierung

GP-Kernel können für eine Vielzahl von finanziellen Zeitreihendaten verwendet werden. Diese Daten können in einem absoluten Format vorliegen, wie z. B. absolute Preise, oder sie können in einem inkrementellen Format vorliegen, wie z. B. Preisänderungen. In diesem Artikel werden wir den GP-Kernel RBF mit letzterem testen. Zu diesem Zweck füllen wir, wie im Code oben von „GetOutput“ zu sehen ist, zunächst den Vektor „_past“ mit der Differenz zweier anderer Vektoren, die beide Close-Preise von verschiedenen Punkten im Abstand von einem Takt kopiert haben.

Darüber hinaus hätten wir diese Preisänderungen normalisieren können, indem wir sie aus ihren Rohpunkten umgerechnet und in einen Bereich von -1,0 bis +1,0 gebracht hätten. Die Funktion „SetOutput“, die für die Nachnormalisierung oder eine andere nutzerdefinierte Methode verwendet wird, könnte auch für diese Datenvorverarbeitung verwendet werden. Für unsere Tests verwenden wir jedoch die reinen Preisänderungen im Datenformat float (double) und wenden die Normalisierung nur auf die Prognosewerte an (was wir oben als Testpunkte bezeichnet haben). Dies geschieht mit der Funktion „SetOutput“, deren Code unten aufgeführt ist:

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
void CSignalGauss::SetOutput(vector &Output)
{  vector _copy;
   _copy.Copy(Output);
   if(Output.HasNan() == 0 && _copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Output.Size()); i++)
      {  if(_copy[i] >= 0.0)
         {  Output[i] = 0.5 + (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
         else if(_copy[i] < 0.0)
         {  Output[i] = (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
      }
   }
   else
   {  Output.Fill(0.5);
   }
}

Wir haben diese Normalisierung bereits in früheren Artikeln dieser Reihe verwendet, und alles, was wir tun, ist eine Neuskalierung der projizierten Vektorwerte, damit sie im Bereich von 0,0 bis +1,0 liegen, mit dem großen Vorbehalt, dass alles unter 0,5 in der de-normalisierten Reihe negativ wäre, während alles über 0,5 positiv gewesen wäre.

Prüfung und Bewertung

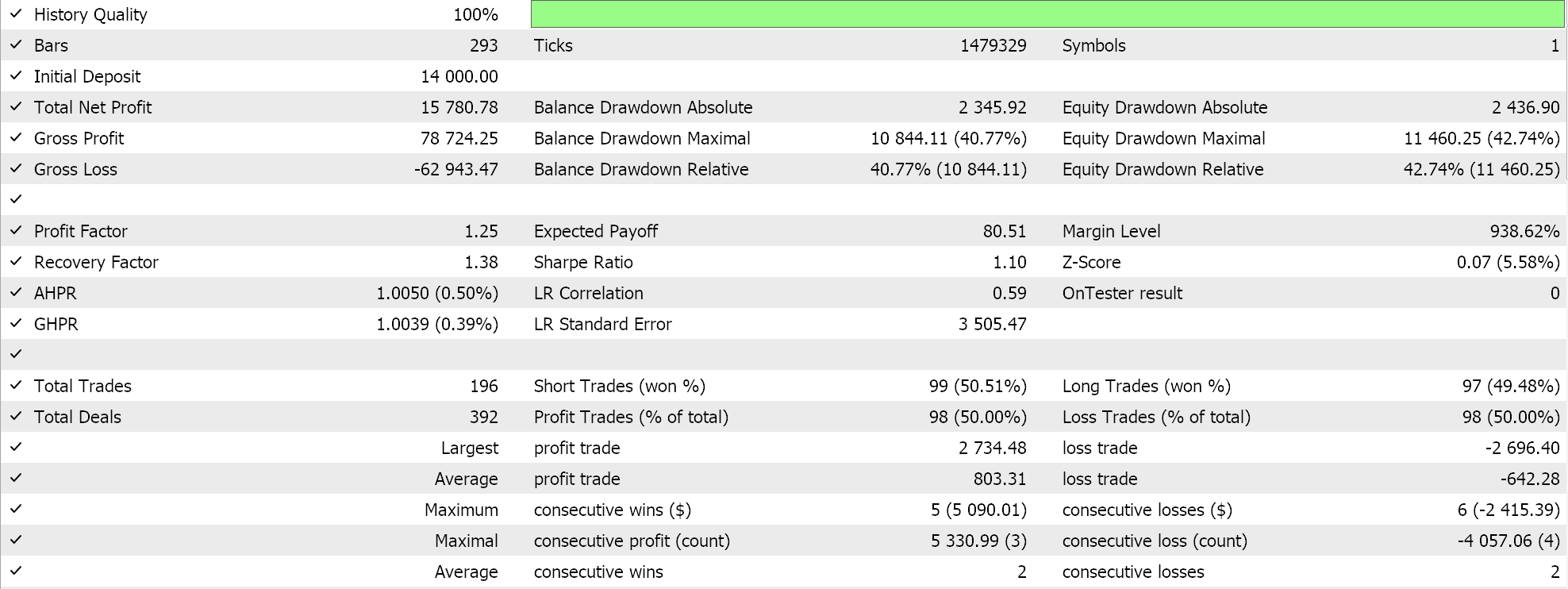
Für unsere Testläufe auf einem GP-Kernel-RBF testen wir das Paar EURUSD für das Jahr 2023 auf dem täglichen Zeitrahmen. Wie so oft, aber nicht immer, stammen diese Einstellungen aus einer sehr kurzen Optimierungsphase und werden nicht durch einen Vorwärtsgang überprüft. Die Anwendung unseres von einem Assistenten zusammengestellten Expert Advisor auf reale Marktbedingungen erfordert mehr unabhängige Sorgfalt seitens des Lesers, um sicherzustellen, dass umfangreiche Tests mit mehr historischen Daten und mit Forward Walks (Kreuzvalidierung) durchgeführt werden. Die Ergebnisse unseres Laufs sind unten aufgeführt:

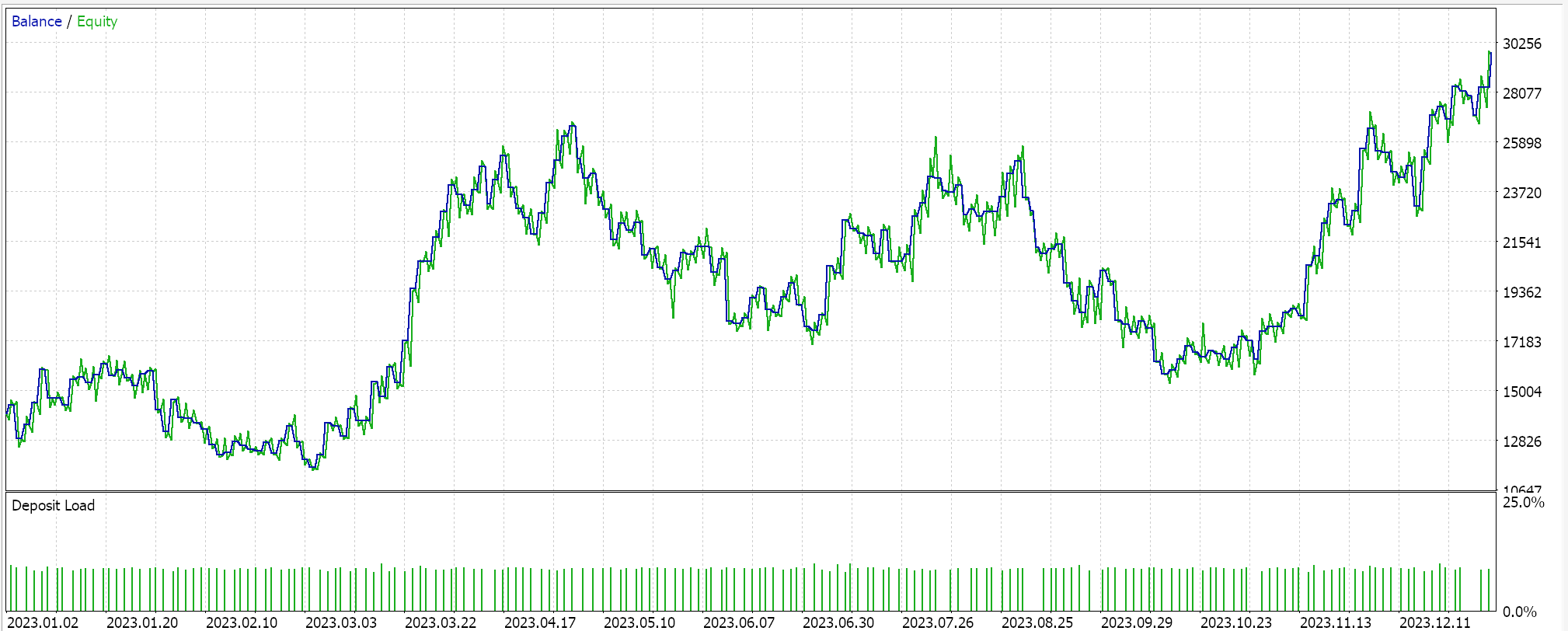
Schlussfolgerung

Abschließend haben wir uns die Gaußschen Prozesskerne als potenzielles Signal für ein Handelssystem angesehen. Der Begriff „Gauß“ erinnert oft an den Zufall oder an die Annahme, dass ein System, das verwendet wird, davon ausgeht, dass seine Umgebung zufällig ist, und dass es daher auf 50:50 Chancen setzt, um Geld zu verdienen. Ihre Befürworter machen jedoch geltend, dass sie eine bereitgestellte Datenstichprobe verwenden, um Prognosen über einen vordefinierten Zeitraum in einem probabilistischen Rahmen zu erstellen. Diese Methode, so wird argumentiert, bietet mehr Flexibilität, da keine Annahmen über die untersuchten Daten getroffen werden (d. h. sie ist nicht parametrisch). Die einzige übergreifende Annahme ist, dass die Daten einer Gaußschen Verteilung folgen. Da die Ungewissheit in den Prozess und die Ergebnisse einfließt, wird argumentiert, dass der Prozess nicht zufallsorientiert ist.

Darüber hinaus haben wir bei der Kodierung und dem Testen der Gauß'schen Prozesskerne die Quantifizierung der Unsicherheit, die sie von anderen Vorhersagemethoden unterscheidet, nicht genutzt. Die Verwendung und der Rückgriff auf Normalverteilungen wirft jedoch die Frage auf, ob Gauß-Prozess-Kerne unabhängig voneinander verwendet werden sollen oder ob sie am besten funktionieren, wenn sie mit einem alternativen Signal gepaart werden. Der MQL5-Assistent, für den neue Leser eine Anleitung finden können hier und hier, erlaubt es problemlos, mehr als ein Signal in einem einzigen Expert Advisor zu testen, da jedes ausgewählte Signal mit einer geeigneten Gewichtung optimiert werden kann. Welches alternative Signal ist es wert, mit diesen Kernels kombiniert zu werden? Nun, die beste Antwort auf diese Frage kann nur der Leser mit seinen eigenen Tests geben, aber wenn ich etwas vorschlagen würde, dann wären es Oszillatoren wie der RSI oder der Stochastik-Oszillator oder ein ausgeglichenes Volumen und sogar einige Stimmungsindikatoren für Nachrichten. Darüber hinaus funktionieren Indikatoren wie einfache gleitende Durchschnitte, gleitende Durchschnittsübergänge, Preiskanäle und Indikatoren mit einer erheblichen Verzögerung im Allgemeinen nicht gut, wenn sie mit Gauß-Prozess-Kernels gepaart sind.

Wir haben auch nur eine Art von Kernel untersucht, die Radialbasisfunktion, die anderen Formate werden in den kommenden Artikeln in veränderten Einstellungen untersucht.