MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 55): SAC mit priorisierter Erfahrungswiederholung

Die zunehmende Komplexität der Modelle neuronaler Netze ist auf die Fähigkeit zurückzuführen, große Datenmengen zu verarbeiten. Traditionelles maschinelles Lernen kämpft mit der Effizienz, während neuronale Netze, wie sie von Plattformen wie DeepSeek, Grok und ChatGPT angeboten werden, leistungsstarke Lösungen bieten.

Das Training dieser Modelle stellt jedoch eine Herausforderung dar, insbesondere bei begrenzten historischen Daten. Die Überanpassung ist ein großes Problem, da die Modelle Gefahr laufen, das Rauschen statt sinnvoller Muster zu lernen. Beim herkömmlichen Training wird häufig der Minimierung von Verlustfunktionen der Vorzug gegeben, was zu einer schlechten Generalisierung führen kann.

Verstärkungslernen (Reinforcement Learning, RL) löst dieses Problem, indem es ein Gleichgewicht zwischen Ausbeutung (Optimierung der Gewichte) und Erkundung (Testen von Alternativen) herstellt. Techniken wie die priorisierter Erfahrungswiederholung (Prioritized Experience Replay, PER) verbessern die Lerneffizienz und entschärfen das Problem der Datenknappheit in Bereichen wie dem Handel, wo die monatlichen Wirtschaftsdaten begrenzt sind.

Zu den wichtigsten RL-Überlegungen gehören der Entwurf einer effektiven Belohnungsfunktion, die Auswahl des richtigen Algorithmus und die Entscheidung zwischen wertbasierten (z.B. Q-Learning, DQN) und richtlinienbasierten Methoden (z.B. PPO, TRPO). Akteurskritische Ansätze (z.B. A3C, SAC) schaffen ein Gleichgewicht zwischen Stabilität und Effizienz. On-Policy-Methoden (PPO, A3C) gewährleisten stabiles Lernen, während Off-Policy-Methoden (DQN, SAC) die Dateneffizienz maximieren.

Die Anpassungsfähigkeit von RL macht es zu einer wertvollen Ergänzung der Pipelines für maschinelles Lernen und ergänzt die traditionellen Ansätze. Wenn komplexe Modelle mit begrenzten Daten trainiert werden, fördert der Vorrang von Gewichtsaktualisierungen vor Verlustminimierung eine bessere Generalisierung und Robustheit.

Priorisierte Erfahrungswiederholung

Die Prioritized Experience Replay (PER) und typische Wiederholungspuffer (für Zufallsstichproben) werden beide in RL mit Off-Policy-Algorithmen wie DQN und SAC verwendet, da sie die Speicherung und Stichprobennahme von vergangenen Erfahrungen ermöglichen. PER unterscheidet sich von einem typischen Wiederholungspuffer darin, wie vergangene Erfahrungen priorisiert und abgetastet werden. 

Bei einem typischen Wiederholungspuffer werden die Erfahrungen gleichmäßig und zufällig ausgewählt, d. h. jede der vergangenen Erfahrungen hat die gleiche Wahrscheinlichkeit, ausgewählt zu werden, unabhängig von ihrer Bedeutung oder Relevanz für den Lernprozess. Bei PER werden vergangene Erfahrungen auf der Grundlage ihrer „Priorität“ abgetastet, eine Eigenschaft, die häufig durch die Größe des Zeitdifferenzfehlers quantifiziert wird. Dieser Fehler dient als Indikator für das Lernpotenzial. Jedem Erlebnis wird ein Wert dieses Fehlers zugewiesen, und Erlebnisse mit hohen Werten werden häufiger in die Stichprobe aufgenommen. Diese Prioritätensetzung kann nach einem proportionalen oder rangbasierten Ansatz erfolgen.

Typische Wiederholungspuffer führen auch keine Verzerrungen ein oder verwenden diese. Dies könnte den Lernprozess in unfairer Weise verzerren. Um dies zu korrigieren, verwendet PER Wichtigkeitsgewichte der Stichproben, um die Auswirkungen jeder Erfahrung in den Stichproben zu korrigieren. Typische Wiederholungspuffer sind daher effizienter bezogen auf die Stichproben, da sie im Gegensatz zu PER viel weniger Dinge im Hintergrund erledigen. Auf der anderen Seite ermöglicht PER ein gezielteres und konstruktiveres Lernen, als dies bei den typischen Puffern der Fall ist.

Es versteht sich daher von selbst, dass die Implementierung eines PER komplexer ist als die eines typischen Wiederholungspuffers; dies wird hier jedoch hervorgehoben, weil PER eine zusätzliche Klasse erfordert, um die Prioritätswarteschlange zu verwalten, die oft als „Summenbaum“ (SumTree) bezeichnet wird. Diese Datenstruktur ermöglicht eine effizientere Auswahl von Erfahrungen auf der Grundlage ihrer Priorität. PER führt tendenziell zu einer schnelleren Konvergenz und besseren Leistung, da es sich auf Erfahrungen konzentriert, die für den Agenten informativer oder herausfordernder sind.

Umsetzung im Modell

Unsere Klasse PER verwendet in Python eine Initialisierung, die ihre Konstruktorparameter, insbesondere den Parameter mode, validiert. Ich könnte mich irren, aber ich glaube, das ist etwas, das mit C/ MQL5 nicht ohne Weiteres möglich ist. Wir deklarieren diese Funktion __init__ wie folgt:

        def __init__(self, capacity, alpha=0.6, beta=0.4, beta_increment=0.001, mode='proportional'):
                self.capacity = capacity
                self.alpha = alpha
                self.beta = beta
                self.beta_increment = beta_increment
                self.mode = mode

                if mode == 'proportional':
                        self.tree = SumTree(capacity)
                elif mode == 'rank':
                        self.priorities = []
                        self.data = []
                else:
                        raise ValueError("Invalid mode. Choose 'proportional' or 'rank'.")

Nachdem die Klasse deklariert wurde, sollte sie als eine der wichtigsten Funktionen eine Methode zum Hinzufügen von Erfahrungen zum Puffer enthalten. Wir setzen dies wie folgt um: 

    def add(self, error, sample):
        p = self._get_priority(error)
        if self.mode == 'proportional':
            self.tree.add(p, sample)
        elif self.mode == 'rank':
            heapq.heappush(self.priorities, -p)
            if len(self.data) < self.capacity:
                self.data.append(sample)
            else:
                heapq.heappop(self.priorities)
                heapq.heappush(self.data, sample)

Beachten Sie, dass bei dieser Hinzufügung von Erfahrungen die Art der Stichprobenziehung der Schlüssel ist, denn wenn wir Erfahrungen auf der Grundlage des Fehleranteils auswählen, fügen wir sie einfach an den Summenbaum an, aber wenn wir auf der Grundlage der Rangfolge der Fehlergröße auswählen, verwenden wir ein importiertes Modul heapq, das wir mit dieser Stichprobe wie oben angegeben aktualisieren. Die Summenbaumklasse wird daher bei der Anteilsstichprobe verwendet und nicht der Rang. So wird es umgesetzt:

class SumTree:
    def __init__(self, capacity):
        self.capacity = capacity
        self.tree = np.zeros(2 * capacity - 1)
        self.data = np.zeros(capacity, dtype=object)
        self.write = 0
        self.n_entries = 0

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2
        self.tree[parent] += change
        if parent != 0:
            self._propagate(parent, change)

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1

        if left >= len(self.tree):
            return idx

        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s - self.tree[left])

    def total(self):
        return self.tree[0]

    def add(self, p, data):
        idx = self.write + self.capacity - 1

        self.data[self.write] = data
        self.update(idx, p)

        self.write += 1
        if self.write >= self.capacity:
            self.write = 0

        if self.n_entries < self.capacity:
            self.n_entries += 1

    def update(self, idx, p):
        change = p - self.tree[idx]
        self.tree[idx] = p
        self._propagate(idx, change)

    def get(self, s):
        idx = self._retrieve(0, s)
        data_idx = idx - self.capacity + 1
        return (idx, self.tree[idx], self.data[data_idx])

Nachdem diese Schlüsselklasse definiert wurde, ist die andere entscheidende Komponente die Musterfunktion selbst, die Teil der PER-Klasse ist. 

def sample(self, batch_size):
        batch = []
        idxs = []
        segment = self.tree.total() / batch_size if self.mode == 'proportional' else len(self.data) / batch_size
        priorities = []

        self.beta = np.min([1., self.beta + self.beta_increment])

        for i in range(batch_size):
            a = segment * i
            b = segment * (i + 1)

            if self.mode == 'proportional':
                s = random.uniform(a, b)
                (idx, p, data) = self.tree.get(s)
                priorities.append(p)
                batch.append(data)
                idxs.append(idx)
            elif self.mode == 'rank':
                idx = random.randint(0, len(self.data) - 1)
                priorities.append(-self.priorities[idx])
                batch.append(self.data[idx])
                idxs.append(idx)

        sampling_probabilities = np.array(priorities) / self.tree.total() if self.mode == 'proportional' else np.array(priorities) / sum(self.priorities)
        is_weights = np.power(len(self.data) * sampling_probabilities, -self.beta)
        is_weights /= is_weights.max()

        return batch, idxs, is_weights

Auch hier ist die Art der Stichprobenziehung, ob proportional oder nach Rangfolge, eine wichtige Überlegung. Diese beiden Ansätze ordnen die Prioritäten jeder Erfahrung unter Berücksichtigung des TD-Fehlers zu, allerdings mit einem feinen Unterschied. Ausmaß des TD-Fehlers und Rang des TD-Fehlers. Der TD-Fehler ist effektiv die Differenz zwischen einem Erfahrungswert und dem Ist- oder Sollwert. Er wird nie in seinem Rohzustand zur Gewichtung der Erfahrungen verwendet, sondern in einen Prioritätswert umgewandelt, wie in dieser Auflistung dargestellt:

def _get_priority(self, error):
        return (error + 1e-5) ** self.alpha

Es ist dieser Prioritätswert, dessen Größe (bei Proportionsstichproben) oder Rang (bei Rangstichproben) bei der Auswahl der Erfahrungen zum Trainieren des Modells verwendet wird. PER wurde von Shaul et al. im Jahr 2015 eingeführt.  Erfahrungen mit höherer Priorität werden häufiger abgerufen, was die Effizienz der Probenahme und die Lerngeschwindigkeit in der RL-Umgebung verbessert. Die Prioritäten werden nach dem Lernen aktualisiert. Die Gewichte der Wichtigkeitsstichprobe werden eingesetzt, um Verzerrungen zu korrigieren, die durch die nicht einheitliche prioritätsbasierte Stichprobe entstehen. Dies ist in der obigen Beispielfunktion der Klasse PER angegeben. Wir wollen uns diese beiden Arten der Probenahme genauer ansehen.

Proportionale Prioritätensetzung

Wie bereits erwähnt, sind die Prioritäten direkt proportional zum Zeitdifferenzfehler (∣δ∣). Die Priorität für eine Erfahrung i würde also wie folgt berechnet:

pi=∣δi∣+ϵ

Dabei ist ϵ, das größer als Null ist, eine kleine Konstante, die sicherstellt, dass nicht alle Erfahrungen eine Priorität von Null haben. Die Stichprobenwahrscheinlichkeit für die Erfahrung wäre also:

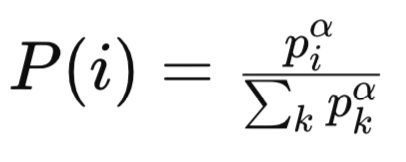
wobei:

• pi ist die Priorität des i-ten Erlebnisses im Wiederholungspuffer. Die Priorität basiert in der Regel auf der Größe des zeitlichen Differenzfehlers (TD) für diese Erfahrung. Erfahrungen mit größeren TD-Fehlern werden als wichtiger angesehen und erhalten eine höhere Priorität.

• α ist ein Hyperparameter, der den Grad der Prioritätensetzung steuert. Wenn (α = 0), werden alle Erfahrungen gleichmäßig ausgewählt (keine Priorisierung). Wenn (α = 1), richtet sich die Probenahme vollständig nach den Prioritäten.

• Sigma/Summe aller k Prioritäten ist der Normalisierungsterm, der sicherstellt, dass die Wahrscheinlichkeiten in der Summe 1 ergeben. Er summiert die Prioritäten aller Erfahrungen im Wiederholungspuffer, erhöht um eine Potenz von (α).

• P(i) ist die Wahrscheinlichkeit, dass das i-te Erlebnis in die Stichprobe aufgenommen wird. Sie ist proportional zur Priorität der Erfahrung (Piα), normiert durch die Summe aller Prioritäten hoch (α).

Ein Summenbaum oder eine Datenstruktur ähnlicher Form kann dann verwendet werden, um die Erfahrungen I. im Verhältnis zu piα effizient zu erfassen. Die Stichprobenverteilung mit proportionaler Priorisierung ist kontinuierlich und direkt mit dem Ausmaß der TD-Fehler verbunden. Erfahrungen mit hohen TD-Fehlern neigen dazu, signifikant hohe Prioritäten zu haben, was zu einer Verteilung mit starten Enden führt.

Dies könnte dazu führen, dass einige Erfahrungen zu häufig in die Stichprobe aufgenommen werden (ein großes Problem, wenn ihre TD-Fehler Ausreißer sind) und andere selten in die Stichprobe aufgenommen werden, weil ihre Fehler gering sind. Die Empfindlichkeit gegenüber Trainingsfehlern kann von Aufgabe zu Aufgabe in den Trainingsphasen variieren, aber es gibt eine Anfälligkeit für eine proportionale Priorisierung gegenüber Ausreißern bei TD-Fehlern, da große Werte die Stichprobenverteilung dominieren können.

Betrachten wir beispielsweise ein Szenario, in dem eine Erfahrung einen Output-Ziel-Abstand von 1000 aufweist, während die anderen einen Wert von 1 haben, so wird dieser große Wert eindeutig überproportional oft abgetastet. Diese Eigenschaft kann zu einer Überanpassung an verrauschte oder ausreißerische Erfahrungen führen, insbesondere in Datenumgebungen mit hoher Varianz der Belohnungen oder Q-Werte. Eine mögliche Maßnahme zur Abschwächung dieses Problems könnte die Begrenzung oder Normalisierung des TD-Fehlers sein. Zum Beispiel:

pi=min⁡(∣δi∣,δmax)+ϵ

Im Wesentlichen wird die Priorität eines Erlebnisses auf das Minimum zwischen seinem eigenen TD-Fehler und dem höchsten TD-Fehler aller Erlebnisse innerhalb des untersuchten Segments plus einem kleinen Wert ungleich Null, Epsilon, festgelegt. Die Komplexität der Ausführungszeit bei der Bearbeitung eines Summenbaums ist bei der Berechnung der Priorität für jede Erfahrung überschaubar, da sie O(1) pro Erfahrung beträgt. Die Abtastung und Aktualisierung der Prioritäten beträgt O(log n) pro Vorgang, wobei n die Puffergröße ist. Da kein zusätzlicher Overhead für die Sortierung und Einstufung anfällt, ist das System bei Aktualisierungen sehr recheneffizient.

Proportionale Priorisierung (PP) kann in Fällen, in denen die TD-Fehler in den verschiedenen Trainingsphasen stark variieren, ein instabiles Training begünstigen, da sich die Stichprobenverteilung schnell ändern würde. Es ist auch empfindlich gegenüber Hyperparametern, sodass die Wahl von Alpha und Epsilon sorgfältig getroffen werden muss, um ein Gleichgewicht zwischen Exploration und Exploitation herzustellen. PP konvergiert vielleicht schneller bei Aufgaben mit „braven“ Fehlern, was auf den Lernwert hindeutet, aber in verrauschten und instationären Umgebungen wird es schwer.

PP eignet sich für Aufgaben, bei denen sich TD-Fehler gut verhalten und direkt auf das Lernpotenzial bzw. den Wert hinweisen. Sie sind sehr effektiv in Umgebungen mit geringem Rauschen und stabilen Q-Werten, wo TD-Fehler direkt proportional zu wichtigen Erfahrungen sind. Beispiele hierfür sind Atari-Spiele mit stabilen Belohnungsstrukturen und kontinuierliche Steuerungsaufgaben mit glatten Wertfunktionen.

Die Gewichte der PP-Wichtigkeitsstichproben variieren aufgrund der Verteilung der Stichproben mit großem Schwanz. Erfahrungen mit niedrigen Prioritätsgewichten und daher niedrigen P(i)-Werten (d. h. Wahrscheinlichkeit der Stichprobenziehung von Erfahrung i), was zu großen Gewichten wi führt (Anpassungsgewichte zur Korrektur von Verzerrungen). Dieser Aufbau kann unbeabsichtigt zu einer Verstärkung der Gradienten und einer Destabilisierung der Ausbildung führen. Das bedeutet also, dass auch Beta sorgfältig abgestimmt werden muss, um ein Gleichgewicht zwischen Verzerrungskorrektur und Stabilität herzustellen.

Zusammenfassend lässt sich sagen, dass PP geeignet ist, wenn sich TD-Fehler gut verhalten und mit dem Lernwert korrelieren, die Datenumgebung geringes Rauschen und stabile Q-Werte aufweist und die Recheneffizienz entscheidend ist, was bedeutet, dass Sortier- und Ranking-Overheads nicht akzeptabel sind. Die Feinabstimmung der Hyperparameter Alpha, Beta und Epsilon kann bei der Behandlung von Ausreißern und der Bewältigung von Instabilitäten helfen.

Rangbasierte Priorisierung

In diesem Modus basieren die Prioritäten auf den Ranglisten-Indexwerten des TD-Fehlers in der sortierten Liste der TD-Fehler. Der Rang eines Erlebnisses i wird festgelegt, indem alle Erlebnisse nach dem Ausmaß des Zeitlichen Differenzfehlers in absteigender Reihenfolge sortiert werden. Warum in absteigender Reihenfolge, weil eine solche Liste intuitiv die Bedeutung einer Erfahrung interpretiert. Je weiter oben auf der Liste, desto wichtiger ist eine Erfahrung. Zweitens ist es vom Standpunkt der Berechnung aus gesehen sinnvoll, die Erfahrungen, auf die am häufigsten Bezug genommen wird, auf den niedrigeren Indizes innerhalb eines Heaps anzuordnen, da der Algorithmus nicht den gesamten Speicherinhalt durchlaufen muss, um zu den Erfahrungen zu gelangen, die den größten Teil des Trainings ausmachen. Die Priorität der Erfahrung i wird normalerweise wie folgt berechnet:

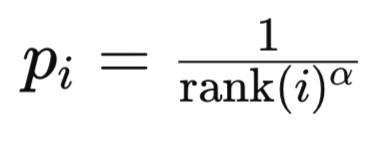
wobei:

- rank(i) ist der Rang der i-ten Erfahrung.

- alpha ist ein Hyperparameter, der die Stärke der Prioritätensetzung steuert.

Die Stichprobenwahrscheinlichkeit für die Erfahrung wird nach einer ähnlichen Formel berechnet, wie wir sie oben bei der proportionalen Priorisierung bereits behandelt haben.

Bei der rangbasierten Priorisierung (RP) ist die Stichprobenverteilung diskret und basiert auf Rängen. Dies macht sie weniger empfindlich gegenüber der absoluten Skala der TD-Fehler. Die Erfahrungen werden nach ihrem Rang und nicht nach der Höhe des Fehlers ausgewählt. Dies führt zu einer gleichmäßigeren Verteilung bei der Stichprobenziehung, da der Unterschied in der Priorisierung zwischen den Erfahrungen nahezu „standardisiert“ ist, da er durch die jeweilige Rangfolge der Erfahrungen (d. h. 1/1, ½, ⅓, usw.) gesteuert wird. Darüber hinaus ist RP weniger anfällig für eine Überanpassung von Ausreißern, da die höchste zugewiesene Priorität für jede Erfahrung auf 1/1 festgelegt ist, unabhängig von der Größe des TD-Fehlers. Diese Robustheit wird jedoch durch eine zu geringe Anzahl von Erfahrungen mit sehr hohen TD-Fehlern überschattet, wenn die rangbasierte Prioritätsfunktion zu schnell abfällt.

Neben dem Risiko der Untererfassung von Schlüsselerfahrungen bleibt jedoch der größte Nachteil von RP die Komplexität der Berechnungen. Die Sortierung eines gesamten Puffers zur Bestimmung der Ränge ist eine operative Berechnungskomplexität der Größenordnung O(nlogn) für einen gesamten Puffer der Größe n. In der Praxis kann diese Sortierung vermieden werden, indem eine sortierte Datenstruktur (wie ein binärer Suchbaum oder ein Heap) für die TD-Fehler beibehalten wird, aber Aktualisierungen erfordern immer noch O(logn) operative Berechnungen pro Erfahrung. Abtastung und Aktualisierung bleiben bei O(logn), wie es bei der proportionalen Abtastung der Fall war. Zusammenfassend lässt sich sagen, dass RP im Vergleich zu PP einen deutlich höheren Rechenaufwand hat.

Beim Training ist die RP stabiler, da die Stichprobenverteilung weniger empfindlich auf Änderungen der TD-Fehlergrößen reagiert. Außerdem liefert es im Laufe der Zeit tendenziell konsistente Stichprobenwahrscheinlichkeiten, da die Ränge relativ sind und weniger von Rauschen und Ausreißern beeinflusst werden. Bei Aufgaben, bei denen absolute TD-Fehler für den Trainingsprozess von entscheidender Bedeutung bzw. sehr informativ sind, konvergiert es möglicherweise langsamer, da es Fehler hoher Größenordnung nicht so aggressiv priorisiert. Sie ist auch etwas einfacher abzustimmen (Anpassung von Hyperparametern), da die rangbasierte Prioritätsfunktion weniger empfindlich auf die Skalierung reagiert.

RP eignet sich in Umgebungen mit geringer Belohnung oder für Aufgaben mit verzögerter Belohnung oder hoher Belohnungsvarianz. RP ist ein bevorzugter Modus, bei dem Stabilität und ausgewogene Stichproben entscheidend sind, auch wenn die Konvergenz langsam sein kann.

Sowohl PP als auch RP führen aufgrund ihrer uneinheitlichen Stichprobenverfahren zu einer Verzerrung, wie bereits erwähnt und in der Stichprobenmethode in der obigen Quelle dargestellt. Die Grundformel hierfür lautet:

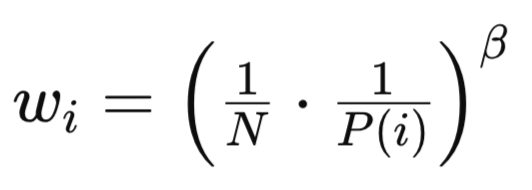
wobei:

- N ist die Gesamtzahl der Erfahrungen im Wiederholungspuffer.

- P(i) ist die Wahrscheinlichkeit, dass das i-te Erlebnis in die Stichprobe aufgenommen wird.

- beta (β∈[0,1]) ist ein Hyperparameter, der die Stärke der Wichtigkeitsstichprobenkorrektur steuert.

Trotz ähnlicher Formeln unterscheiden sich die Gewichte von RP und PP wi in wichtigen Aspekten. Für RP sind die Gewichte der Wichtigkeitsstichprobe gleichmäßiger, da die Verteilung weniger schief ist. Diese geringere Varianz der wi-Werte führt zu einer stabileren Ausbildung und einer geringeren Empfindlichkeit gegenüber Beta. Außerdem ist die Korrektur der Verzerrungen einfacher zu handhaben, da die rangbasierte Verteilung von Natur aus ausgeglichener ist.

Prüfung der Signalklasse

Wenn wir den oben aufgeführten Code verwenden und den Code des SAC-Modells aus dem letzten Artikel ändern, indem wir einen PER anstelle eines typischen/einfachen Wiederholungspuffers verwenden, wären wir in der Lage, das Modell zu trainieren und ein Netz mit seinen Gewichten als ONNX-Datei zu exportieren. Wir haben in diesem letzten Artikel beschrieben, wie dieser Export gehandhabt werden kann, und es gibt hier Anleitungen, wie man ein ONNX-Modell auch aus Python exportieren kann. ONNX-Modelle werden von MQL5 verwendet, indem sie bei der Kompilierung als Ressourcen eingebettet werden. 

Auf der MQL5-Seite in der IDE sollte unsere nutzerdefinierte Signalklasse, die sich streng genommen nicht von dem unterscheidet, was wir im letzten SAC-Artikel hatten, durch den MQL5-Assistenten zusammengestellt werden. Für neue Leser gibt es hier und hier Anleitungen dazu. Tests ohne Kreuzvalidierung für USD JPY auf dem täglichen Zeitrahmen für das Jahr 2023 liefern uns den folgenden Bericht:

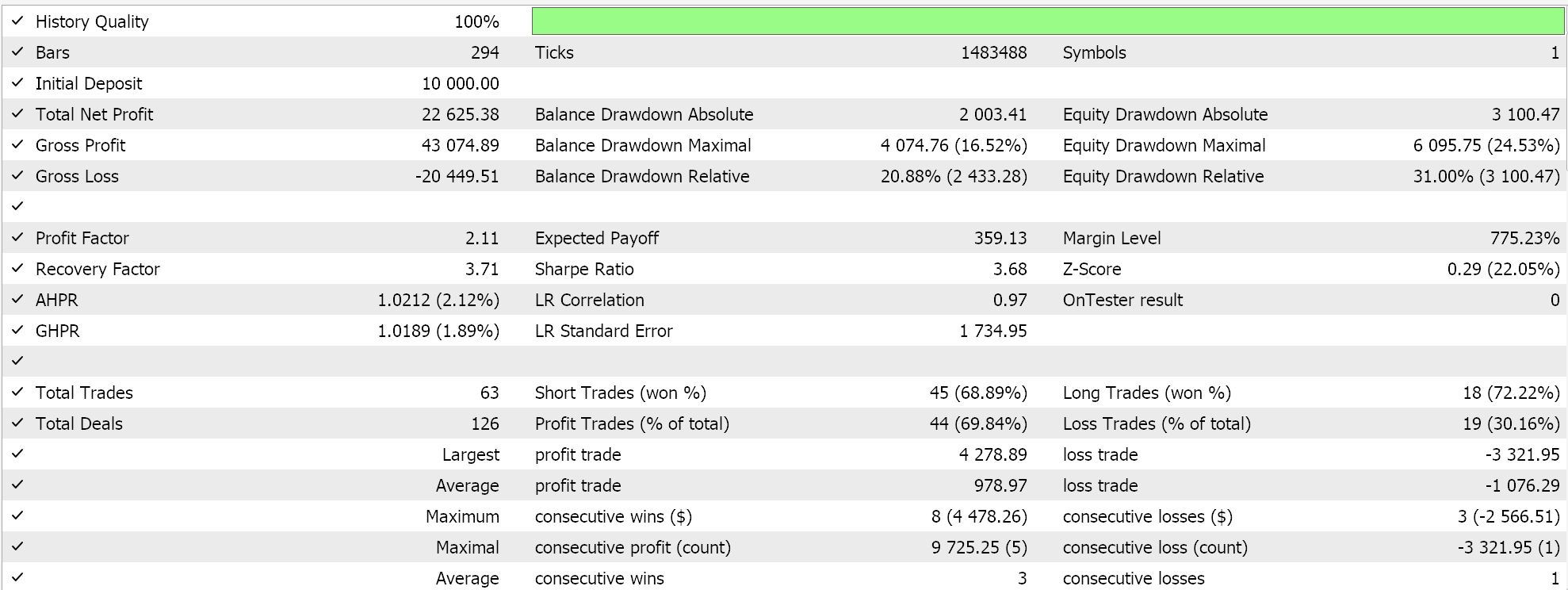
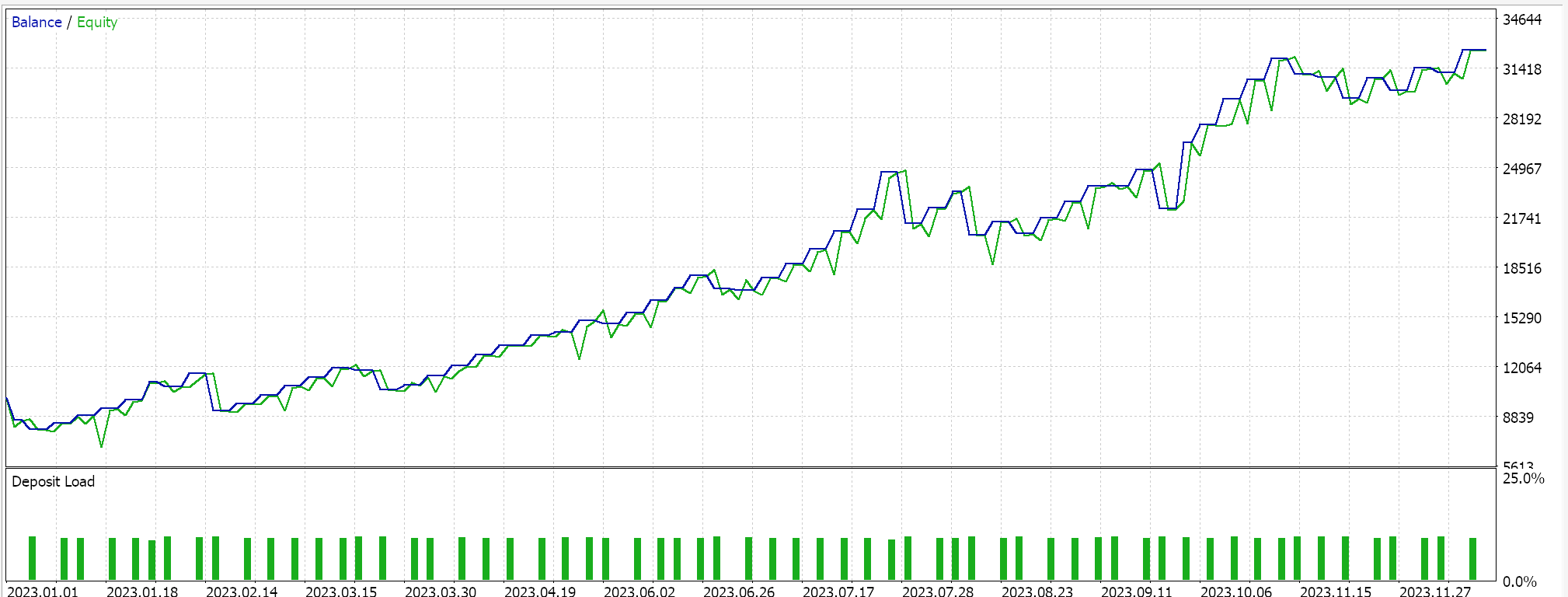
In Zukunft kann die Kreuzvalidierung mit Modellen in Python jedoch sehr effizient durchgeführt werden, sodass ich vielleicht damit beginnen werde, sie in Zukunft in diese Artikel einzubauen. Wie immer gilt jedoch, dass vergangene Leistungen keine Garantie für zukünftige Ergebnisse sind, und der Leser ist stets aufgefordert, seine eigene zusätzliche Sorgfalt walten zu lassen, bevor er sich für die Nutzung oder den Einsatz eines der hier vorgestellten Systeme entscheidet.

Schlussfolgerung

Wir haben die Argumente für das Verstärkungslernen noch einmal aufgegriffen, indem wir dargelegt haben, warum es im heutigen Umfeld komplexer Modelle und eingeschränkter historischer Testdaten sehr wichtig ist, den Prozess der Ermittlung geeigneter Netzgewichte über fiktive verlustarme Funktionswerte zu stellen. Der Prozess ist wichtig. Zu diesem Zweck haben wir einen alternativen Wiederholungspuffer für das Verstärkungslernen vorgestellt, den Priorisierten Erfahrungswiederholungspuffer als Puffer, der nicht nur die jüngsten Erfahrungen für das Training bereithält, sondern auch aus diesem Puffer im Verhältnis zu der Relevanz oder dem Umfang der Erfahrungen, die das Netzwerk aus den gesampelten Erfahrungen lernen muss, Proben nimmt.

Datei	Beschreibung
wz_55.mq5	Ein mit dem Assistenten erstellter Expert Advisor mit Header, der die verwendeten Dateien anzeigt
SignlWZ_55.mqh	Nutzerdefinierte Signalklassendatei
USDJPY.onnx	ONNX-Netzwerkdatei