Возможности Мастера MQL5, которые вам нужно знать (Часть 35): Регрессия опорных векторов

MetaTrader 5 — Торговые системы | 13 марта 2025, 13:36

415

Stephen Njuki

Введение

Регрессия опорных векторов (Support Vector Regression, SVR) - форма регрессии, полученная в рамках метода опорных векторов. По своей сути SVR использует методы ядра для преобразования входных данных в многомерные пространства, что позволяет фиксировать более сложные взаимосвязи, что контрастирует с уменьшением размерности. Однако в этой статье мы изучим лишь ее роль функции потерь при использовании с многослойным персептроном. Связанная, но другая форма регрессии - регрессия гауссовского процесса (Gaussian Process Regression, GPR) была рассмотрена в одной из предыдущих статей. Поэтому, возможно, стоит начать с проведения различий между ними.

Различия между SVR и GPR

Чтобы подчеркнуть различия между двумя разновидностями регрессии, давайте отвлечемся от терминологии машинного обучения и на повседневных примерах покажем важность каждой из них. Представьте, что у вас стартап по производству очень полезного мороженого с низким содержанием сахара, пользующегося большим спросом в вашем городе. Поскольку вы только начинаете и продаете мороженое только в своем городе, большую часть производства вы по-прежнему выполняете вручную. Поэтому вам необходимо начать наращивать производительность, поскольку это, помимо контроля затрат, приносит с собой такие преимущества, как контроль качества и внедрение производственных стандартов.

Такое расширение потребует капитала, который вы не сможете занять у институциональных инвесторов, поскольку у вас нет необходимого обеспечения (или средств), чтобы представить его банкам. Также вы можете сотрудничать с крупным известным брендом мороженого, однако руководители крупных популярных брендов часто оказываются бюрократами и привыкли говорить "нет" независимо от того, что они думают о вашем продукте.

Таким образом, у вас остается единственный вариант привлечения капитала частным, полуофициальным путем с необходимостью масштабировать или расширять свой продукт. Однако по мере того, как вы расширяетесь за пределы своего города, кто даст гарантию, что клиенты обратят внимание на ваш продукт на фоне уже известных брендов? Новые территории требуют нового подхода. Наиболее насущный вопрос, о котором вы, возможно, еще не задумывались, - кто ваши основные клиенты?

Сегментация клиентов — аспект бизнеса, который некоторые предпочитают игнорировать, — имеет несколько типов. Она включает (но не ограничивается) почтовый индекс (или адрес), возраст, уровень образования, род занятий/профессия и уровень дохода. Еще одним "новым" и растущим сегментом благодаря социальным сетям может стать образ жизни/группа интересов. Дополняя данные о продажах сегментацией, мы можем создать несколько интересных наборов данных, которые, если их собрать даже по нашему городу, могут дать представление о том, что произойдет за его пределами.

Регрессия гауссовского процесса, представленная в предыдущей статье, не просто дает прогноз среднего значения, но и привязывает к нему ориентировочный диапазон вместе с уровнем достоверности. Это означает, что он подходит для составления прогнозов в ситуациях, когда спрос на продукт в значительной степени зависит от внешних факторов (не является постоянным) и, следовательно, является предметом роскоши или дорогим продуктом, компенсирующим непостоянство спроса. Если это не люксовый продукт, то, возможно, мы имеем дело с сезонным или нишевым продуктом с высокой ценой и нестабильным спросом. Это означало бы, что наше мороженое должно было бы стоить дороже, чем у конкурентов, чтобы соответствовать нише/люксовому сегменту, наиболее подходящему для использования с GPR.

Кроме того, тип продукта и сегментация клиентов создают совокупность вариантов при выборе набора данных для прогнозирования спроса в будущем, что требует тщательного рассмотрения, как показано в таблице ниже.

Тип сегментации	Лучше с SVR	Лучше с GPR
Почтовый индекс	Товары повседневного спроса	Неидеальна, если не сочетается с другими динамическими данными
Возраст	Одежда, потребительские товары, образовательные инструменты	Неидеальна, если не сочетается с другими динамическими данными
Уровень образования	Образовательная и техническая продукция	Неидеальна, если только не задействованы сложные факторы.
Уровень дохода	Базовые продукты на стабильных рынках	Предметы роскоши, топовая электроника, предметы премиум-класса
Профессия	Продукция, связанная со стабильными профессиями	Сезонные продукты, товары, на которые влияют внешние факторы (например, погода)
Образ жизни, интересы	Предсказуемые группы интересов (например, одежда для фитнеса)	Специализированные или нишевые продукты, сильно изменчивый спрос

Хотя наша таблица выше не обязательно является фактическим отображением взаимосвязи между сегментами потребителей и типами продуктов, она подчеркивает важность их рассмотрения перед выбором соответствующего набора данных для составления прогнозов. Подводя итог, можно сказать, что GPR лучше подходит для компаний, которые часто сталкиваются с неопределенностью и сложными моделями роста, что обуславливает необходимость делать прогнозы с доверительными интервалами.

С другой стороны, регрессии опорных векторов хороши для составления прогнозов, где важны определенность и стабильный рост. Они идеально подходят для случаев, когда решения могут основываться на линейных или умеренно линейных тенденциях. Почему? Потому что SVR устойчива к шуму. Основное внимание уделяется получению границы принятия решения, которая максимизирует погрешность и минимизирует влияние выбросов. Используя погрешность (эпсилон) в качестве классификатора, SVR должна быть эффективна с наборами данных, которые не содержат большого количества выбросов.

Как мы видим из приведенной выше перекрестной таблицы рекомендаций, SVR лучше всего подходит для составления прогнозов по основным продуктам питания или товарам повседневного спроса, спрос на которые практически постоянен, и за исключением вспышки COVID (которая может резко поднять или обрушить спрос), уровень спроса на этот продукт не должен сильно колебаться, если вообще должен. Итак, если рассмотреть нашу ситуацию с расширением продаж мороженого за пределами родного города, SVR будет подходящим инструментом, если цена на него не слишком завышена (как было рекомендовано для GPR выше) и при этом продукт размещается на полках магазинов в местах, где потребители забирают свои ежедневные продукты питания и другие товары, которые могут им понадобиться в течение недели.

Если мы используем перекрестную таблицу в качестве ориентира и если наше мороженое является продуктом премиум-класса, который мы продаем в основном по большим праздникам или только летом, или предлагаем определенным элитным ресторанам, например, то мы будет использовать GPR с данными о продажах, агрегированными по уровню дохода. Кроме того, перекрестная таблица рекомендует группы потребителей по роду занятий и образу жизни/особым интересам, и их также можно учитывать. С другой стороны, SVR работал бы лучше всего, если бы наш продукт продавался преимущественно в крупных магазинах, где важны низкие цены, как утверждалось выше, а главный потребительский сегмент — это адрес (или почтовый индекс). Таким образом, агрегированные данные о продажах по адресам будут более полезны для составления прогнозов с помощью SVR относительно того, насколько быстро или медленно нам следует расширять наше производство мороженого. Это то, что нам нужно будет сделать правильно, поскольку теперь мы используем чужие деньги.

Таким образом, GPR лучше всего подходит для прогнозирования ситуаций, когда высокая степень неопределенности приемлема, в то время как SVR, на которой мы сосредоточимся в этой статье, находится практически на другом конце спектра, поскольку она игнорирует выбросы, которые выходят за пределы заданного порогового значения при определении гиперплоскости наборов данных.

Определение SVR

SVR можно определить как целевую функцию и как функцию принятия решения. If we start with the formula to the objective function it is as follows:

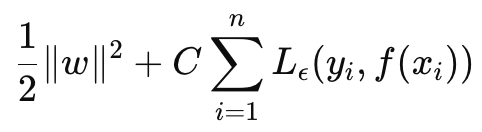
где

w — вектор весов (параметры модели), нас интересует L2-норма весовых матриц,
C — параметр регуляризации, контролирующий компромисс между сложностью модели и устойчивостью к неправильной классификации,
L ϵ — это ϵ-нечувствительная функция потерь, определяемая как:

где

f(xi ) — прогнозируемое значение,
yi — истинное значение,
ϵ — допустимый предел, в пределах которого за ошибки не налагается штраф.

С другой стороны, решающая функция, которая в основном используется в прогнозировании, имеет следующую формулу:

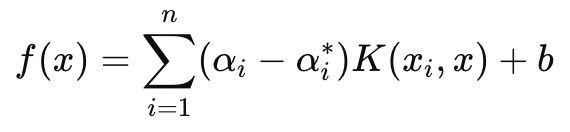
где

αi and αi^∗ — множители Лагранжа,
K (xi , x) — функция ядра (например, линейная, полиномиальная, радиальная базисная (RBF)),
b — член смещения.

Как упоминалось выше, SVR вводит нечувствительный к потерям параметр эпсилон, который следит за тем, чтобы ошибки с величиной меньше эпсилона игнорировались и не приводили к корректировкам весов или параметров для обучаемой модели. Это делает SVR более надежным средством обработки небольших шумов и изменений в данных, что позволяет сосредоточиться на более общей картине или основных тенденциях.

Кроме того, в нашей целевой функции параметр C управляет компромиссом между минимизацией ошибки обучения и минимизацией сложности модели. Более высокое значение C минимизирует ошибку обучения, но повышает риск переобучения, в то время как более низкое значение C на бумаге приведет к большему обобщению и большей гибкости при составлении прогнозов в различных сценариях.

Мы собираемся сосредоточиться исключительно на использовании функции потерь SVR при обучении простого MLP для этой сети. Мы не будем делать прогнозов с ядрами, как это было бы в случае с функцией решения. Однако стоит отметить, что SVR использует функции ядра для преобразования входных данных в многомерное пространство, где можно выявить взаимосвязи, которые могут быть нелинейными в исходном пространстве. К распространенным ядрам для этих целей относятся: линейное ядро, полиномиальное ядро и RBF.

Функцию потерь SVR можно реализовать на языке MQL5 следующим образом:

//+------------------------------------------------------------------+
//| SVR Loss                                                         |
//+------------------------------------------------------------------+
vector Cmlp::SVR_Loss()
{  vector _loss = fabs(output - label);
   for(int i = 0; i < int(_loss.Size()); i++)
   {  if(_loss[i] <= THIS.svr_epsilon)
      {  _loss[i] = 0.0;
      }
   }
   vector _l = THIS.svr_c*_loss;
   double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2);
   vector _weight_norms;
   _weight_norms.Init(_loss.Size());
   _weight_norms.Fill(_w);
   return(_weight_norms + _l);
}

Обычно это значение потерь является скаляром, однако, поскольку эта функция потерь теперь используется в обратном распространении, а некоторые сети имеют более одного конечного выхода, было важно сохранить структуру потерь в векторной форме, даже несмотря на то, что SVR сжимает ее до скаляра. Это то, что мы сделали. Кроме того, мы проверяем, используются ли потери SVR в функции обратного распространения. Делается это так:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
   
   ...


   if(EpochIndex < 0)
   {  printf(__FUNCSIG__ + " Epoch Index Should start from 1. ");
      return;
   }


    ...


   vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss));

    ....
}

Мы можем добавить эту однострочную модификацию, поскольку параметры нашего конструктора находятся в структуре, и мы легко изменили эту структуру (так как этот класс был представлен в предыдущих статьях) следующим образом:

//+------------------------------------------------------------------+
//| Multi-Layer-Perceptron Struct for Constructor Parameters         |
//+------------------------------------------------------------------+
struct Smlp
{  //arch array must be defined with at least 2 non zero values
   //that represent the size of the input layer and output layer
   //If more values than this are provided in the array then the
   //middle values will define the size(s) of the hidden layer(s)
   //first value (index zero) is size of input layer
   //last value (index size-1) is size of output layer
   int               arch[];


  ...


   bool              svr_loss;
   double            svr_c;
   double            svr_epsilon;

                     Smlp()
   {                 ArrayFree(arch);

     ...

      svr_loss = false;
      svr_c = 1.0;
      svr_epsilon = __EPSILON * 5.0;
   };
                    ~Smlp() {};
};

Реализация класса сигнала

Чтобы иметь класс сигнала с MLP, функция потерь которого использует SVR, нам придется использовать наш уже закодированный класс для MLP, который был представлен в предыдущих статьях. Изменения, необходимые для этого класса для использования потери SVR, уже выделены выше, поэтому осталось только показать, как этот класс вызывается и используется в пользовательском экземпляре класса сигнала. Наши MLP, рассмотренные недавно в этой серии, пытаются спрогнозировать следующее изменение цены закрытия на каждом новом баре. Это означает, что на основе таймера (каждый новый бар) производятся новые вычисления относительно того, каким будет следующее изменение цены закрытия.

Входными данными для расчета также являются предыдущие изменения цен закрытия, а основной переменной здесь является количество этих изменений. (Эта переменная устанавливает размер входного слоя). Возможны альтернативы при определении не только того, какие входные данные следует вводить в MLP при прогнозировании изменения цены закрытия следующего бара, но и того, насколько перспективным должен быть прогноз. Последний пункт важен, поскольку для целей нашего тестирования мы используем прогноз по одному ценовому бару. Кроме того, перед составлением каждого прогноза мы выполняем обратное распространение для каждого нового бара, чтобы обучить нашу сеть на заданном размере обучающего набора для определенного количества эпох.

Размер обучающего набора и эпохи также поддаются оптимизации, и это требует баланса между получением идеальных весов сети и обобщением. Это связано с тем, что, хотя больший обучающий набор и большее количество эпох могут указывать на хорошую производительность на выборочных данных, результаты перекрестной проверки наверняка не будут столь радужными, если только сеть не обладает некоторой обобщенностью и не слишком хорошо соответствует своим обучающим данным. Функция Get Output обрабатывает прогнозирование с помощью MLP. Ее исходный код представлен ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old;
         if
         (
            _in_new.Init(__MLP_SIGN_INPUTS) &&
            _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_new.Size() == __MLP_SIGN_INPUTS &&
            _in_old.Init(__MLP_SIGN_INPUTS) &&
            _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) &&
            _in_old.Size() == __MLP_SIGN_INPUTS
         )
         {  _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new, _target_old;
               if
               (
                  _target_new.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) &&
                  _target_new.Size() == __MLP_SIGN_OUTPUTS &&
                  _target_old.Init(__MLP_SIGN_OUTPUTS) &&
                  _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) &&
                  _target_old.Size() == __MLP_SIGN_OUTPUTS
               )
               {  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Она не имеет существенных отличий от реализаций, которые мы рассматривали в предыдущих статьях. Обратное распространение выполняется для каждой точки данных обучающего набора, имеющей метку (или целевое значение). Обычно все данные обучения имеют целевое значение, но поскольку в нашем случае мы объединяем их с прогнозированием, конечная "точка данных обучения" является текущей, а ее возможное изменение цены закрытия — это то, что мы ищем. Таким образом, когда мы получаем текущие входные данные, которые должны дать нам наш прогноз, мы не проводим никакого обучения. Именно поэтому мы ведем обратный отсчет в каждом обучающем наборе, то есть сначала мы обучаемся на очень старых данных, а затем постепенно переходим к текущим данным.

Реализация класса трейлинг-стопа

Прошло некоторое время с тех пор, как в этой серии статей мы рассматривали что-либо, кроме класса пользовательских сигналов, и тем не менее читатели, знакомые с моими предыдущими статьями, помнят, что я часто делился торговыми идеями не только в виде класса сигналов, но и классов трейлинг-стопов и даже классов по управлению капиталом. Итак, вернемся к этим проблемам и рассмотрим пользовательский класс трейлинг-стопа, который можно прикрепить к советнику с помощью Мастера MQL5. Руководство для новых читателей о том, как код, представленный ниже, можно использовать в Мастере MQL5 для создания советника можно найти здесь и здесь.

Таким образом, чтобы реализовать пользовательский класс трейлинга, мы будем проверять, есть ли какая-либо открытая позиция без стоп-лосса и его нужно добавить либо позиция, у которой уже есть стоп-лосс, но его необходимо изменить для лучшей фиксации прибыли. Стоп-лоссы — это немного спорный вопрос, поскольку их выполнение никогда не гарантируется. Гарантируется только выполнение лимитных ордеров. Если по какой-либо причине рынок изменится сильнее, чем ожидало большинство людей, то брокер сможет закрыть ваш ордер только по следующей "доступной цене", а не по вашему стоп-лоссу. Несмотря на это, мы собираемся принимать решения об установке или перемещении стоп-лосса на основе прогнозируемого изменения величины диапазона ценового бара. Мы реализуем этот функционал в другой функции Get Output, отличной от той, что была у нас при работе с пользовательским классом сигнала. Реализация представлена ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingSVR::GetOutput(vector &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo;
         if
         (
            _in_new_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_hi.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_hi.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_hi.Size() == __MLP_TRAIL_INPUTS
            &&
            _in_new_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_new_lo.Size() == __MLP_TRAIL_INPUTS &&
            _in_old_lo.Init(__MLP_TRAIL_INPUTS) &&
            _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) &&
            _in_old_lo.Size() == __MLP_TRAIL_INPUTS
         )
         {  vector _in_new = _in_new_hi - _in_new_lo;
            vector _in_old = _in_old_hi - _in_old_lo;
            _in = _in_new - _in_old;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo;
               if
               (
                  _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS
                  &&
                  _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) &&
                  _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS &&
                  _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) &&
                  _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS
               )
               {  vector _target_new = _target_new_hi - _target_new_lo;
                  vector _target_old = _target_old_hi - _target_old_lo;
                  _target = _target_new - _target_old;
                  MLP.Get(_target);
                  MLP.Backward(m_learning, i);
               }
            }
            Output = MLP.output;
         }
      }
   }
}

Наш код выше, хотя и почти идентичен тому, что был в сигнале, отличается в основном типом получаемых входных данных и ожидаемым выходом. Мы пытаемся определить, нужно ли нам перемещать стоп-лосс, и нашим предварительным предположением для этого является рост волатильности. Поэтому нам необходимо выяснить, каким будет следующее изменение диапазона изменения ценового бара. Подобные данные сами по себе обязательно будут очень изменчивыми (или зашумленными), поэтому более разумно было бы использовать буферы скользящего среднего в качестве входных данных и целевых значений. Полный исходный код приложен ниже и вы можете внести необходимые изменения, однако мы используем изменения максимумов за вычетом минимумов каждого ценового бара в качестве входных данных и ожидаем, что выходным значением будет следующее изменение этих входных значений, как это было с ценами закрытия для сигнала выше.

Таким образом, если прогнозируемое изменение диапазона ценового бара положительно, что означает рост волатильности, мы предпринимаем шаги для перемещения нашего стоп-лосса пропорционально нашему прогнозируемому росту. Это может показаться безрассудным, поскольку, как упоминалось выше, брокеры никогда не гарантируют цену стоп-лосса, поэтому вариант с перемещением стоп-лосса при прогнозируемом снижении волатильности может быть "более надежным", поскольку в менее волатильное время брокеры с большей вероятностью соблюдают стоп-лоссы, чем при наличии волатильности. Я оставляю решение на усмотрение читателя, чтобы он мог внести соответствующие изменения в код в зависимости от своих выводов.

Результаты тестера стратегий

Тестирование проводится на паре USDJPY, на дневном таймфрейме с 2023.01.01 по 2024.01.01. Эти тестовые прогоны выполняются с использованием лучших настроек, полученных с помощью очень быстрых оптимизаций, для которых не проводились прямые проверки или перекрестная проверка. Они представлены здесь просто для того, чтобы продемонстрировать умение размещать сделки и использовать собранный Мастером советник. Более тщательное тестирование на длительных исторических периодах, а также проведение форвард-тестов, если требуется оптимизация, оставлены на усмотрение читателя. Собранные с помощью Мастера советники могут объединять несколько сигналов при разработке торговой системы, поэтому тестирование или оптимизация не обязательно должны проводиться только с использованием пользовательских сигналов, используемых здесь.

Мы разработали собственный сигнал с SVR и собственный класс трейлинга с аналогичным MLP. Таким образом, представленные ниже тестовые прогоны предназначены для двух советников, код интерфейса которых прилагается ниже. Первый вариант использует только пользовательский сигнал без трейлинг-стопа. Его результаты представлены ниже:

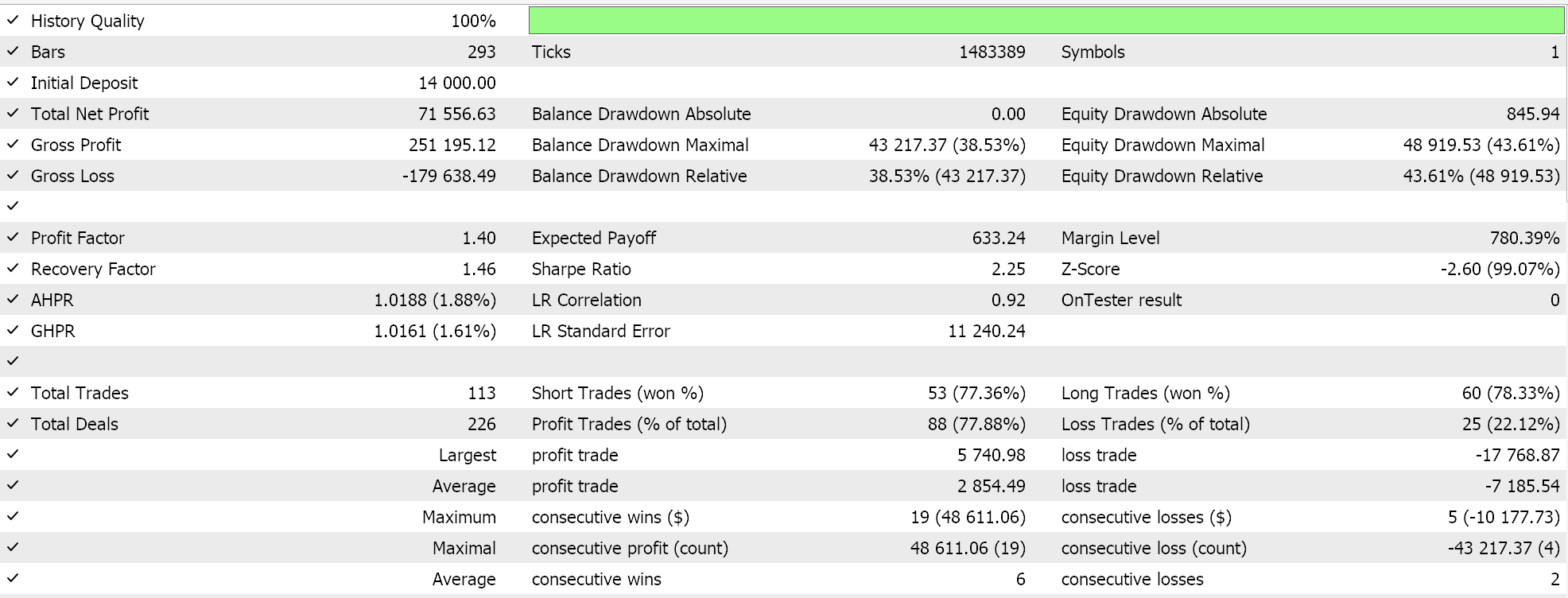
Во втором случае используются пользовательский сигнал и пользовательский трейлинг-класс, которые мы реализовали выше. Результаты также показаны ниже.

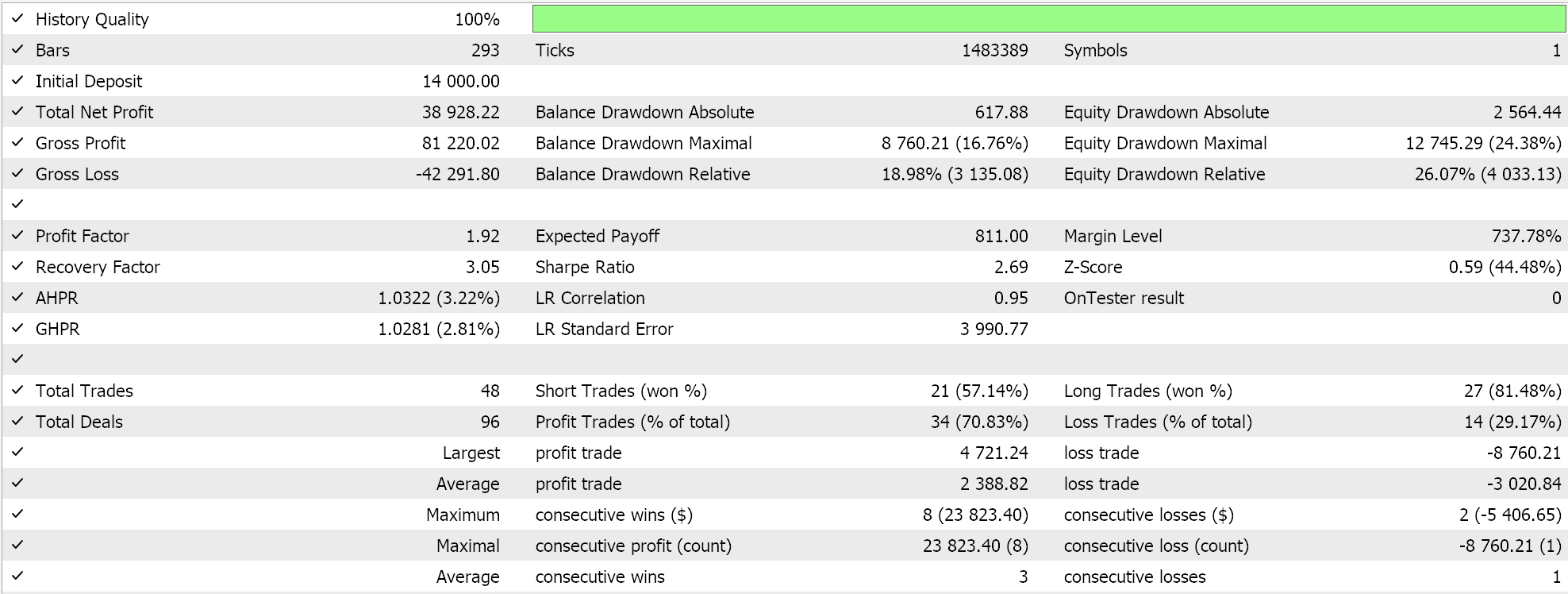
Заключение

Мы рассмотрели регрессию опорных векторов, родственной другой форме регрессии, которую мы рассматривали, когда изучали ядра гауссовских процессов. Эти две регрессии, опорных векторов и гауссовских процессов, являются почти полярными противоположностями в своем применении, поскольку SVR, как правило, больше подходит для менее изменчивых и трендовых наборов данных, в то время как GPR процветает в более изменчивых и менее определенных средах. Регрессия опорных векторов включает в себя целевую функцию и функцию принятия решения. Мы использовали целевую функцию в качестве функции потерь для многослойного перцептрона в классе сигналов и пользовательском классе трейлинг-стопа.

Использование функции принятия решения в качестве инструмента прогнозирования потребовало бы дополнительного использования ядер, что мы рассмотрели в статье о ядрах гауссовских процессов. В этой статье мы не стали этого делать, поскольку использовали в качестве инструмента прогнозирования только многослойный перцептрон. Применение функции принятия решения можно оставить для последующих статей, учитывая, что существуют различные формы ядер, которые можно использовать для выполнения этой задачи, однако в этой статье нашей целью была функция потерь SVR. Применение нечувствительного к потерям параметра эпсилон вместе с растущим списком реализаций функции потерь, некоторые из которых мы рассмотрели здесь, может представить другой способ обучения нейронных сетей.

Этот нечувствительный к потерям параметр эпсилон действует скорее как классификатор, чем как регрессор. Это дает основания для того, чтобы чаще использовать эту функцию потерь в сетях классификаторов, а не регрессоров, как мы делали в этой статье. Однако SVR по-прежнему имеет дело с непрерывными выходными данными (десятичными наборами данных) и прогнозирует числовые значения в аналогичном формате. Она просто использует эпсилон-разницу, чтобы решить, следует ли штрафовать за ошибку, но ее целью остается регрессия, а не классификация.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15692

Прикрепленные файлы |

Загрузить ZIP

Cmlp-.mqh (27.94 KB)

SignalWZ_35.mqh (10.93 KB)

TrailingWZ_35.mqh (10.74 KB)

wz_35.mq5 (7.18 KB)

wz_35_l.mq5 (8.14 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Применение теории игр Нэша с фильтрацией НММ в трейдинге

Настоящая статья посвящена применению теории игр Джона Нэша, в частности теории равновесия Нэша, в трейдинге. В ней обсуждается, как трейдеры могут использовать скрипты Python и платформу MetaTrader 5 для выявления и использования неэффективности рынка спомощью принципов Нэша. В статье приводится пошаговое руководство по реализации этих стратегий, включая использование скрытых Марковских моделей (HMM) и статистического анализа, для повышения эффективности торговли.

Создание самооптимизирующихся советников на языках MQL5 и Python

В этой статье обсудим, как можно создать советник, способный самостоятельно выбирать и менять торговые стратегии в зависимости от преобладающих на рынке условий. Познакомимся с цепями Маркова и с их возможностями с точки зрения пользы для нас, алготрейдеров.

Нейросети в трейдинге: Двойная кластеризация временных рядов (Окончание)

Продолжаем реализацию подходов, предложенных авторами фреймворка DUET, который предлагает инновационный подход к анализу временных рядов, сочетая временную и канальную кластеризацию для выявления скрытых закономерностей в анализируемых данных.

Удаленный профессиональный риск-менеджер Forex на Python

Делаем удаленный профессиональный риск-менеджер Для Forex на Python, разворачиваем его на сервере по шагам. В процессе статьи поймем, как программно управлять рисками на Форекс, и как больше не слить депозит на Форекс.