MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 59): Verstärkungslernen (DDPG) mit gleitendem Durchschnitt und stochastischen Oszillatormustern

Einführung

Im letzten Artikel hatten wir DDPG, einen Algorithmus des Verstärkungslernens, vorgestellt und uns 3drei Die Klasse des Wiedergabepuffers, die Klasse des Akteur-Netzwerks und die Klasse des Kritiker-Netzwerks. Was nicht behandelt wurde, war die DDPG-Agentenklasse, der Import von MetaTrader 5-Kursdaten in Python, Funktionen für den MA und den Stochastik-Oszillator, eine Funktion get-pattern zur Zusammenführung von Daten aus den beiden Indikatoren in einen binären Eingangsvektor für das überwachte Lernnetz (implementiert im früheren Artikel über überwachtes Lernen über MQL5) und schließlich eine Umgebungssimulationsschleife für das Training der Akteurs- und Kritikernetze.

All dies ist Teil des Verstärkungslernens (Reinforcement Learning, RL), das wir als Übergang vom überwachten Lernen (SL) zum Inferenzlernen (IL) (oder unüberwachten Lernen) betrachten. Jeder dieser Modi kann für sich allein verwendet werden, um ein Modell zu trainieren und zu nutzen. In diesen Artikeln wird jedoch versucht, zu zeigen, dass sie zusammen verwendet werden können, um etwas Interessanteres aufzubauen. Wir setzen also unseren Blick auf RL fort, indem wir uns mit der sehr wichtigen Klasse der DDPG-Agenten beschäftigen.

DDPG-Agent

Die Kernarchitektur und Initialisierung dieser Klasse kann wie folgt definiert werden:

def __init__(self, state_dim, action_dim):

    # Actor networks
    self.actor = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target.load_state_dict(self.actor.state_dict())
    self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=LR_ACTOR)
   
    # Critic networks  
    self.critic = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target.load_state_dict(self.critic.state_dict())
    self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=LR_CRITIC)

    self.replay_buffer = ReplayBuffer(BUFFER_SIZE)

Die entscheidenden Komponenten sind hier die duale Netzarchitektur, die Einrichtung des Optimierers und das Erfahrungsmanagement. Die duale Architektur unterhält ein separates Politik- (Akteursnetz) und ein separates Wert-Netz (Kritikernetz), die sich von den beiden Hauptpolitik- und Werte-Netzen unterscheiden. Diese implementieren Zielnetze für beide, was für die Stabilität beim Training wichtig ist. Die Initialisierung der jeweiligen Ziele erfolgt mit denselben Gewichten wie bei ihren Hauptnetzen.

Das Optimierungssetup enthält separate Adam-Optimierer für die Akteurs- und Kritikernetze. Außerdem verwenden wir, wie es üblich ist, getrennte Lernraten für das Politik- und das Wertnetz. Schließlich stellen wir für das Erfahrungsmanagement sicher, dass der Wiedergabepuffer Übergänge für das Off-Policy-Lernen speichert, und durch die Festlegung der Puffergröße verhindern wir eine unbegrenzte Speichernutzung. Wir wählen Aktionen aus, indem wir die Exploration wie folgt einbeziehen:

def select_action(self, state, noise_scale=0.1):
    state = torch.FloatTensor(state).unsqueeze(0).to(device)
    action = self.actor(state).cpu().data.numpy().flatten()
    action += noise_scale * np.random.randn(self.action_dim)
    return np.clip(action, -1, 1)

Die wichtigsten Mechanismen sind hier die Zustandsverarbeitung, die Erkundungsstrategie und das Gerätemanagement. Die Zustandsverarbeitung überwacht die Konvertierung von NumPy-Arrays in das richtige Tensorformat, das Hinzufügen einer Stapeldimension (durch Un-Squeezing) und stellt schließlich sicher, dass die Berechnung auf dem richtigen Gerät erfolgt.

Die Explorationsstrategie fügt der deterministischen Politikausgabe Gaußsches Rauschen hinzu. Die Rauschskala steuert das Ausmaß der Erkundung und die Begrenzung hält einen gültigen Aktionsbereich aufrecht. Das Gerätemanagement sorgt für einen effizienten Wechsel zwischen GPU/CPU, falls erforderlich. Außerdem gibt die Funktion aus Gründen der Umgebungskompatibilität eine endgültige Ausgabe als NumPy-Array zurück. Der Mechanismus der Lernaktualisierung sieht folgendermaßen aus:

def update(self):

    if len(self.replay_buffer) < BATCH_SIZE:

        return

Diese if-Klausel dient als Aktualisierungsgatter, in dem Aktualisierungen so lange übersprungen werden, bis genügend Erfahrungen, die der Losgröße entsprechen, gesammelt wurden. Dies gewährleistet eine aussagekräftige Chargenstatistik. Die Aktualisierung der 2 kritischen Netze erfolgt wie folgt:

# Sample batch

states, actions, rewards, next_states, dones = self.replay_buffer.sample(BATCH_SIZE)

# Target Q calculation
next_actions = self.actor_target(next_states)
target_q = self.critic_target(next_states, next_actions)
target_q = rewards + (1 - dones) * GAMMA * target_q

# Current Q estimation
current_q = self.critic(states, actions)

# Loss computation and backpropagation
critic_loss = nn.MSELoss()(current_q, target_q.detach())
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()

Die wichtigsten Aspekte dieses Codes sind die Zielwertberechnung, die Verlustberechnung und das Gradientenmanagement. Die Zielwertberechnung verwendet Zielnetze, um stabile Q-Ziele zu erhalten. Es implementiert die Bellman-Gleichung mit Abbruchbehandlung, die durch den Erfahrungsparameter „dones“ festgelegt wird. Ein Abzinsungsfaktor von GAMMA steuert die Bedeutung zukünftiger Belohnungen.

Für die Verlustberechnung wird der mittlere quadratische Fehler zwischen den aktuellen und den angestrebten Q-Werten ermittelt. Die Methode detach() verhindert, dass Zielgradienten fließen (oder vom Tensor für die Übertragbarkeit getragen werden). Und es wird das standardmäßige Zeitdifferenzlernen angewendet. Das Gradientenmanagement sorgt lediglich dafür, dass alle Gradienten auf Null gesetzt werden, und die Optimierung des kritischen Netzes ist ein separater Schritt. Aktualisierungen des Akteursnetzwerks werden auch wie folgt durchgeführt:

actor_loss = -self.critic(states, self.actor(states)).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()

Die hier behandelten Besonderheiten des Policy-Gradienten sind die Maximierung von Q-Werten durch die Minimierung von negativem Q, die Differenzierung durch das Akteurs- und das Kritikernetzwerk sowie die Anwendung eines reinen Policy-Gradienten-Ansatzes ohne log-Wahrscheinlichkeiten (da deterministisch). Die Aktualisierungen des Zielnetzes sind wie folgt:

for target, param in zip(self.actor_target.parameters(), self.actor.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

for target, param in zip(self.critic_target.parameters(), self.critic.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

Dieser sanfte Aktualisierungsmechanismus beinhaltet eine Polyak-Mittelung mit einem TAU-Wert, der in der Regel kleiner als 1 ist. Die Gewichte des Netzes werden langsam nachgeführt, da dies eine Alternative zu periodischen harten Aktualisierungen darstellt. Dieser Prozess sorgt insgesamt für Stabilität und ermöglicht gleichzeitig Lernen. Unser Modell muss beständig sein. Es sollte in der Lage sein, zuvor gespeicherte Netzgewichte zu laden und sie auch nach dem Training zu speichern. Dies erreichen wir wie folgt:

def save(self, filename):

    torch.save({
        'actor': self.actor.state_dict(),

        'critic': self.critic.state_dict(),

        'actor_target': self.actor_target.state_dict(),

        'critic_target': self.critic_target.state_dict(),
    }, filename)


def load(self, filename):

    checkpoint = torch.load(filename)
    self.actor.load_state_dict(checkpoint['actor'])
    self.critic.load_state_dict(checkpoint['critic'])
    self.actor_target.load_state_dict(checkpoint['actor_target'])
    self.critic_target.load_state_dict(checkpoint['critic_target'])

Die wichtigsten Merkmale unserer obigen Auflistung sind: Wir speichern/laden alle Netzzustände; wir erhalten die Konsistenz des Zielnetzes aufrecht; wir ermöglichen die Fortsetzung des Trainings; und wir unterstützen die Modellbewertung. Zusammenfassend lässt sich also sagen, dass bei der Implementierung eines DDPG-Agenten einige kritische Designentscheidungen getroffen werden müssen. Diese lassen sich grob in drei Kategorien einteilen, nämlich Auswahl der DDPG-spezifischen Komponenten, Nutzung der Stärken der Implementierung und mögliche Verbesserungen.

Die verwendeten DDPG-Komponenten sind vor allem die Zielnetze, die deterministische Politik und separate Lernraten. Die Zielnetze sind sehr wichtig für ein stabiles Lernen der Belohnungen aus den ausgeführten Aktionen (Q-Learning), wenn es um kontinuierliche Aktionsräume geht. Durch die Verwendung durchgehender Räume ist dies von entscheidender Bedeutung. Diese deterministische Politik erfordert dann eine externe Erkundung mit Rauschen, um Robustheit zu erreichen. Die Verwendung getrennter Lernraten ist ebenfalls eine typische Anwendung, bei der die Politik (Akteursnetz) eine langsamere Lernrate hat als das Wertnetz.

Zu den Entscheidungen, die dies zu einer relativ starken Implementierung machen, gehört eine klare „Trennung der Belange“, bei der wir genau definierte Methoden für die Auswahl von Aktionen und auch für Aktualisierungen haben. Außerdem gibt es eine Geräteerkennung, die eine einheitliche Handhabung von GPU/CPU-Übergängen gewährleistet. Die Stapelverarbeitung wird ebenfalls eingesetzt, um die Tensoroperationen effizienter zu gestalten, und schließlich wird die Formsicherheit an mehreren Stellen überprüft, um eine konsistente Tensordimensionalität zu gewährleisten.

Potenzielle Verbesserungen könnten jedoch sein: Gradientenbeschneidung, um explodierende Gradienten zu vermeiden; die Verwendung eines Lernratenplans, um den Lernprozess zu verfeinern und besser zu kontrollieren; die Verwendung einer prioritären Wiedergabe für effizientes Sampling, wobei dies mit dem bereits im letzten Artikel erwähnten Wiedergabepuffer zusammenhängt; und schließlich parallele Exploration, bei der mehrere Instanzen des Akteurs für eine schnellere Datenerfassung verwendet werden können.

Es gibt auch einige Trainingsdynamiken, die erwähnenswert sind und die mit der Aktualisierungssequenz und den Hyperparametern zu tun haben. Die Aktualisierungsreihenfolge sieht vor, dass die kritischen Netze zuerst aktualisiert werden. Der Grund dafür ist, dass genauere Q-Werte zur Verbesserung der Politik beitragen. Um eine zusätzliche Stabilität zu erreichen, kann die Aktualisierung der Richtlinien auch verzögert werden. Schließlich werden häufige Zielaktualisierungen durchgeführt, um die erlernten Parameter (Netzgewichte) langsam zu verfolgen.

Bei den Überlegungen zu den Hyperparametern sollte der Schwerpunkt auf der TAU liegen, da sie die Geschwindigkeit des Zielnetzes steuert und somit ein wichtiger Faktor für die Stabilität des gesamten Lernprozesses ist. Es sollte eine Skala des Rauschans verwendet werden, die ein Abklingen mit der Zeit ermöglicht. Die Puffergröße ist ebenfalls von entscheidender Bedeutung, da sie sich auf die Lerneffizienz auswirkt und die Stapelgröße einen Einfluss auf die Varianz der Aktualisierungen hat.

MA und stochastische Funktionen

Diese beiden Funktionen sind in Python für das Verstärkungslernen (RL) implementiert, im Gegensatz zu dem Artikel über überwachtes Lernen, in dem wir dies in MQL5 gemacht haben und einfach die Netzwerk-Eingangsdaten zum Training nach Python exportiert haben. Bei unserer Implementierung hier verwenden wir das MetaTrader 5 Python-Modul von MetaTrader, um eine Verbindung zu einer laufenden Terminalinstanz herzustellen und dann Kursdaten abzurufen. In der Dokumentation finden Sie die Anleitungen, wie Sie dies tun können. Unsere nachstehenden Indikatorfunktionen wandeln rohe Preisdaten in technische Indikatordaten um, die nach ihrer Umwandlung/Normalisierung in einen binären Mustervektor als Input für unser überwachtes Lernmodell dienen. 

Die Ergebnisse des überwachten Lernmodells bezeichnen wir als Zustände, da sie im Wesentlichen Veränderungen im Kursgeschehen prognostizieren. Diese Zustände werden dann als Eingaben für den DDPG-RL-Agenten verwendet. Unsere MA-Funktion nimmt als Eingabe einen Panda-Datenrahmen mit Preisen aus dem MetaTrader 5 Python-Modul. Dieser Datenrahmen muss wie folgt validiert und vorbereitet werden:

p = np.asarray(p).flatten()  # Convert to 1D array if not already

if len(p) < window:

    raise ValueError("Window size cannot be larger than the number of prices.")

Hier geht es darum, das Array zu standardisieren, um ein einheitliches 1D-Eingabeformat unabhängig von der Eingabeform zu gewährleisten. Wir haben auch eine Fehlerbehandlung, die ungültige Fenstergrößen verhindert, die zu Berechnungsfehlern führen würden. Die Datenintegrität sorgt auch für einen sauberen Datenfluss durch die Verarbeitungspipeline. Der Berechnungsmechanismus sieht folgendermaßen aus:

return np.convolve(p, np.ones(window), 'valid') / window

Bei dieser Implementierung wird die Faltung zur effizienten Fortschreibung der Durchschnittsberechnung verwendet. Durch die Verwendung des Eingabeparameters „valid“ wird sichergestellt, dass nur vollständig berechnete Fenster zurückgegeben werden. Die Normalisierung erfolgt auch nach Fenstergröße, um einen echten Durchschnitt zu erhalten. Der gesamte Vorgang ist für eine optimale Leistung vektorisiert. Die finanzielle Bedeutung liegt darin, dass die Preisdaten geglättet werden, um Trends zu erkennen, und dass die Größe des verwendeten Fensters (auch als Mittelungszeitraum bezeichnet) die Empfindlichkeit gegenüber Preisänderungen bestimmt. Die Funktion des stochastischen Oszillators validiert ihre Eingaben wie folgt:

p = np.asarray(p).flatten()

if len(p) < k_window:
    raise ValueError("Window size for %K cannot be larger than the number of prices.")

Bei der Gestaltung wurde auf eine einheitliche Eingabeformatierung mit der MA-Funktion geachtet. Für das %K-Berechnungsfenster ist eine separate Validierung erforderlich, wobei bei ungültigen Parametern frühzeitig ein Fehler ausgelöst wird. Die %K-Berechnung erfolgt wie folgt:

for i in range(k_window - 1, len(p)):

    current_close = p[i]
    lowest_low = min(p[i - k_window + 1:i + 1])
    highest_high = max(p[i - k_window + 1:i + 1])
    K = ((current_close - lowest_low) / (highest_high - lowest_low)) * 100
    K_values.append(K)

Wichtige Komponenten sind hier die Analyse des rollenden Fensters, der Marktkontext und die allgemeine Umsetzung. Bei der Analyse des rollenden Fensters muss die Preisspanne über einen Rückblickszeitraum untersucht werden. Dies hilft, die relative Position des aktuellen Schlusskurses zu ermitteln, wobei eine Standardskalierung von 0 bis 100 angewendet wird. Der Marktkontext hilft uns, die überkauften/überverkauften Bedingungen zu beurteilen. Werte in der Nähe von 100 deuten auf eine mögliche Umkehr nach unten hin, während Werte in der Nähe von 0 auf eine Aufwärtsbewegung hindeuten würden. Die Gesamtimplementierung verwendet aus Gründen der Übersichtlichkeit eine explizite Schleife, verwendet eine geeignete Fensterindizierung, um Randfälle zu behandeln, und behält die zeitliche Reihenfolge der Ergebnisse bei. Die Berechnung des %D ist wie folgt:

D_values = MA(K_values, d_window)

Im Wesentlichen handelt es sich um eine Signalverfeinerung, bei der eine geglättete Version des gleitenden %K-Durchschnitts verwendet wird. Die typische Zuteilung für diesen Mittelungszeitraum ist 3, und das ist es, was wir verwenden. Dieser zusätzliche Puffer bietet eine Bestätigung für Schwankungen des %K-Wertes und trägt somit dazu bei, falsche Signale von einem rohen %K-Wert zu reduzieren.

Funktion „Get Pattern“

Diese Funktion wird verwendet, um Daten aus unseren beiden oben genannten Indikatorpuffern in die Lernpipeline zu integrieren. Sie spielt eine Rolle bei der Entwicklung von Funktionen. Der Grund dafür ist, dass sie zur Dimensionenreduktion beiträgt, da sie Rohpreise in aussagekräftigere Signale umwandelt; sie hilft bei der stationären Verbesserung, da Indikatoren oft stabiler sind als Rohpreise; und schließlich ermöglicht sie die Erfassung des zeitlichen Kontextes, da verwitwete Berechnungen zeitliche Abhängigkeiten beibehalten (ein generierter Eingabevektor von z. B. [1,0,0,1] kann mit der Zeit assoziiert werden, zu der er erzeugt wurde, so wie jeder Indikatorwert oder Rohpreis ebenfalls mit der Zeit, zu der er erzeugt wurde, gekennzeichnet wird).

In erster Linie wird es jedoch für die Vorbereitung auf das überwachte Lernen verwendet. Die Merkmale, die es in einem binären Vektor von 0 und 1 ausgibt, trainieren das Modell, um die nächsten Preisänderungen vorherzusagen. Der MA liefert Informationen über den Trend, während die STO-Funktion Informationen über das Momentum und die Umkehrung liefert. Wir haben die kombinierten komplementären Muster aus beiden Indikatoren in Artikel 57 behandelt. Die prognostizierten Preisänderungsausgaben dienen dann als RL-Zustandsdarstellung.

Dies bedeutet, dass die Vorhersagen unseres Modells für überwachtes Lernen zu Zustandsdaten für die DDPG werden. Die von uns verwendeten Indikatoren MA und STO helfen daher dem DDPG-Agenten, indem sie einen Marktkontext liefern, der zum Verständnis einer bestimmten Marktordnung beiträgt. Dadurch wird der Bedarf an Rohdatenpreisen bei der Definition des Zustands verringert.

Zu den Stärken der Implementierung gehören die Robustheit durch die Validierung von Eingaben, um stille Fehler zu vermeiden, die Handhabung von Dimensionen, um konsistente Array-Formen zu gewährleisten, und Fehlermeldungen, um im Falle einer unsachgemäßen Verwendung eindeutige Nachrichten zu erhalten. Außerdem werden leistungsfördernde Überlegungen zur Verwendung vektorisierter Operationen, wo immer dies möglich ist, sowie explizite Schleifen und Speichereffizienz durch ein streamingfreundliches Design angestellt. Sie bleibt für die Händler relevant und verliert sich nicht in Formalitäten. Der Grund dafür ist, dass für die Erstellung der Zustände Standardindikatoren der Branche verwendet werden. Die Indikatoren sind komplementär, da sie Trend- und Impulsmetriken zusammenführen, und die Zustandsausgaben liegen in einem normalisierten Bereich, was für die Konsistenz wichtig ist.

Mögliche Verbesserungen sind die Optimierung von Berechnungen durch die Verwendung einer vektorisierten Implementierung der %K-Berechnung, die Verwendung der Numba-Beschleunigung (importiert aus JIT) zur Beschleunigung von Schleifen in der STO-Funktion und die Zwischenspeicherung von Berechnungen. Eine erweiterte Funktionalität kann durch eine zusätzliche Validierung für NaN/inf-Werte hinzugefügt werden. Dieser Code, der das Verstärkungslernen mit DDPG implementiert, ist sehr umfangreich, und obwohl es angemessen wäre, seine wichtigsten Abschnitte zu kommentieren, werde ich einfach die freigelegten Teile am Ende dieses Artikels anhängen. Dazu gehört vor allem die Funktion „get pattern“.

Tests

Von den zehn Mustern, die wir im Artikel zum überwachten Lernen (Nr. 57) getestet haben, waren nur sieben in der Lage, einen gewinnbringend Vorwärtstest im folgenden Jahr zu machen, nachdem sie für ein Jahr zuvor trainiert worden waren. Da jedes Muster ein eigenes Netz darstellt, müssen wir auch für jedes Muster Verstärkungslernnetze und -umgebungen erstellen. Wir folgen einer ähnlichen Methodik in Artikel 57, wo wir das Paar EUR USD für das Jahr 2023 auf dem täglichen Zeitrahmen trainieren. In diesem Fall trainieren wir unsere Netze des Verstärkungslernens, indem wir das Jahr 2023 als „Live-Markt“ simulieren. Wie in den letzten beiden Artikeln dargelegt, ist das Verstärkungslernen ein System zur Unterstützung und zum Schutz eines bereits etablierten und trainierten Modells, das in unserem Fall das Netz ist, das wir in Artikel 57 durch überwachtes Lernen trainiert haben. 

Dies geschieht durch Backpropagation in Produktions- oder Live-Umgebungen und nicht anhand historischer Daten. Da die Rückübertragung eines ONNX-Netzes von MQL5 aus nicht möglich ist, „simulieren“ wir eine reale Umgebung, die in unserem Fall noch das Jahr 2023 ist.

Anstatt die Frage zu stellen, die wir beim überwachten Lernen gestellt haben, nämlich „Was wird der Preis als Nächstes tun?“, stellen wir die Frage, welche Maßnahmen der Händler angesichts dieser eingehenden Preisänderungen ergreifen sollte. Wir führen also die oben beschriebenen Simulationen für das Jahr 2023 durch und machen dann einen Forward Walk für das Jahr 2024, bei dem unsere Eintrittsbedingungen leicht verändert werden.

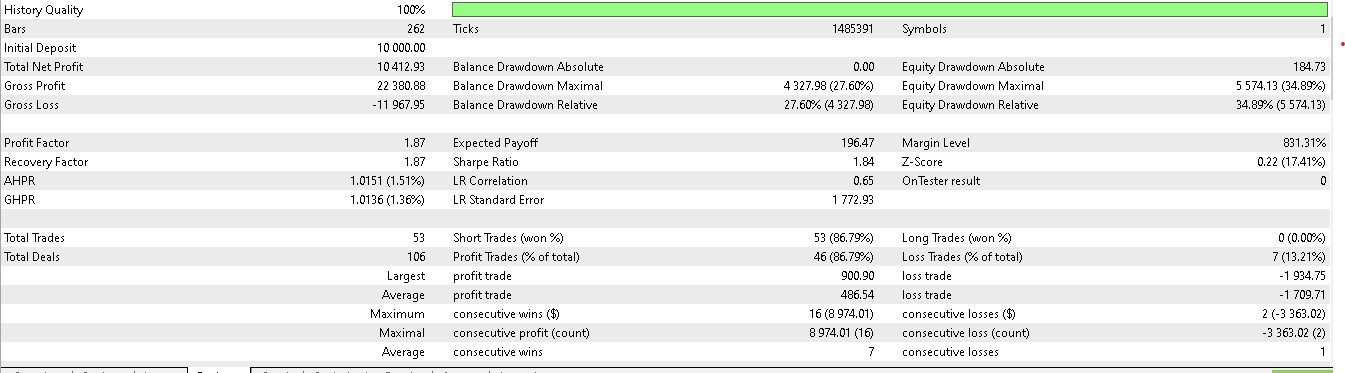
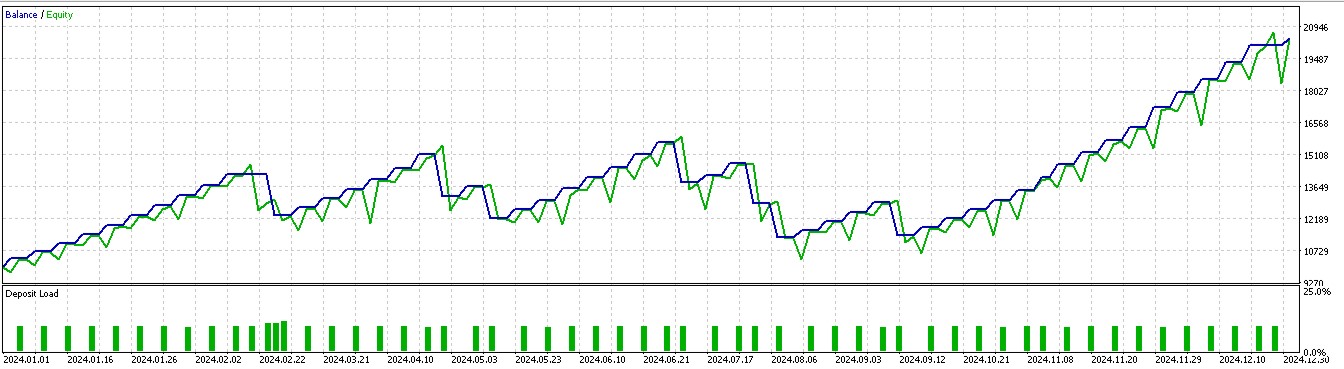
Wir stützen unsere Kauf- oder Verkaufs-Positionen nicht nur darauf, was der Kurs als Nächstes tun wird, sondern überlegen auch, welche Maßnahmen wir angesichts der nächsten Kursentwicklung wirklich ergreifen müssen. Wir berücksichtigen auch, ob sich die Belohnungen lohnen werden. Von den sieben Mustern, die in Artikel 57 einen Vorwärtstest machten, waren nur drei erfolgreich, wenn das Verstärkungslernen eingesetzt wird. Bei unserer Indizierung der 10, die von 0 bis 9 reicht, sind dies die Muster 1, 2 und 5. Ihre Berichte werden im Folgenden vorgestellt:

Für Muster 1:

Für Muster 2:

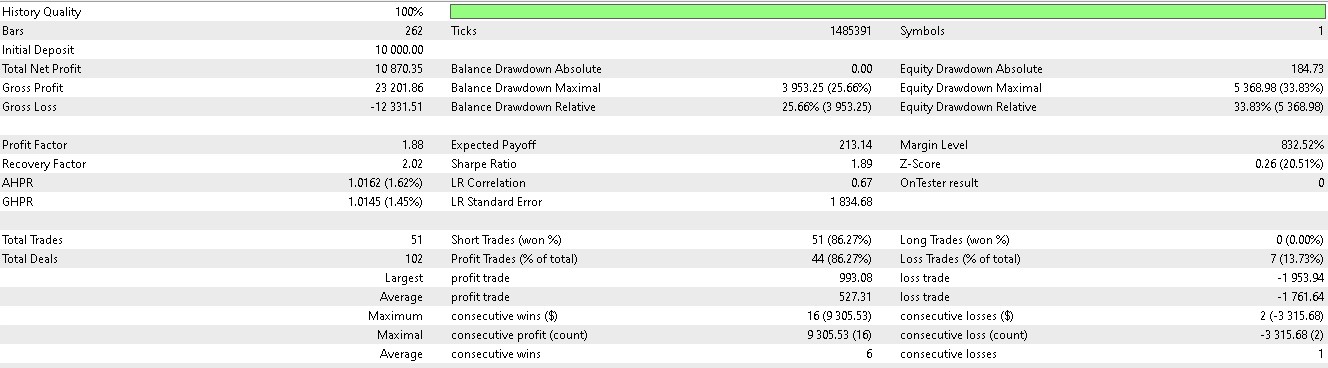
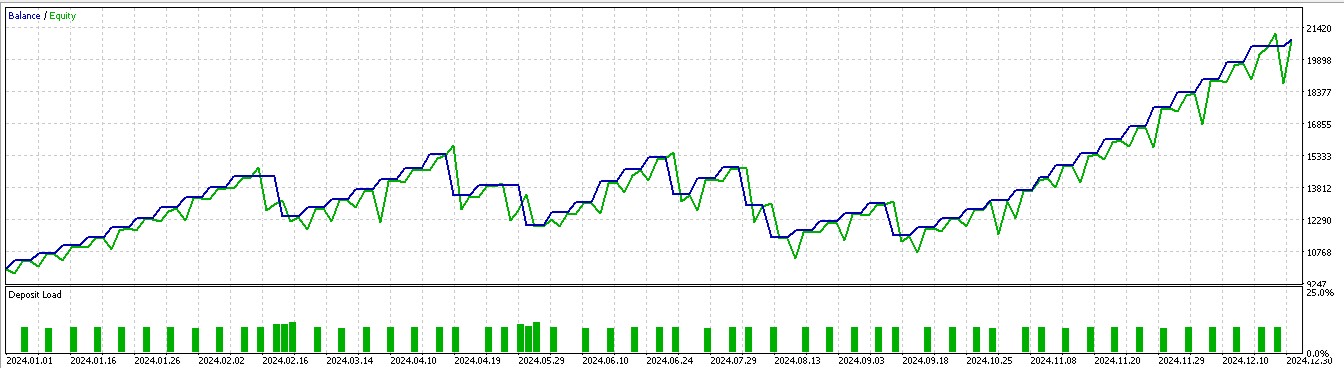
Für Muster 5:

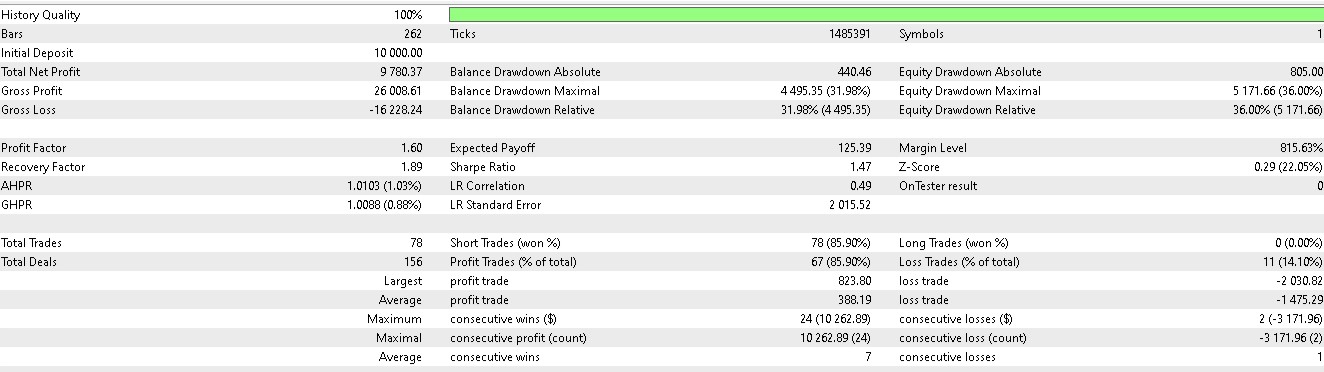
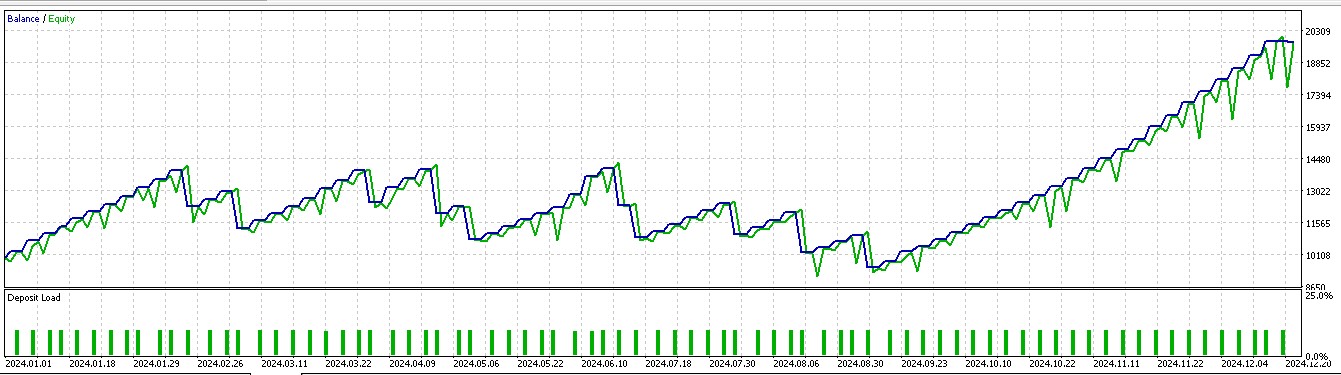
Der getestete Expert Advisor ist wie immer mit einer nutzerdefinierten Signalklasse aufgebaut, deren Code unten beigefügt ist. Wir nehmen Änderungen an der Signalklassendatei vor, die wir in Artikel 57 hatten, indem wir die Funktion „IsPattern“ in „Supervise“ umbenennen. Außerdem führen wir eine neue Funktion „Reinforce“ ein. Der Code für diese beiden Programme ist unten angegeben:

//+------------------------------------------------------------------+
//| Supervised Learning Model Forward Pass.                          |
//+------------------------------------------------------------------+
double CSignal_DDPG::Supervise(int Index, ENUM_POSITION_TYPE T)
{  vectorf _x = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vectorf _y(1);
   _y.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y forecast, err: %i", GetLastError());
      return(double(_y[0]));
   }
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   return(double(_y[0]));
}
//+------------------------------------------------------------------+
//| Reinforcement Learning Model Forward Pass.                       |
//+------------------------------------------------------------------+
double CSignal_DDPG::Reinforce(int Index, ENUM_POSITION_TYPE T, double State)
{  vectorf _x(1);
   _x.Fill(float(State));
   vectorf _y(1);
   _y.Fill(0.0);
   vectorf _y_state(1);
   _y_state.Fill(float(State));
   vectorf _y_action(1);
   _y_action.Fill(0.0);
   vectorf _z(1);
   _z.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles_a[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y action forecast, err: %i", GetLastError());
   }
   _y_action[0] = _y[0];
   ResetLastError();
   if(!OnnxRun(m_handles_c[_i], ONNX_NO_CONVERSION, _y_state, _y_action, _z))
   {  printf(__FUNCSIG__ + " failed to get z reward forecast, err: %i", GetLastError()); 
   }
   //normalize action output & check for state-action alignment
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   else
   {  _y[0] = 0.0f;
   }
   return(double(_y[0]*_z[0]));
}

Diese nutzerdefinierte Signalklassendatei soll mit Hilfe des MQL5-Assistenten zu einem Expert Advisor zusammengestellt werden, und für Leser, die neu sind, gibt es hier und hier eine Anleitung, wie man das macht.

Schlussfolgerung

Wir haben uns mit der Anwendung des Verstärkungslernens befasst, wenn sich die Modelle in der Entwicklung/Produktion befinden. Unser Verstärkungslernen verwendete den tiefen deterministischen Policy-Gradienten-Algorithmus und diese Implementierung hatte die Klassen: Replay-Buffer, Actor, Critic und Agent, wie in diesem und dem letzten Artikel behandelt.  Verstärkungslernen in der Einsatz-/Produktionsphase dient dazu, das Modell auf das zu konzentrieren, was in der Phase des überwachten Lernens gelernt wurde (Verwertung), und gleichzeitig nach neuen, unbekannten Veränderungen in der Umgebung/Marktbedingungen Ausschau zu halten, die bei künftigen Entscheidungen berücksichtigt werden sollten (Verwertung). Um dies korrekt zu tun, müssen wir ein Modell während seiner Verwendung rückwärts propagieren und trainieren. 

Da das Training eines ONNX-Modells in MQL5 jedoch nicht unterstützt wird, haben wir uns für eine Simulation von Live-Handelsbedingungen auf Basis historischer Daten entschieden. Nach der Simulation testeten wir die trainierten Modelle des Verstärkungslernens mit dem Folgejahr nach dem Trainingsjahr, und nur drei der sieben Modelle waren in der Lage, Vorwärtstest zu machen, wenn auch mit verzerrten Handelsergebnissen, da meistens nur Kauf- und Verkaufspositionen gehalten wurden. Dies ist, wie wir in Artikel 57 dargelegt haben, höchstwahrscheinlich auf ein kleines Testfenster zurückzuführen, was bedeutet, dass umfangreiches Training und Testen mit mehr Daten dieses Problem beheben sollte. Als Nächstes befassen wir uns mit der Inferenz.

Typ	Beschreibung
*.*onnx files	ONNX-Modelldateien im Python-Unterordner innerhalb der nutzerdefinierten Signalklassendatei
*.*mqh files	Nutzerdefinierte Signalklassendatei in und Datei mit Funktion zur Verarbeitung von Eingangsnetzdaten (57_X)
*.*mq5 files	Assistent Assemblierter Expert Advisor, dessen Kopfzeile die verwendeten Dateien anzeigt.