MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 54): Verstärkungslernen mit hybriden SAC und Tensoren

Einführung

Soft Actor Critic (SAC) ist einer der Algorithmen, die beim Reinforcement Learning für das Training eines neuronalen Netzes verwendet werden. Zusammenfassend lässt sich sagen, dass das Verstärkungslernen eine aufstrebende Trainingsmethode im Bereich des maschinellen Lernens ist, neben dem überwachten und dem unüberwachten Lernen.

Replay Buffer

Der „Replay Buffer“, ein Wiederholungspuffer, ist eine sehr wichtige Komponente des SAC-Off-Policy-Algorithmus im Reinforcement Learning, da er vergangene Erfahrungen mit dem Zustand, der Aktion, der Belohnung, dem nächsten Zustand und der Erledigt-Flag (um zu protokollieren, ob eine Episode abgeschlossen oder im Gange ist) für das Training in Mini-Stapeln speichert. Sein Hauptzweck besteht darin, verschiedene Erfahrungen zu dekorrelieren, sodass der Agent aus einer vielfältigeren Menge von Erfahrungen lernen kann, was die Lernstabilität und die Stichprobeneffizienz tendenziell verbessert.

Bei der Implementierung von SAC können wir die Sprache MQL5 verwenden, aber die erstellten Netze wären nicht so effizient zu trainieren wie die in Python mit Open-Source-Bibliotheken wie TensorFlow oder PyTorch erstellten. Wie wir im letzten Artikel über Reinforcement Learning gesehen haben, in dem Python zur Modellierung eines rudimentären SAC-Netzwerks verwendet wurde, fahren wir mit Python fort, aber diesmal mit dem Ziel, die Tensor-Graphen zu erforschen und zu nutzen. Es gibt prinzipiell zwei Möglichkeiten, einen Replay Buffer in Python zu implementieren. Der manuelle Ansatz oder der Tensor-basierte Ansatz. 

Bei der manuellen Vorgehensweise werden grundlegende Python-Datenstrukturen wie Listen oder NumPy-Arrays verwendet. Bei der Tensor-basierten Methode werden jedoch Deep-Learning-Frameworks wie TensorFlow oder PyTorch eingesetzt, wobei dieser Ansatz aufgrund der nahtlosen Integration in die Trainings-Pipelines für neuronale Netze effizienter für die GPU-Beschleunigung ist. Beim manuellen Ansatz wird der Wiedergabepuffer mit „NumPy“-Arrays erstellt, was einfach und effektiv für kleine Probleme ist. Dies könnte wie folgt gehandhabt werden:

import numpy as np

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.actions = np.zeros((max_size, action_dim), dtype=np.float32)
        self.rewards = np.zeros(max_size, dtype=np.float32)
        self.next_states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.dones = np.zeros(max_size, dtype=np.float32)
        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
             
        ...

    def sample(self, batch_size):
        idx = np.random.randint(0, self.size, size=batch_size)
        return (
            self.states[idx],
            ...

             self.dones[idx],
        )

Dieser Ansatz ist zwar relativ einfach zu implementieren und ähnelt dem, den wir im vorherigen SAC-Artikel verwendet haben, aber für größere Probleme oder GPU-Beschleunigung ist er möglicherweise nicht gut skalierbar.

Bei der Tensor-basierten Methode wird der Wiedergabepuffer entweder mit PyTorch oder TensorFlow kodiert. Letzteres scheint meiner Erfahrung nach (bisher) etwas problematisch zu sein. Ich war in der Lage, eine GPU so einzurichten, dass sie mit TensorFlow läuft, aber die spezifische Natur der ganzen Kette von Treibern und Versionen der dazugehörigen Softwarebibliotheken, die für eine bestimmte Version nicht nur von TensorFlow, sondern auch von Python vorhanden sein müssen, wenn eine bestimmte GPU verwendet wird, ist sicherlich erdrückend.

Später habe ich PyTorch ausprobiert, und vielleicht lag es an meiner früheren Erfahrung mit TensorFlow, aber der Prozess verlief viel reibungsloser. Die PyTorch-Integration des Trainings neuronaler Netze mit GPU-Beschleunigung ist so reibungslos, dass ein Datensatz mit fast einer Million Zeilen, wenn er mit einem ziemlich komplexen Netz mit 10 Millionen Parametern gefüttert wird, eine einzelne Epoche in etwa 4 Minuten auf einem einfachen NVIDIA T4 laufen lassen kann. Wir können eine rudimentäre Implementierung in Python wie folgt durchführen:

import torch

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = torch.zeros((max_size, state_dim), dtype=torch.float32)
        ...

        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
        self.states[self.ptr] = torch.tensor(state, dtype=torch.float32)
        self.actions[self.ptr] = torch.tensor(action, dtype=torch.float32)
        self.rewards[self.ptr] = torch.tensor(reward, dtype=torch.float32)
        self.next_states[self.ptr] = torch.tensor(next_state, dtype=torch.float32)
        self.dones[self.ptr] = torch.tensor(done, dtype=torch.float32)
        self.ptr = (self.ptr + 1) % self.max_size
        self.size = min(self.size + 1, self.max_size)

    def sample(self, batch_size):
        idx = torch.randint(0, self.size, (batch_size,))
        return (
            self.states[idx],
            self.actions[idx],
            self.rewards[idx],
            self.next_states[idx],
            self.dones[idx],
        )

Diese Methode ist sehr effizient, da sie direkt in die Autograd- und Optimierungspipelines von PyTorch integriert ist. Zusammenfassend lässt sich also sagen, dass der Vergleich zwischen dem manuellen Ansatz und dem Tensor-Ansatz einfach zu implementieren ist und keine Abhängigkeit von Deep-Learning-Frameworks besteht. Die Nachteile sind hingegen die begrenzte Skalierbarkeit und die fehlende GPU-Beschleunigung. Die Vorteile des Tensor-basierten Ansatzes sind die reibungslose Integration von neuronalen Netzen, GPU-Beschleunigung und große Probleme, während die Nachteile eine gewisse Vertrautheit mit den komplexen Implementierungen von TensorFlow/PyTorch sind.

In der Regel sollte man daher bei der Wahl des Ansatzes den Umfang des Problems und die Verfügbarkeit der Hardware berücksichtigen, wobei tensorbasierte Methoden für große Probleme oder GPU-Training bevorzugt werden. Wenn Ihre Umgebung außerdem Zustände variabler Größe hat, wie bei Bildern, dann wäre die tensorbasierte Methode geeignet. Darüber hinaus kann SAC mit Prioritized Experience Replay (PER) erweitert werden, bei dem das Sampling des Wiedergabepuffers auf der relativen Bedeutung der einzelnen Zustände im Puffer basiert, indem der Fehler der zeitlichen Differenz oder andere Schlüsselmetriken gemessen werden. Die PER-Implementierung ist mit tensorbasierten Wiedergabepuffern einfacher, da sie effiziente Prioritätsaktualisierungen und Sampling ermöglicht.

Wie bei jeder Codeauflistung ist es immer eine gute Idee, vor dem Einsatz einige Tests und Debugging durchzuführen, und mit einem Wiedergabepuffer kann dies durch das Hinzufügen von Dummy-Daten und die Überprüfung, ob das Sampling korrekt funktioniert, realisiert werden. Darüber hinaus sollte sichergestellt werden, dass der Wiedergabepuffer auch Randfälle wie leere oder volle Puffer verarbeitet. Zur Validierung der Funktionalität können Python-Assertions oder Unit-Tests verwendet werden. Sobald der Wiedergabepuffer bereit ist, folgt die Integration in die SAC-Trainingsschleife, indem nach jedem Trainingsschritt Erfahrungen gespeichert werden und dann Ministapel für Aktualisierungen abgerufen werden.

Bei der Festlegung der Größe des Wiedergabepuffers wird oft nach einem Gleichgewicht gesucht, denn er sollte groß genug sein, um eine Vielzahl von Erfahrungen zu speichern, aber nicht so groß, dass er den Sampling-Prozess verlangsamt. Der Wiedergabepuffer kann auf Geschwindigkeit und Speicherplatz optimiert werden, indem effiziente Datenstrukturen wie PyTorch-Tensoren verwendet werden, unnötiges Kopieren von Daten vermieden wird und Speicherplatz für den Puffer vorab zugewiesen wird. Das Profiling des Wiedergabepuffers kann helfen, Leistungsengpässe zu erkennen und zu beheben.

Zusammenfassend lässt sich also sagen, dass ein gut implementierter SAC-Puffer für den Erfolg von SAC und vielen Off-Policy-Algorithmen unerlässlich ist. Es gewährleistet eine stabile und effiziente Ausbildung durch die Bereitstellung vielfältiger, unzusammenhängender Erfahrungen.

Critic Network

Bei den SAC-Algorithmen schätzt das Kritiker-Netz (Critic Network) den Q-Wert (oder den Wert der Zustandsaktion oder die nächste Aktion, die der Akteur ausführen soll), wenn ihm der aktuelle Zustand der Umgebung und die Wahl der nächsten Aktion des Akteurs vorgelegt werden. SAC setzt 2 solcher Kritiker-Netze ein, um Überschätzungsfehler zu reduzieren und die Lernstabilität zu verbessern. Da es sich um ein neuronales Netz handelt, das als Eingabe zwei geklammerte Datensätze der Wahrscheinlichkeitsverteilung von Aktionen und „Koordinaten“ von Umgebungszuständen des Akteurs-Netzes benötigt, hängt die Entscheidung, ob NumPy oder Tensors verwendet werden soll, von der Größe des Problems (definiert durch die Größe des Netzes und die Datenmenge, die für das Training verwendet werden soll) und auch von der Verfügbarkeit der Hardware ab.

Bei einer manuellen Nicht-Tensor-Implementierung von Kritiker-Netzen ist NumPy für Matrixoperationen und Gradientenaktualisierungen sehr nützlich. In Fällen, in denen die Netze weniger als 5 Schichten mit einer Größe von jeweils nicht mehr als 15 haben, oder zu Bildungs- und Veranschaulichungszwecken, könnte dies eine praktikable Lösung sein. Bei diesem Ansatz werden Vorwärts- und Rückwärtspropagation manuell implementiert, was bei der Skalierung auf große Trainingsdatensätze fehleranfällig und nicht so effizient sein kann. So könnte eine manuelle Python-Implementierung aussehen:

import numpy as np

class CriticNetwork:
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.hidden_dim = hidden_dim

        # Initialize weights and biases
        self.W1 = np.random.randn(state_dim + action_dim, hidden_dim)
        self.b1 = np.zeros(hidden_dim)
        self.W2 = np.random.randn(hidden_dim, hidden_dim)
        self.b2 = np.zeros(hidden_dim)
        self.W3 = np.random.randn(hidden_dim, 1)
        self.b3 = np.zeros(1)

    def forward(self, state, action):
        x = np.concatenate([state, action], axis=-1)
        x = np.maximum(0, x @ self.W1 + self.b1)  # ReLU activation
        x = np.maximum(0, x @ self.W2 + self.b2)  # ReLU activation
        q_value = x @ self.W3 + self.b3
        return q_value

    def update(self, states, actions, targets, learning_rate=1e-3):
        # Manual gradient descent (simplified)
        q_values = self.forward(states, actions)
        error = q_values - targets
        # Backpropagation and weight updates (not shown for brevity)

Wie bereits erwähnt, ist dieser Ansatz für große Netzwerke oder Datensätze nicht skalierbar und es fehlt die GPU-Beschleunigung. Wenn wir uns hingegen für die Verwendung von Tensoren entscheiden, können wir mit PyTorch die automatische Differenzierung und die GPU-Beschleunigung nutzen. Diese Eigenschaften sind ein gutes Vorzeichen für groß angelegte Probleme und Implementierungen auf Produktionsebene. Ein sehr einfaches Kodierungsbeispiel hierfür könnte wie folgt aussehen:

import torch
import torch.nn as nn
import torch.nn.functional as F

class CriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(CriticNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, 1)

    def forward(self, state, action):
        x = torch.cat([state, action], dim=-1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        q_value = self.fc3(x)
        return q_value

Insbesondere PyTorch enthält einige wichtige Bibliotheken, nämlich „torch.optim“ für die Netzwerkoptimierung und „torch.nn“ für die Einstellung der Netzwerkarchitektur. All dies wird mit einem hoch skalierbaren und effizienten Ansatz erreicht.

Ein manueller Ansatz ist zwar machbar, wie das obige Beispiel zeigt, und bietet die Vorteile der Einfachheit und der Unabhängigkeit von Deep-Learning-Frameworks, aber die mangelnde Skalierbarkeit und die fehlende Möglichkeit, GPUs richtig zu nutzen, sind ein Hindernis für die Akzeptanz.

Die Verwendung von Tensoren in Kritiker-Netzen hätte ähnliche Vor- und Nachteile wie der oben beschriebene Wiederholungspuffer, was im Großen und Ganzen bedeutet, dass der manuelle Ansatz oft in Situationen geeignet ist, in denen die zu lösenden Probleme sehr klein sind und es wichtig ist, die Feinheiten neuronaler Netze zu illustrieren oder zu „lehren“. In der Praxis sind Tensoren jedoch aus den bereits genannten Gründen praktischer.

SAC-Netze verwenden, wie wir uns erinnern, zwei Kritiker-Netze (oft als Q1 und Q2 bezeichnet), um Überschätzungsfehler abzuschwächen. Der Q-Zielwert wird daher als das Minimum der beiden von den Netzen erzeugten Q-Werte bestimmt. Zur Veranschaulichung: Die Kritiker-Netze erzeugen, wie ein Teil der Ausgabe des Akteurs-Netzes, einen Vektor mit geschätzten Belohnungen für jede der verfügbaren Aktionen.

Innerhalb eines solchen Vektors würde natürlich der Index/die Aktion mit dem höchsten Wert die höchste Belohnung vorhersagen. Der Hauptzweck der Kritiker-Netze besteht darin, den Gradienten für die Rückübertragung des Akteurs-Netzes konservativ zu bestimmen.

Während der Aktualisierung des Akteurs-Netzes wird der Gradient der Zielfunktion berechnet und ausgehend vom Minimum der beiden Q-Werte durch das Akteurs-Netz zurückvermittelt. Die minimale Auswahl stellt sicher, dass der Akteur so optimiert ist, dass er Handlungen wählt, die gegenüber den Überschätzungsfehlern der Kritiker robust sind.

Diese Kritiker-Netze, die den Gradienten für die Zielfunktion liefern, die das Akteurs-Netz aktualisiert, müssen ebenfalls trainiert werden. Da sie aber zukünftige Belohnungen aus Handlungen abschätzen, wie wird ihr Trainingsziel festgelegt? Die Antwort ist, dass SAC bei den kritischen Aktualisierungen nicht direkt das Minimum der beiden Q-Werte verwendet. Stattdessen wird für jeden Kritiker (Q1 und Q2) eine Aktualisierung unter Verwendung des aus der weichen Bellman-Gleichung abgeleiteten Ziels durchgeführt.

class DoubleCriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(DoubleCriticNetwork, self).__init__()
        self.Q1 = CriticNetwork(state_dim, action_dim, hidden_dim)
        self.Q2 = CriticNetwork(state_dim, action_dim, hidden_dim)

    def forward(self, state, action):
        q1 = self.Q1(state, action)
        q2 = self.Q2(state, action)
        return q1, q2

Darüber hinaus sind die Ziel-Netze in SAC ein weiterer separater Satz von Netzen (eines für jede Kritik Q1 und Q2), die zur Berechnung der Q-Zielwerte verwendet werden, die für die Rückverfolgung dieser Kritiknetze entscheidend sind. Sie selbst werden langsam durch Polyak-Mittelung aktualisiert, damit sie während des Trainings stabil bleiben. Die Verwendung von Ziel-Netzen ergibt sich aus der Notwendigkeit, ein stabiles Ziel für die Bellman-Gleichung zu liefern, ohne das, so wird argumentiert, die Q-Wert-Schätzungen der Kritiker-Netze aufgrund der Rückkopplungsschleife zwischen den Q-Werten und den Zielen divergieren oder oszillieren würden.

for target_param, param in zip(target_critic.parameters(), critic.parameters()):
    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
```
where `tau` is the polyak averaging coefficient (e.g., 0.005).

Die Verlustfunktion für die Kritiker wäre dann der mittlere quadratische Fehler (MSE) zwischen dem vorhergesagten Q-Wert und dem Ziel-Q-Wert, wie er durch die Bellman-Gleichung mit Hilfe der oben genannten Ziel-Netze ermittelt wurde.

target_q_value = reward + (1 - done) * gamma * min(Q1_target(next_state, next_action), Q2_target(next_state, next_action))
```
where `gamma` is the discount factor.

Um die Kritiker zu trainieren, wird also ein Mini-Batch aus dem Wiedergabepuffer entnommen und der Ziel-Q-Wert berechnet. Damit würden die Kritiker-Netze durch Gradientenabstieg aktualisiert werden. Ein Optimierer wie Adam kann verwendet werden, um das Training effizienter zu gestalten.

optimizer = torch.optim.Adam(critic.parameters(), lr=learning_rate)

Fehlersuche und Tests können durch Einspeisung von Dummy-Eingängen und Überprüfung der Ausgabeform und -werte durchgeführt werden. Es sollte sichergestellt werden, dass das Netz eine Überanpassung an einen kleinen Datensatz vornehmen kann. Wie bereits erwähnt, können Python-Assertions zur Validierung von Eingabedaten verwendet werden. Die Kritiker-Netze werden in die SAC-Trainingsschleife integriert, indem die Q-Werte berechnet, die kritischen Verluste aktualisiert und die Ziel-Netze synchronisiert werden. Es muss sichergestellt werden, dass das Kritiker-Netz zusammen mit den Akteurs- und Wert-Netzen aktualisiert wird, weshalb Tensors und insbesondere der Einsatz von GPUs hier eine große Rolle spielen.

Auch für die Kritiker-Netze könnten einige zusätzliche Optimierungstipps übernommen werden, darunter die Stapelnormalisierung oder die Schichtnormalisierung. Zweitens könnte das Experimentieren mit verschiedenen Aktivierungsfunktionen wie ReLU oder Leaky je nach den getesteten Daten und der Art des verwendeten Netzes unterschiedliche Ergebnisse liefern. Außerdem können Hyperparameter wie Lernrate und Netztiefe fein abgestimmt werden. Die Überwachung des Kritikverlustes während des Trainings ist wichtig, um Probleme wie Überanpassung und Instabilität zu erkennen.

Zusammenfassend lässt sich sagen, dass das Kritiker-Netz eine entscheidende Komponente der SAC ist, die für die Schätzung der Q-Werte und die Steuerung der Aktualisierung der Politik der Akteure von Bedeutung ist. Ein gut implementiertes Kritiker-Netz gewährleistet stabiles und effizientes Lernen.

Wert-Netze

Dieses Netzwerk, das auch als State-Value-Funktion bezeichnet wird, ist ein optionaler Teil von SAC, den wir wahlweise verwenden können. Ihr Zweck ist es, die erwartete kumulative Belohnung eines Zustands unter der aktuellen Politik mit Hilfe der Soft-Value-Funktion zu schätzen. Die Verwendung eines Wertenetzes ist zwar „fakultativ“, bringt aber bei richtiger Umsetzung eine Reihe von Vorteilen mit sich. Erstens ermutigt die Soft-Value-Funktion durch die explizite Berücksichtigung der Entropie die Politik zu einer effizienteren und effektiveren Erkundung. Die Aktion „Soft Value Function“ bietet tendenziell ein weicheres Ziel für das Training, was zur Stabilisierung des Lernprozesses beitragen kann.

Diese Stabilität ist sehr vorteilhaft, wenn man mit hochdimensionierten Eingabedaten konfrontiert ist (wenn der Eingabedatenvektor eine Größe von >10 hat) oder die Aktionsräume kontinuierlicher Natur sind (z.B. eine entgegengesetzte Aktionsoption (0.14, 0.67, 1.51) wie (Kaufen, Verkaufen, Halten)) oder wenn die Datenumgebungen mit mehreren lokalen Optima konfrontiert sind (ein Szenario, in dem viele verschiedene Netzwerkgewichtskonfigurationen gute Ergebnisse zu liefern scheinen, wenn jede Konfiguration auf separaten Datensätzen oder Umgebungen trainiert wird, aber keine dieser Gewichtskonfigurationen in der Lage ist, ihre Leistung auf breiteren Datensätzen zu verallgemeinern oder beizubehalten).

Zusammenfassend kann man sagen, dass Wert-Netze im SAC dazu dienen, den erwarteten Ertrag eines Zustands unabhängig von einer Aktion zu schätzen, was dazu beiträgt, die Varianz in den Q-Wert-Schätzungen zu verringern, indem ein weiches Ziel vorgegeben wird. Die Argumente für die Verwendung von Tensoren im Vergleich zu manuellen Verfahren sind denen sehr ähnlich, die oben für das Kritiker-Netz angeführt wurden. Die meisten modernen SAC-Netze implementieren das Wert-Netz nicht, sondern stützen sich stattdessen auf die zusätzlichen 2 Ziel-Netze, die bei der Festlegung der Trainingsziele für die 2 Kritiker-Netze helfen.

Neben der Verwendung eines einzelnen Wert-Netzes, um die Trainingsziele des Kritiker-Netzes zu moderieren, könnten wir auch 2 Wert-Netze verwenden. In diesem Szenario werden sowohl ein Wert-Netz als auch ein Zielwert-Netz verwendet, um die Wertfunktion zu schätzen, die den erwarteten Ertrag (kumulative Belohnung) aus einem bestimmten Zustand vorhersagt. Insbesondere das Zielwert-Netz wird zur Stabilisierung des Trainings verwendet, nicht nur in diesem Fall, sondern auch bei Deep-QN-Netzen. Da es eine Kopie des Wert-Netzes ist, wird es weniger häufig aktualisiert und bietet ein stabiles Ziel für das Training.

Akteurs-Netz

Dies ist das Hauptnetz, das auch als Politiknetz bezeichnet wird. Es nimmt als Eingabe Umgebungszustände und gibt zwei Vektoren, Mittelwert und Standardabweichung, aus, die als Parameter einer Wahrscheinlichkeitsverteilung über Aktionen dienen, die für stochastische Stichproben verwendet werden können. Die beiden Kritiker-Netze, die zugehörigen Ziel-Netze und das Wert-Netz, sofern es verwendet wird, dienen alle zur Unterstützung der Rückverfolgung und des Trainings dieses Netzes.

Da es sich um ein Netzwerk handelt, sollten wir von der Verwendung des Tensors erheblich profitieren, da er eine zentrale Rolle im SAC spielt. Da alle vorgenannten Netze mit dem Training dieses Netzes, des Akteurs-Netzes, verbunden sind, ist der Einsatz von GPUs zur Parallelisierung und zum gleichzeitigen Training dieser mehreren Netze etwas, das man erforschen sollte, da es viele Effizienzgewinne bringt.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist

class ActorNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(ActorNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_mean = nn.Linear(hidden_dim, action_dim)
        self.fc_log_std = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        mean = self.fc_mean(x)
        log_std = self.fc_log_std(x)
        return mean, log_std

    def sample_action(self, state):
        mean, log_std = self.forward(state)
        std = torch.exp(log_std)
        normal = dist.Normal(mean, std)
        action = normal.rsample()  # Reparameterization trick
        return torch.tanh(action), normal.log_prob(action).sum(dim=-1, keepdim=True)

Wie wir bereits im letzten SAC-Artikel festgestellt haben, gibt das Akteurs-Netz zwei Schlüsselvektoren der Daten aus: den Mittelwert und die Standardabweichung einer Gauß-Verteilung. Diese beiden werden zusammengefügt, um die nächste Aktion auf stochastische Weise zu bestimmen, was für die Exploration und Optimierung in kontinuierlichen Aktionsräumen wichtig ist. Der Mittelwert steht für das Zentrum der Aktionsstreuung oder -verteilung, während die Standardabweichung die Streuung oder Zufälligkeit der Verteilung kontrolliert. Diese beiden definieren eine Gaußsche Verteilung, aus der Aktionen ausgewählt werden können. Der folgende Python-Code hilft Ihnen dabei, dies zu erreichen.

import torch

def select_action(mean, log_std):
    """
    Given the SAC actor's output (mean and log_std), this function selects an action index.
    
    Args:
        mean (torch.Tensor): Mean of the action distribution, shape (n_actions,)
        log_std (torch.Tensor): Log standard deviation, shape (n_actions,)

    Returns:
        int: The index of the selected action.
    """
    std = log_std.exp()  # Convert log standard deviation back to standard deviation
    ....  
    return selected_index

# Example inputs
mean = torch.tensor([0.2, -0.5, 1.0, 0.3])  # Example mean values for 4 actions
log_std = torch.tensor([-1.0, -0.7, -0.2, -0.5])  # Example log std values

# Select action
action_index = select_action(mean, log_std)
print("Selected Action Index:", action_index)

In der Praxis müssten wir diese Funktion jedoch in MQL5 ausführen, da das Modell nach dem Training in Python als ONNX-Datei exportiert würde und als ONNX die Ausgaben bei jedem Vorwärtsdurchlauf ähnlich wären wie die, die beim Training in Python verwendet wurden. Da diese beiden Ausgänge in MQL5 empfangen würden, müsste diese Aktionsauswahlfunktion also auch in MQL5 sein.

Diese beiden Ausgaben definieren eine Gauß- oder Normalverteilung, aus der die Aktionen ausgewählt werden. Die Auswahl der Aktionen erfolgt stochastisch, um die Exploration zu fördern, sodass der Agent nicht immer die gleiche Aktion für einen bestimmten Zustand wählt. Beim der Rückwärtsdurchgang wird aus Gründen der Effizienz eine Neuparametrisierung vorgenommen, damit die Gradienten durch den Abtastprozess fließen können.

Da die meisten Aktionen in realen Anwendungen einen Umfang haben oder begrenzt sind, wendet SAC die Tanh-Funktion an, um die gesampelten Aktionen in den Bereich von -1 bis +1 zu bringen. Dadurch wird sichergestellt, dass die Aktion in einem überschaubaren Rahmen bleibt und der stochastische Charakter des Prozesses erhalten bleibt.

Agent

Der Agent in SAC, den wir hier als Agentenklasse in Python darstellen, kombiniert Politikoptimierung (Akteurs-Netz) mit der Wertfunktionsapproximation (die Paarung der 2 Kritiker-Netze das Wert-Netz und das Zielwert-Netz). Der Agent sollte sehr effizient sein und mit kontinuierlichen Aktionsräumen umgehen können. Denn nicht nur diese Netze, sondern auch der Wiedergabepuffer werden mit dem Ziel zusammengeführt, eine „optimale Politik“ oder geeignete Gewichte und Verzerrungen für das Akteurs-Netz zu lernen.

In Anbetracht der Tatsache, dass es sich um einen Agenten auf hohem Niveau handelt, versteht es sich vielleicht von selbst, dass Tensoren unerlässlich sind, wenn das Netztraining mit einer gewissen Effizienz durchgeführt werden soll. Nachfolgend finden Sie eine Python-Anleitung, die zeigt, wie dies erreicht werden kann:

import torch
import torch.nn.functional as F
import torch.optim as optim

class SACAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=256, replay_buffer_size=1e6, batch_size=256, gamma=0.99, tau=0.005, alpha=0.2):
        self.state_dim = state_dim
        ...

        self.alpha = alpha

        # Initialize networks and replay buffer
        self.actor = ActorNetwork(state_dim, action_dim, hidden_dim)
        ....

        self.value_optimizer = optim.Adam(self.value_network.parameters(), lr=3e-4)

    def select_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        action, _ = self.actor.sample_action(state)
        return action.detach().numpy()[0]

    def update(self):
        # Sample a batch from the replay buffer
        states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size)

        # Convert to tensors
        states = torch.FloatTensor(states)
        ...

        dones = torch.FloatTensor(dones).unsqueeze(1)

        # Update value network
        target_value = self.target_value_network(next_states)
        ...

        # Update critic networks
        q1_value = self.critic1(states, actions)
             
        ...

        self.critic2_optimizer.step()

        # Update actor network
        new_actions, log_probs = self.actor.sample_action(states)
             
        ...

        self.actor_optimizer.step()

        # Update target networks
        for target_param, param in zip(self.target_value_network.parameters(), self.value_network.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

Da wir mit PyTorch Tensoren verwenden, ist es wichtig zu betonen, dass die manuelle Zuweisung eines GPU-Gerätes, falls vorhanden, einen großen Beitrag dazu leistet, dass die Tensoren so effizient wie möglich laufen/ausgeführt werden.

Umgebung

Die Umgebung ist der Ort, an dem die Trainings- und Ziel-/Aktionsdatensätze definiert werden. Sie definiert im Wesentlichen das Problem, das der Agent zu lösen versucht, indem sie dem Agenten auf der Grundlage seiner Aktionen einen Zustand, eine Belohnung und ein Beendigungssignal liefert. Die Umgebung kann manuell implementiert werden (d.h. von 1. Prinzipien) oder durch Vererbung unter Verwendung von Bibliotheken wie OpenAI's Gym für standardisierte Umgebungen. Eine tensorbasierte Umgebung könnte wie folgt implementiert werden:

import torch

class TensorEnvironment:
    def __init__(self):
        self.state_space = 4  # Example: state dimension
        self.action_space = 2  # Example: action dimension
        self.state = torch.zeros(self.state_space)  # Initial state

    def reset(self):
        self.state = torch.randn(self.state_space)  # Reset to a random state
        return self.state

    def step(self, action):
        # Define transition dynamics and reward function
        next_state = self.state + action  # Simple transition
        ...

        self.state = next_state
        return next_state, reward, done, {}

    def render(self):
        print(f"State: {self.state}")

Man würde dann eine Schleife verwenden, um Erfahrungen zu sammeln und den Agenten in regelmäßigen Abständen zu aktualisieren:

for episode in range(num_episodes):
    state = env.reset()
    episode_reward = 0
    for step in range(max_steps):
        action = agent.select_action(state)
        next_state, reward, done, _ = env.step(action)
        agent.replay_buffer.add(state, action, reward, next_state, done)
        state = next_state
        episode_reward += reward
        if len(agent.replay_buffer) > batch_size:
            agent.update()
        if done:
            break
    print(f"Episode {episode}, Reward: {episode_reward}")

Erstellen mit dem Assistenten und die Tests

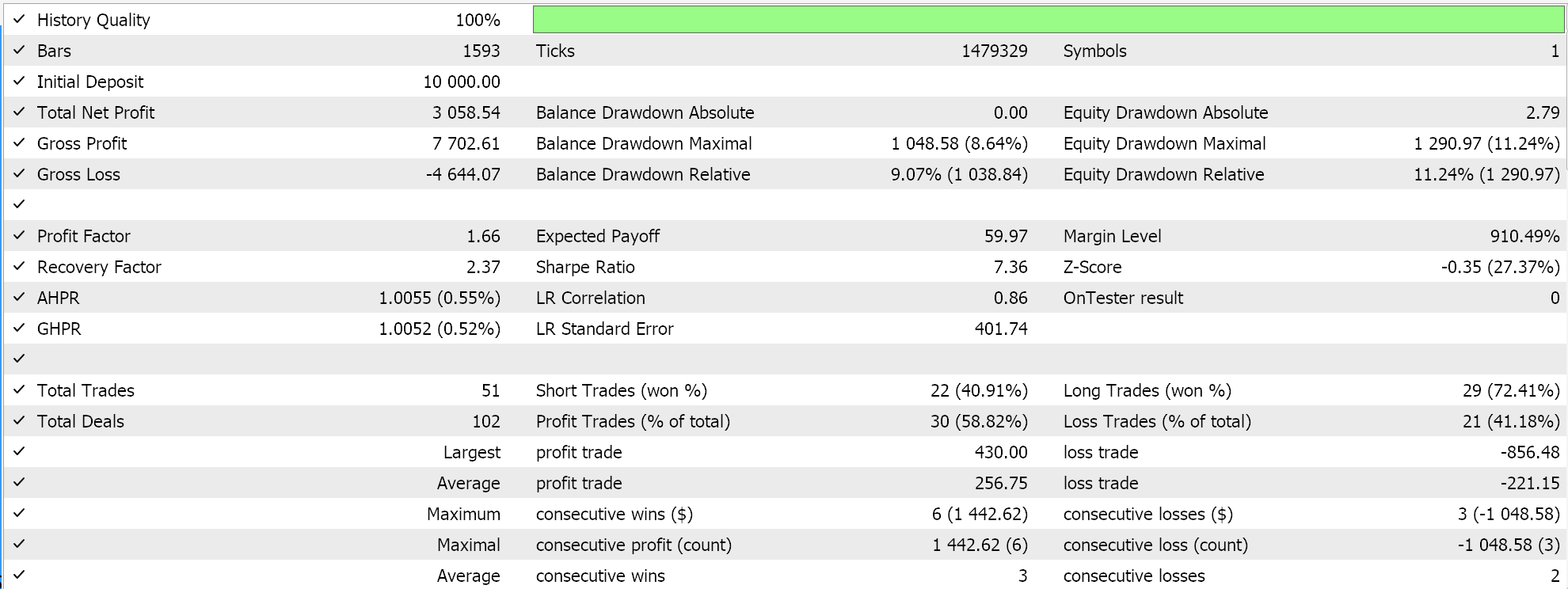
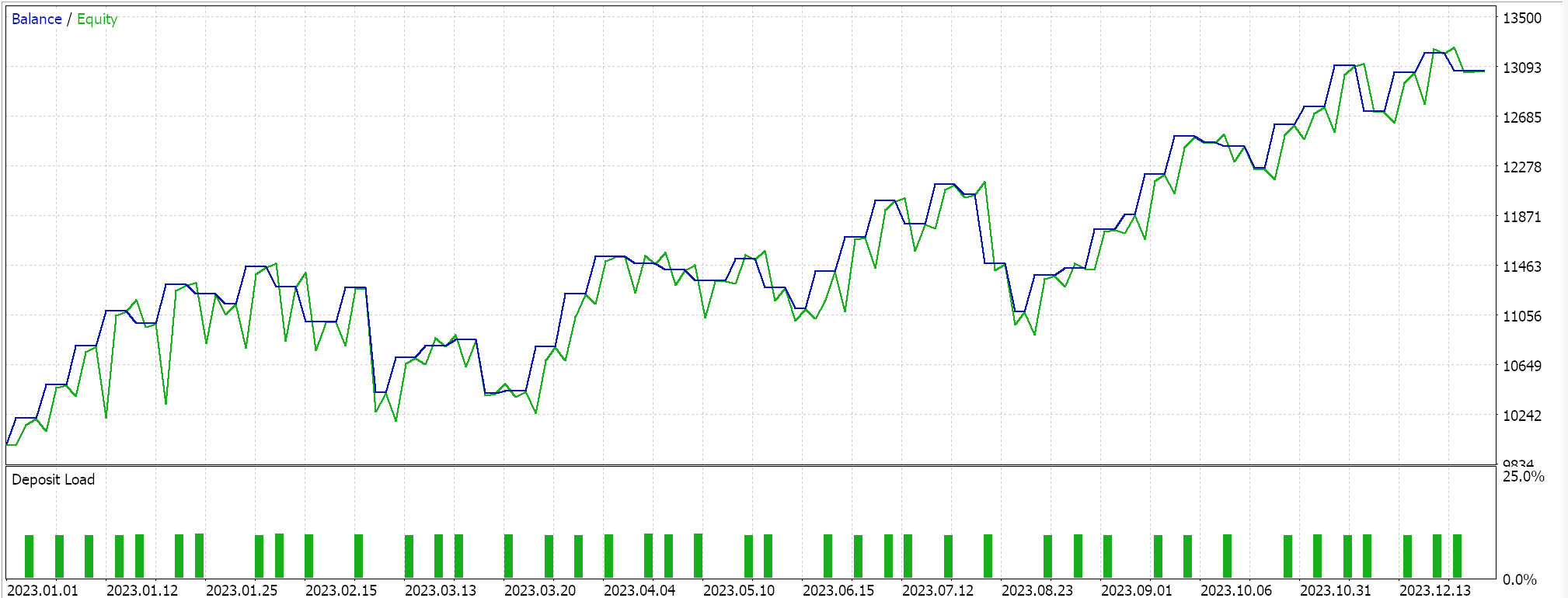
Wir testen unsere tensorbasierte hybride SAC, die neben einem Akteurs-Netz und 2 Kritiker-Netzen ein Wert-Netz und ein Zielwert-Netz anstelle der 2 Ziel-Netze (die die Kritiker trainieren) verwendet. Wir verwenden das EUR-USD-Paar auf dem 4-Stunden-Zeitrahmen für das Jahr 2023.

Sowohl TensorFlow als auch PyTorch erlauben nicht nur das Training von Modellen, sondern auch deren Kreuzvalidierung. TensorFlow erlaubt die Übergabe von validierten x- und y-Datenwerten an seine Fit-Funktion, während PyTorch im Wesentlichen das Gleiche erlaubt, indem es diese Daten an einen data_loader übergibt. Ein Testlauf in einem mit MQL5 kompilierten Expert Advisor, der keine Kreuzvalidierung (oder Inferenz) durchführt, liefert uns die folgenden Ergebnisse für EUR USD über 2023:

Wir verwenden, wie im letzten SAC-Artikel, ONNX, um das Modell aus Python zu exportieren und in MQL5 zu importieren. Wir haben es mit 5 neuronalen Netzen zu tun, von denen jedoch nur eines die von uns benötigten Vorhersagen macht, während die anderen 4 lediglich bei dem Rückwärtsdurchgang helfen. Das Netzwerk, das wir brauchen und exportieren, ist das Netzwerk der Akteure. Dieses Netz gibt jedoch, wie bereits erwähnt, nicht einen, sondern 2 Vektoren aus, den Mittelwert und die Standardabweichung. Bevor wir also das ONNX-Modell in MQL5 verwenden können, müssen wir die Ausgangsformen dieses Modells genau definieren. Die Eingabeform ist einfach. Wir stellen die Formen in MQL5 wie folgt ein:

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period != PERIOD_H4)
   {  Print(" time frame should be H4 ");
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _actor_in_shape[] = {1, __STATES};
   // Set output shapes
   const long _actor_out_shape[] = {1, __ACTIONS};
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 1, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

Dies wird in der Validierungsfunktion unserer nutzerdefinierten Signalklasse behandelt, da das ONNX-Modell nur läuft, wenn diese Formen genau definiert sind. Neue Leser finden hier und hier Anleitungen, wie man einen Expert Advisor aus einer nutzerdefinierten *.*mqh-Datei zusammenstellt.

Schlussfolgerung

Wir haben einen Soft Actor Critic Verstärkungslernalgorithmus in Python mit Hilfe von Tensoren implementiert. Tensoren sind beim maschinellen Lernen von entscheidender Bedeutung, da sie enorme Effizienzgewinne beim Training von Modellen ermöglichen, ein Aspekt, der insbesondere für Händler sehr wichtig ist. Die Größe der Trainingsdatensätze und die Notwendigkeit, komplexere Netze zu entwerfen, führen tendenziell zu langsameren Trainingsverfahren. Dieser Rückschlag wird daher nicht nur durch die Verwendung von Tensoren, sondern auch durch die Nutzung der Leistung von Grafikprozessoren behoben.

Name	Beschreibung
hybrid_sac.mq5	Der mit dem Assistenten erstellte Expert Advisormit einem Header, der die verwendeten Dateien anzeigt.
SignlWZ_54.mqh	NutzerdefinierteSignalklassendatei
model.onnx	ONNX-Netzwerkdatei