MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 34): Preiseinbettung mit einem unkonventionellen RBM

Einführung

Wir setzen diese Serie fort, in der wir verschiedene Handels-Setups und Ideen dank der schnellen Entwicklungs- und Prototyping-Umgebung von MetaTrade-5 mit dem MQL5-Assistenten untersuchen. In diesen Artikeln geht es im Prinzip darum, zu erforschen, wie sich andere Händler von der Masse abheben können, indem sie Ideen erkunden, die vielleicht nicht so üblich sind und dem interessierten Händler einen Vorteil verschaffen könnten, je nachdem, wie er sich entscheidet, sie zu nutzen. Der Grund, warum ein Vorteil so wichtig ist, liegt darin, dass viele der verfügbaren Handelsideen dazu neigen, zu positiv miteinander zu korrelieren.

Das ist super, wenn die Trends nach oben gehen und alle im grünen Bereich sind. Viele sind jedoch der Meinung, dass eine Diversifizierung die Drawdowns bei einer Trendumkehr abmildern würde, und dennoch ist es viel schwieriger, umgekehrt korrelierte Wertpapiere zu finden, als es auf dem Papier scheint. Aus diesem Grund können für einen Händler spezifische Ein- und Ausstiegsmöglichkeiten eine bessere Lösung sein, als sich einfach auf allgemein verwendete Setups zu verlassen. Dieser Artikel befasst sich mit den „Restricted Boltzmann-Maschinen“ (RBMs), wenn sie mit der „Backpropagation“ implementiert werden, im Gegensatz zu ihren traditionellen Implementierungen von „Gibbs Sampling“ und kontrastiver Divergenz.

Es wird argumentiert, dass der Grund für die Verwendung dieser Ansätze zunächst darin lag, dass Mitte der 80er Jahre (ca. 1986, als RBMs unter dem Namen Harmonium eingeführt wurden) die Rechenkosten für die Implementierung der Rückwärtspropagation in Boltzmann-Maschinen einfach nicht machbar waren. Boltzmann-Maschinen, von denen RBMs ihren Namen haben, sind noch komplexer, da sie nicht wie RBMs einen Bipartiter Graphen verwenden, sondern stattdessen Verbindungen zwischen den Neuronen innerhalb einer Schicht haben. Diese Verbindungskomplexität ist es, die selbst eine einfachere Implementierung von Boltzmann-Maschinen wie RBMs dazu veranlasst, sich bei der Feinabstimmung der Parameter (Gewichte und Verzerrungen) des Netzes auf energiebasierten Modellen (EBM) zu stützen, anstatt jeden Parameter einzeln zu verarbeiten, wie es bei anderen neuronalen Netzen und bei der Backpropagation üblich ist.

Gemäß Deep-AI:

Die kontrastive Divergenz befasst sich mit der rechnerischen Herausforderung, die sich aus der Partitionsfunktion in energiebasierten Modellen darstellt. Die wichtigste Erkenntnis hinter der kontrastiven Divergenz ist, dass es möglich ist, diese Modelle zu trainieren, ohne die vollständige Partitionsfunktion berechnen zu müssen. Stattdessen konzentriert sich die CD darauf, die Modellparameter so anzupassen, dass die Wahrscheinlichkeit der beobachteten Daten steigt, während die Wahrscheinlichkeit der vom Modell erzeugten Stichproben sinkt. 

Um dies zu erreichen, führt die kontrastive Divergenz ein Gibbs-Sampling-Verfahren durch, das von den Trainingsdaten ausgeht, um Stichproben zu erzeugen, die das Modell für wahrscheinlich hält. Anhand dieser Stichproben wird dann der Gradient der logarithmischen Wahrscheinlichkeit der Trainingsdaten in Bezug auf die Modellparameter geschätzt. Dieser Gradient wird verwendet, um die Parameter in einer Richtung zu aktualisieren, die die Darstellung der Daten durch das Modell verbessert.

Um also Berechnungen für jede Wahrscheinlichkeit zu vermeiden, waren Gibbs-Sampling und kontrastive Divergenz ein Segen, der eindeutig Sinn machte. Spulen wir in die heutige Zeit vor, und wenn wir vor demselben Problem stehen, kann Backpropagation sicherlich eine praktikable Option sein, insbesondere wenn man bedenkt, dass der Großteil der KI-Arbeitslast nicht mehr von CPUs getragen wird, sondern GPUs diese Aufgaben in erheblichem Umfang und in beschleunigtem Tempo übernehmen. Die Wahl der Hardware ist bei Boltzmann-Maschinen-ähnlichen Netzen (wie dem RBM) von entscheidender Bedeutung, denn obwohl sie nur zwei Schichten haben, sind diese Schichten in der Regel sehr tief, sodass die Anpassung der Gewichte der einzelnen Neuronen gut überlegt sein muss.

Was sind also RBMs angesichts der 2-Schichten-Grenze wirklich? Die kurze Antwort ist ein Klassifikator, der die Dimensionen seiner Eingabedaten reduziert, um verborgene Eigenschaften der Daten in weniger Dimensionen als die Eingabedaten aufzudecken. Dies ist eine stark vereinfachte Definition, denn eine sorgfältige Definition würde sagen, dass es sich um generative stochastische neuronale Netze handelt, die in einem unbeaufsichtigten Umfeld trainiert werden, um die Wahrscheinlichkeitsverteilung ihrer Eingabedaten zu lernen. Die Erkenntnisse aus den Eingabedaten, die in der verborgenen Schicht des Netzes gespeichert werden, können dann zur Klassifizierung, zum Clustering oder als Input für ein anderes Netz verwendet werden.

In diesem Artikel machen wir uns letzteres zunutze, indem wir die Werte unserer RBMs mit versteckter Schicht als Eingabe für ein Multi-Layer-Perceptron verwenden. Die Gesamtstruktur des Artikels folgt im Prinzip dem Format, an das wir uns in dieser Reihe gewöhnt haben.

Price-Embedding

Price-Embedding wird im Rahmen dieses Artikels als ein Prozess verwendet, der der Worteinbettung sehr ähnlich ist; und dies ist, wie einige Leser vielleicht wissen, der voraussetzende Schritt zu Transformator-Netzwerken großer Sprachmodelle. Die Worteinbettung, die als Nummerierung von Wörtern definiert werden kann, hilft in Verbindung mit der Selbstaufmerksamkeit dabei, einen Großteil des online verfügbaren schriftlichen Materials in ein Format umzuwandeln, das neuronale Netze verstehen können. Wir lehnen uns ebenfalls an diesen Ansatz an, indem wir davon ausgehen, dass die Daten der Wertpapierkurse (auch wenn sie numerisch sind) von neuronalen Netzen nicht ohne Weiteres „verstanden“ werden können. Und unser Ansatz, dies verständlicher zu machen, ist die Verwendung eines durch Backpropagation trainierten RBM.

Bei der Umwandlung von Wörtern in Zahlen geht es nicht einfach darum, einem Wort oder einem Buchstaben eine Zahl zuzuordnen, sondern es handelt sich um einen komplizierten Prozess, der, wie bereits erwähnt, Selbstaufmerksamkeit erfordert. Ich glaube, dass sich daraus Parallelen zu RBMs ziehen lassen, wenn man ihren zweiseitigen Graphenaufbau betrachtet.

Quelle

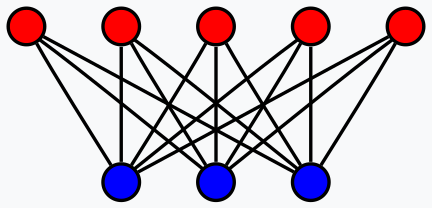
Zwar gibt es innerhalb einer Schicht eines RBM keine direkten Verbindungen von Neuron zu Neuron, doch werden diese Verbindungen, die für die Erfassung der Selbstaufmerksamkeitskomponente der Eingabedaten entscheidend sein könnten, über die verborgene Schicht hergestellt. Bei dieser These protokolliert die verborgene Schicht nicht nur, als was jedes Neuron gezeichnet werden könnte, sondern auch, welche Bedeutung seine Beziehungen zu den anderen Neuronen haben.

Wie immer gilt für Händler, dass der Beweis für die Vorteile dieser Preiseinbettung nur durch Handelsergebnisse erbracht werden kann. Und wir werden zum ersten Teil dieses Prozesses kommen, aber es könnte sich lohnen, hervorzuheben, dass das Ausmaß der Belohnungen, die man durch die Einbettung von Wörtern in Zahlen erhält, nicht mit denen verglichen werden kann, die wir bei der Einbettung von Zahlen in Zahlen betrachten, weil das, was wir hier tun, nicht annähernd so umwälzend ist. Betrachten wir nun, wie wir ein RBM mit Backpropagation rekonstruieren.

Restricted Boltzmann Machines (RBMs)

RBMs arbeiten in zwei Zyklen, die oft als positive und negative Phase bezeichnet werden. Wie bereits erwähnt, handelt es sich dabei häufig um unüberwachtes Lernen (obwohl auch einige überwachte Versionen implementiert wurden), was bedeutet, dass wir zu Beginn des Trainingsprozesses nicht wissen, wie die verborgenen Eigenschaften der einzelnen getesteten Datenpunkte aussehen sollten. Die Trainingsdaten haben keine Labels (oder Zielwerte).

RBMs behalten also die Punkte, indem sie die Werte der verborgenen Schicht rekonstruieren, damit sie mit den Werten der Eingabeschicht in der negativen Phase übereinstimmen. Es gibt also 2 Phasen, die positive Phase, die der Vorwärtspropagation eines normalen MLP ähnelt, liefert Werte an die versteckte Schicht. Diese Werte der verborgenen Schicht sind unser Ziel, da sie eine dimensional reduzierte Darstellung der Eingabedaten sind, die die gesuchten Eigenschaften erfasst.

Bei der Fortpflanzung in Richtung der verborgenen Schicht (der positiven Phase) wird eine Matrix von Gewichten verwendet, wie es in neuronalen Netzen der Fall ist; das Besondere an RBMs ist jedoch, dass in der negativen Phase dieselben Gewichte verwendet werden, um die Eingangsdaten zu rekonstruieren. Diese Rekonstruktion ist, wie bereits erwähnt, die Art und Weise, wie das RBM unbeaufsichtigt trainiert oder die Punktzahl beibehält, und da wir Backpropagation implementieren, dienen die Eingabedaten als De-facto-Etikett (oder Ziel) für sich selbst.

Ich behaupte, dass dies immer noch unüberwacht ist, weil keine zusätzlichen Daten außerhalb der Trainingsdaten des Inputs erforderlich sind, um dieses RBM zu trainieren. In Fällen, in denen ein überwachtes Training mit RBMs durchgeführt wurde, wurden Kennzeichnungen idealer Werte der versteckten Schicht verwendet, was wir hier nicht tun. Für den Anfang müssten wir also die typischen RBM-Funktionen der positiven und negativen Phase rekonstruieren. Dies ist wie folgt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetPositive(void)
{  vector _positive = weights[0].MatMul(inputs), _output;
   _positive += biases[0];
   _positive.Activation(_output, THIS.activation);
   output = _output;
}

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetNegative(void)
{  vector _negative = output.MatMul(weights[0]), _output;
   _negative += biases[1];
   _negative.Activation(_output, THIS.activation);
   label = _output;
}

Unsere MQL5-Klasse „C_u_rbm“ wird von einer anderen Klasse, von „Cmlp“, abgeleitet, die wir in den letzten Artikeln verwendet haben. Die Konstruktion von „C_u_rbm“ muss, obwohl sie von „Cmlp“ erbt, angepasst werden, um sicherzustellen, dass die entsprechende Anzahl von Schichten vorhanden ist und die relevanten Validierungsschritte abgedeckt sind. Die Klasse wird wie folgt konstruiert, wie in ihrer Schnittstelle angegeben:

#include <My\Cmlp-.mqh>
//+------------------------------------------------------------------+
//| Unconventional RBM that uses:                                    |
//| reconstruction-error instead of free-energy                      |
//| and back-propagation instead of contrastive divergence           |
//+------------------------------------------------------------------+
class C_u_rbm : public Cmlp
{
protected:

public:
   void              GetPositive();
   void              GetNegative();
   
   void              BackPropagate(double LearningRate = 0.1);

   double            Get(ENUM_REGRESSION_METRIC R)
   {                 return(label.RegressionMetric(inputs, R));
   }

   void              C_u_rbm(Smlp &MLP) : Cmlp(MLP)
   {  validated = false;
      int _layers =    ArraySize(MLP.arch);
      if(_layers == 2 && MLP.arch[0] > MLP.arch[1])
      {  ArrayResize(biases, _layers);
         //
         ArrayResize(gradients, _layers);
         ArrayResize(gradients_1st_moment, _layers);
         ArrayResize(gradients_2nd_moment, _layers);
         ArrayResize(sum_gradients, _layers);
         ArrayResize(sum_gradients_update, _layers);
         //
         ArrayResize(deltas, _layers);
         ArrayResize(deltas_1st_moment, _layers);
         ArrayResize(deltas_2nd_moment, _layers);
         ArrayResize(sum_deltas, _layers);
         ArrayResize(sum_deltas_update, _layers);
         //
         hidden_layers = 0;
         bool _norm_validated = true;
         for(int i = 0; i < _layers; i++)
         {  int _rows = MLP.arch[_layers - 1 - i], _columns = MLP.arch[i];
            //
            biases[i].Init(_rows);
            biases[i].Fill(MLP.initial_bias);
            //
            gradients[i].Init(_rows, _columns);
            gradients[i].Fill(0.0);
            //
            gradients_1st_moment[i].Init(_rows, _columns);
            gradients_1st_moment[i].Fill(0.0);
            gradients_2nd_moment[i].Init(_rows, _columns);
            gradients_2nd_moment[i].Fill(0.0);
            //
            sum_gradients[i].Init(_rows, _columns);
            sum_gradients[i].Fill(0.0);
            sum_gradients_update[i].Init(_rows, _columns);
            sum_gradients_update[i].Fill(0.0);
            //
            deltas[i].Init(_rows);
            deltas[i].Fill(0.0);
            deltas_1st_moment[i].Init(_rows);
            deltas_1st_moment[i].Fill(0.0);
            deltas_2nd_moment[i].Init(_rows);
            deltas_2nd_moment[i].Fill(0.0);
            sum_deltas[i].Init(_rows);
            sum_deltas[i].Fill(0.0);
            sum_deltas_update[i].Init(_rows);
            sum_deltas_update[i].Fill(0.0);
         }
         validated = true;
      }
      else
      {  printf(__FUNCSIG__ +
                " invalid network arch! Settings size is: %i, Max layer size is: %i, Min layer size is: %i, and activation is %s ",
                _layers, MLP.arch[ArrayMaximum(MLP.arch)], MLP.arch[ArrayMinimum(MLP.arch)], EnumToString(MLP.activation)
               );
      }
   };
   void              ~C_u_rbm(void) { };
};

Bei der Anpassung des Konstruktors für unsere Klasse haben wir das Matrix-Array für die Gewichte weggelassen, da seine Größe immer der Gesamtzahl der Schichten minus eins entspricht, und das ist hier der Fall. Der Konstruktor befasste sich daher mit den Unterschieden: Erstens haben wir zwei Bias-Vektoren, obwohl es nur zwei Schichten sind. Das bedeutet, dass wir auch zwei Delta-Vektoren haben werden, einen für jeden Bias-Vektor. Eine weitere notwendige Anpassung betrifft die Anzahl der Gradientenmatrizen. Obwohl wir nur eine Gewichtungsmatrix haben, haben wir zwei Gradientenmatrizen, weil unsere Backpropagation für die beiden Testzyklen gilt: die positive und die negative Phase.

Dies bedeutet auch, dass unsere einzelne Matrix von Gewichten in jeder Backpropagation zweimal aktualisiert wird. Wie immer werden bei der Backpropagation zunächst die Deltas, dann die Gradienten berechnet und anschließend die Gewichte und Verzerrungen mit diesen Werten aktualisiert. Wir führen unsere Backpropagation wie folgt durch:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::BackPropagate(double LearningRate = 0.1)
{  
//COMPUTE DELTAS
   vector _loss = label.LossGradient(inputs, THIS.loss);
   //
   vector _negative = output.MatMul(weights[0]), _negative_derivative;
   _negative.Derivative(_negative_derivative, THIS.activation);
   deltas[1] = Hadamard(_loss, _negative_derivative);
   //
   vector _positive = weights[0].MatMul(inputs), _positive_derivative;
   _positive.Derivative(_positive_derivative, THIS.activation);
   matrix _weights;
   _weights.Copy(weights[0]);
   _weights.Transpose();
   vector _product = _weights.MatMul(deltas[1]);
   deltas[0] = Hadamard(_product, _positive_derivative);
//COMPUTE GRADIENTS
   gradients[0] = TransposeCol(deltas[0]).MatMul(TransposeRow(inputs));
   gradients[1] = TransposeCol(deltas[1]).MatMul(TransposeRow(output));
   
// UPDATE WEIGHTS AND BIASES
   for(int h = 1; h >= 0;  h--)
   {  matrix _gradients;
      _gradients.Copy(gradients[h]);
      if(h == 1)
      {  _gradients = _gradients.Transpose();
      }
      weights[0] -= LearningRate * _gradients;
      biases[h] -= LearningRate * deltas[h];
   }
}

Diese Funktion fasst also unsere Klasse zusammen, die von „Cmlp“ erbt, wobei alle nicht überschriebenen Funktionen der Basisklasse weiterhin wirksam sind. Zur Klärung der Frage, warum wir zwei Bias-Vektoren, zwei Delta-Vektoren, zwei Gradientenmatrizen und nur eine einzige Gewichtsmatrix haben, sei gesagt, dass wir in der positiven Phase zum ersten Mal auf die Gewichtsmatrix stoßen und das Produkt daraus zum ersten Bias-Vektor addiert werden muss. Dieses Produkt impliziert auch, dass eine Gradientenmatrix erfasst werden muss, um die Gewichte über dieses Produkt korrekt zu aktualisieren. In der zweiten Phase wird derselbe Prozess wiederholt, mit dem entscheidenden Unterschied, dass wir, wie bereits erwähnt, die gleichen Gewichte der positiven Phase verwenden.

Obwohl dieselben Gewichte verwendet werden, wird dem Produkt der zweiten Phase ein neuer (anderer) Verzerrungsvektor hinzugefügt, der unsere Rekonstruktion der Eingabedaten ergibt. Die Differenz zwischen diesen rekonstruierten Daten und den ursprünglichen Eingabedaten definiert dann unsere Deltas, die in die Backpropagation einfließen.

RBM in der nutzerdefinierten Signalklasse

Um die nutzerdefinierte Signalklasse zu erstellen, müssen wir unsere oben erstellte nutzerdefinierte RBM-Klasse in einer neuen Instanz einer nutzerdefinierten Signalklasse referenzieren, die wir über den MQL5-Assistenten zu einem Expert Advisor zusammenstellen. Es gibt hier und hier Anleitungen für Leser, die neu in diesem Bereich sind. Und wenn wir es einmal referenziert und eingerichtet haben, haben wir nur die Hälfte unseres Handelssystems, denn wie in der Einleitung erwähnt, dienen die Werte der versteckten Schicht des RBM als Eingabe für ein anderes neuronales Netz in Form eines mehrschichtigen Perzeptrons (MLP). Die Funktion des RBM besteht darin, Preisänderungen einzubetten, um ihre Entsprechung in einer kleineren Dimension zu entlarven. Für unsere Tests ist unser RBM ein 8-4-Netz, wobei die Zahlen die Größe der sichtbaren und der verborgenen Schicht darstellen. Die RBM-Aufgabe geht meiner Meinung nach mehr in Richtung Klassifizierung als in Richtung Regression, und daher werden die Verlustfunktion und die Aktivierung kategoriale Kreuzentropie und Soft-Sign sein. Diese können noch optimiert werden, um als Klassifikatoren zu funktionieren, wie wir in den letzten Artikeln beschrieben haben, aber wir verwenden diese Einstellungen als Konstanten und sie sind nicht optimierbar.

Die vom RBM ausgeführten Funktionen sind, wie bereits erwähnt, eher auf die Einbettung ausgerichtet, weshalb die Funktion, die in unserer nutzerdefinierten Signalklasse dafür verantwortlich ist, den Namen „Embedder“ trägt. Der Quellcode ist weiter unten zu finden:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalEmbedding::Embedder(vector &Extraction)
{  m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  U_RBM.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old, _out, _out_new, _out_old;
         if
         (
         _in_new.Init(__RBM_VISIBLE) && 
         _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __RBM_VISIBLE) && 
         _in_new.Size() == __RBM_VISIBLE &&
         _in_old.Init(__RBM_VISIBLE) && 
         _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS + 1, __RBM_VISIBLE) && 
         _in_old.Size() == __RBM_VISIBLE
         &&
         _out_new.Init(__MLP_OUTPUTS) &&
         _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_OUTPUTS) &&
         _out_new.Size() == __MLP_OUTPUTS &&
         _out_old.Init(__MLP_OUTPUTS) &&
         _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __MLP_OUTPUTS) &&
         _out_old.Size() == __MLP_OUTPUTS
         )
         {  _in = _in_new - _in_old;
            _out = _out_new - _out_old;
            U_RBM.Set(_in);
            U_RBM.GetPositive();
            U_RBM.GetNegative();
            U_RBM.BackPropagate(m_learning.rate);
            Extraction = Extractor(U_RBM.output, _out, ii > 0);
         }
      }
   }
}

Unsere Datenaufbereitung ist derjenigen in früheren Artikeln sehr ähnlich. Bei den meisten Expert Advisors, die manuell und nicht über den MQL5-Assistenten kodiert werden, müssen zusätzliche Schritte unternommen werden, um sicherzustellen, dass die vom Expert Advisor abgefragten Kursdaten tatsächlich auf dem Server des Brokers verfügbar sind, bevor die Signalberechnungen durchgeführt werden. Wenn ein Assistent den Expert Advisor zusammenstellt, kann dies normalerweise übersprungen werden. In unserem Fall verwenden wir jedoch einfach die if-Klausel, um sicherzustellen, dass die gesuchten Daten tatsächlich in die vorgesehenen Vektoren kopiert werden.

Beim Kopieren von Daten in Vektoren ist auch zu beachten, dass die Daten nicht als Reihe sortiert sind, d. h. der höchste Index im kopierten Vektor hat den neuesten Wert. Hier finden Sie weitere Informationen zu diesem Thema. Da wir eine Kettenanordnung haben, bei der das RBM den Input für das MLP liefert, haben wir uns dafür entschieden, die beiden Netze fast gleichzeitig zu trainieren, wobei wir an jedem Punkt der Trainingsmenge des RBM das RBM trainieren und anschließend auch das MLP trainieren. Dies ist etwas anderes, als wenn man zuerst das Training des RBMs ausschöpft, bevor man den MLP trainiert.

Diese Anordnung kann sicherlich vom Leser geändert werden, da der vollständige Quelltext unten beigefügt ist. Wir haben sie jedoch übernommen, weil sie angesichts der Notwendigkeit, zwei Netze zu trainieren, für unsere Testzwecke effizienter sein könnte. Da wir fast gleichzeitig trainieren, müssen wir die RBM-Eingabe und die MLP-Beschriftungen gleichzeitig erhalten, weshalb unsere if-Klauseln sehr lang sind.

Integration des RBM mit einem MLP

Durch den Trainingsprozess aktualisieren wir also die RBM-Gewichte, was es uns ermöglicht, mehr Eingabedaten zu verarbeiten und ihre versteckten Werte (auch Wahrscheinlichkeitsverteilung genannt) zu erhalten. Diese Wahrscheinlichkeitsverteilung, die wir als Preiseinbettung bezeichnen, wird dann in die MLP eingespeist, und nicht die rohen vorherigen Preisänderungen. Die Verwendung dieser Einbettung erfolgt in der Funktion „Extractor“, die einfach die vom RBM gelieferte Preiseinbettung durch den MLP weiterleitet. Bei der Einspeisung wird auch das MLP trainiert, wenn ein Label (Zielwert) angegeben wird. Da das Training bis zu den letzten Preisänderungen durchgeführt wird, für die es keine Kennzeichnung gibt, müssen wir dies im Auge behalten. Der Tracker ist der dritte Eingabeparameter in der Funktion „Extractor“, die den booleschen Wert „Train“ hat. Standardmäßig ist sie wahr, aber sobald wir das Ende des Trainingssatzes erreichen und keine Kennzeichnung haben, wird sie als falsch eingestuft. Der Code für die Funktion „Extractor“ ist unten angegeben:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CSignalEmbedding::Extractor(vector &Embedding, vector &Labels, bool Train = true)
{  vector _extraction;
   _extraction.Init(MLP.output.Size());
   m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  MLP.LearningType(m_learning, i);
      MLP.Set(Embedding);
      MLP.Forward();
      _extraction = MLP.output;
      if(Train)
      {  MLP.Get(Labels);
         MLP.Backward(m_learning, i);
      }
   }
   return(_extraction);
}

Es gibt einen Vektor zurück, den wir „_extraction“ nennen, aber in unserem Fall sind wir nur an einem Wert interessiert, der nächsten Preisänderung, also ist es wirklich ein einseitiger Vektor. Während das RBM durch seine Aktivierungsfunktion und Verlustfunktion wie ein Klassifikator strukturiert ist, sollte der MLP wahrscheinlich besser funktionieren, wenn er wie ein Regressor strukturiert ist. Der Grund dafür ist die einmalige gleitende Datenausgabe, die negativ sein kann. Als Regressor verwenden wir die Soft-Sign-Aktivierung und die Verlustfunktion ist Huber. Die Gründe dafür, wenn es um Regressor-Netzwerke geht, wurden in kürzlich erschienenen Artikeln behandelt, z. B. hier, sodass neue Leser einen Blick darauf werfen können.

Sowohl das RBM als auch das MLP sind nicht richtig auf optimale Leistung abgestimmt, da sie beispielsweise identische Anfangsgewichte und Vorspannungen verwenden und das Training gleichzeitig stattfindet, was bedeutet, dass beide Netze in einer Sitzung trainiert werden. Eine Alternative dazu sind unterschiedlich große Trainingseinheiten für RBM und MLP, wobei das MLP-Training erst nach Abschluss des RBM-Trainings durchgeführt wird. Darüber hinaus ist die Lernrate für beide Netze festgelegt, und verschiedene Formate, die adaptives Lernen beinhalten, wurden nicht genutzt. Viele dieser zusätzlichen Anpassungen und mehr bleiben dem Leser überlassen, um sie zu überprüfen.

Backtests und Optimierung

Wir führen eine Optimierung für das Jahr 2023 für das Paar GBPUSD auf dem täglichen Zeitrahmen durch und suchen dabei nach den idealen anfänglichen Netzwerkgewichten und Verzerrungen. Es sei daran erinnert, dass wir für diese beiden Werte einen einzigen Eingabeparameter für die beiden Netze haben, was nicht unbedingt ideal ist. Darüber hinaus suchen wir die Eröffnungs- und Schlussschwellen für die Funktionen „LongCondition“ und „ShortCondition“ unserer nutzerdefinierten Signalklasse sowie ein Take-Profit-Niveau in Punkten. Wir führen einige nicht erschöpfende Durchläufe durch, die zu folgenden Ergebnissen führen:

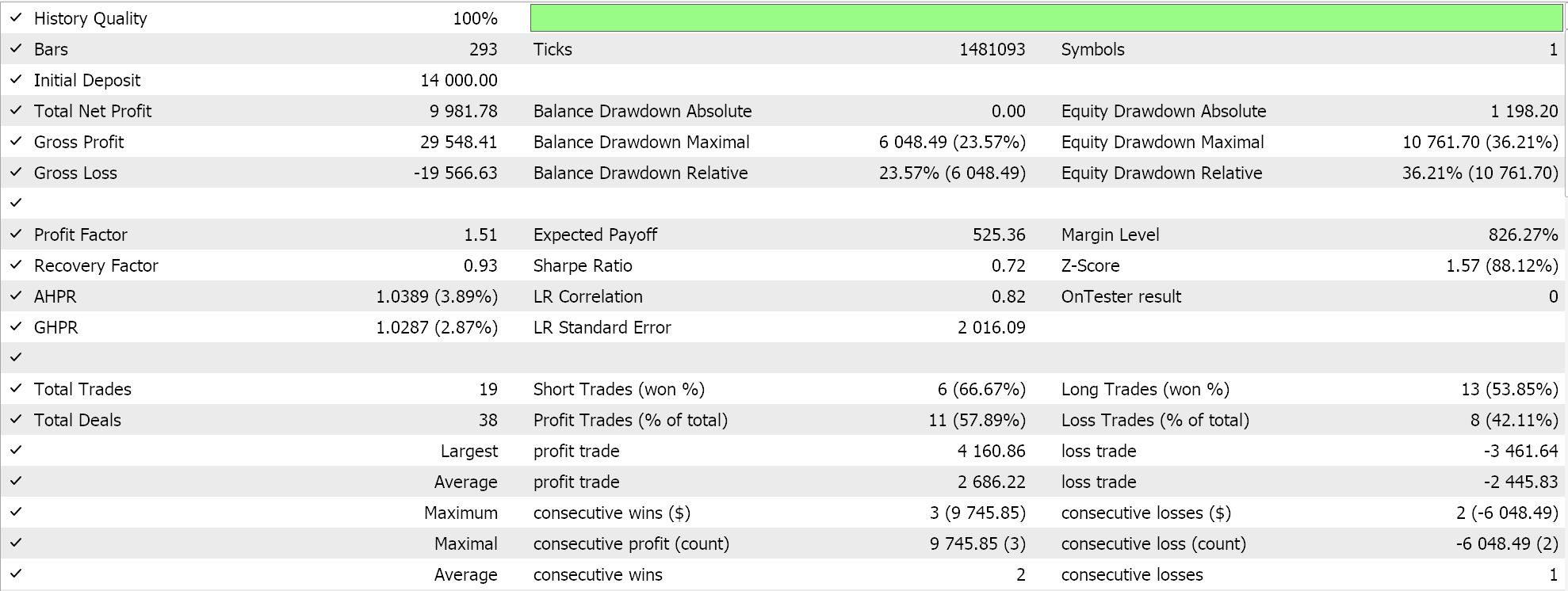
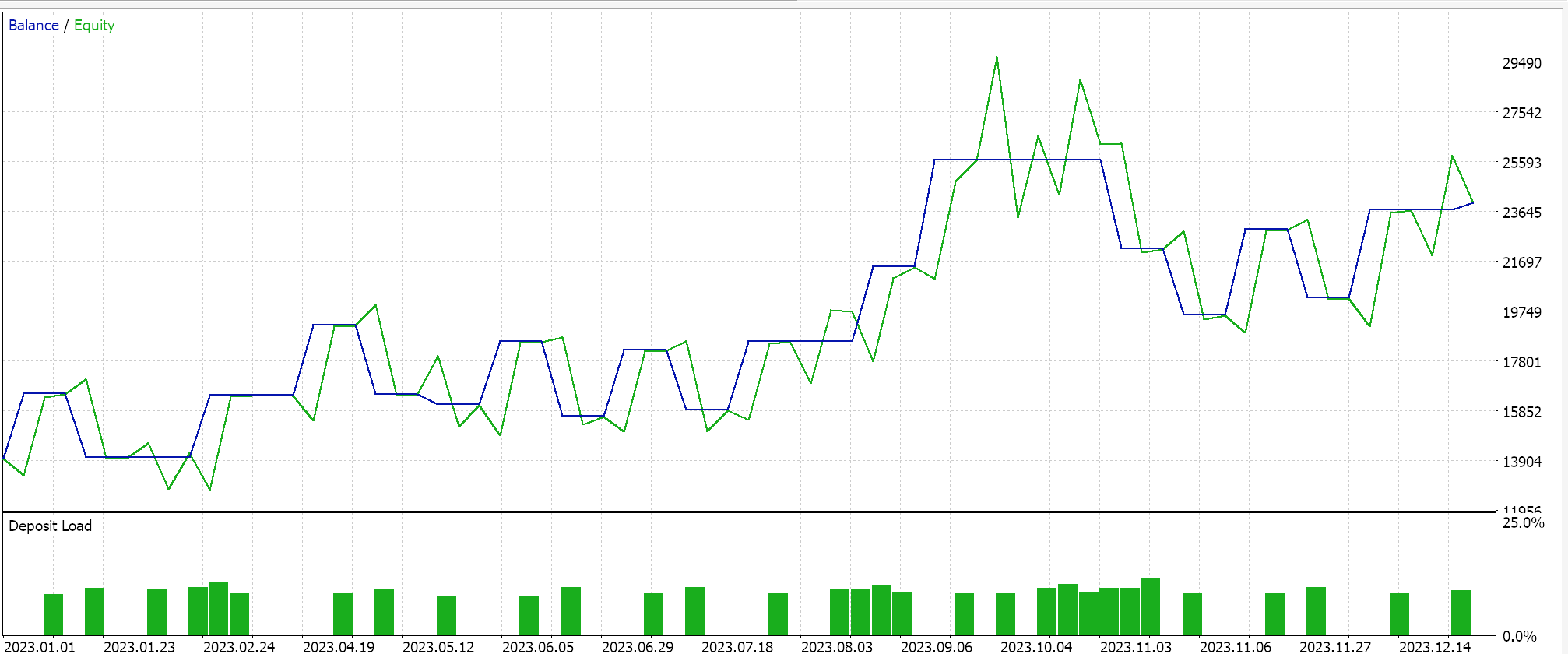
Unser von einem Assistenten zusammengestellter Expert Advisor ist handelbar, aber wie immer ist mehr Sorgfalt erforderlich, was das Testen über längere Zeiträume und das Nachverfolgen von Optimierungen mit Forward Walk Tests angeht. Erwähnenswert ist auch, dass es sich um ein Signal handelt, das auf einem neuronalen Netz basiert, und dass der Nutzer die Aufzeichnung und Speicherung der Gewichte und Verzerrungen des Netzes (hier gibt es zwei) immer einplanen sollte.

Schlussfolgerung

Wir haben ein RBM als Preiseinbettung für eine MLP mit ihren optimierten Handelsergebnissen über ein einziges Jahr zur Verfügung gestellt, aber wie könnte man die Wirksamkeit der „Preiseinbettung“ in dem Kontext beurteilen, in dem sie in diesem Artikel verwendet wird? Nun, die kurze Antwort ist, wenn wir ein anderes reines MLP-Signal haben, das als Input die rohen vorherigen Preisänderungen nimmt und ebenfalls wie das MLP dieses Artikels trainiert wird, um die nächste Preisänderung zu projizieren. Die Einrichtung ist auch deshalb relativ einfach, weil die Ankerklassen für die MLP denen ähnlich sind, die wir bisher verwendet haben, sodass vergleichbare Ergebnisse leicht zu erzielen sind.

Wir haben auch ein RBM gekoppelt, das in eine MLP einfließt und nicht umgekehrt. Dies ist meines Erachtens ein besserer Weg für die Zusammenarbeit dieser beiden Arten von neuronalen Netzen (ein Klassifikator und ein Regressor). Regressoren geben oft, aber nicht immer, einen einzigen Gleitkommawert aus (der negativ sein kann), und durch die Aufnahme von „klassifizierten“ Eingaben könnte diese Paarung gerechtfertigt sein. In Zukunft kann diese Anordnung erweitert werden, und zwar nicht durch Stapeln der RBMs, da diese die Tiefe ausnutzen, sondern indem sie parallel als Eingänge zu transformatorgesteuerten Regressornetzen geschaltet werden. Die Klassifikatoren mit ihrer Tiefe sind meines Erachtens besser für eine „Spezialisierung“ geeignet als Regressornetzwerke.

Abschließend sei darauf hingewiesen, dass wir uns darauf beschränkt haben, Preisänderungen als „Preiseinbettung“ zu klassifizieren. Es können jedoch auch andere Finanzdaten und Zeitreihen in Betracht gezogen werden, wenn es um die „Preiseinbettung“ von Daten in eine MLP geht. Dazu können Kerzen-Kursmuster, Kursindikatorwerte, Wirtschaftsnachrichten usw. gehören. Wie nicht anders zu erwarten, variieren die Leistung und die Testergebnisse für jedes dieser Produkte erheblich, sodass es dem Leser überlassen bleibt, dasjenige zu finden und anzupassen, das am besten zu seinen Vorstellungen von den Märkten passt.