Klassische Strategien neu interpretieren (Teil VII) : Devisenmärkte und die Analyse der Staatsverschuldung bezogen auf USDJPY

Künstliche Intelligenz birgt das Potenzial, neue Handelsstrategien für den modernen Anleger zu entwickeln. Es ist unwahrscheinlich, dass ein einzelner Anleger genügend Zeit hat, jede mögliche Strategie sorgfältig zu prüfen, bevor er sich für eine entscheidet, der er sein Kapital anvertraut. In dieser Artikelserie möchten wir Ihnen die Informationen an die Hand geben, die Sie benötigen, um eine fundierte Entscheidung darüber zu treffen, welche Strategie am besten zu Ihrem speziellen Anlegerprofil passt.

Zusammenfassung der Handelsstrategie

Festverzinsliche Wertpapiere sind Anlagen, mit denen Anleger ihre Portfolios sicher diversifizieren können. Sie sind eine Klasse von Anlagen, die bis zur Fälligkeit einen festen oder variablen Zinssatz zahlen. Bei Fälligkeit wird das Kapital des Anlegers zurückgezahlt, und es werden keine weiteren Zahlungen an den Anleger geleistet. Es gibt viele verschiedene Arten von festverzinslichen Wertpapieren, wie z. B. Anleihen und Einlagenzertifikate.

Anleihen gehören zu den beliebtesten Formen von festverzinslichen Wertpapieren und werden im Mittelpunkt unserer Diskussion stehen. Die Anleihen können von einer Gesellschaft oder einer Regierung ausgegeben werden. Vor allem Staatsanleihen gehören zu den sichersten Anlagen der Welt. Wenn ein Anleger eine bestimmte Staatsanleihe kaufen möchte, muss er dies in der Währung des ausgebenden Staates tun. Wenn eine bestimmte Staatsanleihe international sehr gefragt ist, wird jeder Anleger, der die Anleihe erwerben möchte, zunächst seine Landeswährung in die gewünschte Währung umtauschen. Dies kann wiederum die Vorstellungen des Marktes über eine faire Bewertung des Wechselkurses der beiden Währungen verändern. 

Wie gut sich eine Anleihe entwickelt, wird an der Rendite der Anleihe gemessen. Es besteht ein umgekehrtes Verhältnis zwischen der Rendite einer Anleihe und der Nachfrage nach dieser Anleihe. Mit anderen Worten: Wenn die Nachfrage nach einer bestimmten Anleihe sinkt, steigt die Rendite der Anleihe, um die Nachfrage nach der Anleihe zu erhöhen. Einige erfolgreiche Händler an den Devisenmärkten beziehen diese fundamentale Analyse in ihre Handelsstrategie ein. Durch den Vergleich der Renditen von mittelfristigen Staatsanleihen der beiden Länder zu einem beliebigen Wechselkurs können Devisenhändler einen Eindruck von der wirtschaftlichen Lage der beiden Länder gewinnen.

In der Regel wird die Anleihe, die den Anlegern höhere Zinssätze bietet, beliebter sein, und entsprechend der Strategie wird auch die Währung des Emissionslandes im Laufe der Zeit an Wert gewinnen, während die Währung des Landes, das Anleihen mit niedrigeren Zinssätzen ausgibt, im Laufe der Zeit an Wert verliert. 

Zusammenfassung der Methodik

Um die Strategie zu bewerten, trainieren wir verschiedene Modelle, um den Schlusskurs des USDJPY-Wechselkurses vorherzusagen. Wir verwenden 3 Sätze von Prädiktoren für die Modelle:

1. Die normalen Daten von Open, High, Low, Close und Tick Volume (OHLCV), die vom USDJPY Markt geholt werden.
2. Die OHLCV-Daten der 10-jährigen, japanischen Staatsanleihe und der 10-jährigen, amerikanischen Staatsanleihe (Treasury Note).
3. Ein tolles Setup mit den ersten beiden.

Unser Ziel ist es, herauszufinden, welcher Satz von Prädiktoren ein Modell mit dem niedrigsten RMSE bei ungesehenen Daten ergeben würde. Obwohl die Korrelationsniveaus zwischen den historischen Kursen der Anleihen und dem USDJPY mit -0,85 für beide Staatsanleihen signifikant hoch sind, wurde die niedrigste Testfehlerrate von Modellen erzielt, die mit dem ersten Satz von Prädiktoren trainiert wurden.

Das beste Modell war das Modell der linearen Regression (LR). Sie hat jedoch keine Parameter, die wir einstellen können. Daher haben wir uns für den Linear Support Vector Regressor (LSVR) als Lösungsvorschlag entschieden. Wir haben das LSVR-Modell erfolgreich auf die Hyperparameter abgestimmt, ohne dass es zu einer Überanpassung der Trainingsmenge kam. Darüber hinaus konnte unser maßgeschneidertes LSVR-Modell die Benchmark-Leistung des einfacheren LR-Modells bei Validierungsdaten übertreffen. Die Modelle wurden mit Hilfe von Zeitreihen-Kreuzvalidierung ohne zufälliges Mischen trainiert und verglichen.

Nachdem wir unser Modell erfolgreich abgestimmt hatten, exportierten wir es in das ONNX-Format und integrierten es in unseren maßgeschneiderten Expert Advisor. 

Abrufen von Daten

Fangen wir an, indem wir zunächst die benötigten Bibliotheken importieren.

#Import the libraries we need
import pandas as pd
import numpy as np
import MetaTrader5 as mt5
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import sklearn
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split

Hier sind die Versionen der Bibliotheken, die wir verwenden.

#Show library versions
print(f"Pandas version: {pd.__version__}")
print(f"Numpy version: {np.__version__}")
print(f"MetaTrader 5 version: {mt5.__version__}")
print(f"Matplotlib version: {matplotlib.__version__}")
print(f"Seaborn version: {sns.__version__}")
print(f"Scikit-learn version: {sklearn.__version__}")

Pandas Version: 1.5.3

Numpy-Version: 1.24.4

MetaTrader 5 Version: 5.0.45

Matplotlib-Version: 3.7.1

Version Seaborn: 0.13.0

Scikit-learn-Version: 1.2.2

Initialisieren wir nun unser Terminal .

#Initialize the terminal
mt5.initialize()

True

Festlegung, wie weit wir in die Zukunft vorausschauen wollen.

#Define how far ahead into the future we should forecast
look_ahead = 20

Abruf der benötigten Zeitreihendaten vom MetaTrader 5 Terminal.

#Fetch historical market data 
usa_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("UST10Y_U4",mt5.TIMEFRAME_M1,0,100000))
jpn_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("JGB10Y_U4",mt5.TIMEFRAME_M1,0,100000))
usd_jpy      = pd.DataFrame(mt5.copy_rates_from_pos("USDJPY",mt5.TIMEFRAME_M1,0,100000))

Die Zeitspalte des Datenrahmens muss formatiert werden.

#Convert the time from seconds
usa_10y_bond["time"] = pd.to_datetime(usa_10y_bond["time"],unit="s")
jpn_10y_bond["time"] = pd.to_datetime(jpn_10y_bond["time"],unit="s")
usd_jpy["time"] = pd.to_datetime(usd_jpy["time"],unit="s")

Wir sollten die Zeitspalte als unseren Index festlegen, das wird es uns erleichtern, unsere 3 Datenrahmen zu einem zusammenzufassen.

#Prepare to merge the data
usa_10y_bond.set_index("time",inplace=True)
jpn_10y_bond.set_index("time",inplace=True)
usd_jpy.set_index("time",inplace=True)

Zusammenführung der Datenrahmen.

#Merge the data
merged_data = usa_10y_bond.merge(jpn_10y_bond,how="inner",left_index=True,right_index=True,suffixes=(" usa"," japan"))
merged_data = merged_data.merge(usd_jpy,left_index=True,right_index=True)

Explorative Datenanalyse

Lassen Sie uns eine Kopie des Datenrahmens erstellen, den wir für die Darstellung verwenden werden.

data_visualization = merged_data

Wir müssen den Index der Visualisierungsdaten zurücksetzen.

#Reset the index
data_visualization.reset_index(inplace=True)

Skalieren Sie alle Spaltenwerte so, dass sie alle mit Eins beginnen.

#Let's scale the data so all the first values in the column are one
for i in np.arange(1,data_visualization.shape[1]):
    data_visualization.iloc[:,i] = data_visualization.iloc[:,i] / data_visualization.iloc[0,i]

Zeichnen wir die 3 Zeitreihen auf, um zu sehen, ob es irgendwelche beobachtbaren Beziehungen gibt.

#Let's create a plot
plt.figure(figsize=(10, 5))
plt.plot(data_visualization.loc[:,"open usa"])
plt.plot(data_visualization.loc[:,"open japan"])
plt.plot(data_visualization.loc[:,"open"])
plt.legend(["USA 10Y T-Note","JGB 10Y Bond","USDJPY Fx Rate"])

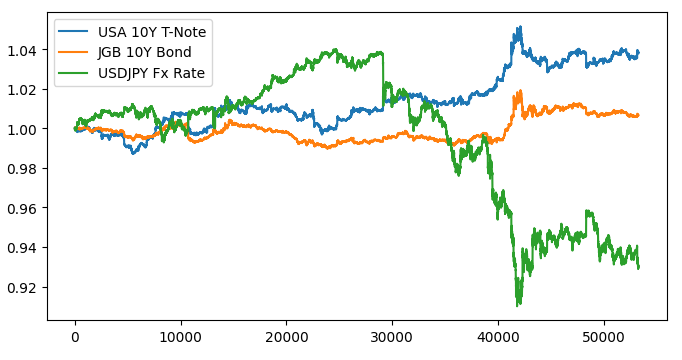
Abb. 1: Visualisierung unserer Marktdaten.

Es scheint keine erkennbare Beziehung zu geben, wenn wir die 3 Märkte überlagern. Versuchen wir, die Darstellung zu vereinfachen, indem wir die Spanne zwischen den amerikanischen und japanischen Anleihen aufzeichnen. Auf diese Weise müssen wir nur den USDJPY-Wechselkurs und den Spread der 10-jährigen USA-JPY-Anleihe berücksichtigen. Mit anderen Worten: Die 3 Kurven, die wir oben aufgezeichnet haben, können durch nur 2 Kurven vollständig dargestellt werden.

Zunächst müssen wir den Spread zwischen den Anleihen berechnen.

#Let's create a new feature to show the spread between the securities
data_visualization["spread"] = data_visualization["open usa"] - data_visualization["open japan"]

Auf der linken Seite des Diagramms sehen wir ein Beispiel für den USDJPY-Wechselkurs. Immer wenn der Wechselkurs über 1 liegt, entwickelt sich der Dollar besser als der Yen, das Gegenteil ist der Fall, wenn der Wechselkurs unter 1 fällt. Wenn der Spread über 0 steigt, entwickeln sich die amerikanischen Anleihen besser als die japanischen, und umgekehrt, wenn der Spread unter 0 fällt. Wenn also der Spread unter 0 liegt, was bedeutet, dass die japanischen Anleihen auf dem Markt besser abschneiden, würden wir auch erwarten, dass sich der Gleichgewichtswechsel zugunsten des Yen verschiebt. Bei einer visuellen Inspektion der Diagramme mit unseren Augen können wir jedoch schnell feststellen, dass diese Erwartung nicht immer zutrifft.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,2,sharex=True,sharey=False,figsize=(8,4))
columns = ["open","spread"]

for i,ax in enumerate(axs.flat):
    ax.plot(data_visualization.loc[:,columns[i]])
    ax.set_title(columns[i])

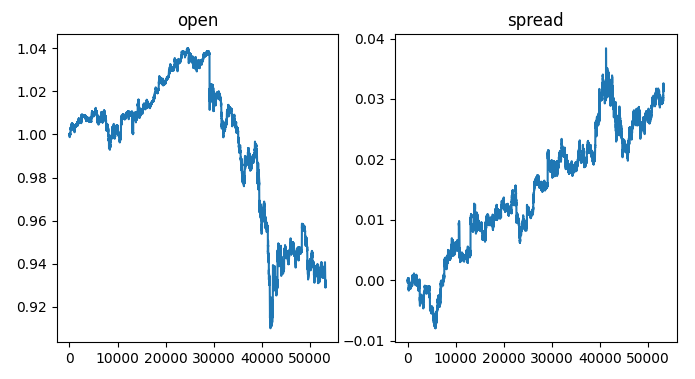
Abb. 2: Visualisierung des Anleihe-Spreads auf den Wechselkurs.

Nun wollen wir unsere Daten beschriften. 

#Label the data
merged_data["target"] = merged_data["close"].shift(-look_ahead)
merged_data["binary target"] = np.nan
merged_data.loc[merged_data["close"] > merged_data["target"],"binary target"] = 0
merged_data.loc[merged_data["close"] < merged_data["target"],"binary target"] = 1
merged_data.dropna(inplace=True)
merged_data.reset_index(inplace=True)
merged_data

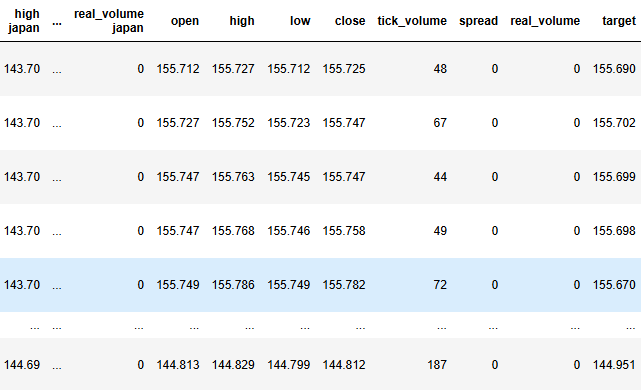
Abb. 3: Der aktuelle Stand unseres Datenrahmens.

Nun müssen wir unser Ziel und unsere Eingaben definieren.

#Define the predictors and target
target = "target"
ohlc_predictors = ['open', 'high', 'low', 'close','tick_volume']
bonds_predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan']
predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan','open', 'high', 'low', 'close','tick_volume']

Analysieren wir nun die Korrelationsniveaus in unserem Datensatz.

#Analyze correlation levels
plt.subplots(figsize=(8,6))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True)

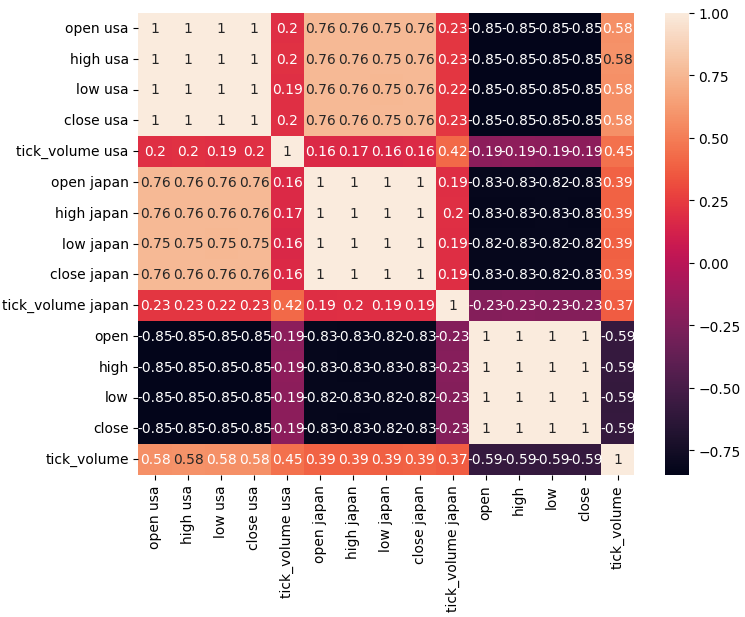
Abb. 4: Unsere Korrelationsmatrix.

Wie wir feststellen können, besteht eine starke Korrelation zwischen den amerikanischen und japanischen Anleihen (0,76). Außerdem weisen sowohl die amerikanischen als auch die japanischen Anleihen eine starke negative Korrelation mit dem USDJPY-Wechselkurs auf. 

Mit Hilfe von Streudiagrammen lassen sich die Beziehungen zwischen Variablen in zwei Dimensionen darstellen. Wir wollen nun anhand der Daten, die wir auf dem Anleihemarkt gesammelt haben, Streudiagramme erstellen. Wir beginnen mit der Erstellung eines Streudiagramms, das den Eröffnungskurs der amerikanischen Staatsanleihe mit dem Eröffnungskurs des USDJPY-Wechselkurses vergleicht.

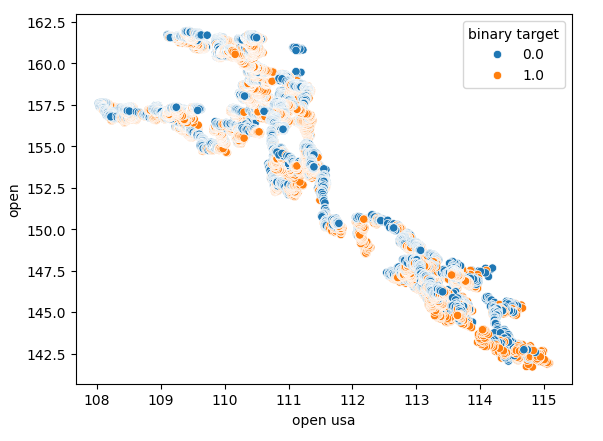
Abb. 5: Ein Streudiagramm des Eröffnungskurses von US-Anleihen gegenüber dem Eröffnungskurs des USDJPY.

Wie man sehen kann, gibt es kein klares Muster oder eine Abhängigkeit, die aus dem Streudiagramm hervorgeht. Es hat den Anschein, dass der Wechselkurs unabhängig von den Veränderungen auf dem Anleihemarkt auf- oder abwerten kann.

Wir haben auch ein weiteres Streudiagramm mit dem Eröffnungskurs der japanischen Staatsanleihe auf der x-Achse und dem Eröffnungskurs des USDJPY-Wechselkurses auf der y-Achse erstellt. Leider war in den Daten immer noch kein Zusammenhang erkennbar.

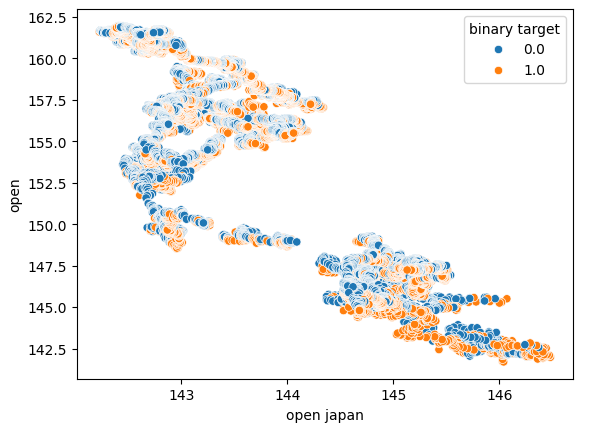
Abb. 6: Ein Streudiagramm des Eröffnungskurses japanischer Staatsanleihen gegenüber dem USDJPY-Eröffnungskurs.

Wir haben auch versucht, ein weiteres Streudiagramm zu erstellen, diesmal mit beiden Staatsanleihen auf jeder Achse. Wir haben den Eröffnungskurs der japanischen Staatsanleihe auf der x-Achse und die amerikanischen Schatzanweisungen auf der y-Achse dargestellt. Unser Streudiagramm zeigte keine interessanten Muster in den Daten, was uns darauf hinweisen könnte, dass es möglicherweise andere Variablen gibt, die wir nicht berücksichtigen und die die Daten ebenfalls beeinflussen.

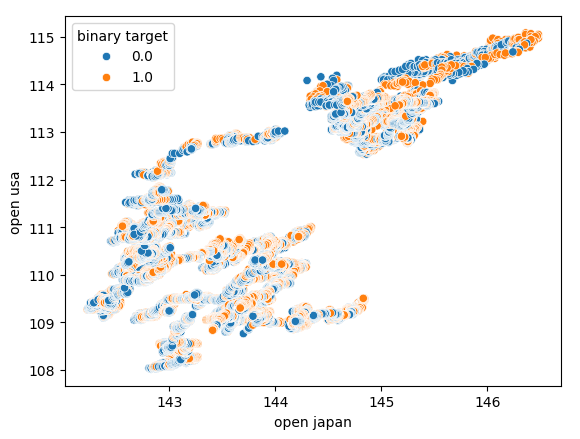
Abb. 7: Ein Streudiagramm des Eröffnungskurses japanischer Staatsanleihen gegenüber dem Eröffnungskurs amerikanischer Staatsanleihen.

Überprüfen wir auch, ob es einen Zusammenhang zwischen dem Tick-Volumen des amerikanischen Anleihemarktes und dem Schlusskurs des USDJPY-Wechselkurses gibt. Leider gibt es keine klare Trennung in der Streuung, wir beobachten viele Fälle, in denen der Preis stieg und fiel auf dem gleichen Tick Volumen Lesung.

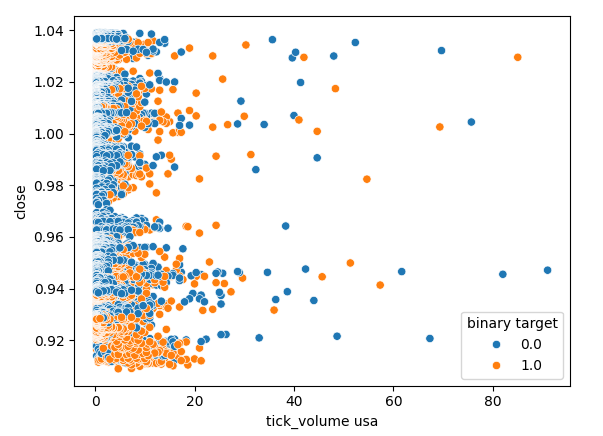
Abb. 8: Ein Streudiagramm des Tick-Volumens amerikanischer Staatsanleihen gegen den USDJPY-Schlusskurs.

Modellierung der Daten

Wir sind nun bereit, mit der Modellierung unserer Daten zu beginnen. Wir beginnen mit der Skalierung und Standardisierung unseres Datensatzes. Dies hilft unseren maschinellen Lernmodellen, effektiv zu lernen.

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

Die eine Hälfte wird zum Trainieren und Optimieren unserer Modelle verwendet, während die zweite Hälfte zur Validierung unserer Modelle und zum Testen auf Überanpassung dient.

#Partition the data
train_X , test_X, train_y, test_y = train_test_split(scaled_data,merged_data.loc[:,target],shuffle=False,test_size=0.5)

Um verschiedene Modelle effektiv zu testen, werden wir unsere Modelle in einer Liste aufbewahren, sodass wir sie in einer Schleife durchgehen und jede ihrer Leistungen nacheinander überprüfen können. Außerdem müssen wir 3 Datenrahmen erstellen:

1. Der erste Datenrahmen speichert unsere Fehlerniveaus, wenn nur gewöhnliche OHLCV-Daten vom USDJPY-Markt verwendet werden.
2. Der zweite Datenrahmen speichert unsere Fehlerquoten, wenn wir uns nur auf die OHCLV-Daten beider Anleihemärkte stützen.
3. Und der letzte Datenrahmen speichert unsere Fehlerniveaus, wenn wir alle verfügbaren Daten einbeziehen.

#Model selection
from sklearn.linear_model import LinearRegression , Lasso , SGDRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import GradientBoostingRegressor , RandomForestRegressor , BaggingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error 
from sklearn.model_selection import TimeSeriesSplit

#Define the columns
columns = [
    "Linear Model",
    "Lasso",
    "SGD",
    "Linear SV",
    "Gradient Boost",
    "Random Forest",
    "Bagging",
    "K Neighbors",
    "Neural Network"
]

#Define the models
models = [
    LinearRegression(),
    Lasso(),
    SGDRegressor(),
    LinearSVR(),
    GradientBoostingRegressor(),
    RandomForestRegressor(),
    BaggingRegressor(),
    KNeighborsRegressor(),
    MLPRegressor(hidden_layer_sizes=(100,40,20,10),shuffle=False)
]

#Create 2 dataframes to store our error on the training and test sets respectively
ohlc_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
ohlc_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Wir werden nun jedes unserer Modelle einer Kreuzvalidierung unterziehen. Die äußere Schleife iteriert über jedes verfügbare Modell, während die innere Schleife jedes Modell kreuzweise validiert und die jeweiligen Trainings- und Testfehlerwerte speichert. Beachten Sie, dass wir die Modelle nur anhand des Trainingssatzes überprüfen.

#Now perform cross validation
for j in np.arange(0,len(models)):
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],predictors],train_y.loc[train[0]:train[-1]])
        all_training_loss.iloc[i,j] = mean_squared_error(train_y.loc[train[0]:train[-1]],model.predict(train_X.loc[train[0]:train[-1],predictors]))
        all_validation_loss.iloc[i,j] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],predictors]))

Betrachten wir nun unsere Fehlerwerte bei der Verwendung gewöhnlicher OHLCV-Daten des USDJPY-Marktes. Wie wir sehen können, schnitt das lineare Modell und der lineare Support-Vector-Regressor in diesem speziellen Setup besonders gut ab.

#Our results using the OHLC data
ohlc_validation_loss

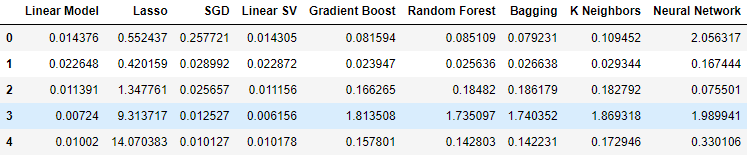
Abb. 9: Unsere OHLCV-Fehlerniveaus.

Lassen Sie uns die Ergebnisse visualisieren. Wir beginnen mit einem Liniendiagramm der Leistung der einzelnen Modelle in unserem 5-fachen Kreuzvalidierungsverfahren.

#Visualizing the results of using the OHLC predictors
plt.plot(ohlc_validation_loss)
plt.legend(columns)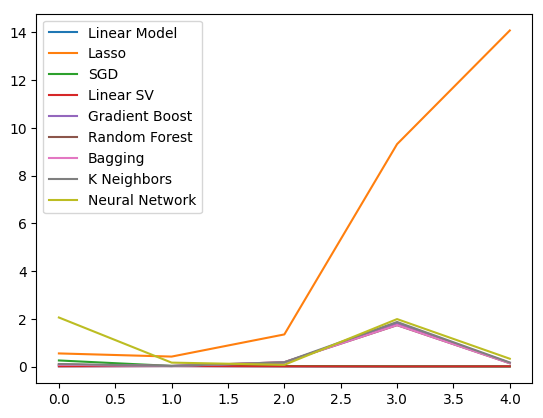

Abb. 10: Liniendiagramme unserer OHLCV-Fehlerwerte. 

Es ist deutlich zu erkennen, dass das Lasso-Modell am schlechtesten abschneidet, seine Validierungsfehlerrate war mit Abstand am höchsten. Es ist jedoch nicht klar, welches Modell die niedrigste Fehlerquote aufweist. Wir können Boxplots verwenden, um diese Frage zu beantworten.

Anhand von Boxplots lässt sich schnell erkennen, welche Modelle bei dieser speziellen Aufgabe gut abschneiden. Wie aus dem nachstehenden Diagramm hervorgeht, weist die lineare Regression die niedrigsten durchschnittlichen Fehlerwerte auf, außerdem scheint sie stabil zu sein und hat den niedrigsten Ausreißerwert.

#Visualizing the results of using the OHLC predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(ohlc_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

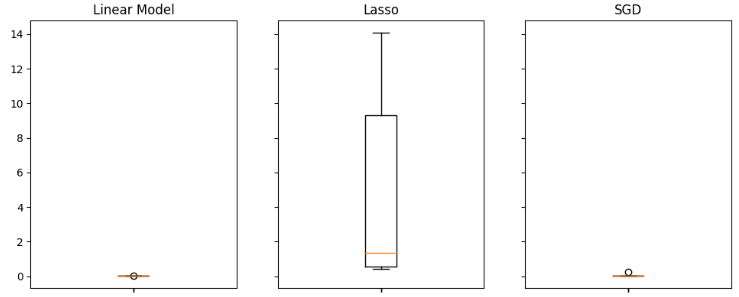
Abb. 11: Einige unserer Fehlerniveaus bei Verwendung des gewöhnlichen USDJP OHLCV

Als wir die Daten zu den Staatsanleihen verwendeten, sank unser Leistungsniveau auf breiter Front. Der lineare Support-Vektor-Regressor (Linear SVR) scheint jedoch mit diesen Daten recht gut umgehen zu können.

#Our results using the bonds data
bonds_validation_loss

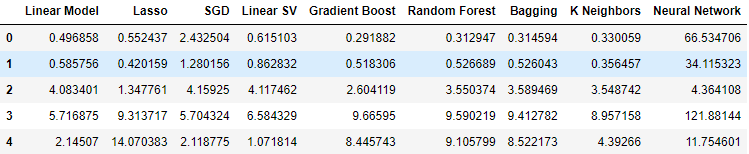
Abb. 12: Unsere Fehlerquoten bei der Verwendung der Anleihendaten.

Lassen Sie uns die Ergebnisse visualisieren.

#Visualizing the results of using the bonds predictors
plt.plot(bonds_validation_loss)
plt.legend(columns)

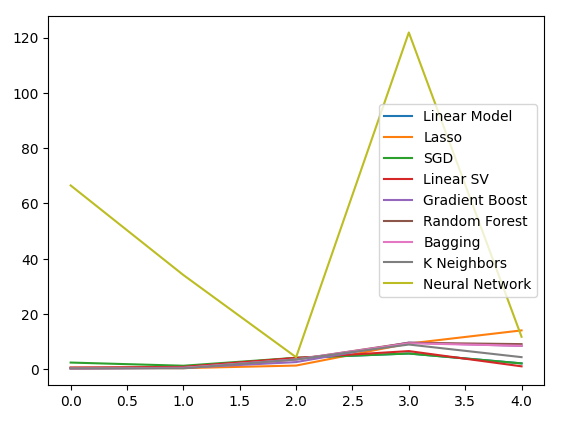
Abb. 13: Ein Liniendiagramm unseres Validierungsfehlers bei der Verwendung von Bonddaten zur Vorhersage des USDJPY-Wechselkurses.

Wir können auch Boxplots verwenden, um unsere Fehlerquoten zu bewerten.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(bonds_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

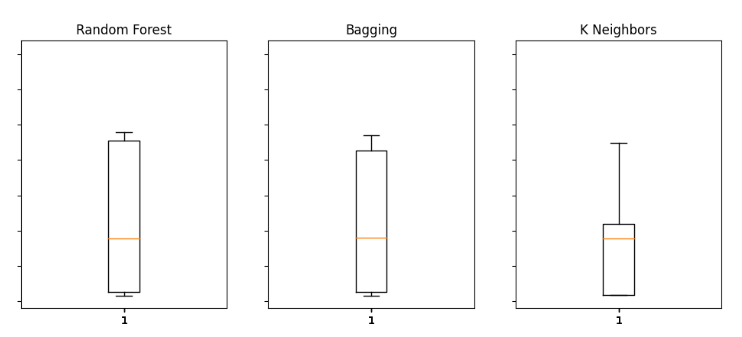
Abb. 14: Einige unserer Fehlerquoten bei der Verwendung von OHLCV-Daten vom Anleihemarkt zur Vorhersage des künftigen Schlusskurses des USDJPY

Als wir schließlich alle verfügbaren Daten einbezogen, verbesserten sich unsere Fehlerquoten im Vergleich zu unserem vorherigen Schritt, sie waren jedoch nicht so zufriedenstellend im Vergleich zu unseren Fehlerquoten, die nur die Marktnotierungen des USDJPY-Marktes verwendeten.

#Our results using all the data we have
all_validation_loss

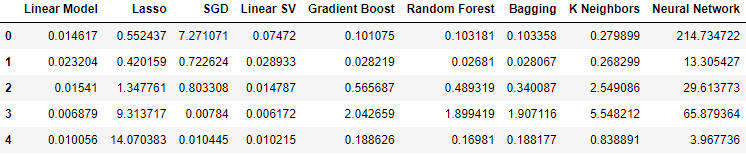
Abb. 15: Unsere Fehlerquote bei Verwendung aller uns vorliegenden Daten.

Machen wir uns ein Bild von unserer Leistung.

#Visualizing the results of using the bonds predictors
plt.plot(all_validation_loss)
plt.legend(columns)

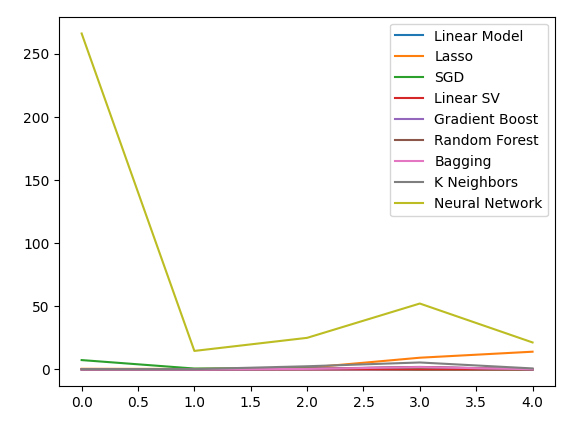
Abb. 16: Unsere Fehlerquote bei der Vorhersage des USDJPY-Schlusskurses unter Verwendung aller uns vorliegenden Daten.

Das Modell der linearen Regression ist hier eindeutig die beste Option. Es gibt jedoch keine Hyperparameter, die uns interessieren. Daher werden wir das zweitbeste Modell, die lineare SVR, auswählen und versuchen, es so einzustellen, dass es das lineare Modell übertrifft, ohne sich zu sehr an die Trainingsmenge anzupassen. Bevor wir das Modell optimieren, sollten wir prüfen, welche Merkmale für das Modell wichtig sind. Wenn unsere Strategie durchführbar ist, würden wir erwarten, dass unsere Algorithmen zur Eliminierung von Merkmalen die Spalte beibehalten. Andernfalls, wenn die Anleihendaten verworfen werden, haben wir möglicherweise Grund, die Strategie zu überarbeiten.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(all_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

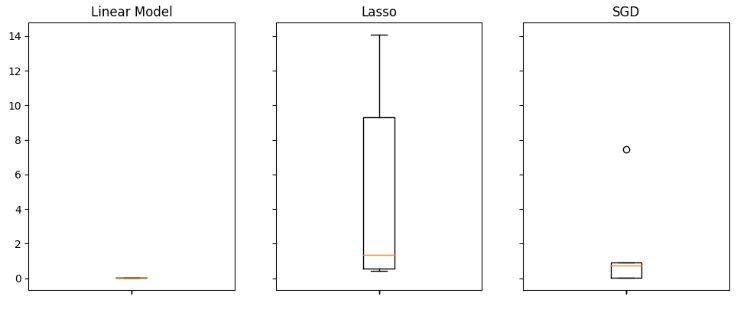
Abb. 17: Unser lineares Modell schnitt bei Verwendung aller verfügbaren Daten am besten ab.

Auswahl der Merkmale

Beginnen wir zunächst mit der Berechnung der Shapley-Werte (SHAP). Die SHAP-Werte sind eine Metrik, die uns darüber informiert, wie sich die einzelnen Eingaben auf die Vorhersagen unseres Modells auswirken, wenn sie mit einem Basiswert für jede Spalte verglichen werden. Nehmen wir zum Beispiel ein Modell, das die Wahrscheinlichkeit vorhersagt, dass ein Autofahrer einen Strafzettel für zu schnelles Fahren bekommt. Wenn wir beurteilen wollten, ob unser Modell in der Lage ist, vernünftige Vorhersagen zu treffen, könnten wir fragen: „Wie interpretiert unser Modell die Tatsache, dass der Blutalkoholspiegel des Fahrers hoch ist?“.

Natürlich würden wir erwarten, dass unser Modell eine höhere Wahrscheinlichkeit vorhersagt, einen Strafzettel zu bekommen, wenn man unter Alkoholeinfluss gefahren ist. SHAP-Werte helfen uns bei der Beantwortung solcher Fragen, indem sie die Frage so umformulieren, dass sie einen Basiswert enthält: „Wie interpretiert unser Modell die Tatsache, dass der Blutalkoholspiegel des Fahrers über dem gesetzlichen Grenzwert liegt?“.

Durch die Einbeziehung des gesetzlichen Grenzwertes haben wir eine Basislinie definiert. Daher berechnen wir unsere SHAP-Werte anhand der Differenz zwischen den Vorhersagen des Modells, wenn der Blutalkoholspiegel des Fahrers unter und über dem gesetzlichen Grenzwert liegt. 

Lassen Sie uns die SHAP-Bibliothek importieren.

#Feature selection
import shap

Nun müssen wir unser Modell trainieren.

#The SVR performed quite well, let's inspect it further
model = LinearSVR()
model.fit(train_X,train_y)

Lassen Sie uns den SHAP-Erklärer einbauen.

#Calculate SHAP Values
explainer = shap.Explainer(model.predict,test_X)
shap_values = explainer(test_X)

Schauen wir uns die SHAP-Darstellung an.

shap.plots.beeswarm(shap_values)

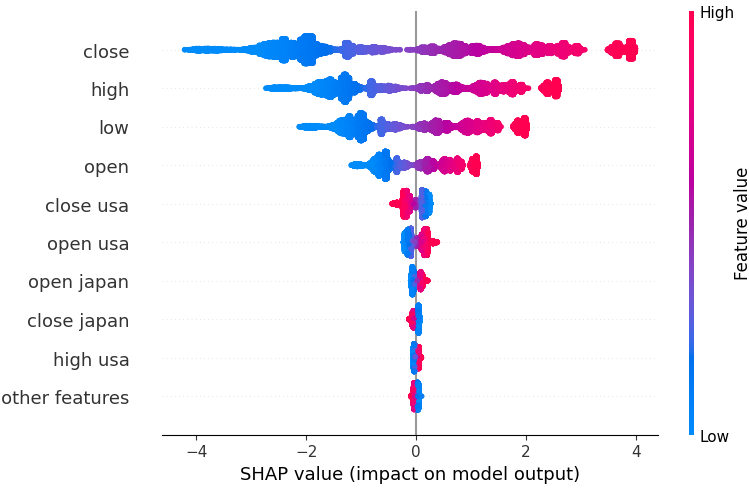
Abb. 18: Unsere SHAP-Werte aus unserem linearen SVR-Modell.

Die Funktionen sind der Reihe nach angeordnet, wobei die wichtigsten oben stehen. Es scheint also, dass der Schlusskurs des USDJPY nach unseren SHAP-Erklärungen das wichtigste Merkmal ist. Darüber hinaus können wir auch sehen, dass unsere Daten zu den Staatsanleihen nur die Preisdaten des Währungspaares waren. Dies ist ein guter Beweis für die Richtigkeit unserer Strategie. Unsere SHAP-Werte berücksichtigen, dass die Anleihendaten wichtiger sind als das Tick-Volumen des USDJPY-Marktes selbst.

Alle Erklärungen zu den Modellen sind jedoch mit Vorsicht zu genießen. Sie sind nicht vor Fehlern gefeit.

Betrachten wir auch die umgekehrte Auswahl. Der Algorithmus für die Rückwärtsauswahl beginnt mit der Anpassung eines vollständigen Modells und eliminiert nacheinander Merkmale, bis der Testfehler nicht mehr verbessert werden kann. 

Lassen Sie uns die Bibliothek mlxtend importieren.

#Let's also perform backward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

Initialisieren wir das Modell,

#Reinitialize the model
model = LinearSVR()

erstellen das Feature-Selektor-Objekt und

#Prepare the feature selector
sfs = SFS(model,
         k_features=(1,train_X.shape[1]),
         forward=False,
          n_jobs = -1,
          scoring="neg_mean_squared_error",
          cv=5)

passen den Funktionswähler an.

#Fit the feature selector
sfs_results = sfs.fit(train_X,train_y)

Schauen wir uns die ausgewählten Merkmale an.

#The best features we identified
sfs_results.k_feature_names_

('open usa',

 'high usa',

 'tick_volume usa',

 'open japan',

 'low japan',

 'close',

 'tick_volume')

Unser Algorithmus zur Rückwärtseliminierung hat den Daten des Anleihemarktes mehr Bedeutung beigemessen als unseren SHAP-Werten. Daher können wir vernünftigerweise davon ausgehen, dass es eine verlässliche Beziehung zwischen unseren Anleihendaten und dem zukünftigen Wechselkurs des USDJPY-Paares geben kann.

Stellen wir die Ergebnisse grafisch dar.

#Prepare the plot
fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev")
plt.title("Backward Selection on our Linear SVR")
plt.grid()

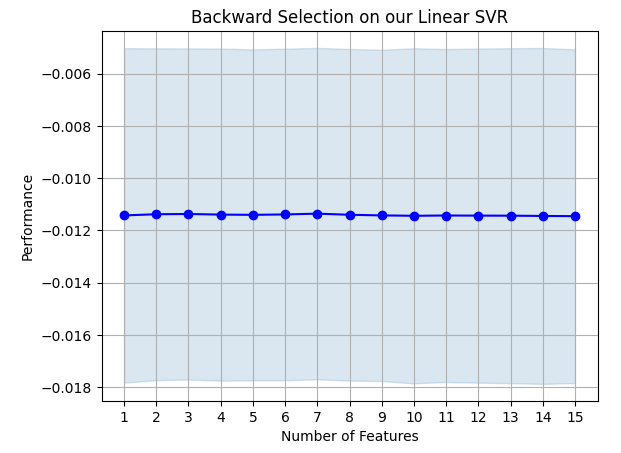
Abb. 19: Unsere Ergebnisse der Rückwärtselimination.

Es zeigt sich, dass die Fehlerquoten unseres Modells nicht stark schwanken, was bedeutet, dass unser Modell auch unter den Bedingungen begrenzter Daten stabil ist. Denken Sie daran, dass der Algorithmus ein Merkmal nach dem anderen eliminiert, bis die Fehlerquote nicht mehr verbessert werden kann, indem eines der vom Algorithmus ausgewählten Merkmale entfernt wird.

Anpassen der Hyperparameter

Optimieren wir nun unser Modell, um die lineare Regression zu übertreffen.

Importieren wir zunächst die benötigten Bibliotheken.

#Parameter tuning 
from sklearn.model_selection import RandomizedSearchCV

Initialisieren wir das Modell,

#Reinitialize the model
model = LinearSVR()

definieren das Tuner-Objekt

tuner = RandomizedSearchCV(model,
                          {
                              "epsilon":[0,0.001,0.01,0.1,25,50,100],
                              "tol": [0.1,0.01,0.001,0.0001,0.00001],
                              "C" : [1,5,10,50,100,1000,10000,100000],
                              "loss":["epsilon_insensitive", "squared_epsilon_insensitive"],
                              "fit_intercept": [False,True]
                          },
                           n_jobs=-1,
                           n_iter=100,
                           scoring="neg_mean_squared_error"
                          )

und stimmen das Modell ab.

tuner_results = tuner.fit(train_X,train_y)

Interessant ist, dass unsere besten Parameter fast identisch mit den Standardeinstellungen sind. Wir wollen jedoch den Unterschied in der Leistung beobachten.

tuner_results.best_params_

{'tol': 0.0001,

 'loss': 'epsilon_insensitive',

 'fit_intercept': True,

 'epsilon': 0,

 'C': 1}

Testen auf Überanpassung

Testen wir nun, ob wir die Trainingsmenge überangepasst haben. Wir werden unsere Modelle instanziieren.

#Testing for overfitting
baseline_model = LinearRegression()
default_model =  LinearSVR()
customized_model = LinearSVR(tol=0.0001,loss='epsilon_insensitive',fit_intercept=True,epsilon=0,C=1)

Nun wollen wir alle 3 Modelle anpassen.

#Fit the models
baseline_model.fit(train_X,train_y)
default_model.fit(train_X,train_y)
customized_model.fit(train_X,train_y)

Vorbereitung auf die Kreuzvalidierung der Leistung der einzelnen Modelle.

#Create a list of models
models = [
    baseline_model,
    default_model,
    customized_model
]

columns = [
    "Linear Regression",
    "Default Linear SVR",
    "Customized Linear SVR"
]

We need to reset the index of our datasets.
#Let's assess our new accuracy levels
test_y = test_y.reset_index()
test_X.reset_index(inplace=True)

Wir definieren das Objekt der Zeitreihenaufteilung neu und erstellen einen Datenrahmen, um unseren Validierungsfehler zu speichern.

#Create our time-series test object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
overfitting_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Cross-validate each model.
for j in np.arange(0,len(columns)):
    model = models[j]
    for i , (train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],predictors],test_y.loc[train[0]:train[-1],"target"])
        overfitting_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"target"],model.predict(test_X.loc[test[0]:test[-1],predictors]))

Schauen wir uns die Ergebnisse an.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,3,sharex=True,sharey=True,figsize=(8,4))

for i,ax in enumerate(axs.flat):
    ax.boxplot(overfitting_error.iloc[:,i])
    ax.set_title(columns[i])

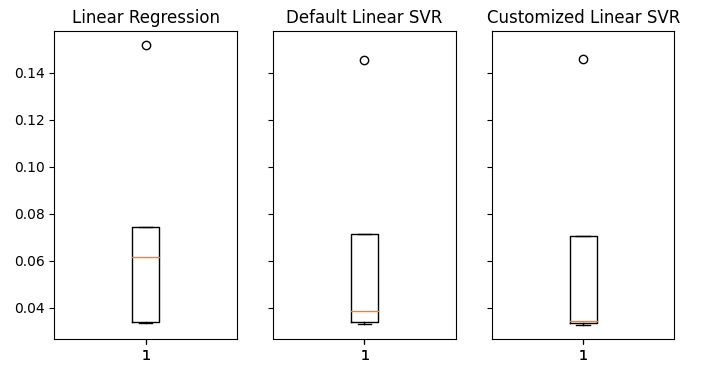
Abb. 20: Unsere Fehlerquote bei ungesehenen Daten

Es ist deutlich zu erkennen, dass unser LinearSVR-Modell den niedrigsten durchschnittlichen Fehler bei der Validierung aufweist. Daher ist es uns gelungen, die vom linearen Modell gesetzte Benchmark zu übertreffen. Darüber hinaus übertrafen wir auch die Standardfehlerrate, ohne die Trainingsmenge zu stark anzupassen.

Exportieren nach ONNX

Bereiten wir nun den Export unseres Modells in das ONNX-Format vor, damit wir es leicht in unser MQL5-Programm integrieren können.

Bevor wir weitermachen können, müssen wir zunächst unsere Daten in einer Weise standardisieren, die wir in MQL5 reproduzieren können. Dies kann erreicht werden, indem der Spaltenmittelwert von jedem einzelnen Spaltenwert subtrahiert und anschließend jede Spalte durch ihre Standardabweichung geteilt wird.

Lassen Sie uns die entsprechenden Werte in eine CSV-Datei schreiben, die im Dateipfad unseres Terminals liegt.

#Create scaling factors
scaling_factors = pd.DataFrame(index=("mean","standard deviation"),columns=predictors)

#Write our the values
for i in np.arange(0,scaling_factors.shape[1]):
    scaling_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
    scaling_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std()
    merged_data.loc[:,predictors[i]] = ((merged_data.loc[:,predictors[i]] - scaling_factors.iloc[0,i]) / scaling_factors.iloc[1,i])

scaling_factors

Abb. 21: Unsere Skalierungsfaktoren.

Jetzt müssen wir die CSV-Datei speichern.

#Save the scaling factors
scaling_factors.to_csv("C:\\Enter \\Your\\Path\\Here\\MetaQuotes\\Terminal\\D0E82094358C8CF3394F550E51FF075\\MQL5\\Files\\usdjpy scaling factors.csv")

Wir trainieren das Modell mit allen uns zur Verfügung stehenden Daten.

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,"target"])

Importieren wir die benötigten Bibliotheken.

#Let's import the libraries we need
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import netron
import onnx

Wir definieren den Eingabetyp und die Form unseres ONNX-Modells,

#Define the initial input types
initial_types = [('float_input',FloatTensorType([1,len(predictors)]))]

erstellen ein ONNX-Modell und

#Create an ONNX representation of the model
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

speichern das ONNX-Modell in einer Datei mit der Erweiterung .onnx.

#Save the ONNX model
onnx_name = "USDJPY M1 FLOAT.onnx"
onnx.save(onnx_model,onnx_name)

Lassen Sie uns das Modell in netron visualisieren.

#Visualize the model
netron.start(onnx_name)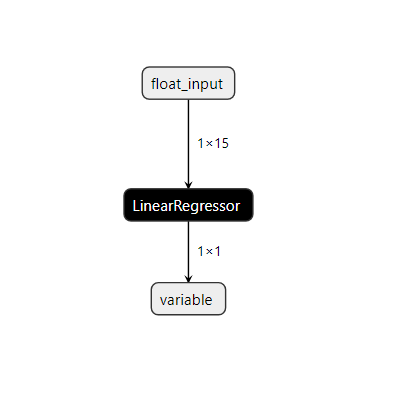

Abb. 22: Visualisierung unseres linearen SVR-Modells.

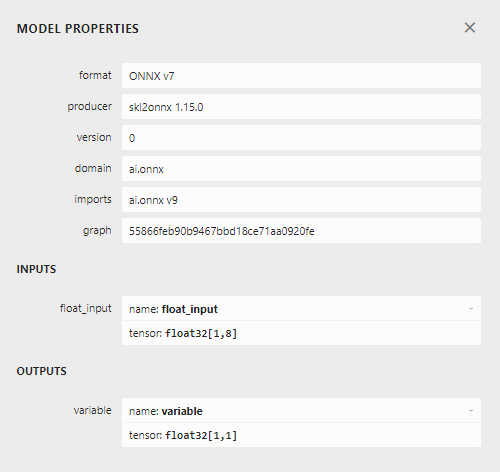
Abb. 23: Unser ONNX-Modell: Eingabe- und Ausgabeform.

Die Form des Inputs und des Outputs unseres Modells entspricht unseren Vorgaben. Fahren wir nun mit der Erstellung des Expert Advisors fort.

Implementation in MQL5

Zunächst benötigen wir unser ONNX-Modell als Ressource, die wir in unser Programm kompilieren werden.

//+------------------------------------------------------------------+
//|                                                 USDJPY Bonds.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource "\\Files\\USDJPY M1 FLOAT.onnx" as const uchar onnx_model_buffer[];

Lassen Sie uns nun einige globale Variablen definieren, die wir in unserem Programm benötigen.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
float mean_values[15],std_values[15];
vector model_output = vector::Zeros(1);
int state = 0;
int prediction = 0;

Wir importieren die Handelsbibliothek, damit wir problemlos Positionen eröffnen und verwalten können.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Nun werden wir Hilfsfunktionen für unseren Expert Advisor definieren. Wir brauchen eine Funktion, die unser ONNX-Modell lädt und seine Eingabe- und Ausgabeformen definiert. Wenn wir an irgendeinem Punkt der Prozedur scheitern, wird unsere Funktion ein Flag zurückgeben, das die Initialisierungsprozedur unterbricht.

//+------------------------------------------------------------------+
//| Load our onnx file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT);

//--- Set the input shape
   ulong input_shape [] = {1,15};

//--- Check if the input shape is valid
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model));
      return(false);
     }

//--- Set the output shape
   ulong output_shape [] = {1,1};

//--- Check if the output shape is valid
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model));
      return(false);
     }
//--- Everything went fine
   return(true);
  }

Wir brauchen auch eine Funktion, die die CSV-Datei mit den Skalierungswerten liest und in einem Array speichert, das wir später in unserer Vorhersagefunktion verwenden können. Beachten Sie, dass die erste Zeile nur die Spaltentitel enthält. Der erste Eintrag in der zweiten Zeile ist die Indexbezeichnung, und der zweite Eintrag in der zweiten Zeile ist der Mittelwert der ersten Spalte. Daher prüft unsere Funktion die aktuelle Schleifeniteration, um zu wissen, wo sie sich befindet und welche Werte wichtig sind.

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
void load_scaling_factors(void)
    {
//--- Read in the file
   string file_name = "usdjpy scaling factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). 

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file
      
      int counter = 0;
      string value = "";
      
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end 
       {
       
         if (counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read
           break; //stop the reading progress
         
         value = FileReadString(result);
         Print("Trying to read string: ",value," count value: ",counter);
         
         //--- Check where we are
         if((counter >= 17) && (counter < 32))
            {
               mean_values[counter - 17] = (float) value;
            }   
         //--- Check where we are
         if((counter >= 33) && (counter < 48))
            {
               std_values[counter - 33] = (float) value;
            }   
         //--- Reading a new row
         if(FileIsLineEnding(result))
           { 
             Print("row++");
           }
         
         counter++;
       }
      //---Close the file
      ArrayPrint(mean_values);
      ArrayPrint(std_values);
      FileClose(result);
     }
//--- We failed to find the file
else 
   {
      Print("Failed to find the file");
   }

  }

Diese Funktion holt unsere Modelleingabewerte und standardisiert sie, bevor sie eine Vorhersage von unserem Modell erhält. Anschließend wird die Vorhersage des Modells als binärer Zustand gespeichert, wobei 1 für die Vorhersage einer Kurssteigerung und 2 für eine des Fallens einer Position steht. So können wir feststellen, wann unser Modell eine Umkehrung vorhersagt.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void model_predict(void)
   {
     //--- Fetch input values
      string symbols[3] = {"UST10Y_U4","JGB10Y_U4","USDJPY"};
      vectorf model_inputs = {iOpen(symbols[0],PERIOD_CURRENT,0),iHigh(symbols[0],PERIOD_CURRENT,0),iLow(symbols[0],PERIOD_CURRENT,0),iClose(symbols[0],PERIOD_CURRENT,0),iTickVolume(symbols[0],PERIOD_CURRENT,0),
                      iOpen(symbols[1],PERIOD_CURRENT,0),iHigh(symbols[1],PERIOD_CURRENT,0),iLow(symbols[1],PERIOD_CURRENT,0),iClose(symbols[1],PERIOD_CURRENT,0),iTickVolume(symbols[1],PERIOD_CURRENT,0),
                      iOpen(symbols[2],PERIOD_CURRENT,0),iHigh(symbols[2],PERIOD_CURRENT,0),iLow(symbols[2],PERIOD_CURRENT,0),iClose(symbols[2],PERIOD_CURRENT,0),iTickVolume(symbols[2],PERIOD_CURRENT,0)
                     };
     //--- Normalize and scale our inputs
     for(int i=0;i < 15;i++)
         {
            model_inputs[i] = ((model_inputs[i] - mean_values[i])/std_values[i]);
         }
     //--- Show the inputs
     Print("Model inputs: ",model_inputs);
     //--- Fetch a forecast from our model
     OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
     //--- Give the user feedback
     Comment("Model forecast: ",model_output[0]);
     
     //--- Store the prediction
     if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 1;
         }
     else if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 2;
         }       
   }

Unsere Initialisierungsprozedur erfordert zunächst, dass wir die ONNX-Datei erfolgreich laden, bevor wir die Skalierungswerte einlesen und schließlich testen, ob unser Modell funktioniert.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Load the ONNX file
   if(!load_onnx_file())
     {
      //--- We failed to load our onnx model
      return(INIT_FAILED);
     }
     
//--- Load scaling factors
load_scaling_factors();

//--- Test if our ONNX model works
model_predict();

//--- Everything worked out
   return(INIT_SUCCEEDED);
   
  }

Wenn unser Programm nicht mehr genutzt wird, müssen wir die nicht mehr benötigten Ressourcen freigeben.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we used for our onnx model
   OnnxRelease(onnx_model);
//--- Release the expert advisor
   ExpertRemove();
  }

Schließlich werden wir bei jeder Veränderung des Preisniveaus zunächst eine Vorhersage aus unserem Modell erhalten. Wenn wir keine offenen Positionen haben, folgen wir der Vorhersage unseres Modells und speichern ein Flag, das unsere aktuelle offene Position darstellt. Andernfalls, wenn wir bereits offene Positionen haben, prüfen wir, ob die Vorhersage unseres Modells mit unseren offenen Positionen übereinstimmt; ist dies nicht der Fall, schließen wir unsere offenen Positionen.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
      //--- Obtain a forecast from our model
      model_predict();
      
      //--- Check if we have any positions
      if(PositionsTotal() == 0)
         {
            //--- Reset the state of our system
            state = 0;
            
            //--- Check for an entry
            if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Buy(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_ASK),SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,"USDJPY Bonds AI");
                  state = 1;
               }
            
             if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Sell(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_BID),SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,"USDJPY Bonds AI");
                  state = 2;
               }
         }
         
      //--- Check for reversals
      if(state != prediction)
         {
            Alert("Reversal detected by the AI system!");
            Trade.PositionClose("USDJPY");
         }
  }
//+------------------------------------------------------------------+

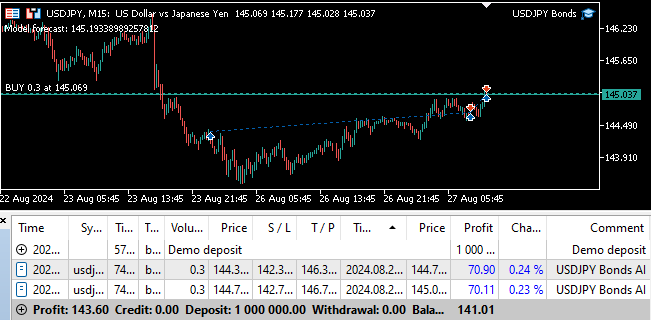
Abb. 24: Der Vorwärtstest unseres Programms

Abb. 25: Unser Expert Advisor kann Positionen automatisch schließen, sobald er eine Umkehrung feststellt.

Schlussfolgerung

In diesem Artikel haben wir gezeigt, wie wir KI einsetzen können, um einer klassischen Handelsstrategie neues Leben einzuhauchen. Ob unsere Strategie ihre Komplexität wert ist, ist fraglich, denn mit einem einfacheren Modell hätten wir eine geringere Genauigkeit erzielen können. Daher können wir vernünftigerweise zu dem Schluss kommen, dass wir, wenn wir nicht mehr Zeit in die Umwandlung der Merkmale investieren, um die Beziehung besser darzustellen, besser dran sind, wenn wir eine einfachere Strategie verwenden, die nur die gewöhnlichen Marktnotierungen umfasst.