您应当知道的 MQL5 向导技术（第 35 部分）：支持向量回归
447
0
概述
支持向量回归（SVR）是一种衍生自支持向量机的回归形式。在其核心处，SVR 使用内核方法将输入数据映射到更高维空间，从而能捕获更复杂的关系，这与降维形成鲜明对比。至于本文，我们将严格探讨它与多层感知器搭配使用时的损失函数作用。我们在早前的文章中视察过一种相关但不同的回归形式，即高斯过程回归。故此，兴许我们从区分两者开始是个关键。
SVR 和 GPR 之间的差异
为了强调这两者之间的区别，我们从机器学习术语中歇一会，并以每日案例来展示为什么每一个都很重要。故此，研究这样一个场景：您正在经营一家初创公司，开发了一款非常健康的低糖冰淇淋，在于您的家乡有健康的需求。因为您刚刚初创，仅在家乡销售冰淇淋，所以您仍然在手工执行大部分制造。由此，您需要开始提高生产力，因之除了成本控制之外，它还能带来益处，像是品质控制，及实现一些生产标准。
这样的扩张需要资本，而您不能从机构筹措到这些资金，因为您缺乏必要的抵押品（或技术设备）来向银行担保；或者，您可与大型知名冰淇淋品牌合作，不过大型知名品牌的雇员通常是官僚主义，无论他们对您的产品有何想法，他们都会说不。
故此，您唯一的选择是通过私人的半正式途径筹集资金，并且它附带告诫，即您必须扩张您的产品。不过，当您扩张到家乡之外时，哪些客户会留意、甚至考虑您的产品与知名品牌对比？作为未知的地域，您不能采取像在家乡那样的方式。那么，这就浮现出一个问题，您在早期忙于满足家庭需求时或许忽略了这个问题，即您的主要客户群是什么？
客户细分，有些人可能选择忽略的一个业务层面，它有多种类型。它包括（但不限于）按邮政编码（或地址）细分，按年龄、教育水平、职业/专业细分，以及按收入水平细分；由于社交媒体，另一个“新兴”和不断增长的细分市场可能是生活方式/兴趣群体。通过这些细分市场来增加销售数据，我们可以创建一些有趣的数据集，当所收集数据集甚至超出我们的家乡时，能够提供一个窗口，了解在我们主要位置之外接下来会发生什么。
正如早前文章中所述的那样，高斯过程回归不仅提供了一个均值投影，而且还为该均值附加了一个指示性范围、和一个置信度。这往往意味着它适合在这种境况下进行预测，即产品需求受到外部因素（不一致）的巨大影响 ，如一种奢侈品或昂贵产品常会造成不一致需求运作。如果它并非奢侈品，那它就可能是季节性很强、或是价格高、且需求波动的小众产品。这意味着我们的冰淇淋必须比竞争对手的价格更高，才能贴合奢侈品定位，更好地配用 GPR。
此外，在选择预测未来需求的数据集以时，产品类型和客户细分会呈现选择洪流，这需要仔细考虑，如下表所概括。
| 细分类型 | 最适合 SVR | 最适合 GPR |
| 邮政编码 | 日用消费品 | 除非与其它动态数据相结合，否则并不理想 |
| 年龄 | 服装、消费品、教育工具 | 除非与其它动态数据相结合，否则并不理想 |
| 教育水平 | 教育产品、科技产品 | 除非有复杂的因素在起作用，否则并不理想 |
| 收入水平 | 稳定市场的基础产品 | 奢侈品、高端电子产品、高档商品 |
| 职业 | 与稳定职业相关的产品 | 季节性商品、受外部因素（例如天气）影响的物件 |
| 生活方式/兴趣群体 | 可预测的利益群体（例如，健身服装） | 特种或小众商品，需求高度变化 |
我们的上表虽然不一定是客户细分和产品类型之间关系的事实描述，但它强调了在选择合适的数据集进行预测之前考虑这些因素的重要性。总而言之，GPR 更适合经常面临不确定性、和复杂增长模式的企业，这些企业需要使用置信区间进行预测。
另一方面，支持向量回归非常适合在确定性和稳定增长发挥作用之处进行预测。当决策可以基于线性或中度线性趋势时，它们是理想的选择。为什么？因为 SVR 对噪声具有稳健性。它专注于获得决策边界，令误差余量最大化，同时把异常值影响最小化。若把误差余量（ε）充当分类器，SVR 应当对于没有大量异常值的数据集有效。
正如我们从上面的交叉表格推荐中所见，SVR 最适合对需求几乎保持不变的基本用品或日常消费品进行预测，除非新冠病毒（COVID）爆发事件（可能会导致需求激增和崩溃），否则对产品的需求水平应当不会有很大波动。故此，考虑到我们在家乡以外冰淇淋销售的扩展状况，如果定价不太浮夸的话，而是摆在商店货柜上并标价，那里是消费者选购一周可能需要的日常杂货和主食之处，SVR 将是一个合适的工具（正如上文对 GPR 的推荐）。
故此，如果我们使用交叉表格作为指导，若冰淇淋是我们在主要的重大节假日、或夏季销售的优质产品、或是提供给特定的高端餐厅，那么我们应看看将 SVR 与按收入水平汇总的销售数据配合使用。此外，交叉表格推荐了消费者职业和生活方式/特殊兴趣群体，这些也是很好的参考。在折叠面，如果我们的产品主要在大卖场销售，SVR 应当作用最佳，如上论调，价廉很重要，而与该消费者细分直接相关的是地址（或邮政编码）。因此，按地址汇总的销售数据可以更好地搭配 SVR 来预测我们应以多快或多慢的速度拓展我们的冰淇淋销售，这就是我们必须正视的事情，因为现在我们正用别人的钱。
故此，SVR 最适合预测可以接受高度不确定性的状况，而我们在本文中关注的 SVR 几乎处于光谱的另一端，因为它在定义数据集的超平面时，会忽略超出设定阈值的异常值。
SVR 定义
SVR 可以公式化为目标函数和决策函数。如果我们从目标函数公式开始，则如下所示：
其中
- w 是权重向量（模型的参数），在我们的例子中，我们对权重矩阵的 L2-Norm 感兴趣，
- C 是正则化参数，控制模型复杂性，与错误分类容忍度之间的权衡，
- L ε 是 ε-不敏感损失函数，定义如下：
其中
- f(xi ) 是预测值，
- yi 是真实值，
- ϵ 定义了一个容错余量，在该范围内不会对错误进行处罚。
另一方面，主要用于预测的决策函数具有以下公式：
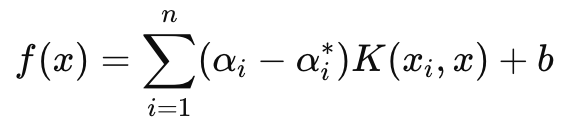
其中
- αi 和 αi∗ 是拉格朗日（Lagrange）乘数，
- K (xi , x) 是内核函数（例如，线性、多项式、RBF），
- b 是乖离项。
如上所述，SVR 引入了一个对损失不敏感的参数 ε，其可确保忽略量级小于 ε 的误差，并且不会导致正在训练的模型权重或参数调整。这令 SVR 在处理小噪声和数据变化方面更加稳健，如此它可专注于更大的全景、或主要趋势。
此外，在我们的目标函数中，C 参数管理训练误差最小化，与模型复杂度最小化之间的权衡。较高的 C 可将训练误差最小化，但风险是过度拟合，而在纸面上，较低的 C 会导致更多的普适化和更好的灵活性，从而在不同场景中进行预测。
在为该网络训练简单的 MLP 时，我们将严格专注于使用 SVR 的损失函数。我们不会像决策函数那样，据其内核进行投影。不过，值得一提的是，SVR 使用内核函数将输入数据转换至更高维的空间，于其中能够精确定位在原始空间中或许不是线性的关系。常见的内核包括：线性内核、多项式内核、和 RBF。
SVR 损失函数能利用 MQL5 实现，如下所示：
//+------------------------------------------------------------------+ //| SVR Loss | //+------------------------------------------------------------------+ vector Cmlp::SVR_Loss() { vector _loss = fabs(output - label); for(int i = 0; i < int(_loss.Size()); i++) { if(_loss[i] <= THIS.svr_epsilon) { _loss[i] = 0.0; } } vector _l = THIS.svr_c*_loss; double _w = 0.5 * WeightsNorm(MATRIX_NORM_P2); vector _weight_norms; _weight_norms.Init(_loss.Size()); _weight_norms.Fill(_w); return(_weight_norms + _l); }
典型情况下，这个损失值是一个标量，但是由于这个损失函数现在被用于反向传播，并且某些网络有多个最终输出，因此即使 SVR 将其压缩为标量，以向量形式维护损失结构也很重要。这就是我们已完成的。此外，在反向传播函数中，我们检查并查看是否用到了 SVR 损失。如下所示：
//+------------------------------------------------------------------+ //| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON. | //+------------------------------------------------------------------+ //| | //| -Extra Validation check of MLP architecture settings is performed| //| at run-time. | //| Chcecking of 'validation' parameter should ideally be performed | //| at class instance initialisation. | //| | //| -Run-time Validation of learning rate, decay rates and epoch | //| index is performed as these are optimisable inputs. | //+------------------------------------------------------------------+ void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1) { if(!validated) { printf(__FUNCSIG__ + " invalid network arch! "); return; } ... if(EpochIndex < 0) { printf(__FUNCSIG__ + " Epoch Index Should start from 1. "); return; } ... vector _last_loss = (THIS.svr_loss? SVR_Loss():output.LossGradient(label, THIS.loss)); .... }
我们之所以能够添加这个单行修改，是因为我们的构造函数参数在一个结构体中，并且我们能很容易地修改这个结构（因为这个类在早前文章中已讲述过了），如下所示：
//+------------------------------------------------------------------+ //| Multi-Layer-Perceptron Struct for Constructor Parameters | //+------------------------------------------------------------------+ struct Smlp { //arch array must be defined with at least 2 non zero values //that represent the size of the input layer and output layer //If more values than this are provided in the array then the //middle values will define the size(s) of the hidden layer(s) //first value (index zero) is size of input layer //last value (index size-1) is size of output layer int arch[]; ... bool svr_loss; double svr_c; double svr_epsilon; Smlp() { ArrayFree(arch); ... svr_loss = false; svr_c = 1.0; svr_epsilon = __EPSILON * 5.0; }; ~Smlp() {}; };
实现信号类
为了得到一个拥有 MLP，且其损失函数使用 SVR 的信号类，我们将取用之前文章中分享的已编码完毕的 MLP 类。上面已经亮明我们用到 SVR 损失时需针对该类进行的必要修改，如此剩下的就是如何在信号类的自定义实例中调用和使用该类。我们最近在这些系列中涵盖的 MLP，都试图预测每根新柱线上下一次收盘价的变化。这意味着在计时器的基础上（每根新柱线）全新计算收盘价的下一次变化。
为计算该结果的输入也是先前的收盘价变化，其中的主要变量是这些变化的数量。（该变量建立输入图层大小）。替代方案不仅可以定义在预测下一根柱线收盘价变化时应将哪些输入投喂到 MLP 当中，还可以定义预测的前瞻性。最后一点很重要，因为对于我们的测试目的，我们正用单根价格柱线的前瞻性展望。此外，在进行每次预测之前，我们会在每根新柱线上执行反向传播，以便在给定的训练集大小上为输入定义的 ε 数量训练我们的网络。
这两个输入参数 'training set size' 和 'epochs' 也是可优化的，这需要在获得网络的理想权重和普适之间取得平衡。这是因为，虽然更大的训练集和更多的 ε 可以表明采样数据的性能良好，但交叉验证必然不会那么乐观，除非网络具有一定的普适性，并且不太过于依赖其训练数据。GetOutput 函数经由 MLP 处理预测，其源代码分享如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalSVR::GetOutput(vector &Output) { m_learning.rate = m_learning_rate; for(int i = m_epochs; i >= 1; i--) { MLP.LearningType(m_learning, i); for(int ii = m_train_set; ii >= 0; ii--) { vector _in, _in_new, _in_old; if ( _in_new.Init(__MLP_SIGN_INPUTS) && _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) && _in_new.Size() == __MLP_SIGN_INPUTS && _in_old.Init(__MLP_SIGN_INPUTS) && _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS + __MLP_SIGN_OUTPUTS, __MLP_SIGN_INPUTS) && _in_old.Size() == __MLP_SIGN_INPUTS ) { _in = _in_new - _in_old; MLP.Set(_in); MLP.Forward(); if(ii > 0) { vector _target, _target_new, _target_old; if ( _target_new.Init(__MLP_SIGN_OUTPUTS) && _target_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_SIGN_OUTPUTS) && _target_new.Size() == __MLP_SIGN_OUTPUTS && _target_old.Init(__MLP_SIGN_OUTPUTS) && _target_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_SIGN_OUTPUTS, __MLP_SIGN_OUTPUTS) && _target_old.Size() == __MLP_SIGN_OUTPUTS ) { _target = _target_new - _target_old; MLP.Get(_target); MLP.Backward(m_learning, i); } } Output = MLP.output; } } } }
它与我们在之前的文章中曾实现的没有太大区别。对已有标签（或目标值）的每个训练集数据点执行反向传播。通常，所有训练数据都有一个目标值，但因为在我们的例子中，我们正在与预测合并，所以最终的“训练数据点”是最新的，其最终的收盘价变化就是我们正在寻找的。故此，当我们获得当前输入数据，假设能为我们提供预测，我们不会执行任何训练。此外，这也是我们在每个训练集中进行倒计数的原因，即我们首先用非常旧的数据进行训练，然后按我们的工作方式向下训练到当前数据。
实现 TrailingStop 类
自从我们研究自定义信号类以外的任何东西以来，本系列已经有一段时间了，而看过我早前文章的读者会记得，我不仅经常分享依据信号类交易的思路，还分享尾随停止类、甚至资金管理类。故此，我们返回这些困境，研究一个自定义尾随停止类，其可由 MQL5 向导附加到智能系统。对于新读者，有关如何在 MQL5 向导中使用下面分享的代码来创建智能系统的指南，可在此处和此处找到。
故此，为了实现自定义尾随类，我们将查看是否有任何持仓，未设止损但需要介入，或者已有止损但需要调整以便更好地锁定持仓的盈利。止损有点争议，因为它们从未得到保证。只有限价单价格才是。如果出于任何原因，市场波动幅度超出大多数人的预期，那么经纪商就只能以下一个“可用价格”为您平仓，而非按您指定的止损。尽管如此，我们仍会基于预测的价格柱线范围量级变化来决定设置或移动止损。我们在另一个 GetOutput 函数中实现这一点，其与自定义信号类类似，但略有不同。它分享如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CTrailingSVR::GetOutput(vector &Output) { m_learning.rate = m_learning_rate; for(int i = m_epochs; i >= 1; i--) { MLP.LearningType(m_learning, i); for(int ii = m_train_set; ii >= 0; ii--) { vector _in, _in_new_hi, _in_new_lo, _in_old_hi, _in_old_lo; if ( _in_new_hi.Init(__MLP_TRAIL_INPUTS) && _in_new_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) && _in_new_hi.Size() == __MLP_TRAIL_INPUTS && _in_old_hi.Init(__MLP_TRAIL_INPUTS) && _in_old_hi.CopyRates(m_symbol.Name(), m_period, 2, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) && _in_old_hi.Size() == __MLP_TRAIL_INPUTS && _in_new_lo.Init(__MLP_TRAIL_INPUTS) && _in_new_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) && _in_new_lo.Size() == __MLP_TRAIL_INPUTS && _in_old_lo.Init(__MLP_TRAIL_INPUTS) && _in_old_lo.CopyRates(m_symbol.Name(), m_period, 4, ii + __MLP_TRAIL_OUTPUTS + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_INPUTS) && _in_old_lo.Size() == __MLP_TRAIL_INPUTS ) { vector _in_new = _in_new_hi - _in_new_lo; vector _in_old = _in_old_hi - _in_old_lo; _in = _in_new - _in_old; MLP.Set(_in); MLP.Forward(); if(ii > 0) { vector _target, _target_new_hi, _target_old_hi, _target_new_lo, _target_old_lo; if ( _target_new_hi.Init(__MLP_TRAIL_OUTPUTS) && _target_new_hi.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) && _target_new_hi.Size() == __MLP_TRAIL_OUTPUTS && _target_old_hi.Init(__MLP_TRAIL_OUTPUTS) && _target_old_hi.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) && _target_old_hi.Size() == __MLP_TRAIL_OUTPUTS && _target_new_lo.Init(__MLP_TRAIL_OUTPUTS) && _target_new_lo.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_TRAIL_OUTPUTS) && _target_new_lo.Size() == __MLP_TRAIL_OUTPUTS && _target_old_lo.Init(__MLP_TRAIL_OUTPUTS) && _target_old_lo.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_TRAIL_OUTPUTS, __MLP_TRAIL_OUTPUTS) && _target_old_lo.Size() == __MLP_TRAIL_OUTPUTS ) { vector _target_new = _target_new_hi - _target_new_lo; vector _target_old = _target_old_hi - _target_old_lo; _target = _target_new - _target_old; MLP.Get(_target); MLP.Backward(m_learning, i); } } Output = MLP.output; } } } }
如上我们的代码虽然与信号中的代码几乎相同，但主要区别在于它接收的输入数据类型及其预期输出。我们正在努力判定是否需要移动止损，我们的先决要求假设波动性上升。因此，我们需要找出价格柱线范围变化的下一个变化是什么。这类数据本身必然非常不稳定（或嘈杂），这就是为什么如果我们使用移动平均缓冲区作为输入数据和目标值，它会更加稳妥。这可以被修改，因为下面附有完整源代码，不过，我们正取每根价格柱线的最高价减去最低价的变化作为输入，我们正在查看输出的下一个变化，就像我们对上述信号的收盘价所做的那样。
故此，如果价格柱线范围的预测变化为正值，意味着波动性正在增加，我们会采取措施依据预测增加比例移动止损。这或许看似很鲁莽，因为如上所述，经纪商从不保证止损价格，这就是为什么仅在预测波动性下降时移动止损的逆选项可能“更确定”，因为在波动性较小的时期，经纪商更有可能比波动性大时遵守止损。是的，故这有点争论，我把这个问题留给读者去探索，并根据他的发现对代码进行相应的调整。
策略测试器结果
我们针对 USDJPY 货币对，在 2023.01.01 至 2024.01.01 的日线时间帧内进行测试。这些测试运行是搭配一些最佳设置执行的，取其快速，且优化未经前向遍历或交叉验证。在此展示它们只是为了简单地演示由向导组装的智能系统进行交易的能力。额外的努力，如覆盖较长历史记录测试，同时在涉及优化时进行前向漫游，则留给读者。同样值得注意的是，向导组装的智能系统在开发交易系统时可以组合多个信号，如此这般测试或优化就不必每次只能单独选取此处可用的自定义信号。
我们开发了一个含有 SVR 的自定义信号，和一个含有类似 MLP 的自定义尾随类。因此，下面所示的测试运行适用于这两款智能系统，其接口代码附在下面。第一个仅用自定义信号，没有尾随停止。其结果如下所示：
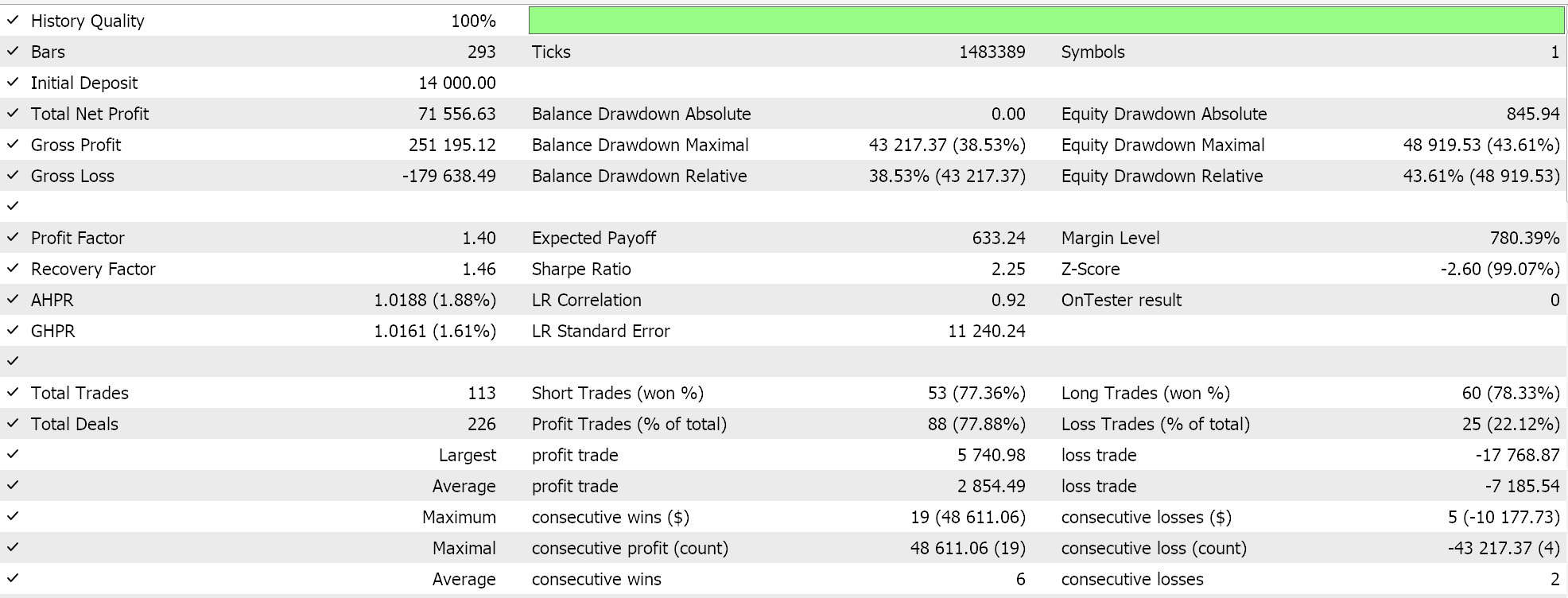
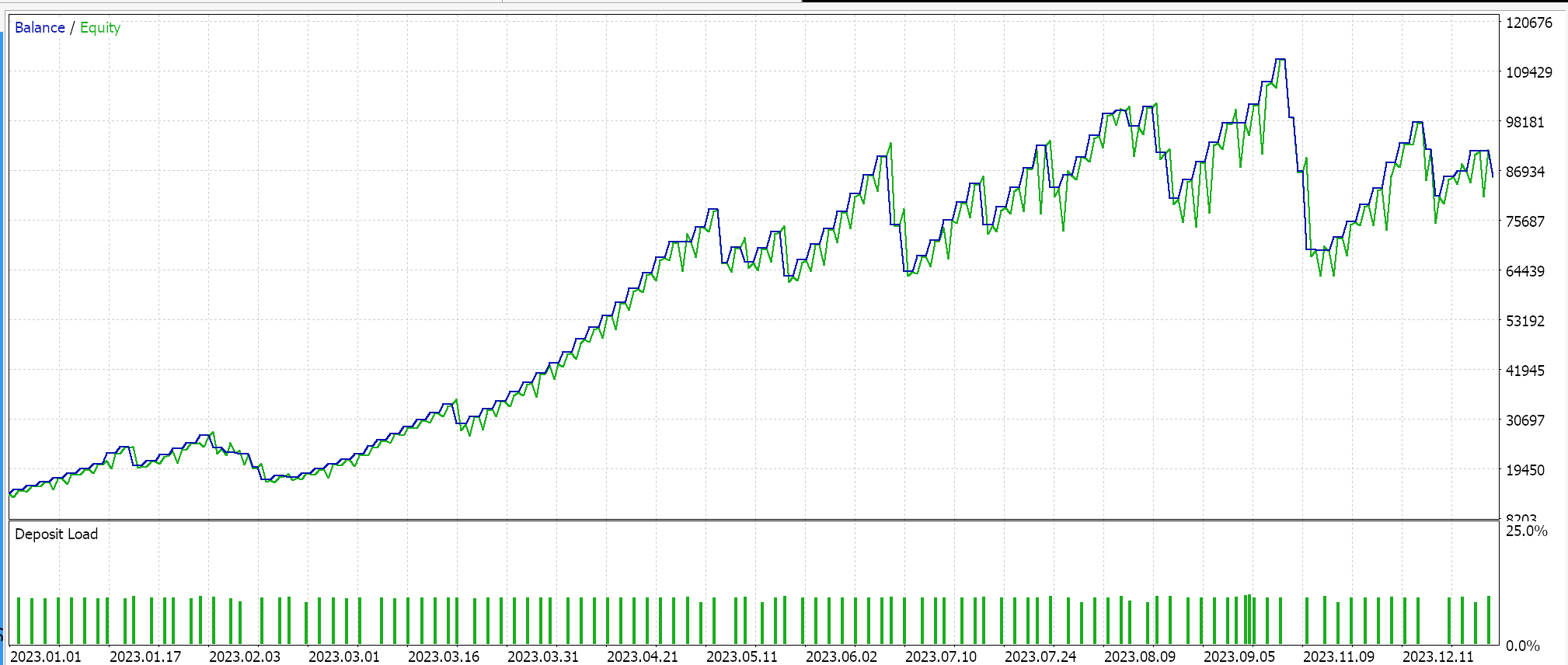
第二个使用我们上面实现的自定义信号和自定义尾随类。其结果也如下所示。
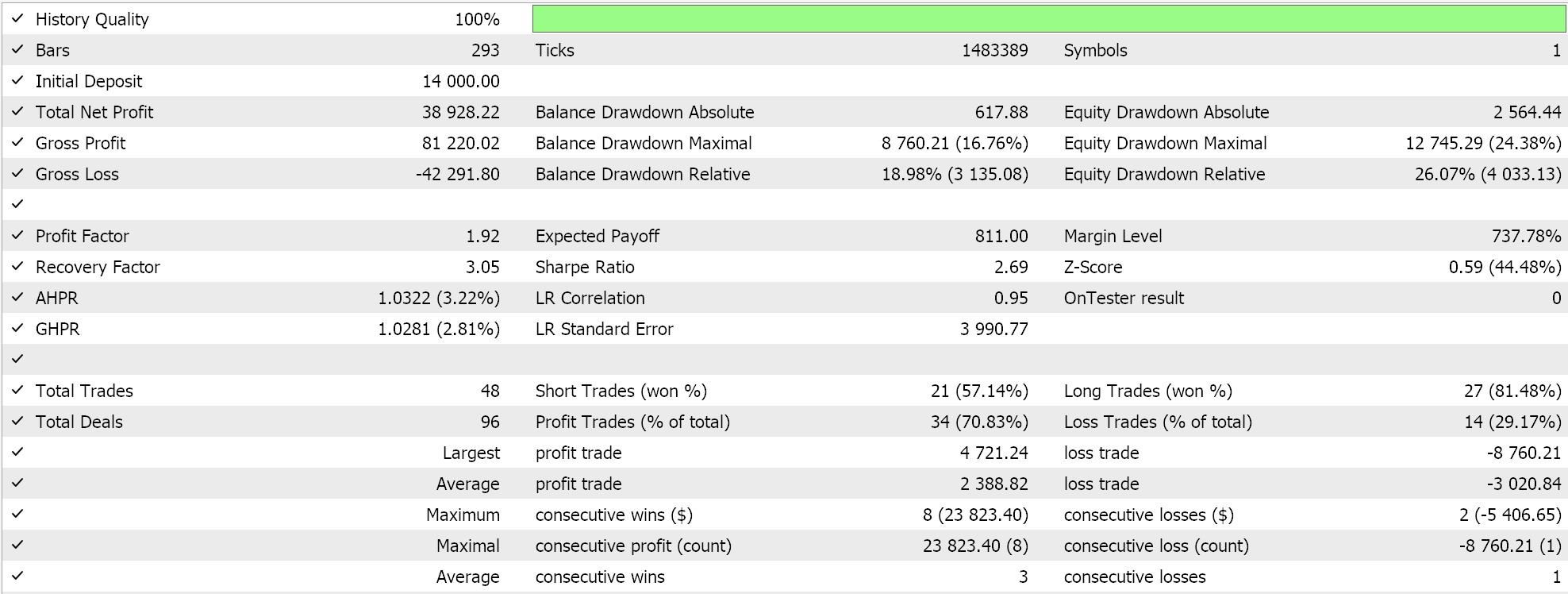
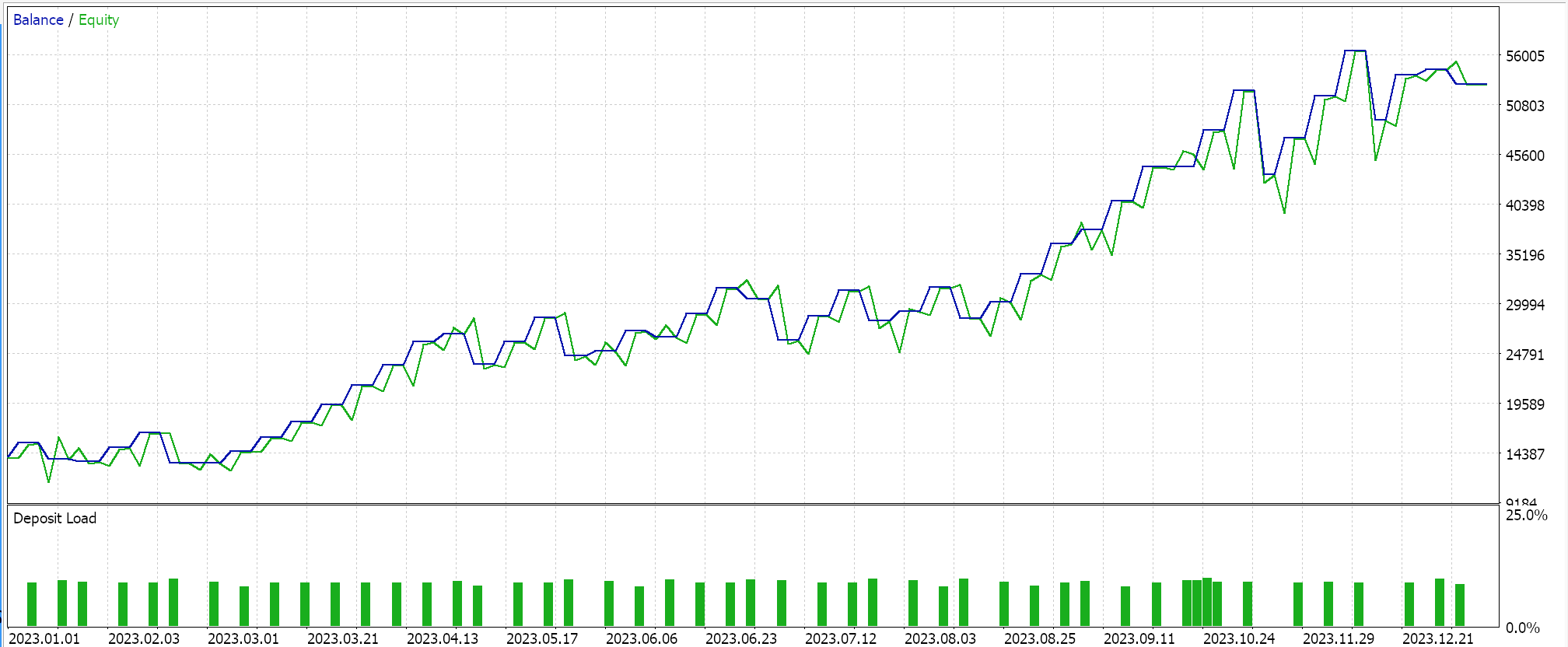
结束语
总而言之，我们已考察了支持向量回归，它遵循了我们在研究高斯过程内核时研究过的另一种回归形式。这两种回归，支持向量回归和高斯过程回归，在其应用中几乎是截然相反的，因为 SVR 往往更适合波动性和趋势性较低的数据集，而 GPR 则在波动性更大和不确定性更低的环境中蓬勃发展。支持向量回归拥有目标函数和决策函数。我们试图利用前者，即目标函数，作为信号类和自定义尾随停止类中多层感知器的损失函数。
使用决策函数，实际作为预测器，需要用到额外内核，我们在高斯过程回归一文中探讨了这一点，但本文未用，因为我们的预测器是一个纯粹的 MLP。在往后的文章中，我们可以研究这一点，因为有不同形式的内核能用于执行此操作，不过 SVR 损失函数是我们本文的目标。通过使用损失不敏感参数 ε，它也可与越来越多的损失函数列表一起（我们在此处涵盖的一些实现），引申出一种不同的神经网络训练方式。
这个对损失不敏感的参数 ε 更像是一个分类器，而非一个回归器，有论调说，这令该损失函数在分类器网络中的使用频度比回归器网络更多，就像我们在这篇文章中所做的那样，这可能是真的。不过，SVR 仍然处置连续输出（十进制数据集），并以类似的格式预测数值。它简单地用 ε 余量来决定是否应该惩罚错误，但其目标仍然是回归，而不是分类。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15692
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
从基础到中级：BREAK 和 CONTINUE 语句
在任何市场中获得优势（第五部分）：联邦储备经济数据库（FRED）欧元兑美元（ EURUSD）可替代数据
神经网络实践：第一个神经元
