William-Gann-Methoden (Teil III): Funktioniert Astrologie?

Einführung

Die Finanzmarktteilnehmer sind ständig auf der Suche nach neuen Methoden der Marktanalyse und -prognose. Selbst die unglaublichsten Konzepte werden nicht ausgelassen. Einer der nicht standardisierten und völlig einzigartigen Ansätze ist die Verwendung der Astrologie im Handel, die durch den berühmten Händler William Gann populär gemacht wurde.

Wir haben uns bereits in früheren Artikeln mit den Werkzeugen von Gann befasst. Hier sind der erste und zweite Teil. Wir werden uns nun darauf konzentrieren, die Auswirkungen der Positionen von Planeten und Sternen auf die Weltmärkte zu untersuchen.

Wir wollen versuchen, die modernsten Technologien mit altem Wissen zu verbinden. Wir werden die Programmiersprache Python sowie die Plattform MetaTrader 5 verwenden, um die Verbindung zwischen astronomischen Phänomenen und den Bewegungen des EURUSD-Paares zu finden. Wir werden den theoretischen Teil der Astrologie im Finanzwesen behandeln und uns im praktischen Teil an der Entwicklung eines Prognosesystems versuchen.

Außerdem werden wir uns mit der Erfassung und Synchronisierung von astronomischen und finanziellen Daten beschäftigen, eine Korrelationsmatrix erstellen und die Ergebnisse visualisieren. 

Theoretische Grundlagen der Astrologie im Finanzwesen

Ich interessiere mich schon seit langem für dieses Thema und möchte heute meine Gedanken über den Einfluss der Astrologie auf die Finanzmärkte mit Ihnen teilen. Dies ist ein wirklich faszinierendes, wenn auch recht umstrittenes Gebiet.

Der Grundgedanke der Finanzastrologie ist meines Erachtens, dass die Bewegungen der Himmelskörper in irgendeiner Weise mit den Marktzyklen zusammenhängen. Dieses Konzept hat eine lange und reiche Geschichte und wurde vor allem von William Gann, einem berühmten Händler des letzten Jahrhunderts, populär gemacht.

Ich habe viel über die Grundprinzipien dieser Theorie nachgedacht. Zum Beispiel die Idee des Zyklizismus, die besagt, dass die Bewegungen der Sterne und Planeten zyklischer Natur sind, ebenso wie die Bewegungen des Marktes. Was die planetarischen Aspekte betrifft, so glauben einige, dass bestimmte Planetenpositionen einen starken Einfluss auf die Märkte haben. Und was ist mit den Tierkreiszeichen? Es wird angenommen, dass der Durchgang der Planeten durch die verschiedenen Tierkreiskonstellationen auch den Markt in gewisser Weise beeinflusst.

Auch die Mondzyklen und die Sonnenaktivität sind erwähnenswert. Ich habe Meinungen gelesen, dass die Mondphasen mit kurzfristigen Marktschwankungen in Verbindung gebracht werden, während Sonneneruptionen mit langfristigen Trends in Verbindung gebracht werden. Interessante Hypothesen, nicht wahr?

William Gunn war ein echter Pionier auf diesem Gebiet. Er entwickelte eine Reihe von Werkzeugen, wie z. B. sein berühmtes 9er-Quadrat, das auf Astronomie, Geometrie und Zahlenfolgen basiert. Seine Werke sorgen noch immer für heftige Diskussionen.

Natürlich ist nicht zu übersehen, dass die wissenschaftliche Gemeinschaft insgesamt der Astrologie skeptisch gegenübersteht. In vielen Ländern ist sie offiziell als Pseudowissenschaft anerkannt. Und offen gesagt, gibt es noch keine eindeutigen Beweise für die Effizienz astrologischer Methoden im Finanzbereich. Oft erweisen sich bestimmte beobachtete Korrelationen einfach als das Ergebnis kognitiver Verzerrungen.

Trotzdem gibt es viele Händler, die die Ideen der Finanzastrologie leidenschaftlich verteidigen.

Deshalb habe ich beschlossen, meine eigenen Nachforschungen anzustellen. Ich möchte versuchen, eine objektive Bewertung des Einflusses der Astrologie auf die Finanzmärkte mit Hilfe von statistischen Methoden und Big Data vorzunehmen. Wer weiß, vielleicht entdecken wir ja etwas Interessantes. In jedem Fall wird es eine faszinierende Reise in die Welt der Sterne und der Aktiencharts sein.

Überblick über die verwendeten Python-Bibliotheken

Ich werde ein ganzes Arsenal von Python-Bibliotheken benötigen. 

Zunächst habe ich beschlossen, das Skyfield-Paket zu verwenden, um astronomische Daten zu erhalten. Ich habe viel Zeit damit verbracht, das richtige Werkzeug auszuwählen, und Skyfield hat mich mit seiner Präzision beeindruckt. Mit seiner Hilfe werde ich in der Lage sein, Informationen über die Positionen von Himmelskörpern und die Mondphasen mit sehr hoher Genauigkeit im Dezimalbereich zu sammeln - alles, was ich für meine Datensätze benötige.

Was die Marktdaten betrifft, so fiel meine Wahl auf die offizielle MetaTrader 5-Bibliothek für Python. Es ermöglicht das Herunterladen von historischen Daten zu Währungspaaren und sogar das Eröffnen von Geschäften, falls erforderlich.

Pandas werden unsere treuen Begleiter bei der Arbeit mit Daten sein. Ich habe diese Bibliothek in der Vergangenheit häufig verwendet und sie ist für die Arbeit mit Zeitreihen einfach unverzichtbar. Ich werde es für die Vorverarbeitung und Synchronisierung aller gesammelten Daten verwenden.

Für die statistische Analyse habe ich mich für die SciPy-Bibliothek entschieden. Beeindruckend ist der große Funktionsumfang, insbesondere die Tools für Korrelations- und Regressionsanalysen. Ich hoffe, dass sie mir helfen werden, interessante Muster zu finden.

Um die Ergebnisse zu visualisieren, entschied ich mich, meine guten alten Freunde Matplotlib und Seaborn zu verwenden. Ich liebe diese Bibliotheken wegen ihrer Flexibilität bei der Erstellung von Diagrammen. Ich bin sicher, dass sie dazu beitragen werden, alle Ergebnisse zu veranschaulichen.

Das ganze Set ist zusammengebaut. Es ist, als würde man einen leistungsstarken PC aus hervorragenden Komponenten zusammenstellen. Wir haben nun alles, was wir brauchen, um eine umfassende Studie über den Einfluss astrologischer Faktoren auf die Finanzmärkte durchzuführen. Ich kann es kaum erwarten, in die Daten einzutauchen und meine Hypothesen zu testen!

Sammeln astronomischer Daten

import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests

# Loading planet ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    # Get solar activity data from NOAA API
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    # Convert date to 'YYYY-MM' format
    target_date = date.strftime("%Y-%m")
    
    # Find the closest date in the data
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

start_date = datetime(2024, 4, 1, tzinfo=utc)
end_date = datetime(2024, 5, 31, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)
    
    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame
df = pd.DataFrame(astronomical_data)

# Save data to CSV file
df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Data saved to astronomical_data_2018_2024.csv")

Dieser Python-Code sammelt astronomische Daten, die wir in Zukunft für Marktanalysen verwenden werden.

Der Code bezieht sich auf den Zeitraum vom 1. Januar 2018 bis zum 31. Mai 2024 und erfasst eine Reihe von Daten wie z. B.:

• Positionen der Planeten - Venus, Merkur, Mars, Jupiter, Saturn, Uranus und Neptun
• Mondphasen
• Sonnenaktivität
• Planetenaspekte (wie die Planeten zueinander ausgerichtet sind)

Das Skript enthält Bibliotheksimporte, die Hauptschleife und das Speichern von Daten im Excel-Format. Der Code verwendet die bereits erwähnte Skyfield-Bibliothek zur Berechnung von Planetenpositionen, Pandas für Daten und Anfragen zum Erhalt von Sonnenaktivitätsdaten.

Zu den bemerkenswerten Funktionen gehören get_planet_positions() zur Ermittlung der Planetenpositionen (Rektaszension und Deklination), get_moon_phase() zur Ermittlung der aktuellen Mondphase, get_solar_activity() zur direkten Lieferung von Daten zur Sonnenaktivität von der NOAA-API und calculate_aspects() zur Berechnung von Aspekten - den Positionen der Planeten zueinander.

Wir gehen jeden Tag als Teil des Zyklus durch und sammeln alle Daten. Deshalb speichern wir alles in einer Excel-Datei zur späteren Verwendung. 

Abrufen von Finanzdaten über MetaTrader 5

Um Finanzdaten zu erhalten, werden wir die MetaTrader 5-Bibliothek für Python verwenden. Die Bibliothek wird es uns ermöglichen, Finanzdaten direkt vom Broker herunterzuladen und Zeitreihen von Preisen für jedes Instrument zu erhalten. Hier ist unser Code zum Laden historischer Daten: 

import MetaTrader5 as mt5
import pandas as pd
from datetime import datetime

# Connect to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set query parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2018, 1, 1)
end_date = datetime(2024, 12, 31)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
df = pd.DataFrame(rates)
df['time'] = pd.to_datetime(df['time'], unit='s')

# Save data to CSV file
df.to_csv(f'{symbol}_data.csv', index=False)

# Terminate the connection to MetaTrader5
mt5.shutdown()

Das Skript stellt eine Verbindung zum Handelsterminal her, empfängt Daten zu EURUSD D1, erstellt dann einen Datenrahmen und speichert ihn in einer einzigen CSV-Datei. 

Synchronisierung von astronomischen und finanziellen Daten

Wir haben also Daten zur Astronomie, wir haben auch Daten zum EURUSD. Jetzt müssen wir sie synchronisieren. Fassen wir die Daten nach Daten zusammen, sodass ein einziger Datensatz alle notwendigen Informationen enthält, sowohl finanzielle als auch astronomische.

import pandas as pd

# Load data
astro_data = pd.read_csv('astronomical_data_2018_2024.csv')
financial_data = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_data['date'] = pd.to_datetime(astro_data['date'])
financial_data['time'] = pd.to_datetime(financial_data['time'])

# Merge data
merged_data = pd.merge(financial_data, astro_data, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)

Das Skript lädt alle gespeicherten Daten, formatiert Datumsspalten im Datumsformat und kombiniert Datensätze nach Datum. Als Ergebnis erhalten wir eine CSV-Datei, die alle Daten enthält, die wir für zukünftige Analysen benötigen.

Statistische Analyse der Korrelationen

Weiter geht's. Wir haben einen gemeinsamen Satz, einen gemeinsamen Datensatz, und es ist an der Zeit herauszufinden, ob es in den Daten irgendwelche Beziehungen zwischen Astronomie und Marktbewegungen gibt. Wir werden die Funktionen corr() aus der Pandas-Bibliothek verwenden. Außerdem werden wir unsere beiden Codes zu einem einzigen zusammenfassen.

Hier ist das endgültige Skript:

import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt

# Part 1: Collecting astronomical data

# Loading planetary ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']

    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()

    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()

    target_date = date.strftime("%Y-%m")

    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))

    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees

            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"

    return aspects

# Collecting astronomical data
start_date = datetime(2024, 3, 1, tzinfo=utc)
end_date = datetime(2024, 7, 30, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)

    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)

    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame and save
astro_df = pd.DataFrame(astronomical_data)
astro_df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Astronomical data saved to astronomical_data_2018_2024.csv")

# Part 2: Retrieving financial data via MetaTrader5

# Initialize connection to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set request parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2024, 3, 1)
end_date = datetime(2024, 7, 30)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
financial_df = pd.DataFrame(rates)
financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')

# Save financial data
financial_df.to_csv(f'{symbol}_data.csv', index=False)
print(f"Financial data saved to {symbol}_data.csv")

# Shutdown MetaTrader5 connection
mt5.shutdown()

# Part 3: Synchronizing astronomical and financial data

# Load data
astro_df = pd.read_csv('astronomical_data_2018_2024.csv')
financial_df = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
financial_df['time'] = pd.to_datetime(financial_df['time'])

# Merge data
merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)
print("Merged data saved to merged_astro_financial_data.csv")

# Part 4: Statistical analysis of correlations

# Select numeric columns for correlation analysis
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Create lags for astronomical data
for col in numeric_columns:
    if col not in ['open', 'high', 'low', 'close', 'tick_volume', 'spread', 'real_volume']:
        for lag in range(1, 6):  # Create lags from 1 to 5
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)

# Update list of numeric columns
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Calculate correlation matrix
correlation_matrix = merged_data[numeric_columns].corr()

# Create heatmap of correlations
plt.figure(figsize=(20, 16))
sns.heatmap(correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0)
plt.title('Correlation Matrix of Astronomical Factors (with Lags) and EURUSD Prices')
plt.tight_layout()
plt.savefig('correlation_heatmap_with_lags.png')
plt.close()

# Output the most significant correlations with the closing price
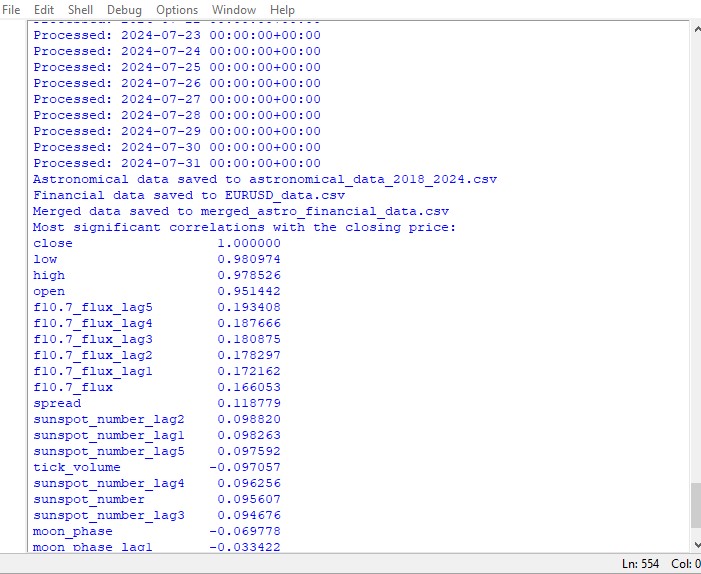
significant_correlations = correlation_matrix['close'].sort_values(key=abs, ascending=False)
print("Most significant correlations with the closing price:")
print(significant_correlations)

# Create a separate correlation matrix for astronomical data with lags and the current price
astro_columns = [col for col in numeric_columns if col not in ['open', 'high', 'low', 'tick_volume', 'spread', 'real_volume']]
astro_columns.append('close')  # Add the current closing price
astro_correlation_matrix = merged_data[astro_columns].corr()

# Create heatmap of correlations for astronomical data with lags and the current price
import seaborn as sns
import matplotlib.pyplot as plt

# Increase the header and axis label font
plt.figure(figsize=(18, 14))
sns.heatmap(astro_correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0, cbar_kws={'label': 'Correlation'})
plt.title('Correlation matrix of astronomical factors (with lags) and current EURUSD price', fontsize=24)
plt.xlabel('X-axis Label', fontsize=30)
plt.ylabel('Y-axis Label', fontsize=30)
plt.xticks(fontsize=30)
plt.yticks(fontsize=30)
plt.tight_layout()
plt.savefig('astro_correlation_heatmap_with_lags.png')
plt.close()

print("Analysis completed. Results saved in CSV and PNG files.")

Dieses Skript zeigt eine Karte der Korrelationen zwischen allen Zahlen im Datensatz und eine Matrix aller Korrelationen im Heatmap-Format an und erstellt eine Liste der wichtigsten Korrelationen mit den Schlusskursen.

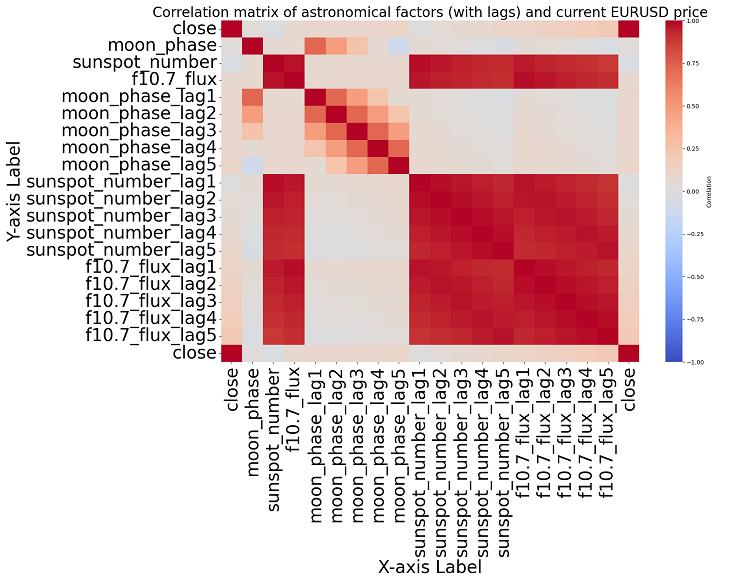
Das Vorhandensein oder Nichtvorhandensein einer Korrelation impliziert nicht das Vorhandensein oder Nichtvorhandensein eines Kausalzusammenhangs. Selbst wenn wir starke Korrelationen zwischen astronomischen Daten und Preisbewegungen feststellen würden, würde dies nicht bedeuten, dass der eine Faktor den anderen bestimmt und umgekehrt. Es sind neue Forschungen erforderlich, da die Korrelationskarte nur die grundlegendste Sache ist.

Wenn wir uns näher mit dem Thema beschäftigen, können wir keine signifikante Korrelation in den Daten finden. Es gibt keine eindeutigen Korrelationen zwischen früheren Astronomiedaten und Marktindikatoren.

Maschinelles Lernen zur Rettung

Ich überlegte, was ich als Nächstes tun sollte, und beschloss, ein maschinelles Lernmodell anzuwenden. Ich habe zwei Skripte mit der CatBoost-Bibliothek erstellt, die versuchen, künftige Preise vorherzusagen, indem sie Daten aus dem Datensatz als Merkmale verwenden. Hier ist das erste der Modelle - ein Regressionsmodell: 

import pandas as pd
import numpy as np
from catboost import CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder

# Loading data
data = pd.read_csv('merged_astro_financial_data.csv')

# Converting date to datetime
data['date'] = pd.to_datetime(data['date'])

# Creating lags for financial data
for col in ['open', 'high', 'low', 'close']:
    for lag in range(1, 6):  # Creating lags from 1 to 5
        data[f'{col}_lag{lag}'] = data[col].shift(lag)

# Creating lags for astronomical data
astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
for col in astro_cols:
    data[f'{col}_ra'] = data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
    data[f'{col}_dec'] = data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
    for lag in range(1, 6):  # Lags from 1 to 5
        data[f'{col}_ra_lag{lag}'] = data[f'{col}_ra'].shift(lag)
        data[f'{col}_dec_lag{lag}'] = data[f'{col}_dec'].shift(lag)
    data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

# Converting aspects to numerical features
aspect_cols = ['mercury_saturn', 'venus_mars', 'venus_jupiter', 'venus_uranus', 
               'mars_jupiter', 'mars_uranus', 'jupiter_uranus', 'mercury_neptune', 
               'venus_saturn', 'venus_neptune', 'mars_saturn', 'mercury_venus', 
               'mars_neptune', 'mercury_uranus', 'saturn_neptune', 'mercury_jupiter', 
               'mercury_mars', 'jupiter_saturn']

# Using LabelEncoder for encoding aspects
label_encoders = {}
for col in aspect_cols:
    label_encoders[col] = LabelEncoder()
    data[col] = label_encoders[col].fit_transform(data[col].astype(str))

# Filling missing values with mean values for numeric columns
numeric_cols = data.select_dtypes(include=[np.number]).columns
data[numeric_cols] = data[numeric_cols].fillna(data[numeric_cols].mean())

# Removing rows with missing values
data = data.dropna()

# Preparing features and target variable
features = [col for col in data.columns if col not in ['date', 'time', 'close']]
X = data[features]
y = data['close']

# Splitting data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

# Creating and training the CatBoost model
model = CatBoostRegressor(iterations=500, learning_rate=0.1, depth=9, random_state=1)
model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

# Evaluating the model
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
print(f"Mean Absolute Error: {mae}")
print(f"R-squared Score: {r2}")

# Visualizing feature importance
feature_importance = model.feature_importances_
feature_names = X.columns
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
plt.figure(figsize=(12, 6))
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(feature_names)[sorted_idx])
plt.xlabel('Feature Importance')
plt.title('Feature Importance')
plt.show()

# Predicting the next value
def predict_next():
    # Selecting the last row of data
    last_data = data.iloc[-1]
    input_features = last_data[features].values.reshape(1, -1)
    # Prediction
    prediction = model.predict(input_features)
    print(f"Prediction for the next closing price: {prediction[0]}")

# Example of using the function to predict the next value
predict_next()

Das zweite Modell ist die Klassifizierung:

import pandas as pd
import numpy as np
from skyfield.api import load, utc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.preprocessing import LabelEncoder

# Part 1: Collecting astronomical data

planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    target_date = date.strftime("%Y-%m")
    
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

# Part 2: Obtaining financial data through MetaTrader5

def get_financial_data(symbol, start_date, end_date):
    if not mt5.initialize():
        print("initialize() failed")
        mt5.shutdown()
        return None

    timeframe = mt5.TIMEFRAME_D1

    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    mt5.shutdown()

    financial_df = pd.DataFrame(rates)
    financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')
    return financial_df

# Part 3: Synchronizing astronomical and financial data

def sync_data(astro_df, financial_df):
    astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
    financial_df['time'] = pd.to_datetime(financial_df['time'])
    merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')
    return merged_data

# Part 4: Training the model and making predictions

def train_and_predict(merged_data):
    # Converting aspects to numerical features
    aspect_cols = [col for col in merged_data.columns if '_' in col and col not in ['date', 'time']]
    label_encoders = {}
    for col in aspect_cols:
        label_encoders[col] = LabelEncoder()
        merged_data[col] = label_encoders[col].fit_transform(merged_data[col].astype(str))
    
    # Creating lags for financial data
    for col in ['open', 'high', 'low', 'close']:
        for lag in range(1, 6):
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)
    
    # Creating lags for astronomical data
    astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
    for col in astro_cols:
        merged_data[f'{col}_ra'] = merged_data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
        merged_data[f'{col}_dec'] = merged_data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
        for lag in range(1, 6):
            merged_data[f'{col}_ra_lag{lag}'] = merged_data[f'{col}_ra'].shift(lag)
            merged_data[f'{col}_dec_lag{lag}'] = merged_data[f'{col}_dec'].shift(lag)
        merged_data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

    # Filling missing values with mean values for numeric columns
    numeric_cols = merged_data.select_dtypes(include=[np.number]).columns
    merged_data[numeric_cols] = merged_data[numeric_cols].fillna(merged_data[numeric_cols].mean())

    merged_data = merged_data.dropna()

    # Creating binary target variable
    merged_data['price_change'] = (merged_data['close'].shift(-1) > merged_data['close']).astype(int)

    # Removing rows with missing values in the target variable
    merged_data = merged_data.dropna(subset=['price_change'])

    features = [col for col in merged_data.columns if col not in ['date', 'time', 'close', 'price_change']]
    X = merged_data[features]
    y = merged_data['price_change']

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

    model = CatBoostClassifier(iterations=500, learning_rate=0.1, depth=9, random_state=1)
    model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    clf_report = classification_report(y_test, y_pred)
    conf_matrix = confusion_matrix(y_test, y_pred)

    print(f"Accuracy: {accuracy}")
    print("Classification Report:")
    print(clf_report)
    print("Confusion Matrix:")
    print(conf_matrix)

    # Visualizing feature importance
    feature_importance = model.feature_importances_
    feature_names = X.columns
    sorted_idx = np.argsort(feature_importance)
    pos = np.arange(sorted_idx.shape[0]) + 0.5

    plt.figure(figsize=(12, 6))
    plt.barh(pos, feature_importance[sorted_idx], align='center')
    plt.yticks(pos, np.array(feature_names)[sorted_idx])
    plt.xlabel('Feature Importance')
    plt.title('Feature Importance')
    plt.show()

    # Predicting the next value
    def predict_next():
        last_data = merged_data.iloc[-1]
        input_features = last_data[features].values.reshape(1, -1)
        prediction = model.predict(input_features)
        print(f"Price change prediction (0: will decrease, 1: will increase): {prediction[0]}")

    predict_next()

# Main program
start_date = datetime(2023, 3, 1)
end_date = datetime(2024, 7, 30)

astro_data = []
current_date = start_date

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    astro_data.append({
        'date': current_date,
        'mercury': str(planet_positions['mercury']),
        'venus': str(planet_positions['venus']),
        'mars': str(planet_positions['mars']),
        'jupiter': str(planet_positions['jupiter']),
        'saturn': str(planet_positions['saturn']),
        'uranus': str(planet_positions['uranus']),
        'neptune': str(planet_positions['neptune']),
        'moon_phase': moon_phase,
        **solar_activity,
        **aspects
    })
    
    current_date += timedelta(days=1)

astro_df = pd.DataFrame(astro_data)

symbol = "EURUSD"
financial_data = get_financial_data(symbol, start_date, end_date)

if financial_data is not None:
    merged_data = sync_data(astro_df, financial_data)
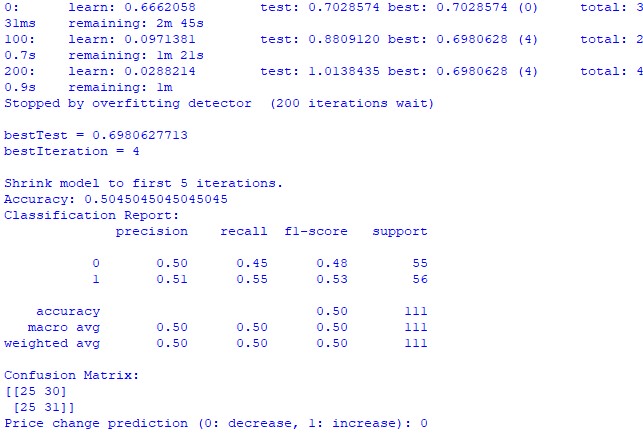
    train_and_predict(merged_data)

Leider sind beide Modelle nicht sehr genau. Die Klassifizierungsgenauigkeit liegt bei etwas mehr als 50 %, was bedeutet, dass wir genauso gut eine Vorhersage auf der Grundlage eines Münzwurfs treffen können.

Vielleicht kann das Ergebnis noch verbessert werden, da dem Regressionsmodell wenig Aufmerksamkeit geschenkt wurde und es in der Tat möglich ist, die Preise anhand der Planetenpositionen und der Aktivität von Mond und Sonne vorherzusagen. Ich werde einen weiteren Artikel zu diesem Thema schreiben, wenn ich in der Stimmung bin.

Ergebnisse

Es ist also an der Zeit, die Ergebnisse zusammenzufassen. Nach der Durchführung einer einfachen Analyse und der Erstellung von zwei Prognosemodellen sehen wir die Ergebnisse der Studie über die möglichen Auswirkungen der Astrologie auf den Markt. 

Die Korrelationsanalyse. Die Korrelationskarte, die wir erhielten, zeigte keine starke Korrelation zwischen den Planetenpositionen und dem EURUSD-Schlusskurs. Alle unsere Korrelationen sind schwächer als 0,3, was uns zu der Annahme veranlasst, dass die Position von Sternen oder Planeten überhaupt nicht mit den Finanzmärkten zusammenhängt.

Das Regressionsmodell CatBoost. Die endgültigen Ergebnisse des Regressionsmodells zeigten, dass die Fähigkeit zur Vorhersage künftiger Schlusskurse auf der Grundlage astronomischer Daten sehr gering ist.

Die sich daraus ergebenden Modellleistungskennzahlen, wie MSE, MAE und R-Quadrat, sind sehr schwach und erklären die Daten sehr schlecht. Gleichzeitig zeigt das Modell, dass die wichtigsten Merkmale Verzögerungen und frühere Preiswerte sind, und nicht die Planetenpositionen. Heißt das also, dass der Preis ein besserer Indikator ist als die Position eines beliebigen Planeten in unserem Sonnensystem?

Das Klassifizierungsmodell CatBoost. Das Klassifizierungsmodell ist extrem schlecht bei der Vorhersage zukünftiger Preissteigerungen oder -senkungen. Die Genauigkeit übersteigt kaum 50 %, was ebenfalls bestätigt, dass die Astronomie auf dem realen Markt nicht funktioniert.

Schlussfolgerung

Die Ergebnisse der Studie sind eindeutig: Die Methoden der Astrologie und die Versuche, die Preise auf dem realen Markt auf der Grundlage astronomischer Daten vorherzusagen, sind völlig nutzlos. Vielleicht werde ich auf dieses Thema zurückkommen, aber im Moment sehen die Lehren von William Gann wie Versuche aus, nicht funktionierende Lösungen zu verschleiern, die nur geschaffen wurden, um Bücher und Handelskurse zu verkaufen.

Könnte es sein, dass ein verbessertes Modell, das auch die Gann-Winkelwerte, das 9er-Quadrat und die Gann-Rasterwerte verwendet, besser abschneiden würde? Das wissen wir noch nicht. Ich bin ein wenig enttäuscht von den Ergebnissen der Studie.

Ich bin aber nach wie vor der Meinung, dass die Gann-Winkel auf die eine oder andere Weise verwendet werden können, um funktionierende Kursprognosen zu erhalten. Der Preis wirkt sich auf die eine oder andere Weise auf die Winkel aus, er reagiert auf sie, was aus den Ergebnissen der vorangegangenen Studie ersichtlich ist. Es ist auch möglich, dass Winkel als Arbeitsmerkmale für das Training von Modellen verwendet werden können. Ich werde versuchen, einen solchen Datensatz zu erstellen und sehen, was dabei herauskommt.