Neuronales Netz in der Praxis: Skizze eines Neurons

Einführung

Hallo und herzlich willkommen zu einem weiteren Artikel über neuronale Netze.

Im vorherigen Artikel Neuronales Netzwerk in der Praxis: Pseudoinverse (II) habe ich die Bedeutung spezieller Rechensysteme und die Gründe für ihre Entwicklung erörtert. In diesem neuen Artikel über neuronale Netze werden wir uns näher mit dem Thema befassen. Die Erstellung von Material für diese Phase ist keine einfache Aufgabe. Auch wenn es einfach zu sein scheint, kann es eine Herausforderung sein, etwas zu erklären, das oft für große Verwirrung sorgt.

Was werden wir in dieser Phase behandeln? In dieser Serie möchte ich zeigen, wie ein neuronales Netz lernt. Bislang haben wir untersucht, wie ein neuronales Netz Korrelationen zwischen verschiedenen Datenpunkten herstellt. Die bisher diskutierten Methoden sind jedoch nur anwendbar, wenn mit einem vorverarbeiteten und gefilterten Datensatz gearbeitet wird. So kann das neuronale Netz auf der Grundlage der vorhandenen Informationen optimale Lösungen ermitteln. Aber was passiert, wenn die Daten ungefiltert sind? Wie stellt ein neuronales Netz in solchen Fällen Korrelationen her? Hier glauben viele Menschen fälschlicherweise, dass ein neuronales Netz über eine Art von Intelligenz verfügt. Sie gehen davon aus, dass es auf autonome, menschenähnliche Weise „lernt“, Dinge zu klassifizieren.

Dieses weit verbreitete Missverständnis macht es besonders schwierig, neuronale Netze zu erklären. Oft fehlt denjenigen, die sie verstehen wollen, das Grundwissen, wie man die verschiedenen Arten von Informationen sortiert, selbst wenn die Daten in einem gewissen Zusammenhang stehen. Dies ist der verwirrendste Punkt für diejenigen, die nicht damit arbeiten. Infolgedessen können sie Erklärungen falsch interpretieren, was zu weiterer Verwirrung über die Funktionsweise neuronaler Netze führt.

Um das klarzustellen: Ich behaupte nicht, dass neuronale Netze auf die gleiche Weise lernen wie Menschen. Sie verfügen über keine versteckte Intelligenz. Jeder, der etwas anderes glaubt, irrt. Ein neuronales Netz ist nichts anderes als eine komplexe, mathematische Gleichung. Diese Gleichung hat jedoch die bemerkenswerte Fähigkeit, Daten zu analysieren und zu klassifizieren. Sobald ein Datensatz klassifiziert ist, wird jedem neuen Datenpunkt, der einer bestehenden Klassifizierung ähnelt, eine Wahrscheinlichkeit zugeordnet, zu einer bekannten Kategorie zu gehören.

Dieses Konzept wurde bereits in früheren Artikeln behandelt, aber hier werden wir einen etwas anderen Ansatz wählen. Dieser Ansatz ist ebenso grundlegend wie faszinierend. Wir werden mit den absoluten Grundlagen beginnen und uns schrittweise bis zur Konstruktion eines neuronalen Netzes mit künstlichen Neuronen vorarbeiten.

Die Grundlagen

Um wirklich zu verstehen, wie ein neuronales Netz lernt, wenn wir ihm Informationen zeigen, bitte ich Sie, alles zu vergessen, was Sie über künstliche Intelligenz und neuronale Netze zu wissen glauben. Vieles von dem, was Sie zu wissen (glauben), ist wahrscheinlich reiner Unsinn oder eine Fehlinformation, vor allem, wenn Sie es auf Nachrichtenseiten oder anderen solchen Quellen gelesen haben. Das Thema neuronale Netze ist vor allem deshalb in den Blickpunkt der Öffentlichkeit gerückt, weil einige Unternehmer darin eine Chance zum Geldverdienen sahen, aber neuronale Netze werden schon seit Jahrzehnten entwickelt. Sie sind weder neu noch funktionieren sie so, wie sie oft dargestellt werden. Obwohl sie sehr nützlich sind, richten sie sich in erster Linie an Personen, die ein starkes Interesse am Programmieren haben.

Im Kern beruhen alle neuronalen Netze (die manche als künstliche Intelligenz bezeichnen) auf einem einfachen mathematischen Prinzip, das bereits in früheren Artikeln erläutert wurde. Im Folgenden werden wir dieses Konzept näher betrachten. Dies ist die Sekante. Ungeachtet dessen, was andere behaupten, läuft bei neuronalen Netzen alles auf dieses grundlegende Konzept hinaus - die Suche nach einer Sekante, die sich der Tangente annähert. Es ist eigentlich ganz einfach.

In früheren Diskussionen haben wir diesen Schritt umgangen und sind direkt zur Bestimmung der Tangente übergegangen. Dies erklärt die zuvor eingeführten Formeln. Diese Formeln wurden speziell entwickelt, um den Prozess abzukürzen und direkt zur Tangente zu gelangen. All dieses Material bezieht sich auf eine ganz bestimmte Tatsache: wenn wir gefilterte, ausgewählte Informationen in unserer Datenbank haben. In diesem Fall brauchen wir keine Sekante, sondern gehen direkt zur Tangente über und erstellen eine Formel, die den Inhalt dieses Datensatzes am besten wiedergibt. Wenn also ein Suchprogramm diesen Datensatz abfragt, kann es ein nahezu perfektes Ergebnis zu einer bestimmten Information liefern. Viele Menschen bezeichnen diese Art von Programm als künstliche Intelligenz. In Fällen, in denen die Datensätze unvollständig oder unstrukturiert sind, ist jedoch ein anderer Ansatz erforderlich. Das neuronale Netz muss in der Lage sein, Korrelationen zwischen scheinbar unverbundenen Datenpunkten herzustellen. Dieser Prozess wird als Training bezeichnet. Einfach ausgedrückt: Wir haben Rohdaten, die zunächst keine Korrelation aufzuweisen scheinen. Diese Daten werden systematisch in das neuronale Netz eingespeist, das nach und nach lernt, die Tangente zu approximieren. Dieser Prozess führt letztendlich zu einer mathematischen Gleichung, die es dem KI-System ermöglicht, nützliche Vorhersagen zu treffen. Dies wird bestätigt, wenn Daten, die dem Netz unbekannt sind, aber von einem Menschen sortiert wurden, zur Prüfung der Gleichung verwendet werden.

Ich weiß nicht, ob Sie es geschafft haben, zu verstehen, wie das alles funktioniert, aber ich werde versuchen, es für diejenigen, die noch keine Programmierer sind, aber bereits Erfahrung in der Arbeit auf dem Finanzmarkt haben, klarer zu erklären. Wenn Sie mit der Arbeit am Markt beginnen, müssen Sie als erstes einen so genannten Backtest durchführen. Wir wählen ein Modell für den Handel aus, gehen zum Chart und suchen nach allen Signalen, in denen dieses Modell erscheint. Dies entspricht der Trainingsphase eines neuronalen Netzes. Sobald das Modell eine gewisse Zeit lang vollständig getestet wurde, gehen wir in die Testphase über. Hier wählen wir zufällige Zeiträume aus, um zu überprüfen, ob das Modell gültig bleibt. Wenn wir das Modell immer wieder erkennen können, auch wenn seine Muster weniger offensichtlich sind, haben wir es tatsächlich verinnerlicht und können es mathematisch ausdrücken. Der letzte Schritt ist der Blindtest. Hier steigen wir mit einem Demokonto in den Markt ein, um zu prüfen, ob unser mathematisches Modell zuverlässig ist. Wenn Sie das schon einmal gemacht haben, dann wissen Sie, dass das System nie zu 100 % genau ist, sondern immer Raum für Fehler hat. Ein Modell mit einer geringen Fehlermarge gilt jedenfalls als effektiv.

Genau das versucht ein neuronales Netz zu erreichen: Es formuliert eine Gleichung, die es ihm ermöglicht, Muster zu erkennen, sei es in Handschriften, bei der Gesichtserkennung, bei Molekularstrukturen, Pflanzenarten, Tieren, Tönen, Bildern oder jeder anderen Form der Klassifizierung.

Lassen Sie uns nun zum nächsten Thema übergehen und untersuchen, wie wir dies erreichen können.

Das Neuron

Nachdem wir nun das vorhergehende Thema behandelt haben, wollen wir mit dem einfachsten Element beginnen, das Sie erstellen können: einem einzelnen Neuron. Unterschätzen Sie jedoch nicht seine Bedeutung. Während wir mit einem einzigen Neuron beginnen, wird die Komplexität schnell zunehmen. Daher möchte ich Sie ermutigen, methodisch vorzugehen und die einzelnen Komponenten nach und nach zu verstehen. Dieser schrittweise Ansatz wird entscheidend sein, wenn wir mit dem Aufbau ganzer neuronaler Netzarchitekturen beginnen.

Beginnen wir also mit dem folgenden Code.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    Print("The first neuron...");
}
//+------------------------------------------------------------------+

Dieser scheinbar uninteressante Code gibt einfach eine Meldung auf dem Terminal aus. Das war's! Denken Sie aber daran, dass es sich um ein Skript handelt, auch wenn es zu einem Dienst werden kann. Für den Moment belassen wir es bei einem einfachen Skript. Was also soll ein Neuron tun? Sie können an tausend verschiedene Dinge denken, aber versuchen Sie, sie auf ein gemeinsames Ziel zu reduzieren. Dies ist der erste Teil, in dem alles auf eine Aufgabe hinausläuft, die das Neuron erfüllen muss.

Ein Neuron muss wissen, wie es Berechnungen durchführen kann. Dies ist wichtig, weil sie einige Informationen zurückgeben muss. Wir wissen jedoch noch nicht, wie diese Berechnungen aussehen, wir haben nur die Daten, die zum Trainieren des Neurons benötigt werden. Der obige Code wird also geändert und verwandelt sich in den unten gezeigten Code.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };

    Print("The first neuron...");
}
//+------------------------------------------------------------------+

Wenn man sich die Trainingsdaten ansieht, wird sofort klar, dass sie eine Art Muster enthalten. Das heißt, wir multiplizieren die erste Zahl mit zwei. Aber unser Neuron weiß das noch nicht. Wir wollen, dass es lernt, wie man eine Gleichung entwickelt, sodass es die richtige Antwort auf eine Zahl geben kann. Das Neuron verwendet dann die Gleichung, die es erstellt hat, um auf der Grundlage des Gelernten eine Ausgabe zu erzeugen.

Klingt gut, aber wie bringen wir das Neuron dazu, diese Formel zu entdecken? Und hier ist der Haken: Wir können nicht einfach das Wissen aus früheren Artikeln verwenden. Wie können wir also das Neuron dazu bringen, die Gleichung zu finden, die die Trainingsdaten am besten repräsentiert?

Dies ist der Punkt, an dem viele Menschen dazu neigen, sich zu verwirren. Wir werden dem Neuron einfach sagen, dass es mit einem Zufallswert beginnen und diesen als Grundlage für die Suche nach der richtigen mathematischen Gleichung verwenden soll. Dies ist ein wesentlicher Punkt des Missverständnisses. Wir sagen dem Neuron nicht, dass es nach der genauen Zahl suchen soll, die bei der Multiplikation verwendet werden soll. Schließlich könnten wir Addition, Division oder sogar Zufallsdaten verwenden. Was wir eigentlich wollen, ist, dass das Neuron eine Gleichung findet, nicht nur einen einzelnen Wert. Der Anfangswert, den wir ihm zugestehen, ist nichts weiter als ein Startpunkt, das ist alles. Lassen Sie uns nun unseren Code ein wenig verfeinern, wie unten gezeigt.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
}
//+------------------------------------------------------------------+

Also gut, wir machen Fortschritte! Doch bevor wir weitermachen, sollten wir etwas Wichtiges besprechen. Normalerweise wird die MathSrand-Funktion mit einem Wert der Systemuhr initialisiert. Dadurch wird sichergestellt, dass der Zufallszahlengenerator jedes Mal, wenn er gestartet wird, an einem anderen Punkt beginnt. Nur zur Erinnerung: Die generierten Zahlen sind nicht wirklich zufällig, sondern pseudozufällig. Das bedeutet, dass sie zwar nicht völlig zufällig sind, aber es ist schwierig, die nächste Zahl in der Folge vorherzusagen. Da wir den Startpunkt kontrollieren wollen, geben wir MathSrand explizit einen Anfangswert vor, was eine konsistentere Prüfung ermöglicht. Entscheidend ist der Wert, der in der Variablen „weight“ (Gewicht) gespeichert ist. Dieser Wert sagt unserem Neuron, ob es auf dem richtigen Weg ist oder nicht. Da er als Zufallswert beginnt, hat er noch keine bestimmte Richtung.

Ein weiterer wichtiger Punkt: Der Gewichtswert liegt zwischen 0 und 1. Das liegt daran, dass in unserem Makro das Ergebnis der Funktion „rand“ durch ihren maximal möglichen Rückgabewert geteilt wird. Weitere Einzelheiten hierzu finden Sie in der Dokumentation. Ich beschränke das Gewicht auf diesen Bereich, um die nächsten Schritte zu vereinfachen. Es steht Ihnen jedoch frei, den rohen Randwert zu verwenden, wenn Sie dies bevorzugen; Sie sollten sich nur bewusst sein, dass später einige Anpassungen erforderlich sein werden, wenn wir weitere Berechnungen durchführen.

Und jetzt lasst uns anfangen, die Dinge in die Tat umzusetzen! Unser Neuron beginnt Gestalt anzunehmen. Doch bevor wir weitermachen, müssen wir zunächst eine erste mathematische Formel definieren, die er verwenden soll. Von nichts kommt nichts - wir müssen dem neuronalen Netz sagen, wie es funktionieren soll. Sie kann sich nicht selbst aus dem Nichts erschaffen. Wenn Sie auch nur ein Grundverständnis für mathematische Berechnungen haben, wissen Sie, dass sich alles, von den einfachsten Gleichungen bis hin zu den komplexesten Polynomen, auf ein einziges Grundkonzept reduzieren lässt. Ich spreche von Derivaten. Aber nicht irgendeine Ableitung, sondern eine, die so einfach wie möglich ist. In früheren Artikeln habe ich gezeigt, dass die Gleichung einer Geraden die einfachste mögliche Gleichung ist. Jedes Polynom oder jede Gleichung lässt sich auf diese lineare Gleichung reduzieren, wenn man sie auf ihre einfachste Form herunterdifferenziert. Wenn wir weiter differenzieren, könnten wir schließlich bei einer Konstante landen. Aber das wäre für uns nicht von Nutzen. Was wir brauchen, ist ein Derivat, das als minimales Berechnungsinstrument dient. Damit sind wir wieder bei der unten stehenden Gleichung.

In diesem Stadium spielt die Reihenfolge der Ableitung keine Rolle. Wichtig ist, dass wir, wenn wir zu sehr vereinfachen, eine Konstante erhalten, die in diesem Fall nutzlos ist. Die Konstante < b > (der Achsenabschnitt) sollte jedoch vorerst als Null betrachtet werden. In der Zwischenzeit wird die Konstante <a > (die Steigung) auf den in Gewicht gespeicherten Wert gesetzt. Mit diesem Ansatz können wir nun unseren Code weiter verfeinern, wie unten gezeigt:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, x;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    for (uint c = 0; c < Train.Size() / 2; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
    }
}
//+------------------------------------------------------------------+

Nachdem Sie diesen Code ausgeführt haben, sehen Sie im MetaTrader-Terminal ein Bild ähnlich dem unten abgebildeten.

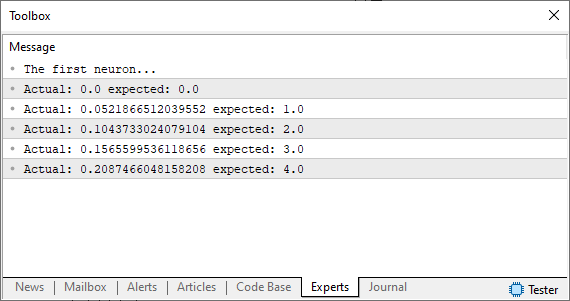
Beachten Sie, dass wir eine Annahme verwenden, d. h. dieselbe Zufallszahl, die nicht annähernd dem entspricht, was wir erwarten oder erreichen wollen. Wie können wir die Situation verbessern? Okay, unser Basisneuron ist auf dem Weg. Jetzt müssen wir das gleiche Prinzip wie in den vorherigen Artikeln anwenden. Mit anderen Worten: Wir werden ein Fehlersystem definieren, damit das Neuron weiß, wohin es sich bewegen muss, um die am besten geeignete Gleichung zu finden. Dies ist recht einfach, wie Sie im folgenden Code sehen können.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, dx, x, err;
    const uint nTrain = Train.Size() / 2;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
    err = 0;
        
    for (uint c = 0; c < nTrain; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
        dx = fx - Train[c][1];
        err += MathPow(dx, 2);
    }
    Print("Err: ", err / nTrain);
}
//+------------------------------------------------------------------+

Wenn Sie diesen Code ausführen, sollten Sie etwas ähnliches wie das folgende Bild sehen.

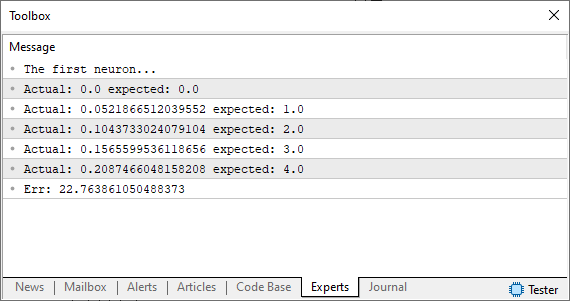
An diesem Punkt befinden wir uns an einem Scheideweg. Das ist genau der Moment, in dem wir bisher die Werte manuell anpassen mussten, um Fehler zu minimieren. Wenn Sie sich nicht sicher sind, was ich meine, lesen Sie die vorherigen Artikel, um den Zusammenhang zu verstehen. Anstatt jedoch wie bisher manuelle Einstellungen vorzunehmen, lassen wir diesmal den Computer die Arbeit machen. Anstatt die Tangente auf die gleiche Weise zu finden wie zuvor, werden wir uns ihr über die Sekante nähern. Und jetzt wird es interessant - die Maschine beginnt nun, bei der Suche nach der bestmöglichen Passform „verrückt“ zu spielen. Manchmal konvergiert sie in Richtung der richtigen Lösung, und manchmal weicht sie völlig ab.

Unser Ziel ist es, den Wert der Variablen „err“ zu verringern. Dies ist der Grund für das unberechenbare Verhalten der Maschine. Um dies besser zu verstehen, wollen wir uns einem neuen Thema zuwenden.

Verwendung der Sekante

In dem Artikel „Neuronale Netze in der Praxis: Die Sekante“ Ich habe kurz erwähnt, dass die Sekante eine grundlegende Rolle in neuronalen Netzen spielt. Dort habe ich ein Diagramm gezeigt, das Sie unten einsehen können.

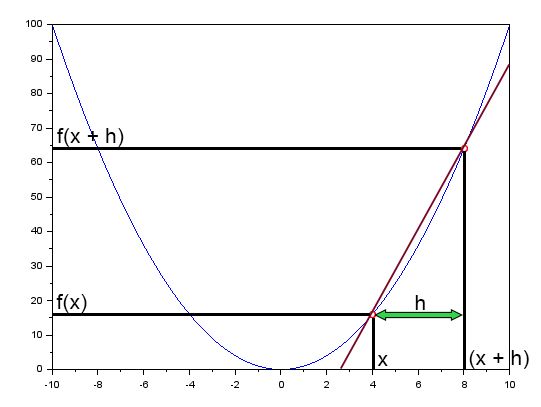
Dieses Diagramm veranschaulicht die Fehlerkurve zusammen mit einer geraden Linie. Dies ist die Sekante. Wenn man das Diagramm vereinfacht und nur die Sekante beibehält, erhält man das folgende Bild.

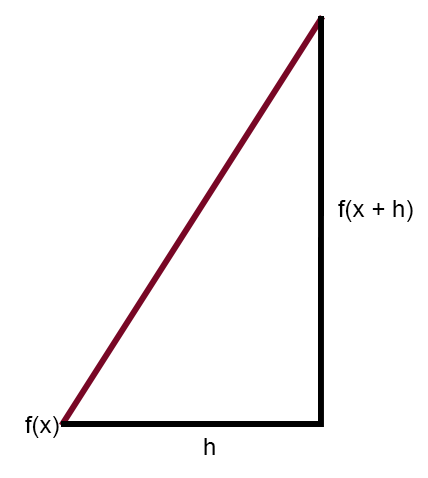
Wenn man nun dieses Diagramm so verändert, dass die Konstante < h > gleich Null ist, erhält man den folgenden Ausdruck:

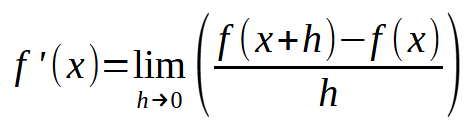
Jetzt wird es spannend. Die obige Formel ist im Wesentlichen die „Zauberformel“, die es einem neuronalen Netz ermöglicht, aus seinen Fehlern zu lernen. Durch die Anwendung dieser Gleichung können wir den Computer zwingen, die Linie zu finden, die am besten zu den Eingabedaten passt. Auf diese Weise kann die Maschine lernen, wie sie ein bestimmtes Problem lösen kann, ganz gleich, um welches Problem es sich handelt. Unabhängig davon, welche Daten Sie in das neuronale Netz einspeisen, bleibt die zugrunde liegende Berechnung dieselbe. Achten Sie jedoch genau darauf: Der Schlüssel liegt in der Wahl eines geeigneten Wertes für < h >. Wenn der Wert eine bestimmte Grenze überschreitet, wird die Maschine bei der Suche nach der besten Liniengleichung „verrückt“. Wenn der Wert zu klein ist, verbringt die Maschine viel Zeit mit der Suche nach der am besten passenden Gleichung, sodass ein wenig gesunder Menschenverstand in dieser Angelegenheit nicht schaden kann. Hier ist also ein gutes Urteilsvermögen gefragt. Seien Sie nicht übermäßig anspruchsvoll, aber auch nicht zu nachlässig. Finden Sie einen ausgewogenen Näherung.

Wie können wir dies nun in unser Neuron einbauen? Bevor wir irgendwelche Änderungen vornehmen, sollten wir zunächst einen kleinen Test durchführen. Nachfolgend sehen Sie, wie unser aktualisierter Code aussehen sollte.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 2},
                    {2, 4},
                    {3, 6},
                    {4, 8},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((Train[c][0] * w) - Train[c][1], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    Print("Err: ", Cost(weight));
    Print("Err: ", Cost(weight + eps));
}
//+------------------------------------------------------------------+

Wow! Jetzt fängt es an, sich wie ein richtiges Programm anzufühlen. Wenn Sie es ausführen, sollten Sie etwas ähnliches wie das folgende Bild sehen.

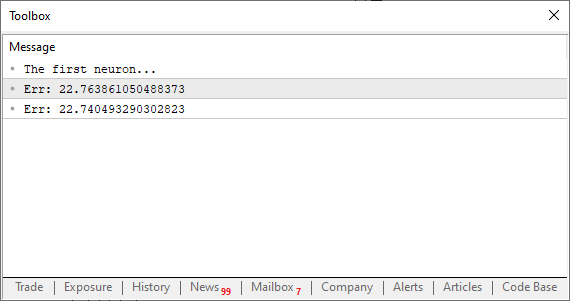
In diesem Stadium kommt es vor allem darauf an, ob der Fehlerwert sinkt oder steigt. Der tatsächliche Zahlenwert selbst ist nicht wichtig. Passen Sie jetzt gut auf: Die Variable „eps“ entspricht dem < h >, das wir in der Formel zuvor gesehen haben. Je näher dieser Wert an Null herankommt, desto mehr bringt uns jede Iteration näher an die Tangente. Dies geschieht, weil die Sekante in Richtung eines Grenzpunktes konvergiert. Was ist also unser nächster Schritt? Etwas ganz Einfaches: Wir müssen eine Schleife erstellen, die den Fehler (oder die Kosten) mit jeder Iteration verringert. Irgendwann erreichen wir einen Punkt, an dem der Fehler nicht mehr abnimmt, sondern zunimmt. Genau in diesem Moment sollte das Programm diese Änderung erkennen und die Schleife verlassen. Andernfalls würden wir Gefahr laufen, in eine Endlosschleife zu geraten. Alternativ können wir auch eine andere Art von Schutzmaßnahmen einführen, um Endlosschleifen zu verhindern. Ein gängiger Ansatz besteht darin, die Anzahl der Iterationen zu begrenzen und sicherzustellen, dass das Programm anhält, wenn es nicht konvergiert oder anfängt, „verrückt zu spielen“. Diese Instabilität kann auftreten, wenn die Schrittweite nicht gut gewählt ist. Wir werden dieses Thema später noch ausführlicher behandeln. Machen Sie sich also vorerst nicht zu viele Gedanken darüber. Es steht Ihnen jedoch frei, das Programm so zu gestalten, dass Sie den geringstmöglichen Kostenwert erzielen. Es liegt ganz bei Ihnen, wann Sie die Schleife beenden. Aber um die Dinge einfach zu halten, wollen wir sehen, wie das in der Praxis aussieht. Sehen Sie sich den nachstehenden Code an, um zu verstehen, wie er funktioniert.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err;
31. 
32.     Print("The first neuron...");
33.     MathSrand(512);
34.     weight = (double)macroRandom;
35. 
36.     for(ulong c = 0; c < 10; c++)
37.     {
38.         err = ((Cost(weight + eps) - Cost(weight)) / eps);
39.         weight -= (err * eps);
40.         Print(c, "  -->  ", weight, " :: ", err);
41.     }
42.     Print("Weight: ", weight);
43. }
44. //+------------------------------------------------------------------+

Wenn Sie diesen Code ausführen, sehen Sie im Terminal etwas Ähnliches wie das folgende Bild.

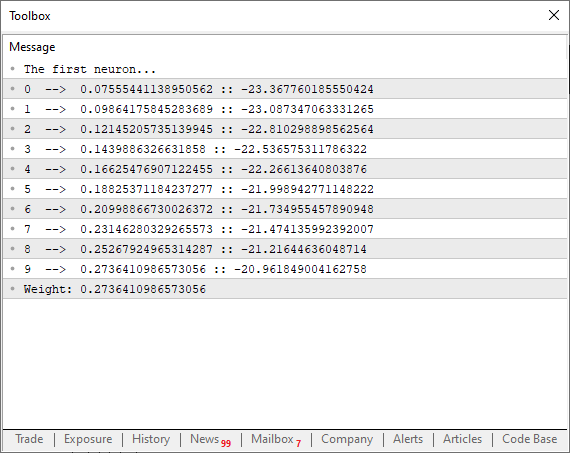
Schauen Sie sich nun ein interessantes Detail genauer an. In Zeile 38 führen wir die exakte Berechnung durch, die wir vorhin besprochen haben. Wir zwingen die Sekante, nach dem niedrigsten möglichen Grenzwert zu suchen, was der Funktion hilft, zu konvergieren. Beachten Sie jedoch in Zeile 39, dass wir den Kurvenpunkt nicht nur anhand des Rohfehlers oder des Gesamtkostenwerts anpassen. Aber warum? Wenn wir das täten, würde das Programm anfangen, chaotisch entlang der Kurve der Funktion hin und her zu springen. Und das ist nicht das, was wir wollen. Die Anpassungen müssen reibungslos und kontrolliert erfolgen. Warum aber nicht „eps“ verwenden, um den nächsten Punkt auf der Parabelkurve fein abzustimmen? Nun, wenn wir das täten, müssten wir ständig überprüfen, ob der Fehler zunimmt oder abnimmt. Das wird völlig unnötig, wenn wir die Faktorisierung in Zeile 39 anwenden. Dieser Ansatz hat einen weiteren Vorteil, denn er zwingt das Neuron, zu Beginn des Prozesses schneller zu konvergieren. Je mehr sie sich dem Idealwert nähert, desto glatter wird die Abklingkurve und verhält sich wie eine invertierte, logarithmische Abklingfunktion. Und das ist wirklich großartig! Das bedeutet, dass wir viel schneller einen optimalen Fehlerwert erreichen.

Aber wir können diesen Code noch besser machen! Wir können zusätzliche Analysetools hinzufügen, um die Vorgänge besser zu verstehen. Gleichzeitig können wir einen zusätzlichen Test einführen, der es ermöglicht, die Schleife zu beenden, sobald sie den minimalen Konvergenzpunkt erreicht, noch bevor sie die maximale Anzahl von Iterationen erreicht hat. In diesem Sinne ist hier die verbesserte Version des Codes:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err, e1;
31.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
32. 
33.     Print("The first neuron...");
34.     MathSrand(512);
35.     weight = (double)macroRandom;
36. 
37.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight)) > eps); c++)
38.     {
39.         err = (Cost(weight + eps) - e1) / eps;
40.         weight -= (err * eps);
41.         if (f != INVALID_HANDLE)
42.             FileWriteString(f, StringFormat("%I64u;%f;%f\n", c, err, e1));
43.     }
44.     if (f != INVALID_HANDLE)
45.         FileClose(f);
46.     Print("Weight: ", weight);
47. }
48. //+------------------------------------------------------------------+

Das Schöne an diesem Code ist, dass es unglaublich viel Spaß macht, mit ihm zu experimentieren. Es ist so konzipiert, dass Sie es studieren, optimieren und ausprobieren können. Ich habe beschlossen, die Werte nicht im MetaTrader 5 Terminal, sondern in einer Datei auszugeben. Auf diese Weise können wir ein Diagramm erstellen und die Vorgänge genauer analysieren. Mit der aktuellen Konfiguration sieht das resultierende Diagramm wie folgt aus:

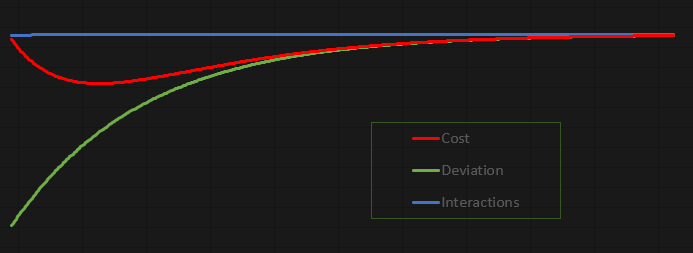
Dieses Diagramm wurde in Excel auf der Grundlage der Werte erstellt, die in der vom Neuron erzeugten Datei gespeichert sind. Ich gebe zu, dass die Art und Weise, wie die Datei erstellt wird, ein wenig klobig ist. Aber da dies eine lehrreiche und unterhaltsame Übung sein soll, sehe ich kein Problem darin, wie wir die Daten in die Datei übertragen.

Abschließende Überlegungen

In diesem Artikel haben wir ein grundlegendes Neuron gebaut. Sicher, es ist einfach, und manche mögen denken, der Code sei zu einfach oder sinnlos. Aber ich möchte, dass Sie, mein Leser, damit herumspielen und Spaß haben. Scheuen Sie sich nicht, den Code zu ändern, denn das Ziel ist es, ihn vollständig zu verstehen. Der Code ist beigefügt, damit Sie die Funktionsweise eines einfachen Neurons untersuchen können. Nehmen Sie sich die Zeit, diesen Artikel zu lesen. Versuchen Sie, den Code von Grund auf neu einzugeben, anstatt ihn zu kopieren und einzufügen. Testen Sie jeden Schritt, bis Sie die endgültige Version erreicht haben. Kopieren Sie nicht einfach meinen Ansatz, sondern bauen Sie ihn so auf, dass er für Sie Sinn macht. Der Schlüssel liegt darin, dasselbe Endergebnis zu erzielen: die Korrelation zwischen den Trainingsdaten im Array zu finden. Es ist eigentlich ganz einfach.

Da der Code im Anhang enthalten ist, finden Sie hier einige interessante Änderungen, die Sie ausprobieren können. Denken Sie daran, jede Änderung in Ruhe zu prüfen. Das erste Element ist das Trainings-Array, das sich in der sechsten Zeile des Anwendungscodes befindet. Sie können dort verschiedene Werte eingeben und das Neuron versuchen lassen, eine Korrelation zwischen ihnen zu finden.

Ein weiterer sehr interessanter Punkt ist die Änderung des Wertes der Konstante in Zeile 15. Ändern Sie ihn auf einen höheren oder niedrigeren Wert und beobachten Sie das Ergebnis, das das Neuron am Ende seiner Arbeit meldet. Sie werden feststellen, dass bei niedrigeren Werten die Verarbeitung länger dauert, das Ergebnis aber viel näher am Idealwert liegt.

Ein weiterer interessanter Punkt findet sich in Zeile 35, wo wir ein Gewicht zuweisen, das zwischen Null und Eins schwankt. Sie können ihn ändern, indem Sie den vom Makro zurückgegebenen Wert multiplizieren. Versuchen Sie zum Beispiel, in Zeile 35 etwas Ähnliches zu schreiben.

weight = (double)macroRandom * 50;

Sie werden feststellen, dass alles ganz anders sein wird, einfach weil Sie das Anfangsgewicht, mit dem das Neuron startet, geändert haben. Und wenn Sie sich ganz sicher sind, können Sie den Code in Zeile 34 in den unten gezeigten ändern.

MathSrand(GetTickCount()); 

Sie werden feststellen, dass alles viel interessanter ist, als viele Leute denken. Vor allem aber werden Sie anfangen zu verstehen, wie ein einzelnes Neuron in einem neuronalen Netz etwas lernen kann. Im nächsten Artikel werden wir dieses Neuron in etwas noch Interessanteres verwandeln. Bevor Sie also mit dem nächsten Artikel fortfahren, sollten Sie diesen Code studieren und mit ihm experimentieren. Denn dies ist erst der Anfang.