Neuronale Netze im Handel: Zustandsraummodelle
141
0
Einführung
In jüngster Zeit hat sich das Paradigma der Anpassung großer Modelle an neue Aufgaben immer mehr durchgesetzt. Diese Modelle werden mit umfangreichen Datensätzen trainiert, die beliebige Rohdaten aus einem breiten Spektrum von Bereichen enthalten, darunter Text, Bilder, Audio, Zeitreihen und vieles mehr.
Obwohl dieses Konzept nicht an eine bestimmte Architektur gebunden ist, basieren die meisten Modelle auf einer einzigen Architektur – dem Transformer und seiner Kernschicht, der Selbstaufmerksamkeit (Self-Attention). Die Effizienz der Selbstaufmerksamkeit wird auf die Fähigkeit zurückgeführt, Informationen innerhalb eines kontextuellen Fensters zu verdichten, was die Modellierung komplexer Daten ermöglicht. Diese Eigenschaft hat jedoch grundlegende Einschränkungen: die Unfähigkeit, etwas zu modellieren, was über das endliche Fenster hinausgeht, und die quadratische Skalierung in Bezug auf die Fensterlänge.
Eine alternative Lösung für Sequenzmodellierungsaufgaben besteht in der Verwendung strukturierter Sequenzmodelle im Zustandsraum (Space Sequence Models, SSM). Diese Modelle können als eine Kombination aus rekurrenten neuronalen Netzen (RNNs) und faltigen neuronalen Netzen (CNNs) interpretiert werden. Diese Klasse von Modellen kann sehr effizient mit linearer oder nahezu linearer Skalierung der Sequenzlänge berechnet werden. Außerdem verfügt es über inhärente Mechanismen zur Modellierung weitreichender Abhängigkeiten in bestimmten Datenmodalitäten.
Ein Algorithmus, der die Verwendung von Zustandsraummodellen für die Zeitreihenprognose ermöglicht, wurde in dem Beitrag „Mamba: Linear-Time Sequence Modeling with Selective State Spaces“. In diesem Beitrag wird eine neue Klasse von selektiven Zustandsraummodellen vorgestellt.
Die Autoren stellen eine wesentliche Einschränkung bestehender Modelle fest: die Fähigkeit, Informationen auf der Grundlage von Eingabedaten effektiv zu filtern (d. h. sich auf bestimmte Eingabedaten zu konzentrieren oder sie zu ignorieren). Sie entwickeln einen einfachen Auswahlmechanismus, der die SSM-Parameter von den Eingabedaten abhängig macht. Auf diese Weise kann das Modell irrelevante Informationen herausfiltern und relevante Informationen auf unbestimmte Zeit beibehalten.
Die Autoren vereinfachen frühere Architekturen für tiefe Sequenzmodelle, indem sie die SSM-Architektur mit MLP in einen einzigen Block integrieren, was zu einer einfachen und homogenen Architektur (Mamba) führt, die selektive Zustandsräume einschließt.
Selektive SSMs und folglich auch die Mamba-Architektur sind vollständig rekurrente Modelle mit Schlüsseleigenschaften, die sie als Grundlage für allgemeine sequenzbasierte Modelle geeignet machen.
- Hohe Qualität: Die Selektivität gewährleistet eine hohe Leistung in dichten Modalitäten.
- Schnelles Training und Inferenz: Die Berechnungen und der Speicherplatz skalieren linear mit der Sequenzlänge während des Trainings, während die Entwicklung des autoregressiven Modells während der Inferenz nur eine konstante Zeit pro Schritt benötigt, da es keine vorherigen Elemente zwischenspeichern muss.
- Langfristiger Kontext: Die Kombination aus Qualität und Effizienz steigert die Leistung bei der Bearbeitung großer Sequenzen.
1. Der Mamba-Algorithmus
Die Autoren von Mamba argumentieren, dass die grundlegende Herausforderung bei der Sequenzmodellierung darin besteht, den Kontext in einen kleineren Zustand zu komprimieren. Die Kompromisse der gängigen Sequenzmodelle können unter diesem Gesichtspunkt betrachtet werden. So ist beispielsweise die Aufmerksamkeit gleichzeitig effizient und ineffizient, da sie den Kontext nicht explizit komprimiert. Dies zeigt sich daran, dass die autoregressive Inferenz die explizite Speicherung des gesamten Kontexts (d. h. des Cache von Key-Value) erfordert, was zu einer langsamen Inferenz mit linearer Zeit und einem Transformer-Training mit quadratischer Zeit führt.
Umgekehrt sind rekurrente Modelle effizient, weil sie einen endlichen Zustand beibehalten, was Inferenz in konstanter Zeit und Training in linearer Zeit bedeutet. Ihre Effizienz wird jedoch dadurch eingeschränkt, wie gut dieser Zustand den Kontext komprimiert.
Um dieses Prinzip zu veranschaulichen, konzentrieren sich die Autoren auf die Lösung von zwei synthetischen Aufgaben:
- Der Aufgabe von einem selektiven Kopieren. Es erfordert ein inhaltsbezogenes Denken, um sich relevante Token zu merken und irrelevante herauszufiltern.
- Der Aufgabe von einem Induktionskopf. Das erklärt die meisten LLM-Fähigkeiten im kontextuellen Lernen. Die Lösung dieser Aufgabe erfordert kontextabhängiges Denken, um zu bestimmen, wann die richtige Ausgabe im entsprechenden Kontext abgerufen werden soll.
Diese Aufgaben zeigen Fehlermöglichkeiten in LTI-Modellen auf. Aus einer rekurrenten Perspektive verhindert ihre feste Dynamik, dass sie die richtigen Informationen aus ihrem Kontext auswählen oder den verborgenen Zustand, der durch die Sequenz übertragen wird, auf der Grundlage von Eingabedaten beeinflussen können. Aus der Sicht der Faltung können globale Faltungen die Aufgabe des reinen Kopierens lösen, da sie nur ein Bewusstsein für die Zeit erfordern, aber sie haben Probleme mit dem selektiven Kopieren, da ihnen ein Bewusstsein für den Inhalt fehlt. Insbesondere variiert der Abstand zwischen Eingängen und Ausgängen und kann nicht mit statischen Faltungskernen (convolutional kernels) modelliert werden.
Der Effizienzkompromiss bei Sequenzmodellen ist also dadurch gekennzeichnet, wie gut sie ihren Zustand komprimieren. Im Gegenzug schlagen die Autoren vor, dass das grundlegende Prinzip bei der Entwicklung von Sequenzmodellen die Selektivität ist, d. h. die kontextabhängige Fähigkeit, sich auf Eingabedaten in sequenziellen Zuständen zu konzentrieren oder diese herauszufiltern. Der Auswahlmechanismus steuert, wie sich Informationen entlang der Sequenzdimension ausbreiten oder interagieren.
Eine Methode zur Einbeziehung von Selektionsmechanismen in Modelle besteht darin, die Parameter, die die Sequenzinteraktionen beeinflussen, von den Eingabedaten abhängig zu machen. Der entscheidende Unterschied besteht darin, dass mehrere Parameter Δ B, C von den Eingabedaten abhängen und sich die Tensorformen entsprechend ändern. Konkret haben diese Parameter jetzt eine Längenabmessung L. Dies bedeutet, dass das Modell von zeitinvariant zu zeitvariabel übergeht.
Die Autoren wählen gezielt:
- SB(x) = LinearN(x)
- SC(x) = LinearN(x)
- SΔ(x) = BroadcastD(Linear1(x))
- τΔ = SoftPlus
Die Wahl von SΔ und τΔ ist durch ihre Verbindung zu RNN-Steuermechanismen begründet.
Ziel der Autoren ist es, selektive SSMs auf moderner Hardware (GPUs) effizient zu machen. Bei rekurrenten Modellen wie SSMs besteht immer ein Gleichgewicht zwischen Effizienz und Geschwindigkeit: Modelle mit höherer Dimensionalität des verborgenen Zustands sollten effizienter, aber langsamer sein. Die Herausforderung für Mamba bestand also darin, die versteckte Zustandsdimension zu maximieren, ohne die Modellgeschwindigkeit zu beeinträchtigen oder den Speicherverbrauch zu erhöhen.
Der Auswahlmechanismus überwindet die Einschränkungen von LTI-Modellen. Allerdings bleibt die rechnerische Herausforderung der SSM bestehen. Die Autoren gehen dies mit drei klassischen Techniken an: Kernel-Fusion, paralleles Scannen und Neuberechnung. Sie machen zwei wichtige Feststellungen:
- Naive rekurrente Berechnungen benötigen O(BLDN)FLOP, die Faltungsberechnungen hingegen O(BLD log(L)) FLOP. Ersterer hat einen niedrigeren Koeffizienten. Bei langen Sequenzen und nicht allzu großen Zustandsdimensionen N kann der rekurrente Modus also tatsächlich weniger FLOPs verwenden.
- Die beiden größten Herausforderungen sind die sequentielle Natur der Wiederholung und der hohe Speicherbedarf. Um letzteres zu erreichen, versuchen sie, wie beim Faltungsmodus, die Berechnung des vollständigen Zustands h zu vermeiden.
Der Kerngedanke besteht darin, moderne Beschleuniger (GPUs) zu nutzen, um h nur auf effizienteren Ebenen der Speicherhierarchie zu berechnen. Die meisten Vorgänge sind an die Speicherbandbreite gebunden, auch das Scannen. Die Autoren nutzen die Kernel-Fusion, um Speicher-E/A-Operationen zu reduzieren, was die Ausführung im Vergleich zu einer Standardimplementierung erheblich beschleunigt.
Darüber hinaus wenden sie sorgfältig eine klassische Neuberechnungstechnik an, um den Speicherbedarf zu verringern: Zwischenzustände werden nicht gespeichert, sondern während der Eingabeverarbeitung in umgekehrter Richtung neu berechnet.
Selektive SSMs funktionieren als autonome Sequenztransformationen, die flexibel in neuronale Netze eingebettet werden können.
Der Auswahlmechanismus ist ein umfassenderes Konzept, das auf andere Parameter oder durch verschiedene Transformationen angewendet werden kann.
Die Selektivität ermöglicht es uns, irrelevante Rausch-Token zu entfernen, die in den relevanten Eingabedaten vorkommen können. Ein Beispiel hierfür ist das Problem des selektiven Kopierens, das bei allen gängigen Datenmodalitäten auftritt, insbesondere bei diskreten Daten. Diese Eigenschaft ergibt sich, weil das Modell mechanisch alle spezifischen Eingabedaten Xt herausfiltern kann.
Empirische Beobachtungen zeigen, dass viele Sequenzmodelle mit längerem Kontext nicht besser werden, trotz des Grundsatzes, dass mehr Kontext grundsätzlich die Leistung verbessern sollte. Die Erklärung dafür ist, dass viele Sequenzmodelle irrelevante Zusammenhänge nicht wirksam ignorieren können, wenn dies erforderlich ist.
Umgekehrt können Selektionsmodelle ihren Zustand jederzeit zurücksetzen, um überflüssige Daten zu verwerfen, sodass sich ihre Leistung bei längerem Kontext monoton verbessert.
Die originale Visualisierung der Methode ist unten dargestellt.
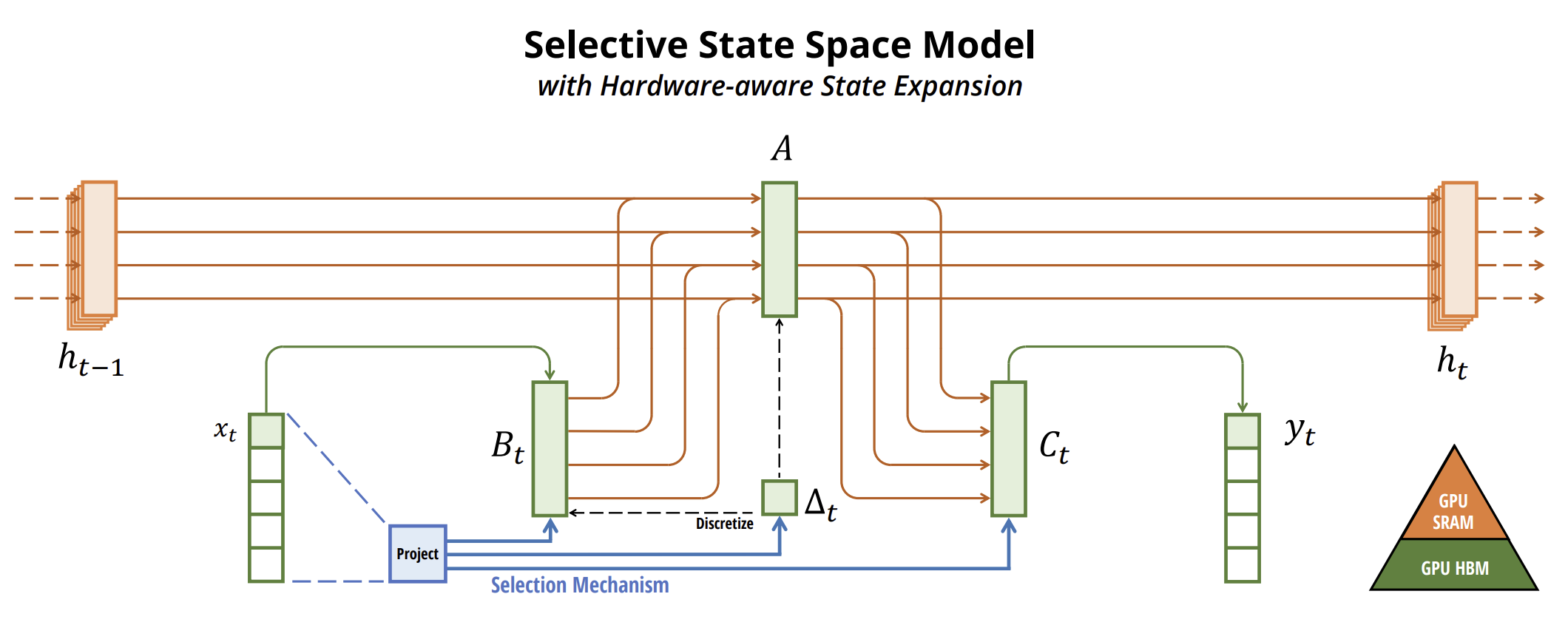
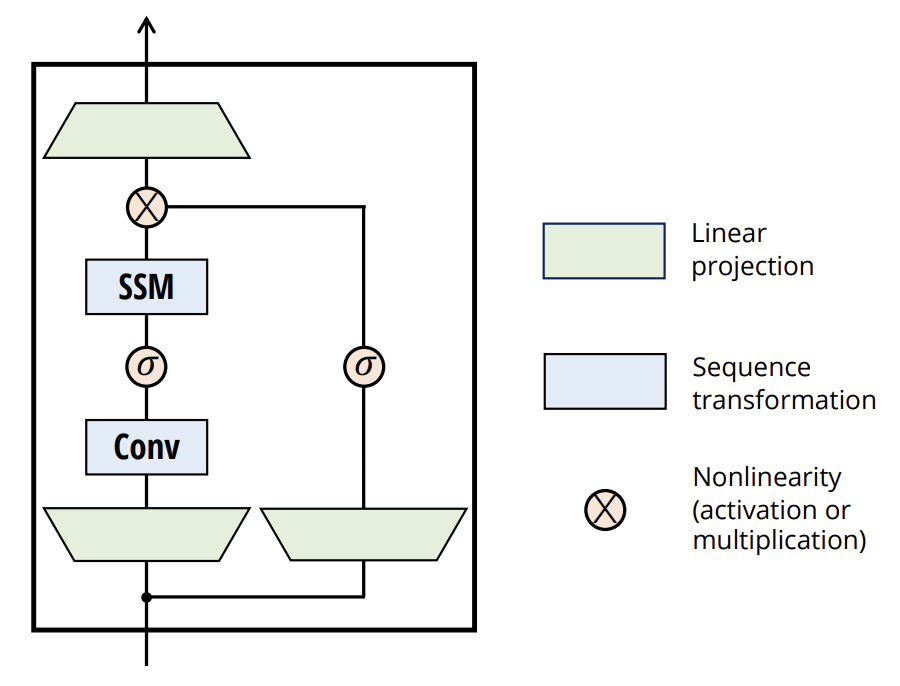
2. Implementation in MQL5
Nachdem wir die theoretischen Aspekte der Mamba-Methode erläutert haben, gehen wir zur praktischen Umsetzung der vorgeschlagenen Ansätze mit MQL5 über. Diese Arbeit gliedert sich in zwei Phasen. Zunächst konstruieren wir die Klasse, die den SSM-Algorithmus implementiert, der als eine der verschachtelten Schichten der umfassenden Mamba-Methode dient. Dann erstellen wir die algorithmischen Prozesse der obersten Ebene.
2.1 SSM-Implementierung
Es gibt zahlreiche Algorithmen für die Konstruktion von SSMs. Für dieses Experiment bin ich leicht von der ursprünglichen Mamba-Implementierung abgewichen und habe eines der einfachsten Modelle für die Auswahl des Zustandsraums erstellt. Dies wurde in der Klasse CNeuronSSMOCL implementiert. Als übergeordnetes Objekt verwenden wir die Basisklasse CNeuronBaseOCL (fully connected neural layer). Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronSSMOCL : public CNeuronBaseOCL { protected: uint iWindowHidden; CNeuronBaseOCL cHiddenStates; CNeuronConvOCL cA; CNeuronConvOCL cB; CNeuronBaseOCL cAB; CNeuronConvOCL cC; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronSSMOCL(void) {}; ~CNeuronSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
In der vorgestellten Struktur sehen wir die Deklaration einer Konstante, die die Dimension des verborgenen Zustands eines Elements (iWindowHidden) definiert, und 5 interne neuronale Schichten. Wir werden uns ihre Funktionalität während der Implementierung ansehen.
Die Menge der überschreibbaren Methoden in unserer Klasse ist ziemlich standardmäßig. Und ich denke, Sie haben bereits erraten, wozu sie dienen.
Alle internen Objekte der Klasse werden statisch deklariert, was es uns ermöglicht, den Klassenkonstruktor und -destruktor leer zu lassen. Die Initialisierung aller deklarierten und geerbten Objekte wird in der Methode Init durchgeführt. In den Parametern dieser Methode erhalten wir Konstanten, anhand derer wir eindeutig feststellen können, welches Objekt der Nutzer erstellen wollte.
bool CNeuronSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Hier gibt es 3 solcher Parameter:
- window – die Vektorgröße eines Elements in der Sequenz;
- window_key – Größe des Vektors der internen Darstellung eines Elements in der Sequenz;
- units_count – die Größe der zu analysierenden Sequenz.
Wie ich bereits erwähnt habe, verwenden wir in diesem Experiment einen vereinfachten SSM-Algorithmus. Insbesondere ist es nicht möglich, eine multimodale Sequenz in unabhängige Kanäle aufzuteilen.
Innerhalb des Methodenkörpers rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf, die bereits die Initialisierung der geerbten Objekte und Variablen sowie die minimale und notwendige Validierung der vom externen Programm erhaltenen Parameter enthält.
Sobald die Methode der übergeordneten Klasse erfolgreich ausgeführt wurde, fahren wir mit der Initialisierung der in dieser Klasse deklarierten Objekte fort. Zunächst initialisieren wir die interne Schicht, die für die Speicherung des verborgenen Zustands zuständig ist.
if(!cHiddenStates.Init(0, 0, OpenCL, window_key * units_count, optimization, iBatch)) return false; cHiddenStates.SetActivationFunction(None); iWindowHidden = window_key;
Außerdem speichern wir die Größe des internen Zustandsvektors eines einzelnen Sequenzelements sofort in einer lokalen Variablen.
Es ist wichtig zu beachten, dass wir diesen Parameterwert absichtlich speichern, ohne eine Validierung durchzuführen. Die Idee dabei ist, dass wir bewusst zuerst die interne Schicht initialisiert haben, deren Größe durch diesen Parameter bestimmt wird. Wenn der Nutzer einen falschen Wert angibt, würden bei der Initialisierung der Klasse selbst Fehler auftreten. Die sorgfältige Initialisierung der internen Schicht führt also implizit eine Parametervalidierung durch. Dies macht zusätzliche Kontrollen in diesem Stadium überflüssig.
Es ist auch erwähnenswert, dass das Objekt cHiddenStates nur für die temporäre Datenspeicherung verwendet wird, und wir deaktivieren ausdrücklich die Aktivierungsfunktion darin.
Als Nächstes initialisieren wir zwei Datenprojektionsschichten, die steuern, wie die Eingabedaten das Ergebnis beeinflussen. Zunächst initialisieren wir die verborgene Projektionsschicht für den Zustand:
if(!cA.Init(0, 1, OpenCL, iWindowHidden, iWindowHidden, iWindowHidden, units_count, 1, optimization, iBatch)) return false; cA.SetActivationFunction(SIGMOID);
Hier verwenden wir eine Faltungsschicht, die es uns ermöglicht, unabhängige Projektionen des verborgenen Zustands für jedes Sequenzelement durchzuführen. Um den Einfluss der einzelnen Elemente auf das Endergebnis zu regulieren, verwenden wir Sigmoid als Aktivierungsfunktion dieser Schicht. Wie Sie wissen, bildet die Sigmoidfunktion Werte in den Bereich [0, 1] ab. Bei „0“ hat das Element keinen Einfluss auf das Gesamtergebnis.
Anschließend wird die Projektionsschicht für die Eingangsdaten auf ähnliche Weise initialisiert:
if(!cB.Init(0, 2, OpenCL, window, window, iWindowHidden, units_count, 1, optimization, iBatch)) return false; cB.SetActivationFunction(SIGMOID);
Es ist zu beachten, dass beide Projektionsschichten Tensoren zurückgeben, die der Größe des verborgenen Zustands entsprechen, auch wenn ihre Eingabetensoren unterschiedliche Dimensionen haben können. Dies zeigt sich an der Größe des Datenfensters und seinem Schritt bei der Initialisierung der Objekte.
Um den kombinierten Einfluss der Eingabedaten und des verborgenen Zustands auf das Ergebnis zu berechnen, verwenden wir die gewichtete Summierung. Um die Anzahl der Operationen zu optimieren und zu reduzieren, haben wir beschlossen, diesen Schritt mit der Projektion auf die Zielergebnisdimension zu kombinieren. Daher verketten wir die Daten zunächst zu einem gemeinsamen Tensor entlang der Dimension der Sequenzelemente.
if(!cAB.Init(0, 3, OpenCL, 2 * iWindowHidden * units_count, optimization, iBatch)) return false; cAB.SetActivationFunction(None);
Als Nächstes wird eine weitere interne Faltungsschicht angewendet.
if(!cC.Init(0, 4, OpenCL, 2*iWindowHidden, 2*iWindowHidden, window, units_count, 1, optimization, iBatch)) return false; cC.SetActivationFunction(None);
Am Ende der Initialisierungsmethode leiten wir die Zeiger auf die Ergebnis- und Gradientenpuffer unserer Klasse auf die entsprechenden Puffer der internen Ergebnisprojektionsschicht um. Dieser einfache Schritt ermöglicht es uns, unnötiges Kopieren von Daten sowohl beim Vorwärts- als auch beim Rückwärtsdurchlauf zu vermeiden.
SetActivationFunction(None); if(!SetOutput(cC.getOutput()) || !SetGradient(cC.getGradient())) return false; //--- return true; }
Natürlich überwachen wir auch den Erfolg aller durchgeführten Operationen und geben dem aufrufenden Programm am Ende der Methode einen booleschen Wert zurück, der den Erfolg anzeigt.
Nachdem die Initialisierung der Klasse abgeschlossen ist, kommen wir zur Erstellung des Algorithmus für den Vorwärtsdurchgang. Wie Sie wissen, ist diese Funktionalität in der überschriebenen Methode feedForward implementiert. Hier ist alles ganz unkompliziert.
bool CNeuronSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cA.FeedForward(cHiddenStates.AsObject())) return false; if(!cB.FeedForward(NeuronOCL)) return false;
Die Methodenparameter enthalten einen Zeiger auf das vorangehende Objekt der neuronalen Schicht, das die Eingabedaten liefert.
Innerhalb der Methode führen wir sofort zwei Projektionen (der Eingabedaten und des verborgenen Zustands) in ein kompatibles Format durch. Dies geschieht mit den Vorwärtsdurchgangsmethoden der entsprechenden internen Faltungsschichten.
Die erhaltenen Projektionen werden zu einem einzigen Tensor entlang der Dimension der Sequenzelemente verkettet.
if(!Concat(cA.getOutput(), cB.getOutput(), cAB.getOutput(), iWindowHidden, iWindowHidden, cA.Neurons() / iWindowHidden)) return false;
Schließlich projizieren wir die verkettete Ebene auf die gewünschte Ergebnisdimension.
if(!cC.FeedForward(cAB.AsObject())) return false;
Hier sind zwei Punkte zu beachten. Zunächst kopieren wir das Ergebnis nicht in den Ergebnispuffer der aktuellen Ebene – dieser Vorgang ist nicht erforderlich, da wir die Datenpufferzeiger umleiten.
Zweitens haben Sie vielleicht bemerkt, dass wir den verborgenen Status nicht aktualisiert haben. Daher erscheint die Vorwärtsdurchgangsmethode an dieser Stelle unvollständig. Das Problem besteht jedoch darin, dass wir für den Rückwärtsdurchgang (Backpropagation) immer noch den aktuellen verborgenen Zustand benötigen. Daher ist es sinnvoll, den verborgenen Zustand während des Rückwärtsdurchgangs zu aktualisieren, da er nur innerhalb des Algorithmus der aktuellen Schicht verwendet wird.
Es gibt jedoch einen Nachteil: Während der Modellinferenz (Entwicklung) verwenden wir keine Rückwärtsdurchgangsmethoden. Wenn wir die Aktualisierung des verborgenen Zustands auf den Rückwärtsdurchgang verschieben, würde er während der Inferenz nie aktualisiert werden, was die gesamte Logik des Algorithmus verletzen würde.
Wir überprüfen also den aktuellen Betriebsmodus des Modells und aktualisieren den verborgenen Zustand erst während der Inferenz. Wir erreichen dies, indem wir die Projektionen des vorherigen verborgenen Zustands und der Eingabedaten addieren und normalisieren.
if(!bTrain) if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true)) return false; //--- return true; }
Damit ist unsere Vorwärtsdurchgangsmethode abgeschlossen, und wir geben dem aufrufenden Programm einen booleschen Status des erfolgreichen Vorgangs zurück.
Nach der Implementierung des Vorwärtsdurchgangs gehen wir zu den Rückwärtsdurchgangsmethoden über. Wie üblich setzen wir zwei Methoden außer Kraft:
- calcInputGradients — für die Fehlergradientenverteilung.
- updateInputWeights — für die Aktualisierung der Modellparameter.
Der Algorithmus zur Verteilung des Fehlergradienten spiegelt den Vorwärtsdurchgang in umgekehrter Reihenfolge wider. Ich schlage vor, Sie untersuchen diese Methode selbst - sie ist im beigefügten Code enthalten. Besondere Aufmerksamkeit verdient jedoch die Methode der Parameteraktualisierung. Denn wir haben den Prozess der Aktualisierung des verborgenen Zustands als Teil des Modelltrainings einbezogen.
bool CNeuronSSMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cA.UpdateInputWeights(cHiddenStates.AsObject())) return false; if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true)) return false;
Hier passen wir zunächst die Parameter der internen versteckten Projektionsschicht an. Erst danach wird der verborgene Zustand selbst aktualisiert.
Beachten Sie, dass wir den Betriebsmodus des Modells hier nicht überprüfen, da diese Methode nur während des Trainings aufgerufen wird.
Anschließend rufen wir die entsprechenden Methoden zur Aktualisierung der Parameter der verbleibenden internen Objekte mit lernbaren Parametern auf.
if(!cB.UpdateInputWeights(NeuronOCL)) return false; if(!cC.UpdateInputWeights(cAB.AsObject())) return false; //--- return true; }
Nach Abschluss aller Operationen gibt die Methode einen booleschen Status an das aufrufende Programm zurück.
Damit ist die Diskussion über die Methoden der SSM-Implementierungsklasse abgeschlossen. Den vollständigen Code für alle diese Methoden finden Sie im Anhang.
2.2 Mamba-Methode Klasse
Wir haben die Klasse für die SSM-Schicht implementiert. Jetzt können wir mit dem Aufbau des Top-Level-Algorithmus der Mamba-Methode fortfahren. Um die Methode zu implementieren, erstellen wir eine Klasse CNeuronMambaOCL, die, wie die vorherige, die Basisfunktionalität von der Klasse CNeuronBaseOCL erbt. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronMambaOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL cXProject; CNeuronConvOCL cZProject; CNeuronConvOCL cInsideConv; CNeuronSSMOCL cSSM; CNeuronBaseOCL cZSSM; CNeuronConvOCL cOutProject; CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaOCL(void) {}; ~CNeuronMambaOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMambaOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Hier sehen wir einen vertrauten Satz überschreibbarer Methoden und die Deklaration interner Schichten des neuronalen Netzes, deren Funktionalitäten wir bei der Implementierung der Klassenmethoden erkunden werden.
Gleichzeitig gibt es keine internen Variablen, die zur Speicherung von Konstanten deklariert sind. Wir werden die Entscheidungen erörtern, die es uns ermöglicht haben, das Speichern von Konstanten während der Implementierungsphase zu vermeiden.
Wie üblich werden alle internen Objekte statisch deklariert. Daher bleiben sowohl der Konstruktor als auch der Destruktor der Klasse leer. Die Initialisierung von Objekten wird in der Methode Init durchgeführt.
bool CNeuronMambaOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Eine Liste von Parametern in dieser Methode ähnelt der gleichnamigen Methode in der zuvor besprochenen Klasse CNeuronSSMOCL. Es ist nicht schwer zu erraten, dass sie ähnliche Funktionen haben.
Im Hauptteil der Methode wird zunächst die Initialisierungsmethode der übergeordneten Klasse aufgerufen, die geerbte Objekte und Variablen behandelt.
Wie Sie sich vielleicht aus der theoretischen Erklärung der Mamba-Methode erinnern, folgen die Eingabedaten hier zwei parallelen Strömen. Für beide Streams führen wir Datenprojektionen durch, die mithilfe von Faltungsschichten ausgeführt werden.
if(!cXProject.Init(0, 0, OpenCL, window, window, window_key + 2, units_count, 1, optimization, iBatch)) return false; cXProject.SetActivationFunction(None); if(!cZProject.Init(0, 1, OpenCL, window, window, window_key, units_count, 1, optimization, iBatch)) return false; cZProject.SetActivationFunction(SIGMOID);
Im ersten Stream verwenden wir eine Faltungsschicht und einen SSM-Block. Im zweiten Schritt wenden wir eine Aktivierungsfunktion an, woraufhin die Daten zur Zusammenführung gelangen. Folglich müssen die Ausgaben beider Ströme Tensoren von vergleichbarer Größe sein. Um dies zu erreichen, erhöhen wir die Projektionsgröße des ersten Streams geringfügig, was durch die Datenkompression während der Faltung kompensiert wird.
Beachten Sie, dass die Aktivierungsfunktion nur für die Projektion des zweiten Streams verwendet wird.
Der nächste Schritt ist die Initialisierung der Faltungsschicht.
if(!cInsideConv.Init(0, 2, OpenCL, 3, 1, 1, window_key, units_count, optimization, iBatch)) return false; cInsideConv.SetActivationFunction(SIGMOID);
Hier führen wir eine unabhängige Faltung innerhalb einzelner Sequenzelemente durch. Daher geben wir die Größe des verborgenen Zustandstensors als die Anzahl der Faltungselemente an. Wir fügen auch die Anzahl der Sequenzelemente als unabhängige Variablen hinzu.
Die Größe des Faltungsfensters und die Schrittweite stimmen mit unserer erhöhten Projektionsgröße für den ersten Datenstrom überein.
An diesem Punkt fügen wir auch eine Aktivierungsfunktion hinzu, um die Vergleichbarkeit der Daten in beiden Streams zu gewährleisten.
Als Nächstes kommt unser SSM-Block, der die Zustandsauswahl durchführt.
if(!cSSM.Init(0, 3, OpenCL, window_key, window_key, units_count, optimization, iBatch)) return false;
Um den Algorithmus zu vervollständigen und Nichtlinearität in die Zusammenführung der beiden Datenströme einzubringen, verketten wir die Ausgaben zu einem einheitlichen Tensor.
if(!cZSSM.Init(0, 4, OpenCL, 2 * window_key * units_count, optimization, iBatch)) return false; cZSSM.SetActivationFunction(None);
Anschließend projizieren wir die resultierenden Daten mithilfe einer weiteren Faltungsschicht auf die erforderliche Größe innerhalb jedes Sequenzelements.
if(!cOutProject.Init(0, 5, OpenCL, 2*window_key, 2*window_key, window, units_count, 1, optimization, iBatch)) return false; cOutProject.SetActivationFunction(None);
Zusätzlich wird ein Puffer zur Speicherung von Zwischenergebnissen zugewiesen
if(!Temp.BufferInit(window * units_count, 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false;
und die Zeiger vertauscht, um auf diese Puffer zu verweisen.
if(!SetOutput(cOutProject.getOutput())) return false; if(!SetGradient(cOutProject.getGradient())) return false; SetActivationFunction(None); //--- return true; }
Schließlich gibt die Methode ein boolesches Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück.
Nach Abschluss der Klasseninitialisierung wird der Vorwärtsdurchgangsalgorithmus in der Methode feedForward implementiert. Ein Teil dieses Algorithmus wurde bereits bei der Erstellung der Initialisierungsmethode erwähnt. Schauen wir uns nun die Umsetzung in Code an.
bool CNeuronMambaOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cXProject.FeedForward(NeuronOCL)) return false; if(!cZProject.FeedForward(NeuronOCL)) return false;
Die Methode erhält einen Zeiger auf das Objekt der vorherigen Schicht, dessen Puffer unsere Eingabedaten enthält. Innerhalb des Methodenkörpers projizieren wir die eingehenden Daten sofort, indem wir die Vorwärtsdurchgangsmethoden unserer Projektionsfaltungsschichten aufrufen.
An diesem Punkt schließen wir die Operationen des zweiten Informationsstroms ab. Wir müssen jedoch noch den Hauptdatenstrom verarbeiten. Hier beginnen wir mit der Datenfaltung.
if(!cInsideConv.FeedForward(cXProject.AsObject())) return false;
Danach führen wir eine Zustandsauswahl durch.
if(!cSSM.FeedForward(cInsideConv.AsObject())) return false;
Sobald die Operationen beider Ströme abgeschlossen sind, werden die Ergebnisse zu einem einheitlichen Tensor zusammengeführt.
if(!Concat(cSSM.getOutput(), cZProject.getOutput(), cZSSM.getOutput(), 1, 1, cSSM.Neurons())) return false;
Es ist wichtig zu beachten, dass wir die Dimension des internen Zustands eines einzelnen Sequenzelements nicht gespeichert haben. Das ist kein Problem. Wir wissen, dass die Tensoren der beiden Informationsströme gleich groß sind. Daher können wir nacheinander ein Element aus jedem Tensor kombinieren, ohne die Gesamtstruktur zu stören.
Schließlich projizieren wir die Daten auf die gewünschte Ausgabedimension.
if(!cOutProject.FeedForward(cZSSM.AsObject())) return false; //--- return true; }
Die Methode schließt mit der Rückgabe eines booleschen Ergebnisses an das aufrufende Programm ab, das den Erfolg der Operationen anzeigt.
Wie Sie sehen, ist der Algorithmus für den Vorwärtsdurchgang nicht besonders komplex. Das Gleiche gilt für die Methoden des Rückwärtsdurchgangs. Daher werden wir ihre Algorithmen in diesem Artikel nicht im Detail betrachten. Der vollständige Code dieser Klasse und alle ihre Methoden sind in den beigefügten Dateien enthalten.
2.3 Modellarchitektur
In den vorangegangenen Abschnitten haben wir unsere Interpretation der von den Mamba-Autoren vorgeschlagenen Ansätze vorgestellt. Die geleistete Arbeit sollte jedoch zu Ergebnissen führen. Um die Effizienz der implementierten Algorithmen zu bewerten, müssen wir sie in unser Modell integrieren. Sie haben vielleicht schon geahnt, dass wir die neu erstellten Ebenen dem Modell des Umgebungszustands (Environment State Encoder) hinzufügen werden. Schließlich ist dies das Modell, das wir im Rahmen der Vorhersage künftiger Kursbewegungen trainieren.
Die Architektur dieses Modells wird in der Methode CreateEncoderDescriptions dargestellt.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Die Methode empfängt einen Zeiger auf ein dynamisches Array, in das wir die Architekturbeschreibung des zu erstellenden Modells schreiben werden.
Im Hauptteil der Methode prüfen wir die Relevanz des empfangenen Zeigers und erstellen ggf. eine neue Instanz des Objekts. Nach diesem vorbereitenden Schritt fahren wir mit der Beschreibung der Modellarchitektur fort.
Die erste Schicht ist für die Eingabe von Rohdaten in das Modell vorgesehen. Wie üblich verwenden wir eine vollständig verknüpfte Schicht von ausreichender Größe.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Normalerweise geben wir die „rohen“ Ausgangsdaten in das Modell in der Form ein, in der wir sie vom Terminal erhalten. Natürlich gehören diese Eingaben zu unterschiedlichen Verteilungen. Wir wissen, dass sich die Effizienz eines jeden Modells erheblich verbessert, wenn mit normalisierten und vergleichbaren Werten gearbeitet wird. Um die unterschiedlichen Eingabedaten auf eine vergleichbare Skala zu bringen, verwenden wir daher eine Batch-Normalisierungsschicht.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Als Nächstes erstellen wir einen Block aus drei identischen Mamba-Ebenen. Dazu definieren wir eine einzelne Architekturbeschreibung für den Block und fügen sie dem Array die erforderliche Anzahl von Malen hinzu.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMambaOCL; descr.window = BarDescr; //window descr.window_out = 4 * BarDescr; //Inside Dimension prev_count = descr.count = HistoryBars; //Units descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; for(int i = 2; i <= 4; i++) if(!encoder.Add(descr)) { delete descr; return false; }
Beachten Sie, dass die Größe des analysierten Datenfensters der Anzahl der Elemente entspricht, die ein einzelnes Sequenzelement beschreiben, und die Größe der internen Darstellung viermal größer ist. Dies entspricht der Empfehlung der Autoren, bei der Mamba-Methode eine expandierende Projektion durchzuführen.
Die Anzahl der Sequenzelemente entspricht der Tiefe der analysierten Datenhistorie.
Wie ich bereits bei der Einführung der Klasse erwähnt habe, haben wir in dieser Version keine separaten Informationskanäle zugewiesen. Dennoch verarbeitet unser Algorithmus unabhängige Sequenzelemente. Wenn Sie unabhängige Kanäle analysieren müssen, können Sie die Daten vortransponieren und die Ebenenparameter entsprechend anpassen. Aber das ist ein Thema für ein anderes Experiment.
Wir werden jedoch Sequenzen über unabhängige Kanäle hinweg vorhersagen. Deshalb transponieren wir die Daten nach dem Mamba-Block.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = prev_count; descr.window = BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Dann wenden wir zwei Faltungsschichten an, um die nächsten Werte für die unabhängigen Kanäle vorherzusagen.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = prev_count; descr.window_out = 4 * NForecast; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = 4 * NForecast; descr.window_out = NForecast; descr.activation = TANH; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Danach kehren wir die vorhergesagten Werte in ihre ursprüngliche Darstellung zurück.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Zusätzlich fügen wir statistische Merkmale der ursprünglichen Datenverteilung hinzu, die bei der Normalisierung ermittelt wurden.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Der letzte Schritt unseres Modells ist die Anpassung der Ergebnisse im Frequenzbereich.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Die Architekturen der Modelle Akteur (Actor) und Kritiker (Critic) bleiben unverändert. Auch bei den Programmen zur Interaktion mit der Umwelt waren keine Änderungen erforderlich. Allerdings mussten wir einige gezielte Änderungen in den Modellausbildungsprogrammen vornehmen. Dies liegt daran, dass die Verwendung des verborgenen Zustands innerhalb des SSM-Blocks eine Anpassung der Abfolge der Eingabedaten in einer für rekurrente Modelle charakteristischen Weise erfordert. Solche Anpassungen sind üblich, wenn Modelle mit verborgenen Zuständen verwendet werden, bei denen sich Informationen mit der Zeit ansammeln. Ich möchte Sie ermutigen, sie in der Anlage zu lesen. Der vollständige Code für alle Programme und Klassen, die bei der Erstellung dieses Artikels verwendet wurden, ist dort enthalten. Damit schließen wir die Beschreibung der Implementierung ab und gehen zu den praktischen Tests mit realen historischen Daten über.
3. Tests
Unsere Arbeit steht kurz vor dem Abschluss, und wir gehen zur letzten Phase über – dem Training der Modelle und dem Testen der erzielten Ergebnisse. Die Modelle werden auf historischen EURUSD-Daten für das Jahr 2023 mit einem H1-Zeitrahmen trainiert. Die Parameter aller Indikatoren sind auf Standardwerte eingestellt.
In der ersten Phase trainieren wir den Encoder des Umgebungszustands, um zukünftige Preisbewegungen über einen bestimmten Zeithorizont vorherzusagen. Dieses Modell analysiert nur historische Preisdaten und lässt die Handlungen des Akteurs völlig außer Acht. Auf diese Weise können wir ein umfassendes Modelltraining mit zuvor gesammelten Datensätzen durchführen, ohne diese aktualisieren zu müssen. Solche Aktualisierungen können jedoch erforderlich sein, wenn der historische Ausbildungszeitraum geändert oder verlängert wird.
Die erste Feststellung ist, dass sich das Modell als kompakt und schnell erwiesen hat. Der Ausbildungsprozess war relativ stabil und robust. Das Modell zeigte interessante Ergebnisse.
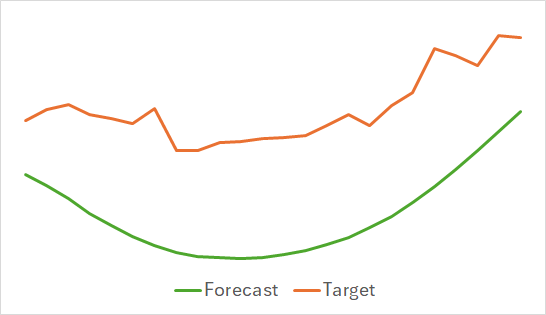
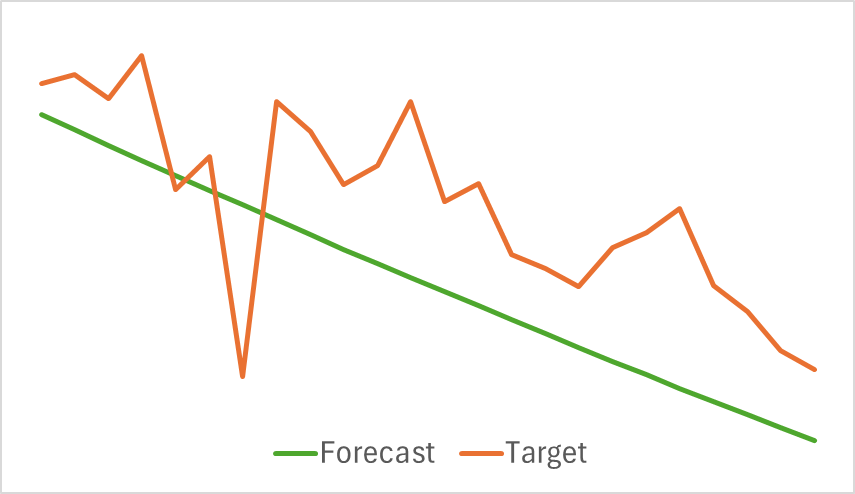
Die obigen Diagramme zeigen die voraussichtlichen Kursbewegungen für die nächsten 24 Stunden. Bemerkenswert ist, dass die Prognoselinie im ersten Schaubild eine fließende Trendänderung anzeigt, während sie im zweiten Fall fast linear den anhaltenden Trend widerspiegelt.
In der zweiten Phase führten wir ein iteratives Training der Politik des Akteurs durch. Wir haben auch die Wertfunktion des Kritikers trainiert. Die Rolle des Kritikers besteht darin, den Akteur bei der Verbesserung seiner politischen Effizienz anzuleiten.
Wie bereits erwähnt, ist die zweite Trainingsphase iterativ. Das bedeutet, dass wir den Trainingsdatensatz während des Trainings regelmäßig aktualisieren, um Daten aufzunehmen, die für die aktuelle Politik des Akteurs relevant sind. Die Pflege eines aktuellen Trainingssatzes ist entscheidend für ein aktualisiertes Modelltraining.
Während des Trainings haben wir jedoch keine Politik mit einem klar definierten Trend zum Einlagenwachstum erreicht. Obwohl es dem Modell gelang, auf den historischen Testdaten für Januar 2024 Gewinne zu erzielen, konnte kein konsistenter Trend beobachtet werden.
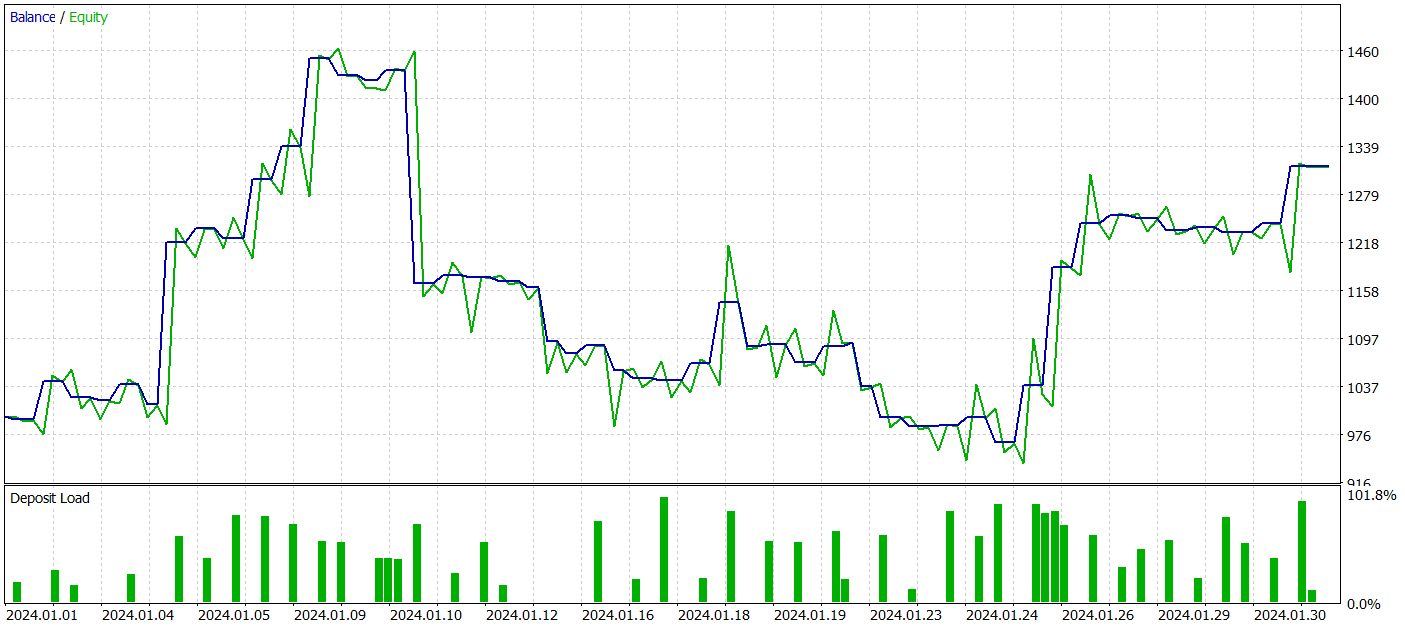
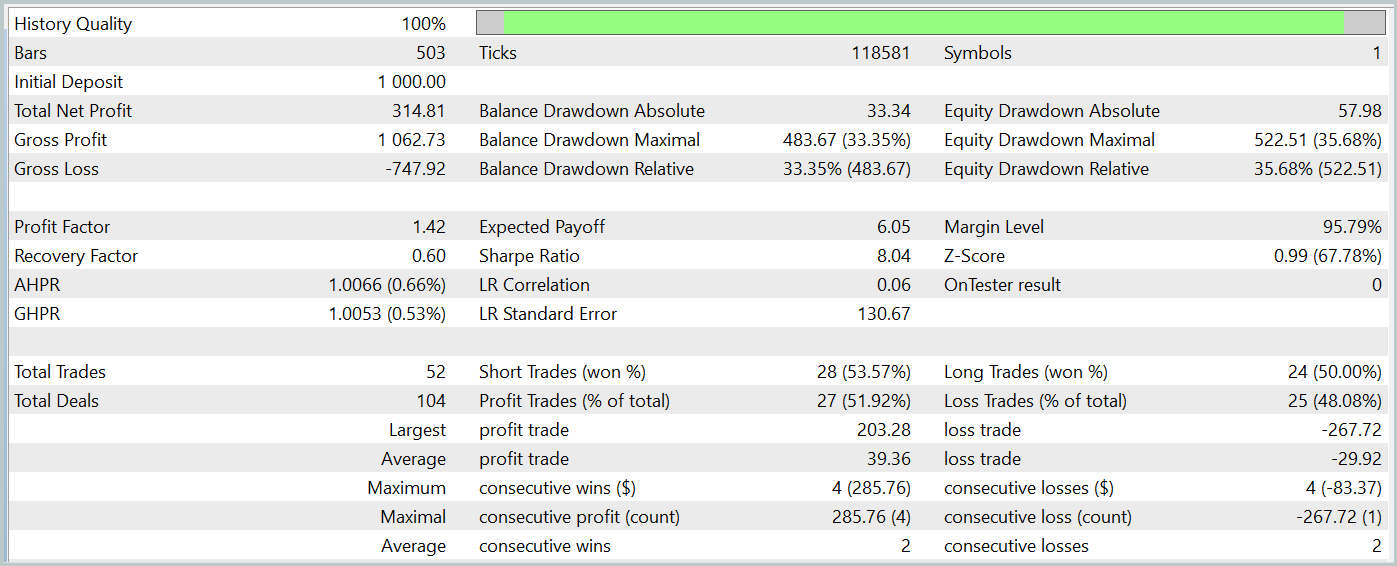
Während des Testzeitraums führte das Modell 52 Handelsgeschäfte aus, von denen 27 mit einem Gewinn abgeschlossen wurden, d. h. fast 52 %. Der durchschnittliche Gewinn überstieg den durchschnittlichen Verlust pro Handel (39,36 vs. -29,82). Allerdings war der maximale Verlust um 30 % höher als der maximale Gewinn. Außerdem beobachteten wir einen Rückgang des Eigenkapitals um mehr als 35 %. Es ist klar, dass dieses Modell weiter verfeinert werden muss.
Interessant ist auch die Aufschlüsselung von Gewinn und Verlust nach Stunden und Tagen.
Freitags sind die Gewinne besonders hoch, während mittwochs Verluste zu verzeichnen sind. Es gibt auch bestimmte Intraday-Perioden mit einer Häufung von gewinn- und verlustbringenden Handelsgeschäften. Dies bedarf einer weiteren Analyse. Zumal die durchschnittliche Haltedauer einer Position etwas mehr als eine Stunde betrug, mit einem Maximum von zwei Stunden.
Schlussfolgerung
In diesem Artikel haben wir eine neue Zeitreihenprognosemethode namens Mamba vorgestellt, die eine effiziente Alternative zu traditionellen Architekturen wie dem Transformer darstellt. Durch die Integration des Models Sample State Space (SSM) bietet Mamba einen hohen Durchsatz und eine lineare Skalierung der Sequenzlänge.
Im praktischen Teil unseres Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben Modelle mit realen Daten trainiert und dabei unterschiedliche Ergebnisse erzielt.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Trainings-EA des Modells |
| 4 | StudyEncoder.mq5 | EA | Trainings-EA des Encoders |
| 5 | Test.mq5 | EA | Modeltest-EA |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15546
Entwicklung eines Replay-Systems (Teil 60): Abspielen des Dienstes (I)
William-Gann-Methoden (Teil III): Funktioniert Astrologie?
Von der Grundstufe bis zur Mittelstufe: Übergabe als Wert oder Referenz
Künstlicher Algenalgorithmus (AAA)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.