
Erstellen von 3D-Balken auf der Grundlage von Zeit, Preis und Volumen
Einführung
Es ist sechs Monate her, dass ich mit diesem Projekt begonnen habe. Ein halbes Jahr nach der Idee, die mir dumm vorkam, bin ich nicht mehr darauf zurückgekommen und habe nur noch mit bekannten Händlern darüber gesprochen.
Am Anfang stand eine einfache Frage: Warum versuchen Händler immer wieder, einen 3D-Markt anhand von 2D-Charts zu analysieren? Kursbewegung, technische Analyse, Wellentheorie - all das funktioniert mit der Projektion des Marktes auf eine Ebene. Was aber, wenn wir versuchen, die tatsächliche Struktur von Preis, Volumen und Zeit zu erkennen?
Bei meiner Arbeit an algorithmischen Systemen bin ich immer wieder auf die Tatsache gestoßen, dass traditionelle Indikatoren kritische Beziehungen zwischen Preis und Volumen übersehen.
Die Idee zu den 3D-Bars kam nicht sofort. Zunächst gab es ein Experiment mit der 3D-Visualisierung der Markttiefe. Dann tauchten die ersten Entwürfe für Volumen-Preis-Cluster auf. Und als ich die Zeitkomponente hinzufügte und den ersten 3D-Balken erstellte, wurde mir klar, dass dies eine grundlegend neue Art war, den Markt zu betrachten.
Heute möchte ich Ihnen die Ergebnisse dieser Arbeit vorstellen. Ich zeige Ihnen, wie Sie mit Python und MetaTrader 5 Volumenbalken in Echtzeit erstellen können. Ich werde über die Mathematik hinter den Berechnungen sprechen und darüber, wie man diese Informationen im praktischen Handel nutzen kann.
Was ist anders an der 3D-Leiste?
Solange wir den Markt durch das Prisma zweidimensionaler Charts betrachten, entgeht uns das Wichtigste - seine wirkliche Struktur. Die traditionelle technische Analyse arbeitet mit Preis-Zeit-, Volumen-Zeit-Projektionen, zeigt aber nie das vollständige Bild der Interaktion dieser Komponenten.
Die 3D-Analyse unterscheidet sich grundlegend, da sie uns erlaubt, den Markt als Ganzes zu betrachten. Wenn wir einen Volumenbalken konstruieren, erstellen wir buchstäblich einen „Schnappschuss“ des Marktzustands, wobei jede Dimension wichtige Informationen enthält:
- die Höhe des Balkens zeigt die Amplitude der Kursbewegung an
- die Breite spiegelt die Zeitskala wider
- Tiefe visualisiert die Volumenverteilung
Warum ist das wichtig? Stellen Sie sich zwei identische Kursbewegungen in einem Chart vor. In zwei Dimensionen sehen sie identisch aus. Wenn wir jedoch die Volumenkomponente hinzufügen, ändert sich das Bild dramatisch - eine Bewegung kann durch massives Volumen gestützt werden und einen tiefen und stabilen Balken bilden, während sich eine andere als oberflächlicher Spritzer mit minimaler Unterstützung für echte Trades entpuppt.
Ein integrierter Ansatz, der 3D-Balken verwendet, löst ein klassisches Problem der technischen Analyse - die Signalverzögerung. Die volumetrische Struktur des Balkens beginnt sich ab den ersten Ticks zu formen und ermöglicht es uns, die Entstehung einer starken Bewegung zu erkennen, lange bevor sie in einem regulären Chart erscheint. Im Wesentlichen erhalten wir ein prädiktives Analysewerkzeug, das nicht auf historischen Mustern, sondern auf der realen Dynamik des aktuellen Handels basiert.
Die multivariate Datenanalyse ist mehr als nur eine hübsche Visualisierung; sie ist eine grundlegend neue Art, die Mikrostruktur des Marktes zu verstehen. Jeder 3D-Balken enthält Informationen über:
- Verteilung des Volumens innerhalb der Preisspanne
- Positionen Akkumulationsgeschwindigkeit
- Ungleichgewichte zwischen Käufern und Verkäufern
- Volatilität auf der Mikroebene
- Bewegungsimpuls
All diese Komponenten wirken wie ein einziger Mechanismus, der es Ihnen ermöglicht, die wahre Natur der Preisbewegung zu erkennen. Wo die klassische technische Analyse nur eine Kerze oder einen Balken sieht, zeigt die 3D-Analyse die komplexe Struktur des Zusammenspiels von Angebot und Nachfrage.
Gleichungen für die Berechnung der wichtigsten Metriken. Grundprinzipien der Konstruktion von 7D-Balken. Die Logik der Kombination verschiedener Dimensionen in einem einzigen System
Das mathematische Modell der 3D-Balken entstand aus der Analyse der realen Marktmikrostruktur. Jeder Balken im System kann als dreidimensionale Figur dargestellt werden, wobei:
class Bar3D: def __init__(self): self.price_range = None # Price range self.time_period = None # Time interval self.volume_profile = {} # Volume profile by prices self.direction = None # Movement direction self.momentum = None # Impulse self.volatility = None # Volatility self.spread = None # Average spread
Entscheidend ist die Berechnung des volumetrischen Profils im Inneren des Stabes. Im Gegensatz zu den klassischen Balken analysieren wir die Verteilung des Volumens nach Preisniveaus.
def calculate_volume_profile(self, ticks_data): volume_by_price = defaultdict(float) for tick in ticks_data: price_level = round(tick.price, 5) volume_by_price[price_level] += tick.volume # Normalize the profile total_volume = sum(volume_by_price.values()) for price in volume_by_price: volume_by_price[price] /= total_volume return volume_by_price
Das Momentum wird als Kombination aus der Änderungsrate von Preis und Volumen berechnet:
def calculate_momentum(self): price_velocity = (self.close - self.open) / self.time_period volume_intensity = self.total_volume / self.time_period self.momentum = price_velocity * volume_intensity * self.direction
Besondere Aufmerksamkeit wird der Analyse der Volatilität der innerhalb der Balken gewidmet. Wir verwenden eine modifizierte ATR-Gleichung, die die Mikrostruktur der Bewegung berücksichtigt:
def calculate_volatility(self, tick_data): tick_changes = np.diff([tick.price for tick in tick_data]) weighted_std = np.std(tick_changes * [tick.volume for tick in tick_data[1:]]) time_factor = np.sqrt(self.time_period) self.volatility = weighted_std * time_factor
Der grundlegende Unterschied zu den klassischen Balken besteht darin, dass alle Metriken in Echtzeit berechnet werden, sodass wir die Entstehung der Balkenstruktur sehen können:
def update_bar(self, new_tick): self.update_price_range(new_tick.price) self.update_volume_profile(new_tick) self.recalculate_momentum() self.update_volatility(new_tick) # Recalculate the volumetric center of gravity self.volume_poc = self.calculate_poc()
Alle Messungen werden durch ein System von Gewichtungsfaktoren kombiniert, die für ein bestimmtes Instrument angepasst werden:
def calculate_bar_strength(self): return (self.momentum_weight * self.normalized_momentum + self.volatility_weight * self.normalized_volatility + self.volume_weight * self.normalized_volume_concentration + self.spread_weight * self.normalized_spread_factor)
Im realen Handel ermöglicht uns dieses mathematische Modell, solche Aspekte des Marktes zu erkennen wie:
- Ungleichgewichte in der Volumenakkumulation
- Anomalien in der Geschwindigkeit der Preisbildung
- Konsolidierungs- und Ausbruchszonen
- die wahre Stärke eines Trends anhand der Volumenmerkmale
Jeder 3D-Balken ist nicht nur ein Punkt auf dem Chart, sondern ein vollwertiger Indikator für den Zustand des Marktes zu einem bestimmten Zeitpunkt.
Eine detaillierte Analyse des Algorithmus zur Erstellung von 3D-Balken. Merkmale der Arbeit mit MetaTrader 5. Besonderheiten der Datenverarbeitung
Nach der Fehlersuche im Hauptalgorithmus kam ich schließlich zum interessantesten Teil - der Implementierung von mehrdimensionalen Balken in Echtzeit. Ich gebe zu, anfangs schien es eine entmutigende Aufgabe zu sein. MetaTrader 5 ist nicht besonders freundlich zu externen Skripten, und die Dokumentation bietet manchmal kein richtiges Verständnis. Aber lassen Sie mich Ihnen sagen, wie ich es geschafft habe, dies zu überwinden.
Ich habe mit einer Grundstruktur für die Speicherung von Daten begonnen. Nach mehreren Iterationen wurde die folgende Klasse geboren:
class Bar7D: def __init__(self): self.time = None self.open = None self.high = None self.low = None self.close = None self.tick_volume = 0 self.volume_profile = {} self.direction = 0 self.trend_count = 0 self.volatility = 0 self.momentum = 0
Der schwierigste Teil war herauszufinden, wie man die Blockgröße korrekt berechnet. Nach vielen Experimenten bin ich auf diese Gleichung gekommen:
def calculate_brick_size(symbol_info, multiplier=45): spread = symbol_info.spread point = symbol_info.point min_price_brick = spread * multiplier * point # Adaptive adjustment for volatility atr = calculate_atr(symbol_info.name) if atr > min_price_brick * 2: min_price_brick = atr / 2 return min_price_brick
Ich hatte auch große Probleme mit den Volumina. Zuerst wollte ich einen volume_brick mit fester Größe verwenden, merkte aber schnell, dass das nicht funktioniert. Die Lösung kam in Form eines adaptiven Algorithmus:
def adaptive_volume_threshold(tick_volume, history_volumes): median_volume = np.median(history_volumes) std_volume = np.std(history_volumes) if tick_volume > median_volume + 2 * std_volume: return median_volume + std_volume return max(tick_volume, median_volume / 2)
Aber ich glaube, ich habe es mit der Berechnung der statistischen Kennzahlen ein wenig übertrieben:
def calculate_stats(df): df['ma_5'] = df['close'].rolling(5).mean() df['ma_20'] = df['close'].rolling(20).mean() df['volume_ma_5'] = df['tick_volume'].rolling(5).mean() df['price_volatility'] = df['price_change'].rolling(10).std() df['volume_volatility'] = df['tick_volume'].rolling(10).std() df['trend_strength'] = df['trend_count'] * df['direction'] # This is probably too much df['zscore_price'] = stats.zscore(df['close'], nan_policy='omit') df['zscore_volume'] = stats.zscore(df['tick_volume'], nan_policy='omit') return df
Es ist lustig, aber der schwierigste Teil war nicht das Schreiben des Codes, sondern das Debuggen unter realen Bedingungen.
Hier ist das Endergebnis der Funktion mit der Normalisierung im Bereich 3-9. Warum 3-9? Sowohl Gann als auch Tesla behaupteten, dass in diesen Zahlen eine Art Magie verborgen sei. Ich habe auch persönlich einen Händler auf einer bekannten Plattform gesehen, der angeblich ein erfolgreiches Umkehrskript auf der Grundlage dieser Zahlen erstellt hat. Aber wir wollen uns nicht in Verschwörungstheorien und Mystizismus verlieren. Versuchen wir stattdessen dies:
def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000): """ Creates 3D Renko bars with extended analytics """ rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None # Convert time to numeric and scale everything scaler = MinMaxScaler(feature_range=(3, 9)) # Convert datetime to numeric (seconds from start) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Scale all numeric data together columns_to_scale = ['time_numeric', 'open', 'high', 'low', 'close', 'tick_volume'] df[columns_to_scale] = scaler.fit_transform(df[columns_to_scale]) renko_blocks = [] current_price = float(df.iloc[0]['close']) current_tick_volume = 0 current_time = df.iloc[0]['time'] current_time_numeric = float(df.iloc[0]['time_numeric']) current_spread = float(symbol_info.spread) current_type = 0 prev_direction = 0 trend_count = 0 try: for idx, row in df.iterrows(): if pd.isna(row['tick_volume']) or pd.isna(row['close']): continue current_tick_volume += float(row['tick_volume']) volume_bricks = int(current_tick_volume / volume_brick) price_diff = float(row['close']) - current_price if pd.isna(price_diff) or pd.isna(min_price_brick): continue price_bricks = int(price_diff / min_price_brick) if volume_bricks > 0 or abs(price_bricks) > 0: direction = np.sign(price_bricks) if price_bricks != 0 else 1 if direction == prev_direction: trend_count += 1 else: trend_count = 1 renko_block = { 'time': current_time, 'time_numeric': float(row['time_numeric']), 'open': float(row['open']), 'close': float(row['close']), 'high': float(row['high']), 'low': float(row['low']), 'tick_volume': float(row['tick_volume']), 'direction': float(direction), 'spread': float(current_spread), 'type': float(current_type), 'trend_count': trend_count, 'price_change': price_diff, 'volume_intensity': float(row['tick_volume']) / volume_brick, 'price_velocity': price_diff / (volume_bricks if volume_bricks > 0 else 1) } if volume_bricks > 0: current_tick_volume = current_tick_volume % volume_brick if price_bricks != 0: current_price += min_price_brick * price_bricks prev_direction = direction renko_blocks.append(renko_block) except Exception as e: print(f"Error processing data: {e}") if len(renko_blocks) == 0: return None, None if len(renko_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(renko_blocks) # Scale derived metrics to same range derived_metrics = ['price_change', 'volume_intensity', 'price_velocity', 'spread'] result_df[derived_metrics] = scaler.fit_transform(result_df[derived_metrics]) # Add analytical metrics using scaled data result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brickUnd so sieht die Reihe von Balken aus, die wir auf einer einzigen Skala erhalten haben. Nicht sehr stationär, oder?
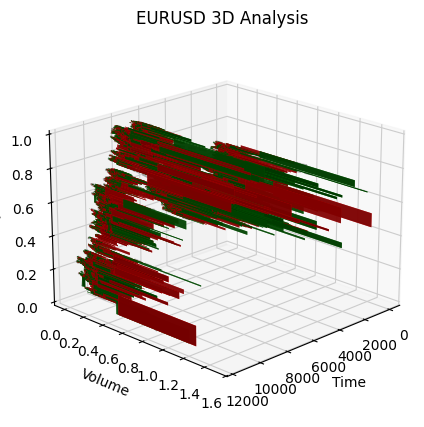
Natürlich war ich mit einer solchen Reihe nicht zufrieden, denn mein Ziel war es, eine mehr oder weniger stationäre Reihe zu schaffen - eine stationäre Zeit-Volumen-Preis-Reihe. Als Nächstes habe ich Folgendes getan:
Einführung in die Volatilitätsmessung
Bei der Implementierung der Funktion create_stationary_4d_features habe ich einen grundlegend anderen Weg eingeschlagen. Im Gegensatz zu den ursprünglichen 3D-Balken, bei denen wir die Daten einfach in den Bereich 3-9 skaliert haben, habe ich mich hier auf die Erstellung wirklich stationärer Reihen konzentriert.
Der Kerngedanke der Funktion besteht darin, eine vierdimensionale Darstellung des Marktes durch stationäre Merkmale zu erstellen. Anstatt einfach zu skalieren, wird jede Dimension auf besondere Weise transformiert, um Stationarität zu erreichen:
- Zeitliche Dimension: Hier habe ich die trigonometrische Transformation angewandt und die Stunden in Sinus- und Kosinuswellen umgewandelt. Die Gleichungen sin(2π * Stunde/24) und cos(2π * Stunde/24) erzeugen zyklische Merkmale und beseitigen das Problem der täglichen Saisonalität vollständig.
- Preismessung: Anstelle von absoluten Preiswerten werden deren relative Veränderungen verwendet. Im Code wird dies durch die Berechnung des typischen Preises (Hoch + Tief + Schluss)/3 und die anschließende Berechnung der Renditen und ihrer Beschleunigung umgesetzt. Bei diesem Ansatz ist die Reihe unabhängig vom Preisniveau stationär.
- Messung des Volumens: Hier ist ein interessanter Punkt - wir messen nicht nur die Veränderungen des Volumens, sondern auch ihre relativen Zuwächse. Dies ist wichtig, weil die Mengen oft sehr ungleichmäßig verteilt sind. Im Code wird dies durch die aufeinanderfolgende Anwendung von pct_change() und diff() umgesetzt.
- Messung der Volatilität: Hier habe ich eine zweistufige Umwandlung vorgenommen - zuerst wird die laufende Volatilität durch die Standardabweichung der Renditen berechnet, und dann werden die relativen Veränderungen dieser Volatilität ermittelt. In der Tat erhalten wir eine „Volatilität der Volatilität“.
Jeder Datenblock wird in einem gleitenden Fenster von 20 Perioden gebildet. Dabei handelt es sich nicht um eine Zufallszahl, sondern um einen Kompromiss zwischen der Erhaltung der lokalen Struktur der Daten und der Gewährleistung der statistischen Signifikanz der Berechnungen.
Alle berechneten Merkmale werden schließlich auf den Bereich 3-9 skaliert, aber dies ist bereits eine sekundäre Transformation, die auf bereits stationäre Reihen angewendet wird. Dadurch können wir die Kompatibilität mit der ursprünglichen Implementierung von 3D-Balken beibehalten und gleichzeitig einen grundlegend anderen Ansatz für die Datenvorverarbeitung verwenden.
Ein besonders wichtiger Punkt ist die Beibehaltung aller wichtigen Metriken der ursprünglichen Funktion - gleitende Durchschnitte, Volatilität, z-Scores. Dadurch kann die neue Implementierung als direkter Ersatz für die ursprüngliche Funktion verwendet werden, während gleichzeitig stationäre Daten von höherer Qualität erhalten werden.
Als Ergebnis erhalten wir eine Reihe von Merkmalen, die nicht nur im statistischen Sinne stationär sind, sondern auch alle wichtigen Informationen über die Marktstruktur enthalten. Durch diesen Ansatz eignen sich die Daten viel besser für die Anwendung von Methoden des maschinellen Lernens und der statistischen Analyse, wobei der Bezug zum ursprünglichen Handelskontext erhalten bleibt.
Hier ist die Funktion:
def create_true_3d_renko(symbol, timeframe, min_spread_multiplier=45, volume_brick=500, lookback=20000): """ Creates 4D stationary features with same interface as 3D Renko """ rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, lookback) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None scaler = MinMaxScaler(feature_range=(3, 9)) df_blocks = [] try: # Time dimension df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24) df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Price dimension df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3 df['price_return'] = df['typical_price'].pct_change() df['price_acceleration'] = df['price_return'].diff() # Volume dimension df['volume_change'] = df['tick_volume'].pct_change() df['volume_acceleration'] = df['volume_change'].diff() # Volatility dimension df['volatility'] = df['price_return'].rolling(20).std() df['volatility_change'] = df['volatility'].pct_change() for idx in range(20, len(df)): window = df.iloc[idx-20:idx+1] block = { 'time': df.iloc[idx]['time'], 'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(), 'open': float(window['price_return'].iloc[-1]), 'high': float(window['price_acceleration'].iloc[-1]), 'low': float(window['volume_change'].iloc[-1]), 'close': float(window['volatility_change'].iloc[-1]), 'tick_volume': float(window['volume_acceleration'].iloc[-1]), 'direction': np.sign(window['price_return'].iloc[-1]), 'spread': float(df.iloc[idx]['time_sin']), 'type': float(df.iloc[idx]['time_cos']), 'trend_count': len(window), 'price_change': float(window['price_return'].mean()), 'volume_intensity': float(window['volume_change'].mean()), 'price_velocity': float(window['price_acceleration'].mean()) } df_blocks.append(block) except Exception as e: print(f"Error processing data: {e}") if len(df_blocks) == 0: return None, None if len(df_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(df_blocks) # Scale all features features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction'] result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale]) # Add same analytical metrics as in original function result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brick
So sieht es in 2D aus:
Als Nächstes wollen wir versuchen, mit Plotly ein interaktives 3D-Modell für 3D-Preise zu erstellen. In der Nähe sollte ein normales zweidimensionales Chart zu sehen sein. Hier ist der Code:
import plotly.graph_objects as go from plotly.subplots import make_subplots def create_interactive_3d(df, symbol, save_dir): """ Creates interactive 3D visualization with smoothed data and original price chart """ try: save_dir = Path(save_dir) # Smooth all series with MA(100) df_smooth = df.copy() smooth_columns = ['close', 'tick_volume', 'price_volatility', 'volume_volatility'] for col in smooth_columns: df_smooth[f'{col}_smooth'] = df_smooth[col].rolling(window=100, min_periods=1).mean() # Create subplots: 3D view and original chart side by side fig = make_subplots( rows=1, cols=2, specs=[[{'type': 'scene'}, {'type': 'xy'}]], subplot_titles=(f'{symbol} 3D View (MA100)', f'{symbol} Original Price'), horizontal_spacing=0.05 ) # Add 3D scatter plot fig.add_trace( go.Scatter3d( x=np.arange(len(df_smooth)), y=df_smooth['tick_volume_smooth'], z=df_smooth['close_smooth'], mode='markers', marker=dict( size=5, color=df_smooth['price_volatility_smooth'], colorscale='Viridis', opacity=0.8, showscale=True, colorbar=dict(x=0.45) ), hovertemplate= "Time: %{x}<br>" + "Volume: %{y:.2f}<br>" + "Price: %{z:.5f}<br>" + "Volatility: %{marker.color:.5f}", name='3D View' ), row=1, col=1 ) # Add original price chart fig.add_trace( go.Candlestick( x=np.arange(len(df)), open=df['open'], high=df['high'], low=df['low'], close=df['close'], name='OHLC' ), row=1, col=2 ) # Add smoothed price line fig.add_trace( go.Scatter( x=np.arange(len(df_smooth)), y=df_smooth['close_smooth'], line=dict(color='blue', width=1), name='MA100' ), row=1, col=2 ) # Update 3D layout fig.update_scenes( xaxis_title='Time', yaxis_title='Volume', zaxis_title='Price', camera=dict( up=dict(x=0, y=0, z=1), center=dict(x=0, y=0, z=0), eye=dict(x=1.5, y=1.5, z=1.5) ) ) # Update 2D layout fig.update_xaxes(title_text="Time", row=1, col=2) fig.update_yaxes(title_text="Price", row=1, col=2) # Update overall layout fig.update_layout( width=1500, # Double width to accommodate both plots height=750, showlegend=True, title_text=f"{symbol} Combined Analysis" ) # Save interactive HTML fig.write_html(save_dir / f'{symbol}_combined_view.html') # Create additional plots with smoothed data (unchanged) fig2 = make_subplots(rows=2, cols=2, subplot_titles=('Smoothed Price', 'Smoothed Volume', 'Smoothed Price Volatility', 'Smoothed Volume Volatility')) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['close_smooth'], name='Price MA100'), row=1, col=1 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['tick_volume_smooth'], name='Volume MA100'), row=1, col=2 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['price_volatility_smooth'], name='Price Vol MA100'), row=2, col=1 ) fig2.add_trace( go.Scatter(x=np.arange(len(df_smooth)), y=df_smooth['volume_volatility_smooth'], name='Volume Vol MA100'), row=2, col=2 ) fig2.update_layout( height=750, width=750, showlegend=True, title_text=f"{symbol} Smoothed Data Analysis" ) fig2.write_html(save_dir / f'{symbol}_smoothed_analysis.html') print(f"Interactive visualizations saved in {save_dir}") except Exception as e: print(f"Error creating interactive visualization: {e}") raise
So sieht unsere neue Preisspanne aus:
Insgesamt sieht es sehr interessant aus. Wir sehen bestimmte Sequenzen der Preisgruppierung nach Zeit und Ausreißer bei der Preisgruppierung nach Volumen. So entsteht das Gefühl (und wird durch die Erfahrung führender Händler direkt bestätigt), dass wir es, wenn der Markt unruhig ist, wenn riesige Volumina herausgepumpt werden, wenn die Volatilität hereinbricht, mit einem gefährlichen Ausbruch zu tun haben, der über die Statistik hinausgeht - den berüchtigten Risiken der Ausläufer. Daher können wir hier sofort einen solchen „abnormalen“ Ausstieg des Preises auf solchen Koordinaten erkennen. Allein dafür möchte ich mich bei der Idee der multivariaten Preis-Charts bedanken!
Bitte beachten:
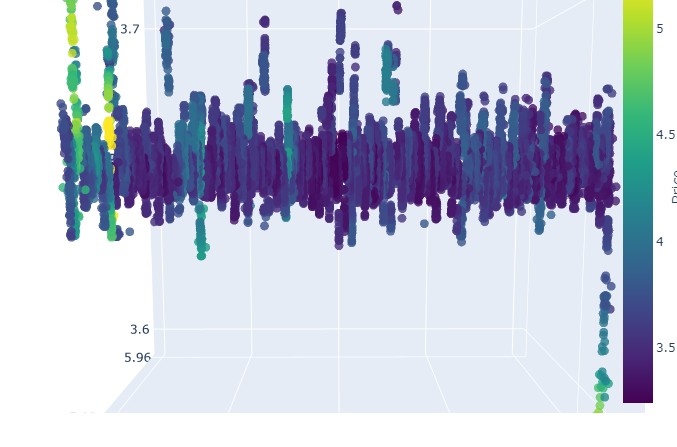
Untersuchung des Patienten (3D-Grafik)
Als Nächstes schlage ich vor, zu visualisieren. Aber nicht unsere strahlende Zukunft unter einer Palme, sondern 3D-Kurs-Charts. Unterteilen wir die Situationen in drei Gruppen: Aufwärtstrend, Abwärtstrend, Umkehr vom Aufwärtstrend zum Abwärtstrend und Umkehr vom Abwärtstrend zum Aufwärtstrend. Dazu müssen wir den Code ein wenig ändern: Wir brauchen die Balkenindizes nicht mehr, sondern laden Daten zu bestimmten Daten. Um dies zu tun, müssen wir nur zu mt5.copy_rates_range gehen.
def create_true_3d_renko(symbol, timeframe, start_date, end_date, min_spread_multiplier=45, volume_brick=500): """ Creates 4D stationary features with same interface as 3D Renko """ rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date) if rates is None: print(f"Error getting data for {symbol}") return None, None df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') if df.isnull().any().any(): print("Missing values detected, cleaning...") df = df.dropna() if len(df) == 0: print("No data for analysis after cleaning") return None, None symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") return None, None try: min_price_brick = symbol_info.spread * min_spread_multiplier * symbol_info.point if min_price_brick <= 0: print("Invalid block size") return None, None except AttributeError as e: print(f"Error getting symbol parameters: {e}") return None, None scaler = MinMaxScaler(feature_range=(3, 9)) df_blocks = [] try: # Time dimension df['time_sin'] = np.sin(2 * np.pi * df['time'].dt.hour / 24) df['time_cos'] = np.cos(2 * np.pi * df['time'].dt.hour / 24) df['time_numeric'] = (df['time'] - df['time'].min()).dt.total_seconds() # Price dimension df['typical_price'] = (df['high'] + df['low'] + df['close']) / 3 df['price_return'] = df['typical_price'].pct_change() df['price_acceleration'] = df['price_return'].diff() # Volume dimension df['volume_change'] = df['tick_volume'].pct_change() df['volume_acceleration'] = df['volume_change'].diff() # Volatility dimension df['volatility'] = df['price_return'].rolling(20).std() df['volatility_change'] = df['volatility'].pct_change() for idx in range(20, len(df)): window = df.iloc[idx-20:idx+1] block = { 'time': df.iloc[idx]['time'], 'time_numeric': scaler.fit_transform([[float(df.iloc[idx]['time_numeric'])]]).item(), 'open': float(window['price_return'].iloc[-1]), 'high': float(window['price_acceleration'].iloc[-1]), 'low': float(window['volume_change'].iloc[-1]), 'close': float(window['volatility_change'].iloc[-1]), 'tick_volume': float(window['volume_acceleration'].iloc[-1]), 'direction': np.sign(window['price_return'].iloc[-1]), 'spread': float(df.iloc[idx]['time_sin']), 'type': float(df.iloc[idx]['time_cos']), 'trend_count': len(window), 'price_change': float(window['price_return'].mean()), 'volume_intensity': float(window['volume_change'].mean()), 'price_velocity': float(window['price_acceleration'].mean()) } df_blocks.append(block) except Exception as e: print(f"Error processing data: {e}") if len(df_blocks) == 0: return None, None if len(df_blocks) == 0: print("Failed to create any blocks") return None, None result_df = pd.DataFrame(df_blocks) # Scale all features features_to_scale = [col for col in result_df.columns if col != 'time' and col != 'direction'] result_df[features_to_scale] = scaler.fit_transform(result_df[features_to_scale]) # Add same analytical metrics as in original function result_df['ma_5'] = result_df['close'].rolling(5).mean() result_df['ma_20'] = result_df['close'].rolling(20).mean() result_df['volume_ma_5'] = result_df['tick_volume'].rolling(5).mean() result_df['price_volatility'] = result_df['price_change'].rolling(10).std() result_df['volume_volatility'] = result_df['tick_volume'].rolling(10).std() result_df['trend_strength'] = result_df['trend_count'] * result_df['direction'] # Scale moving averages and volatility ma_columns = ['ma_5', 'ma_20', 'volume_ma_5', 'price_volatility', 'volume_volatility', 'trend_strength'] result_df[ma_columns] = scaler.fit_transform(result_df[ma_columns]) # Add statistical metrics and scale them result_df['zscore_price'] = stats.zscore(result_df['close'], nan_policy='omit') result_df['zscore_volume'] = stats.zscore(result_df['tick_volume'], nan_policy='omit') zscore_columns = ['zscore_price', 'zscore_volume'] result_df[zscore_columns] = scaler.fit_transform(result_df[zscore_columns]) return result_df, min_price_brick
Hier ist unser geänderter Code:
def main(): try: # Initialize MT5 if not mt5.initialize(): print("MetaTrader5 initialization error") return # Analysis parameters symbols = ["EURUSD", "GBPUSD"] timeframes = { "M15": mt5.TIMEFRAME_M15 } # 7D analysis parameters params = { "min_spread_multiplier": 45, "volume_brick": 500 } # Date range for data fetching start_date = datetime(2017, 1, 1) end_date = datetime(2018, 2, 1) # Analysis for each symbol and timeframe for symbol in symbols: print(f"\nAnalyzing symbol {symbol}") # Create symbol directory symbol_dir = Path('charts') / symbol symbol_dir.mkdir(parents=True, exist_ok=True) # Get symbol info symbol_info = mt5.symbol_info(symbol) if symbol_info is None: print(f"Failed to get symbol info for {symbol}") continue print(f"Spread: {symbol_info.spread} points") print(f"Tick: {symbol_info.point}") # Analysis for each timeframe for tf_name, tf in timeframes.items(): print(f"\nAnalyzing timeframe {tf_name}") # Create timeframe directory tf_dir = symbol_dir / tf_name tf_dir.mkdir(exist_ok=True) # Get and analyze data print("Getting data...") df, brick_size = create_true_3d_renko( symbol=symbol, timeframe=tf, start_date=start_date, end_date=end_date, min_spread_multiplier=params["min_spread_multiplier"], volume_brick=params["volume_brick"] ) if df is not None and brick_size is not None: print(f"Created {len(df)} 7D bars") print(f"Block size: {brick_size}") # Basic statistics print("\nBasic statistics:") print(f"Average volume: {df['tick_volume'].mean():.2f}") print(f"Average trend length: {df['trend_count'].mean():.2f}") print(f"Max uptrend length: {df[df['direction'] > 0]['trend_count'].max()}") print(f"Max downtrend length: {df[df['direction'] < 0]['trend_count'].max()}") # Create visualizations print("\nCreating visualizations...") create_visualizations(df, symbol, tf_dir) # Save data csv_file = tf_dir / f"{symbol}_{tf_name}_7d_data.csv" df.to_csv(csv_file) print(f"Data saved to {csv_file}") # Results analysis trend_ratio = len(df[df['direction'] > 0]) / len(df[df['direction'] < 0]) print(f"\nUp/Down bars ratio: {trend_ratio:.2f}") volume_corr = df['tick_volume'].corr(df['price_change'].abs()) print(f"Volume-Price change correlation: {volume_corr:.2f}") # Print warnings if anomalies detected if df['price_volatility'].max() > df['price_volatility'].mean() * 3: print("\nWARNING: High volatility periods detected!") if df['volume_volatility'].max() > df['volume_volatility'].mean() * 3: print("WARNING: Abnormal volume spikes detected!") else: print(f"Failed to create 3D bars for {symbol} on {tf_name}") print("\nAnalysis completed successfully!") except Exception as e: print(f"An error occurred: {e}") import traceback print(traceback.format_exc()) finally: mt5.shutdown()
Nehmen wir den ersten Datenabschnitt - EURUSD, vom 1. Januar 2017 bis zum 1. Februar 2018. In der Tat, ein sehr starker Aufwärtstrend. Möchten Sie sehen, wie es in 3D-Balken aussieht?
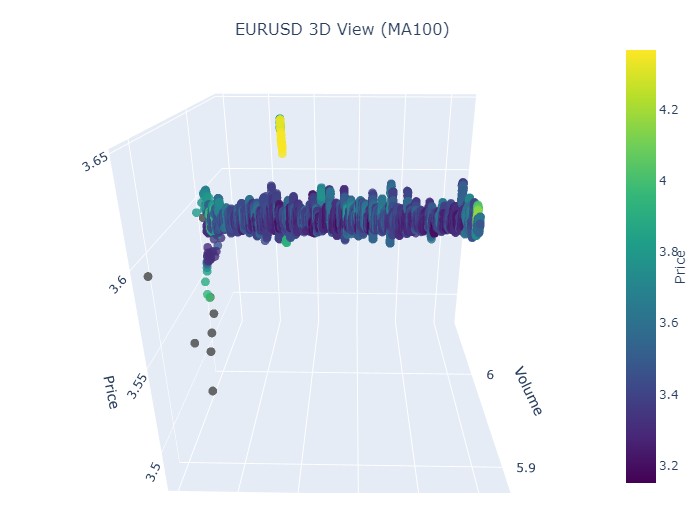
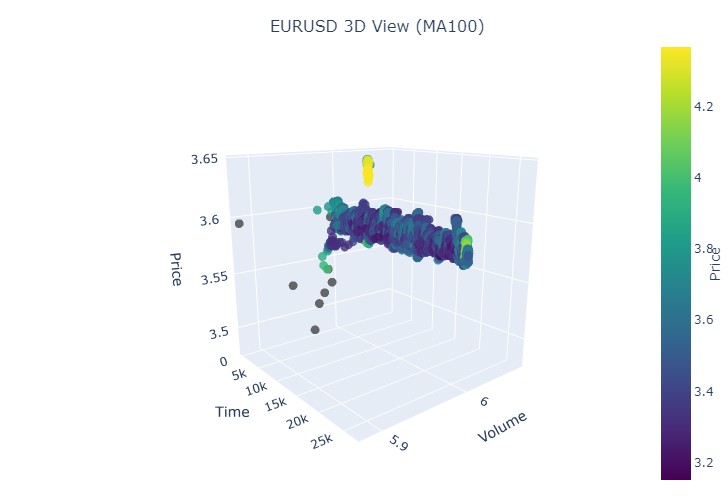
So sieht eine andere Visualisierung aus:
Achten wir auf den Beginn des Aufwärtstrends:
Und bis zum Ende:
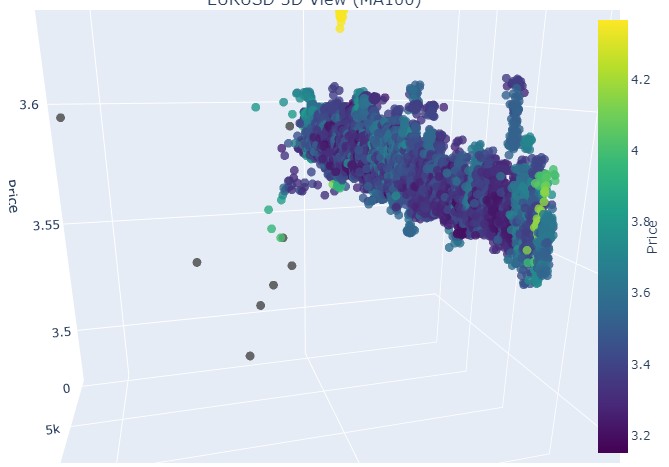
Schauen wir uns nun den Abwärtstrend an. Vom 1. Februar 2018 bis zum 20. März 2020:
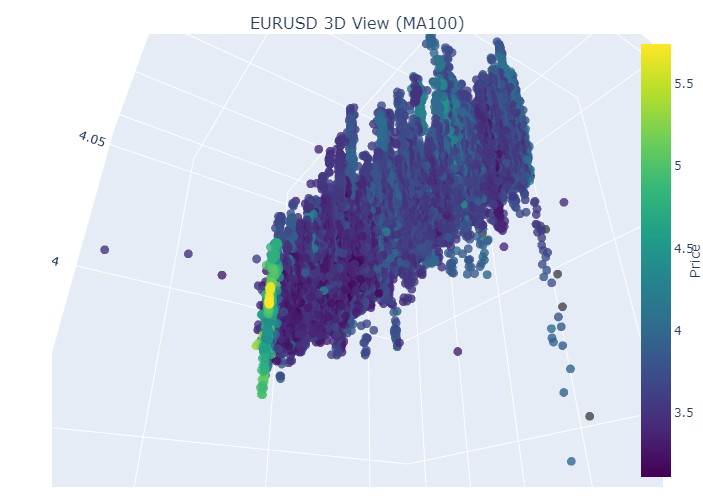
Hier ist der Beginn des Abwärtstrends:
Und hier ist sein Ende:
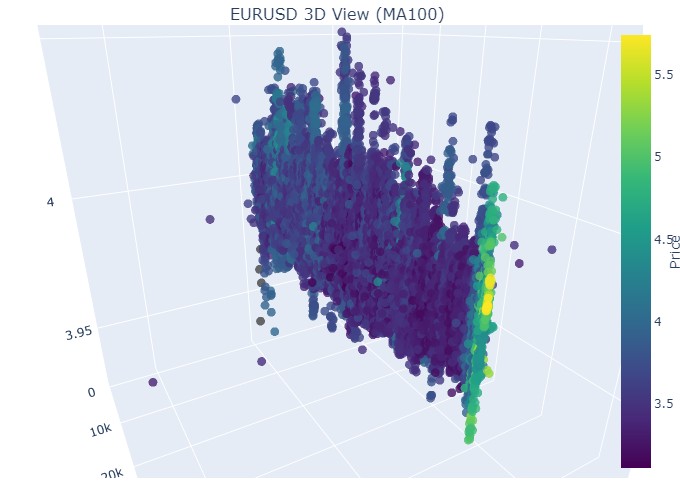
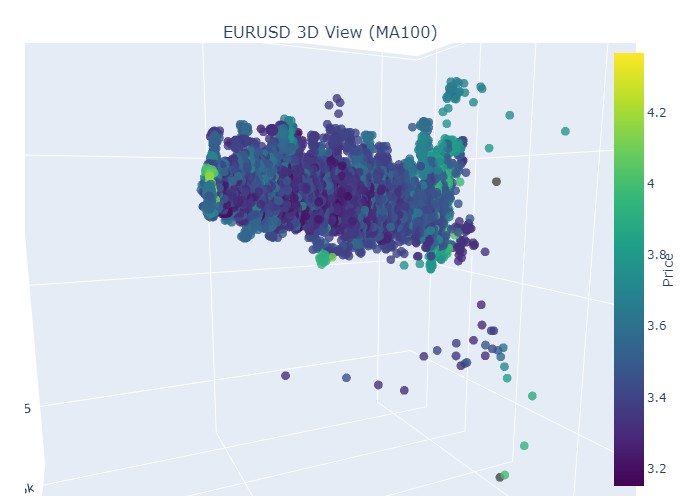
Wir sehen also, dass beide Trends (sowohl der Abwärts- als auch der Aufwärtstrend) in der 3D-Darstellung als ein Bereich von Punkten unterhalb der 3D-Punktdichte begannen. Das Ende des Trends war in beiden Fällen durch ein leuchtend gelbes Farbschema gekennzeichnet.
Zur Beschreibung dieses Phänomens und des Kursverhaltens von EURUSD in Aufwärts- und Abwärtstrends kann die folgende universelle Gleichung verwendet werden:
P(t) = P_0 + \int_{t_0}^{t} A \cdot e^{k(t-u)} \cdot V(u) \, du + N(t)
wobei:
- P(t) - Währungspreis zu einem bestimmten Zeitpunkt.
- P_0 - Anfangspreis zu einem bestimmten Zeitpunkt.
- A - Trendamplitude, die das Ausmaß der Preisänderungen kennzeichnet.
- k - Verhältnis, das die Änderungsrate bestimmt (k > 0 bedeutet Aufwärtstrend; k < 0 bedeutet Abwärtstrend).
- V(u) - Handelsvolumen zu einem bestimmten Zeitpunkt, das die Marktaktivität beeinflusst und die Bedeutung von Preisänderungen erhöhen kann.
- N(t) - Zufallsrauschen, das unvorhersehbare Marktschwankungen widerspiegelt.
Erläuterung zum Text
Diese Gleichung beschreibt, wie sich der Preis einer Währung im Laufe der Zeit in Abhängigkeit von einer Reihe von Faktoren verändert. Der Anfangskurs ist der Ausgangspunkt, nach dem das Integral den Einfluss der Trendamplitude und deren Veränderungsrate berücksichtigt und den Kurs je nach Größe exponentiell wachsen oder fallen lässt. Das durch die Funktion dargestellte Handelsvolumen fügt eine weitere Dimension hinzu und zeigt, dass die Marktaktivität auch die Preisänderungen beeinflusst.
Dieses Modell ermöglicht die Visualisierung von Preisbewegungen unter verschiedenen Trends, indem es sie im 3D-Raum anzeigt, wo die Zeitachse, der Preis und das Volumen ein umfassendes Bild der Marktaktivität ergeben. Die Helligkeit des Farbschemas in diesem Muster kann die Stärke des Trends anzeigen, wobei hellere Farben höheren Derivatpreis- und Handelsvolumenwerten entsprechen, die starke Volumenbewegungen auf dem Markt signalisieren.
Anzeige der Umkehrung
Hier ist der Zeitraum vom 14. bis 28. November. Etwa in der Mitte dieses Zeitraums wird es zu einer Umkehrung der Kurse kommen. Wie sieht das in 3D-Koordinaten aus? Und zwar so:
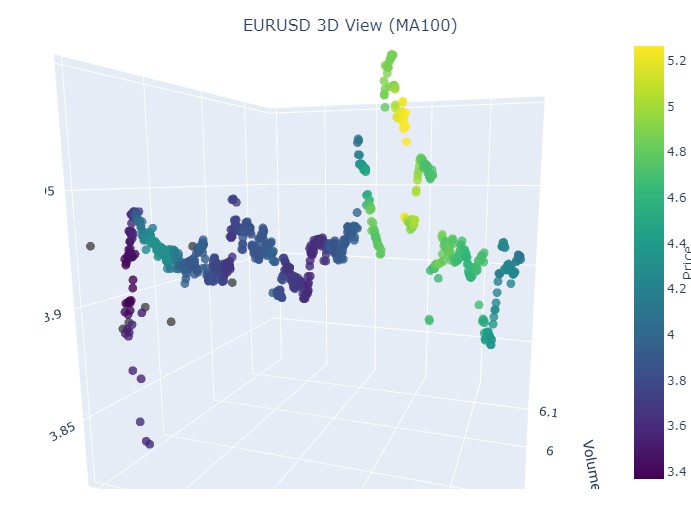
Wir sehen die bereits bekannte gelbe Farbe im Moment der Umkehrung und des Anstiegs der normalisierten Preiskoordinate. Betrachten wir nun einen weiteren Kursabschnitt mit einer Trendwende, vom 13. September 2024 bis zum 10. Oktober desselben Jahres:
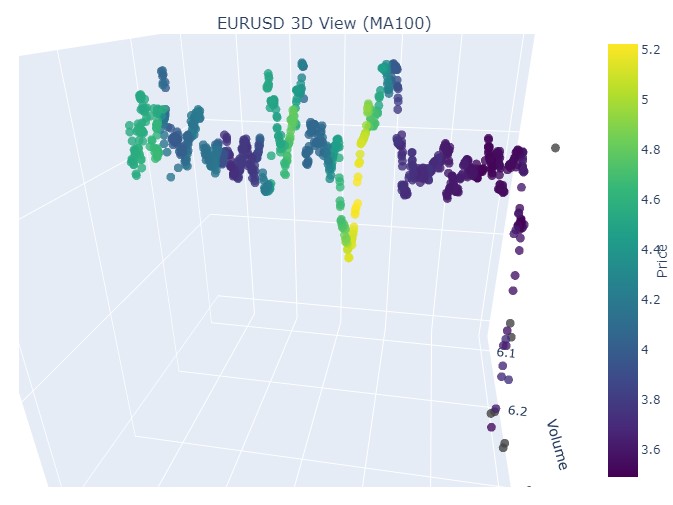
Wir sehen dasselbe Bild noch einmal, nur dass die gelbe Farbe und ihre Anhäufung jetzt ganz unten sind. Sieht interessant aus.
19. August 2024 - 30. August 2024, eine exakte Trendumkehr ist in der Mitte dieses Datumsbereichs zu erkennen. Schauen wir uns unsere Koordinaten an.
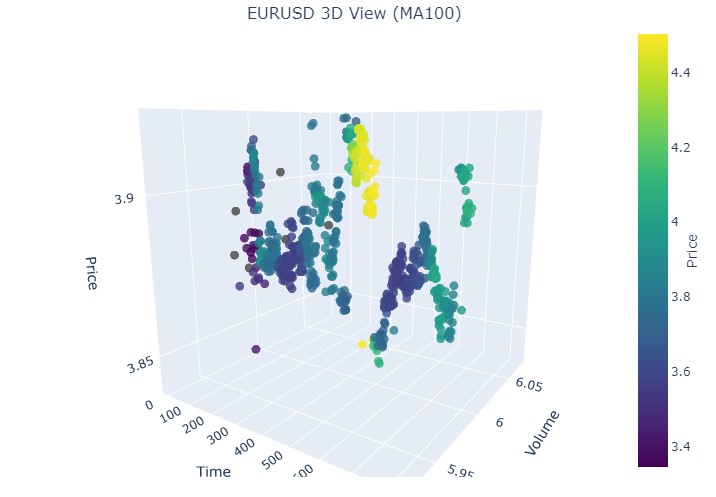
Wiederum genau das gleiche Bild. Betrachten wir den Zeitraum vom 17. Juli 2024 bis zum 8. August 2024. Zeigt das Modell bald Anzeichen einer Umkehrung?
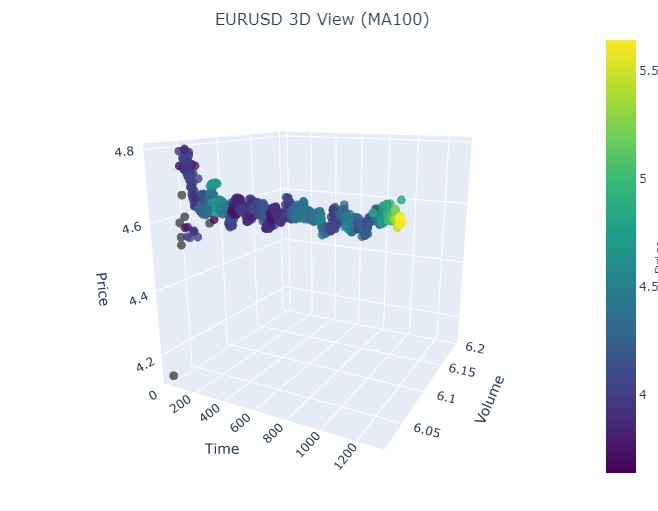
Der letzte Zeitraum erstreckt sich vom 21. April bis zum 10. August 2023. Der Aufwärtstrend endete dort.
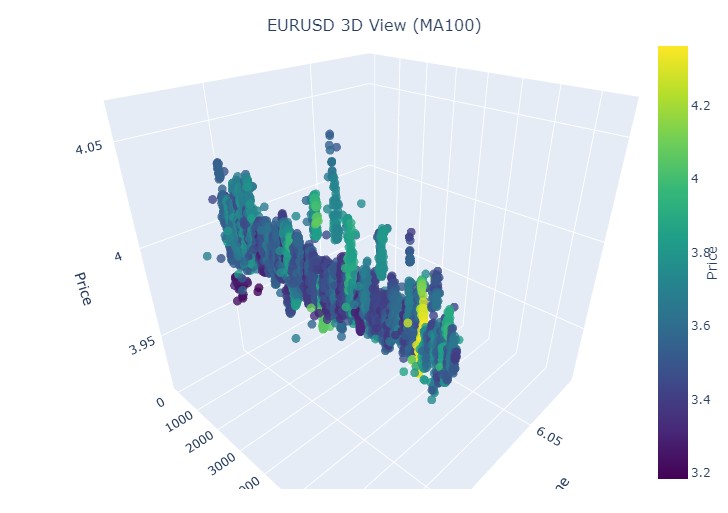
Wir sehen wieder die vertraute gelbe Farbe.
Gelbe Cluster
Bei der Entwicklung von 3D-Balken bin ich auf ein sehr interessantes Merkmal gestoßen - gelbe volumen-volatile Cluster. Ich war fasziniert von ihrem Verhalten auf dem Chart Nachdem ich eine Menge historischer Daten durchgesehen hatte (mehr als 400.000 Balken für 2022-2024, um genau zu sein), stellte ich etwas Überraschendes fest.
Zunächst traute ich meinen Augen nicht - von den etwa 100 Tausend gelben Balken waren fast alle (97 %!) nahe an einer Kursumkehr. Außerdem funktionierte dies in einem Bereich von plus oder minus drei Balken. Interessant ist, dass nur 40 % der Umkehrungen (und es gab insgesamt etwa 169 Tausend davon) gelbe Balken aufweisen. Es zeigt sich, dass ein gelber Balken fast eine Garantie für eine Umkehr ist, obwohl Umkehrungen auch ohne ihn stattfinden können.
Bei näherer Betrachtung der Trends ist mir ein klares Muster aufgefallen. Zu Beginn und während des Trends gibt es fast keine gelben Balken, sondern nur regelmäßige 3D-Balken in einer dichten Gruppe. Doch vor der Umkehrung leuchten die gelben Cluster auf dem Chart.
Dies zeigt sich besonders deutlich in langen Trends. Nehmen wir zum Beispiel das Wachstum des EURUSD von Anfang 2017 bis Februar 2018 und dann den Rückgang bis März 2020. In beiden Fällen erschienen diese gelben Cluster vor der Umkehrung, und ihre 3D-Platzierung zeigte buchstäblich an, wohin der Kurs gehen würde!
Ich habe die Sache auch in kurzen Zeiträumen getestet - ich habe 2024 mehrere 2-3-wöchige Abschnitte genommen. Es funktionierte wie am Schnürchen! Jedes Mal, wenn ein Umschwung bevorstand, erschienen gelbe Balken, wie zur Warnung: „Hey, Mann, der Trend ist dabei, sich umzukehren!“
Dies ist nicht nur ein Indikator. Ich denke, wir sind auf etwas wirklich Wichtiges in der Marktstruktur selbst gestoßen - die Art und Weise, wie die Volumina verteilt sind und wie sich die Volatilität vor einem Trendwechsel verändert. Wenn ich jetzt gelbe Cluster in einem 3D-Chart sehe, weiß ich, dass es Zeit ist, sich auf eine Umkehr vorzubereiten!
Schlussfolgerung
Zum Abschluss unserer Erkundung von 3D-Balken komme ich nicht umhin zu bemerken, wie sehr dieser Tauchgang mein Verständnis der Marktmikrostruktur verändert hat. Was als Visualisierungsexperiment begann, hat sich zu einer grundlegend neuen Art und Weise entwickelt, den Markt zu sehen und zu verstehen.
Bei der Arbeit an diesem Projekt ist mir immer wieder aufgefallen, wie sehr wir durch die traditionelle zweidimensionale Darstellung von Preisen eingeschränkt sind. Der Übergang zur dreidimensionalen Analyse hat völlig neue Horizonte für das Verständnis der Beziehungen zwischen Preis, Volumen und Zeit eröffnet. Besonders beeindruckt hat mich, wie deutlich die Muster, die wichtigen Marktereignissen vorausgehen, im dreidimensionalen Raum erscheinen.
Die wichtigste Entdeckung war die Fähigkeit, potenzielle Trendumkehrungen frühzeitig zu erkennen. Die charakteristische Häufung von Volumina und die Veränderung des Farbschemas in der 3D-Darstellung haben sich als überraschend zuverlässige Indikatoren für bevorstehende Trendwechsel erwiesen. Dies ist nicht nur eine theoretische Feststellung, sondern wir haben sie durch zahlreiche historische Beispiele bestätigt.
Das von uns entwickelte mathematische Modell ermöglicht es uns, die Marktdynamik nicht nur zu visualisieren, sondern auch quantitativ zu bewerten. Die Integration moderner Visualisierungstechnologien und Softwaretools hat es möglich gemacht, diese Methode im realen Handel anzuwenden. Ich nutze diese Tools täglich und sie haben meine Herangehensweise an die Marktanalyse stark verändert.
Ich glaube jedoch, dass wir erst am Anfang der Reise stehen. Dieses Projekt öffnete die Tür zur Welt der multivariaten Mikrostrukturanalyse des Marktes, und ich bin zuversichtlich, dass weitere Forschungen in dieser Richtung viele weitere interessante Entdeckungen bringen werden. Der nächste Schritt könnte die Integration von maschinellem Lernen zur automatischen Erkennung von 3D-Mustern oder die Entwicklung neuer Handelsstrategien auf der Grundlage multivariater Analysen sein.
Letztlich liegt der wahre Wert dieser Forschung nicht in den hübschen Charts oder komplexen Gleichungen, sondern in den neuen Markteinblicken, die sie bietet. Als Forscher bin ich fest davon überzeugt, dass die Zukunft der technischen Analyse in einem multivariaten Ansatz zur Analyse von Marktdaten liegt.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16555
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Parametereffizienter Transformer mit segmentierter Aufmerksamkeit (letzter Teil)
Neuronale Netze im Handel: Parametereffizienter Transformer mit segmentierter Aufmerksamkeit (letzter Teil)
 Neuronale Netze im Handel: Ein parameter-effizienter Transformer mit segmentierter Aufmerksamkeit (PSformer)
Neuronale Netze im Handel: Ein parameter-effizienter Transformer mit segmentierter Aufmerksamkeit (PSformer)
 Algorithmischer Handel auf der Grundlage von 3D-Umkehrmustern
Algorithmischer Handel auf der Grundlage von 3D-Umkehrmustern
 Der Indikator Market Profile (Teil 2) Optimierung und Rendering auf Leinwand
Der Indikator Market Profile (Teil 2) Optimierung und Rendering auf Leinwand
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Es stellt sich sofort die Frage: Warum? Ein flaches Diagramm reicht für eine genaue Analyse nicht aus? Das ist der Punkt, an dem die normale Schulgeometrie funktioniert.
Jeder Algorithmus erforscht im Wesentlichen räumliche Dimensionen. Indem wir Algorithmen entwickeln, versuchen wir, das grundlegende Problem der kombinatorischen Explosion durch mehrdimensionale Suche zu lösen. Das ist unsere Art, durch ein unendliches Meer von Möglichkeiten zu navigieren.
(Entschuldigung, wenn die Übersetzung nicht perfekt ist)
Jeder Algorithmus erforscht im Wesentlichen räumliche Dimensionen. Indem wir Algorithmen entwickeln, versuchen wir, das grundlegende Problem der kombinatorischen Explosion durch mehrdimensionale Suche zu lösen. Das ist unsere Art, durch ein unendliches Meer von Möglichkeiten zu navigieren.
(Entschuldigung, wenn die Übersetzung nicht perfekt ist)
Das ist klar. Wenn wir die Trendvorhersage nicht durch einfache geometrische Schulformeln lösen können, erfinden die Leute einen Lysaped mit Turboaufladung, mit Smartphone-Steuerung, mit Smiley-Gesichtern und anderem Lametta! Nur gibt es keine Räder, und es wird auch nicht erwartet, dass sie Räder haben. Und ohne Räder kann man mit einem Rahmen nicht weit kommen.
Aha. Wenn es unmöglich ist, die Trendvorhersage mit einfachen geometrischen Formeln zu lösen, dann erfinden die Leute ein lisaped mit Turboaufladung, mit Smartphone-Steuerung, mit Smiley-Gesichtern und anderem Lametta! Nur gibt es keine Räder, und es wird auch nicht erwartet, dass sie Räder haben. Und ohne Räder kann man auf einem Rahmen nicht weit kommen.