MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 32): Regularisierung

Einführung

Die Regularisierung ist eine weitere Facette von Algorithmen des maschinellen Lernens, die eine gewisse Sensibilität für die Leistung von neuronalen Netzen mit sich bringt. Im Verlauf eines Netzes besteht häufig die Tendenz, einige Parameter auf Kosten anderer zu stark zu gewichten. Dies „Bias“ auf bestimmte Parameter (Netzgewichte) kann die Leistung des Netzes beeinträchtigen, wenn die Tests mit Daten durchgeführt werden, die nicht aus der Stichprobe stammen. Aus diesem Grund wurde die Regularisierung entwickelt.

Es handelt sich im Wesentlichen um einen Mechanismus, der den Konvergenzprozess verlangsamt, indem er das Ergebnis der Verlustfunktion im Verhältnis zur Magnitude der an jeder Schichtverbindung verwendeten Gewichte erhöht (oder bestraft). Dies geschieht häufig entweder durch: Early-Stopping, Lasso, Ridge, Elastic-Net, oder Drop-Out. Jedes dieser Formate ist ein wenig anders. Wir werden aber nicht auf alle Typen eingehen, sondern uns auf Lasso, Ridge und Drop-Out beschränken.

Wir betrachten die Vorteile und die Verwendung der Regularisierung im Zusammenhang mit einer geeigneten oder synchronisierten Paarung mit Aktivierungs- und Verlustfunktionen. Die richtige Auswahl und Paarung dieser Funktionen verhindert zumindest das Problem des Explodierens/der verschwindenden Gradienten, weshalb der Autor in den letzten Artikeln (dieser Reihe) die Verwendung von Sigmoid- und Soft-Max-Aktivierung zusammen mit Binär-Kreuzentropie- oder kategorialen Kreuzentropie-Verlustfunktionen bei der Behandlung von Klassifizierungsnetzwerken befürwortet hat. Umgekehrt könnte die TANH der Soft-Sign-Aktivierung in Verbindung mit MSE- oder MAE- oder Huber-Verlustfunktionen geeignet sein, wenn es um regressive neuronale Netze geht.

In einem früheren Artikel haben wir auch betont, wie wichtig es ist, diese ausgewählten Aktivierungsfunktionen mit geeigneten bereichsgebundenen Batch-Normalisierungsalgorithmen zu kombinieren, wobei die Verlustfunktion jedoch ungebunden ist. Das bedeutet, dass der zusätzliche Term zur Verlustfunktion (die Regularisierung) nicht unbedingt mit einer Aktivierungsfunktion oder einer Batch-Normalisierungsfunktion gepaart sein muss, die in einem idealen Bereich (-1 bis +1 für Regressoren und 0 bis 1 für Klassifikatoren) liegt.

Dennoch muss bei der Wahl des Regularisierungstyps berücksichtigt werden, ob es sich bei dem Netzwerk um einen Regressor oder einen Klassifikator handelt. Wenn wir zum Beispiel L1 Lasso verwenden, indem wir nur den absoluten Wert der Gewichte bestrafen, neigt der Trainingsprozess dazu, viele der Gewichte in den Netzschichten auf Null zu reduzieren, während nur die kritischen Gewichte auf akzeptablen kleinen Nicht-Null-Werten belassen werden. Dies führt naturgemäß zu einer spärlichen Ausgabe, eine Situation, die sich gut für Klassifizierungsnetze eignet, deren Merkmalswahrscheinlichkeiten vorhergesagt werden. Dies ist vor allem in Situationen relevant, in denen innerhalb der prognostizierten Merkmalswahrscheinlichkeiten nur einige wenige Merkmale von Bedeutung sein dürften.

Umgekehrt wird bei Regressionsnetzen, bei denen die endgültige Ausgabeschicht oft eine Größe von 1 hat (anders als z. B. bei Klassifikationsnetzen), erwartet, dass der Beitrag der verschiedenen Gewichte „demokratischer“ ist. Um dies zu erreichen, ist der L2 oder Ridge-Regulierer besser geeignet, da er nach dem Quadrat der Gewichte gewichtet ist, was zu einem gleichmäßigeren Beitrag der Schichtengewichte zur endgültigen Ausgabe führt. Die Drop-out-Regularisierung könnte eine Alternative zur Regularisierung von Klassifizierungsnetzwerken sein, da auch sie aufgrund der zufälligen Annullierung einiger Gewichte eine gewisse Sparsamkeit in die Ausgabeergebnisse einbringt. Wir stellen den Code dafür in den Anhängen unten zur Verfügung, aber unsere Tests konzentrieren sich auf L1 und L2.

Regularisierung in neuronalen Netzen

Die beiden Formate der Regularisierung, die wir im Folgenden testen, bestrafen die Verlustfunktion im Verhältnis zur Magnitude des Netzgewichts. Diese „Magnitude“ wird durch eine Normfunktion berechnet, die in unserem Fall in mehreren Varianten angeboten wird. Streng genommen müsste diese Norm jedoch die Summe der Magnituden aller Matrixwerte sein. Diese Absolutwertsumme kann in MQL5 leicht wie folgt realisiert werden:

//+------------------------------------------------------------------+
//| Typical Norm function                                            |
//+------------------------------------------------------------------+
double Norm(matrix &M)
{  double _norm = 0.0;
   for(int i = 0; i < int(M.Rows()); i++)
   {  for(int ii = 0; ii < int(M.Cols()); ii++)
      {  _norm += M[i][ii];
      }
   }
   return(_norm);
}

Wir tauchen jedoch in die Matrixnorm ein (dank der verschiedenen Funktionen, die im Datentyp Matrix verfügbar sind). Die Matrixnormen sind im Gegensatz zu den einfachen absoluten Normen nicht so seltsam, wie es auf den ersten Blick scheinen mag, denn es wird argumentiert, dass sie ein strukturelles Bewusstsein in den Prozess der Regularisierungsgewichtung einbringen. Darüber hinaus ermöglichen sie die Kontrolle über bestimmte gewünschte Netzeigenschaften, wie z. B. die Glattheit von Regressor-Netzen, und bieten gleichzeitig die Flexibilität, die gewünschte Sparsamkeit der Klassifizierungsnetz-Ausgänge fein abzustimmen. Die Berücksichtigung dieser zusätzlichen Eigenschaften, die oft nuanciert erscheinen, bei der Bewertung der Gewichtungsmatrizen für die Regularisierung ist also das, was wir in unseren Testergebnissen unten anwenden werden. Zur Verdeutlichung: Wir ziehen bis zu neun verschiedene Matrixnormen für jeden der beiden Regularisierungsansätze in Betracht, die wir für ein Regressor- und Klassifizierungsnetzwerk testen werden.

Im letzten Artikel, in dem wir uns mit der Verlustfunktion beschäftigt haben, hatten wir zwei Netzwerktypen, einen Regressor und einen Klassifikator. Wir werden auch in diesem Artikel bei diesen Formaten bleiben, um die Regularisierung zu veranschaulichen.

L1-Regularisierung (Lasso)

Bei der Lasso- (oder L1-) Regularisierung wird die Verlustfunktion proportional zum absoluten Wert der Gewichte oder zu den Matrixnormen der Gewichte bestraft, wie oben beschrieben. Dies wird formal durch die nachstehende Gleichung definiert:

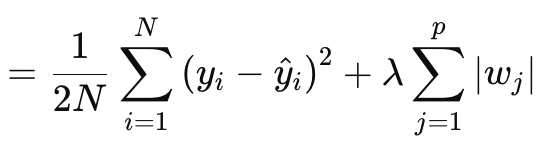
wobei:

• N ist die Anzahl der Datenpunkte.
• p ist die Gesamtzahl der Schichten, für die es Gewichtungsmatrizen gibt
• yi ist der Zielwert (oder Label) für den i-ten Datenpunkt.
• y^i ist der vorhergesagte Wert für den i-ten Datenpunkt.
• wj sind die Koeffizienten (Gewichte) des Modells.

§λ ist der Regularisierungsparameter, der die Stärke der Regularisierung steuert. Ein größeres λ erhöht die Strafe für große Gewichte und fördert die Sparsamkeit. Sein optimaler Bereich kann 10^-4 bis 10^-1 für Soft-Max- oder Sigmoid-Aktivierungsnetze bzw. 10^-5 bis 10^-2 für Soft-Sign- oder TANH-Netze betragen.

Anders ausgedrückt, der Regularisierungswert besteht aus dem MSE, der Differenz zwischen den prognostizierten und den tatsächlichen Werten (linke Seite), plus der Normalsumme der Gewichte über alle Schichten. Wir setzen dies in MQL5 wie folgt um:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();
   if(THIS.regularization == REGULARIZE_L1)
   {  _term = _mse + (Lambda * _weights_norm);
   }
   
        ....

   _regularized.Fill(_term);
   return(_regularized);
}

Die Ausgabe ist ein skalarer Wert, kein Vektor, und das ist ein großer Unterschied zu dem, was wir als Ausgaben der Verlustfunktion behandelt haben. Denn wenn wir unsere Aktualisierungsdeltas definieren müssen, die uns dann helfen, die Aktualisierungsgradienten bei der Rückwärtspropagation festzulegen, wird der Verlust als Vektor quantifiziert. Dieser Vektor fließt in die Delta-Vektoren ein, die ihrerseits die Gradientenmatrizen aktualisieren. Um dies beizubehalten, erstellen wir einen Vektor, der mit replizierten Werten des Regularisierungswertes gefüllt ist, und verwenden diesen als Ausgabe. Dieser Standardvektorwert wird dann zu allen Verlustwerten im Verlustvektor addiert, wie sie durch die verwendete Verlustfunktion definiert sind. Dies würde wie folgt umgesetzt werden:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }

   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss);
   _last_loss += RegularizeTerm(label, THIS.regularization_lambda);

   deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative);
   
        ...

}

Es wird also eine einheitliche Strafe auf alle Merkmale/Klassen des Ausgangsvektors angewandt, und vielleicht könnte man sich deshalb für die Verwendung von Matrixnormen und nicht nur ihres Absolutwerts aussprechen, da die Normen die Matrixstruktur bei ihren Berechnungen berücksichtigen.

Bei der Berechnung des Regularisierungsterms stehen eine Reihe von Matrixnormen zur Verfügung, die zwar alle für die Bestimmung des Lassos verwendet werden können, aber nicht alle geeignet sind. Die Frobenius-Norm ist besser auf L2 abgestimmt, da sie große Gewichte direkt bestraft, ohne Sparsamkeit zu erzwingen, was im Widerspruch zu Lasso steht, das darauf abzielt, dass unkritische Gewichte auf Null gesetzt werden. Die Kernnorm eignet sich besser für die Förderung von Matrizen mit niedrigem Rang, die für das Problem der Matrix-Vervollständigung relevant sind. Es ist nicht auf Lasso abgestimmt, das elementweise Sparsamkeit im Gegensatz zu Rank-Sparsamkeit fördert. Die Spektralnorm wird auch verwendet, um den maximalen Einfluss einer Matrix auf einen Vektor zu kontrollieren und nicht um die Sparsamkeit zu gewährleisten.

Während Unendlichkeitsnormen eine Form von Sparsamkeit erzeugen können, sind sie für die Erzeugung elementweiser Sparsamkeit weniger geeignet. Die Minus-Unendlichkeitsnorm konzentriert sich auf die Minimierung der kleinsten Zeilensummen, was nicht mit dem Lasso-Ziel der Sparsamkeit übereinstimmt. Das Gleiche gilt für Minus P1 und Minus P2, da sie beide versuchen, den Einfluss kleiner Elemente zu minimieren.

Aus dieser Enumeration von neun Normen ergibt sich, dass nur die P1-Norm am besten mit Lasso funktioniert, weil sie die Sparsamkeit mit dem Ziel der elementweisen Sparsamkeit fördert. P2, die endgültige Norm der Neun, ist besser für die L2 oder Ridge Regularisierung geeignet. Um es noch einmal zusammenzufassen: Die L1-Regularisierung wurde oben als ideal für Klassifizierungsnetzwerke erwähnt. Dies impliziert eine Klassifikator-L1-P1-Beziehung, die nur wenige Alternativen für die Funktion der Matrixnormen des Gewichts bietet.

L2-Regularisierung (Ridge)

Die L2- oder Ridge-Regularisierung ist der L1-Formel sehr ähnlich, mit dem offensichtlichen Unterschied, dass die Normen der Gewichte quadriert werden, anstatt den Rohwert zu verwenden. Dies wird wie folgt angegeben:

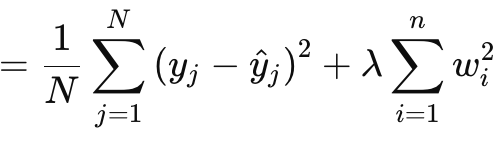
wobei:

• λ ist der Regularisierungsparameter, der die Stärke der Strafe steuert.
• w i sind die Gewichte oder Koeffizienten des Modells.
• n ist die Anzahl der Schichten mit einer vorangehenden Gewichtsmatrix.
• N ist die Anzahl der Datenpunkte.
• y j ist der tatsächliche Zielwert.
• y^ j ist der vorhergesagte Wert.

Wie bei L1 gibt es einen MSE und einen Term, der in diesem Fall eine Summe der quadrierten Gewichte ist. Wir setzen dies in MQL5 wie folgt um:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...

   else if(THIS.regularization == REGULARIZE_L2)
   {  _term = _mse + (Lambda * _weights_norm * _weights_norm);
   }
   

...

   _regularized.Fill(_term);
   return(_regularized);
}

Die Quadrierung der Gewichte, wie oben beschrieben, führt zu einer Glättung der Regularisierung, was diesen Ansatz zu einem idealen Kandidaten für Regressor-Netzwerke macht. Darüber hinaus wird die Regularisierung am besten durch Frobenius-Matrixnormen oder P2-Normen gehandhabt. Soweit ich weiß, handelt es sich dabei um dieselben Begriffe, wobei Frobenius häufig für Matrizen und P2 für Vektoren verwendet wird. In den Matrixnormen-Funktionen von MQL5 kann nun neben Frobenius auch P2 ausgewählt werden, und die beiden liefern leicht unterschiedliche Ergebnisse. Es gibt hier einen Beitrag über die Unterschiede zwischen den beiden.

Aus all dem ergibt sich, dass die Regressor-L2-Frobenius-Paarung bei regressiven neuronalen Netzen ideal wäre.

Regularisierung von Ausfällen

Schließlich gibt es noch die Drop-out-Regularisierung, die sich deutlich von den beiden oben beschriebenen Typen unterscheidet. Nebenbei bemerkt können L1 und L2 in einem gewichteten Format zu einem so genannten Elastic-Net kombiniert werden, aber das bleibt dem Leser überlassen, um es auszuprobieren und zu implementieren, denn alles, was erforderlich wäre, ist ein zusätzlicher Alpha-Parameter für die Proportionierung der Gewichte. Beim Drop-out wird ein Neuron zufällig ausgewählt, das beim Training im Vorwärtsdurchlauf weggelassen wird. Dies setzen wir in unserer MLP-Klasse wie folgt um:

//+------------------------------------------------------------------+
//| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON.          |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Input data is normalized if normalization type was selected at  |
//|  class instance initialisation.                                  |
//+------------------------------------------------------------------+
void Cmlp::Forward(bool Training = false)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
//
   for(int h = 0; h <= hidden_layers; h++)
   {  vector _output;
      _output.Init(output.Size());

...

      if(Training && THIS.regularization == REGULARIZE_DROPOUT)
      {  int _drop = MathRand() % int(_output.Size());
         _output[_drop] = 0.0;
      }
      _output += biases[h];

...


   }
}

Beim Training und bei der Anpassung der Gewichte können einige Gewichte auf Null gesetzt werden, sodass die Tatsache, dass wir einige der Werte der Ausgangsneuronen auf Null gesetzt haben, für das Erreichen des gewünschten Ergebnisses unwirksam sein könnte. Auch eine manuelle Multiplikation mit for-Schleifen, in denen wir zufällig Neuronen auslassen, wäre ein besserer Ansatz für die Umsetzung des Drop-outs gewesen. Es erfordert mehr Kodierung, aber der Leser ist eingeladen, dies zu versuchen.

Wir führen keine Tests mit der Drop-Out-Regularisierung durch, da deren Vorteile in der Regel nur bei sehr tiefen und transformatorisch gestapelten Netzen sichtbar sind. Für die Zwecke dieses Artikels testen wir nur L1 und L2, der Code für Drop-Out ist jedoch beigefügt und steht für Änderungen und Tests in großen Netzwerken zur Verfügung.

Die Drop-Out-Regularisierung ist aus einer Reihe von Gründen für die Implementierung beliebt, und so wollen wir versuchen, ein paar von ihnen durchzugehen. Erstens wird eine übermäßige Anpassung des Modells verhindert, indem das Netz gezwungen wird, redundante Darstellungen zu lernen. Dadurch wird sichergestellt, dass das Netz nicht zu sehr von bestimmten Neuronen oder Eingangsmerkmalen/-klassen abhängig ist. Dies deutet auf eine verbesserte Generalisierung hin. Durch das zufällige Fallenlassen von Neuronen entsteht im Trainingsprozess aus einem einzigen neuronalen Netz ein Ensemble von Modellen. Diese verbesserte Generalisierung macht das Netzwerk robuster bei der Klassifizierung von ungesehenen Daten, insbesondere in komplexen, hochdimensionalen Datensituationen.

Darüber hinaus macht Drop-out ein Netzwerk widerstandsfähiger gegenüber verrauschten Daten, da es sicherstellt, dass kein Neuron den Entscheidungsprozess dominiert. Dies ist nicht nur bei verrauschten oder weniger zuverlässigen Testdaten wichtig, sondern auch in Situationen, in denen die Eingabedaten ein hohes Maß an Varianz aufweisen. Darüber hinaus wird die gegenseitige Abhängigkeit der Neuronen reduziert oder die Unterbrechung der Koadaption der Neuronen gefördert. Dies ermutigt jedes Neuron, unabhängig zu lernen, was das Netz robuster macht. Hinzu kommt, dass die Verwendung von Drop-Out in sehr tiefen und transformatorisch gestapelten Netzen nicht nur den Testprozess effizienter machen könnte (wenn der Prozess die Neuronen manuell fallen lässt, anstatt den Post-Output-Vektor-Ansatz zu verwenden, den wir gewählt haben), sondern auch das Risiko einer Überanpassung angesichts der großen Anzahl von Parametern verhindert.

Es ist auf verschiedene Netzwerkformate wie MLPs oder CNNs anwendbar und auch skalierbar. Im Vergleich zu L1 und L2 tendiert Drop-out eher zu L1, da das Fallenlassen von Neuronen beim Testen zu spärlicheren Ausgabeergebnissen führt, die in Klassifizierungsnetzwerken entscheidend sind. Der Grund dafür ist, dass die meisten der oben erwähnten Ausstiegsprofis für Klassifizierungsnetze relevant sind. Diese Netze sind oft tiefer als Regressor-Netze, und diese Vielzahl von Parametern macht sie anfällig für Overfitting. Die oben erwähnte Ausmusterung wirkt dem entgegen, indem sie das Netz zwingt, allgemeinere und robustere Merkmale zu lernen. Die Generalisierung ist der Schlüssel zu Klassifizierern, die durch Drop-Out verbessert werden; verrauschte Daten können sie (im Vergleich zu Regressor-Netzwerken) unverhältnismäßig stark beeinträchtigen, und Drop-Out trägt dazu bei, diese Auswirkungen zu mildern. Dies und viele der oben bereits erwähnten Merkmale implizieren die Eignung für Klassifizierungsnetze, da Klassifizierungsnetze im Allgemeinen, aber nicht immer, dazu neigen, sehr wenige, aber große Schichten zu haben. Sie sind sehr tief. Andererseits haben Regressornetzwerke in der Regel kleine, aber gestapelte Schichten. Sie tendieren eher zu Transformatoren. Dies ist vielleicht eine weitere wichtige Überlegung, die nicht nur bei der Festlegung der Regularisierung eines Netzes, sondern auch bei der Bestimmung der Gesamtzahl und Größe der Schichten berücksichtigt werden sollte.

Test Ergebnisse

Wie versprochen, führen wir wie immer Tests mit einem von einem Assistenten zusammengestellten Expert Advisor durch. Für neue Leser muss der beigefügte Code zu einem Expert Advisor zusammengesetzt werden, indem man den Richtlinien folgt, die hier und hier verfügbar sind. Diesmal testen wir EURUSD auf dem täglichen Zeitrahmen für das Jahr 2023. Wie im letzten Artikel testen wir ein Regressor-Netzwerk und ein Klassifikator-Netzwerk.

Wie bereits in den vorangegangenen Artikeln dargelegt, funktionieren Klassifizierungsnetze am besten mit Soft-Max- oder Sigmoid-Aktivierungen. Darüber hinaus eignen sie sich, wie bereits erwähnt, besser für die Arbeit mit kategorialen oder binären Cross-Entropie-Verlustfunktionen und L1-Regularisierung, die speziell P1-Matrixnormen verwendet. Wenn wir also Tests mit diesen Einstellungen durchführen und dabei schwebende Aufträge (pending orders) ohne Stop-Loss platzieren, erhalten wir die folgenden Ergebnisse:

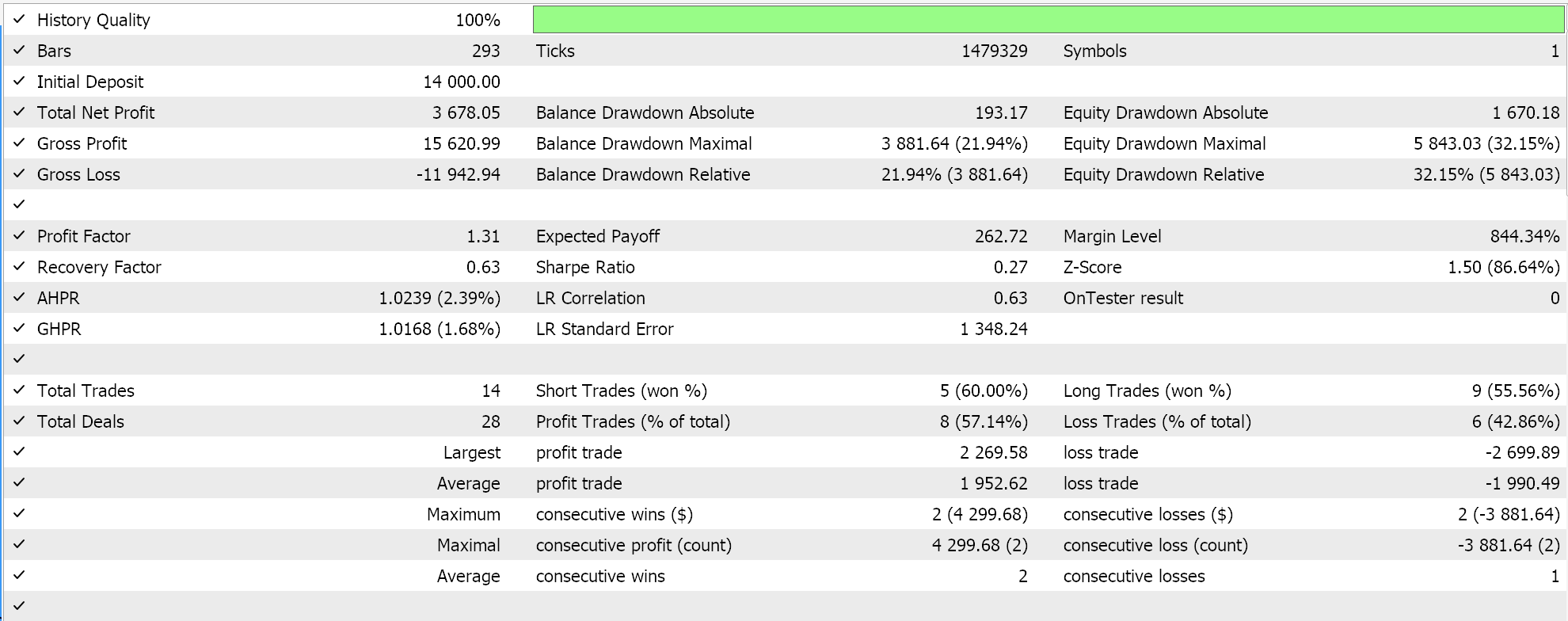
Die Kapitalkurven:

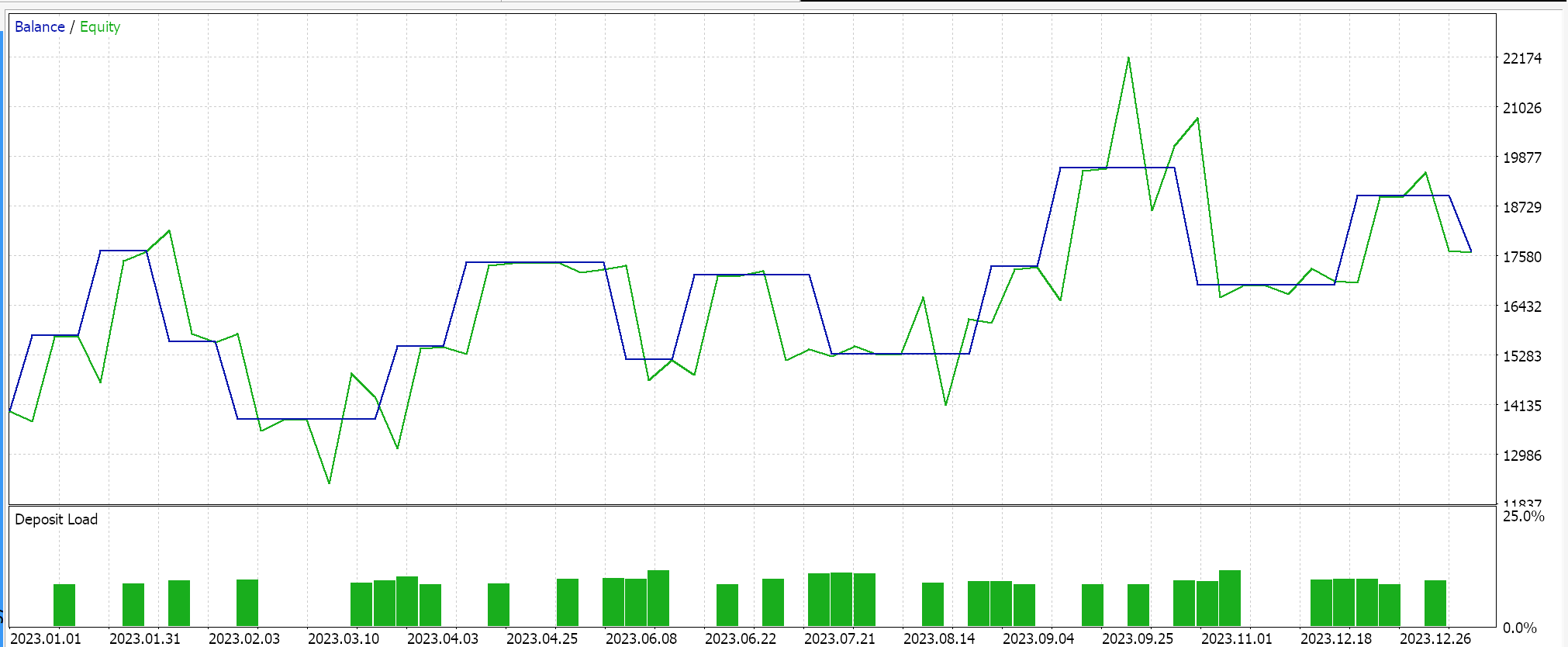
Umgekehrt erhalten wir für das Regressor-Netzwerk die folgenden Ergebnisse, wenn wir Tests mit Soft-Sign-Aktivierung und L2-Ridge-Regularisierung zusammen mit der Huber-Verlustfunktion durchführen:

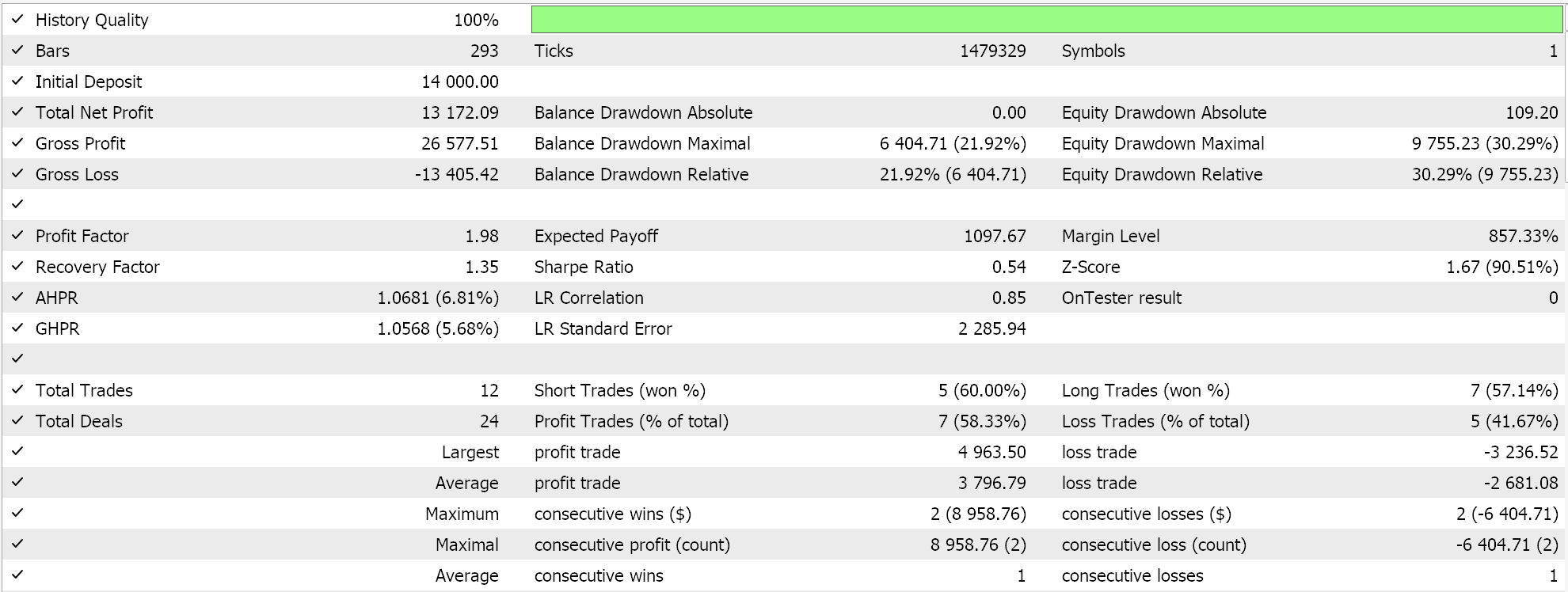
Und die Kapitalkurven:

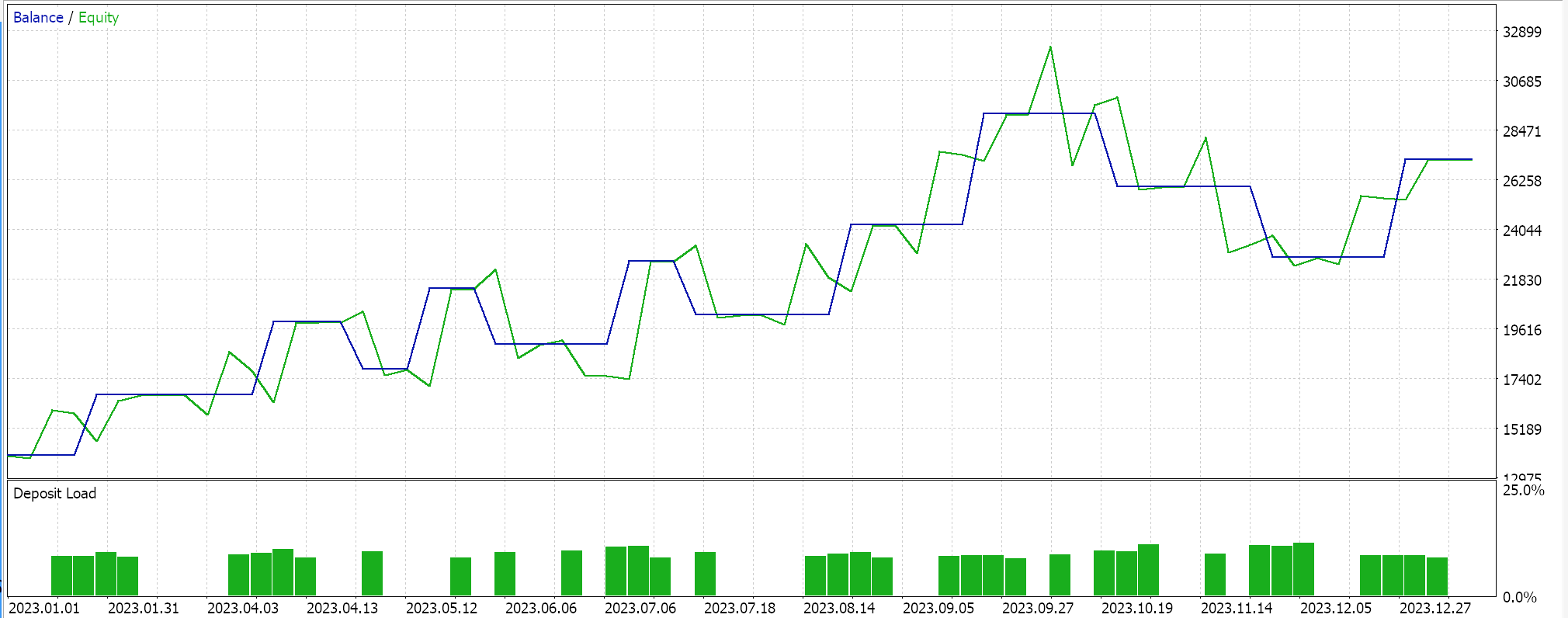
Um diese Ergebnisse zu kontrollieren, müsste man das Netz mit umgekehrten Regularisierungsoptionen oder gar ohne Regularisierung trainieren. Testläufe mit identischen Einstellungen wie oben für das Regressor- und das Klassifikatornetzwerk, aber ohne Regularisierung, führen zu den gleichen Ergebnissen. Dies könnte bedeuten, dass die Regularisierung nicht so entscheidend ist wie andere Faktoren wie die Verlustfunktion, Aktivierungsfunktionen und sogar die typischen Einstiegs- und Abschlussschwellen des Expert Advisors. Es könnte jedoch auch ein gegenteiliges und vielleicht glaubwürdiges Argument vorgebracht werden, dass die Vorteile der Regularisierung insbesondere im Klassifizierungsnetz am besten zu erkennen sind, wenn nicht nur über längere Zeiträume getestet wird, die über ein Jahr hinausgehen, sondern auch mit sehr tiefen Netzen, die eine breitere Ausgangsklasse aufweisen.

Schlussfolgerung

Abschließend haben wir die Regularisierung als Schlüsselkomponente von Algorithmen des maschinellen Lernens, wie z.B. neuronalen Netzen, untersucht, indem wir ihre Rolle in zwei speziellen Situationen betrachteten. Klassifikatornetze und Regressornetze. Klassifizierungsnetze haben oft, aber nicht immer, nur sehr wenige Schichten, aber jede ihrer Schichten ist sehr tief. Andererseits haben Regressor-Netze in der Regel kleine Schichten, die aber in mehreren übereinander gestapelt werden, um die fehlende Tiefe auszugleichen. Während unsere Testergebnisse darauf hindeuten, dass die Leistung des Expert Advisors nicht auf die Regularisierung anspricht, sind auf der Grundlage der EURUSD-Läufe auf dem täglichen Zeitrahmen für 2023 weitere Tests erforderlich, bevor eine solch drastische Schlussfolgerung gezogen werden kann. Das liegt daran, dass die verwendeten Netze nicht nur ein kleines Testfenster hatten, sondern auch eine sehr bescheidene Größe, bei der es unwahrscheinlich ist, dass die Vorteile der Regularisierung voll zum Tragen kommen.

Epilog

Ich hatte vor, die Elastic-Net-Regularisierung nicht zu erwähnen, aber da der Artikel nicht allzu lang ist, dachte ich, ich könnte ihn hier kurz anfügen. Die Gleichung für Elastic-Net lautet wie folgt:

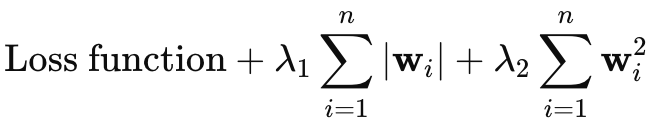
Wobei

• wi steht für die einzelnen Gewichte des Modells.
• λ1 steuert die Stärke der L1-Strafe (Lasso), die die Sparsamkeit des Modells fördert, indem sie einige Gewichte auf Null schrumpfen lässt.
• λ2 steuert die Stärke der L2-Strafe (Ridge), die kleine Gewichte begünstigt, sie aber im Allgemeinen nicht auf Null reduziert.

Um die Regularisierung des elastischen Netzes zu unserer Klasse hinzuzufügen, müssten wir zunächst die Hauptenumeration wie folgt ändern, um sie aufzunehmen:

//+------------------------------------------------------------------+
//| Regularization Type Enumerator                                   |
//+------------------------------------------------------------------+
enum Eregularize
{  REGULARIZE_NONE = -1,
   REGULARIZE_L1 = 1,
   REGULARIZE_L2 = 2,
   REGULARIZE_DROPOUT = 3,
   REGULARIZE_ELASTIC = 4
};

Dann müssten wir zweitens die Funktion „RegularizeTerm“ ändern, um diese Elastic-Net-Option zu behandeln, indem wir eine dritte Klausel hinzufügen, und das implementieren wir wie folgt:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...


   else if(THIS.regularization == REGULARIZE_ELASTIC)
   {  _term =  _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) +
               ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm));
   }
   _regularized.Fill(_term);
   return(_regularized);
}

Dies ergibt sich eindeutig aus der oben dargestellten Formel, da sie einen gewichteten Mittelwert mit einem positiven Alpha-Wert von höchstens 1 verwendet. Dies würde normalerweise im Bereich von 0,0 bis 1,0 optimiert werden. In unserer obigen Code-Implementierung verwenden wir jedoch eine einzige Matrixnorm-Aufzählung, was die Erfassung der unabhängigen Eigenschaften von L1 und L2 verhindern würde. Eine Möglichkeit, dies zu umgehen, besteht darin, zwei Variablen „_weight_norm“ zu haben, die jeweils ihre eigenen Matrixnormfunktionen haben, aber dies würde auch bedeuten, dass die Konstruktorstruktur geändert werden müsste, um beide unterzubringen. Alternativ könnte man auch die Unendlichkeitsnormen als Kompromiss für beide Regularisierungsformate verwenden.