知っておくべきMQL5ウィザードのテクニック（第32回）：正則化

はじめに

正規化は、機械学習アルゴリズムのもう一つの側面であり、ニューラルネットワークの性能に感度をもたらします。ネットワークのプロセスでは、しばしば、あるパラメータに過度の重み付けをし、他のパラメータを犠牲にする傾向があります。特定のパラメータ（ネットワークの重み）に対するこの「偏り」は、サンプル外のデータでテストをおこなった場合、ネットワークのパフォーマンスを妨げることになります。これが正則化が開発された理由です。

これは基本的に、各層の接合部で使用される重みの大きさに比例して損失関数の結果を増加させる（またはペナルティを課す）ことにより、収束プロセスを遅くするメカニズムとして機能します。これは多くの場合、次のいずれかの方法でおこなわれます。アーリーストッピング、ラッソ回帰、リッジ回帰、エラスティックネット、ドロップアウト。これらの形式はそれぞれ少しずつ異なるので、すべての種類を検討することはしませんが、代わりに、ラッソ回帰、リッジ回帰、ドロップアウトを取り上げることにします。

活性化関数と損失関数との適切なペアリング、あるいは同期をとるという文脈の中で、正則化の利点とその利用について考えます。これらの適切な選択と組み合わせは、最低限、勾配の爆発や消失の問題を防ぐことができます。そのため、筆者は本連載の最近の記事で、分類器ネットワークを扱う際に、シグモイドとソフトマックスの活性化とバイナリクロスエントロピーまたはカテゴリクロスエントロピー損失関数を併用することを提唱してきました。逆に、ソフトサイン活性化のTANHは、MSEやMAE、Huber損失関数と組み合わせることで、回帰型ニューラルネットワークを扱う場合に適しています。

また、関連する過去の記事で、これらの選択活性化関数と適切な範囲拘束バッチ正規化アルゴリズムを組み合わせることの重要性を強調しましたが、損失関数は非拘束です。つまり、損失関数の追加項（正則化）は、必ずしも理想的な範囲（回帰関数の場合は-1～+1、分類関数の場合は0～1）に束縛される活性化関数やバッチ正規化関数と対になるとは限りません。

とはいえ、正則化のタイプは、ネットワークが回帰器なのか分類器なのかを考慮する必要があります。例えば、L1ラッソ回帰を使用する場合、重みの絶対値だけでペナルティをかけることで、学習プロセスはネットワーク層の重みの多くをゼロにし、重要なものだけを許容できる小さな非ゼロ値に残す傾向があります。これは本来、出力にスパース性をもたらすもので、特徴確率を予測する分類器ネットワークには好都合な状況です。これは、予測特徴確率の中で、いくつかの特徴だけが重要であると予想される場合に特に関連します。

逆に、（例えば分類ネットワークの確率とは異なり）最終出力層のサイズが1であることが多い回帰型ネットワークでは、様々な重みの寄与はしばしば「より民主的」であることが期待されます。これを達成するためには、L2正則化器またはリッジ正則化器が適しています。重みの2乗に対して重み付けされるので、最終出力に対する各層の重みの寄与がより均等になるからです。ドロップアウト正規化は、一部の重みをランダムに無効化することにより出力結果にある程度スパース性を導入するため、分類器ネットワークを正規化する代わりに使用できます。このコードは以下の添付ファイルで共有していますが、テストはL1とL2に焦点を当てています。

ニューラルネットワークにおける正則化

以下で試す2種類の正則化は、ネットワーク重みの大きさに比例して損失関数にペナルティを与えます。この「大きさ」はノルム関数によって計算されます。私たちの場合、かなり多くの種類が提供されています。しかし厳密に言えば、このノルムはすべての行列値の大きさの和であるべきです。この絶対値和は、MQL5で次のように簡単に実現できます。

//+------------------------------------------------------------------+
//| Typical Norm function                                            |
//+------------------------------------------------------------------+
double Norm(matrix &M)
{  double _norm = 0.0;
   for(int i = 0; i < int(M.Rows()); i++)
   {  for(int ii = 0; ii < int(M.Cols()); ii++)
      {  _norm += M[i][ii];
      }
   }
   return(_norm);
}

ただし、ここでは行列ノルムについて少し触れておきます（行列データ型内で利用できるさまざまな関数のおかげです）。行列ノルムは単純な絶対値とは異なり、正則化の重み付けプロセスに構造的な認識を導入するものであるため、最初は奇妙に見えるかもしれないが、それほど適合しているわけではありません。さらに、分類器ネットワークの出力に望ましいスパース性を微調整する柔軟性を提供しながら、回帰器ネットワークの平滑性のような特定の望ましいネットワーク特性を制御することができます。そこで、正則化のための重み行列を評価する際に、しばしば微妙に見えるこれらの余分な特性を考慮することが、以下のテスト結果で適用されることになります。はっきりさせるために、回帰器と分類器ネットワークに対してテストする2つの正則化アプローチのそれぞれに対して、最大9つの異なる行列規範を考慮しています。

損失関数に注目した前回の記事では、2つのネットワークタイプ、回帰型とクラシファイアーを用意しました。この記事でも、正則化の説明にはこれらの形式にこだわることにします。

L1正則化（ラッソ）

Lasso（またはL1）正則化では、上述したように、重みの絶対値または重みの行列ノルムに比例して損失関数にペナルティを与えます。これは正式には以下の式で定義されます。

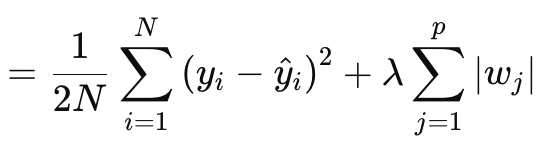
ここで

• Nはデータポイントの数
• pは重み行列が存在する層の総数
• yiはi番目のデータポイントのターゲット（またはラベル）値
• y^iはi番目のデータポイントの予測値
• wjはモデルの係数（重み）

§λは正則化の強さを制御する正則化パラメータです。λを大きくすると、大きな重みに対するペナルティが大きくなり、スパース性が促進されます。その最適範囲は、ソフトマックスやシグモイド活性化ネットワークでは10^-4～10^-1、ソフトサインやTANHネットワークでは10^-5～10^-2となります。

別の言い方をすれば、正則化値は、予測値と実際値（左側）の差のMSEに、全層にわたる重みのノルム和を加えたものです。MQL5では次のように実装しています。

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();
   if(THIS.regularization == REGULARIZE_L1)
   {  _term = _mse + (Lambda * _weights_norm);
   }
   
        ....

   _regularized.Fill(_term);
   return(_regularized);
}

出力はベクトルではなくスカラー値であり、これは損失関数の出力としてこれまで扱ってきたものと大きく対照的です。なぜなら、逆伝播をおこなう際に更新勾配を設定するのに役立つ更新デルタを定義する必要があるとき、損失はベクトルとして定量化されるからです。このベクトルは、デルタベクトルへの入力に役立ち、それによって勾配行列が更新されます。これを維持するために、正則化値の複製値で満たされたベクトルを作成し、これを出力として使用します。この標準ベクトルの値は、使用されている損失関数によって定義されるように、損失ベクトルのすべての損失値に加算されます。これは以下のように実装されます。

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }

   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss);
   _last_loss += RegularizeTerm(label, THIS.regularization_lambda);

   deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative);
   
        ...

}

したがって、出力ベクトルのすべての特徴/クラスに均一なペナルティが適用されます。おそらくこれが、ノルムが計算で行列構造を考慮するため、絶対値だけでなく行列ノルムを使用することを主張できる理由です。

正則化項を計算する際、多くの行列ノルムのオプションが利用可能であり、その全てがラッソを決定する際に利用可能ですが、全てが適しているわけではありません。フロベニウス ノルムは、スパース性を強制せずに大きな重みを直接過剰にペナルティするため、L2とよりよく一致しています。これは、重要でない重みをゼロに調整することを目指すラッソ回帰とは矛盾しています。核ノルムは、行列補充問題(matrix completion problems)（英語）に関連する低ランク行列を促進するのに適しています。ランクスパースとは対照的に要素ごとのスパース性を促進するラッソ回帰とは一致しません。スペクトルノルムは、行列がベクトルに与える最大の影響を制御するためにも使用され、スパース性を保証するものではありません。

無限ノルムはスパース性を作り出すことができるが、要素ごとのスパース性を作り出すにはあまり適していない。マイナス無限大ノルムは、最小の行和を最小化することに重点を置いており、これはラッソ回帰のスパース性の目的とは一致しません。マイナスP1もマイナスP2も、小要素の影響を最小限にしようとするものだから、同じことが言えます。

つまり、この9つのノルムの列挙体から、P1ノルムだけが、要素ごとのスパース性を目標にスパース性を促進するため、ラッソ回帰と最も相性が良いことが判明しました。P2 9の最終ノルムはL2またはRidge正則化に適しています。要約すると、L1正則化は分類器ネットワークに理想的であるということです。このことは、Classifier-L1-P1の関係には、重みの行列の規範関数の選択肢がほとんどないことを意味します。

L2正則化（リッジ）

L2正則化またはリッジ正則化は、L1正則化と式が非常に似ているが、明らかな違いは、生の値を使うのとは対照的に、重みのノルムを2乗することです。これは次のように与えられます。

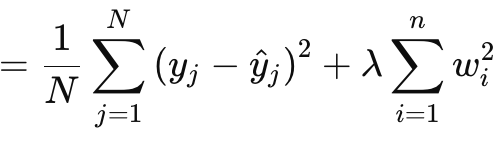
ここで

• λはペナルティの強さを制御する正則化パラメータ
• w i はモデルの重みまたは係数
• nは先行する重み行列を持つ層の数
• Nはデータポイントの数
• y jは実際の目標値
• y^ jは予測値

これはL1と同様、MSEと項を特徴とし、この場合は重みの二乗和です。MQL5では次のように実装しています。

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...

   else if(THIS.regularization == REGULARIZE_L2)
   {  _term = _mse + (Lambda * _weights_norm * _weights_norm);
   }
   

...

   _regularized.Fill(_term);
   return(_regularized);
}

上述したように、重みの2乗は正則化に滑らかさを導入するので、このアプローチは回帰型ネットワークにとって理想的な候補となります。さらに、正則化は、フロベニウス行列ノルムかP2ノルムで処理するのが最適です。これら2つは実際には同じです。フロベニウスは行列で、P2はベクトルでよく使われます。MQL5の行列ノルム関数では、フロベニウスと並んでP2も選択することができ、この2つはわずかに異なる結果を返します。この2つの違いについては、こちらに投稿があります。

これらのことから、回帰-L2-フロベニウスの組み合わせは、回帰型ニューラルネットワークと理想的な組み合わせであると言えます。

ドロップアウト正則化

最後に、ドロップアウト正則化ですが、これは上で見てきた2つのタイプとは明らかに異なります。ちなみに、L1 と L2 は、エラスティックネットと呼ばれる重み付け形式で組み合わせることができますが、重みを比例させるための追加のアルファパラメータだけが必要なので、試して実装するのは読者の責任となります。ドロップアウトの話に戻ると、フォワードフィードパスで訓練する際に、省略するニューロンをランダムに選ぶことになります。このMLPクラスは次のように実装されています。

//+------------------------------------------------------------------+
//| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON.          |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Input data is normalized if normalization type was selected at  |
//|  class instance initialisation.                                  |
//+------------------------------------------------------------------+
void Cmlp::Forward(bool Training = false)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
//
   for(int h = 0; h <= hidden_layers; h++)
   {  vector _output;
      _output.Init(output.Size());

...

      if(Training && THIS.regularization == REGULARIZE_DROPOUT)
      {  int _drop = MathRand() % int(_output.Size());
         _output[_drop] = 0.0;
      }
      _output += biases[h];

...


   }
}

訓練や重み調整の過程で、重みの一部がゼロに調整されることがあるため、出力ニューロンの値の一部をゼロにしたことは、意図した結果を達成する上で効果がない可能性があります。また、ニューロンをランダムに省略するforループを使用する手動乗算は、ドロップアウトを実装する上でより良いアプローチだったかもしれません。もっとコーディングが必要ですが、それは読者の自由です。

ドロップアウト正則化の利点は、通常、非常に深く、変圧器を積み重ねたネットワークにのみ現れるからです。この記事ではL1とL2についてのみテストしているが、ドロップアウトのコードは添付されており、大規模なネットワークでの修正やテストに利用できます。

ドロップアウト正則化は、いくつかの実装上の理由で人気があります。まず、ネットワークに冗長な表現を学習させることで、モデルの過剰適合を防ぎます。これにより、ネットワークが特定のニューロンや入力特徴クラスに過度に依存しないようになります。これは汎化性の向上を示しています。ニューロンをランダムに削除することで、訓練プロセスは1つのニューラルネットワークからモデルのアンサンブルを作り出します。この改善された汎化性により、特に複雑で高次元のデータ状況において、未見のデータを分類するネットワークがより強固になります。

さらに、ドロップアウトは、1つのニューロンが意思決定プロセスを支配しないようにすることで、ノイズの多いデータに強いネットワークを作る傾向があります。これは、ノイズの多いテストデータや信頼性の低いテストデータだけでなく、入力データに大きなばらつきがある場合にも重要です。さらに、神経細胞の相互依存性を低下させたり、神経細胞の共適応を阻害したりします。これにより、各ニューロンが独立して学習するようになり、ネットワークがより強固になります。加えて、非常に深いネットワークや変形の積み重ねられたネットワークでドロップアウトを使用することで、テストプロセスに効率を導入できるだけでなく（私たちが採用したポスト出力ベクトルアプローチではなく、手動でニューロンをドロップするプロセスを採用した場合）、関係するパラメータの数が多いため、過剰適合のリスクも防ぐことができます。

MLPやCNNのような様々なネットワーク形式に適用でき、スケーラブルでもあります。L1とL2を比較すると、ドロップアウトはL1に傾く傾向があります。テスト時にニューロンを落とすと、分類器ネットワークの鍵となる出力結果が疎になるからです。というのも、前述のドロップアウトの長所のほとんどは、クラシファイアネットワークに当てはまるからです。これらのネットワークは回帰型ネットワークよりも深いことが多く、多数のパラメータがあるため、過剰適合を起こしやすいです。前述したように、ドロップアウトは、より一般的でロバストな特徴をネットワークに学習させることで、これに対抗します。 一般化は、ドロップアウトを強化する分類器では重要な鍵となります。ノイズの多いデータは（回帰型ネットワークと比較して）分類器に不釣り合いな影響を与える可能性があり、ドロップアウトはその影響を軽減するのに役立ちます。この点と、すでに述べた多くの特徴は、分類ネットワークに適していることを意味します。なぜなら、分類ネットワークは、常にそうであるとは限りませんが、一般的には、層の数は非常に少ないものの、サイズの大きい層を持つ傾向があるからです。これらはとても深いです。一方、回帰型ネットワークは、層は小さいが積み重ねられる傾向があります。これらはTransformer寄りです。そのため、ネットワークをどのように正則化するかを定義するときだけでなく、全体の層数とサイズを決定する際にも、この点を考慮する必要があります。

テスト結果

お約束どおり、いつものように、ウィザードで組み立てたEAでテストをおこないます。新しい読者のために、添付のコードは、こちらと こちらで入手可能なガイドラインに従ってEAに組み立てる必要があります。今回はEURUSDで、2023年の日足でテストします。前回の記事でおこなったように、回帰器ネットワークと分類器ネットワークをテストしています。

この記事のリード記事ですでに論じたように、分類器ネットワークは、ソフトマックスまたはシグモイド活性で最もうまく機能します。加えて、上述したように、カテゴリクロスエントロピーやバイナリクロスエントロピーの損失関数や、特にP1行列ノルムを使用するL1正則化に適しています。従って、これらの設定をして、ストップロスなしで未決済注文を出しながらテストをおこなうと、次のような結果が得られます。

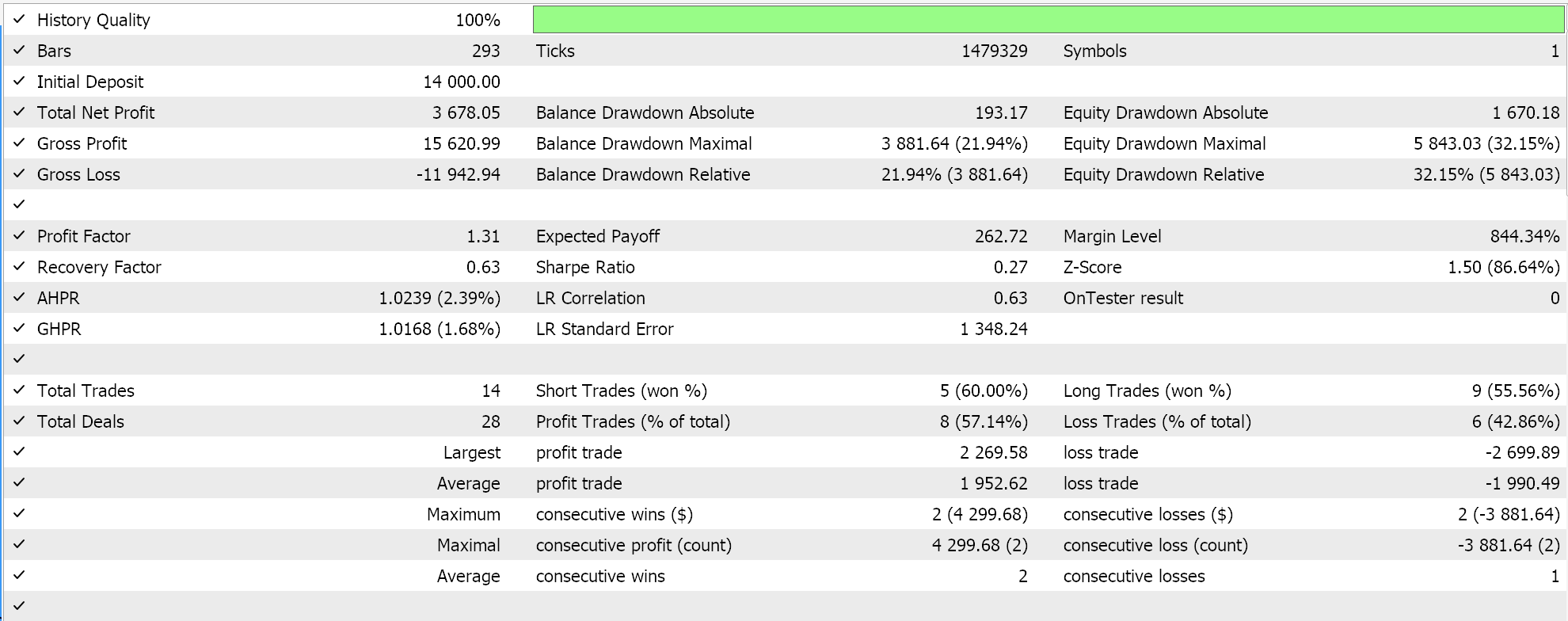
エクイティカーブで：

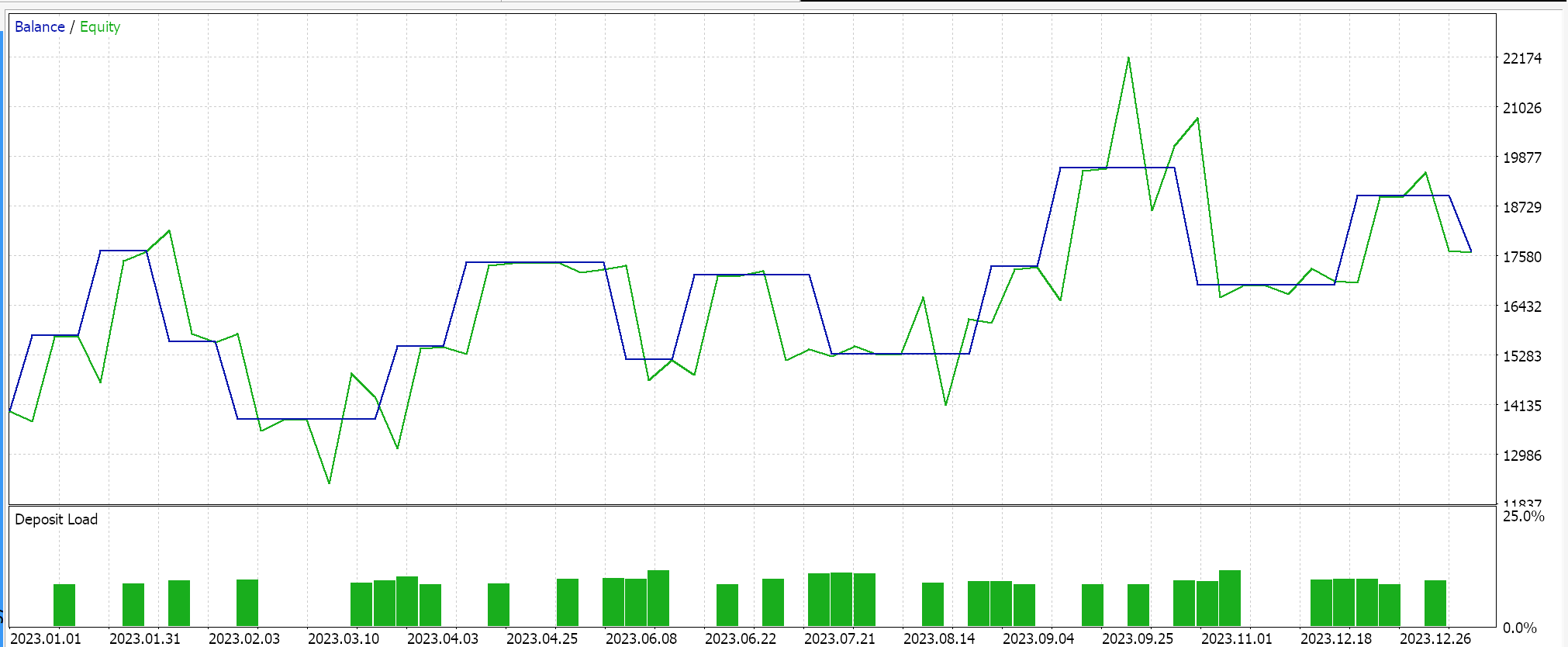
逆に、ソフトサイン活性化とL2リッジ正則化とHuber損失関数を使ったテストを回帰型ネットワークでおこなうと、次のような結果が得られます。

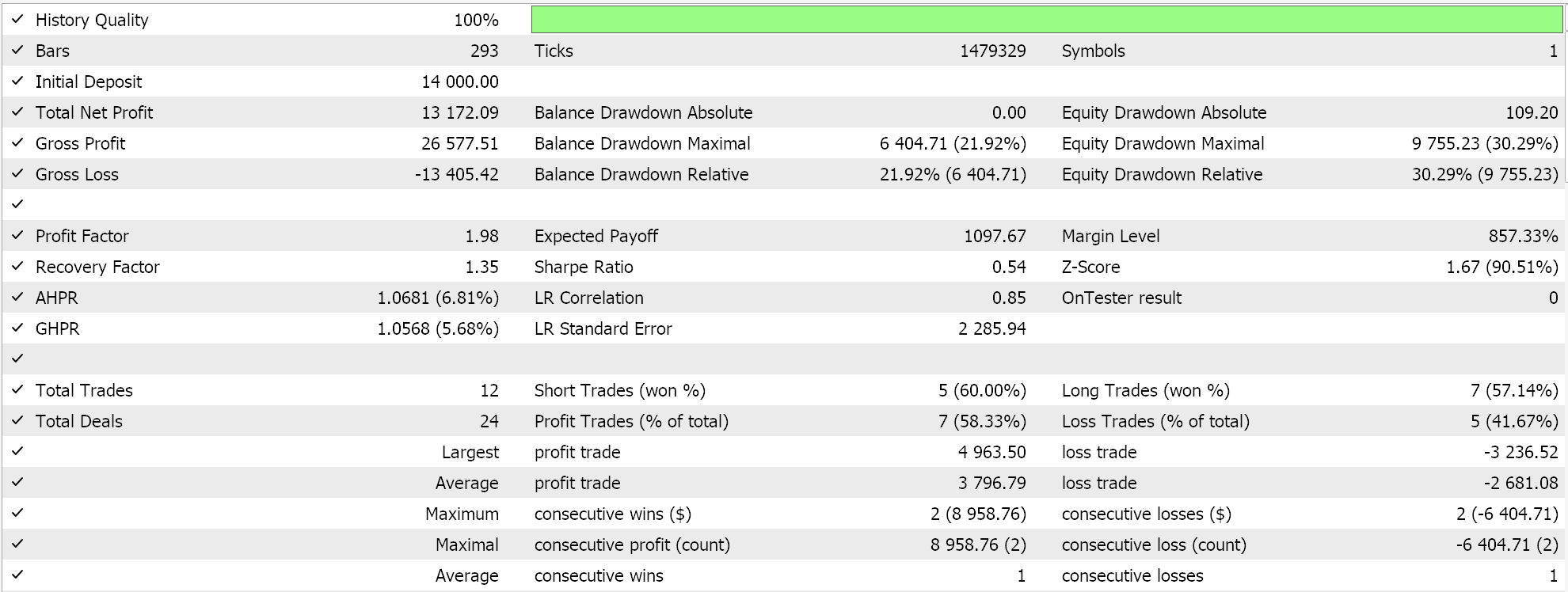
エクイティカーブ：

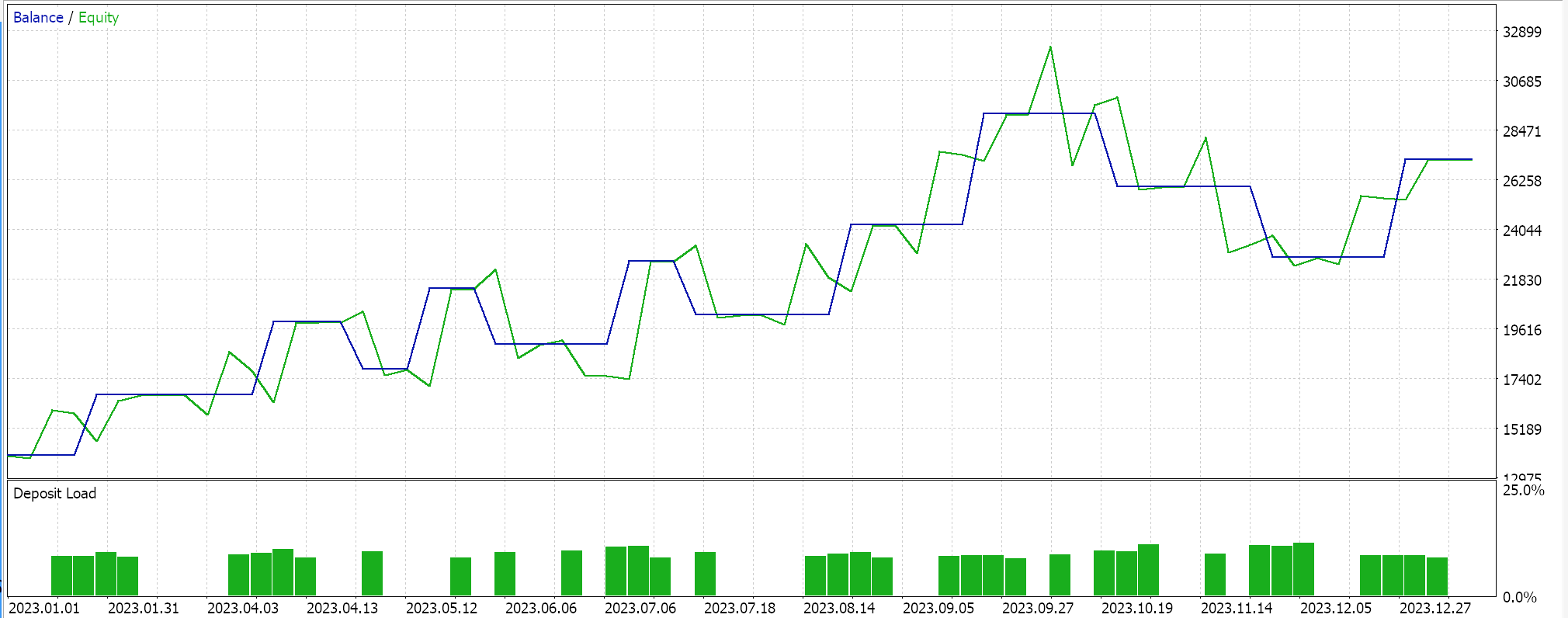
これらの結果をコントロールするためには、正則化のオプションを逆にするか、正則化をまったくしないでネットワークを訓練する必要があります。回帰型と分類器ネットワークの両方で上記と同じ設定をおこないましたが、正則化をおこなわなかったテスト実行でも同じ結果が得られました。これは、正則化が、損失関数、活性化関数、さらにはEAの典型的なエントリとクロージングのしきい値のような他の要因ほど重要ではないことを示唆している可能性があります。しかし、特に分類器ネットワークにおける正則化の利点は、1年を超えるような長期間のテストだけでなく、より幅広い出力クラスを特徴とする非常に深いネットワークでテストすることによって、最もよく理解できるという反論も、おそらく信頼できるものでしょう。

結論

結論として、ニューラルネットワークのような機械学習アルゴリズムの重要な構成要素としての正則化について、2つの特定の設定におけるその役割を見てきました。分類器ネットワークと回帰器ネットワークです。分類器ネットワークは、常にではないが、層数が非常に少ないことが多く、各層は非常に深いです。一方、回帰型ネットワークは小さな層を持つ傾向がありますが、深さの不足を「補う」ために多重に積み重ねられています。テスト結果はEAのパフォーマンスが正則化の影響を受けないことを示していますが、2023年の日足時間枠でのEURUSDの実行に基づくと、そのような抜本的な結論を下す前に、より多くのテストが必要です。これは、テストウィンドウが小さいことに加え、使用されたネットワークが非常に小規模で、正則化のメリットを完全に享受できそうにないからです。

おわりに

エラスティックネット正則化については省略するつもりでしたが、記事がそれほど長くないので、ここで簡単に補足しておこうと思います。エラスティックネットの方程式は以下の通りです。

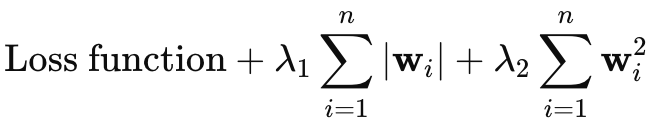
ここで

• wiはモデルの各重みを表します。
• λ1はL1ペナルティ（ラッソ回帰）の強さを制御し、一部の重みをゼロに縮小することでモデルのスパース性を促します。
• λ2はL2ペナルティ(Ridge)の強さを制御し、小さな重みを奨励しますが、一般的に重みをゼロにすることはありません。

エラスティックネット正則化をクラスに追加するには、まずメイン列挙体を以下のように修正する必要があります。

//+------------------------------------------------------------------+
//| Regularization Type Enumerator                                   |
//+------------------------------------------------------------------+
enum Eregularize
{  REGULARIZE_NONE = -1,
   REGULARIZE_L1 = 1,
   REGULARIZE_L2 = 2,
   REGULARIZE_DROPOUT = 3,
   REGULARIZE_ELASTIC = 4
};

次に、RegularizeTerm関数に3番目のif句を追加して、このエラスティックネットオプションを扱えるようにする必要があります。

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...


   else if(THIS.regularization == REGULARIZE_ELASTIC)
   {  _term =  _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) +
               ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm));
   }
   _regularized.Fill(_term);
   return(_regularized);
}

これは、上記で共有された式から明らかに導かれるもので、正で1を超えないアルファ値を使用する加重平均を実施しているからです。これは通常、0.0から1.0の範囲で最適化されます。しかし、上記のコード実装を見る限り、単一の行列ノルムの列挙体を使用しており、L1とL2の独立した特性の捕捉を妨げています。この問題を回避するには、それぞれ独自の行列ノルム関数を持つ 2 つの「_weight_norm」変数を用意しますが、これは、両方に対応するようにコンストラクタ構造体を変更する必要があることも意味します。あるいは、両正則化形式の妥協点として無限大ノルムを使うこともできます。