Características del Wizard MQL5 que debe conocer (Parte 32): Regularización

Introducción

La regularización es otra faceta de los algoritmos de aprendizaje automático que aporta cierta sensibilidad al rendimiento de las redes neuronales. En el proceso de una red, a menudo se tiende a asignar una ponderación excesiva a algunos parámetros en detrimento de otros. Este "sesgo" hacia parámetros particulares (pesos de la red) puede llegar a obstaculizar el rendimiento de la red cuando las pruebas se realizan en datos fuera de la muestra. Por esta razón se desarrolló la regularización.

Básicamente actúa como un mecanismo que ralentiza el proceso de convergencia al aumentar (o penalizar) el resultado de la función de pérdida en proporción a la magnitud de los pesos utilizados en cada unión de capas. Esto se hace a menudo mediante: Detención temprana, Lasso, Ridge, Elastic-Net o Drop-Out. Cada uno de estos formatos es un poco diferente, y no consideraremos todos los tipos, sino que nos detendremos en Lasso, Ridge y Drop-Out.

Consideramos los beneficios y el uso de la regularización dentro del contexto de tener un emparejamiento adecuado o sincronizado con las funciones de activación y pérdida. La selección y el emparejamiento adecuados de estas funciones evitan, como mínimo, los problemas de explosión/desvanecimiento de gradientes, razón por la cual este autor, en los artículos recientes (de esta serie), ha sido partidario de utilizar la activación sigmoide y soft-max junto con las funciones de pérdida de Entropía cruzada binaria o Entropía cruzada categórica al manejar redes de clasificadores. Por el contrario, TANH de activación de signo suave cuando se empareja con funciones de pérdida MSE o MAE o Huber podría ser adecuado cuando se trata de redes neuronales regresoras.

En un artículo anterior también destacamos la importancia de emparejar estas funciones de activación selectas con algoritmos de normalización de lotes con límites de rango adecuados, aunque la función de pérdida no está limitada. Esto significa que el término adicional a la función de pérdida (la regularización) no está necesariamente ligado a una función de activación o a una función de normalización por lotes que esté ligada a un rango ideal (de -1 a +1 para los regresores y de 0 a 1 para los clasificadores).

Sin embargo, el tipo de regularización seleccionado debe tener en cuenta si la red es un regresor o un clasificador. Si, por ejemplo, utilizáramos L1 Lasso, al penalizar sólo con el valor absoluto de los pesos, el proceso de entrenamiento tiende a reducir a cero muchos de los pesos de las capas de la red, dejando sólo los críticos con valores pequeños aceptables distintos de cero. Esto crea de forma inherente una dispersión en la salida, una situación que va bien con las redes clasificadoras cuyas probabilidades de características se están pronosticando. Esto es especialmente relevante en situaciones en las que, dentro de las probabilidades de las características pronosticadas, se espera que solo unas pocas características sean importantes.

Por el contrario, en redes regresoras donde a menudo la capa de salida final tiene un tamaño de 1 (a diferencia de las probabilidades de la red de clasificación, por ejemplo), a menudo se espera que la contribución de los diversos pesos sea "más democrática". Y para lograr esto, el regularizador L2 o Ridge es más adecuado, ya que está ponderado hacia el cuadrado de los pesos, lo que genera una contribución más uniforme entre los pesos de las capas hacia el resultado final. La regularización por abandono (Drop-out) podría ser una alternativa a la regularización de las redes de clasificadores, ya que también introduce cierta escasez en los resultados de salida debido a la anulación aleatoria de algunos pesos. Compartimos el código para esto en los archivos adjuntos a continuación, sin embargo nuestras pruebas se centran en L1 y L2.

Regularización en redes neuronales

Los dos formatos de regularización que probamos a continuación penalizan la función de pérdida en proporción a la magnitud del peso de la red. Esta «magnitud» se calcula mediante una función Norm, que en nuestro caso se ofrece en bastantes variedades. Sin embargo, en sentido estricto, esta norma debería ser la suma de magnitudes de todos los valores de la matriz. Esta suma de valor absoluto podría realizarse fácilmente en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Typical Norm function                                            |
//+------------------------------------------------------------------+
double Norm(matrix &M)
{  double _norm = 0.0;
   for(int i = 0; i < int(M.Rows()); i++)
   {  for(int ii = 0; ii < int(M.Cols()); ii++)
      {  _norm += M[i][ii];
      }
   }
   return(_norm);
}

Sin embargo, nos estamos sumergiendo en normas matriciales (gracias a las diversas funciones disponibles dentro del tipo de datos matricial). Las normas matriciales, a diferencia de las absolutas simples, no son un ajuste tan extraño, como podría parecer en un principio, porque se argumenta que introducen conciencia estructural en el proceso de ponderación de la regularización. Además, permiten controlar ciertas propiedades deseadas de la red, como la suavidad en las redes regresoras, al tiempo que ofrecen flexibilidad para ajustar con precisión la dispersión deseada en las salidas de la red clasificadora. Así pues, la consideración de estas propiedades adicionales, que a menudo parecen matizadas, en la evaluación de las matrices de pesos para la regularización es lo que aplicaremos en los resultados de nuestras pruebas a continuación. Para que quede claro, estamos considerando hasta nueve normas matriciales diferentes para cada uno de los 2 enfoques de regularización que probaremos para una red de regresores y clasificadores.

En el último artículo en el que nos centramos en la función de pérdida, teníamos dos tipos de red, un regresor y un clasificador. Nos ceñiremos a esos formatos para ilustrar la regularización también en este artículo.

Regularización L1 (Lasso)

La regularización Lasso (o L1) consiste en penalizar la función de pérdida en proporción al valor absoluto de los pesos o a las normas matriciales de los pesos, como se ha comentado anteriormente. Esto se define formalmente mediante la siguiente ecuación:

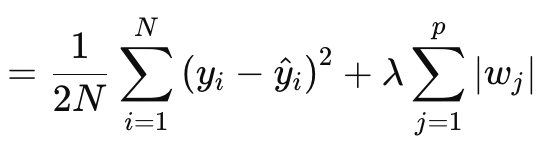
Donde:

• N es el número de puntos de datos.
• p es el número total de capas para las que existen matrices de pesos
• yi es el valor objetivo (o etiqueta) del i-ésimo punto de datos.
• y^i es el valor previsto para el i-ésimo punto de datos.
• wj son los coeficientes (ponderaciones) del modelo.

§λ es el parámetro de regularización que controla la fuerza de la regularización. Un λ mayor aumenta la penalización por pesos grandes, promoviendo la dispersión. Su rango óptimo puede ser de 10^-4 a 10^-1 para redes de activación suave-max o sigmoide, o de 10^-5 a 10^-2 para redes de signo suave o TANH.

Dicho de otro modo, el valor de regularización consiste en el MSE de la diferencia entre los valores previstos y los valores reales (lado izquierdo), más la suma de las normas de los pesos en todas las capas. Lo implementamos en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();
   if(THIS.regularization == REGULARIZE_L1)
   {  _term = _mse + (Lambda * _weights_norm);
   }
   
        ....

   _regularized.Fill(_term);
   return(_regularized);
}

La salida es un valor escalar, no un vector y esto contrasta mucho con lo que hemos estado tratando como salidas de la función de pérdida. Porque cuando necesitamos definir nuestros deltas de actualización que luego nos ayudan a establecer los gradientes de actualización al hacer una retropropagación, la pérdida se cuantifica como un vector. Este vector ayuda a alimentar los vectores delta, que a su vez actualizan las matrices de gradiente. Para mantenerlo, creamos un vector que se rellena con valores replicados del valor de regularización y lo utilizamos como salida. A continuación, este valor del vector estándar se suma a todos los valores de pérdida del vector de pérdidas, según lo definido por la función de pérdida en uso. Esto se llevaría a cabo de la siguiente manera:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }

   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss);
   _last_loss += RegularizeTerm(label, THIS.regularization_lambda);

   deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative);
   
        ...

}

Por lo tanto, se aplica una penalización uniforme a todas las características/clases del vector de salida y quizás por eso se podría argumentar a favor de utilizar normas matriciales y no sólo su valor absoluto, ya que las normas tienen en cuenta la estructura matricial en sus cálculos.

A la hora de calcular el término de regularización, se dispone de varias opciones de normas matriciales y, aunque todas ellas son utilizables para determinar el Lasso, no todas son adecuadas. La norma de Frobenius se ajusta mejor a L2, ya que penaliza directamente los pesos grandes sin imponer la dispersión, lo que contradice a Lasso, cuyo objetivo es que los pesos no críticos se ajusten a cero. La norma nuclear es más adecuada para promover matrices de bajo rango que sean relevantes para problemas de terminación de matrices. No está alineado con Lasso, que promueve la escasez de elementos en lugar de la escasez de rangos. La norma espectral también se utiliza para controlar el efecto máximo que tiene una matriz sobre un vector y no para garantizar la escasez.

Si bien las normas de infinito pueden crear una forma de escasez, son menos ideales para crear escasez a nivel de elementos. La norma menos infinito se centra en minimizar las sumas de filas más pequeñas, y esto no se alinea con el objetivo de escasez de Lasso. Lo mismo puede decirse de menos P1 y menos P2, ya que ambos buscan minimizar la influencia de elementos pequeños.

Entonces, de esta enumeración de nueve normas, resulta que solo la norma P1 funciona mejor con Lasso porque promueve la escasez con el objetivo de lograr escasez de elementos. P2 la norma final de las nueve es más adecuada para la regularización L2 o Ridge. Sólo para recapitular, la regularización L1 se mencionó anteriormente como ideal para redes de clasificadores. Esto implica una relación Clasificador-L1-P1 que tiene pocas alternativas para la función de normas de la matriz de pesos.

Regularización L2 (Ridge)

La regularización L2 o Ridge es muy similar a la fórmula L1, con la diferencia obvia de elevar al cuadrado las normas de los pesos en lugar de utilizar el valor bruto. Esto se da como:

Donde:

• λ es el parámetro de regularización que controla la intensidad de la penalización.
• w i son las ponderaciones o coeficientes del modelo.
• n es el número de capas con una matriz de pesos precedente.
• N es el número de puntos de datos.
• y j es el valor objetivo real.
• y^ j es el valor previsto.

Al igual que L1, presenta un MSE y un término, que en este caso es una suma de los pesos al cuadrado. Lo implementamos en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...

   else if(THIS.regularization == REGULARIZE_L2)
   {  _term = _mse + (Lambda * _weights_norm * _weights_norm);
   }
   

...

   _regularized.Fill(_term);
   return(_regularized);
}

La cuadratura de los pesos, como ya se ha comentado, introduce suavidad en la regularización, lo que hace de este enfoque un candidato ideal para las redes regresoras. Además, la regularización se realiza mejor mediante normas matriciales de Frobenius o normas P2. En realidad son lo mismo, por lo que he podido averiguar, pero Frobenius se utiliza a menudo con matrices y P2 con vectores. Ahora desde las funciones de normas de matriz de MQL5, P2 también se puede seleccionar junto con Frobenius y los dos devuelven resultados ligeramente diferentes. Hay una publicación aquí sobre las diferencias entre ambos.

De todo esto, por tanto, el binomio Regresor-L2-Frobenius sería ideal con redes neuronales regresoras.

Regularización "drop-out"

Por último, tenemos la regularización por "abandono" (Drop-out), que es notablemente diferente de los dos tipos que hemos visto anteriormente. Como nota al margen, L1 y L2 se pueden combinar en un formato ponderado a lo que se llama Elastic-Net, pero eso queda en manos del lector para que lo pruebe e implemente, ya que todo lo que se requeriría es un parámetro alfa adicional para proporcionar los pesos. Volviendo al tema del drop-out, se trata de elegir aleatoriamente una neurona para la omisión, durante el entrenamiento en el pase de alimentación hacia adelante. Implementamos esto en nuestra clase MLP de la siguiente manera:

//+------------------------------------------------------------------+
//| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON.          |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Input data is normalized if normalization type was selected at  |
//|  class instance initialisation.                                  |
//+------------------------------------------------------------------+
void Cmlp::Forward(bool Training = false)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
//
   for(int h = 0; h <= hidden_layers; h++)
   {  vector _output;
      _output.Init(output.Size());

...

      if(Training && THIS.regularization == REGULARIZE_DROPOUT)
      {  int _drop = MathRand() % int(_output.Size());
         _output[_drop] = 0.0;
      }
      _output += biases[h];

...


   }
}

En el proceso de entrenamiento y ajuste de peso, algunos pesos se pueden ajustar a cero, por lo que el hecho de poner en cero algunos de los valores de las neuronas de salida podría ser ineficaz para lograr el resultado previsto. Además, una multiplicación manual que utiliza bucles for durante los cuales omitimos neuronas aleatoriamente podría haber sido un mejor enfoque para implementar la eliminación. Implica más codificación, pero el lector puede intentarlo.

No realizamos pruebas con regularización de abandono porque los beneficios de esto generalmente solo son evidentes en redes muy profundas y con apilados transformadores. Para los propósitos de este artículo sólo estamos probando para L1 y L2, sin embargo, el código para el abandono se adjunta y está disponible para su modificación y pruebas en grandes redes.

La regularización de abandonos es popular por varias razones de aplicación, así que vamos a intentar repasar algunas de ellas. En primer lugar, evita el sobreajuste del modelo obligando a la red a aprender representaciones redundantes. Esto garantiza que la red no dependa excesivamente de determinadas neuronas o características/clases de entrada. Esto apunta a una mejora de la generalización. Al eliminar neuronas aleatoriamente, el proceso de entrenamiento crea un conjunto de modelos a partir de una única red neuronal. Esta generalización mejorada hace que la red sea más robusta a la hora de clasificar datos no vistos, especialmente en situaciones de datos complejos y de alta dimensionalidad.

Además, el abandono tiende a hacer que una red sea más resistente a los datos ruidosos al garantizar que ninguna neurona domine el proceso de toma de decisiones. Esto es clave no sólo con datos de prueba ruidosos o menos fiables, sino también en situaciones en las que los datos de entrada tienen un alto grado de varianza. Además, reduce la interdependencia neuronal o favorece la coadaptación neuronal de ruptura. Esto anima a cada neurona a aprender de forma independiente, lo que hace que la red sea más robusta. Además, el uso del drop-out en redes muy profundas y apiladas por transformadores no sólo podría introducir eficiencia en el proceso de prueba (si el proceso deja caer manualmente las neuronas en lugar del enfoque de vector post-salida que hemos adoptado), sino que también evita el riesgo de sobreajuste dado el gran número de parámetros implicados.

Es aplicable a varios formatos de red, como MLP o CNN, y también es escalable. En comparación con L1 y L2, el abandono tiende a inclinarse más hacia L1, ya que la eliminación de neuronas durante la prueba conduce a resultados de salida más dispersos, que son clave en las redes de clasificación. Esto se debe a que la mayoría de los profesionales de deserción mencionados anteriormente son pertinentes a las redes de clasificadores. Estas redes suelen ser más profundas que las redes regresoras y esta multitud de parámetros las hace propensas al sobreajuste. La deserción, como se mencionó anteriormente, combate esto al obligar a la red a aprender características más generales y sólidas. La generalización es clave en los clasificadores que mejoran la deserción; los datos ruidosos pueden afectarlos desproporcionadamente (en comparación con las redes regresoras) y la deserción ayuda a mitigar sus efectos. Ésta y muchas de las características ya mencionadas anteriormente implican la idoneidad para las redes de clasificación porque, en general, aunque no siempre, las redes de clasificación tienden a tener muy pocas capas pero de gran tamaño. Son muy profundos. Por otro lado, las redes regresoras suelen tener capas de pequeño tamaño pero apiladas. Se inclinan más hacia los transformadores. Por lo tanto, esta es quizás otra consideración clave que se debe tener en cuenta no solo al definir cómo se debe regularizar una red, sino también al determinar el número y el tamaño general de sus capas.

Resultados de la prueba

Como prometimos, como siempre, realizamos pruebas con un Asesor Experto montado por un asistente. Para los nuevos lectores, el código adjunto necesita ser ensamblado en un Asesor Experto siguiendo las directrices que están disponibles aquí y aquí. Esta vez estamos probando el EURUSD en el marco temporal diario para el año 2023. Como hicimos en el último artículo, estamos probando una red regresora y una red clasificadora.

Como ya se ha argumentado en los artículos previos a este, las redes de clasificación funcionan mejor con activaciones soft-max o sigmoideas. Además, como se mencionó anteriormente, son más adecuados para trabajar con funciones de pérdida de entropía cruzada categórica o entropía cruzada binaria y regularización L1 que utiliza específicamente normas de matriz P1. Por lo tanto, si realizamos pruebas con estas configuraciones mientras colocamos órdenes pendientes sin stop loss, obtenemos los siguientes resultados:

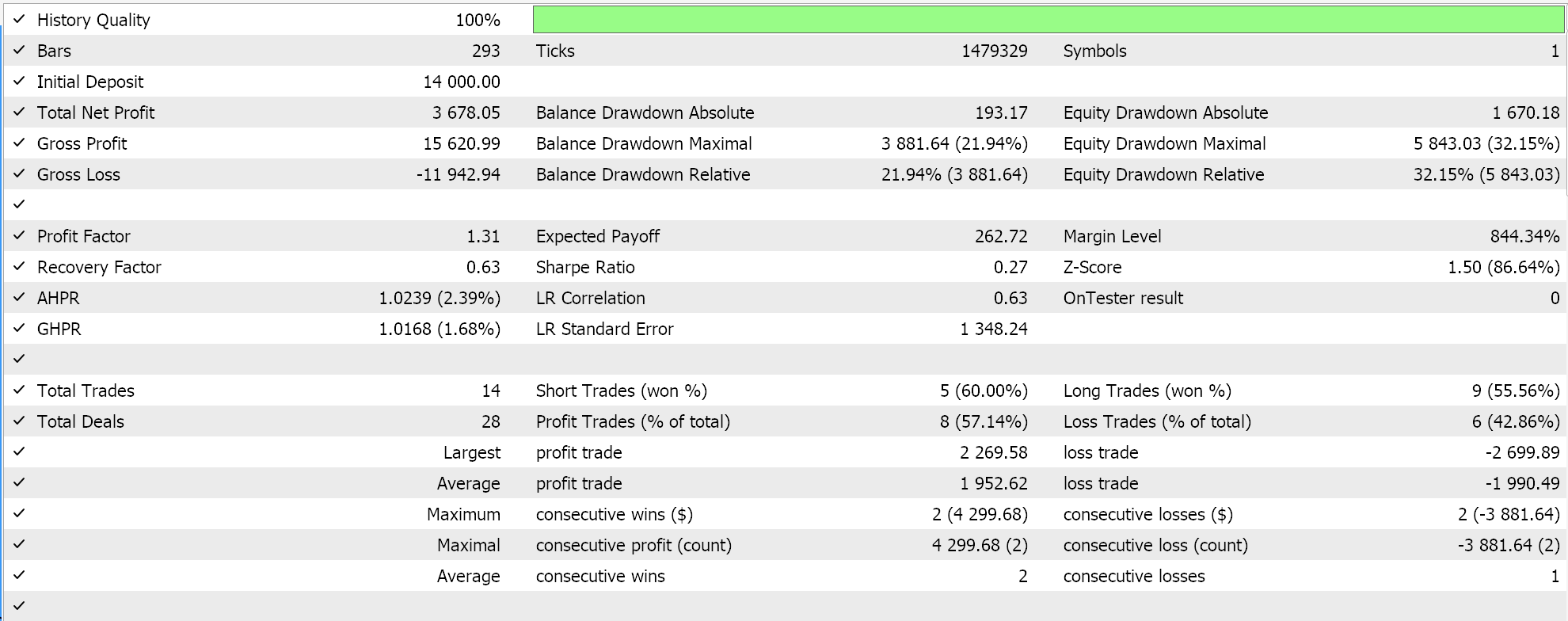
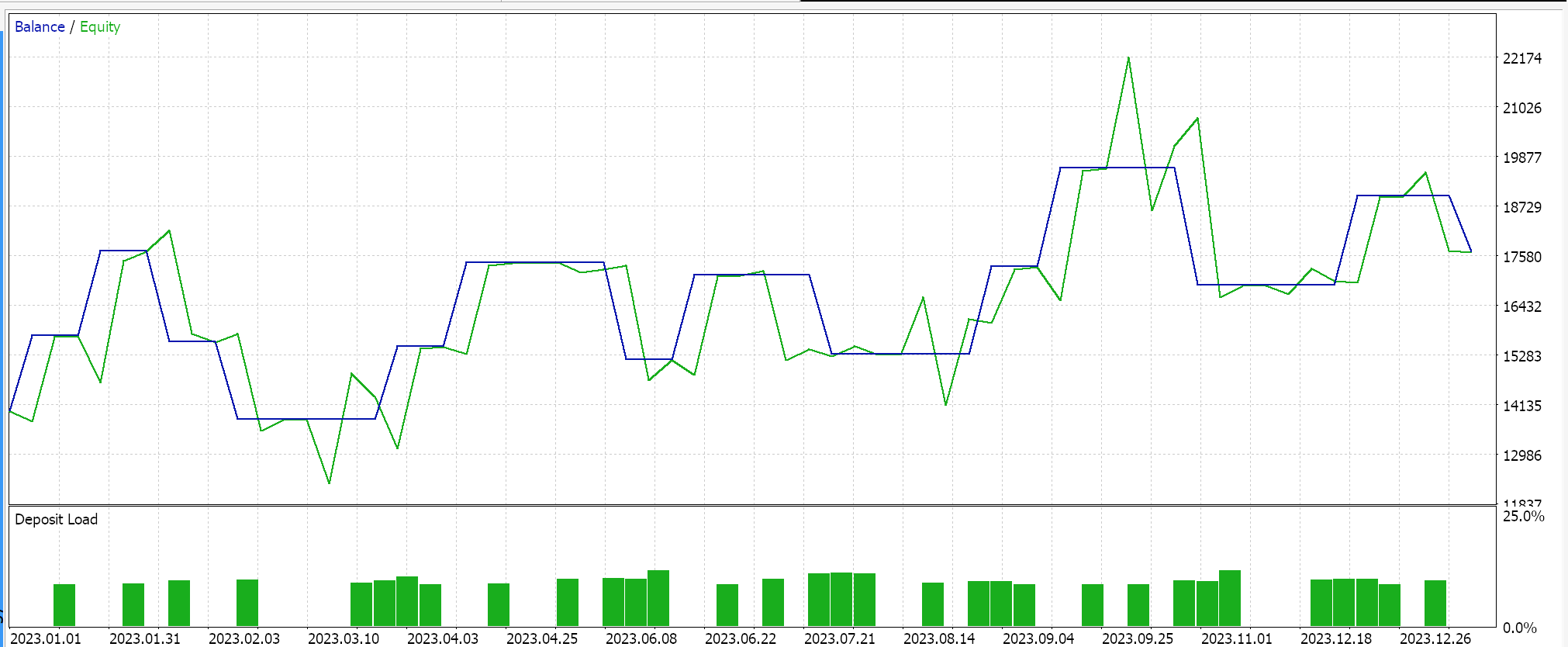
Con la curva de equidad:

Por el contrario, para la red regresora, si realizamos pruebas utilizando activación de signo suave y regularización L2 Ridge junto con la función de pérdida de Huber, obtenemos los siguientes resultados:

Y la curva de capital:

Como control de estos resultados, sería necesario entrenar la red con opciones de regularización inversa o sin regularización alguna. Las pruebas ejecutadas con configuraciones idénticas a las utilizadas anteriormente para las redes del regresor y del clasificador, pero sin regularización, producen los mismos resultados. Esto podría implicar que la regularización no es tan crítica como otros factores como la función de pérdida, las funciones de activación e incluso los umbrales de entrada y cierre típicos del Asesor Experto. Sin embargo, también se podría presentar un argumento contrario y quizás creíble: que los beneficios de la regularización, especialmente en la red de clasificadores, se pueden apreciar mejor con pruebas no solo durante períodos más largos que se extiendan más allá de un año, sino con redes muy profundas que presenten una clase de salida más amplia.

Conclusión

En conclusión, hemos examinado la regularización como un componente clave de los algoritmos de aprendizaje automático, como las redes neuronales, observando su papel en dos entornos particulares. Redes clasificadoras y redes regresoras. Las redes clasificadoras a menudo, pero no siempre, tienen muy pocas capas, pero cada una de sus capas es muy profunda. Por otro lado, las redes regresoras tienden a tener capas de tamaño pequeño, pero están apiladas en múltiples capas que "compensan" la falta de profundidad. Si bien los resultados de nuestras pruebas indican que el rendimiento del Asesor Experto no es sensible a la regularización, según las ejecuciones del EURUSD en el marco de tiempo diario para 2023, se justifican más pruebas antes de poder llegar a una conclusión tan drástica. Esto se debe a que, además de la pequeña ventana de prueba, las redes utilizadas eran de una escala muy modesta y es poco probable que aprovechen todos los beneficios de la regularización.

Epílogo

Tenía la intención de omitir la regularización de Elastic-Net, sin embargo, como el artículo no es demasiado largo, pensé que podría agregarlo brevemente aquí. La ecuación para Elastic-Net es la siguiente:

Donde:

• wi representa los pesos individuales del modelo.
• λ1 controla la fuerza de la penalización L1 (Lasso), que fomenta la dispersión en el modelo reduciendo algunos pesos a cero.
• λ2 controla la fuerza de la penalización L2 (Ridge), que fomenta los pesos pequeños pero generalmente no los reduce a cero.

Para añadir la regularización Elastic-Net a nuestra clase, en primer lugar tendríamos que modificar la enumeración principal para incluirla de la siguiente manera:

//+------------------------------------------------------------------+
//| Regularization Type Enumerator                                   |
//+------------------------------------------------------------------+
enum Eregularize
{  REGULARIZE_NONE = -1,
   REGULARIZE_L1 = 1,
   REGULARIZE_L2 = 2,
   REGULARIZE_DROPOUT = 3,
   REGULARIZE_ELASTIC = 4
};

En segundo lugar, tendríamos que modificar la función ‘RegularizeTerm’ para manejar esta opción Elastic-Net agregando una tercera cláusula if, que implementamos de la siguiente manera:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...


   else if(THIS.regularization == REGULARIZE_ELASTIC)
   {  _term =  _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) +
               ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm));
   }
   _regularized.Fill(_term);
   return(_regularized);
}

Esto se desprende claramente de la fórmula compartida anteriormente, ya que aplica una media ponderada que utiliza un valor alfa positivo y no superior a uno. Por lo general, se optimiza entre 0,0 y 1,0. Sin embargo, desde nuestra implementación de código anterior, estamos utilizando una sola enumeración de la norma de la matriz, lo que impediría la captura de las propiedades independientes de L1 y L2. Una forma de evitar esto es tener dos variables '_weight_norm' cada una con sus propias funciones de norma matricial, pero esto también significaría que la estructura del constructor debería ser modificada para acomodar ambas. Alternativamente, podríamos utilizar las normas infinitas como compromiso para ambos formatos de regularización.