Técnicas do MQL5 Wizard que você deve conhecer (Parte 32): Regularização

Introdução

Regularização é outra faceta dos algoritmos de aprendizado de máquina que traz sensibilidade ao desempenho das redes neurais. No processo de uma rede, frequentemente há uma tendência de atribuir peso excessivo a alguns parâmetros em detrimento de outros. Esse ‘viés’ em direção a parâmetros específicos (pesos da rede) pode prejudicar o desempenho da rede quando os testes são realizados com dados fora da amostra. Foi por isso que a regularização foi desenvolvida.

Ela essencialmente atua como um mecanismo que desacelera o processo de convergência, aumentando (ou penalizando) o resultado da função de perda em proporção à magnitude dos pesos usados em cada junção de camada. Isso é frequentemente feito por meio de: Early-Stopping, Lasso, Ridge, Elastic-Net ou Drop-Out. Cada um desses formatos é um pouco diferente, e não vamos considerar todos os tipos, mas vamos nos concentrar no Lasso, Ridge e Drop-Out.

Consideramos os benefícios e o uso da regularização no contexto de ter um emparelhamento adequado ou sincronizado com funções de ativação e perda. A seleção adequada e o emparelhamento dessas funções evitam, no mínimo, os problemas de gradientes explosivos/desaparecendo, razão pela qual este autor, nos artigos recentes (dessa série), tem defendido o uso das funções de ativação sigmoide & soft-max juntamente com as funções de perda Binary-Cross Entropy ou Categorical Cross Entropy ao lidar com redes classificadoras. Por outro lado, o ativador TANH de soft-sign, quando emparelhado com funções de perda MSE, MAE ou Huber, pode ser adequado ao lidar com redes neurais de regressão.

Também enfatizamos a importância de emparelhar essas funções de ativação selecionadas com algoritmos apropriados de normalização em lotes com limite de intervalo em um artigo relacionado, porém a função de perda não possui limites. Isso significa que o termo adicional na função de perda (a regularização) não é necessariamente emparelhado com uma função de ativação ou de normalização de lote que esteja no intervalo ideal (-1 a +1 para regressões e de 0 a 1 para classificadores).

No entanto, o tipo de regularização selecionado deve ser considerado com base em se a rede é uma rede de regressão ou de classificação, e aqui está o motivo. Se usássemos o L1 Lasso, por exemplo, penalizando com o valor absoluto dos pesos, o processo de treinamento tende a reduzir muitos dos pesos nas camadas da rede a zero, deixando apenas os críticos em valores não zero pequenos aceitáveis. Isso cria uma escassez inerente entre os resultados, uma situação que é vantajosa para redes classificadoras, cujas probabilidades de recursos estão sendo previstas. Isso é especialmente relevante em situações onde, dentro das probabilidades de recursos previstas, apenas alguns recursos são esperados para serem importantes.

Por outro lado, em redes de regressão, onde frequentemente a camada de saída final tem um tamanho de 1 (diferente das probabilidades da rede de classificação, por exemplo), a contribuição dos diversos pesos é frequentemente esperada para ser ‘mais democrática’. E, para alcançar isso, o regularizador L2, ou Ridge, é mais adequado, pois é ponderado em relação ao quadrado dos pesos, o que leva a uma contribuição mais equilibrada dos pesos das camadas para a saída final. A regularização Drop-Out poderia ser uma alternativa para regularizar redes classificadoras, pois ela também introduz certa escassez nos resultados de saída devido à anulação aleatória de alguns pesos. Compartilhamos o código para isso nos anexos abaixo, no entanto, nossos testes se concentram no L1 e L2.

Regularização em Redes Neurais

Os dois formatos de regularização que estamos testando abaixo penalizam a função de perda em proporção à magnitude dos pesos da rede. Essa ‘magnitude’ é calculada por meio de uma função Norm, que, no nosso caso, é oferecida em várias variedades. Falando estritamente, essa norma deveria ser a soma da magnitude de todos os valores da matriz. Essa soma do valor absoluto poderia ser facilmente realizada em MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| Typical Norm function                                            |
//+------------------------------------------------------------------+
double Norm(matrix &M)
{  double _norm = 0.0;
   for(int i = 0; i < int(M.Rows()); i++)
   {  for(int ii = 0; ii < int(M.Cols()); ii++)
      {  _norm += M[i][ii];
      }
   }
   return(_norm);
}

No entanto, estamos começando a explorar normas de matriz (graças às várias funções disponíveis dentro do tipo de dado matriz). As normas de matriz, ao contrário do simples valor absoluto, não são tão estranhas quanto parecem inicialmente, pois argumenta-se que elas introduzem uma conscientização estrutural no processo de ponderação da regularização. Além disso, elas permitem controle sobre certas propriedades desejadas da rede, como suavidade em redes de regressão, enquanto ainda oferecem flexibilidade para ajustar a escassez desejada nos resultados de saída das redes classificadoras. Portanto, a consideração dessas propriedades adicionais, que muitas vezes parecem sutis, ao avaliar as matrizes de pesos para regularização é o que aplicaremos nos nossos resultados de teste abaixo. Para ser claro, estamos considerando até nove normas diferentes de matrizes para cada uma das duas abordagens de regularização que testaremos para uma rede de regressão e uma rede classificadora.

No último artigo em que nos concentramos na função de perda, tínhamos dois tipos de rede, uma de regressão e uma de classificação. Manteremos esses formatos ao ilustrar a regularização para este artigo também.

Regularização L1 (Lasso)

A regularização Lasso (ou L1) envolve penalizar a função de perda em proporção ao valor absoluto dos pesos ou das normas das matrizes de pesos, conforme discutido acima. Isso é formalmente definido pela equação abaixo:

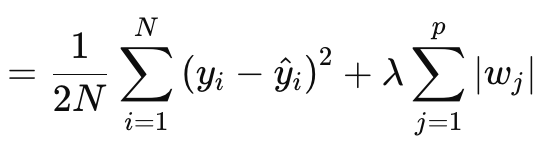
onde:

• N é o número de pontos de dados.
• p é o número total de camadas para as quais existem matrizes de pesos
• yi é o valor alvo (ou rótulo) para o i-ésimo ponto de dados.
• y^i é o valor previsto para o i-ésimo ponto de dados.
• wj são os coeficientes (pesos) do modelo.

§λ é o parâmetro de regularização que controla a intensidade da regularização. Um λ maior aumenta a penalização para pesos grandes, promovendo a escassez. Seu intervalo ótimo pode ser de 10^-4 a 10^-1 para redes de ativação soft-max ou sigmoide, ou de 10^-5 a 10^-2 para redes soft-sign ou TANH.

De outra forma, o valor da regularização consiste no MSE, a diferença entre os valores previstos e os valores reais (lado esquerdo), mais a soma das normas dos pesos em todas as camadas. Implementamos isso em MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();
   if(THIS.regularization == REGULARIZE_L1)
   {  _term = _mse + (Lambda * _weights_norm);
   }
   
        ....

   _regularized.Fill(_term);
   return(_regularized);
}

A saída é um valor escalar, não um vetor, e isso contrasta bastante com o que temos lidado como saídas da função de perda. Porque, quando precisamos definir nossos deltas de atualização, que depois ajudam a definir os gradientes de atualização ao fazer uma retropropagação, a perda é quantificada como um vetor. Esse vetor ajuda a alimentar os vetores delta, que, por sua vez, atualizam as matrizes de gradientes. Para manter isso, criamos um vetor preenchido com valores replicados do valor de regularização e usamos isso como a saída. Esse valor padrão do vetor então é somado a todos os valores de perda no vetor de perda, conforme definido pela função de perda em uso. Isso seria implementado da seguinte maneira:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }

   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss);
   _last_loss += RegularizeTerm(label, THIS.regularization_lambda);

   deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative);
   
        ...

}

Portanto, uma penalização uniforme é aplicada a todas as características/classes do vetor de saída, e talvez seja por isso que se pode argumentar a favor do uso de normas de matriz e não apenas de seus valores absolutos, já que as normas consideram a estrutura da matriz em seus cálculos.

Ao calcular o termo de regularização, várias opções de normas de matriz estão disponíveis e, embora todas elas possam ser usadas para determinar o Lasso, nem todas são adequadas. A norma de Frobenius está mais alinhada com L2, pois penaliza excessivamente os pesos grandes sem impor escassez, o que entra em conflito com o Lasso, que visa ajustar os pesos não críticos para zero. A norma nuclear é mais adequada para promover matrizes de baixa classificação, relevantes para problemas de completação de matriz. Ela não está alinhada com o Lasso, que promove escassez elementar em vez de escassez por classificação. A norma espectral também é usada para controlar o efeito máximo que uma matriz tem sobre um vetor e não garante escassez.

Enquanto as normas de infinito podem criar uma forma de escassez, elas são menos ideais para criar escassez elementar. A norma de menos infinito foca em minimizar as menores somas das linhas, e isso não se alinha ao objetivo de escassez do Lasso. O mesmo pode ser dito para as normas de menos P1 e menos P2, pois ambas buscam minimizar a influência de pequenos elementos.

Então, dessa enumeração de nove normas, acontece que apenas a norma P1 funciona melhor com o Lasso, pois elas promovem escassez com o objetivo de escassez elementar. A norma P2, a última das nove, é mais adequada para a regularização L2 ou Ridge. Portanto, para recapitular, a regularização L1 foi mencionada acima como ideal para redes classificadoras. Isso implica uma relação Classificador-L1-P1, que tem poucas alternativas para a função das normas da matriz de pesos.

Regularização L2 (Ridge)

A regularização L2 ou Ridge é muito similar à L1 na fórmula, com a diferença óbvia sendo o quadrado das normas dos pesos em vez de usar o valor bruto. Isso é dado como:

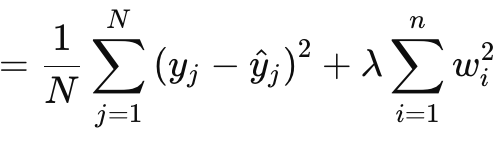
onde:

• λ é o parâmetro de regularização que controla a força da penalização.
• w i são os pesos ou coeficientes do modelo.
• n é o número de camadas com uma matriz de pesos anterior.
• N é o número de pontos de dados.
• y j é o valor alvo real.
• y^ j é o valor previsto.

Ela, como a L1, possui um MSE e um termo, que, neste caso, é uma soma dos pesos quadrados. Implementamos isso em MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...

   else if(THIS.regularization == REGULARIZE_L2)
   {  _term = _mse + (Lambda * _weights_norm * _weights_norm);
   }
   

...

   _regularized.Fill(_term);
   return(_regularized);
}

O quadrado dos pesos, conforme discutido acima, realmente introduz suavidade na regularização, o que torna essa abordagem uma candidata ideal para redes de regressão. Além disso, a regularização é melhor tratada por meio das normas de matriz Frobenius ou das normas P2. Os dois são, na verdade, o mesmo, pelo que pude perceber, com o Frobenius sendo frequentemente usado com matrizes e o P2 com vetores. Agora, nas funções de normas de matriz do MQL5, o P2 também pode ser selecionado juntamente com o Frobenius, e os dois retornam resultados ligeiramente diferentes. Há um post aqui sobre as diferenças entre os dois.

Portanto, a combinação Regressor-L2-Frobenius seria ideal para redes neurais de regressão.

Regularização Dropout

Por fim, temos a regularização drop-out, que é notavelmente diferente dos dois tipos que vimos acima. Como observação, o L1 e o L2 podem ser combinados em um formato ponderado para o que é chamado de Elastic-Net, mas isso fica a critério do leitor tentar e implementar, já que tudo o que seria necessário é um parâmetro alfa extra para a distribuição dos pesos. Voltando ao drop-out, ele envolve a escolha aleatória de um neurônio para omissão, durante o treinamento na passagem de alimentação direta. Isso implementamos em nossa classe MLP da seguinte forma:

//+------------------------------------------------------------------+
//| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON.          |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Input data is normalized if normalization type was selected at  |
//|  class instance initialisation.                                  |
//+------------------------------------------------------------------+
void Cmlp::Forward(bool Training = false)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
//
   for(int h = 0; h <= hidden_layers; h++)
   {  vector _output;
      _output.Init(output.Size());

...

      if(Training && THIS.regularization == REGULARIZE_DROPOUT)
      {  int _drop = MathRand() % int(_output.Size());
         _output[_drop] = 0.0;
      }
      _output += biases[h];

...


   }
}

No processo de treinamento e ajuste de pesos, alguns pesos podem ser ajustados para zero, portanto, o fato de termos anulado alguns valores de neurônios de saída pode ser ineficaz para alcançar nosso resultado pretendido. Além disso, uma multiplicação manual que usa laços for, durante os quais omitemos aleatoriamente neurônios, poderia ter sido uma abordagem melhor para implementar o drop-out. Envolve mais codificação, mas o leitor está convidado a tentar isso.

Não realizamos testes com a regularização drop-out porque os benefícios disso geralmente são evidentes apenas em redes muito profundas e empilhadas do tipo transformer. Para os propósitos deste artigo, estamos testando apenas o L1 e L2, no entanto, o código para drop-out está anexado e disponível para modificação e teste em redes grandes.

A regularização drop-out é popular por várias razões de implementação, então vamos tentar passar por algumas delas. Primeiramente, ela previne o overfitting do modelo, forçando a rede a aprender representações redundantes. Isso garante que a rede não dependa excessivamente de neurônios ou características de entrada/classe específicas. Isso resulta em uma melhor generalização. Ao omitir aleatoriamente neurônios, o processo de treinamento cria um conjunto de modelos a partir de uma única rede neural. Essa melhor generalização torna a rede mais robusta para classificar dados não vistos, especialmente em situações complexas e de dados de alta dimensionalidade.

Além disso, o drop-out tende a tornar a rede mais resiliente a dados ruidosos, garantindo que nenhum neurônio domine o processo de tomada de decisão. Isso é fundamental não apenas com dados de teste ruidosos ou menos confiáveis, mas também em situações onde os dados de entrada têm um alto grau de variância. Além disso, ele reduz a interdependência entre os neurônios ou incentiva a quebra da co-adaptação entre os neurônios. Isso faz com que cada neurônio aprenda de forma independente, o que torna a rede mais robusta. Adicione a isso, o uso do drop-out em redes muito profundas e empilhadas do tipo transformer poderia não só introduzir eficiência no processo de teste (se o processo eliminar neurônios manualmente, em vez da abordagem pós-vetor de saída que adotamos), mas também previne o risco de overfitting, dado o grande número de parâmetros envolvidos.

Ele é aplicável em vários formatos de rede, como MLPs ou CNNs, e também é escalável. Quando comparado ao L1 e L2, o drop-out tende a se inclinar mais para o L1, pois a omissão de neurônios durante os testes leva a resultados de saída mais esparsos, o que é fundamental em redes classificadoras. Isso ocorre porque a maioria dos benefícios do drop-out mencionados acima são pertinentes para redes classificadoras. Essas redes geralmente são mais profundas do que as redes de regressão, e essas multitudes de parâmetros as tornam propensas ao overfitting. O drop-out, como mencionado acima, combate isso forçando a rede a aprender características mais gerais e robustas. A generalização é fundamental em classificadores, e o drop-out a melhora; dados ruidosos podem afetá-los desproporcionalmente (quando comparados às redes de regressão), e o drop-out ajuda a mitigar seus efeitos. Isso e muitas das características já mencionadas acima implicam que é mais adequado para redes classificadoras, pois, em geral, mas não sempre, as redes classificadoras tendem a ter camadas muito poucas, mas grandes. Elas são muito profundas. Por outro lado, as redes de regressão tendem a ter camadas pequenas, mas empilhadas. Elas se inclinam mais para transformers. Portanto, isso talvez seja outra consideração importante que deve ser levada em conta não apenas ao definir como uma rede será regularizada, mas também ao determinar o número e o tamanho geral de suas camadas.

Resultados dos Testes

Como prometido, como sempre, realizamos testes com um Expert Advisor montado por um assistente. Para novos leitores, o código anexado precisa ser montado em um Expert Advisor, seguindo as diretrizes que estão disponíveis aqui e aqui. Estamos testando no EURUSD desta vez, no período diário para o ano de 2023. Como fizemos no último artigo, estamos testando uma rede de regressão e uma rede classificadora.

Como já argumentado em artigos anteriores a este, redes classificadoras funcionam melhor com ativações soft-max ou sigmoide. Além disso, como discutido acima, elas são mais adequadas para trabalhar com funções de perda Categorical Cross Entropy ou Binary Cross Entropy e com regularização L1, que usa especificamente as normas de matriz P1. Portanto, se realizarmos testes com essas configurações em vigor, enquanto colocamos ordens pendentes sem stop-loss, obtemos os seguintes resultados:

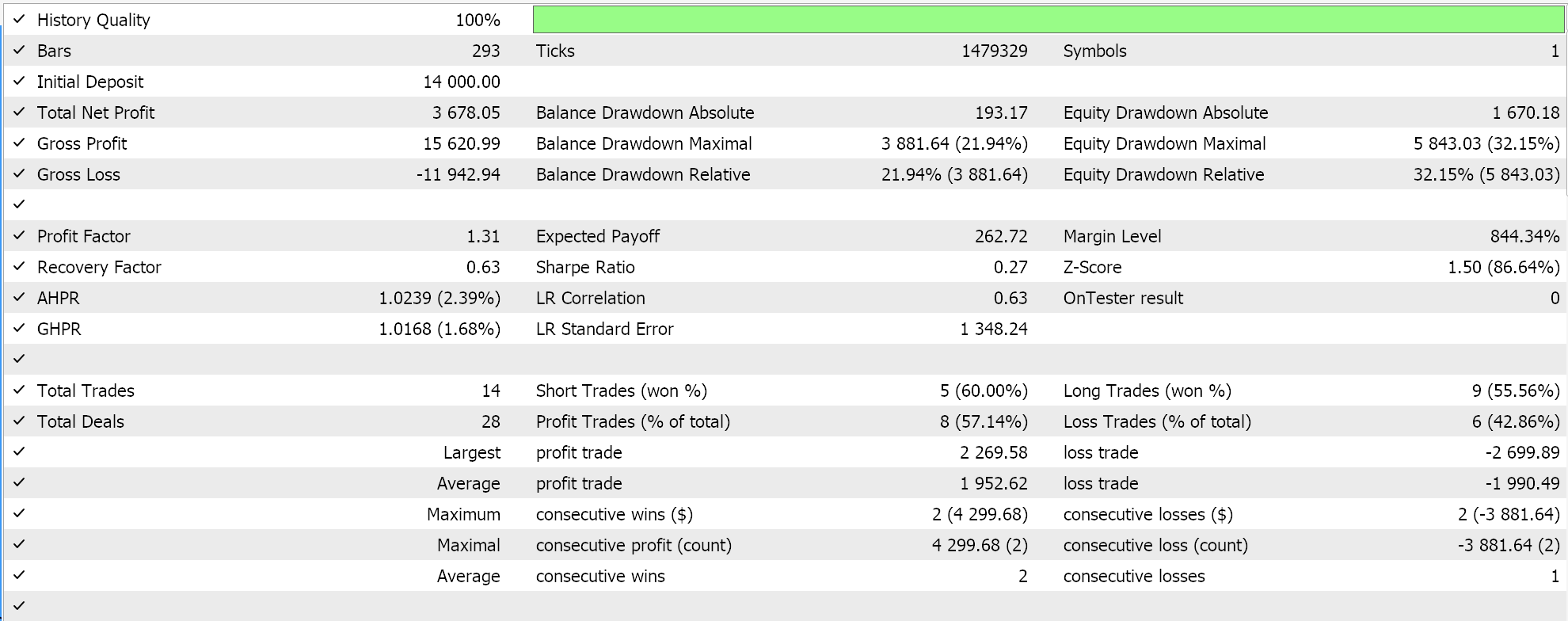
Com a curva de equidade:

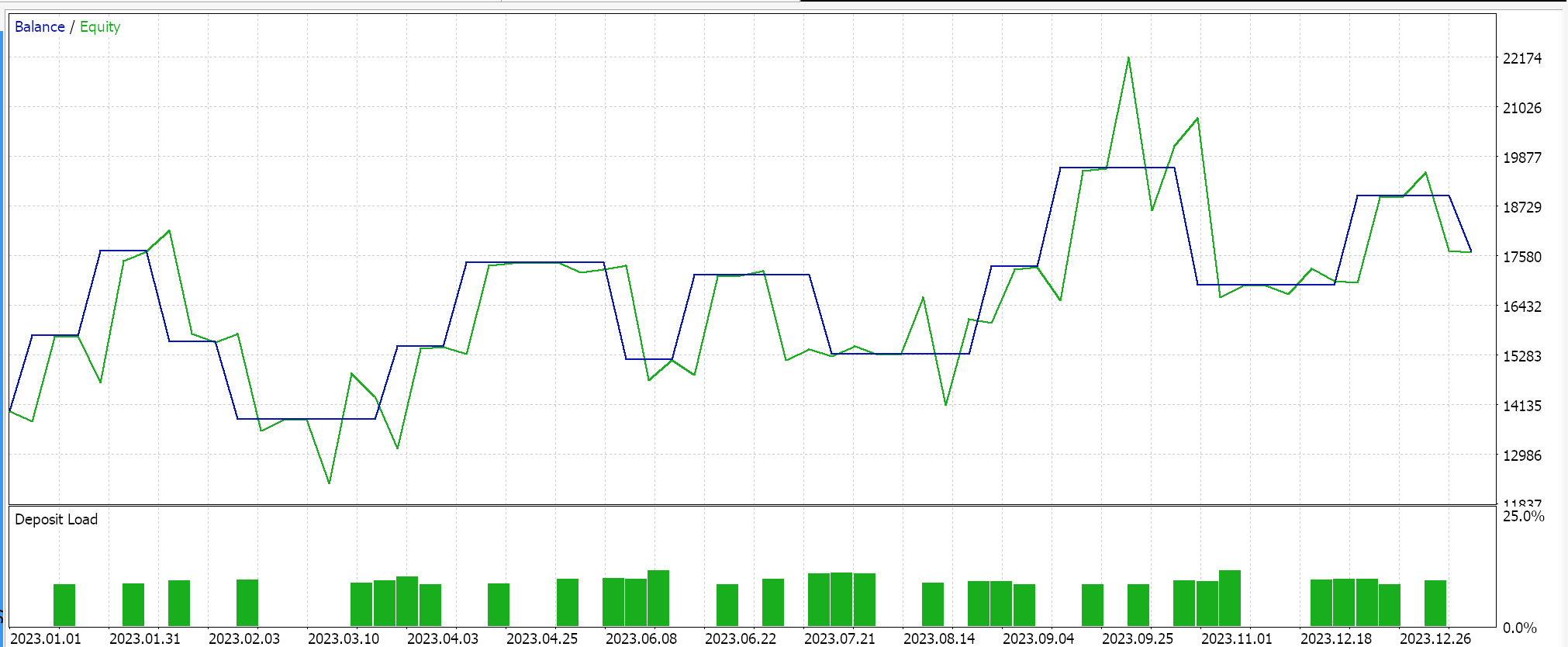
Por outro lado, para a rede de regressão, se realizarmos testes usando a ativação soft-sign e a regularização L2 Ridge juntamente com a função de perda Huber, obtemos os seguintes resultados:

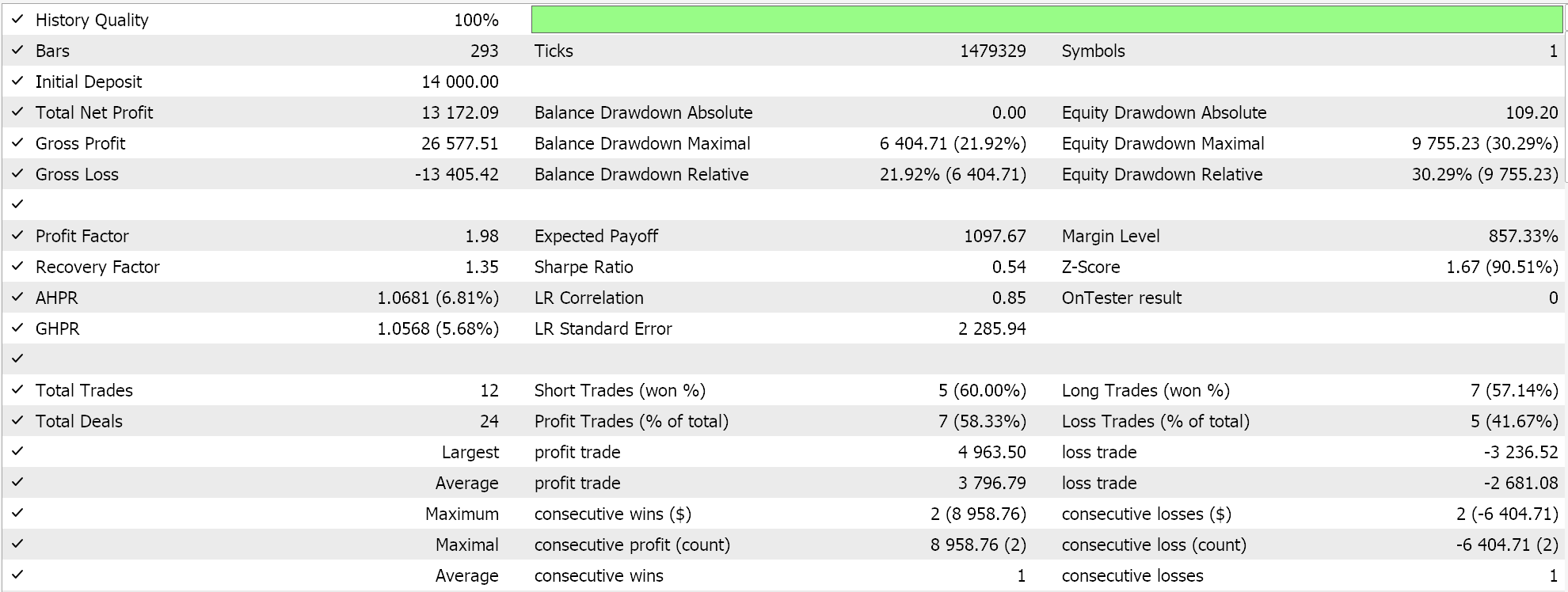
Com a curva de equidade:

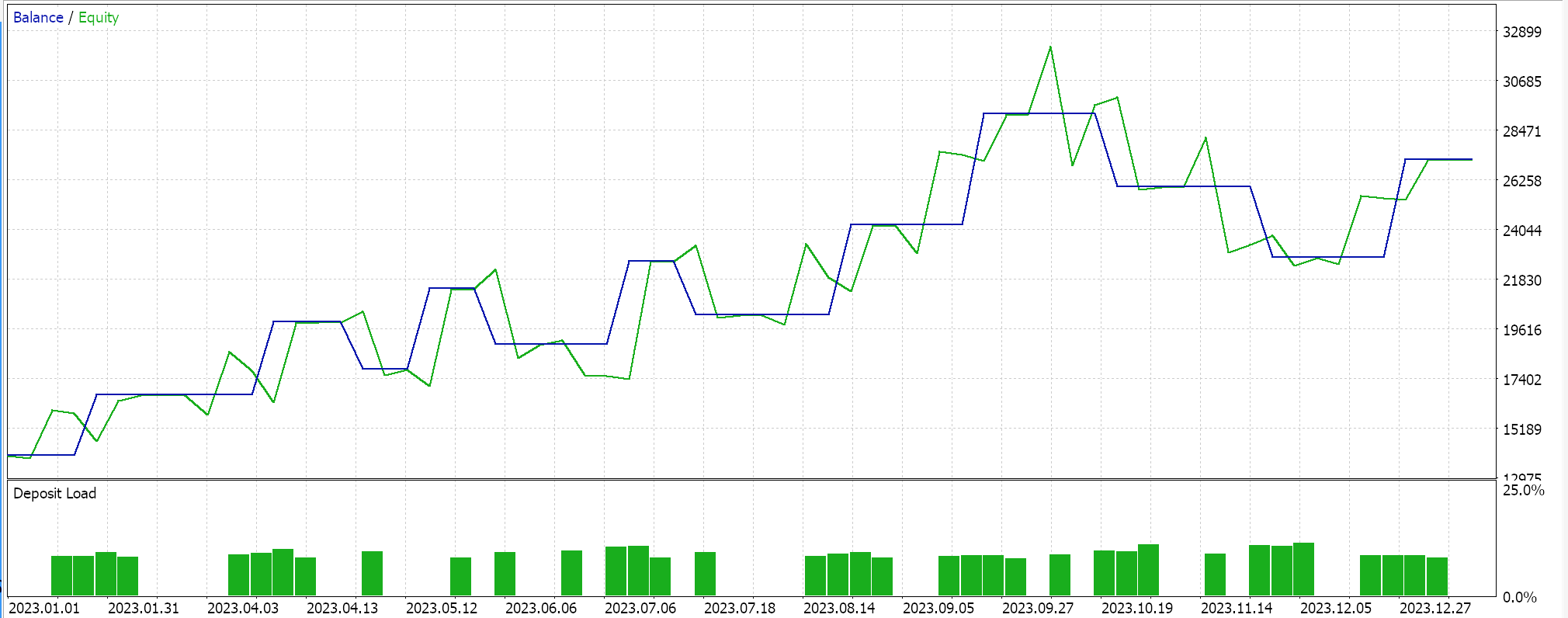
Como controle para esses resultados, seria necessário treinar a rede com opções de regularização revertidas ou sem regularização alguma. Testes realizados com as mesmas configurações das usadas acima para as redes de regressão e classificação, mas sem regularização, produzem os mesmos resultados. Isso pode implicar que a regularização não seja tão crítica quanto outros fatores, como a função de perda, funções de ativação e até mesmo os limiares típicos de entrada e fechamento do Expert Advisor. No entanto, um argumento contraposto e talvez credível também poderia ser feito de que os benefícios da regularização, especialmente na rede classificadora, podem ser melhor apreciados com testes não apenas por períodos mais longos que se estendem por mais de um ano, mas com redes muito profundas que apresentam uma classe de saída mais ampla.

Conclusão

Em conclusão, examinamos a regularização como um componente chave dos algoritmos de aprendizado de máquina, como as redes neurais, observando seu papel em dois cenários específicos. Redes classificadoras e redes de regressão. Redes classificadoras frequentemente, mas não sempre, têm poucas camadas, mas cada uma delas é muito profunda. Por outro lado, as redes de regressão tendem a ter camadas pequenas, mas empilhadas em múltiplos, que compensam a falta de profundidade. Embora nossos resultados de teste indiquem que o desempenho do Expert Advisor não é sensível à regularização, com base nas execuções do EURUSD no período diário para 2023, mais testes são necessários antes que tal conclusão drástica possa ser feita. Isso porque, além da pequena janela de teste, as redes usadas estavam em uma escala muito modesta, o que torna improvável que aproveitem completamente os benefícios da regularização.

Epílogo

Eu pretendia omitir a cobertura da regularização Elastic-Net, no entanto, como o artigo não é muito longo, pensei que poderia adicionar brevemente aqui. A equação para o Elastic-Net é a seguinte:

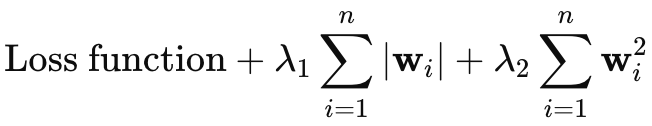
Onde

• wi representa os pesos individuais do modelo.
• λ1 controla a intensidade da penalização L1 (Lasso), que incentiva a escassez no modelo, diminuindo alguns pesos para zero.
• λ2 controla a intensidade da penalização L2 (Ridge), que incentiva pesos pequenos, mas geralmente não os reduz a zero.

Para adicionar a regularização elastic-net à nossa classe, primeiro precisaríamos modificar a enumeração principal para incluí-la da seguinte forma:

//+------------------------------------------------------------------+
//| Regularization Type Enumerator                                   |
//+------------------------------------------------------------------+
enum Eregularize
{  REGULARIZE_NONE = -1,
   REGULARIZE_L1 = 1,
   REGULARIZE_L2 = 2,
   REGULARIZE_DROPOUT = 3,
   REGULARIZE_ELASTIC = 4
};

Então, em segundo lugar, precisaríamos modificar a função ‘RegularizeTerm’ para lidar com essa opção Elastic-Net, adicionando uma cláusula if de 3^rd, e implementamos isso da seguinte maneira:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...


   else if(THIS.regularization == REGULARIZE_ELASTIC)
   {  _term =  _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) +
               ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm));
   }
   _regularized.Fill(_term);
   return(_regularized);
}

Isso segue claramente a fórmula compartilhada acima, pois implementa uma média ponderada que usa um valor alfa que é positivo e não excede um. Isso normalmente seria otimizado no intervalo de 0.0 a 1.0. Com a implementação do código acima, no entanto, estamos usando uma única enumeração de normas de matriz, o que impediria a captura das propriedades independentes do L1 e L2. Uma solução seria ter duas variáveis ‘_weight_norm’, cada uma com suas próprias funções de normas de matriz, mas isso também significaria que a estrutura do construtor deveria ser modificada para acomodar ambas. Alternativamente, poderíamos usar as normas de infinito como um compromisso para ambos os formatos de regularização.