Klassische Strategien neu interpretieren (Teil VI): Analyse mehrerer Zeitrahmen
134
0
Einführung
Es gibt potenziell unendlich viele Möglichkeiten, wie ein moderner Anleger künstliche Intelligenz (KI) integrieren kann, um seine Handelsentscheidungen zu verbessern. Leider ist es unwahrscheinlich, dass Sie alle diese Strategien bewerten können, bevor Sie entscheiden, welcher Strategie Sie Ihr hart verdientes Kapital anvertrauen. In dieser Artikelserie werden wir Handelsstrategien untersuchen, um zu beurteilen, ob wir die Strategie mit KI verbessern können. Unser Ziel ist es, Ihnen die Informationen zur Verfügung zu stellen, die Sie benötigen, um eine fundierte Entscheidung zu treffen, ob diese Strategie für Ihr individuelles Anlegerprofil geeignet ist.
Überblick über die Handelsstrategie
In diesem Artikel greifen wir eine bekannte Strategie der Analyse mehrerer Zeitrahmen wieder auf. Eine große Gruppe erfolgreicher Händler auf der ganzen Welt ist davon überzeugt, dass es von Vorteil ist, mehr als einen Zeitrahmen zu analysieren, bevor man Anlageentscheidungen trifft. Es gibt viele verschiedene Varianten dieser Strategie. Sie alle neigen jedoch dazu, die allgemeine Überzeugung zu vertreten, dass ein Trend, der in einem höheren Zeitrahmen festgestellt wird, auch in allen niedrigeren Zeitrahmen fortbesteht.
Wenn wir also zum Beispiel auf dem Tages-Chart ein zinsbullisches Kursverhalten beobachten, können wir davon ausgehen, dass wir auch auf dem Stunden-Chart zinsbullische Kursmuster sehen werden. Bei dieser Strategie wird die Idee noch erweitert, indem Kursschwankungen, die mit dem auf dem höheren Zeithorizont beobachteten Trend übereinstimmen, stärker gewichtet werden sollten.
Mit anderen Worten, um auf unser einfaches Beispiel zurückzukommen: Wenn wir auf dem Tages-Chart einen Aufwärtstrend beobachten, würden wir eher zu Kaufgelegenheiten auf dem Stunden-Chart tendieren und nur ungern Positionen gegen den auf dem Tages-Chart beobachteten Trend eingehen.
Im Allgemeinen fällt die Strategie auseinander, wenn sich der auf dem höheren Zeitrahmen beobachtete Trend umkehrt. Dies liegt in der Regel daran, dass die Umkehrung nur in einem niedrigeren Zeitrahmen beginnt. Es sei daran erinnert, dass bei dieser Strategie Fluktuationen, die in niedrigeren Zeitrahmen beobachtet werden und im Gegensatz zum höheren Zeitrahmen stehen, wenig Gewicht beigemessen wird. Daher würden Händler, die diese Strategie verfolgen, in der Regel warten, bis die Umkehrung auf dem höheren Zeitrahmen zu beobachten ist. Daher kann es zu starken Kursschwankungen kommen, während sie auf die Bestätigung des höheren Zeitrahmens warten.
Überblick über die Methodik
Um die Vorzüge dieser Strategie empirisch bewerten zu können, mussten wir sorgfältig aussagekräftige Daten aus unserem MetaTrader 5 Terminal extrahieren. Unser Ziel in diesem Artikel war die Vorhersage des zukünftigen Schlusskurses des EURUSD 20 Minuten in die Zukunft. Um dieses Ziel zu erreichen, haben wir 3 Gruppen von Prädiktoren gebildet:
- Gewöhnliche Informationen von Eröffnungs-, Höchst-, Tiefst- und Schlusskursen.
- Änderungen des Preisniveaus über längere Zeiträume
- Eine übergeordnete Menge der beiden oben genannten Sätze.
Wir haben eine relativ schwache Korrelation zwischen den normalen Preisdaten und den Preisänderungen in den höheren Zeiträumen festgestellt. Die stärksten Korrelationswerte wurden zwischen den Preisänderungen auf der M15 und den Preisniveaus auf der M1 beobachtet, etwa -0,1.
Wir erstellten eine große Anzahl verschiedener Modelle und trainierten sie auf alle 3 Sätze von Prädiktoren, um die Veränderungen in der Genauigkeit zu beobachten. Die besten Fehlerquoten wurden bei der Verwendung der ersten Gruppe von Prädiktoren, den gewöhnlichen Marktdaten, erzielt. Aus unseren Beobachtungen geht hervor, dass das Modell der linearen Regression am besten funktioniert, gefolgt vom Modell des Gradient Boosting Regressor (GBR).
Da das lineare Modell keine für uns interessanten Tuning-Parameter hat, wählten wir das GBR-Modell als unseren Lösungsvorschlag, und die Fehlerwerte des linearen Modells wurden zu unserem Leistungsmaßstab. Unser Ziel war es nun, das GBR-Modell so zu optimieren, dass es die Benchmark-Leistung des linearen Modells übertrifft.
Bevor wir mit dem Optimierungsprozess begannen, führten wir eine Merkmalsauswahl mit dem Algorithmus der Rückwärtsauswahl durch. Alle Merkmale, die sich auf die Preisveränderungen in höheren Zeiträumen beziehen, wurden vom Algorithmus verworfen, was möglicherweise darauf hindeutet, dass die Beziehung nicht zuverlässig ist, oder wir können dies auch so interpretieren, dass wir die Assoziation nicht auf sinnvolle Weise in unser Modell aufgenommen haben.
Wir verwendeten einen randomisierten Suchalgorithmus mit 1000 Iterationen, um optimale Einstellungen für unser GBR-Modell zu finden. Anschließend haben wir die Ergebnisse unserer randomisierten Suche als Ausgangspunkt für eine lokale Optimierung der kontinuierlichen GBR-Parameter mit Hilfe des Algorithmus Limited Memory Broyden Fletcher Goldfarb And Shanno (L-BFGS-B) verwendet.
Bei den Validierungsdaten konnten wir das Standard-GBR-Modell nicht übertreffen, was möglicherweise darauf hindeutet, dass wir die Trainingsdaten zu stark angepasst haben. Außerdem konnten wir bei der Validierung die Benchmark-Leistung des linearen Modells nicht übertreffen.
Datenextraktion
Ich habe ein nützliches MQL5-Skript zum Extrahieren von Daten aus unserem MetaTrader 5-Terminal erstellt. Das Skript holt auch die Preisänderungen aus einer Auswahl höherer Zeitrahmen und gibt die Datei im Pfad aus: „MetaTrader 5\MQL5\Files\...“
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 5; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + " multiple timeframe 20 step look ahead .csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= -1;i<=size;i++) { if(i == -1) { FileWrite(file_handle,"Time","Open","High","Low","Close","M5","M15","M30","H1","D1"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), (iClose(Symbol(),PERIOD_M5,i) - iClose(Symbol(),PERIOD_M5,i+20)), (iClose(Symbol(),PERIOD_M15,i) - iClose(Symbol(),PERIOD_M15,i+20)), (iClose(Symbol(),PERIOD_M30,i) - iClose(Symbol(),PERIOD_M30,i+20)), (iClose(Symbol(),PERIOD_H1,i) - iClose(Symbol(),PERIOD_H1,i+20)), (iClose(Symbol(),PERIOD_D1,i) - iClose(Symbol(),PERIOD_D1,i+20)) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Einlesen der Daten
Beginnen wir damit, die benötigten Bibliotheken zu laden.
import pandas as pd imort numpy as np
Beachten Sie, dass die Daten von der nahen Gegenwart bis in die ferne Vergangenheit reichen. Wir müssen die Daten umkehren, so dass sie von der Vergangenheit bis zur nahen Gegenwart reichen.
#Let's format the data so it starts with the oldest date market_data = market_data[::-1] market_data.reset_index(inplace=True)
Nun werden wir unseren Prognosehorizont festlegen.
look_ahead = 20 Kennzeichnung der Daten. Unser Ziel wird der zukünftige Schlusskurs des EURUSD sein.
#Let's label the data market_data["Target"] = market_data["Close"].shift(-look_ahead)
Jetzt lassen wir alle Zeilen mit fehlenden Werten weg.
#Drop rows with missing values
market_data.dropna(inplace=True)
Explorative Datenanalyse
Analyse der Korrelationsniveaus.
#Let's see if there is any correlation market_data.iloc[:,2:-1].corr()
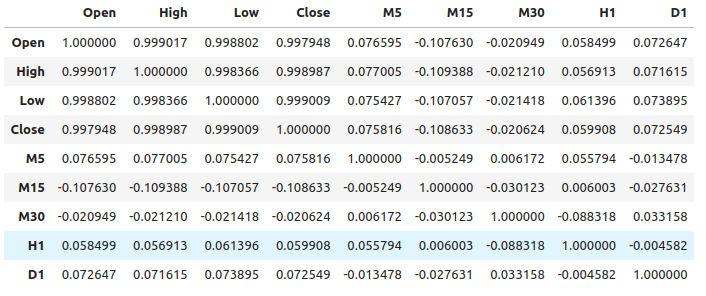
Abb. 1: Korrelationsniveaus über verschiedene Zeiträume hinweg
Wie wir sehen, sind die Korrelationen in unserem Datensatz nur mäßig ausgeprägt. Beachten Sie, dass die Korrelation nicht unbedingt beweist, dass eine Beziehung zwischen den beobachteten Variablen besteht.
Die gegenseitige Information ist ein Maß für das Potenzial eines Prädiktors, unser Ziel zu erklären. Betrachten wir zunächst eine Variable, von der wir wissen, dass sie ein großes Potenzial für die Vorhersage des Ziels hat, nämlich den Eröffnungskurs.
from sklearn.feature_selection import mutual_info_regression
Als Benchmark ist dies ein guter Wert für die gegenseitige Information (MI).
#MI Score for the Open price
print(f'Open price has MI score: {mutual_info_regression(market_data.loc[:,["Open"]],market_data.loc[:,"Target"])[0]}') Betrachten wir nun den MI-Score für die Preisänderungen auf dem M5-Zeitrahmen im Verhältnis zum zukünftigen Preis auf dem M1-Zeitrahmen.
#MI Score for the M5 change in price
print(f'M5 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M5"]],market_data.loc[:,"Target"])[0]}') Unsere MI-Punktzahl ist wesentlich geringer, was bedeutet, dass wir die Beziehung möglicherweise nicht sinnvoll aufgedeckt haben oder dass es keine Abhängigkeit zwischen den Preisniveaus in verschiedenen Zeiträumen gibt!
#MI Score for the M15 change in price
print(f'M15 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M15"]],market_data.loc[:,"Target"])[0]}') Das Gleiche gilt für die übrigen von uns ausgewählten Zeitrahmen.
Modellierung der Beziehung
Definieren wir also unsere Prädiktoren und unser Ziel.
#Let's define our predictors and our target ohlc_predictors = [ "Open", "High", "Low", "Close" ] time_frame_predictors = [ "M5", "M15", "M30", "H1", "D1" ] all_predictors = ohlc_predictors + time_frame_predictors target = "Target"
Jetzt importieren wir die Bibliotheken, die wir brauchen.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import SGDRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit,RandomizedSearchCV from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
Dann definieren wir die Parameter für unser Zeitserien-Split-Objekt.
#Define the time series split object gap = look_ahead splits = 10
Bereiten wir nun unsere Modelle vor und erstellen wir auch Datenrahmen, um unsere Genauigkeitsstufen zu speichern. Auf diese Weise können wir beobachten, wie sich die Genauigkeit ändert, wenn wir unsere Modelleingaben ändern.
#Store our models in a list models = [ LinearRegression(), SGDRegressor(), RandomForestRegressor(), BaggingRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), MLPRegressor(hidden_layer_sizes=(100,20),early_stopping=True) ] #Create a list of column titles for each model columns = [ "Linear Regression", "SGD Regressor", "Random Forest Regressor", "Bagging Regressor", "Gradient Boosting Regressor", "AdaBoost Regressor", "K Neighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neurla Network" ] #Create data frames to store our accuracy ohlc_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) multiple_time_frame_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) all_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns)
Bereiten wir nun die Prädiktoren vor und skalieren wir unsere Daten.
#Preparing to perform cross validation
current_predictors = all_predictors
scaled_data = pd.DataFrame(RobustScaler().fit_transform(market_data.loc[:,all_predictors]),columns=all_predictors)
Erstellen des geteilten Zeitreihenobjekts.
#Create the time series split object
tscv = TimeSeriesSplit(gap=gap,n_splits=splits)
Nun werden wir eine Kreuzvalidierung durchführen. Die erste Schleife durchläuft die Liste der zuvor erstellten Modelle, die zweite Schleife führt eine Kreuzvalidierung jedes Modells durch.
#First we will iterate over all the available models for i in np.arange(0,len(models)): #First select the model model = models[i] #Now we will cross validate this current model for j , (train,test) in enumerate(tscv.split(scaled_data)): #First define the train and test data train_X = scaled_data.loc[train[0]:train[-1],current_predictors] train_y = market_data.loc[train[0]:train[-1],target] test_X = scaled_data.loc[test[0]:test[-1],current_predictors] test_y = market_data.loc[test[0]:test[-1],target] #Now we will fit the model model.fit(train_X,train_y) #And finally record the accuracy all_accuracy.iloc[j,i] = root_mean_squared_error(test_y,model.predict(test_X))
Unsere Genauigkeitsstufen bei Verwendung gewöhnlicher Eingaben für unser Modell.
ohlc_accuracy
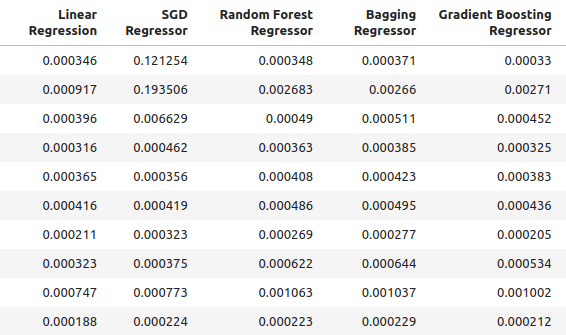
Abb. 2: Unsere normale Genauigkeitsstufen.
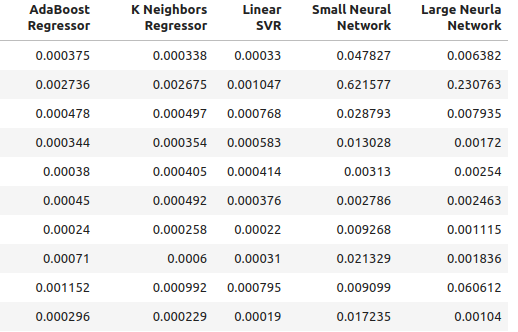
Abb. 3: Unsere normale Genauigkeitsstufen II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {ohlc_accuracy.iloc[:,i].mean()}")
Die lineare Regression hatte einen Fehlerwert von 0,00042256332959154886
SGD Regressor hatte einen Fehlerwert 0.0324320107406244
Der Random Forest Regressor hatte einen Fehlerwert von 0,0006954883552094012
Der Bagging-Regressor hatte einen Fehlerwert von 0,0007030697054783931
Der Gradient-Boosting-Regressor hatte einen Fehlerwert von 0,0006588749449742309
Der AdaBoost-Regressor hatte einen Fehlerwert von 0,0007159624774453208
K Neighbors Regressor hatte einen Fehlerwert 0.0006839218661791973
Die lineare SVR hatte einen Fehlerwert von 0,000503277800807813
Das kleine neuronale Netz hatte eine einen Fehlerwert von 0,07740701832606754
Das große neuronale Netz hatte einen Fehlerwert von 0,03164056895135391
Unsere Genauigkeit bei der Verwendung der neuen Eingaben, die wir erstellt haben.
multiple_time_frame_accuracy
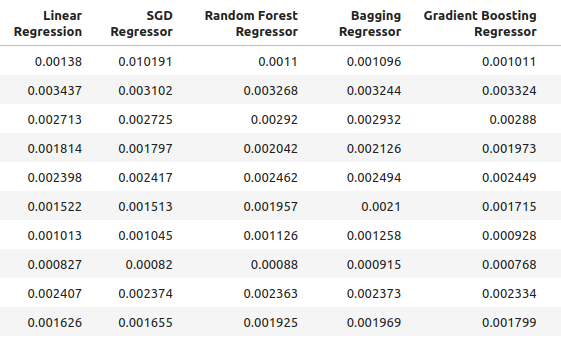
Abb. 4: Unsere neuen Genauigkeitsstufen
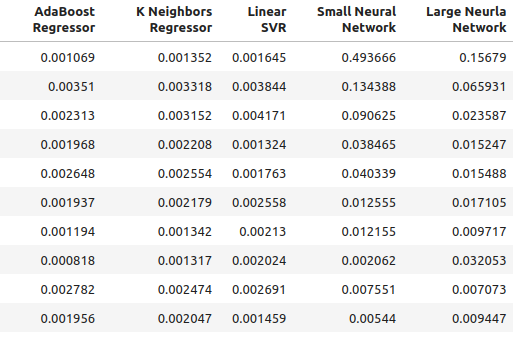
Abb. 5: Unsere neuen Genauigkeitsstufen II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {multiple_time_frame_accuracy.iloc[:,i].mean()}")
Die lineare Regression hatte einen Fehlerwert von 0,001913639795583766
SGD Regressor hatte einen Fehlerwert 0.0027638553835377206
Der Random Forest Regressor hatte einen Fehlerwert von 0,0020041047670504254
Der Bagging-Regressor hatte einen Fehlerwert von 0,0020506512726394415
Der Gradient-Boosting-Regressor hatte einen Fehlerwert von 0,0019180687958290775
Der AdaBoost-Regressor hatte einen Fehlerwert von 0,0020194136735787625
K Neighbors Regressor hatte einen Fehlerwert 0.0021943350208868213
Die lineare SVR hatte einen Fehlerwert von 0,0023609474919917338
Das kleine neuronale Netz hatte einen Fehlerwert von 0,08372469596701271
Das große neuronale Netz hatte einen Fehlerwert von 0,035243897461061074
Abschließend wollen wir unsere Genauigkeit bei Verwendung aller verfügbaren Prädiktoren betrachten.
all_accuracy
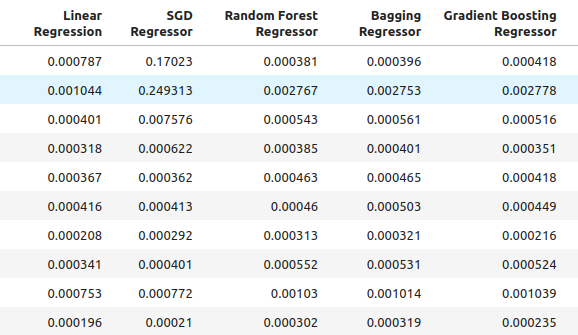
Abb. 6: Unsere Genauigkeitsstufen bei Verwendung aller uns zur Verfügung stehenden Prädiktoren.
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {all_accuracy.iloc[:,i].mean()}")
Die lineare Regression hatte Genauigkeit insgesamt von 0,00048307488099524497
SGD Regressor hatte Genauigkeit insgesamt 0.043019079499194125
Der Random Forest Regressor hatte Genauigkeit insgesamt von 0,0007196920919204373
Der Bagging-Regressor hatte Genauigkeit insgesamt von 0,0007263444909545053
Der Gradient-Boosting-Regressor hatte Genauigkeit insgesamt von 0,0006943964783049555
Der AdaBoost-Regressor hatte Genauigkeit insgesamt von 0,0007217149661087063
K Neighbors Regressor hatte Genauigkeit insgesamt 0.000872811528292862
Die lineare SVR hatte Genauigkeit insgesamt von 0,0006457525216512596
Das kleine neuronale Netz hatte Genauigkeit insgesamt von 0,14002618062102
Das große neuronale Netz hatte Genauigkeit insgesamt von 0,06774795252887988
Wie man sieht, war das lineare Modell in allen Tests das beste Modell. Außerdem schnitt es am besten ab, wenn gewöhnliche OHLC-Daten verwendet wurden. Das Modell hat jedoch keine für uns interessanten Tuning-Parameter. Daher wählen wir das zweitbeste Modell, den Gradient Boosting Regressor (GBR), und versuchen, das lineare Modell zu übertreffen.
Auswahl der Merkmale
Nun wollen wir sehen, welche Merkmale für unser GBR-Modell am wichtigsten waren.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS
Wählen Sie das Modell aus.
#We'll select the Gradient Boosting Regressor as our chosen model model = GradientBoostingRegressor()
Wir werden den Algorithmus der Rückwärtsauswahl verwenden. Wir beginnen mit einem Modell, das alle Prädiktoren enthält, und lassen nach und nach die einzelnen Merkmale weg. Ein Merkmal wird nur dann gestrichen, wenn es zu einer verbesserten Leistung des Modells führt.
#Let us prepare the Feature Selector Object sfs = SFS(model, k_features=(1,len(all_predictors)), forward=False, n_jobs=-1, scoring="neg_root_mean_squared_error", cv=10 )
Durchführen der Merkmalsauswahl.
#Select the best feature sfs_results = sfs.fit(scaled_data.loc[:,all_predictors],market_data.loc[:,"Target"])
Der Algorithmus behielt nur das Hoch bei und ließ alle anderen Merkmale außer Acht.
#The best feature we found
sfs_results.k_feature_names_
Lassen Sie uns unsere Ergebnisse visualisieren.
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on Gradient Boosting Regressor") plt.grid()
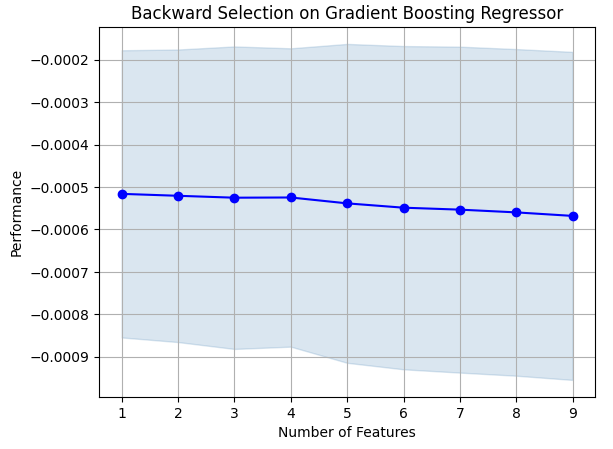
Abb. 7: Visualisierung des Merkmalsauswahlprozesses
Wie man sieht, waren Modellgröße und Fehlerniveau direkt proportional. Mit anderen Worten: Je größer unser Modell wurde, desto größer wurden auch unsere Fehlerquoten.
Einstellung der Parameter
Wir wollen nun die Parameter unseres GBR-Modells abstimmen. Wir haben 11 Parameter des Modells identifiziert, die es wert sind, abgestimmt zu werden, und wir werden 1000 Iterationen des Abstimmungsobjekts zulassen, bevor wir den Optimierungsprozess beenden.
#Let us try to tune our model
from sklearn.model_selection import RandomizedSearchCV
Bevor wir mit der Abstimmung unseres Modells beginnen, sollten wir unsere Daten in zwei Teile aufteilen. Die eine Hälfte wird für das Training und die Optimierung unseres Modells verwendet, die andere für die Validierung und die Prüfung auf Überanpassung.
#Before we try to tune our model, let's first create a train and test set train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = market_data.loc[:(market_data.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = market_data.loc[(market_data.shape[0]//2):,"Target"]
Definieren wir das Abstimmobjekt.
#Time the process import time start_time = time.time() #Prepare the tuning object tuner = RandomizedSearchCV(GradientBoostingRegressor(), { "loss": ["squared_error","absolute_error","huber"], "learning_rate": [0,(10.0 ** -1),(10.0 ** -2),(10.0 ** -3),(10.0 ** -4),(10.0 ** -5),(10.0 ** -6),(10.0 ** -7)], "n_estimators": [5,10,25,50,100,200,500,1000], "max_depth": [1,2,3,5,9,10], "min_samples_split":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0], "criterion":["friedman_mse","squared_error"], "min_samples_leaf":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9], "min_weight_fraction_leaf":[0.0,0.1,0.2,0.3,0.4,0.5], "max_features":[1,2,3,4,5,20], "max_leaf_nodes": [2,3,4,5,10,20,50,90,None], "min_impurity_decrease": [0,1,10,(10.0 ** 2),(10.0 ** 3),(10.0 ** 4)] }, cv=5, n_iter=1000, return_train_score=False, scoring="neg_mean_squared_error" )
Abstimmen des GBR-Modells.
#Tune the GradientBoostingRegressor tuner.fit(train_X,train_y) end_time = time.time() print(f"Process completed in {end_time - start_time} seconds.")
Sehen wir uns die Ergebnisse in der Reihenfolge der besten bis schlechtesten Ergebnisse an.
#Let's observe the results tuner_results = pd.DataFrame(tuner.cv_results_) params = ["param_loss", "param_learning_rate", "param_n_estimators", "param_max_depth", "param_min_samples_split", "param_criterion", "param_min_samples_leaf", "param_max_features", "param_max_leaf_nodes", "param_min_impurity_decrease", "param_min_weight_fraction_leaf", "mean_test_score"] tuner_results.loc[:,params].sort_values(by="mean_test_score",ascending=False)
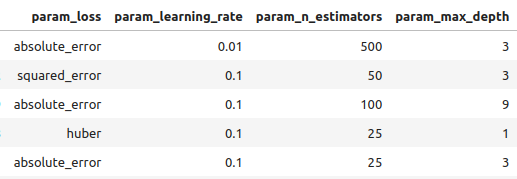
Abb. 8: Einige unserer besten Ergebnisse.
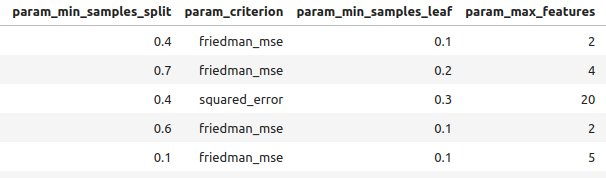
Abb. 9: Einige unserer besten Ergebnisse II
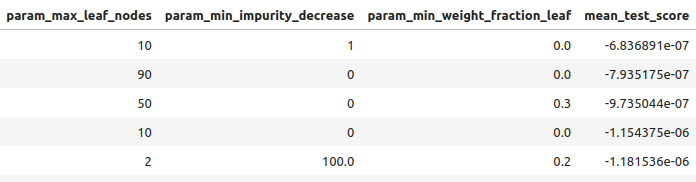
Abb. 10: Einige unserer besten Ergebnisse III
Die besten Parameter, die wir gefunden haben.
#Best parameters we found
tuner.best_params {'n_estimators': 500,
'min_weight_fraction_leaf': 0.0,
'min_samples_split': 0.4,
'min_samples_leaf': 0.1,
'min_impurity_decrease': 1,
'max_leaf_nodes': 10,
'max_features': 2,
'max_depth': 3,
'loss': 'absolute_error',
'learning_rate': 0.01,
'criterion': 'friedman_mse'}
Tiefergehende Parameterabstimmung
Abb. 11: Das SciPy-Logo
SciPy ist eine Python-Bibliothek, die für wissenschaftliche Berechnungen verwendet wird. SciPy steht für wissenschaftliches Python. Mal sehen, ob wir nicht noch bessere Parameter finden können. Wir werden die SciPy-Optimierungsbibliothek verwenden, um Parameter zu finden, die die Leistung unseres Modells verbessern.
#Let's see if we can't find better parameters #We may be overfitting the training data! from scipy.optimize import minimize
Um die SciPy-Optimierungsbibliothek zu verwenden, müssen wir eine Zielfunktion definieren. Unsere Zielfunktion ist der Durchschnitt der kreuzvalidierten Fehlerwerte, die unser Modell in der Trainingsmenge erreicht. Unser SciPy-Optimierer wird nach Koeffizienten suchen, die unseren Trainingsfehler reduzieren.
#Define the objective function def objective(x): #Create a dataframe to store our new accuracy current_error = pd.DataFrame(index=[0],columns=["error"]) #x is an array of possible values to use for our Gradient Boosting Regressor model = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=x[0], min_samples_split=x[1], min_samples_leaf=x[2], learning_rate=x[3]) model.fit(train_X.loc[:,:],train_y.loc[:]) current_error.iloc[0,0] = root_mean_squared_error(train_y.loc[:],model.predict(train_X.loc[:,:])) #Record our progress mean_error = current_error.loc[:].mean() #Return the average error return mean_error
Beginnen wir nun mit dem Optimierungsprozess. Beachten Sie, dass einige Parameter im GBR-Modell keine negativen Werte zulassen und unser SciPy-Optimierer negative Werte weitergibt, wenn wir keine Grenzen für den Optimierer angeben. Außerdem erwartet der Optimierer, dass wir ihm einen Startpunkt geben. Wir verwenden den Endpunkt des vorherigen Optimierungsalgorithmus als Ausgangspunkt für diesen Algorithmus.
#Let's optimize these parameters again #Fist define the bounds bounds = ((0.0,0.5),(0.3,0.5),(0.001,0.2),(0.001,0.1)) #Then define the starting points for the L-BFGS-B algorithm pt = np.array([tuner.best_params_["min_weight_fraction_leaf"], tuner.best_params_["min_samples_split"], tuner.best_params_["min_samples_leaf"], tuner.best_params_["learning_rate"] ])
Minimierung von Trainingsfehlern.
lbfgs = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
Schauen wir uns die Ergebnisse an.
lbfgs
success: True
status: 0
fun: 0.0005766670348377334
x: [ 5.586e-06 4.000e-01 1.000e-01 1.000e-02]
nit: 3
jac: [-6.216e+00 -4.871e+02 -2.479e+02 8.882e+01]
nfev: 180
njev: 36
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
Testen auf Überanpassung
Vergleichen wir nun die Genauigkeit unserer beiden angepassten Modelle mit dem Standard-GBR-Modell. Darüber hinaus werden wir auch darauf achten, ob wir das lineare Modell übertroffen haben.
#Let us now see how well we're performing on the validation set linear_regression = LinearRegression() default_gbr = GradientBoostingRegressor() grid_search_gbr = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=0, min_samples_split=0.4, min_samples_leaf=0.1, learning_rate=0.01 ) lbfgs_grid_search_gbr = GradientBoostingRegressor( n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=lbfgs.x[0], min_samples_split=lbfgs.x[1], min_samples_leaf=lbfgs.x[2], learning_rate=lbfgs.x[3] )Unsere Genauigkeit mit dem linearen Modell.
#Linear Regression
linear_regression.fit(train_X,train_y)
root_mean_squared_error(test_y,linear_regression.predict(test_X)) Unsere Genauigkeit mit dem Standard-GBR-Modell.
#Default Gradient Boosting Regressor
default_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,default_gbr.predict(test_X)) Unsere Genauigkeit mit dem GBR-Modell angepasst durch zufällige Suche.
#Random Search Gradient Boosting Regressor
grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,grid_search_gbr.predict(test_X)) Unsere Genauigkeit bei der Verwendung des GBR-Modells, angepasst durch Zufallssuche und L-BFGS-B.
#L-BFGS-B Random Search Gradient Boosting Regressor
lbfgs_grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,lbfgs_grid_search_gbr.predict(test_X))
Wie wir sehen, ist es uns nicht gelungen, das lineare Modell zu übertreffen. Außerdem haben wir das Standard-GBR-Modell nicht übertroffen. Daher werden wir zu Demonstrationszwecken mit dem Standard-GBR-Modell fortfahren. Es ist jedoch zu beachten, dass die Auswahl des linearen Modells zu einer höheren Genauigkeit geführt hätte.
Exportieren nach ONNX
Open Neural Network Exchange (ONNX) ist ein Protokoll, das es uns ermöglicht, Modelle des maschinellen Lernens als Berechnungsgraphen mit Knoten und Kanten darzustellen. Dabei stehen die Knoten für mathematische Operationen und die Kanten für den Datenfluss. Wenn wir unser maschinelles Lernmodell in das ONNX-Format exportieren, können wir unsere KI-Modelle problemlos in unserem Expert Advisor verwenden.
Lassen Sie uns nun unser ONNX-Modell exportieren.
#We failed to beat the linear regression model, in such cases we should pick the linear model! #However for demonstrational purposes we'll pick the gradient boosting regressor #Let's export the default GBR to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnx
Nun müssen wir unsere Daten so skalieren, dass wir sie im MetaTrader 5 reproduzieren können. Die einfachste Umwandlung besteht darin, den Mittelwert zu subtrahieren und durch die Standardabweichung zu dividieren.
#We need to save the scale factors for our inputs scale_factors = pd.DataFrame(index=["mean","standard deviation"],columns=all_predictors) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = market_data.iloc[:,i+2].mean() scale_factors.iloc[1,i] = market_data.iloc[:,i+2].std() market_data.iloc[:,i+2] = ((market_data.iloc[:,i+2] - market_data.iloc[:,i+2].mean()) / market_data.iloc[:,i+2].std()) scale_factors
Abb. 12: Unsere Skalenfaktoren
Definieren wir die Eingabetypen für unser ONNX-Modell.
#Define our initial types initial_types = [("float_input",FloatTensorType([1,test_X.shape[1]]))]
Anpassen des Modells an alle Daten, die wir haben.
#Fit the model on all the data we have model = GradientBoostingRegressor().fit(market_data.loc[:,all_predictors],market_data.loc[:,"Target"])
Erstellen der ONNX-Darstellung.
#Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Speichern des ONNX-Modells.
#Now save the ONNX model onnx_model_name = "GBR_M1_MultipleTF_Float.onnx" onnx.save(onnx_model,onnx_model_name)
Visualisierung des Modells
Netron ist ein Open-Source-Visualisierungsprogramm für die Untersuchung von Machine-Learning-Modellen. Derzeit bietet netron Unterstützung für eine begrenzte Anzahl von Frameworks. Im Laufe der Zeit und mit zunehmender Reife der Bibliothek wird die Unterstützung jedoch auf verschiedene maschinelle Lernsysteme ausgeweitet werden.
Importieren wir die benötigten Bibliotheken.
#Import netron so we can visualize the model
import netron
Starten von netron.
netron.start(onnx_model_name)
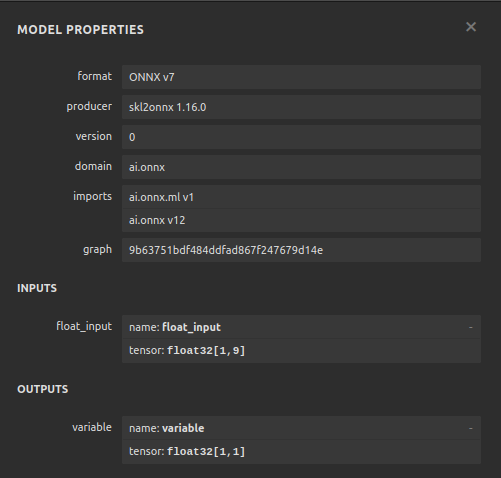
Abb. 13: Die Eigenschaften unseres Gradient Boosting Regressor ONNX-Modells
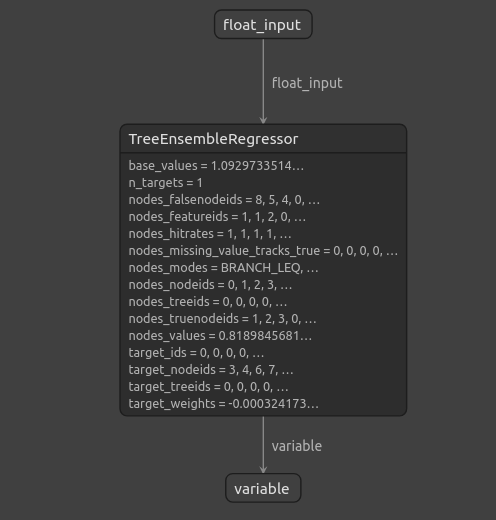
Abb. 14: Die Struktur unseres Gradient-Boosting-Regressors
Da wir sehen können, dass die Eingabe- und Ausgabeform unseres ONNX-Modells dort ist, wo wir sie erwarten, gibt uns dies die Zuversicht, fortzufahren und einen Expert Advisor auf der Grundlage unseres ONNX-Modells zu erstellen.
Implementierung in MQL5
Um mit dem Aufbau unseres Expert Advisors mit integriertem KI-Modul zu beginnen, benötigen wir zunächst das ONNX-Modell.//+------------------------------------------------------------------+ //| Multiple Time Frame.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the onnx file | //+------------------------------------------------------------------+ #resource "\\Files\\GBR_M1_MultipleTF_Float.onnx" as const uchar onnx_model_buffer[];
Jetzt laden wir die Handelsbibliothek.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Definieren wir die Eingaben definieren, die unser Endnutzer ändern kann.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input double max_risk = 20; //How much profit/loss should we allow before closing input double sl_width = 1; //How wide should out sl be?
Nun werden wir globale Variablen definieren, die in unserem Programm verwendet werden.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_variance[9],std_variance[9]; //Our scaling factors vector model_forecast = vector::Zeros(1); //Model forecast vector model_inputs = vector::Zeros(9); //Model inputs double ask,bid; //Market prices double trading_volume; //Our trading volume int lot_multiple = 20; //Our lot size int state = 0; //System state
Lassen Sie uns Hilfsfunktionen definieren, die wir in unserem Programm verwenden werden. Zunächst benötigen wir eine Funktion zur Erkennung von Umkehrungen und zur Warnung des Endnutzers vor der Gefahr, die unser KI-System vorausgesagt hat. Wenn unser KI-System eine Umkehrung feststellt, schließen wir die offenen Positionen, die wir in diesem Markt haben.
//+------------------------------------------------------------------+ //| Check reversal | //+------------------------------------------------------------------+ void check_reversal(void) { //--- Check for reversal if(((state == 1) && (model_forecast[0] < iClose(Symbol(),PERIOD_M1,0))) || ((state == 2) && (model_forecast[0] > iClose(Symbol(),PERIOD_M1,0)))) { Alert("Reversal predicted."); Trade.PositionClose(Symbol()); } //--- Check if we have breached our maximum risk levels if(MathAbs(PositionGetDouble(POSITION_PROFIT) > max_risk)) { Alert("We've breached our maximum risk level."); Trade.PositionClose(Symbol()); } }
Jetzt werden wir eine Funktion definieren, um Markteintrittsmöglichkeiten zu finden. Wir betrachten einen Eintrag nur dann als gültig, wenn wir von höheren Zeitrahmen eine Bestätigung der Bewegung erhalten. Bei diesem Expert Advisor sollen sich unser Handel an der Preisentwicklung im Wochenchart orientieren.
//+------------------------------------------------------------------+ //| Find an entry | //+------------------------------------------------------------------+ void find_entry(void) { //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bullish momentum if(model_forecast[0] > iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a buy Trade.Buy(trading_volume,Symbol(),ask,(ask - sl_width),(ask + sl_width),"Multiple Time Frames AI"); state = 1; } } //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bearish momentum if(model_forecast[0] < iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a sell Trade.Sell(trading_volume,Symbol(),bid,(bid + sl_width),(bid - sl_width),"Multiple Time Frames AI"); state = 2; } } }
Wir brauchen auch eine Funktion zum Abrufen der aktuellen Marktpreise.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); }
Unser ONNX-Modell kann nur verwendet werden, wenn wir die Eingaben standardisieren und normalisieren. Mit dieser Funktion werden die Skalierungsfaktoren abgerufen, die wir beim Training unseres ONNX-Modells verwendet haben.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- EURUSD OHLC mean_variance[0] = 1.0930010861272836; std_variance[0] = 0.0017987600829890852; mean_variance[1] = 1.0930721822927123; std_variance[1] = 0.001810556238082839; mean_variance[2] = 1.092928371812889; std_variance[2] = 0.001785041172362313; mean_variance[3] = 1.093000590242923; std_variance[3] = 0.0017979420556511476; //--- M5 Change mean_variance[4] = (MathPow(10.0,-5) * 1.4886568962056413); std_variance[4] = 0.000994902152654042; //--- M15 Change mean_variance[5] = (MathPow(10.0,-5) * 1.972093957036524); std_variance[5] = 0.0017104874192072138; //--- M30 Change mean_variance[6] = (MathPow(10.0,-5) * 1.5089339490060967); std_variance[6] = 0.002436078407827825; //--- H1 Change mean_variance[7] = 0.0001529512146155358; std_variance[7] = 0.0037675774501395387; //--- D1 Change mean_variance[8] = -0.0008775667536639223; std_variance[8] = 0.03172437243836734; }
Bei der Definition der Funktion, die für das Abrufen von Vorhersagen aus unserem Modell verantwortlich ist, ist zu beachten, dass wir die Eingaben skalieren, bevor wir sie an unser ONNX-Modell weitergeben. Die Vorhersagen werden mit Hilfe des Befehls OnnxRun aus dem Modell gewonnen.
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- EURD OHLC model_inputs[0] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[0]) / std_variance[0]); model_inputs[1] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[1]) / std_variance[1]); model_inputs[2] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[2]) / std_variance[2]); model_inputs[3] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[3]) / std_variance[3]); //--- M5 CAHNGE model_inputs[4] = (((iClose(Symbol(),PERIOD_M5,0) - iClose(Symbol(),PERIOD_M5,20)) - mean_variance[4]) / std_variance[4]); //--- M15 CHANGE model_inputs[5] = (((iClose(Symbol(),PERIOD_M15,0) - iClose(Symbol(),PERIOD_M15,20)) - mean_variance[5]) / std_variance[5]); //--- M30 CHANGE model_inputs[6] = (((iClose(Symbol(),PERIOD_M30,0) - iClose(Symbol(),PERIOD_M30,20)) - mean_variance[6]) / std_variance[6]); //--- H1 CHANGE model_inputs[7] = (((iClose(Symbol(),PERIOD_H1,0) - iClose(Symbol(),PERIOD_H1,20)) - mean_variance[7]) / std_variance[7]); //--- D1 CHANGE model_inputs[8] = (((iClose(Symbol(),PERIOD_D1,0) - iClose(Symbol(),PERIOD_D1,20)) - mean_variance[8]) / std_variance[8]); //--- Fetch forecast OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
Nun werden wir eine Funktion definieren, die unser Onnx-Modell lädt und die Eingabe- und Ausgabeform definiert.
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,9}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
Wir können nun die Initialisierungsprozedur des Programms definieren. Unser Experte lädt die Onnx-Datei, lädt die Skalierungsfaktoren und holt die Marktdaten.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Get trading volume trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
Wann immer unser Programm nicht genutzt wird, geben wir die nicht mehr benötigten Ressourcen frei. Wir werden das Onnx-Modell freigeben und den Expert Advisor aus dem Chart entfernen.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
Immer wenn neue Preise angeboten werden, holen wir zunächst eine Vorhersage aus unserem Modell und aktualisieren dann unsere Marktpreise. Wenn wir keine offene Position haben, werden wir versuchen, eine Eröffnung zu finden. Andernfalls, wenn es eine Position gibt, die verwaltet werden muss, werden wir aufmerksam nach einer möglichen Umkehrung Ausschau halten.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a prediction from our model model_predict(); //--- Show the model forecast Comment("Model forecast ",model_forecast); //--- Fetch market prices update_market_prices(); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find entry find_entry(); //--- Update state state = 0; } //--- If we have an open position, manage it else { //--- Check if our AI is predicting a reversal check_reversal(); } }
Jetzt können wir unsere Anwendung in Aktion sehen.
Abb. 15: Die Schnittstelle unseres Expert Advisors
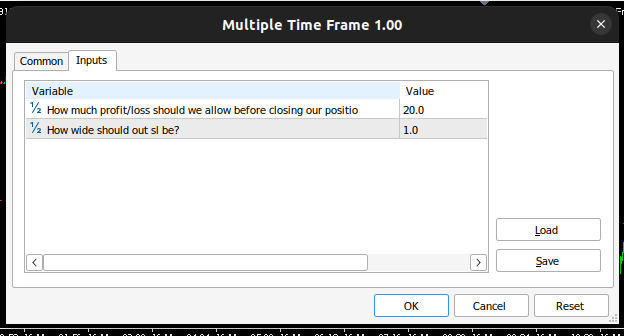
Abb. 16: Die Eingaben unseres Expert Advisors
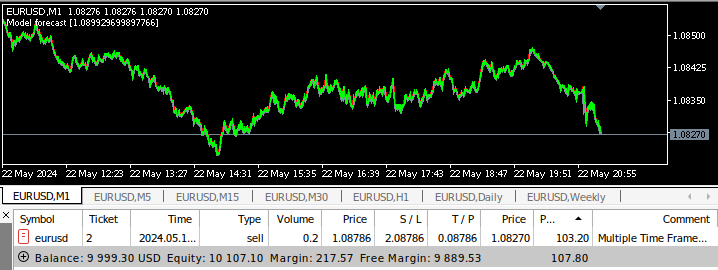
Abb. 17: Expert Advisor für mehrere Zeitrahmen im Backtest
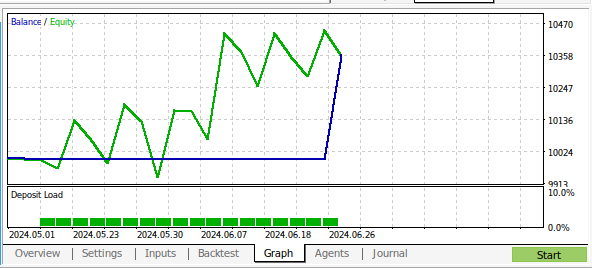
Abb. 18: Die Ergebnisse des Backtests unseres Programms über 1 Monat M1-Daten
Schlussfolgerung
In diesem Artikel haben wir gezeigt, dass es möglich ist, einen KI-gestützten Expert Advisor zu erstellen, der mehrere Zeitrahmen analysiert. Obwohl wir mit gewöhnlichen OHLC-Daten höhere Genauigkeitsstufen erreicht haben, gibt es viele verschiedene Möglichkeiten, die wir nicht untersucht haben, zum Beispiel haben wir keine Indikatoren auf höheren Zeitrahmen hinzugefügt. Es gibt viele Möglichkeiten, wie wir KI in unsere Handelsstrategie einbinden können. Hoffentlich haben Sie jetzt neue Ideen für die Möglichkeiten, die in Ihrer MetaTrader 5-Installation darauf warten, genutzt zu werden.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15610
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 33): Gauß-Prozess-Kerne
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 32): Regularisierung
Aufbau des Kerzenmodells Trend-Constraint (Teil 8): Entwicklung eines Expert Advisors (II)
Verschaffen Sie sich einen Vorteil auf jedem Markt (Teil III): Visa-Ausgabenindex
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.