Klassische Strategien neu interpretieren (Teil V): Analyse mehrerer Symbole für USDZAR

Einführung

Es gibt unzählige Möglichkeiten, wie wir KI in unsere Handelsstrategien integrieren können, aber leider können wir nicht jede einzelne davon bewerten, bevor wir entscheiden, welcher wir unser Kapital anvertrauen. Heute greifen wir eine beliebte Handelsstrategie der Mehrfachsymbolanalyse wieder auf, um festzustellen, ob wir die Strategie mithilfe von KI verbessern können. Wir liefern Ihnen die Informationen, die Sie benötigen, um eine fundierte Entscheidung darüber zu treffen, ob diese Strategie für Ihr Anlegerprofil geeignet ist.

Überblick über die Handelsstrategie

Handelsstrategien, die sich der Analyse mehrerer Symbole bedienen, beruhen hauptsächlich auf der Korrelation, die zwischen dem Korb von Symbolen beobachtet wird. Die Korrelation ist ein Maß für die lineare Abhängigkeit zwischen zwei Variablen. Die Korrelation wird jedoch oft als Hinweis auf eine Beziehung zwischen zwei Variablen verstanden, was nicht immer der Fall ist.   

Händler auf der ganzen Welt haben sich ihr grundlegendes Verständnis korrelierter Vermögenswerte zunutze gemacht, um ihre Anlageentscheidungen zu treffen, das Risikoniveau zu messen und sogar als Ausstiegssignal zu dienen. Betrachten wir zum Beispiel das Währungspaar USDZAR. Die amerikanische Regierung ist einer der größten Erdölexporteure der Welt, während die südafrikanische Regierung der größte Goldexporteur der Welt ist.

Da diese Rohstoffe einen erheblichen Anteil am Bruttoinlandsprodukt dieser beiden Länder haben, könnte man natürlich erwarten, dass die Preisniveaus dieser Rohstoffe einen Teil der Varianz des Währungspaares USDZAR erklären können. Wenn also Öl auf dem Kassamarkt besser abschneidet als Gold, können wir erwarten, dass der Dollar stärker ist als der Rand und umgekehrt.

Überblick über die Methodik

Um die Beziehung zu beurteilen, haben wir alle unsere Marktdaten von unserem MetaTrader 5-Terminal mit Hilfe eines in MQL5 geschriebenen Skripts exportiert. Wir haben verschiedene Modelle trainiert und dabei 2 Gruppen von möglichen Eingaben für die Modelle verwendet:

1. Gewöhnliche OHLC-Kurse für den USDZAR.
2. Eine Kombination aus Öl- und Goldpreisen.

Aus den gesammelten Daten geht hervor, dass Öl eine stärkere Korrelation mit dem Währungspaar UDZAR aufweist als Gold.

Da unsere Daten auf unterschiedlichen Skalen lagen, haben wir die Daten vor dem Training standardisiert und normalisiert. Wir haben eine 10-fache Kreuzvalidierung ohne zufälliges Mischen durchgeführt, um unsere Genauigkeit mit den verschiedenen Eingabesätzen zu vergleichen.

Unsere Ergebnisse deuten darauf hin, dass die erste Gruppe den geringsten Fehler aufweisen könnte. Das beste Modell war die lineare Regression unter Verwendung gewöhnlicher OHLC-Daten. In der letztgenannten Gruppe 2 war das beste Modell jedoch der KNeigborsRegressor-Algorithmus.

Wir haben die Abstimmung der Hyperparameter erfolgreich mit 500 Iterationen einer randomisierten Suche über 5 Parameter des Modells durchgeführt. Wir testeten auf Überanpassung, indem wir die Fehlerniveaus unseres angepassten Modells mit denen eines Standardmodells auf einem Validierungssatz verglichen, der während der Optimierung ausgeklammert wurde. Nachdem wir beide Modelle auf gleichwertigen Trainingssätzen trainiert hatten, übertrafen wir das Standardmodell auf dem Validierungssatz.

Schließlich haben wir unser angepasstes Modell in das ONNX-Format exportiert und es in unseren Expert Advisor in MQL5 integriert.

Datenextraktion

Ich habe ein praktisches Skript erstellt, das mir die erforderlichen Daten aus dem MetaTrader 5-Terminal extrahiert. Ziehen Sie das Skript einfach auf Ihr gewünschtes Symbol, und es wird die Daten für Sie extrahieren und in den Pfad einfügen: „\MetaTrader 5\MQL5\Files\...“

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//---Amount of data requested
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
//---File name
   string file_name = "Market Data " + Symbol() + ".csv";

//---Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i));
        }
     }

  }
//+------------------------------------------------------------------+

Explorative Datenanalyse in Python

Wir beginnen mit dem Import von Standardbibliotheken.

#Libraries
import pandas as pd
import numpy as np
import seaborn as sns

Lassen Sie uns nun die Daten einlesen, die wir zuvor extrahiert haben.

#Dollar VS Rand
USDZAR = pd.read_csv("/home/volatily/market_data/Market Data USDZAR.csv")
#US Oil
USOIL = pd.read_csv("/home/volatily/market_data/Market Data US Oil.csv")
#SA Gold
SAGOLD = pd.read_csv("/home/volatily/market_data/Market Data XAUUSD.csv")

Einsichtnahme in die Daten.

USOIL

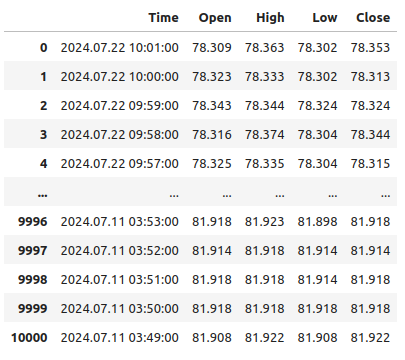
Abb. 1: Unsere Daten laufen in der Zeit rückwärts

Beachten Sie, dass unsere Zeitstempel von der Gegenwart bis weit in die Vergangenheit zurückreichen, was für Aufgaben des maschinellen Lernens unerwünscht ist. Kehren wir die Reihenfolge der Daten um, sodass wir in die Zukunft und nicht in die Vergangenheit prognostizieren.

#Format the data
USDZAR = USDZAR[::-1]
USOIL = USOIL[::-1]
SAGOLD = SAGOLD[::-1]

Bevor wir unsere Datensätze zusammenführen können, müssen wir zunächst sicherstellen, dass sie alle die Datumsspalte als Index verwenden. Auf diese Weise können wir sicherstellen, dass wir nur Tage auswählen, die von allen Datensätzen in der richtigen chronologischen Reihenfolge gemeinsam genutzt werden.

#Set the indexes
USOIL = USOIL.set_index("Time")
SAGOLD = SAGOLD.set_index("Time")
USDZAR = USDZAR.set_index("Time")

Zusammenführung der Datensätze.

#Merge the dataframes
merged_df = pd.merge(USOIL,SAGOLD,how="inner",left_index=True,right_index=True,suffixes=(" US OIL"," SA GOLD"))
merged_df = pd.merge(merged_df,USDZAR,how="inner",left_index=True,right_index=True)

Festlegung des Prognosehorizonts.

#Define the forecast horizon
look_ahead = 10

Das Ziel wird der zukünftige Schlusskurs des USDZAR-Paares sein, wir werden auch ein binäres Ziel zu Visualisierungszwecken einfügen.

#Label the data
merged_df["Target"] = merged_df["Close"].shift(-look_ahead)
merged_df["Binary Target"] = 0
merged_df.loc[merged_df["Close"] < merged_df["Target"],"Binary Target"] = 1

Lassen wir alle leeren Zeilen weg.

#Drop empty rows
merged_df.dropna(inplace=True)

Schauen wir uns die Korrelationsniveaus an.

#Let's observe the correlation levels
merged_df.corr()

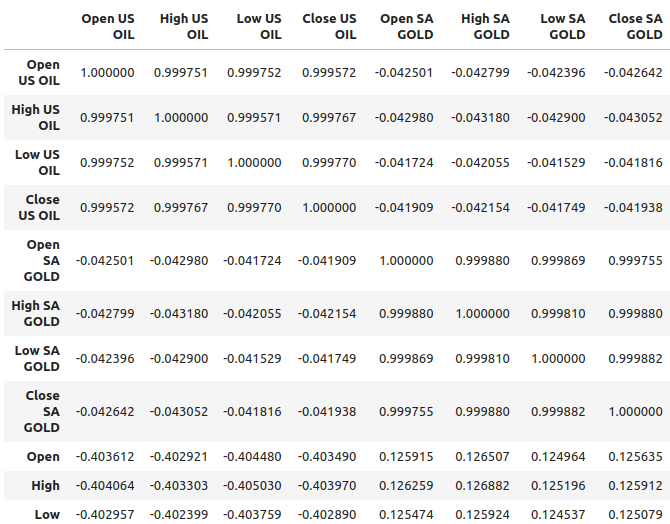
Abb. 2: Korrelationsniveaus in unserem Datensatz

Öl scheint eine relativ stärkere Korrelation mit dem USDZAR-Paar aufzuweisen, etwa -0,4, während Gold eine relativ schwächere Korrelation mit dem Währungspaar aufweist, etwa 0,1. Es ist wichtig, sich daran zu erinnern, dass Korrelation nicht immer bedeutet, dass eine Beziehung zwischen den Variablen besteht, manchmal resultiert die Korrelation aus einer gemeinsamen Ursache, die beide Variablen beeinflusst.

In der Vergangenheit war das Verhältnis zwischen Gold und dem Dollar beispielsweise umgekehrt. Immer wenn der Dollar an Wert verlor, zogen die Händler ihr Geld aus dem Dollar ab und investierten es stattdessen in Gold. Dies führte in der Vergangenheit immer dann zu einem Anstieg des Goldpreises, wenn sich der Dollar schlecht entwickelte. Die gemeinsame Ursache wären in diesem einfachen Beispiel also die Händler, die an beiden Märkten beteiligt waren.

Streudiagramme helfen uns, die Beziehung zwischen zwei Variablen zu visualisieren. Daher haben wir ein Streudiagramm der Ölpreise gegen die Goldpreise erstellt und die Punkte eingefärbt, je nachdem, ob das Preisniveau des USDZAR gestiegen (rot) oder gesunken (grün) ist. Wie man sieht, gibt es keine eindeutige Trennung in den Daten. Tatsächlich deutet keine der von uns erstellten Streudiagramme auf eine starke Beziehung hin.

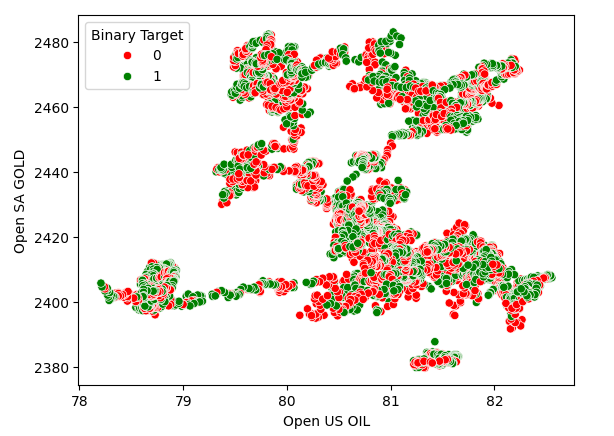
Abb. 3: Ein Streudiagramm des Goldpreises im Vergleich zum Ölpreis

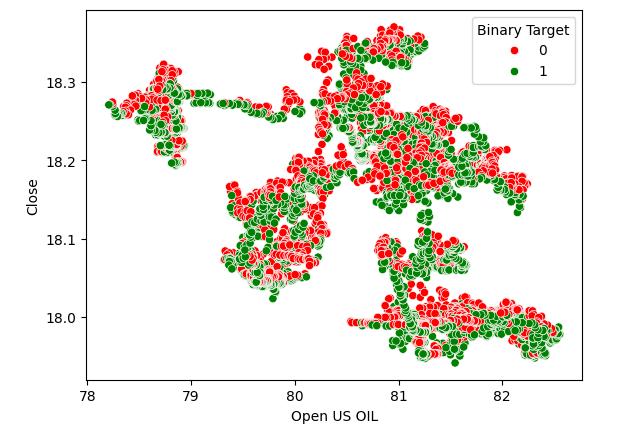
Abb. 4: Streudiagramm der Ölpreise gegen den USDZAR-Schlusskurs

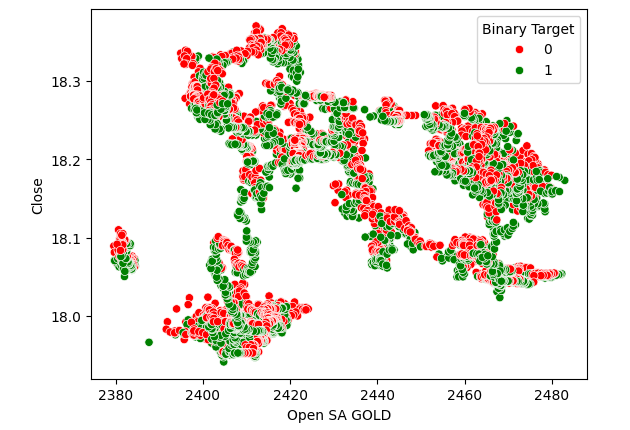
Abb. 5: Streudiagramm des Goldpreises gegenüber dem USDZAR-Schlusskurs

Modellierung der Beziehung

Setzen wir den Index unseres Datensatzes zurück, damit wir eine Kreuzvalidierung durchführen können.

#Reset the index
merged_df.reset_index(inplace=True)

Nun werden wir die Bibliotheken importieren, die wir für die Modellierung der Beziehungen in den Daten benötigen.

#Import the libraries we need
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.ensemble import BaggingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import LinearSVR
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import root_mean_squared_error
from sklearn.preprocessing import RobustScaler

Definition der Prädiktoren und des Ziels.

#Define the predictors
normal_predictors = ["Open","High","Low","Close"]
oil_gold_predictors = ["Open US OIL","High US OIL","Low US OIL","Close US OIL","Open SA GOLD","High SA GOLD","Low SA GOLD","Close SA GOLD"]
target = "Target"

Skalierung der Daten.

#Scale the data
all_predictors = normal_predictors + oil_gold_predictors
scaler = RobustScaler()
scaled_data = pd.DataFrame(scaler.fit_transform(merged_df.loc[:,all_predictors]),columns=all_predictors,index=np.arange(0,merged_df.shape[0]))

Initialisierung der Modelle.

#Now prepare the models
models = [
        LinearRegression(),
        Lasso(),
        GradientBoostingRegressor(),
        RandomForestRegressor(),
        AdaBoostRegressor(),
        BaggingRegressor(),
        KNeighborsRegressor(),
        LinearSVR(),
        MLPRegressor(hidden_layer_sizes=(10,5),early_stopping=True),
        MLPRegressor(hidden_layer_sizes=(50,15),early_stopping=True)
]

columns = [
        "Linear Regression",
        "Lasso",
        "Gradient Boosting Regressor",
        "Random Forest Regressor",
        "AdaBoost Regressor",
        "Bagging Regressor",
        "KNeighbors Regressor",
        "Linear SVR",
        "Small Neural Network",
        "Large Neural Network"
]

Instanziierung des Zeitreihen-Kreuzvalidierungsobjekts.

#Prepare the time-series split object
splits = 10
tscv = TimeSeriesSplit(n_splits=splits,gap=look_ahead)

Erstellen eines Datenrahmens zum Speichern unserer Fehlerstufen.

#Prepare the dataframes to store the error levels
normal_error = pd.DataFrame(columns=columns,index=np.arange(0,splits))
new_error = pd.DataFrame(columns=columns,index=np.arange(0,splits))

Nun führen wir eine Kreuzvalidierung mit einer verschachtelten for-Schleife durch. Die erste Schleife durchläuft die Liste der Modelle, während die zweite Schleife jedes Modell kreuzweise validiert und die Fehlerwerte speichert.

#First we iterate over all the models we have available
for j in np.arange(0,len(models)):
        #Now we have to perform cross validation with each model
        for i,(train,test) in enumerate(tscv.split(scaled_data)):
        #Get the data
        X_train = scaled_data.loc[train[0]:train[-1],oil_gold_predictors]
        X_test = scaled_data.loc[test[0]:test[-1],oil_gold_predictors]
        y_train = merged_df.loc[train[0]:train[-1],target]
        y_test = merged_df.loc[test[0]:test[-1],target]
        #Fit the model
        models[j].fit(X_train,y_train)
        #Measure the error
        new_error.iloc[i,j] = root_mean_squared_error(y_test,models[j].predict(X_test))

Unsere Fehlerniveaus unter Verwendung der gewöhnlichen Modelleingaben.

normal_error

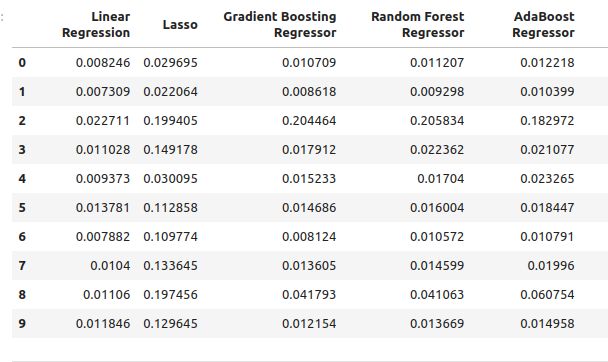
Abb. 6: Unsere Fehlerquoten bei der Vorhersage mit OHLC-Prädiktoren

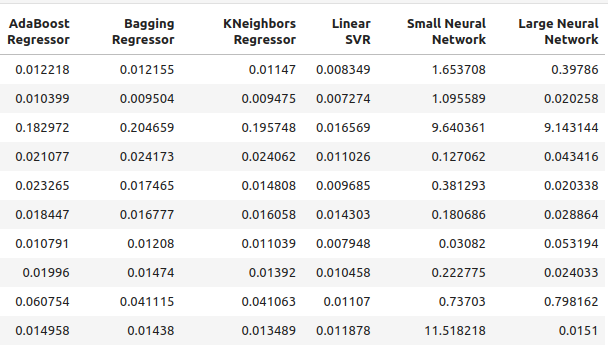
Abb. 7: Unsere Fehlerquoten bei Vorhersagen mit OHLC-Prädiktoren II

Werfen wir nun einen Blick auf unsere Fehlerquoten, indem wir nur die Öl- und Goldpreise verwenden.

new_error

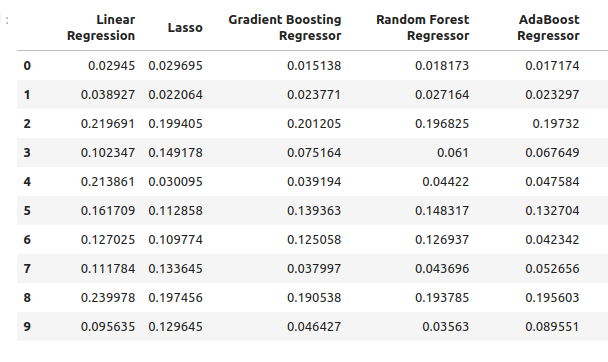
Abb. 8: Unsere Prognosegenauigkeit bei der Verwendung von Öl- und Goldpreisen

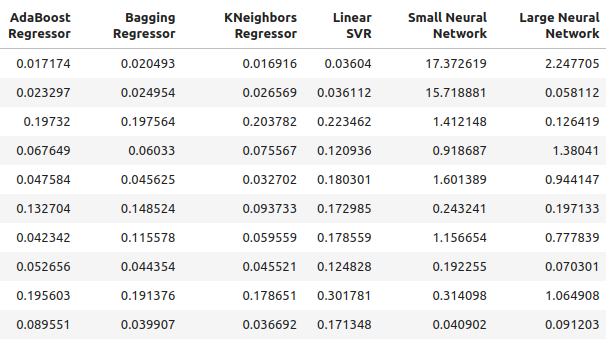
Abb. 9: Unsere Prognosegenauigkeit bei der Verwendung von Öl- und Goldpreisen II

Schauen wir uns die durchschnittliche Leistung jedes Modells mit gewöhnlichen Prädiktoren an.

#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
        print(f"{models[i]} normal error {((normal_error.iloc[:,i].mean()))}")

LinearRegression() normal error 0.01136361865358375
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.03472997520534606
RandomForestRegressor() normal error 0.03616484012058101
AdaBoostRegressor() normal error 0.037484107657877755
BaggingRegressor() normal error 0.03670486223028821
KNeighborsRegressor() normal error 0.035113189373409175
LinearSVR() normal error 0.01085610361276552
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 2.558754334716706
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 1.0544369296125597

Nun werden wir unsere durchschnittliche Leistung unter Verwendung der neuen Prädiktoren bewerten.

#Let's see our average performance on the new dataset
for i in (np.arange(0,normal_error.shape[0])):
        print(f"{models[i]} normal error {((new_error.iloc[:,i].mean()))}")

LinearRegression() normal error 0.13404065973045615
Lasso() normal error 0.11138143304314707
GradientBoostingRegressor() normal error 0.0893855335909897
RandomForestRegressor() normal error 0.08957454602573789
AdaBoostRegressor() normal error 0.08658796789785872
BaggingRegressor() normal error 0.08887059320664067
KNeighborsRegressor() normal error 0.07696901077705855
LinearSVR() normal error 0.15463529064256165
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) normal error 3.8970873719426784
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) normal error 0.6958177634524169

Schauen wir uns nun die Veränderungen der Genauigkeit an.

#Let's see our average performance on the normal dataset
for i in (np.arange(0,normal_error.shape[0])):
    print(f"{models[i]} changed by {((normal_error.iloc[:,i].mean()-new_error.iloc[:,i].mean()))/normal_error.iloc[:,i].mean()}%")

LinearRegression() changed by -10.795596439535894%
Lasso() changed by 0.0%
GradientBoostingRegressor() changed by -1.573728690057642%
RandomForestRegressor() changed by -1.4768406476311784%
AdaBoostRegressor() changed by -1.3099914419240863%
BaggingRegressor() changed by -1.421221271695885%
KNeighborsRegressor() changed by -1.1920256220116057%
LinearSVR() changed by -13.244087580439862%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(10, 5)) changed by -0.5230408480672479%
MLPRegressor(early_stopping=True, hidden_layer_sizes=(50, 15)) changed by 0.34010489967561475%

Auswahl der Eigenschaften

Unser leistungsfähigstes Modell unter den Öl- und Goldprädiktoren ist der KNeighbors-Regressor, und wir wollen sehen, welche Eigenschaften für ihn am wichtigsten sind.

#Our best performing model was the KNeighbors Regressor
#Let us perform feature selection to test how stable the relationship is
from mlxtend.feature_selection import SequentialFeatureSelector as SFS

Erstellen wir eine neue Instanz des Modells.

#Let us select our best model
model = KNeighborsRegressor()

Wir werden die Vorwärtsselektion verwenden, um die wichtigsten Eigenschaften für unser Modell zu ermitteln. Wir werden unserem Modell nun Zugang zu allen Prädiktoren auf einmal geben.

#Create the sequential selector object
sfs1 = SFS(
        model,
        k_features=(1,len(all_predictors)),
        forward=True,
        scoring="neg_mean_squared_error",
        cv=10,
        n_jobs=-1
)

Anpassen der sequentiellen Eigenschaftsauswahl.

#Fit the sequential selector
sfs1 = sfs1.fit(scaled_data.loc[:,all_predictors],merged_df.loc[:,"Target"])

Betrachtet man die besten vom Algorithmus ausgewählten Eigenschaften, könnte man zu dem Schluss kommen, dass weder der Öl- noch der Goldpreis für die Vorhersage des USDZAR von großem Nutzen sind, da unser Algorithmus nur drei Eigenschaften ausgewählt hat, nämlich die Preise von Eröffnungs-, Tiefst- und Schlusskurses des USDZAR.

#Now let us see which predictors were selected
sfs1.k_feature_names_

('Open', 'Low', 'Close')

Anpassen der Hyperparameter

Versuchen wir, die Abstimmung der Hyperparameter mit dem Modul RandomizedSearchCV von scikit-learn durchzuführen. Der Algorithmus hilft uns, eine Antwortfläche zu beproben, die möglicherweise zu groß ist, um sie vollständig zu beproben. Wenn wir Modelle mit zahlreichen Parametern verwenden, wächst die Gesamtzahl der Kombinationen von Eingaben sehr schnell. Daher bevorzugen wir den randomisierten Suchalgorithmus, wenn wir es mit vielen Parametern zu tun haben, die viele mögliche Werte haben.

Der Algorithmus bietet einen Kompromiss zwischen der Genauigkeit der Ergebnisse und dem Zeitaufwand für die Berechnungen. Dieser Kompromiss wird durch Anpassung der Anzahl der zulässigen Iterationen gesteuert. Beachten Sie, dass es aufgrund des zufälligen Charakters des Algorithmus schwierig sein kann, die in diesem Artikel gezeigten Ergebnisse exakt zu reproduzieren.

Import the scikit-learn module.
#Now we will load the libraries we need
from sklearn.model_selection import RandomizedSearchCV

Bereiten Sie spezielle Trainings- und Testsets vor.

#Let us see if we can tune the model
#First we will create train test splits
train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:]
train_y = merged_df.loc[:(merged_df.shape[0]//2),"Target"]

test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:]
test_y = merged_df.loc[(merged_df.shape[0]//2):,"Target"]

Um die Parameterabstimmung durchzuführen, müssen wir einen Schätzer übergeben, der die scikit-learn-Schnittstelle implementiert, gefolgt von einem Lexikon, das die Schlüssel enthält, die den Parametern des Schätzers entsprechen, und die Werte, die dem Bereich der zulässigen Eingaben für jeden Parameter entsprechen. Danach geben wir an, dass wir eine 5-fache Kreuzvalidierung durchführen möchten, und dann müssen wir die Bewertungsmetrik als negativen mittleren quadratischen Fehler angeben.

#Create the tuning object
rs = RandomizedSearchCV(KNeighborsRegressor(n_jobs=-1),{
        "n_neighbors": [1,2,3,4,5,8,10,16,20,30,60,100],
        "weights":["uniform","distance"],
        "leaf_size":[1,2,3,4,5,10,15,20,40,60,90],
        "algorithm":["ball_tree","kd_tree"],
        "p":[1,2,3,4,5,6,7,8]
},cv=5,n_iter=500,return_train_score=False,scoring="neg_mean_squared_error")

Durchführen der Parameterabstimmung an der Trainingsmenge.

#Let's perform the hyperparameter tuning
rs.fit(train_X,train_y)

Betrachtet man die Ergebnisse, die wir erhalten haben, von den besten bis zu den schlechtesten.

#Let's store the results from our hyperparameter tuning
tuning_results = pd.DataFrame(rs.cv_results_)
tuning_results.loc[:,["param_n_neighbors","param_weights","param_leaf_size","param_algorithm","param_p","mean_test_score"]].sort_values(by="mean_test_score",ascending=False)

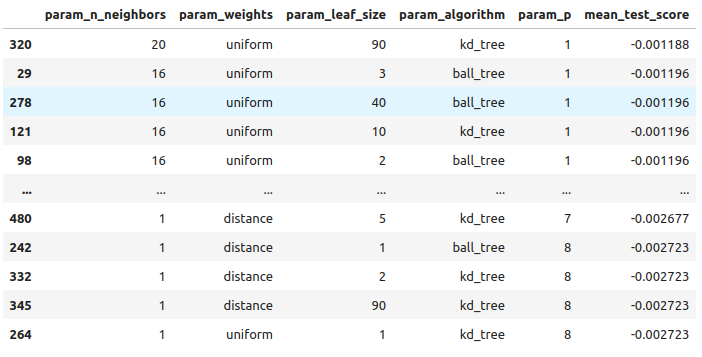
Abb. 10: Die Ergebnisse der Abstimmung unseres besten Modells

Dies sind die besten Parameter, die wir gefunden haben.

#The best parameters we came across
rs.best_params_

{'weights': 'distance',
 'p': 1,
 'n_neighbors': 4,
 'leaf_size': 15,
 'algorithm': 'ball_tree'}

Prüfen auf Überanpassung

Vergleichen wir nun unsere angepasstes mit dem Standardmodell. Beide Modelle werden auf identischen Trainingssätzen trainiert. Wenn das Standardmodell unser nutzerdefiniertes Modell in der Validierungsmenge übertrifft, kann dies ein Zeichen dafür sein, dass wir die Trainingsdaten zu stark angepasst haben. Wenn unser angepasstes Modell jedoch besser abschneidet, kann dies darauf hindeuten, dass wir die Modellparameter erfolgreich angepasst haben, ohne dass es zu einer Überanpassung kam.

#Create instances of the default model and the custmoized model
default_model = KNeighborsRegressor()
customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"])

Messen wir zuerst die Genauigkeit des Standardmodells:

#Measure the accuracy of the default model
default_model.fit(train_X,train_y)
root_mean_squared_error(test_y,default_model.predict(test_X))

0.06633226373900612

Und nun die Genauigkeit des angepassten Modells.

#Measure the accuracy of the customized model
customized_model.fit(train_X,train_y)
root_mean_squared_error(test_y,customized_model.predict(test_X))

0.04334616246844129

Es scheint, dass wir das Modell gut abgestimmt haben, ohne es zu überarbeiten! Lassen Sie uns nun unser angepasstes Modell in das ONNX-Format exportieren.

Exportieren ins ONNX-Format

Open Neural Network Exchange (ONNX) ist ein interoperabler Rahmen für die Erstellung und den Einsatz von Modellen für maschinelles Lernen in einer sprachunabhängigen Weise. Durch die Verwendung von ONNX können unsere Modelle für maschinelles Lernen problemlos in jeder Programmiersprache verwendet werden, sofern diese Sprache die ONNX-API unterstützt. Zum Zeitpunkt der Erstellung dieses Berichts wird die ONNX-API von einem Konsortium der größten Unternehmen der Welt entwickelt und gepflegt.

Import the libraries we need
#Let's prepare to export the customized model to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Wir müssen sicherstellen, dass unsere Daten so skaliert und normalisiert sind, dass wir sie im MetaTrader 5-Terminal wiedergeben können. Deshalb werden wir eine Standardtransformation durchführen, die wir später immer in unserem Terminal durchführen können. Wir subtrahieren den Mittelwert jeder Spalte und zentrieren so unsere Daten. Anschließend wird jeder Wert durch die Standardabweichung der jeweiligen Spalte geteilt, damit unser Modell die Veränderungen zwischen den Variablen auf den verschiedenen Skalen besser erfassen kann.

#Train the model on all the data we have
#But before doing that we need to first scale the data in a way we can repeat in MQL5
scale_factors = pd.DataFrame(columns=all_predictors,index=["mean","standard deviation"])
for i in np.arange(0,len(all_predictors)):
        scale_factors.iloc[0,i] = merged_df.loc[:,all_predictors[i]].mean()
        scale_factors.iloc[1,i] = merged_df.loc[:,all_predictors[i]].std()
scale_factors

Abb. 12: Einige der Werte, die wir zur Skalierung und Standardisierung unserer Daten verwenden werden, werden nicht in allen Spalten angezeigt

Nun wollen wir die Normalisierung und Standardisierung durchführen.

for i in all_predictors:
        merged_df.loc[:,i] = (merged_df.loc[:,i] - merged_df.loc[:,i].mean()) / merged_df.loc[:,i].std()

Schauen wir uns nun unsere Daten an.

merged_df

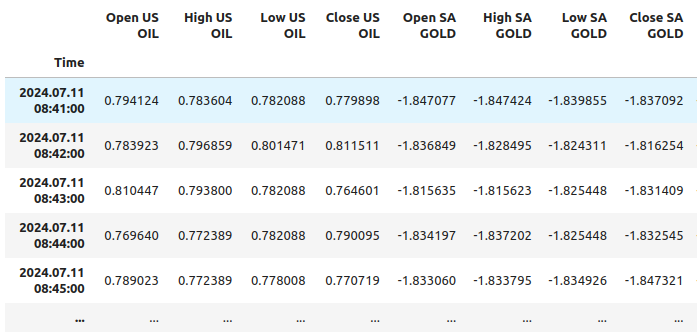
Abb. 11: So sehen unsere Daten nach der Skalierung aus, wobei nicht alle Spalten angezeigt werden

Initialisieren unseres angepassten Modells.

customized_model = KNeighborsRegressor(p=rs.best_params_["p"],weights=rs.best_params_["weights"],n_neighbors=rs.best_params_["n_neighbors"],leaf_size=rs.best_params_["leaf_size"],algorithm=rs.best_params_["algorithm"])
customized_model.fit(merged_df.loc[:,all_predictors],merged_df.loc[:,"Target"])

Definieren der Eingabeform unseres Modells.

#Define the input shape and type
initial_type = [("float_tensor_type",FloatTensorType([1,train_X.shape[1]]))]

Erstellen der ONNX-Darstellung.

#Create an ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_type)

Speichern des ONNX-Modell.

#Store the ONNX model
onnx_model_name = "USDZAR_FLOAT_M1.onnx"
onnx.save_model(onnx_model,onnx_model_name)

Visualisierung des ONNX-Modells

Netron ist ein Open-Source-Visualisierungsprogramm für maschinelle Lernmodelle. Netron unterstützt neben ONNX auch viele andere Frameworks wie Keras. Wir werden netron verwenden, um sicherzustellen, dass unser ONNX-Modell die von uns erwartete Eingabe- und Ausgabeform hat.

Importieren des netron-Moduls.

#Let's visualize the model in netron
import netron

Jetzt können wir das Modell mit netron visualisieren.

#Run netron
netron.start(onnx_model_name)

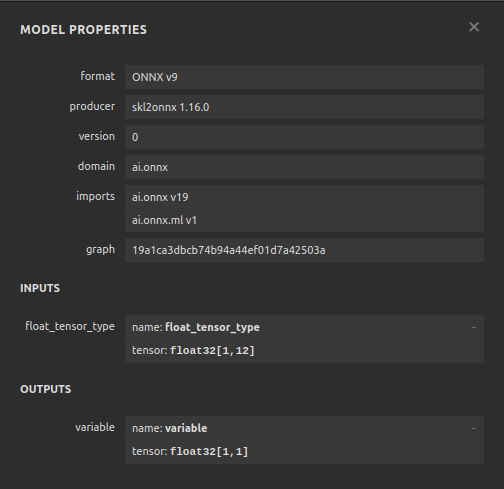
Abb. 12: Die Spezifikationen unseres ONNX-Modells

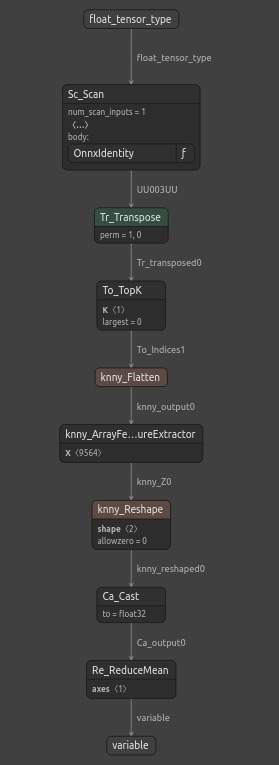
Abb. 13: Die Struktur unseres ONNX-Modells

Unser ONNX-Modell erfüllt unsere Erwartungen, die Input- und Output-Form sind genau dort, wo wir sie erwarten. Wir können nun mit der Erstellung eines Expert Advisors auf der Grundlage unseres ONNX-Modells fortfahren.

Implementation in MQL5

Wir können nun mit dem Aufbau unseres Expert Advisors beginnen. Zunächst integrieren wir unser ONNX-Modell in unsere Anwendung. Wenn wir die ONNX-Datei als Ressource angeben, wird die ONNX-Datei in das kompilierte Programm mit der Erweiterung .ex5 aufgenommen.

//+------------------------------------------------------------------+
//|                                                       USDZAR.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+-----------------------------------------------------------------+
//| Require the ONNX file                                           |
//+-----------------------------------------------------------------+
#resource "\\Files\\USDZAR_FLOAT_M1.onnx" as const uchar onnx_model_buffer[];

Nun werden wir die Handelsbibliothek importieren.

//+-----------------------------------------------------------------+
//| Libraries we need                                               |
//+-----------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Definieren wir die Eingaben, die der Endnutzer kontrollieren kann.

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
double input sl_width = 0.4;              //How tight should our stop loss be?
int input lot_multiple = 10;              //How many times bigger than minimum lot should we enter?
double input max_risk = 10;               //After how much profit/loss should we close?

Jetzt brauchen wir ein paar globale Variablen.

//+------------------------------------------------------------------+
//| Global Variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;                          //Our onnx model
double mean_values[12],std_values[12];    //The scaling factors we used for our data
vector model_inputs = vector::Zeros(12);  //Our model's inputs
vector model_forecast = vector::Zeros(1); //Our model's output
double bid,ask;                           //Market prices
double minimum_volume;                    //Smallest lot size
double state = 0;                         //0 means we have no positions, 1 means we have buy position, 2 means we have sell position.

Definieren wir nun Hilfsfunktionen für Aufgaben, die wir möglicherweise wiederholt ausführen müssen. Wenn der Gesamtgewinn/-verlust unsere festgelegten Risikostufen überschreitet, wird die Position automatisch geschlossen.

//+------------------------------------------------------------------+
//| Check if we have reached our risk level                          |
//+------------------------------------------------------------------+
void check_risk_level(void)
  {
//--- Check if we have surpassed our maximum risk level
   if(MathAbs(PositionGetDouble(POSITION_PROFIT)) > max_risk)
     {
      //--- We should close our positions
      Trade.PositionClose("USDZAR");
     }
  }

Da wir über ein integriertes KI-System verfügen, sollten wir es nutzen, um Umkehrungen zu erkennen. Wenn unser System vorhersagt, dass sich der Preis gegen uns entwickeln wird, schließen wir die Position und informieren den Endnutzer, dass eine potenzielle Umkehr erkannt wurde.

//+------------------------------------------------------------------+
//| Check if there is a reversal may be coming                       |
//+------------------------------------------------------------------+
void check_reversal(void)
  {
   if(((state == 1) && (model_forecast[0] < iClose("USDZAR",PERIOD_M1,0))) ||((state == 2) && (model_forecast[0] > iClose("USDZAR",PERIOD_M1,0))))
     {
      //--- There may be a reversal coming
      Trade.PositionClose("USDZAR");
      //--- Give the user feedback
      Alert("Potential reversal detected");
     }
  }

Wir brauchen jetzt eine Funktion, die uns Einstiegsmöglichkeiten findet. Wir betrachten einen Einstieg nur dann als gültig, wenn die Vorhersage unseres Modells mit den Veränderungen der Preisniveaus auf höheren Zeitrahmen übereinstimmt. 

//+------------------------------------------------------------------+
//| Find an entry opportunity                                        |
//+------------------------------------------------------------------+
void find_entry(void)
  {
//---Check for the change in price on higher timeframes
   if(iClose("USDZAR",PERIOD_D1,0) > iClose("USDZAR",PERIOD_D1,21))
     {
      //--- We're looking for buy oppurtunities
      if(model_forecast[0] > iClose("USDZAR",PERIOD_M1,0))
        {
         //--- Open the position
         Trade.Buy(minimum_volume,"USDZAR",ask,(ask - sl_width),(ask + sl_width),"USDZAR AI");
         //--- Update the system state
         state = 1;
        }
     }
//---Check for the change in price on higher timeframes
   else
      if(iClose("USDZAR",PERIOD_D1,0) < iClose("USDZAR",PERIOD_D1,21))
        {
         //--- We're looking for sell oppurtunities
         if(model_forecast[0] < iClose("USDZAR",PERIOD_M1,0))
           {
            //--- Open sell position
            Trade.Sell(minimum_volume,"USDZAR",bid,(bid + sl_width),(bid - sl_width),"USDZAR AI");
            //--- Update the system state
            state = 2;
           }
        }
  }

Jetzt brauchen wir eine Funktion, die eine Vorhersage aus unserem Modell abruft. Dazu müssen wir zunächst die aktuellen Marktpreise ermitteln und sie dann durch Subtraktion des Mittelwerts und Division durch die Standardabweichung umrechnen.

//+------------------------------------------------------------------+
//| Obtain a forecast from our model                                 |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//Let's fetch our model's inputs
//--- USDZAR
   model_inputs[0] = ((iOpen("USDZAR",PERIOD_M1,0) - mean_values[0]) / std_values[0]);
   model_inputs[1] = ((iHigh("USDZAR",PERIOD_M1,0) - mean_values[1]) / std_values[1]);
   model_inputs[2] = ((iLow("USDZAR",PERIOD_M1,0) - mean_values[2]) / std_values[2]);
   model_inputs[3] = ((iClose("USDZAR",PERIOD_M1,0) - mean_values[3]) / std_values[3]);
//--- XTI OIL US
   model_inputs[4] = ((iOpen("XTIUSD",PERIOD_M1,0) - mean_values[4]) / std_values[4]);
   model_inputs[5] = ((iHigh("XTIUSD",PERIOD_M1,0) - mean_values[5]) / std_values[5]);
   model_inputs[6] = ((iLow("XTIUSD",PERIOD_M1,0) - mean_values[6]) / std_values[6]);
   model_inputs[7] = ((iClose("XTIUSD",PERIOD_M1,0) - mean_values[7]) / std_values[7]);
//--- GOLD SA
   model_inputs[8] = ((iOpen("XAUUSD",PERIOD_M1,0) - mean_values[8]) / std_values[8]);
   model_inputs[9] = ((iHigh("XAUUSD",PERIOD_M1,0) - mean_values[9]) / std_values[9]);
   model_inputs[10] = ((iLow("XAUUSD",PERIOD_M1,0) - mean_values[10]) / std_values[10]);
   model_inputs[11] = ((iClose("XAUUSD",PERIOD_M1,0) - mean_values[11]) / std_values[11]);
//--- Get a prediction
   OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast);
  }

Da wir mehrere Symbole analysieren, müssen wir sie zur Marktbeobachtung hinzufügen.

//+------------------------------------------------------------------+
//| Load the symbols we need and add them to the market watch        |
//+------------------------------------------------------------------+
void load_symbols(void)
  {
   SymbolSelect("XAUUSD",true);
   SymbolSelect("XTIUSD",true);
   SymbolSelect("USDZAR",true);
  }

Wir brauchen eine Funktion, die für das Laden unserer Skalierungsfaktoren, des Mittelwerts und der Standardabweichung jeder Spalte zuständig ist.

//+------------------------------------------------------------------+
//| Load the scale values                                            |
//+------------------------------------------------------------------+
void load_scale_values(void)
  {
//--- Mean
//--- USDZAR
   mean_values[0] = 18.14360511919699;
   mean_values[1] = 18.145737421580925;
   mean_values[2] = 18.141568574864074;
   mean_values[3] = 18.14362306984525;
//--- XTI US OIL
   mean_values[4] = 80.76956702216644;
   mean_values[5] = 80.7864452112087;
   mean_values[6] = 80.75236177331661;
   mean_values[7] = 80.76923546633206;
//--- GOLD SA
   mean_values[8] = 2430.5180384776245;
   mean_values[9] = 2430.878959640318;
   mean_values[10] = 2430.1509598494354;
   mean_values[11] = 2430.5204140526976;
//--- Standard Deviation
//--- USDZAR
   std_values[0] = 0.11301636249300206;
   std_values[1] = 0.11318116432297631;
   std_values[2] = 0.11288670156099372;
   std_values[3] = 0.11301994613848391;
//--- XTI US OIL
   std_values[4] = 0.9802409859148413;
   std_values[5] = 0.9807944310705999;
   std_values[6] = 0.9802449355481064;
   std_values[7] = 0.9805961626626833;
//--- GOLD SA
   std_values[8] = 26.397404261230328;
   std_values[9] = 26.414599597905003;
   std_values[10] = 26.377605644853944;
   std_values[11] = 26.395208330942864;
  }

Schließlich brauchen wir eine Funktion, die für das Laden unserer ONNX-Datei verantwortlich ist.

//+------------------------------------------------------------------+
//| Load the onnx file from buffer                                   |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT);

//--- The input size for our onnx model
   ulong input_shape [] = {1,12};

//--- Check if we have the right input size
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Comment("Incorrect input shape, the model has input shape ",OnnxGetInputCount(onnx_model));
      return(false);
     }

//--- The output size for our onnx model
   ulong output_shape [] = {1,1};

//--- Check if we have the right output size
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Comment("Incorrect output shape, the model has output shape ",OnnxGetOutputCount(onnx_model));
      return(false);
     }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

Nachdem wir nun diese Hilfsfunktionen definiert haben, können wir sie in unserem Expert Advisor verwenden. Lassen Sie uns zunächst das Verhalten unserer Anwendung definieren, wenn sie zum ersten Mal geladen wird. Wir beginnen mit dem Laden unseres ONNX-Modells, bereiten die Skalierungswerte vor und holen dann die Marktdaten ab.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the onnx file
   if(!load_onnx_file())
     {
      return(INIT_FAILED);
     }

//--- Load our scaling values
   load_scale_values();

//--- Add the symbols we need to the market watch
   load_symbols();

//--- The smallest lotsize we can use
   minimum_volume = SymbolInfoDouble("USDZAR",SYMBOL_VOLUME_MIN) * lot_multiple;

//--- Everything went fine
   return(INIT_SUCCEEDED);
  }

Wenn unser Programm deaktiviert wurde, müssen wir die nicht mehr benötigten Ressourcen freigeben.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we used for our onnx model
   OnnxRelease(onnx_model);

//--- Remove the expert advisor
   ExpertRemove();
  }

Schließlich müssen wir bei jeder Preisänderung eine neue Prognose von unserem Modell abrufen, aktualisierte Marktpreise erhalten und dann entweder eine neue Position eröffnen oder die derzeit offenen Positionen verwalten.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- We always need a forecast from our model
   model_predict();
//--- Fetch market prices
   bid = SymbolInfoDouble("USDZAR",SYMBOL_BID);
   ask = SymbolInfoDouble("USDZAR",SYMBOL_ASK);

//--- If we have no open positions, find an entry
   if(PositionsTotal() == 0)
     {
      //--- Find an entry
      find_entry();
      //--- Reset the system state
      state = 0;
     }

//--- If we have open postitions, manage them
   else
     {
      //--- Check for a reveral warning from our AI
      check_reversal();
      //--- Check if we have not reached our max risk levels
      check_risk_level();
     }

  }

Wenn wir all dies zusammennehmen, können wir unser Programm in Aktion sehen. 

Abb. 17: Unser Expert Advisor

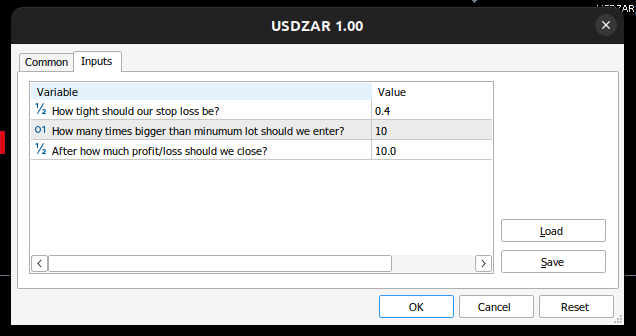
Abb. 14: Die Eingaben für unseren Expert Advisor

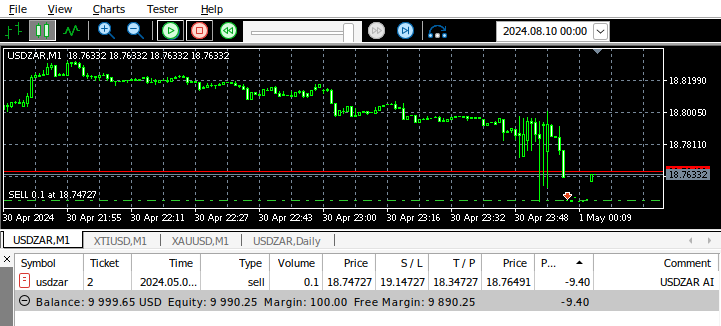
Abb. 15: Unser Programm in Aktion

Schlussfolgerung

In diesem Artikel haben wir gezeigt, wie Sie einen Expert Advisor mit mehreren Symbolen und KI erstellen können. Obwohl wir mit gewöhnlichem OHLC niedrigere Fehlerniveaus erreicht haben, bedeutet dies nicht unbedingt, dass dies auch für alle Symbole in Ihrem MetaTrader 5-Terminal gilt. Es kann einen Korb verschiedener Symbole geben, die niedrigere Fehler als die USDZAR OHLC-Kurse aufweisen.