Возможности Мастера MQL5, которые вам нужно знать (Часть 32): Регуляризация

Введение

Регуляризация - еще один аспект алгоритмов машинного обучения, который влияет на производительность нейронных сетей. В процессе работы сети часто наблюдается тенденция придавать избыточный вес одним параметрам за счет других. Такое "смещение" в сторону определенных параметров (весов сети) может привести к снижению производительности сети, если тестирование проводится на данных, отличных от выборки. Вот почему была разработана регуляризация.

По сути, оно действует как механизм, который замедляет процесс сходимости, увеличивая (или штрафуя) результат функции потерь пропорционально величине весов, используемых на каждом стыке слоев. Это часто достигается с помощью ранней остановки (Early-Stopping), Лассо-, Ридж-регрессии, эластичной сети (Elastic-Net) или исключения (Drop-Out). Каждый из этих форматов немного отличается, и мы не будем рассматривать все типы, а вместо этого остановимся на лассо, ридже и исключении.

Мы рассматриваем преимущества и использование регуляризации в контексте наличия надлежащего или синхронизированного сопряжения с функциями активации и потерь. Правильный выбор и сочетание этих факторов как минимум предотвращают проблемы взрывного роста/исчезновения градиентов, поэтому автор в последних статьях (этой серии) выступает за использование сигмоиды и softmax-активации вместе с функциями потерь двоичной перекрестной энтропии (Binary-Cross Entropy) или категориальной перекрестной энтропии (Categorical Cross Entropy) при работе с сетями классификаторов. Напротив, TANH Softsign-активации в сочетании с функциями потерь MSE, MAE или Huber может быть подходящим при работе с регрессорными нейронными сетями.

В предыдущей статье мы также подчеркивали важность объединения этих функций активации с соответствующими алгоритмами пакетной нормализации с ограничением по диапазону, однако функция потерь остается несвязанной. Это означает, что дополнительный член функции потерь (регуляризация) не обязательно должен быть связан с функцией активации или функцией пакетной нормализации, которая ограничена идеальным диапазоном (от -1 до +1 для регрессоров и от 0 до 1 для классификаторов).

Тем не менее, при выборе типа регуляризации необходимо учитывать, является ли сеть регрессором или классификатором, и вот почему. Если бы мы использовали, например, L1 Lasso, штрафуя только абсолютные значения весов, процесс обучения имел бы тенденцию уменьшать многие веса в слоях сети до нуля, оставляя только наиболее важные с приемлемыми небольшими ненулевыми значениями. Это по сути создает разреженность выходных данных, что хорошо подходит для сетей классификаторов, вероятности признаков которых прогнозируются. Это особенно актуально в ситуациях, когда среди вероятностей прогнозируемых признаков ожидается, что важными окажутся лишь несколько признаков.

Напротив, в сетях регрессоров, где часто конечный выходной слой имеет размер 1 (в отличие, например, от вероятностей классификационных сетей), вклад различных весов часто ожидается "более демократичным". Для достижения этой цели лучше подходит регуляризатор L2 или Ridge, поскольку он взвешивается по квадрату весов, что приводит к более равномерному распределению весов по слоям в конечном результате. Регуляризация методом исключения может быть альтернативой регуляризации сетей классификаторов, поскольку она также вносит некоторую разреженность в выходные результаты из-за случайного обнуления некоторых весов. Необходимый код приложен ниже, однако наше тестирование сосредоточено на L1 и L2.

Регуляризация в нейронных сетях

Два формата регуляризации, которые мы тестируем ниже, накладывают штраф на функцию потерь пропорционально величине веса сети. Эта "величина" вычисляется с помощью функции Norm, которая в нашем случае предлагается в довольно большом количестве разновидностей. Строго говоря, эта норма должна быть суммой величин всех значений матрицы. Эту абсолютную сумму значений можно легко реализовать на языке MQL5 следующим образом:

//+------------------------------------------------------------------+
//| Typical Norm function                                            |
//+------------------------------------------------------------------+
double Norm(matrix &M)
{  double _norm = 0.0;
   for(int i = 0; i < int(M.Rows()); i++)
   {  for(int ii = 0; ii < int(M.Cols()); ii++)
      {  _norm += M[i][ii];
      }
   }
   return(_norm);
}

Однако мы окунаемся в нормы матрицы (благодаря различным функциям, доступным в матричном типе данных). Матричные нормы, в отличие от простых абсолютных, не столь странны, как может показаться на первый взгляд, поскольку утверждается, что они вносят структурную осведомленность в процесс взвешивания регуляризации. Кроме того, они позволяют контролировать определенные желаемые свойства сети, такие как гладкость в сетях регрессоров, при этом обеспечивая гибкость для тонкой настройки желаемой разреженности в выходных данных сетей классификаторов. Таким образом, рассмотрение этих дополнительных свойств, которые часто кажутся нюансами, при оценке матриц весов для регуляризации — это то, что мы применим в наших результатах теста ниже. Для ясности: мы рассматриваем до девяти различных матричных норм для каждого из двух подходов регуляризации, которые мы будем тестировать для сети регрессора и классификатора.

В последней статье, где мы рассматривали функцию потерь, у нас было два типа сетей: регрессор и классификатор. Мы также будем придерживаться этих форматов при иллюстрации регуляризации в этой статье.

Регуляризация L1 (Lasso)

Регуляризация Лассо (или L1) подразумевает штрафование функции потерь пропорционально абсолютному значению весов или нормам матрицы весов, как обсуждалось выше. Формально это определяется уравнением ниже:

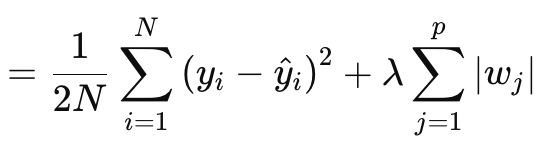
где:

• N — количество точек данных.
• p — общее количество слоев, для которых существуют матрицы весов.
• yi — целевое (или меточное) значение для i-й точки данных.
• y^i — прогнозируемое значение для i-й точки данных.
• wj — коэффициенты (веса) модели.

§λ — параметр регуляризации, который контролирует силу регуляризации. Большее значение λ увеличивает штраф за большие веса, способствуя разреженности. Возможный оптимальный диапазон - от 10^-4 до 10^-1для сетей активации soft-max или сигмоиды, или от 10^-5 до 10^-2 для сетей Soft-sign или TANH.

Другими словами, значение регуляризации состоит из MSE — разницы между прогнозируемыми значениями и фактическими значениями (левая часть), а также суммы норм весов по всем слоям. Реализуем это в MQL5 следующим образом:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();
   if(THIS.regularization == REGULARIZE_L1)
   {  _term = _mse + (Lambda * _weights_norm);
   }
   
        ....

   _regularized.Fill(_term);
   return(_regularized);
}

Выход представляет собой скалярное значение, а не вектор, и это сильно контрастирует с тем, с чем мы имели дело, работая с данными функции потерь. Потому что, когда нам нужно определить наши дельты обновления, которые затем помогают нам установить градиенты обновления при выполнении обратного распространения, потери количественно определяются как вектор. Этот вектор помогает взаимодействовать с дельта-векторами, которые, в свою очередь, обновляют матрицы градиентов. Мы создаем вектор, заполненный реплицированными значениями регуляризации, и используем его в качестве выходных данных. Затем это стандартное векторное значение добавляется ко всем значениям потерь в векторе потерь, как определено используемой функцией потерь. Реализация представлена ниже:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }

   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss);
   _last_loss += RegularizeTerm(label, THIS.regularization_lambda);

   deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative);
   
        ...

}

Таким образом, ко всем признакам/классам выходного вектора применяется единообразный штраф, и, возможно, именно поэтому можно было бы обосновать необходимость использования матричных норм, а не только их абсолютного значения, поскольку нормы учитывают структуру матрицы в своих вычислениях.

При вычислении члена регуляризации доступно несколько вариантов матричных норм, и хотя все они применимы для определения Лассо, не все из них подходят. Норма Фробениуса лучше согласуется с L2, поскольку она напрямую штрафует большие веса, не обеспечивая разреженности, что противоречит норме Лассо, которая стремится свести некритические веса к нулю. Ядерная норма лучше подходит для продвижения матриц низкого ранга, которые имеют отношение к задачам завершения матрицы (matrix completion problems). Это не соответствует принципу Лассо, который продвигает разреженность по элементам, а не по рангам. Спектральная норма также используется для контроля максимального воздействия матрицы на вектор, а не для обеспечения разреженности.

Хотя нормы бесконечности могут создавать форму разреженности, они менее идеальны для создания поэлементной разреженности. Норма минус бесконечности фокусируется на минимизации наименьших сумм строк, и это не согласуется с целью разреженности Лассо. То же самое можно сказать и о минус P1 и минус P2, поскольку они оба стремятся минимизировать влияние малых элементов.

Итак, из этого перечисления девяти норм оказывается, что только норма P1 лучше всего работает с Lasso, поскольку она способствует разреженности с целью поэлементной разреженности. P2 — конечная норма из девяти — лучше подходит для регуляризации L2, или Ridge. Итак, подведем итог: регуляризация L1 была упомянута выше как идеальная для сетей классификаторов. Это подразумевает связь Классификатор-L1-P1, которая имеет мало альтернатив для функции норм матрицы веса.

Регуляризация L2 (Ridge)

Регуляризация L2, или Ридж, очень похожа на формулу L1, при этом очевидным отличием является возведение в квадрат норм весов, а не использование необработанного значения. Формула выглядит так:

где:

• λ — параметр регуляризации, который контролирует силу штрафа.
• w i — веса или коэффициенты модели.
• n — количество слоев с предыдущей матрицей весов.
• N — количество точек данных.
• y j — фактическое целевое значение.
• y^ j — прогнозируемое значение.

Как и L1, он включает в себя среднеквадратичную ошибку и член, который в данном случае представляет собой сумму квадратов весов. Реализуем это в MQL5 следующим образом:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...

   else if(THIS.regularization == REGULARIZE_L2)
   {  _term = _mse + (Lambda * _weights_norm * _weights_norm);
   }
   

...

   _regularized.Fill(_term);
   return(_regularized);
}

Возведение весов в квадрат, как обсуждалось выше, вносит гладкость в регуляризацию, что делает этот подход идеальным кандидатом для сетей регрессоров. Кроме того, регуляризация лучше всего осуществляется либо с помощью норм матрицы Фробениуса, либо с помощью норм P2. Насколько я могу судить, это на самом деле одно и то же, причем Фробениус часто используется с матрицами, а P2 — с векторами. Теперь из функций норм матриц MQL5 можно выбрать P2 наряду с функцией Фробениуса, и эти две функции вернут немного разные результаты. Здесь можно почитать о различиях между ними.

Исходя из всего этого, сопряжение Регрессор-L2-Фробениус была бы идеальной для нейронных сетей регрессоров.

Регуляризация методом исключения

Наконец, у нас есть регуляризация методом исключения, которая заметно отличается от двух типов, рассмотренных нами выше. В качестве примечания: L1 и L2 можно объединить в весовом формате в так называемую эластичную сеть (Elastic-Net). Я рекомендую читателям реализовать ее самостоятельно, поскольку для пропорционального распределения весов потребуется лишь дополнительный параметр альфа. Исключение подразумевает случайный выбор нейрона для его исключения при обучении в прямом распространении. Реализуем это в нашем классе MLP следующим образом:

//+------------------------------------------------------------------+
//| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON.          |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Input data is normalized if normalization type was selected at  |
//|  class instance initialisation.                                  |
//+------------------------------------------------------------------+
void Cmlp::Forward(bool Training = false)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }
//
   for(int h = 0; h <= hidden_layers; h++)
   {  vector _output;
      _output.Init(output.Size());

...

      if(Training && THIS.regularization == REGULARIZE_DROPOUT)
      {  int _drop = MathRand() % int(_output.Size());
         _output[_drop] = 0.0;
      }
      _output += biases[h];

...


   }
}

В процессе обучения и корректировки весов некоторые веса могут быть скорректированы до нуля, поэтому тот факт, что мы обнулили некоторые выходные значения нейронов, может оказаться неэффективным для достижения желаемого результата. Кроме того, ручное умножение с использованием циклов for, в ходе которых мы случайным образом исключаем нейроны, могло бы стать лучшим подходом к реализации исключения. Это потребует больше кода, но вы может попытаться его реализовать.

Мы не проводим тестирование с регуляризацией методом исключения, поскольку ее преимущества обычно очевидны только в очень глубоких и многослойных сетях с трансформерами. В данной статье мы проводим тестирование только для L1 и L2, однако код для метода исключения приложен и доступен для модификации и тестирования в крупных сетях.

Регуляризация методом исключения популярна по ряду причин, связанных с ее реализацией, поэтому давайте попробуем рассмотреть некоторые из них. Во-первых, она предотвращает переобучение модели, заставляя сеть изучать избыточные представления. Это гарантирует, что сеть не будет чрезмерно зависеть от конкретных нейронов или входных характеристик/классов. Это указывает на улучшение обобщения. Путем случайного удаления нейронов процесс обучения создает ансамбль моделей из одной нейронной сети. Благодаря такому улучшенному обобщению сеть становится более надежной при классификации невидимых данных, особенно в сложных ситуациях с данными высокой размерности.

Более того, исключение делает сеть более устойчивой к зашумленным данным, гарантируя, что ни один нейрон не будет доминировать в процессе принятия решений. Это важно не только в случае зашумленных или менее надежных тестовых данных, но и в ситуациях, когда входные данные имеют высокую степень дисперсии. Кроме того, оно снижает взаимозависимость нейронов или способствует нарушению их коадаптации. Это побуждает каждый нейрон обучаться независимо, что делает сеть более надежной. К этому следует добавить, что использование исключения в очень глубоких и трансформаторных сетях может не только повысить эффективность тестирования (если процесс выполняется вручную вместо подхода с использованием вектора пост-выходных данных, который мы приняли), но и предотвратить риск переобучения, учитывая большое количество задействованных параметров.

Оно применимо в различных сетевых форматах, таких как MLP или CNN. Кроме того, оно также масштабируется. При сравнении с L1 и L2, исключение больше тяготеет к L1, поскольку исключение нейронов при тестировании приводит к более разреженным выходным результатам, которые являются ключевыми в сетях классификаторов. Это связано с тем, что большинство вышеупомянутых преимуществ исключения актуальны для сетей классификаторов. Эти сети часто оказываются глубже сетей регрессоров, и такое множество параметров делает их склонными к переобучению. Как упоминалось выше, исключение позволяет бороться с этим, заставляя сеть изучать более общие и надежные признаки. Обобщение - ключевой фактор в классификаторах, которые улучшаются благодаря исключению. Зашумленные данные могут непропорционально сильно влиять на них (по сравнению с сетями регрессоров), а исключение помогает смягчить влияние шума. Эта и многие из уже упомянутых выше особенностей подразумевают пригодность для сетей классификаторов, поскольку в целом, хотя и не всегда, сети классификаторов имеют тенденцию иметь очень мало слоев, но большого размера. Они очень глубокие. С другой стороны, сети регрессоров, как правило, имеют небольшие по размеру, но многоуровневые слои. Они больше тяготеют к трансформерам. Это, возможно, еще одно ключевое соображение, которое следует учитывать не только при определении того, как должна быть регуляризована сеть, но и при определении ее размера и общего количества слоев в ней.

Результаты тестирования

Как и обещали, мы проводим тестирование с помощью собранного вручную советника. Прилагаемый код необходимо собрать в виде советника. Подробности можно найти здесь и здесь. На этот раз мы тестируем EURUSD на дневном таймфрейме за 2023 год. Как и в предыдущей статье, мы тестируем сеть регрессора и сеть классификатора.

Как уже утверждалось в предыдущих статьях, сети классификаторов лучше всего работают с активациями soft-max или сигмоидой. Кроме того, как уже отмечалось выше, они больше подходят для работы с функциями потерь категориальной или бинарной кросс-энтропии и регуляризацией L1, которая специально использует нормы матрицы P1. Таким образом, если мы проведем тесты с этими настройками, размещая отложенные ордера без стоп-лосса, мы получим следующие результаты:

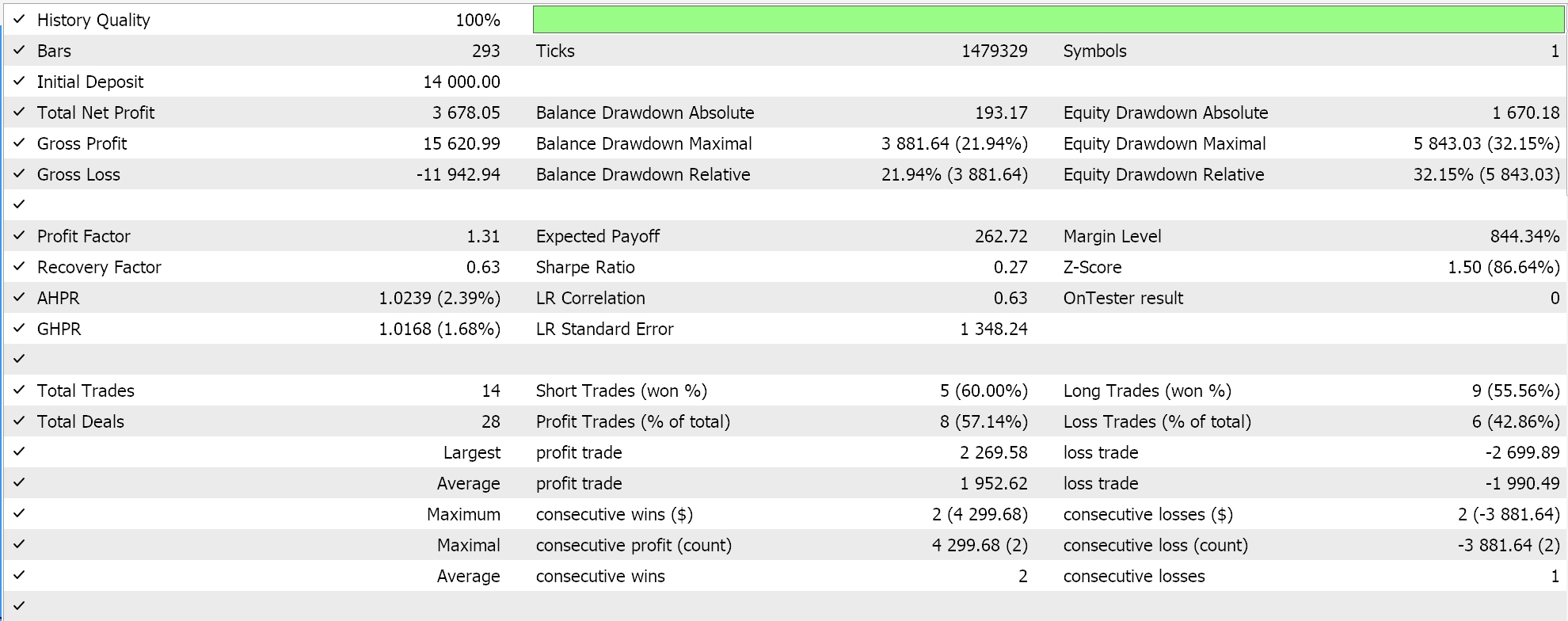
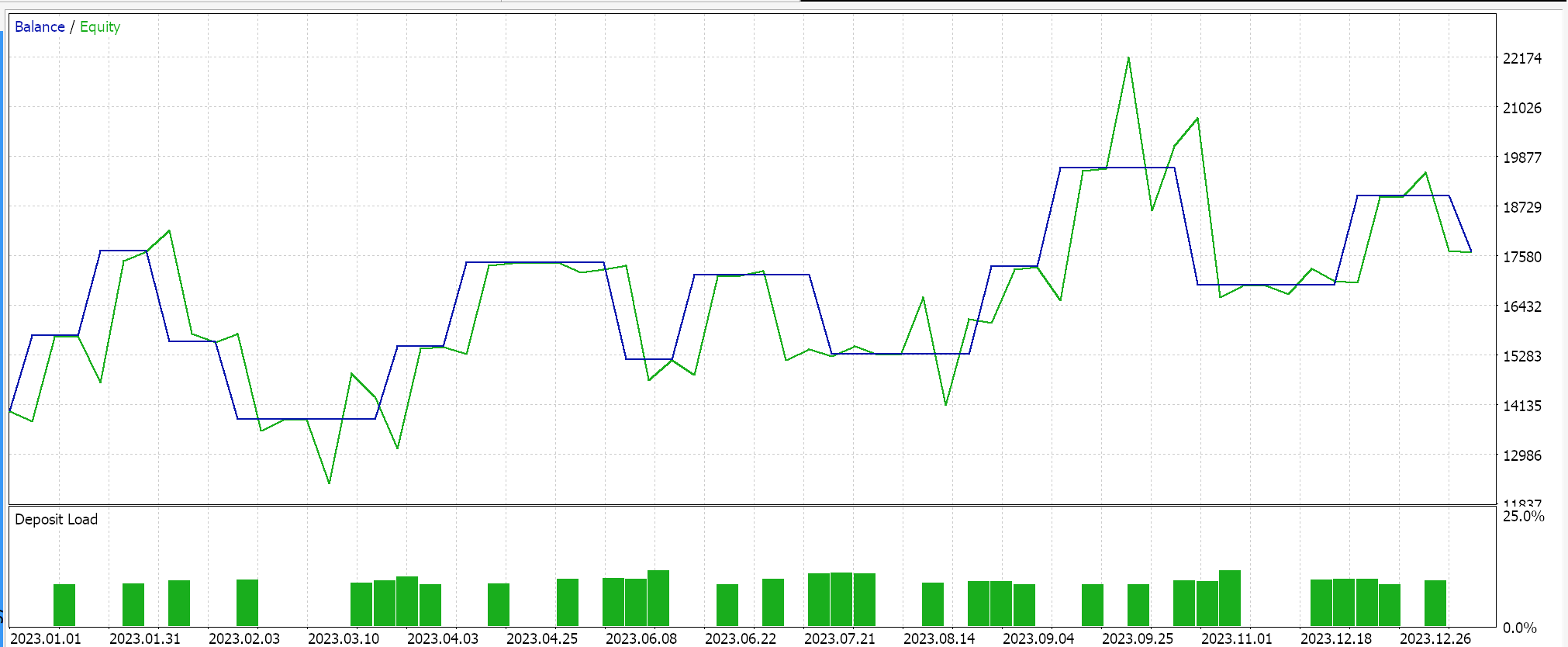
С кривой эквити:

Наоборот, для сети регрессора, если мы выполним тесты с использованием активации Soft-sign и регуляризации L2 Ridge вместе с функцией потерь Хьюбера, мы получим следующие результаты:

Кривая эквити:

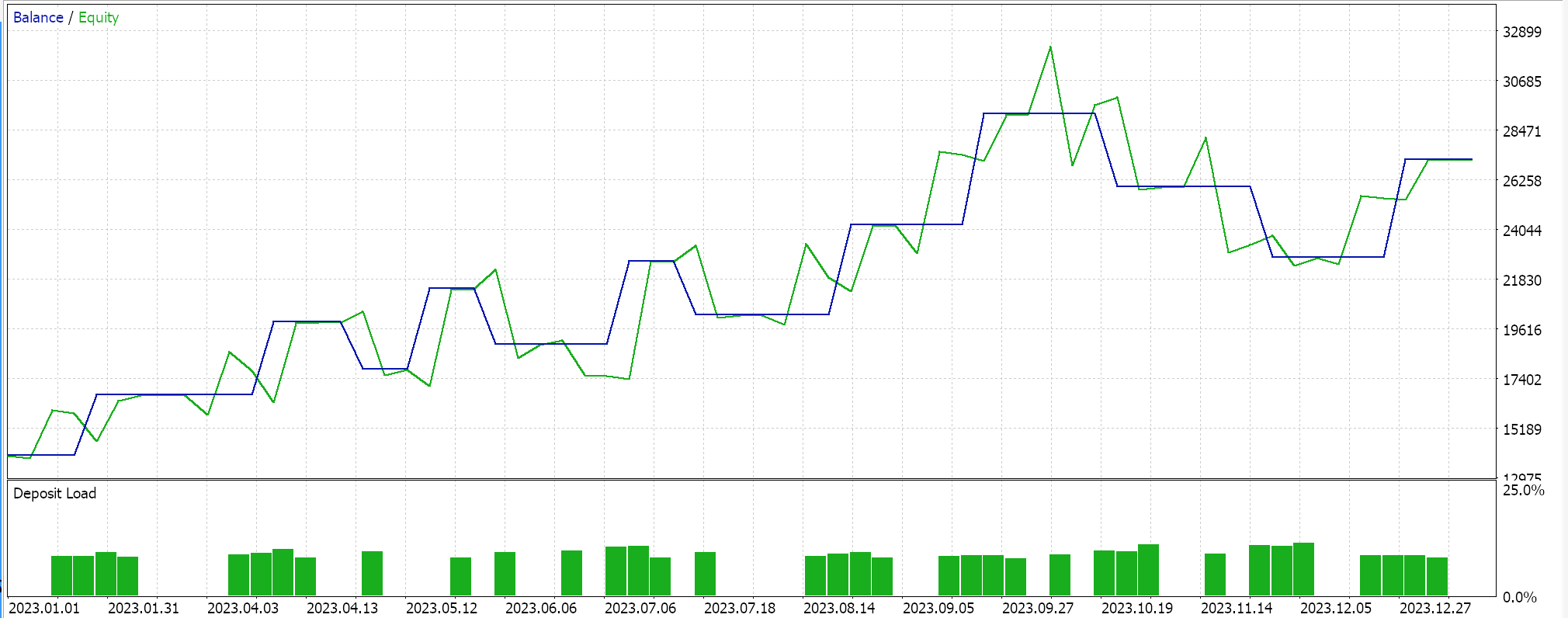
Для контроля этих результатов необходимо обучить сеть с обратными вариантами регуляризации или вообще без регуляризации. Тестовые прогоны с идентичными настройками, использованными выше для сетей регрессора и классификатора, но без регуляризации не дают одинаковых результатов. Это может означать, что регуляризация не так критична, как другие факторы, такие как функция потерь, функции активации и даже типичные пороги входа и закрытия советника. Однако можно также привести встречный и, возможно, заслуживающий доверия аргумент о том, что преимущества регуляризации, особенно в сети классификаторов, можно лучше всего оценить при тестировании не только в течение более длительных периодов, выходящих за рамки года, но и с использованием очень глубоких сетей, которые характеризуются более широким выходным классом.

Заключение

Мы рассмотрели регуляризацию как ключевой компонент алгоритмов машинного обучения, таких как нейронные сети, изучив ее роль в двух конкретных ситуациях. Сети классификаторов и сети регрессоров. Сети классификаторов часто, хотя и не всегда, имеют очень мало слоев, но каждый из них очень глубок. С другой стороны, сети регрессоров, как правило, имеют слои небольшого размера, но они уложены в несколько слоев, что "компенсирует" недостаток глубины. Хотя результаты наших тестов указывают на то, что производительность советника не чувствительна к регуляризации, судя по результатам работы EURUSD на дневном таймфрейме за 2023 год, необходимо провести больше тестов, прежде чем можно будет сделать столь радикальный вывод. Это связано с тем, что, помимо небольшого тестового окна, используемые сети имели очень скромный масштаб, который вряд ли позволит в полной мере воспользоваться преимуществами регуляризации.

Эпилог

Я намеревался пропустить рассмотрение регуляризации эластичной сети, однако, поскольку статья не слишком длинная, я подумал, что могу кратко описать ее здесь. Формула эластичной сети выглядит так:

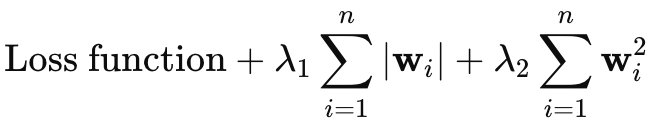
где

• wi - индивидуальные веса модели.
• λ1 - штраф L1 (Лассо), который способствует разреженности модели за счет уменьшения некоторых весов до нуля.
• λ2 - штраф L2 (Ридж), который поощряет небольшие веса, но, как правило, не сводит их к нулю.

Чтобы добавить регуляризацию эластичной сети в наш класс, сначала нам придется изменить основное перечисление, включив его следующим образом:

//+------------------------------------------------------------------+
//| Regularization Type Enumerator                                   |
//+------------------------------------------------------------------+
enum Eregularize
{  REGULARIZE_NONE = -1,
   REGULARIZE_L1 = 1,
   REGULARIZE_L2 = 2,
   REGULARIZE_DROPOUT = 3,
   REGULARIZE_ELASTIC = 4
};

Во-вторых, нам нужно будет изменить функцию RegularizeTerm для обработки опции Elastic-Net путем добавления третьего выражения if. Реализуем это следующим образом:

//+------------------------------------------------------------------+
//| Regularize Term Function                                         |
//+------------------------------------------------------------------+
vector Cmlp::RegularizeTerm(vector &Label, double Lambda)
{  vector _regularized;
   _regularized.Init(Label.Size());
   double _term = 0.0;
   double _mse = output.Loss(Label, LOSS_MSE);
   double _weights_norm = WeightsNorm();

...


   else if(THIS.regularization == REGULARIZE_ELASTIC)
   {  _term =  _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) +
               ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm));
   }
   _regularized.Fill(_term);
   return(_regularized);
}

Это ясно следует из приведенной выше формулы, поскольку она реализует взвешенное среднее значение, использующее положительное значение альфа, не превышающее единицу. Обычно этот показатель оптимизируется в диапазоне от 0,0 до 1,0. Однако в нашей реализации кода выше мы используем перечисление с одной матричной нормой, что не позволяет получить независимые свойства L1 и L2. Обойти эту проблему можно, имея две переменные _weight_norm, каждая со своей собственной функцией нормы матрицы, но это также означало бы, что структуру конструктора следует изменить, чтобы учесть обе переменные. В качестве альтернативы мы могли бы использовать нормы бесконечности в качестве компромисса для обоих форматов регуляризации.