您应当知道的 MQL5 向导技术（第 32 部分）：正则化
94
0
概述
正则化是机器学习算法的另一面，它为神经网络的性能带入了一些敏感性。在网络过程中，常有以牺牲其它参数为代价，只为某些参数过度分配权重的倾向。当依据样本之外数据执行测试时，这种对特定参数（网络权重）的“倾向”可能会阻碍网络的性能。这就是开发正则化的原因。
它本质上是一种机制，即按损失函数的结果成比例增加（或惩罚）各层结点所用的权重量级，来减慢收敛过程。这通常按以下方式完成：提早停止、索套（Lasso）、山脊、弹性网、或舍弃。这些格式中的每种都略有不同，我们不会研究所有类型，但我们将着重讨论索套、山脊、和舍弃。
我们研究正则化的益处和用处，是在协同激活和损失函数进行正确或同步配对的情境下。这样正确选择和配对至少可以防止梯度膨胀/消失的问题，这就是为什么这位作者在最近的文章（该系列的）中一直支持使用 sigmoid 和 soft-max 激活，以及二元交叉熵、或分类交叉熵损失函数来处理分类器网络。相较之，当与 MSE 或 MAE 或 Huber 损失函数配对时，soft-sign 激活的 TANH 更适合与回归神经网络打交道。
在之前的相关文章中，我们还强调了将这些选择激活函数与相应范围界定批量归一化算法配对的重要性，但是损失函数是未界定的。这意味着损失函数的附加项（正则化）不一定要与界定在理想范围内（回归变量为 -1 到 +1，分类器为 0 到 1）的激活函数或批量归一化函数配对。
无论多寡，所选正则化类型需要参考网络是回归器、亦或是分类器，原因如下。举例，若我们使用 L1 套索，通过仅对权重的绝对值进行惩罚，训练过程往往会将网络层中的较大权重降低至零，而把关键权重保持在可接受的非零较小值。本质上这会在输出之间造成稀疏性，这种情形对于正在预测特征概率的分类器网络来说是个好兆头。这在预测特征概率中，预计只有少数特征很重要的情形下尤其重要。
相较之，在最终输出层的大小通常为 1 的回归器网络中（例如，与分类网络的概率不同），各种权重的贡献往往被期待“更民主”。为了达成这一点，L2 或山脊正则化器更适合，因为它的权重偏向权重的平方，这导致跨层权重对最终输出的贡献更加均匀。舍弃正则化可能是正则化分类器网络的替代方案，故因某些权重的随机无效化，它也给输出结果带来了一些稀疏性。我们在下面的附件中分享了这方面的代码，不过我们的测试侧重于 L1 和 L2。
神经网络中的正则化
我们下面测试的两种正则化格式针对与网络权重量级成正比惩罚损失函数。这个 “量级” 是通过 Norm 函数计算的，在我们的例子中，该函数有很多变种。然而，严格来说，这个范数应该是所有矩阵值的量级和。这个绝对值合计能够很容易在 MQL5 中实现，如下所示：
//+------------------------------------------------------------------+ //| Typical Norm function | //+------------------------------------------------------------------+ double Norm(matrix &M) { double _norm = 0.0; for(int i = 0; i < int(M.Rows()); i++) { for(int ii = 0; ii < int(M.Cols()); ii++) { _norm += M[i][ii]; } } return(_norm); }
不过，我们正在涉足矩阵范数（这要归功于矩阵数据类型中可用的各种函数）。'矩阵范数不像简单绝对值，初看它有点奇怪，因为有论调说它们为正则化加权过程引入了结构意识。此外，它们还允许控制某些所需的网络属性，像是回归器网络中的平滑度，同时仍提供灵活性来优调分类器网络输出中所需的稀疏性。故此，在评估正则化的权重矩阵时，参考这些通常看起来无足轻重的额外属性，在下面的测试结果中我们会应用这些。需要明确的是，我们针对测试回归器和分类器网络的 2 种正则化方式的每一种，正在研究多达 9 种不同的矩阵范数。
在上一篇文章中，我们重点介绍了损失函数，我们已有两种网络类型，一个回归器、以及一个分类器。在本文中，我们会坚持使用这些格式来概括正则化。
L1 正则化（套索）
如上所述，套索（或 L1）正则化涉及按绝对权重值、或权重矩阵范数成比例惩罚损失函数。其按以下方程正式定义：
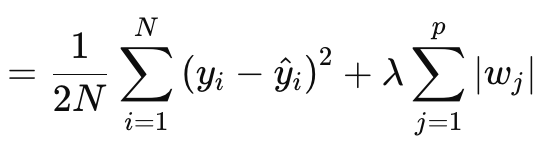
其中：
- N 是数据点的数量。
- p 是存在权重矩阵的层总数
- yi 是第 i 个数据点的目标（或标签）值。
- y^i 是第 i 个数据点的预测值。
- wj 是模型的系数（权重）。
§λ 是控制正则化强度的正则化参数。较大的 λ 会增加较大权重的惩罚，促进稀疏性。对于 soft-max 或 sigmoid 激活网络，其最优范围可以是 10-4 到 10-1，对于 soft-sign 或 TANH 网络，则是 10-5到 10-2。
换种方式，正则化值由 MSE 预测值与实际值之间的差值（左侧），加上所有层的权重范数合计组成。我们的 MQL5 实现如下：
//+------------------------------------------------------------------+ //| Regularize Term Function | //+------------------------------------------------------------------+ vector Cmlp::RegularizeTerm(vector &Label, double Lambda) { vector _regularized; _regularized.Init(Label.Size()); double _term = 0.0; double _mse = output.Loss(Label, LOSS_MSE); double _weights_norm = WeightsNorm(); if(THIS.regularization == REGULARIZE_L1) { _term = _mse + (Lambda * _weights_norm); } .... _regularized.Fill(_term); return(_regularized); }
输出是一个标量值，而非一个向量，这与我们一直在处理的损失函数的输出形成鲜明对比。因为当我们需要定义更新增量，然后帮助我们在进行反向传播中设置更新梯度时，损失被量化为向量。该向量有助于投喂到增量向量，而其又会更新梯度矩阵。为了维护这一点，我们创建了一个向量，往其中填充正则化值的再生值，并将其用作输出。然后，该标准向量值将添加到损失向量中的所有损失值当中，如正在使用的损失函数所定义。这将按如下方式实现：
//+------------------------------------------------------------------+ //| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON. | //+------------------------------------------------------------------+ //| | //| -Extra Validation check of MLP architecture settings is performed| //| at run-time. | //| Chcecking of 'validation' parameter should ideally be performed | //| at class instance initialisation. | //| | //| -Run-time Validation of learning rate, decay rates and epoch | //| index is performed as these are optimisable inputs. | //+------------------------------------------------------------------+ void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1) { .... //COMPUTE DELTAS vector _last, _last_derivative; _last.Init(inputs.Size()); if(hidden_layers == 0) { _last = weights[hidden_layers].MatMul(inputs); } else if(hidden_layers > 0) { _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]); } _last.Derivative(_last_derivative, THIS.activation); vector _last_loss = output.LossGradient(label, THIS.loss); _last_loss += RegularizeTerm(label, THIS.regularization_lambda); deltas[hidden_layers] = Hadamard(_last_loss, _last_derivative); ... }
如此，跨越输出向量的所有特征/类都应用了统一的惩罚，也许这就是为什么可以使用矩阵范数的原因，不仅是它们的绝对值，还在于范数在计算中参考了矩阵结构。
在计算正则化项时，有许多矩阵范数选项可用，虽然它们都可用于判定套索，但并非所有选项都合适。Frobenius 范数与 L2 更一致，因为它直接过度惩罚较大权重，而不强制进行稀疏性，这与旨在将非关键权重调整为零的套索相悖。核范数更适合于提升与矩阵完成问题相关的低秩矩阵。它与套索不一致，后者提倡元素稀疏性，而与秩稀疏性相悖。谱范数还用于控制矩阵对向量的最大影响，且不会确保稀疏性。
虽然无穷大范数能够产生某种形式的稀疏性，但它们对于创建元素稀疏性并不理想。负无穷大范数注重于最小化最小行合计，这与套索稀疏性目标不一致。负 P1 和负 P2 也是如此，因为它们都试图最小化较小元素的影响。
故此，从这九个范数中，事实证明只有 P1 范数最适合套索，因为它们促进了稀疏性，目标是元素稀疏性。P2 是九个当中的最终范数，更适合 L2 或山脊正则化。那么回顾一下，上面提到了 L1 正则化是分类器网络的理想选择。这意味着分类器-L1-P1 关系，即对于权重的矩阵范数函数几乎没有其它选择。
L2 正则化（山脊）
L2 或山脊正则化在公式上与 L1 非常相似，明显的区别在于权重范数的平方，而并非使用原始值。其给出如下：
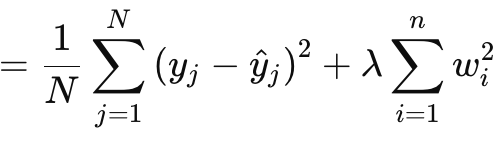
其中：
- λ 是控制惩罚强度的正则化参数。
- w i 是模型的权重或系数。
- n 是具有前导权重矩阵的层数。
- N 是数据点的数量。
- y j 是实际的目标值。
- y^ j 是预测值。
它与 L1 一样，具有一个 MSE 和一个项，在本例中是权重的平方和。我们的 MQL5 实现如下：
//+------------------------------------------------------------------+ //| Regularize Term Function | //+------------------------------------------------------------------+ vector Cmlp::RegularizeTerm(vector &Label, double Lambda) { vector _regularized; _regularized.Init(Label.Size()); double _term = 0.0; double _mse = output.Loss(Label, LOSS_MSE); double _weights_norm = WeightsNorm(); ... else if(THIS.regularization == REGULARIZE_L2) { _term = _mse + (Lambda * _weights_norm * _weights_norm); } ... _regularized.Fill(_term); return(_regularized); }
如上所述，权重的平方为正则化引入了平滑度，这令该方式成为回归器网络的理想选择。此外，正则化最好由弗罗贝纽斯（Frobenius）矩阵范数、或 P2 范数处理。从我收集到的信息来看，这两者实际上是相同的，弗罗贝纽斯经常与矩阵搭配使用，而 P2 与向量搭配使用。现在，从 MQL5 的矩阵范数函数中，也可以选择 P2 和弗罗贝纽斯，两者返回的结果略有不同。此处有一篇关于两者之间差异的帖子。
因此，综上所述，回归-L2-弗罗贝纽斯配对将是回归神经网络的理想选择。
舍弃正则化
最后，我们有舍弃正则化，这与我们上面看到的两种类型明显不同。旁注，L1 和 L2 能够以加权格式组合成所谓的弹性网t，但这留给读者去尝试和实现，因为所需要的只是一个额外的 alpha 参数来分配权重。回到舍弃，它涉及在前向前向通验训练时随机选择一个神经元进行舍弃。我们的 MLP 类实现如下：
//+------------------------------------------------------------------+ //| FORWARD PROPAGATION THROUGH THE MULTI-LAYER-PERCEPTRON. | //+------------------------------------------------------------------+ //| | //| -Extra Validation check of MLP architecture settings is performed| //| at run-time. | //| Chcecking of 'validation' parameter should ideally be performed | //| at class instance initialisation. | //| | //| -Input data is normalized if normalization type was selected at | //| class instance initialisation. | //+------------------------------------------------------------------+ void Cmlp::Forward(bool Training = false) { if(!validated) { printf(__FUNCSIG__ + " invalid network arch! "); return; } // for(int h = 0; h <= hidden_layers; h++) { vector _output; _output.Init(output.Size()); ... if(Training && THIS.regularization == REGULARIZE_DROPOUT) { int _drop = MathRand() % int(_output.Size()); _output[_drop] = 0.0; } _output += biases[h]; ... } }
在训练和权重调整过程中，一些权重可以调整为零，如此我们将一些输出神经元值归零，而事实上可能无法有效地达成我们预期的结果。此外，使用 for 循环手动乘法，在此期间我们随机省略神经元，这可能是实现舍弃的更好方式。它涉及更多的编码，但欢迎读者尝试。
我们不会用舍弃正则化进行测试，因为其益处通常只在非常深、以及变换器堆叠的网络上才会显现。对于本文目的，我们只测试 L1 和 L2，不过也已附上了舍弃的代码，且可在大型网络上进行修改和测试。
舍弃正则化之所以流行，出于众多实现原因，所以我们来尝试遍览其中的一些。首先，它通过强制网络学习冗余表示来防止模型过度拟合。这确保了网络不会过度依赖特定的神经元、或输入特征/类别。这一点改善了普适性。通过随机舍弃神经元，训练过程会从单个神经网络创建一组融汇模型。这种改进的普适性令网络在针对没见过的数据进行分类时更加健壮，尤其是在复杂的高维数据状况下。
甚至，舍弃倾向于通过确保没有一个神经元能主导决策过程，这令网络对嘈杂数据更具弹性。这不仅对于噪声较大、或不太可靠的测试数据至关重要，而且在输入数据具有高度方差的情况下也是如此。此外，它还降低了神经元的相互依赖性，或鼓励破除神经元的共适。这样鼓励每个神经元独立学习，从而令网络更加健壮。此外，在非常深的变换器堆叠网络中使用舍弃，不仅能够提高测试过程的效率（如果手动处理舍弃神经元，替代我们采用的后输出向量方法），且还能防止由于涉及大量参数而出现过拟合的风险。
它适用于 MLP 或 CNN 等各种网络格式，并且还具有可扩展性。当与 L1 和 L2 相比时，舍弃更倾向于 L1，因为在测试时舍弃的神经元会导致输出结果更稀疏，这在分类器网络中是关键。这是因为上述大多数舍弃优点都与分类器网络相关。这些网络往往比回归器网络更深，并且这些众多参数令它们容易出现过拟合。如上所述，舍弃通过强制网络学习更通用和更健壮特征来抗击这个问题。普适性是分类器的关键，即舍弃强化；嘈杂的数据可能会不成比例地影响它们（与回归器网络相比），而舍弃有助于减轻其影响。这意味着它和上面已经提到的许多特征都适用于分类器网络，就通常而言，但并非总是，分类器网络往往具有非常少但较尺度的层。它们非常深。另一方面，回归器网络倾向于具有小尺寸但堆叠的层。它们更朝着变压器偏斜。故此，这可能是另一个关键考虑因素，不仅在定义如何正则化网络时，且在判定其整体层数和大小时也应牢记。
测试结果
正如承诺的那样，一如既往，我们使用向导组装的智能系统执行测试。对于新读者，需要按照此处和此处提供的指南，将所附代码组装到智能交易系统之中。我们这次在 EURUSD 上进行测试，依据 2023 年的日线时间帧。正如我们在上一篇文章中所做的，我们正在测试回归器网络和分类器网络。
正如在本文的后续文章中已经讨论的那样，分类器网络最适合 soft-max 或 Sigmoid 激活。此外，如上所述，它们更适合搭配分类交叉熵、或二元交叉熵损失函数，以及专门使用 P1 矩阵范数的 L1 正则化。因此，如果我们在无止损下挂单条件下，使用这些设置进行测试，我们会得到以下结果：
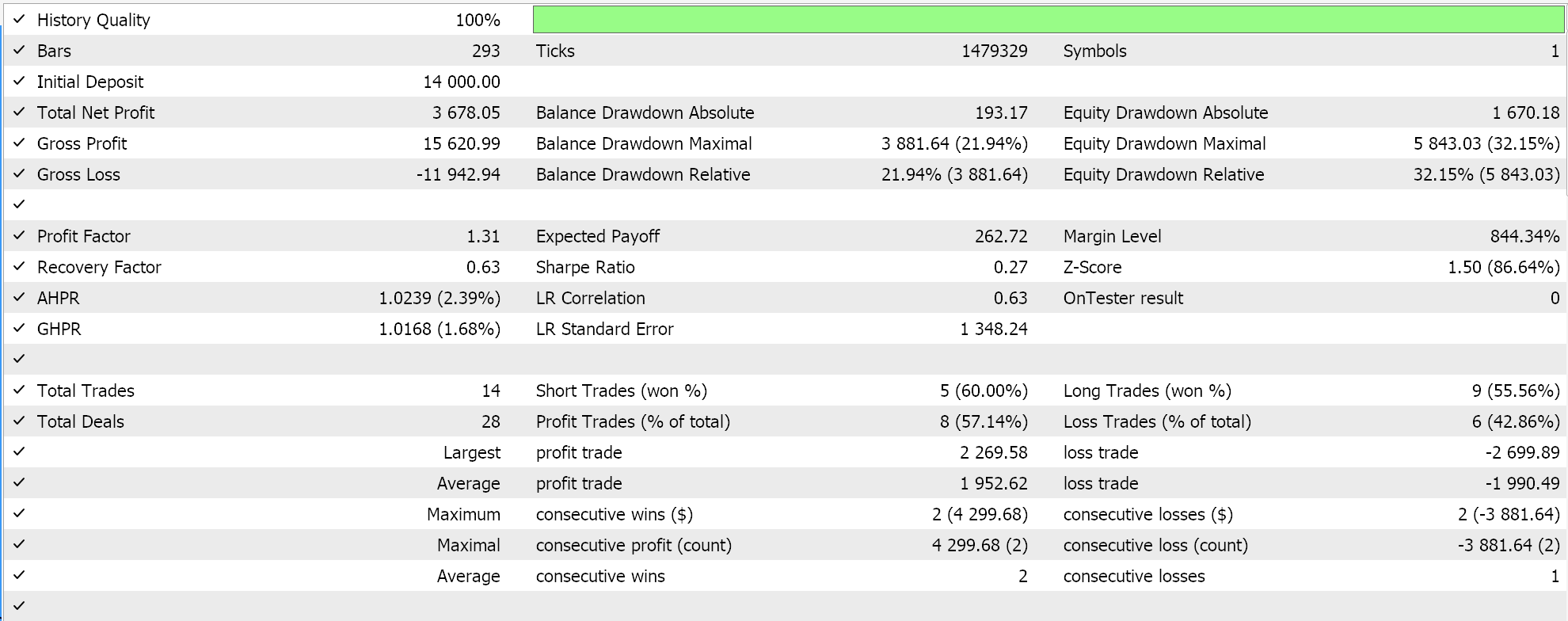
净值曲线：
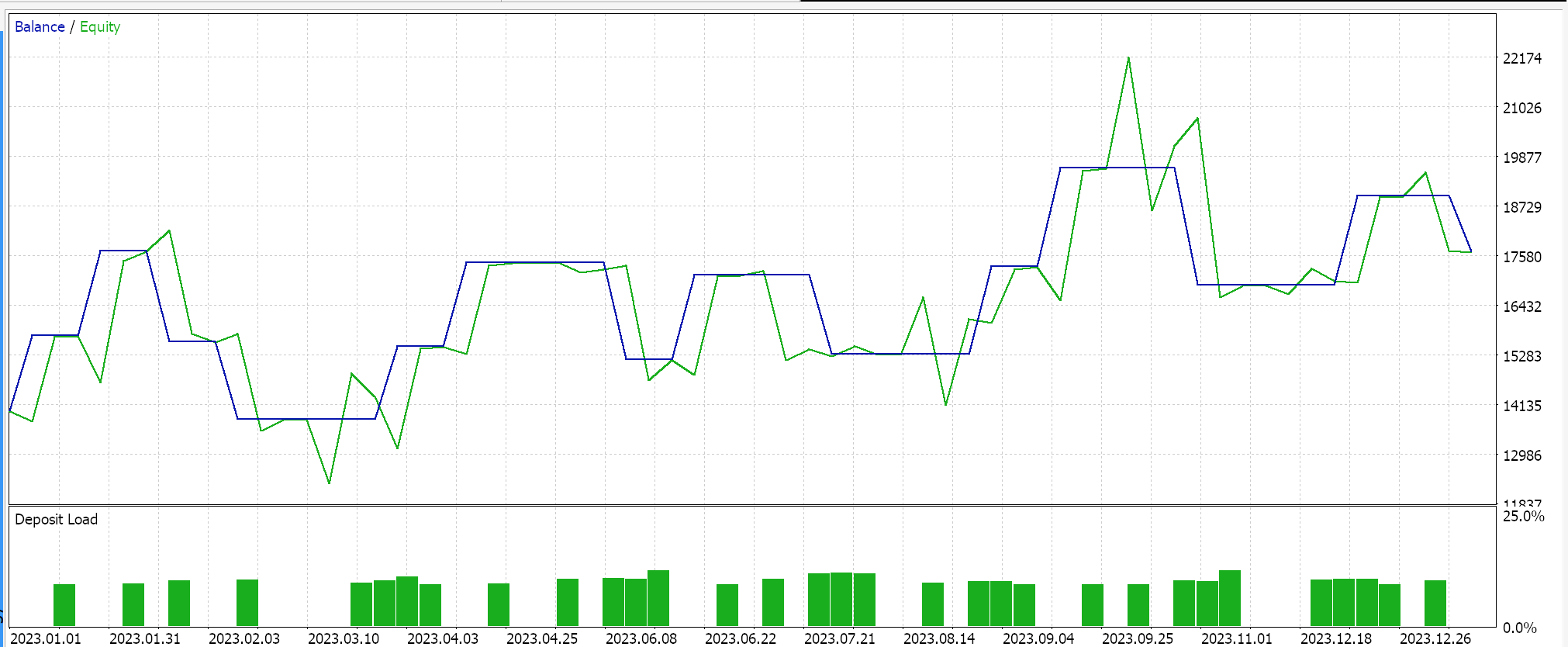
相较之，对于回归器网络，如果我们使用 soft-sign 激活和 L2 山脊正则化，以及 Huber 损失函数来执行测试，我们就会得到以下结果：
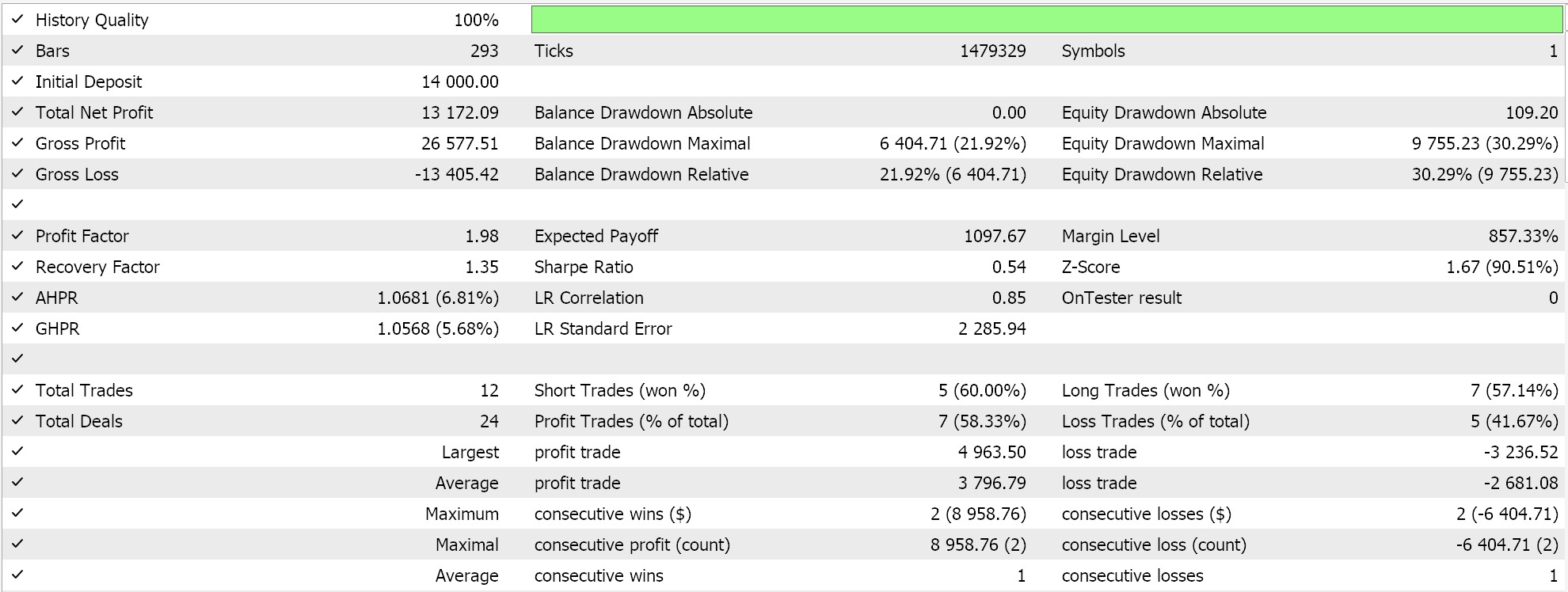
净值曲线：
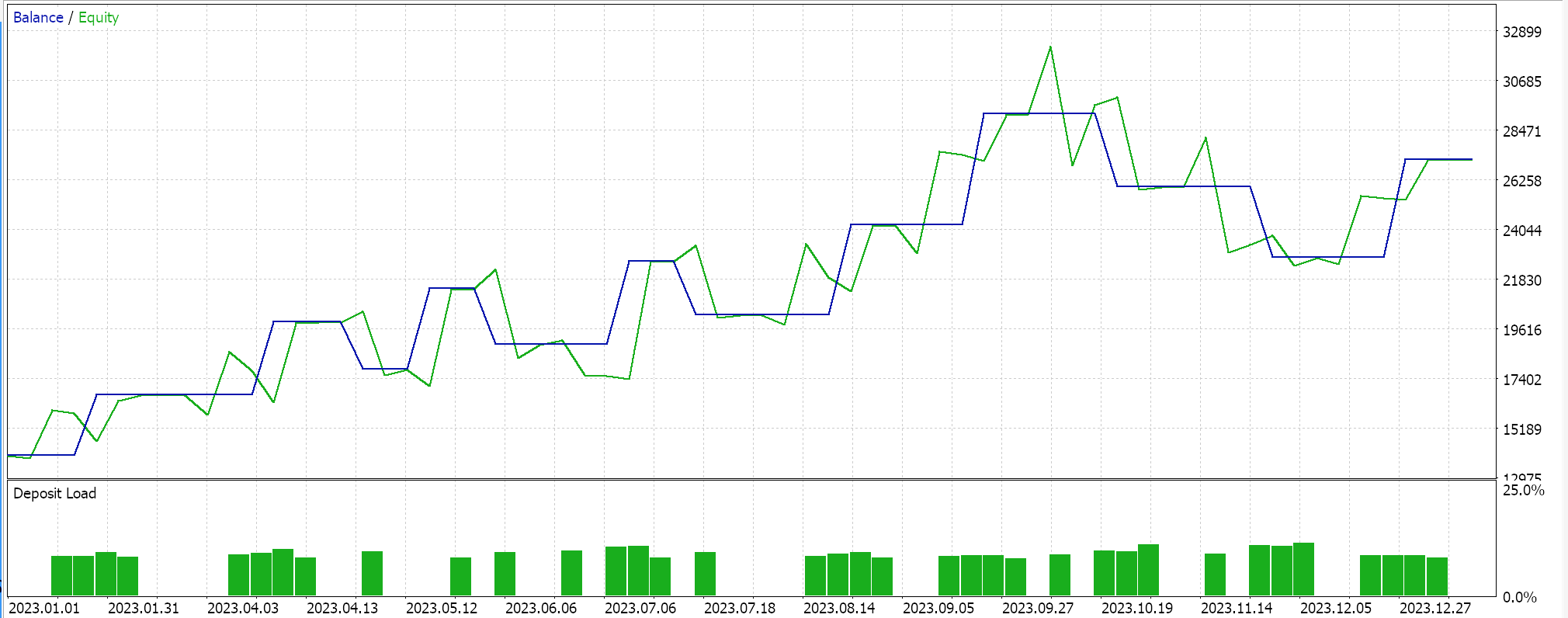
作为这些结果的对照，需要使用反向正则化选项、或压根不用正则化来训练网络。使用与上述回归器和分类器网络相同的设置（但没有正则化）的测试运行会产生相同的结果。这可能意味着正则化不像其它因素（如损失函数、激活函数，甚至智能系统的典型入场和平仓阈值）那么重要。然而，反论也许是可信的论点，即正则化的益处，尤其是在分类器网络中，不仅可以通过超过一年较长时间进行测试，而且可以通过具有更广泛输出类的非常深的网络来最好地理解。
结束语
总之，我们通过考察它在两个特定设定中的作用，验证了正则化可作为机器学习算法（如神经网络）的关键组成部分。分类器网络和回归器网络。分类器网络往往，但并非总是，具有非常少的层，但每个层都非常深。另一方面，回归器网络往往具有较小尺寸的层，但它们会多重堆叠，这“弥补”了深度的不足。虽然我们基于 EURUSD 的 2023 年日线时间帧的运行测试结果表明智能系统的性能对正则化不敏感，但在做出如此激进的结论之前，需要进行更多测试。这是因为除了测试窗口较小外，所使用的网络规模非常小，不太可能体现正则化的全部益处。
后记
我本来打算省略对弹性网络正则化的介绍，但由于这篇文章并不太长，我想我可以在此处简述它。弹性网络的公式如下：
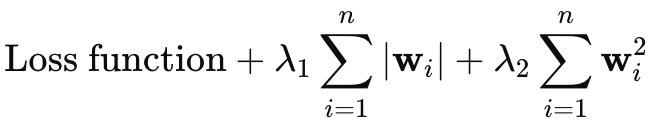
其中
- wi 表示各个模型的权重。
- λ1 控制 L1 惩罚（套索）的强度，它通过将一些权重缩至零来鼓励模型中的稀疏性。
- λ2 控制 L2 惩罚（山脊）的强度，它鼓励使用较小权重，但通常不会将它们减至零。
为了将弹性网络正则化添加到我们的类中，首先我们必须修改主要枚举以便能包含它，如下所示：
//+------------------------------------------------------------------+ //| Regularization Type Enumerator | //+------------------------------------------------------------------+ enum Eregularize { REGULARIZE_NONE = -1, REGULARIZE_L1 = 1, REGULARIZE_L2 = 2, REGULARIZE_DROPOUT = 3, REGULARIZE_ELASTIC = 4 };
然后其次，我们需要修改 'RegularizeTerm' 函数，通过添加第 3 个 if 子句来处理这个弹性网络选项，我们按如下方式实现：
//+------------------------------------------------------------------+ //| Regularize Term Function | //+------------------------------------------------------------------+ vector Cmlp::RegularizeTerm(vector &Label, double Lambda) { vector _regularized; _regularized.Init(Label.Size()); double _term = 0.0; double _mse = output.Loss(Label, LOSS_MSE); double _weights_norm = WeightsNorm(); ... else if(THIS.regularization == REGULARIZE_ELASTIC) { _term = _mse + (THIS.regularization_alpha * (Lambda * _weights_norm)) + ((1.0 - THIS.regularization_alpha) * (Lambda * _weights_norm * _weights_norm)); } _regularized.Fill(_term); return(_regularized); }
这显然遵循上面共享的公式，因为它实现了一个加权平均值，该值使用正值、且不超过 1 的 alpha 值。典型情况下会在 0.0 到 1.0 的范围内进行优化。不过，从上面的代码实现来看，我们使用的是单个矩阵范数枚举，这将阻止捕获 L1 和 L2 的独立属性。变通的方法是有两个 '_weight_norm' 变量，每个变量都有自己的矩阵范数函数，但这也意味着应该修改构造函数结构，以便容纳两者。备案是，我们能采用无穷大范数作为两种正则化格式的折衷方案。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15576
新手在交易中的10个基本错误
构建蜡烛图趋势约束模型（第8部分）：EA开发（II）
